Vortex Dynamics and Pinning in CaKFe4As4 Single Crystals from DC Magnetization Relaxation and AC Susceptibility
Abstract
:1. Introduction
2. Results
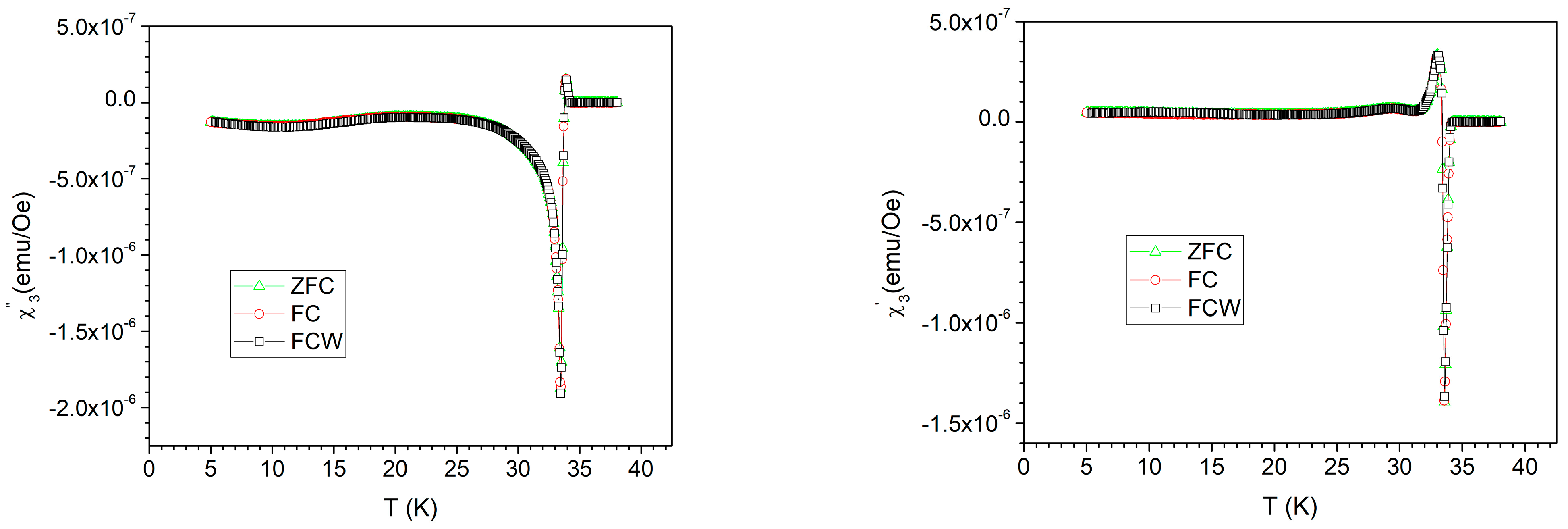
2.1. Magnetic Memory Effects
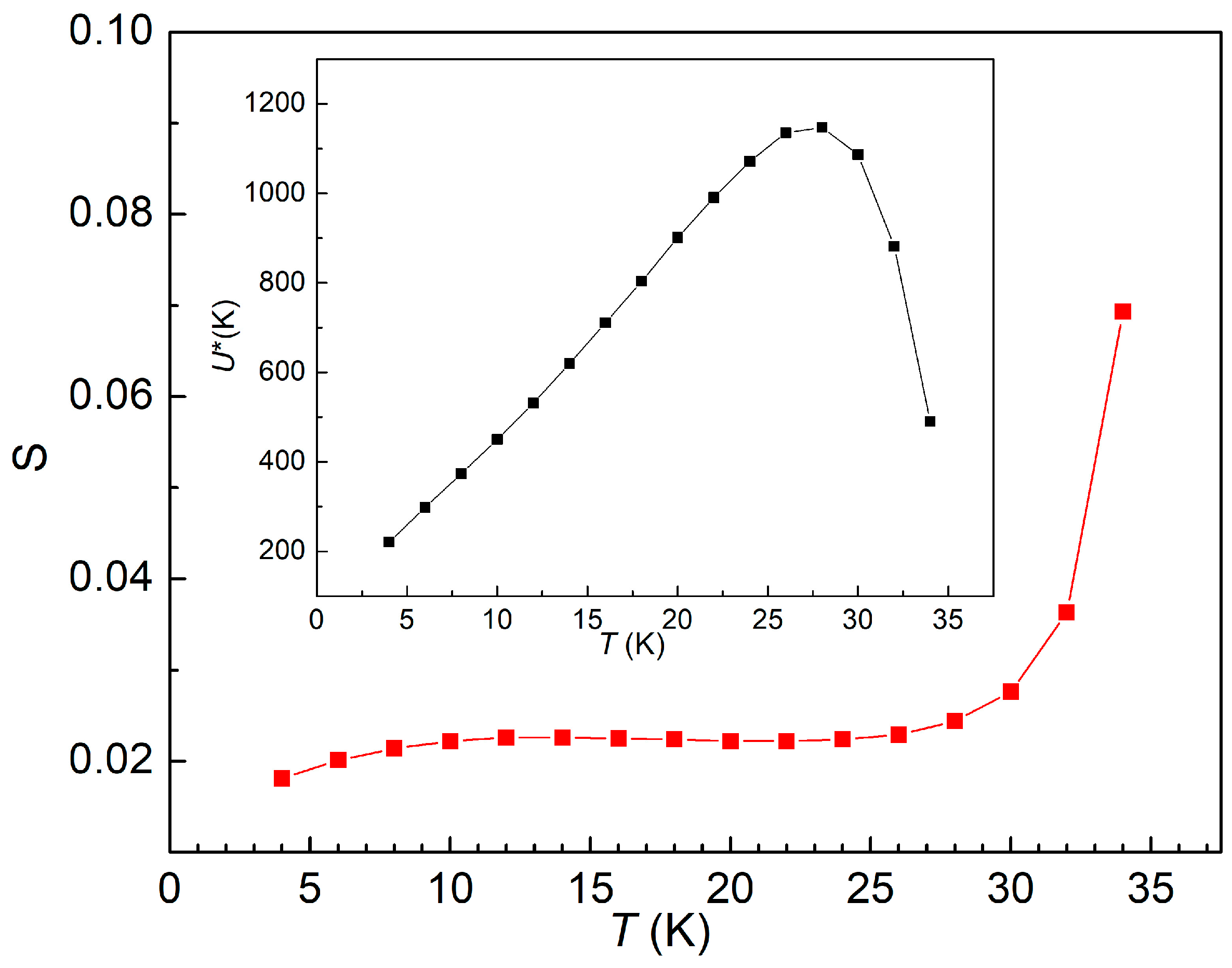
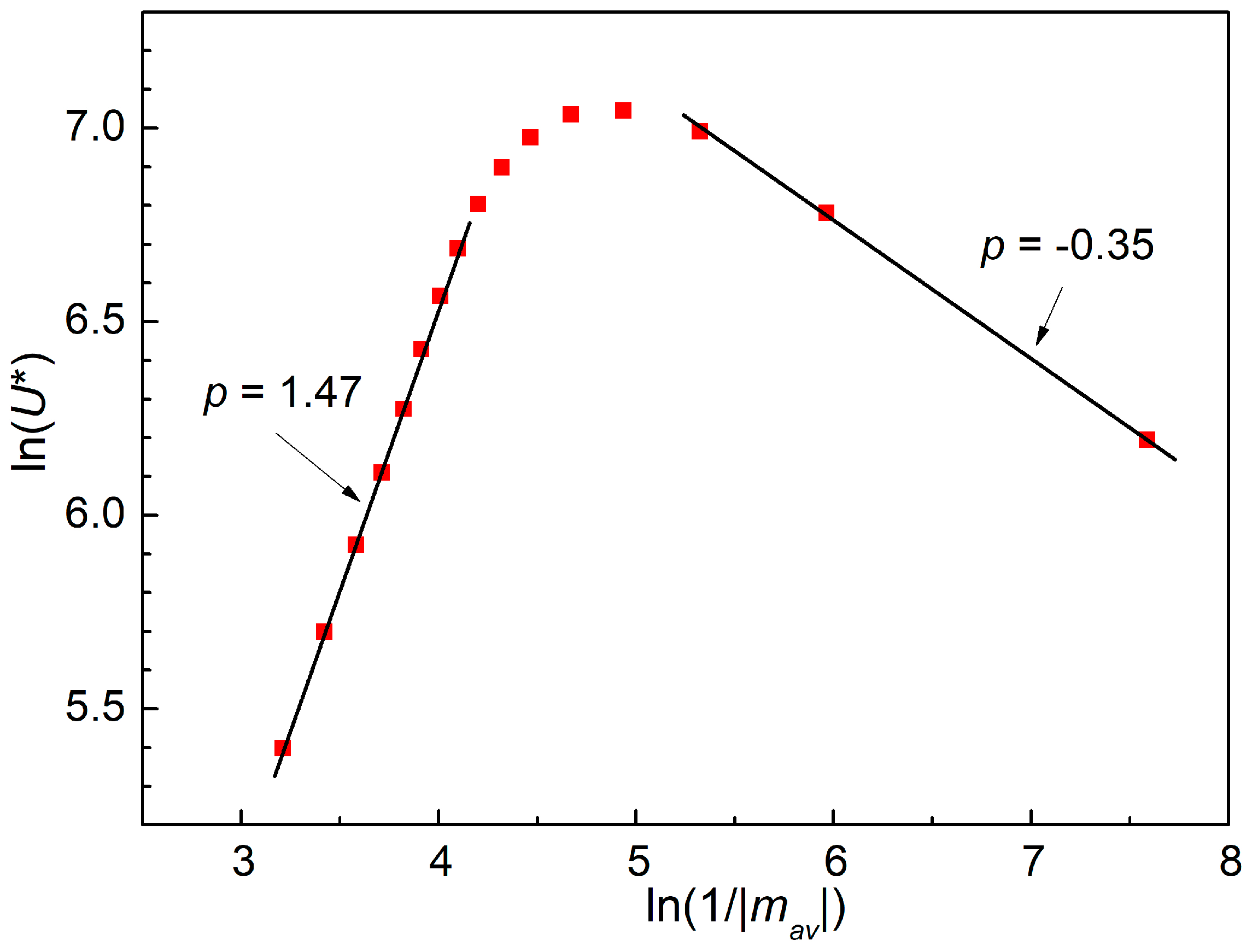
2.2. Magnetization Relaxation
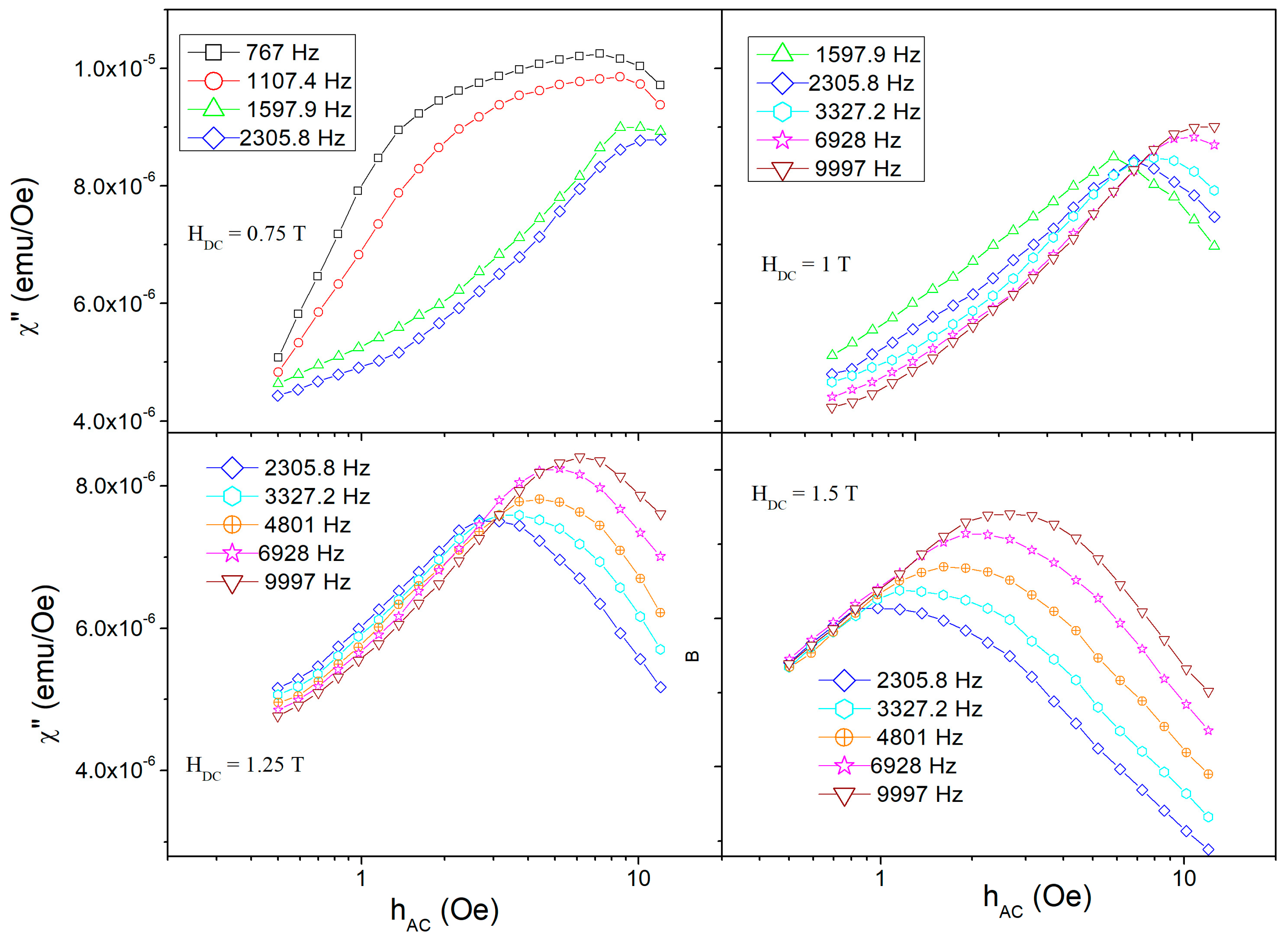
2.3. Frequency-Dependent AC Susceptibility
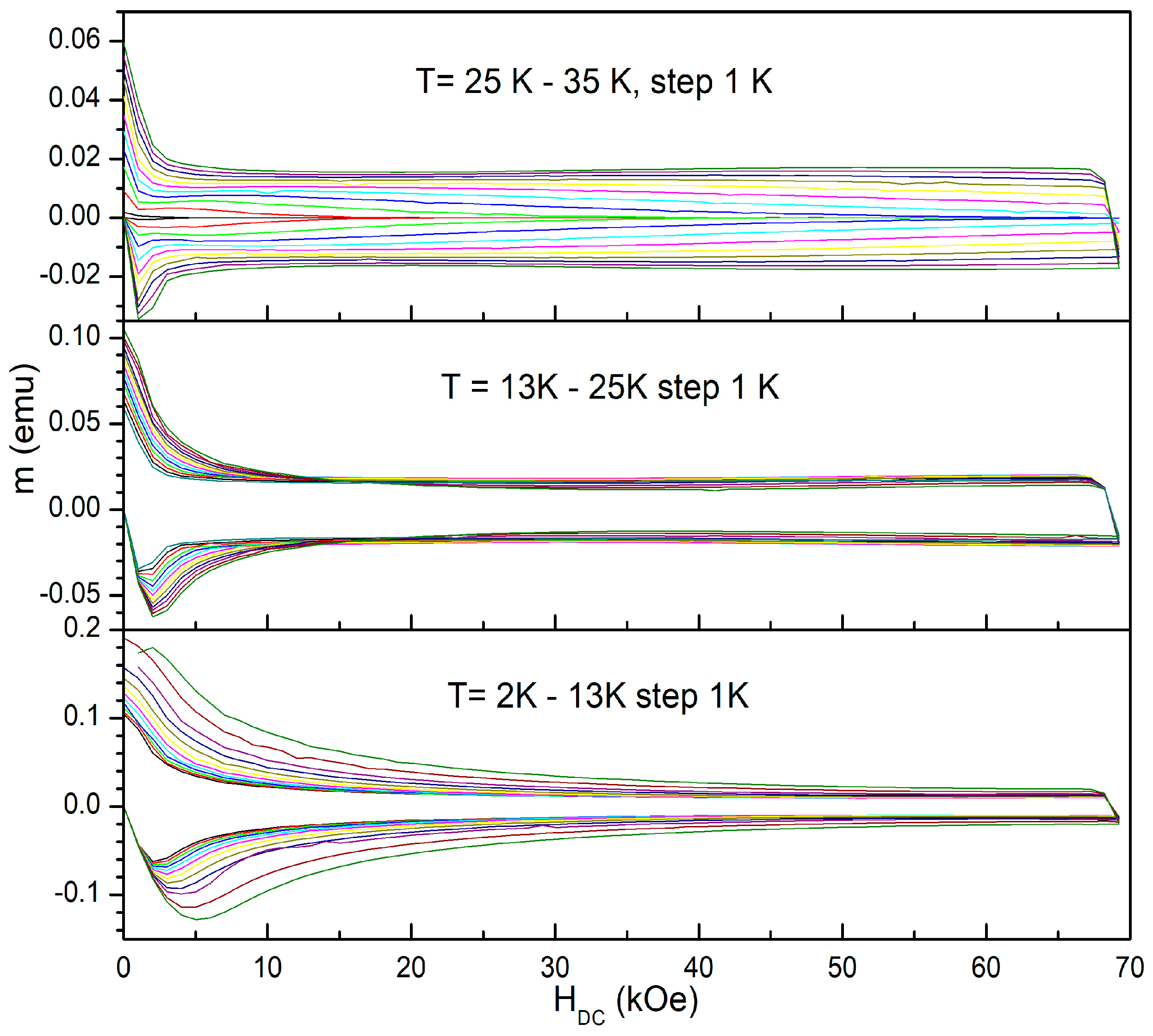
2.4. Magnetic Hysteresis Loops and Critical Current Density
3. Discussion
4. Materials and Methods
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rotter, M.; Tegel, M.; Johrendt, D. Superconductivity at 38 K in the iron arsenide (Ba1−xKx)Fe2As2. Phys. Rev. Lett. 2008, 101, 107006. [Google Scholar] [CrossRef] [PubMed]
- Yuan, H.Q.; Singleton, J.; Balakirev, F.F.; Baily, S.A.; Chen, G.F.; Luo, J.L.; Wang, N.L. Nearly isotropic superconductivity in (Ba,K)Fe2As2. Nature 2009, 457, 565–568. [Google Scholar] [CrossRef] [PubMed]
- Altarawneh, M.M.; Collar, K.; Mielke, C.H.; Ni, N.; Bud’Ko, S.L.; Canfield, P.C. Determination of anisotropic Hc2 up to 60 T in Ba0.55K0.45Fe2As2 single crystals. Phys. Rev. B-Condens. Matter Mater. Phys. 2008, 78, 220505. [Google Scholar] [CrossRef]
- Iyo, A.; Kawashima, K.; Kinjo, T.; Nishio, T.; Ishida, S.; Fujihisa, H.; Gotoh, Y.; Kihou, K.; Eisaki, H.; Yoshida, Y. New-Structure-Type Fe-Based Superconductors: CaAFe4As4 (A = K, Rb, Cs) and SrAFe4As4 (A = Rb, Cs). J. Am. Chem. Soc. 2016, 138, 3410–3415. [Google Scholar] [CrossRef] [PubMed]
- Ishida, S.; Iyo, A.; Ogino, H.; Eisaki, H.; Takeshita, N.; Kawashima, K.; Yanagisawa, K.; Kobayashi, Y.; Kimoto, K.; Abe, H.; et al. Unique defect structure and advantageous vortex pinning properties in superconducting CaKFe4As4. npj Quantum Mater. 2019, 4, 27. [Google Scholar] [CrossRef]
- Ichinose, A.; Pyon, S.; Tamegai, T.; Ishida, S. Elucidating the origin of planar defects that enhance critical current density in CaKFe4As4single crystals. Supercond. Sci. Technol. 2021, 34, 034003. [Google Scholar] [CrossRef]
- Polichetti, M.; Adesso, M.G.; Pace, S. Third harmonics of the AC magnetic susceptibility: A method for the study of flux dynamics in high temperature superconductors. Eur. Phys. J. B 2003, 36, 27–36. [Google Scholar] [CrossRef]
- Blatter, G.; Feigelman, M.V.; Geshkenbein, V.B.; Larkin, A.I.; Vinokur, V.M. Vortices in high-temperature superconductors. Rev. Mod. Phys. 1994, 66, 1125–1388. [Google Scholar] [CrossRef]
- Malozemoff, A.P. Flux creep in high temperature superconductors. Phys. C 1991, 185, 264–269. [Google Scholar] [CrossRef]
- Geshkenbein, V.B.; Larkin, A. Time dependence of the magnetic moment of high-temperature superconductors. Sov. Phys. JETP 1989, 69, 639. [Google Scholar]
- Yeshurun, Y.; Malozemoff, A.P.; Shaulov, A. Magnetic relaxation in high-temperature superconductors. Rev. Mod. Phys. 1996, 68, 911–949. [Google Scholar] [CrossRef]
- Ionescu, A.M.; Ivan, I.; Crisan, D.N.; Galluzzi, A.; Polichetti, M.; Ishida, S.; Iyo, A.; Eisaki, H.; Crisan, A. Pinning potential in highly performant CaKFe4As4 superconductor from DC magnetic relaxation and AC multi-frequency susceptibility studies. Sci. Rep. 2022, 12, 19132. [Google Scholar] [CrossRef] [PubMed]
- Bean, C.P. Magnetization of high-field superconductors. Rev. Mod. Phys. 1964, 36, 31–39. [Google Scholar] [CrossRef]
- Brandt, E.H. Thin superconductors in a perpendicular magnetic ac field: General formulation and strip geometry. Phys. Rev. B 1994, 49, 9024–9040. [Google Scholar] [CrossRef] [PubMed]
- Crisan, A.; Awang Kechik, M.M.; Mikheenko, P.; Dang, V.S.; Sarkar, A.; Abell, J.S.; Paturi, P.; Huhtinen, H. Critical current density and pinning potential in YBa2Cu3O7−δ thick films ablated from a BaZrO3-doped nanocrystalline target. Supercond. Sci. Technol. 2009, 22, 045014. [Google Scholar] [CrossRef]
- Feigelman, M.V.; Geshkenbein, V.B.; Larkin, A.I.; Vinokur, V.M. Theory of collective flux creep. Phys. Rev. Lett. 1989, 63, 2303–2306. [Google Scholar] [CrossRef] [PubMed]
- Abulafia, Y.; Shaulov, A.; Wolfus, Y.; Prozorov, R.; Burlachkov, L.; Yeshurun, Y.; Majer, D.; Zeldov, E.; Wühl, H.; Geshkenbein, V.B.; et al. Plastic vortex creep in YBa2Cu3O7−x crystals. Phys. Rev. Lett. 1996, 77, 1596–1599. [Google Scholar] [CrossRef] [PubMed]
- Anderson, P.W.; Kim, Y.B. Hard superconductivity: Theory of the motion of abrikosov flux lines. Rev. Mod. Phys. 1964, 36, 39–43. [Google Scholar] [CrossRef]
- Zeldov, E.; Amer, N.M.; Koren, G.; Gupta, A.; Gambino, R.J.; McElfresh, M.W. Optical and Electrical Enhancement of Flux Creep in YBa2Cu3O7−x Epitaxial Films. Phys. Rev. Lett. 1989, 62, 3093–3096. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ionescu, A.M.; Ivan, I.; Miclea, C.F.; Crisan, D.N.; Galluzzi, A.; Polichetti, M.; Crisan, A. Vortex Dynamics and Pinning in CaKFe4As4 Single Crystals from DC Magnetization Relaxation and AC Susceptibility. Condens. Matter 2023, 8, 93. https://doi.org/10.3390/condmat8040093
Ionescu AM, Ivan I, Miclea CF, Crisan DN, Galluzzi A, Polichetti M, Crisan A. Vortex Dynamics and Pinning in CaKFe4As4 Single Crystals from DC Magnetization Relaxation and AC Susceptibility. Condensed Matter. 2023; 8(4):93. https://doi.org/10.3390/condmat8040093
Chicago/Turabian StyleIonescu, Alina M., Ion Ivan, Corneliu F. Miclea, Daniel N. Crisan, Armando Galluzzi, Massimiliano Polichetti, and Adrian Crisan. 2023. "Vortex Dynamics and Pinning in CaKFe4As4 Single Crystals from DC Magnetization Relaxation and AC Susceptibility" Condensed Matter 8, no. 4: 93. https://doi.org/10.3390/condmat8040093
APA StyleIonescu, A. M., Ivan, I., Miclea, C. F., Crisan, D. N., Galluzzi, A., Polichetti, M., & Crisan, A. (2023). Vortex Dynamics and Pinning in CaKFe4As4 Single Crystals from DC Magnetization Relaxation and AC Susceptibility. Condensed Matter, 8(4), 93. https://doi.org/10.3390/condmat8040093











