The Depairing Current Density of a Fe(Se,Te) Crystal Evaluated in Presence of Demagnetizing Factors
Abstract
1. Introduction
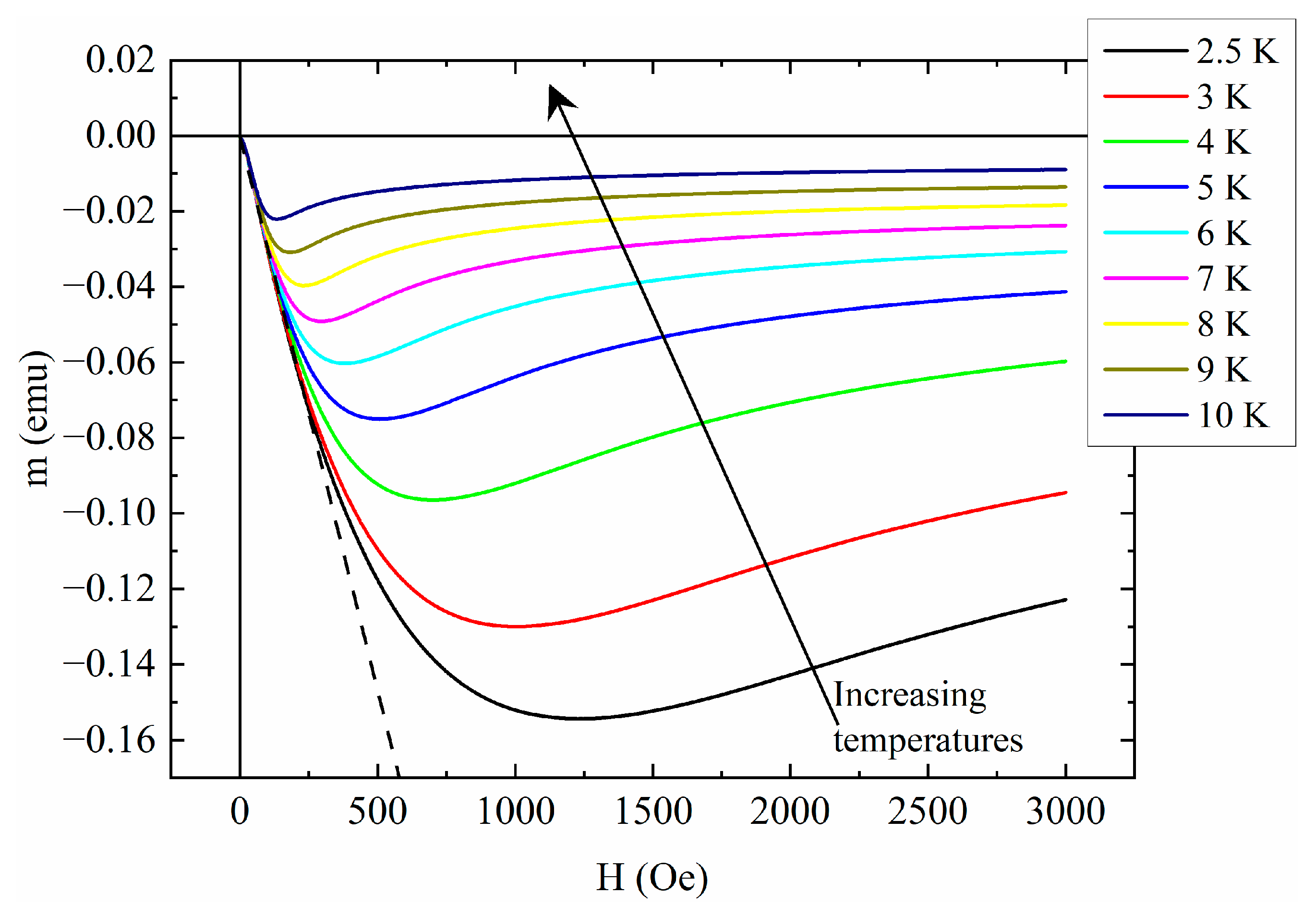
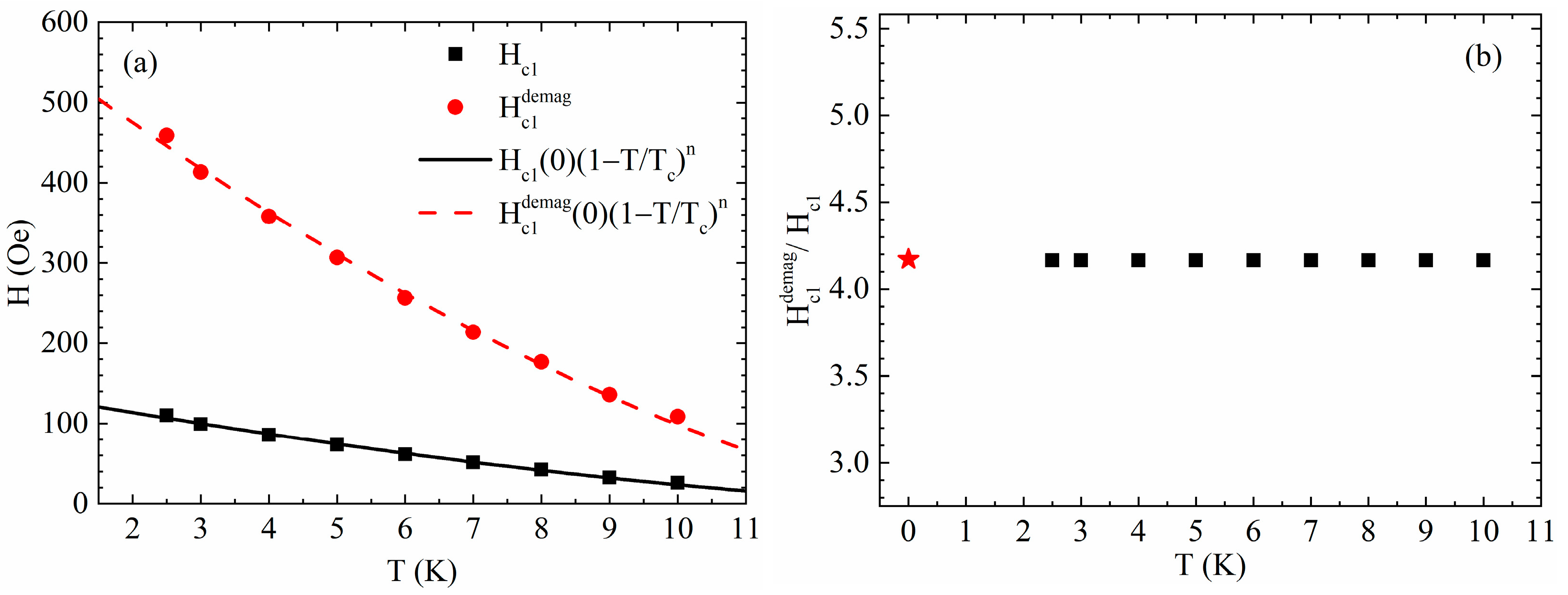
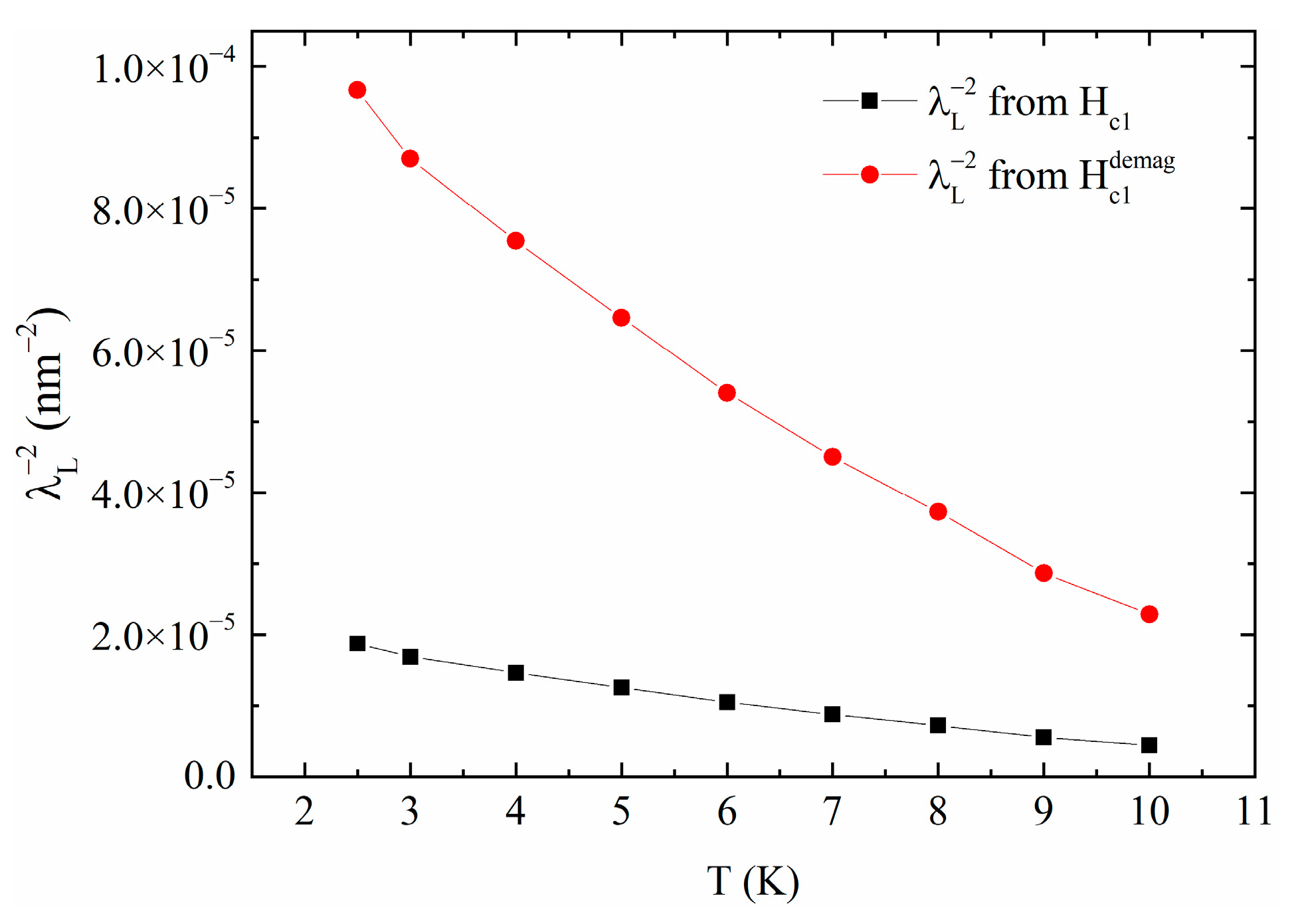
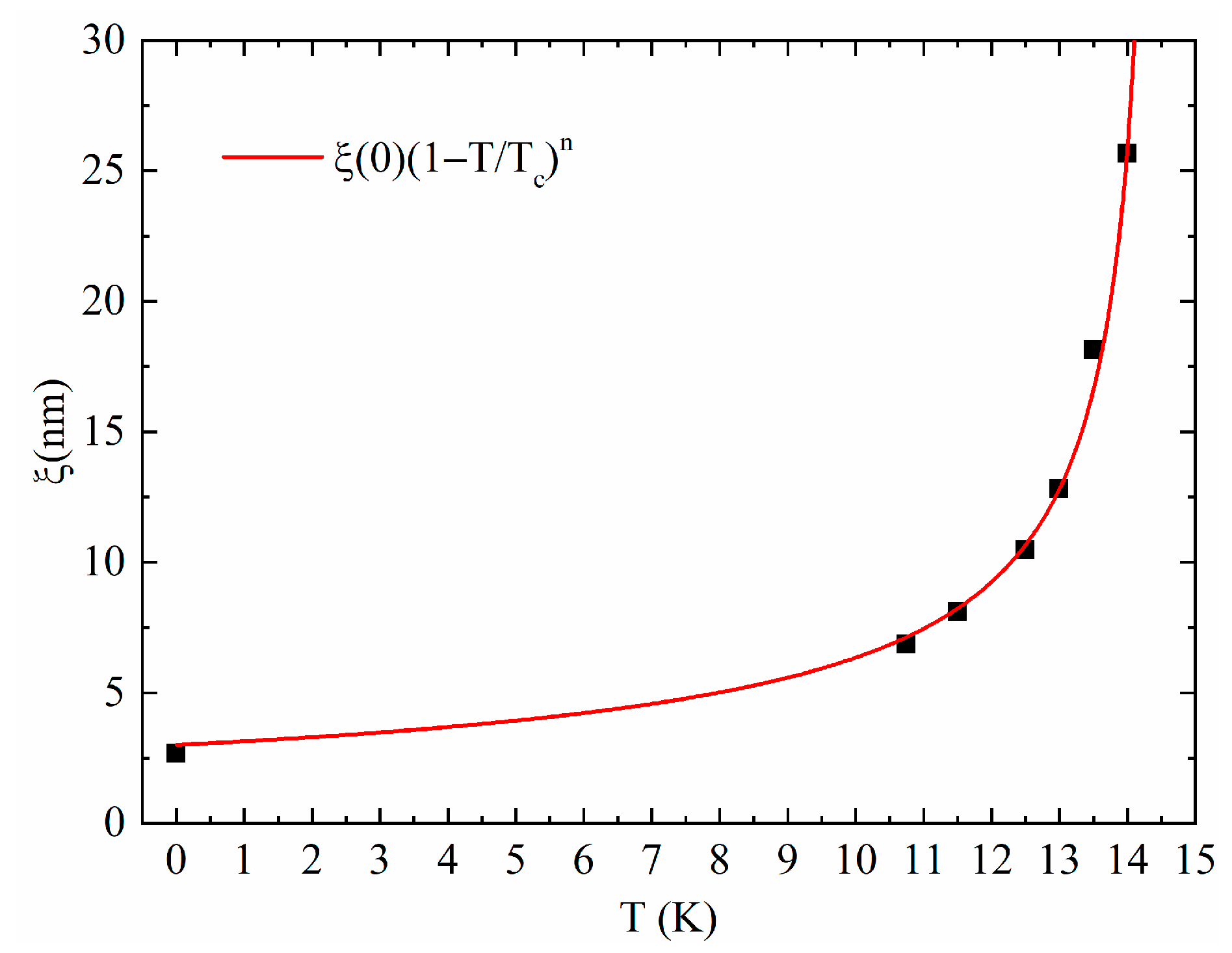
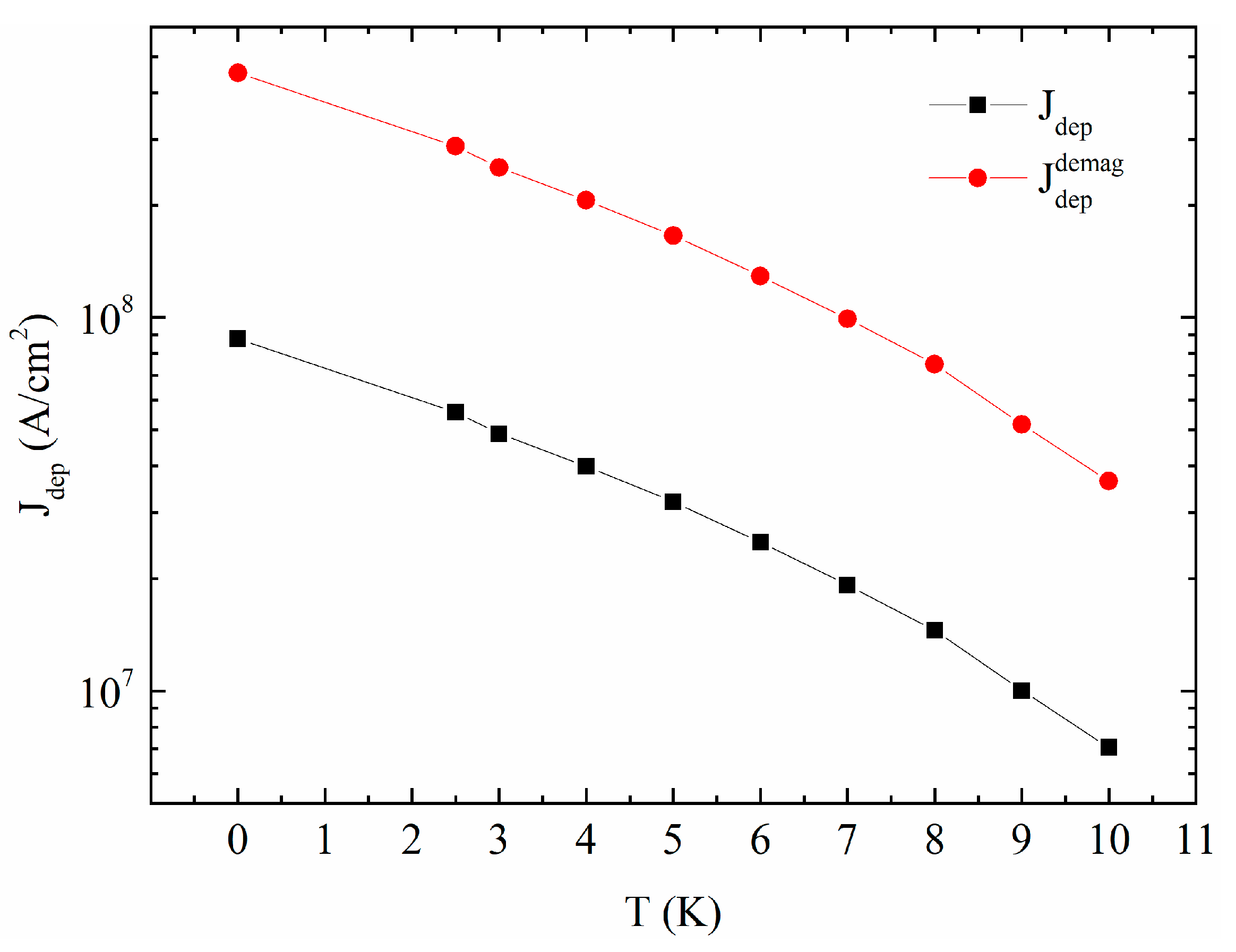
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kamihara, Y.; Watanabe, T.; Hirano, M.; Hosono, H. Iron-based layered superconductor La[O1−xFx]FeAs (x = 0.05–0.12) with Tc = 26 K. J. Am. Chem. Soc. 2008, 130, 3296–3297. [Google Scholar] [CrossRef]
- Bednorz, J.G.; Müller, K.A. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z. Phys. B Condens. Matter 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Hsu, F.-C.; Luo, J.-Y.; Yeh, K.-W.; Chen, T.-K.; Huang, T.-W.; Wu, P.M.; Lee, Y.-C.; Huang, Y.-L.; Chu, Y.-Y.; Yan, D.-C.; et al. Superconductivity in the PbO-type structure α-FeSe. Proc. Natl. Acad. Sci. USA 2008, 105, 14262–14264. [Google Scholar] [CrossRef] [PubMed]
- Galluzzi, A.; Buchkov, K.; Tomov, V.; Nazarova, E.; Leo, A.; Grimaldi, G.; Nigro, A.; Pace, S.; Polichetti, M. Evidence of pinning crossover and the role of twin boundaries in the peak effect in FeSeTe iron based superconductor. Supercond. Sci. Technol. 2018, 31, 015014. [Google Scholar] [CrossRef]
- Galluzzi, A.; Buchkov, K.; Nazarova, E.; Tomov, V.; Grimaldi, G.; Leo, A.; Pace, S.; Polichetti, M. Transport properties and high upper critical field of a Fe(Se,Te) iron based superconductor. Eur. Phys. J. Spec. Top. 2019, 228, 725–731. [Google Scholar] [CrossRef]
- Galluzzi, A.; Buchkov, K.; Nazarova, E.; Tomov, V.; Leo, A.; Grimaldi, G.; Pace, S.; Polichetti, M. Magnetic field sweep rate influence on the critical current capabilities of a Fe(Se,Te) crystal. J. Appl. Phys. 2020, 128, 073902. [Google Scholar] [CrossRef]
- Hosono, H.; Yamamoto, A.; Hiramatsu, H.; Ma, Y. Recent advances in iron-based superconductors toward applications. Mater. Today 2018, 21, 278–302. [Google Scholar] [CrossRef]
- Yuan, H.Q.; Singleton, J.; Balakirev, F.F.; Baily, S.A.; Chen, G.F.; Luo, J.L.; Wang, N.L. Nearly isotropic superconductivity in (Ba,K)Fe2As2. Nature 2009, 457, 565–568. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, A.; Jaroszynski, J.; Tarantini, C.; Balicas, L.; Jiang, J.; Gurevich, A.; Larbalestier, D.C.; Jin, R.; Sefat, A.S.; McGuire, M.A.; et al. Small anisotropy, weak thermal fluctuations, and high field superconductivity in Co-doped iron pnictide Ba(Fe1−xCox)2As2. Appl. Phys. Lett. 2009, 94, 062511. [Google Scholar] [CrossRef]
- Grimaldi, G.; Leo, A.; Martucciello, N.; Braccini, V.; Bellingeri, E.; Ferdeghini, C.; Galluzzi, A.; Polichetti, M.; Nigro, A.; Villegier, J.-C.; et al. Weak or Strong Anisotropy in Fe(Se,Te) Superconducting Thin Films Made of Layered Iron-Based Material? IEEE Trans. Appl. Supercond. 2019, 29, 1–4. [Google Scholar] [CrossRef]
- Leo, A.; Braccini, V.; Bellingeri, E.; Ferdeghini, C.; Galluzzi, A.; Polichetti, M.; Nigro, A.; Pace, S.; Grimaldi, G. Anisotropy effects on the quenching current of Fe(Se,Te) Thin Films. IEEE Trans. Appl. Supercond. 2018, 28, 8234633. [Google Scholar] [CrossRef]
- Eley, S.; Willa, R.; Chan, M.K.; Bauer, E.D.; Civale, L. Vortex phases and glassy dynamics in the highly anisotropic superconductor HgBa2CuO4+δ. Sci. Rep. 2020, 10, 10239. [Google Scholar] [CrossRef]
- Polichetti, M.; Galluzzi, A.; Buchkov, K.; Tomov, V.; Nazarova, E.; Leo, A.; Grimaldi, G.; Pace, S. A precursor mechanism triggering the second magnetization peak phenomenon in superconducting materials. Sci. Rep. 2021, 11, 7247. [Google Scholar] [CrossRef] [PubMed]
- Llovo, I.F.; Sónora, D.; Mosqueira, J.; Salem-Sugui, S.; Sundar, S.; Alvarenga, A.D.; Xie, T.; Liu, C.; Li, S.L.; Luo, H.Q. Vortex dynamics and second magnetization peak in the iron-pnictide superconductor Ca0.82La0.18Fe0.96Ni0.04As2. Supercond. Sci. Technol. 2021, 34, 115010. [Google Scholar] [CrossRef]
- Yi, X.; Xing, X.; Meng, Y.; Zhou, N.; Wang, C.; Sun, Y.; Shi, Z. Anomalous Second Magnetization Peak in 12442-Type RbCa2Fe4As4F2 Superconductors. Chin. Phys. Lett. 2023, 40, 027401. [Google Scholar] [CrossRef]
- Lopes, P.V.; Sundar, S.; Salem-Sugui, S.; Hong, W.; Luo, H.; Ghivelder, L. Second magnetization peak, anomalous field penetration, and Josephson vortices in KCa2Fe4As4F2 bilayer pnictide superconductor. Sci. Rep. 2022, 12, 20359. [Google Scholar] [CrossRef]
- Prozorov, R.; Ni, N.; Tanatar, M.A.; Kogan, V.G.; Gordon, R.T.; Martin, C.; Blomberg, E.C.; Prommapan, P.; Yan, J.Q.; Bud’ko, S.L.; et al. Vortex phase diagram of Ba(Fe0.93Co0.07)2As2 single crystals. Phys. Rev. B 2008, 78, 224506. [Google Scholar] [CrossRef]
- Sun, Y.; Taen, T.; Tsuchiya, Y.; Pyon, S.; Shi, Z.; Tamegai, T. Magnetic relaxation and collective vortex creep in FeTe0.6Se0.4 single crystal. Europhys. Lett. 2013, 103, 57013. [Google Scholar] [CrossRef]
- Pramanik, A.K.; Harnagea, L.; Nacke, C.; Wolter, A.U.B.; Wurmehl, S.; Kataev, V.; Büchner, B. Fishtail effect and vortex dynamics in LiFeAs single crystals. Phys. Rev. B 2011, 83, 094502. [Google Scholar] [CrossRef]
- Sundar, S.; Salem-Sugui, S.; Amorim, H.S.; Wen, H.H.; Yates, K.A.; Cohen, L.F.; Ghivelder, L. Plastic pinning replaces collective pinning as the second magnetization peak disappears in the pnictide superconductor Ba0.75K0.25Fe2As2. Phys. Rev. B 2017, 95, 134509. [Google Scholar] [CrossRef]
- Taen, T.; Tsuchiya, Y.; Nakajima, Y.; Tamegai, T. Critical current densities and vortex dynamics in FeTexSe1−x single crystals. Phys. C Supercond. Appl. 2010, 470, 1106–1108. [Google Scholar] [CrossRef]
- Ren, C.; Wang, Z.S.; Luo, H.Q.; Yang, H.; Shan, L.; Wen, H.H. Evidence for two energy gaps in superconducting Ba0.6K0.4Fe2As2 single crystals and the breakdown of the uemura plot. Phys. Rev. Lett. 2008, 101, 257006. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.L.; Dou, S.X.; Ren, Z.A.; Yi, W.; Li, Z.C.; Zhao, Z.X.; Lee, S.I. Unconventional superconductivity of NdFeAsO0.82F0.18 indicated by the low temperature dependence of the lower critical field Hc1. J. Phys. Condens. Matter 2009, 21, 205701. [Google Scholar] [CrossRef]
- Martin, C.; Gordon, R.T.; Tanatar, M.A.; Kim, H.; Ni, N.; Bud’Ko, S.L.; Canfield, P.C.; Luo, H.; Wen, H.H.; Wang, Z.; et al. Nonexponential London penetration depth of external magnetic fields in superconducting Ba1−xKxFe2As2 single crystals. Phys. Rev. B 2009, 80, 020501. [Google Scholar] [CrossRef]
- Abdel-Hafiez, M.; Ge, J.; Vasiliev, A.N.; Chareev, D.A.; Van De Vondel, J.; Moshchalkov, V.V.; Silhanek, A.V. Temperature dependence of lower critical field Hc1(T) shows nodeless superconductivity in FeSe. Phys. Rev. B 2013, 88, 174512. [Google Scholar] [CrossRef]
- Song, Y.J.; Ghim, J.S.; Yoon, J.H.; Lee, K.J.; Jung, M.H.; Ji, H.S.; Shim, J.H.; Bang, Y.; Kwon, Y.S. Small anisotropy of the lower critical field and the s±- wave two-gap feature in single-crystal LiFeAs. Europhys. Lett. 2011, 94, 57008. [Google Scholar] [CrossRef][Green Version]
- Prozorov, R.; Kogan, V.G. London penetration depth in iron-based superconductors. Rep. Prog. Phys. 2011, 74, 124505–124525. [Google Scholar] [CrossRef]
- Rosenstein, B.; Li, D. Ginzburg-Landau theory of type II superconductors in magnetic field. Rev. Mod. Phys. 2010, 82, 109–168. [Google Scholar] [CrossRef]
- Tahara, S.; Anlage, S.M.; Halbritter, J.; Eom, C.B.; Fork, D.K.; Geballe, T.H.; Beasley, M.R. Critical currents, pinning, and edge barriers in narrow YBa2Cu3O7−δ thin films. Phys. Rev. B 1990, 41, 11203–11208. [Google Scholar] [CrossRef] [PubMed]
- Tinkham, M. Introduction to Superconductivity; Dover Publications: Mineola, NY, USA, 2004; ISBN 0486134725. [Google Scholar]
- Arpaia, R.; Nawaz, S.; Lombardi, F.; Bauch, T. Improved nanopatterning for YBCO nanowires approaching the depairing current. IEEE Trans. Appl. Supercond. 2013, 23, 1101505. [Google Scholar] [CrossRef]
- Wang, T.; Ma, Y.; Li, W.; Chu, J.; Wang, L.; Feng, J.; Xiao, H.; Li, Z.; Hu, T.; Liu, X.; et al. Two-gap superconductivity in CaFe0.88Co0.12AsF revealed by temperature dependence of the lower critical field Hc1c(T). npj Quantum Mater. 2019, 4, 33. [Google Scholar] [CrossRef]
- Musolino, N.; Bals, S.; Van Tendeloo, G.; Clayton, N.; Walker, E.; Flükiger, R. Modulation-free phase in heavily Pb-doped (Bi,Pb)2212 crystals. Phys. C Supercond. Its Appl. 2003, 399, 1–7. [Google Scholar] [CrossRef]
- Galluzzi, A.; Leo, A.; Masi, A.; Varsano, F.; Nigro, A.; Grimaldi, G.; Polichetti, M. Magnetic Vortex Phase Diagram for a Non-Optimized CaKFe4As4 Superconductor Presenting a Wide Vortex Liquid Region and an Ultra-High Upper Critical Field. Appl. Sci. 2023, 13, 884. [Google Scholar] [CrossRef]
- Felner, I.; Kopelevich, Y. Magnetization measurement of a possible high-temperature superconducting state in amorphous carbon doped with sulfur. Phys. Rev. B 2009, 79, 233409. [Google Scholar] [CrossRef]
- Yadav, C.S.; Paulose, P.L. Upper critical field, lower critical field and critical current density of FeTe0.60Se0.40 single crystals. New J. Phys. 2009, 11, 103046. [Google Scholar] [CrossRef]
- Stoner, E.C. XCVII. The demagnetizing factors for ellipsoids. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1945, 36, 803–821. [Google Scholar] [CrossRef]
- Prando, G.; Giraud, R.; Aswartham, S.; Vakaliuk, O.; Abdel-Hafiez, M.; Hess, C.; Wurmehl, S.; Wolter, A.U.B.; Büchner, B. Evidence for a vortex–glass transition in superconducting Ba(Fe0.9Co0.1)2As2. J. Phys. Condens. Matter 2013, 25, 505701. [Google Scholar] [CrossRef] [PubMed]
- Yeshurun, Y.; Malozemoff, A.P.; Shaulov, A. Magnetic relaxation in high-temperature superconductors. Rev. Mod. Phys. 1996, 68, 911–949. [Google Scholar] [CrossRef]
- Maheshwari, P.K.; Gahtori, B.; Gupta, A.; Awana, V.P.S. Impact of Fe site Co substitution on superconductivity of Fe1−xCoxSe0.5Te0.5 (x = 0.0 to 0.10): A flux free single crystal study. AIP Adv. 2017, 7, 15006. [Google Scholar] [CrossRef]
- Murugesan, K.; Lingannan, G.; Ishigaki, K.; Uwatoko, Y.; Sekine, C.; Kawamura, Y.; Junichi, H.; Joseph, B.; Vajeeston, P.; Maheswari, P.K.; et al. Pressure Dependence of Superconducting Properties, Pinning Mechanism, and Crystal Structure of the Fe0.99Mn0.01Se0.5Te0.5 Superconductor. ACS Omega 2021, 6, 30419–30431. [Google Scholar] [CrossRef] [PubMed]
- Lei, H.; Hu, R.; Petrovic, C. Critical fields, thermally activated transport, and critical current density of β-FeSe single crystals. Phys. Rev. B 2011, 84, 014520. [Google Scholar] [CrossRef]
- Dutta, P.; Pramanick, S.; Chatterjee, S. Effect of S-doping on the magnetic and electrical properties of FeSe superconductor. Phys. C Supercond. Appl. 2022, 602, 1354126. [Google Scholar] [CrossRef]
- Fletcher, J.D.; Serafin, A.; Malone, L.; Analytis, J.G.; Chu, J.H.; Erickson, A.S.; Fisher, I.R.; Carrington, A. Evidence for a nodal-line superconducting state in LaFePO. Phys. Rev. Lett. 2009, 102, 147001. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, H.; Imai, Y.; Komiya, S.; Tsukada, I.; Maeda, A. Anomalous temperature dependence of the superfluid density caused by a dirty-to-clean crossover in superconducting FeSe0.4Te0.6 single crystals. Phys. Rev. B 2011, 84, 132503. [Google Scholar] [CrossRef]
- Bendele, M.; Weyeneth, S.; Puzniak, R.; Maisuradze, A.; Pomjakushina, E.; Conder, K.; Pomjakushin, V.; Luetkens, H.; Katrych, S.; Wisniewski, A.; et al. Anisotropic superconducting properties of single-crystalline FeSe0.5Te0.5. Phys. Rev. B 2010, 81, 224520. [Google Scholar] [CrossRef]
- Milošević, M.V.; Perali, A. Emergent phenomena in multicomponent superconductivity: An introduction to the focus issue. Supercond. Sci. Technol. 2015, 28, 060201. [Google Scholar] [CrossRef]
- Weyeneth, S.; Puzniak, R.; Mosele, U.; Zhigadlo, N.D.; Katrych, S.; Bukowski, Z.; Karpinski, J.; Kohout, S.; Roos, J.; Keller, H. Anisotropy of superconducting single crystal SmFeAsO0.8F0.2 studied by torque magnetometry. J. Supercond. Nov. Magn. 2009, 22, 325–329. [Google Scholar] [CrossRef]
- Gonnelli, R.S.; Daghero, D.; Tortello, M.; Ummarino, G.A.; Stepanov, V.A.; Kremer, R.K.; Kim, J.S.; Zhigadlo, N.D.; Karpinski, J. Point-contact Andreev-reflection spectroscopy in ReFeAsO1−xFx (Re = La, Sm): Possible evidence for two nodeless gaps. Phys. C Supercond. Appl. 2009, 469, 512–520. [Google Scholar] [CrossRef]
- Szabó, P.; Pribulová, Z.; Pristáš, G.; Bud’ko, S.L.; Canfield, P.C.; Samuely, P. Evidence for two-gap superconductivity in Ba0.55K 0.45Fe2As2 from directional point-contact Andreev-reflection spectroscopy. Phys. Rev. B 2009, 79, 012503. [Google Scholar] [CrossRef]
- Mu, G.; Luo, H.; Wang, Z.; Shan, L.; Ren, C.; Wen, H.H. Low temperature specific heat of the hole-doped Ba0.6K0.4Fe2As2 single crystals. Phys. Rev. B 2009, 79, 174501. [Google Scholar] [CrossRef]
- Bekaert, J.; Vercauteren, S.; Aperis, A.; Komendová, L.; Prozorov, R.; Partoens, B.; Milošević, M.V. Anisotropic type-I superconductivity and anomalous superfluid density in OsB2. Phys. Rev. B 2016, 94, 144506. [Google Scholar] [CrossRef]
- Klein, T.; Braithwaite, D.; Demuer, A.; Knafo, W.; Lapertot, G.; Marcenat, C.; Rodière, P.; Sheikin, I.; Strobel, P.; Sulpice, A.; et al. Thermodynamic phase diagram of Fe(Se0.5Te0.5) single crystals in fields up to 28 tesla. Phys. Rev. B 2010, 82, 184506. [Google Scholar] [CrossRef]
- Diaconu, A.; Martin, C.; Hu, J.; Liu, T.; Qian, B.; Mao, Z.; Spinu, L. Possible nodal superconducting gap in Fe1+y(Te1−xSex) single crystals from ultralow temperature penetration depth measurements. Phys. Rev. B 2013, 88, 104502. [Google Scholar] [CrossRef]
- Kumar, R.; Varma, G.D. Study of TAFF and vortex phase of FexTe0.60Se0.40 (0.970 ≤ x ≤ 1.030) single crystals. Phys. Scr. 2020, 95, 045814. [Google Scholar] [CrossRef]
- Poole, C.; Farach, H.; Creswick, R.; Prozorov, R. Superconductivity; Academic Press: Cambridge, MA, USA, 2007; ISBN 0080550487. [Google Scholar]
- Peri, A.; Mangel, I.; Keren, A. Superconducting Stiffness and Coherence Length of FeSe0.5Te0.5 Measured in a Zero-Applied Field. Condens. Matter 2023, 8, 39. [Google Scholar] [CrossRef]
- Bardeen, J. Critical fields and currents in superconductors. Rev. Mod. Phys. 1962, 34, 667–681. [Google Scholar] [CrossRef]
- Maiorov, B.; Mele, P.; Baily, S.A.; Weigand, M.; Lin, S.Z.; Balakirev, F.F.; Matsumoto, K.; Nagayoshi, H.; Fujita, S.; Yoshida, Y.; et al. Inversion of the upper critical field anisotropy in FeTeS films. Supercond. Sci. Technol. 2014, 27, 044005. [Google Scholar] [CrossRef]
- Her, J.L.; Kohama, Y.; Matsuda, Y.H.; Kindo, K.; Yang, W.H.; Chareev, D.A.; Mitrofanova, E.S.; Volkova, O.S.; Vasiliev, A.N.; Lin, J.Y. Anisotropy in the upper critical field of FeSe and FeSe0.33Te0.67 single crystals. Supercond. Sci. Technol. 2015, 28, 045013. [Google Scholar] [CrossRef]
- Sun, Y.; Pan, Y.; Zhou, N.; Xing, X.; Shi, Z.; Wang, J.; Zhu, Z.; Sugimoto, A.; Ekino, T.; Tamegai, T.; et al. Comparative study of superconducting and normal-state anisotropy in Fe1+yTe0.6Se0.4 superconductors with controlled amounts of interstitial excess Fe. Phys. Rev. B 2021, 103, 224506. [Google Scholar] [CrossRef]
- Mishev, V.; Nakajima, M.; Eisaki, H.; Eisterer, M. Effects of introducing isotropic artificial defects on the superconducting properties of differently doped Ba-122 based single crystals. Sci. Rep. 2016, 6, 27783. [Google Scholar] [CrossRef] [PubMed]
- Kondo, K.; Motoki, S.; Hatano, T.; Urata, T.; Iida, K.; Ikuta, H. NdFeAs(O,H) epitaxial thin films with high critical current density. Supercond. Sci. Technol. 2020, 33, 09LT01. [Google Scholar] [CrossRef]
- Li, J.; Yuan, J.; Yuan, Y.H.; Ge, J.Y.; Li, M.Y.; Feng, H.L.; Pereira, P.J.; Ishii, A.; Hatano, T.; Silhanek, A.V.; et al. Direct observation of the depairing current density in single-crystalline Ba0.5K0.5Fe2As2 microbridge with nanoscale thickness. Appl. Phys. Lett. 2013, 103, 62603. [Google Scholar] [CrossRef]
- Bristow, M.; Knafo, W.; Reiss, P.; Meier, W.; Canfield, P.C.; Blundell, S.J.; Coldea, A.I. Competing pairing interactions responsible for the large upper critical field in a stoichiometric iron-based superconductor CaKFe4As4. Phys. Rev. B 2020, 101, 134502. [Google Scholar] [CrossRef]
- Sun, Y.; Ohnuma, H.; Ayukawa, S.-Y.; Noji, T.; Koike, Y.; Tamegai, T.; Kitano, H. Achieving the depairing limit along the c axis in Fe1+yTe1−xSex single crystals. Phys. Rev. B 2020, 101, 134516. [Google Scholar] [CrossRef]
- Galluzzi, A.; Buchkov, K.; Tomov, V.; Nazarova, E.; Kovacheva, D.; Leo, A.; Grimaldi, G.; Pace, S.; Polichetti, M. Mixed state properties of iron based Fe(Se,Te) superconductor fabricated by Bridgman and by self-flux methods. J. Appl. Phys. 2018, 123, 233904. [Google Scholar] [CrossRef]
- Tsurkan, V.; Deisenhofer, J.; Günther, A.; Kant, C.; Klemm, M.; von Nidda, H.-A.; Schrettle, F.; Loidl, A. Physical properties of FeSe0.5Te0.5 single crystals grown under different conditions. Eur. Phys. J. B 2011, 79, 289–299. [Google Scholar] [CrossRef]
- Wittlin, A.; Aleshkevych, P.; Przybylińska, H.; Gawryluk, D.J.; Dłuzewski, P.; Berkowski, M.; Puźniak, R.; Gutowska, M.U.; Wiśniewski, A. Microstructural magnetic phases in superconducting FeTe0.65Se0.35. Supercond. Sci. Technol. 2012, 25, 065019. [Google Scholar] [CrossRef][Green Version]
- Sivakov, A.G.; Bondarenko, S.I.; Prokhvatilov, A.I.; Timofeev, V.P.; Pokhila, A.S.; Koverya, V.P.; Dudar, I.S.; Link, S.I.; Legchenkova, I.V.; Bludov, A.N.; et al. Microstructural and transport properties of superconducting FeTe0.65Se0.35 crystals. Supercond. Sci. Technol. 2017, 30, 015018. [Google Scholar] [CrossRef]
- McQueen, T.M.; Huang, Q.; Ksenofontov, V.; Felser, C.; Xu, Q.; Zandbergen, H.; Hor, Y.S.; Allred, J.; Williams, A.J.; Qu, D.; et al. Extreme sensitivity of superconductivity to stoichiometry in Fe1+δSe. Phys. Rev. B 2009, 79, 014522. [Google Scholar] [CrossRef]
- Onar, K.; Yakinci, M.E. Solid state synthesis and characterization of bulk β-FeSe superconductors. J. Alloys Compd. 2015, 620, 210–216. [Google Scholar] [CrossRef]
- Fiamozzi Zignani, C.; De Marzi, G.; Grimaldi, G.; Leo, A.; Guarino, A.; Vannozzi, A.; della Corte, A.; Pace, S. Fabrication and Physical Properties of Polycrystalline Iron-Chalcogenides Superconductors. IEEE Trans. Appl. Supercond. 2017, 27, 1–5. [Google Scholar] [CrossRef]
- Galluzzi, A.; Nigro, A.; Fittipaldi, R.; Guarino, A.; Pace, S.; Polichetti, M. DC magnetic characterization and pinning analysis on Nd1.85Ce0.15CuO4 cuprate superconductor. J. Magn. Magn. Mater. 2019, 475, 125–129. [Google Scholar] [CrossRef]
- Galluzzi, A.; Mancusi, D.; Cirillo, C.; Attanasio, C.; Pace, S.; Polichetti, M. Determination of the Transition Temperature of a Weak Ferromagnetic Thin Film by Means of an Evolution of the Method Based on the Arrott Plots. J. Supercond. Nov. Magn. 2018, 31, 1127–1132. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galluzzi, A.; Buchkov, K.; Tomov, V.; Nazarova, E.; Leo, A.; Grimaldi, G.; Crisan, A.; Polichetti, M. The Depairing Current Density of a Fe(Se,Te) Crystal Evaluated in Presence of Demagnetizing Factors. Condens. Matter 2023, 8, 91. https://doi.org/10.3390/condmat8040091
Galluzzi A, Buchkov K, Tomov V, Nazarova E, Leo A, Grimaldi G, Crisan A, Polichetti M. The Depairing Current Density of a Fe(Se,Te) Crystal Evaluated in Presence of Demagnetizing Factors. Condensed Matter. 2023; 8(4):91. https://doi.org/10.3390/condmat8040091
Chicago/Turabian StyleGalluzzi, Armando, Krastyo Buchkov, Vihren Tomov, Elena Nazarova, Antonio Leo, Gaia Grimaldi, Adrian Crisan, and Massimiliano Polichetti. 2023. "The Depairing Current Density of a Fe(Se,Te) Crystal Evaluated in Presence of Demagnetizing Factors" Condensed Matter 8, no. 4: 91. https://doi.org/10.3390/condmat8040091
APA StyleGalluzzi, A., Buchkov, K., Tomov, V., Nazarova, E., Leo, A., Grimaldi, G., Crisan, A., & Polichetti, M. (2023). The Depairing Current Density of a Fe(Se,Te) Crystal Evaluated in Presence of Demagnetizing Factors. Condensed Matter, 8(4), 91. https://doi.org/10.3390/condmat8040091














