Single-Band versus Two-Band Description of Magnetism in Infinite-Layer Nickelates

Abstract

We present a weak-coupling analysis of magnetism in infinite-layer nickelates, where we compare a single-band description with a two-band model. Both models predict that (i) hybridization due to hopping is negligible, and ($ii$) the magnetic properties are characterized by very similar dynamic structure factors, $S(\overrightarrow{k},\omega )$, at the points $(\pi ,\pi ,0)$ and $(\pi ,\pi ,\pi )$. This gives effectively a two-dimensional description of the magnetic properties.

1. Introduction: Superconducting Infinite-Layer Nickelates Nd${}_{1-x}$Sr${}_x$NiO${}_2$

The discovery of Bednorz and Müller [1] marks a new era in the superconductivity research dominated by the search for novel superconductors with high values in the critical temperature $T_c$. However, in spite of the huge effort in the theory, the mechanism responsible for the pairing in cuprates is still unknown [2], being one of the fundamental open problems in modern condensed matter theory. Perhaps less spectacular was the more recent discovery of superconductivity in infinite-layer NdNiO${}_2$ doped by Sr [3], as the values of $T_c$ are here “only” close to 15 K [4]. However, certainly, it attracted more attention to the superconductivity in strongly correlated materials.

The nickelate superconductors are rather similar to cuprate superconductors [5,6,7]—here also, the two-dimensional (2D) planes of transition metal ions play a central role. At each Ni${}^{+}$ ion, one has one hole, i.e., $d^9$ electronic configuration and apical oxygens are absent. Using perturbation theory, such states in a NiO${}_2$ layer give the magnetic short-range order, similar to CuO${}_2$ layer; in cuprates, we even find antiferromagnetic (AFM) long-range order. We find that the charge-transfer gap in a NiO${}_2$ plane is larger than the one in the CuO${}_2$ plane [8,9,10,11]. Doped holes reside at oxygen sites in cuprates forming the Zhang–Rice singlet [12]. On the contrary, doped holes likely reside at Ni ions within Nd${}_{1-x}$Sr${}_x$NiO${}_2$. This justifies AFM correlations in the one–band model with $x^2-y^2$ orbitals, which is an effective model of not only superconducting cuprates but also nickelates [5,13]. However, nickelates also need another band that crosses the Fermi energy and is described by a two-band model [14,15,16]. Here, we present and compare valuable insights from the random phase approximation (RPA), first obtained for cuprates [17].

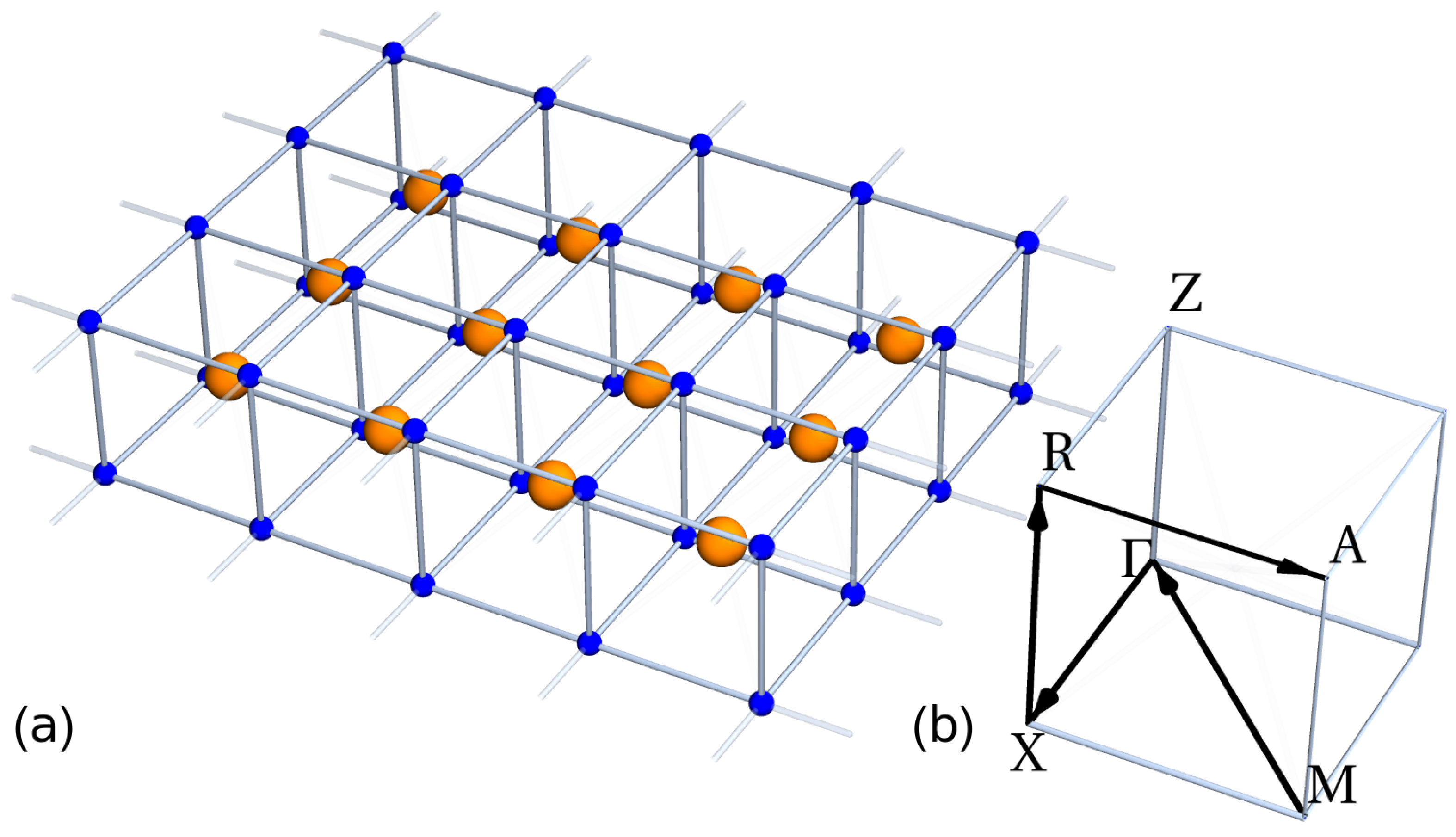
2. The Two-Band Model and One-Band Model for Infinite-Layer Nickelate

In this paper, we consider (i) a two-orbital Hubbard model and (ii) a one-orbital Hubbard model of infinite-layer nickelate. In (i), the two-orbital model is derived from first principles and is similar to that in Ref. [15]. The first orbital (denoted as d) is centered on the Ni atom and has antibonding Ni($3d_{x^2-y^2}$)/O($2p_{\sigma }$) character; the Ni($3d_{x^2-y^2}$) character is dominant. The second orbital (denoted as s) is centered on the Nd atom and has mixed Nd($5d_{3z^2-r^2}$) and interstitial s character; the Nd($5d_{3z^2-r^2}$) character is dominant along the $\mathrm{\Gamma }$-X-M-$\mathrm{\Gamma }$ path shown in Figure 1, and the interstitial s character is dominant along the Z-R-A-Z path. There is one d orbital and one s orbital per unit cell, and the total filling of both orbitals is one electron. At the DFT level, the occupation number of the nearly half-filled d orbital is 0.91 and that of the nearly empty s orbital is 0.09.

Figure 1. (a) Schematic lattice structure of the two-band model for NiNdO${}_2$, with Ni(d) blue orbital and Ni(s) orange orbital. The latter orbital is spatially shifted by (0.5, 0.5, 0.5) relative to the Ni(d). (b) Brillouin zone used for the two-band model along high-symmetry special points. Special points are: M $\equiv (\pi ,\pi ,0)$; $\mathrm{\Gamma }\equiv (0,0,0)$; X $\equiv (\pi ,0,0)$; R $\equiv (\pi ,0,\pi )$; A $\equiv (\pi ,\pi ,\pi )$; Z $\equiv (0,0,\pi )$.

The sketch of the model is shown in Figure 1a. To obtain the two-band model, we use the generalized gradient approximation (GGA). The ab initio electronic structure calculations using density functional theory (DFT) were performed employing the Quantum Espresso code [18,19] and using a specific choice of pseudopotentials [20]. The computational details are the following: We use the structural data from Ref. [21]. The self-consistent DFT calculation considers a sampling of the full Brillouin zone with an 8 × 8 × 8 $\overrightarrow{k}$-point grid and 100 bands. The resulting band structure is used as a starting point for the subsequent calculations.

Then, we perform the Wannier projections by using the Respack code [22,23]. The initial guesses for the Wannier orbitals are an $x^2-y^2$ atomic orbital centered on the Ni atom, and a $3z^2-r^2$ atomic orbital centered on the Nd atom. To preserve the DFT band dispersion in the Wannier projection, we used an inner window between the Fermi level and +0.7 eV above the Fermi level. Then, we calculate the maximally localized Wannier functions [24,25]. After the calculation, the first orbital d has antibonding Ni$(3d{x}^2-y^2)$/O$\left(2p_{\sigma }\right)$ character, and the second orbital s has mixed interstitial s/Nd($5d_{3z^2-r^2}$) character. Finally, we disentangle [26] the other six bands in the band window from the two Wannier bands.

The Hamiltonian of the two-orbital model is

$$\mathcal{H}=H_{dd}+H_{ss}+H_{ds}+H_{\mathrm{int}}.$$

(1)

The first three terms in the Hamiltonian (1) stand for the kinetic energy: $H_{dd}$ includes the Ni$\left(d\right)$-Ni$\left(d\right)$ hoppings $\propto t_{mn}^{dd}$, $H_{ss}$ includes the Ni$\left(s\right)$-Ni$\left(s\right)$ hoppings $\propto t_{mn}^{ss}$, and $H_{ds}$ includes the $d-s$ hybridization $\propto t_{mn}^{ds}$,

$$\begin{array}{ccc}\hfill H_{dd}& =& \sum _{\{m\mu ;n\nu \},\sigma }\left(t_{mn}^{dd}{\widehat{a}}_{m\alpha \sigma }^{†}{\widehat{a}}_{n\nu \sigma }+\mathrm{H}.\mathrm{c}.\right),\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill H_{ss}& =& \sum _{\{m\mu ;n\nu \},\sigma }\left(t_{mn}^{ss}{\widehat{a}}_{m\mu \sigma }^{†}{\widehat{a}}_{n\nu \sigma }+\mathrm{H}.\mathrm{c}.\right),\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill H_{ds}& =& \sum _{\{m\mu ;n\nu \},\sigma }\left(t_{mn}^{ds}{\widehat{a}}_{m\mu \sigma }^{†}{\widehat{a}}_{n\nu \sigma }+\mathrm{H}.\mathrm{c}.\right),\hfill \end{array}$$

(4)

where ${\widehat{a}}_{m\mu \sigma }^{†}$ (${\widehat{a}}_{n\nu \sigma }$) is the creation (annihilation) operator of an electron at nickel site m in an orbital $\mu \in \{d,s\}$. The hopping parameters $t_{mn}^{mn}$ used in this calculation are set above 0.001 eV, where the three dominant hoppings are: $t_{100}^{dd}=t_{010}^{dd}=0.369$, $t_{002}^{ss}=0.286$ and $t_{001}^{ss}=0.208$ (all in eV). The large kinetic exchange $t_{00z}^{ss}$ along the z-axis is due to its mixing character of Nd$\left(5d_{3z^2-r^2}\right)$ and the interstitial s. The d-s hybridization is fairly small compared to intra-orbital hoppings. The crystal-field splitting obtained from the Wannier projections is ${ϵ}_d=0.270$ eV and ${ϵ}_s=1.510$ eV, respectively. The Coulomb interaction is as follows [27,28]:

$$\begin{array}{cc}\hfill H_{\mathrm{int}}& =\sum _{m\alpha }{U}_{\alpha }{n}_{m\alpha \uparrow }{n}_{m\alpha \downarrow },\hfill \end{array}$$

(5)

where $\alpha =d,s$ orbitals. $n_{m\mu \sigma }$ is a density operator at site m orbital $\mu$ with spin $\sigma$. In the two-orbital model, as shown in Figure 1a, the s orbital is spatially shifted by $(0.5,0.5,0.5)$. Here, we consider only the on-site Coulomb interaction, i.e., $U_d=3.26$ eV and $U_s=0.76$ eV. The calculation of $U_d$ and $U_s$ was carried out by using the constrained random phase approximation (cRPA) [29,30], as implemented in the Respack code (details of the cRPA framework can be found in Refs. [22,23]). The computational details are the following: We consider 100 bands, a planewave cutoff energy of 8 Ry for the cRPA polarization and the same 8 × 8 × 8 k-point grid as that in the Wannier projection. The Hund’s couplings between the two-orbitals at each site are smaller and are neglected in our two-band model. In (ii), the one-orbital model considers only the d orbital; it is obtained by taking the above-defined effective Hamiltonian for the two-orbital model and removing all effective parameters that involve the s orbital.

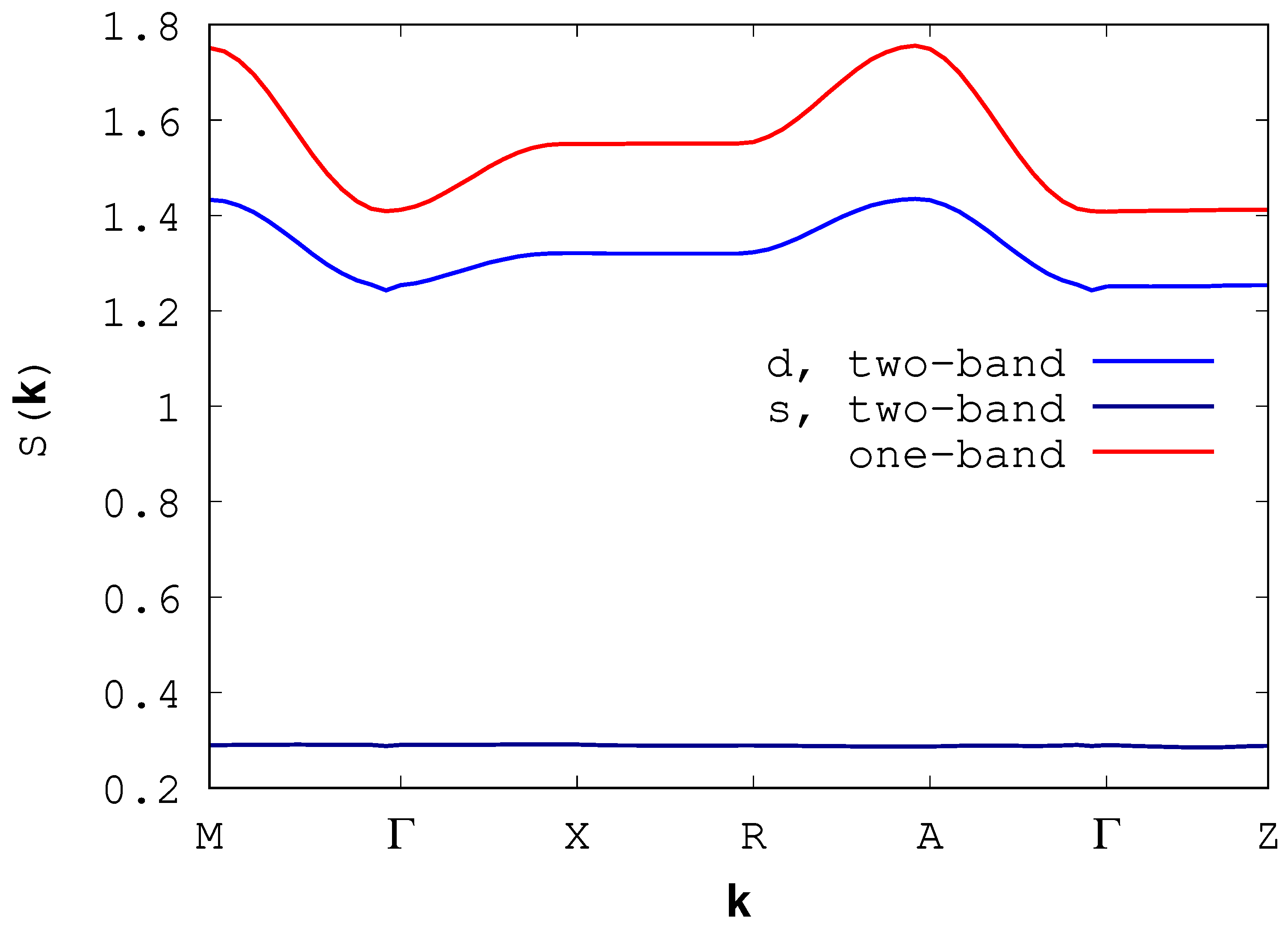
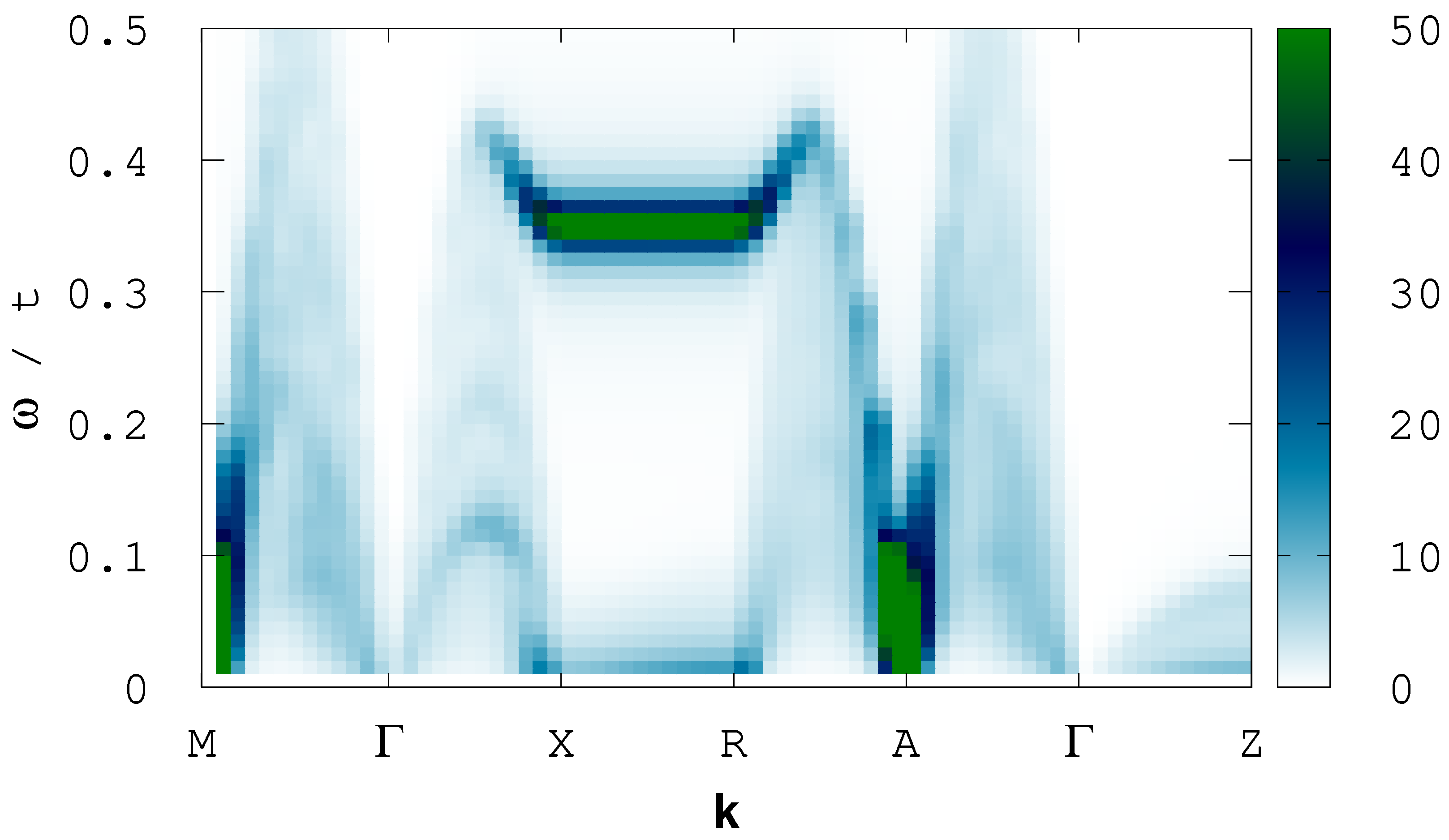
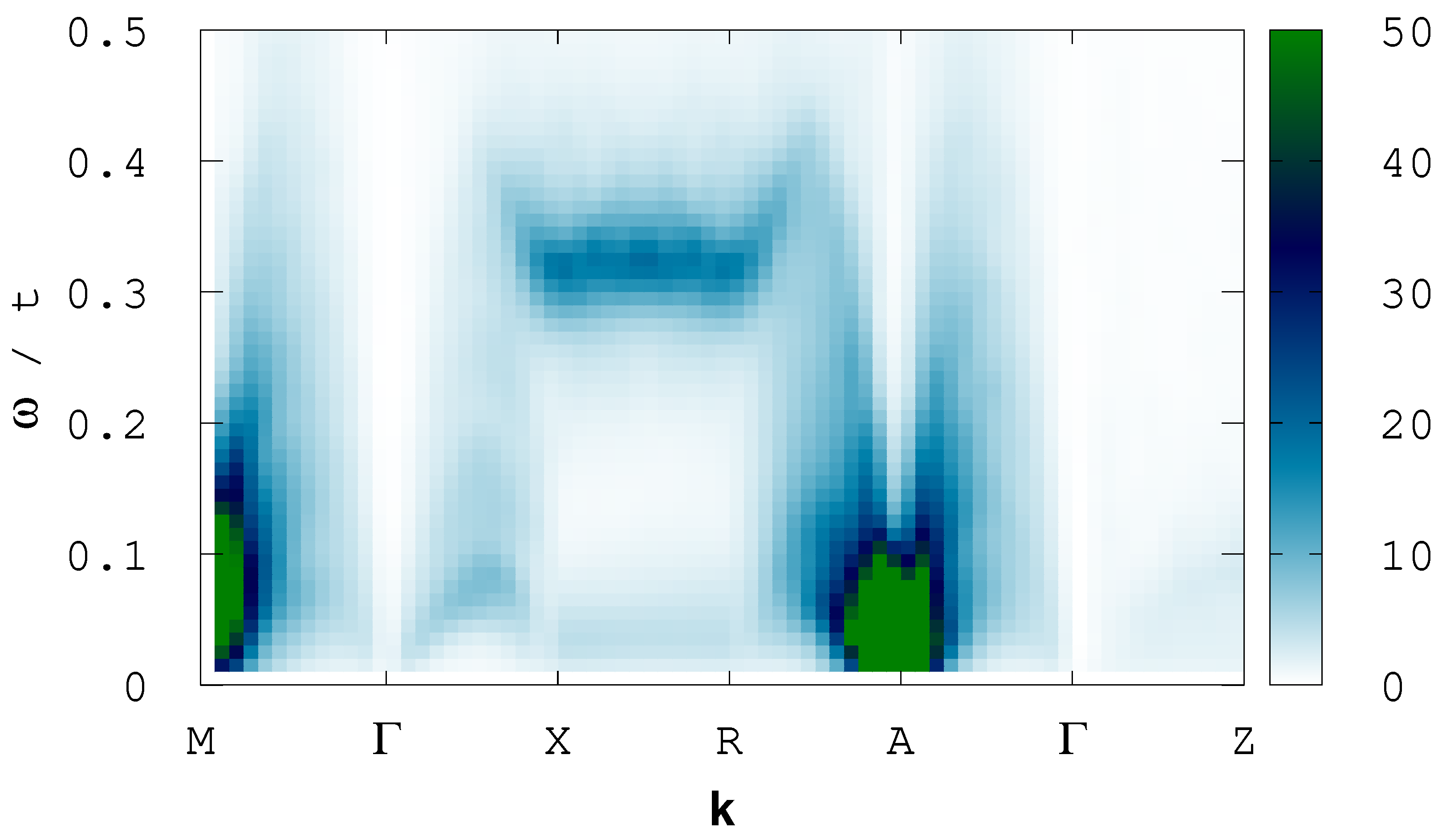
3. Results and Discussion

The static structure factor $S(\overrightarrow{k})$ (9) is shown in Figure 2 in the PM state at high temperatures along a high-symmetry path through the first Brillouin zone. The results are shown both for the two-band model and for the one-band model defined in Section 2. In the two-band model, the signal coming from the d-band is much stronger than that coming from the s-band, which can already be explained by the different band fillings. Moreover, the modulation is much more pronounced for the d-band, which reflects the stronger correlations in these states. The results for the s-band show quite good agreement with those of the d band.

Figure 2. Static spin-structure factor $S(\overrightarrow{k})$ for the PM phase at high temperatures for the two-band model (blue and black) and for the one-band model (red). The special points are as in Figure 1.

The structure factor $S(\overrightarrow{k})$ is shown along a high-symmetry path, and we have verified that at $(\pi ,\pi ,\pi )$, i.e., at the A-point, we have indeed found the global maximum. A two-site unit cell can, thus, be expected to capture the magnetic pattern. We, therefore, use a corresponding mean-field Ansatz and indeed find a magnetic ordering transition. This does not reflect the physics of infinite-layer nickelate superconductors but is likely an artifact of the mean-field approach used here.

The structure factor obtained for M = $(\pi ,\pi ,0)$ corresponds here to C-type magnetic order, i.e., to C-AFM order. In contrast, at the A = $(\pi ,\pi ,\pi )$ point, we find an AFM order of G-type, with magnetization alternation in every cubic direction. Both AFM orders are of very similar amplitude. In the uncorrelated two-band model, the M point shows the slightly stronger overall signal; however, the d-band prefers the A point already without interaction. When temperature is lowered towards the magnetic transition, the contributions of the d states are stronger enhanced, so that the signal at the M point finally dominates. Thus, we conclude that the present models prefer G-type alternating magnetic ordering over C-type. However, this preference is weak, so that relatively small additions to the present two-band model can be expected to promote C-type tendencies. In contrast, the in-plane component of the magnetic correlations is clearly peaked at the M point. The magnetic interactions are, thus, rather 2D in both the two-band and the single-band models. This can be explained by the predominantly in-plane hoppings within the d-band.

While the actual materials do not show long-range magnetic order, short-range correlations are present, which the mean-field approximation is unable to capture. Accordingly, magnetic excitations are magnon-like and somewhat similar to those found in cuprates [31,32]. However, the weak-coupling approach used here cannot model localized magnetic moments without long-range magnetic order and this cannot treat short-range magnetic correlations. We, therefore, investigate the ordered state as a proxy for the one with shorter-ranged correlations.

The magnetic excitation spectrum $S(\overrightarrow{k},\omega )$ obtained in the low-temperature AFM phase of the one-band and two-band models are shown in Figure 3 and Figure 4, respectively. We see the magnetic Bragg peak emerge at $(\pi ,\pi ,\pi )$ and $\omega \to 0$. At $(\pi ,\pi ,0)$ and $\omega \approx 0.08\mathrm{eV}$, the high intensity reflects the competing—but loosing—ordering tendency. In addition to these peaks, we find low-energy magnon-like modes with an in-plane dispersion in both models, see Figure 3 and Figure 4. These magnon-like modes are damped, which is likely due to hole doping of the correlated d band. Similar models were also observed in experiments at energies $\omega \approx 0.1\mathrm{eV}$ [31,32]. There is, thus, good agreement between the experiment and the present one-band model and qualitative agreement with the two-band model.

Figure 3. Dynamic spin-structure factor $S(\overrightarrow{k},\omega )$ in the AFM phase of the single-band model, at $\beta =10$ below the mean-field ordering temperature. Special points as in Figure 1.

Figure 4. Dynamic spin-structure factor $S(\overrightarrow{k},\omega )$ in the AFM phase of the two-band model at $\beta =2$ below the mean-field ordering temperature. Special points as in Figure 1. The state is unstable at $\beta =10$.

The energies of magnetic states are rather close—for instance, DFT using the dynamical mean field theory (DFT+DMFT) approach [33] gives the paramagnetic ground state with the lowest energy, followed by C-AFM with energy higher by 20 meV/atom, and G-AFM with energy higher by 105 meV/atom. The C-AFM state has parallel spins along the c axis, while G-AFM phase has antiparallel spin alignment to its nearest neighbor in all directions.

Figure 5 shows the band structure of the two-band model. Panel (a) shows uncorrelated bands, which do not depend on temperature. The two colors refer to orbital character, and we see the small hybridization between the bands: Each band is overwhelmingly of one character, with only a little orbital mixing along the $\mathrm{\Gamma }$-X direction. The correlated bands at temperature $T=0.01\mathrm{eV}$ are given in Figure 5b. The correlations broaden both bands in the electronic structure. The d-band becomes gapped, while the s band remains ungapped but splits into two along the path shown in the $\overrightarrow{k}$-space. Even though magnetic correlations dominate in the d states, the s band also reflects magnetic ordering, and we notice some backfolding of the A = $(\pi ,\pi ,\pi )$ point towards the $\mathrm{\Gamma }$-point. The infinite-layer nickelate, thus, combines localized and itinerant aspects.

Figure 5. One-particle spectral density $A(\overrightarrow{k},\omega )$ for the two-band model at $\beta =100$. (a) shows results without correlations and (b) with on-site interactions included and in the AFM phase. Blue and red refer to the s- and d bands, respectively.

4. Materials and Methods

We discuss here the static and dynamic spin-structure factors, as well as the one-particle Green’s functions. The latter are obtained in Hartree–Fock mean-field theory and are for the one-site unit cell above the ordering transition given by the band structure. In a two-site unit cell, where the Brillouin zone is folded in half, we continue to show results for the first Brillouin zone of the one-site unit cell for easier comparison. (This corresponds to the first two Brillouin zones in the reduced-zone scheme.) The orbital-resolved weights’ spectral densities are thus given by

$$\begin{array}{c}\hfill A^{\alpha }(\overrightarrow{k},\omega )=\sum _{\sigma ,\nu }\delta (\omega -{ϵ}_{\alpha ,\nu ,\overrightarrow{k}}){\left|\sum _m{\mathrm{e}}^{i\overrightarrow{k}{\overrightarrow{r}}_i}{u}_{\sigma ,\nu ,\overrightarrow{k},i}^{\alpha }\right|}^2.\end{array}$$

(6)

Band $\nu$, spin $\sigma$ and momentum $\overrightarrow{k}$ are good quantum numbers defining the one-electron states in the bands. Component $u_{\sigma ,\nu ,\overrightarrow{k},m}^{\alpha }$ corresponds to orbital $\alpha =s,d$ and then refers to the orbital weight determining the matrix element. Sublattice index m runs over the one or two sites of one unit cell and ${\overrightarrow{r}}_m$ refers to the intra-unit-cell distances.

Magnetism is tracked through transverse spin susceptibilities,

$$\begin{array}{c}\hfill {\chi }^{\mu ,\nu }(\overrightarrow{k},i{\omega }_n)=\frac{1}{N}{\int }_0^{\beta }\mathrm{d}\tau {\mathrm{e}}^{i{\omega }_n\tau }⟨T_{\tau }{S}_{\mu }^{+}(\overrightarrow{k},\tau )S_{\nu }^{-}(-\overrightarrow{k},\tau )⟩,\end{array}$$

(7)

where $\mu$ and $\nu$ refer to the orbital, ${\omega }_n$ is the Matsubara frequency, and $T_{\tau }$ is the time-order operator. The spin raising operator

$$\begin{array}{c}\hfill S_{\mu }^{+}(\overrightarrow{k})=\frac{1}{\sqrt{N}}\sum _{m=1}^N{\mathrm{e}}^{i\overrightarrow{k}{\overrightarrow{r}}_m}{a}_{m,\alpha ,\uparrow }^{†}{a}_{m,\alpha ,\downarrow }^{\phantom{†}},\end{array}$$

(8)

and the adjoint $S_{\nu }^{-}(-\overrightarrow{k})$ are defined as usual, with $a_{m,\alpha ,\sigma }^{†}$ ($a_{m,\alpha ,\sigma }^{\phantom{†}}$) creating (annihilating) an electron with spins $\sigma$ in orbital $\alpha =s,d$ at site m. The sum runs over all N lattice sites.

Here, we are interested in the static spin-structure factor ($\omega \to 0$), which becomes equivalent to

$$S(\overrightarrow{k})=\sum _{mn}{e}^{i\overrightarrow{k}({\overrightarrow{r}}_m-{\overrightarrow{r}}_n)}⟨{\overrightarrow{S}}_m·{\overrightarrow{S}}_n⟩$$

(9)

in an isotropic system, i.e., above the magnetic ordering transition. We also look at the retarded Green’s functions describing magnetic excitations, which are given by the analytic continuation of (7), i.e., $({\omega }_n\to \omega +i{0}^{+})$.

In order to obtain the susceptibility, we use a multi-orbital implementation of the random-phase approximation (RPA), similar to the approach used in Ref. [34]. However, we replace the ’non-interacting’ Green’s functions entering the RPA formalism by Hartree–Fock Green’s functions, as proposed in [35]. Above the ordering transition, this leads to some Hartree shifts affecting the relative energy of the two bands. This would double-count interactions to some extent, and we fix this by adjusting the crystal-field splitting so that overall band fillings remain similar to those found in DFT. Above the ordering transition, this largely reduces the Hartree–Fock bands to the non-interacting ones. However, we can in this way include magnetically ordered states where bands become different from non-interacting ones. Such an approach has been used to reproduce magnetic excitations observed by inelastic neutron scattering in ${\mathrm{La}}_2{\mathrm{CuO}}_4$ from a single-band Hubbard model [17]. This previous success in a strongly correlated system leads us to expect insights also for the case of nickelates, even though a weak-coupling treatment may not a priori appear justified.

Finally, we remark on the role played by Nd($4f$) electronic states. We suggest that instead of them, the empty Nd($5d$) orbitals may model the striking electron pocket at the $\mathrm{\Gamma }$ point in the band structure [7]. In such an effective model, the rare-earth atoms are included into Ni atoms via s orbital, indicating the model is three-dimensional, and the Coulomb interaction, as well as Hund’s coupling, need to be screened. For instance, the two electrons occupying an s orbital could be located either at Nd or at Ni atom. Therefore, the Coulomb repulsion between these two electrons within the s orbital is reduced. We introduce a parameter $\alpha \in [0,1]$ to represent the reduced Coulomb interaction and Hund’s coupling, i.e., $U_2=\alpha U_1$ and $J=\alpha J_H$. $\alpha =1\left(0\right)$ stands for the weak (strong) screening effect from rare-earth atoms; more details were given in Ref. [11], and we do not repeat them here. We study the effective two-band model via the Lanczos algorithm [11,36] on a $2\times 2\times 2$ unit cell.

5. Summary and Conclusions

In summary, we have investigated and compared magnetism in two effective models for the infinite-layer nickelate superconductor NdNiO${}_2$. One model includes both bands found near the Fermi surface, one of d character (with a large $x^2-y^2$ contribution from Ni ions) and the other one of s character (with large rare-earth weight and centered between Ni ions). We only keep on-site interactions here, which are intra-orbital, since the d and s orbitals are spatially separated here.

We then used a combination of Hartree–Fock mean-field theory and a multi-band multi-site implementation of the random-phase approximation to obtain spectral densities and spin-structure factors. This weak-coupling has been successfully applied to cuprates before [17], suggesting its usefulness here. While it is not able to treat states with short-range magnetic correlations, without long-range order, we were able to infer some tendencies and qualitative aspects of the short-range–correlated state observed in these materials.

We find that ordering vectors A = $(\pi ,\pi ,\pi )$ and M = $(\pi ,\pi ,0)$ closely compete, suggesting that inter-layer couplings are weak. Indeed, this can be rationalized by the fact that magnetic correlations are mostly due to the stronger correlated d bands, which have an almost exclusively 2D band structure, see the band structure on Figure 5. In the ordered state, magnetic excitations show damped in-plane magnon-like modes similar to those observed in infinite-layer nickelates.

Notably, we find here that the one-band and two-band models behave very similarly to each other, with the second band providing basically only self-doping [13]. This can be readily understood from the Hamiltonian, since the bands are only coupled via hopping hybridization, which is very small. A more complete description including long-range Coulomb interactions or coupling to the lattice might change this assessment, however.