Multiband Superconductivity in High-Pressure Sulfur Hydrides
Abstract
1. Introduction
2. The Model
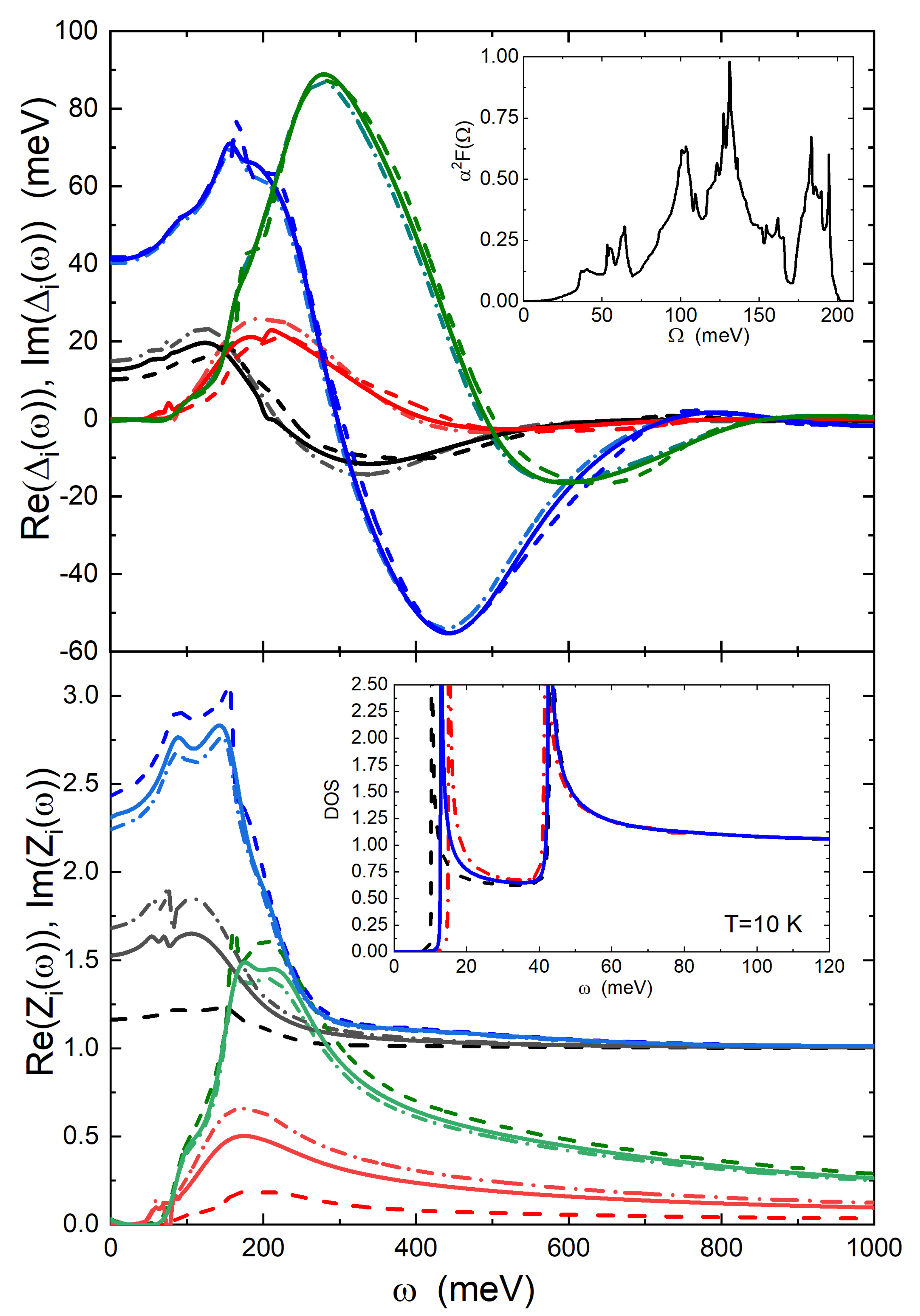
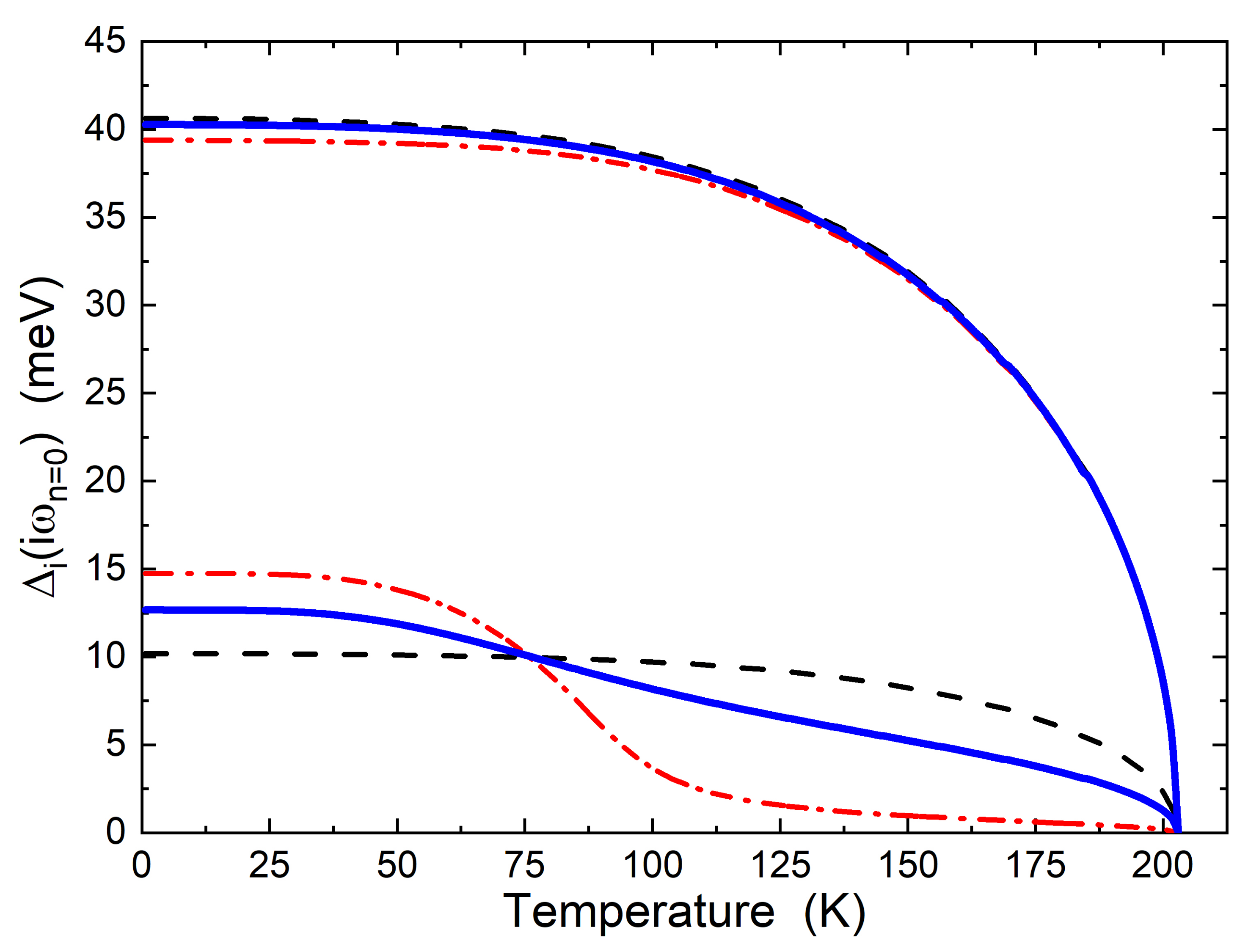
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carbotte, J.P. Properties of boson-exchange superconductors. Rev. Mod. Phys. 1990, 62, 1027. [Google Scholar] [CrossRef]
- Ummarino, G.A. Eliashberg Theory. In Emergent Phenomena in Correlated Matter; Pavarini, E., Koch, E., Schollwöck, U., Eds.; Forschungszentrum Jülich GmbH and Institute for Advanced Simulations: Jülich, Germany, 2013; pp. 13.1–13.36. [Google Scholar]
- Hafstrom, J.W.; MacVicar, M.L.A. Case for a second energy gap in superconducting niobium. Phys. Rev. B 1970, 2, 4511. [Google Scholar] [CrossRef]
- Bianconi, A.; Valletta, A.; Perali, A.; Saini, N.L. Superconductivity of a striped phase at the atomic limit. Phys. C Supercond. 1998, 296, 269–280. [Google Scholar] [CrossRef]
- Nagamatsu, J.; Nakagawa, N.; Muranaka, T.; Zenitani, Y.; Akimitsu, J. Superconductivity at 39 K in magnesium diboride. Nature 2001, 410, 63–64. [Google Scholar] [CrossRef]
- Ummarino, G.A.; Gonnelli, R.S.; Massidda, S.; Bianconi, A. Two-band Eliashberg equations and the experimental Tc of the diboride Mg1-xAlxB2. Phys. C 2004, 407, 121–127. [Google Scholar] [CrossRef][Green Version]
- Daghero, D.; Calzolari, A.; Ummarino, G.A.; Tortello, M.; Gonnelli, R.S.; Stepanov, V.A.; Tarantini, C.; Manfrinetti, P.; Lehmann, E. Point-contact spectroscopy in neutron-irradiated M11B2. Phys. Rev. B 2006, 74, 174519. [Google Scholar] [CrossRef]
- Innocenti, D.; Caprara, S.; Poccia, N.; Ricci, A.; Valletta, A.; Bianconi, A. Shape resonance for the anisotropic superconducting gaps near a Lifshitz transition: The effect of electron hopping between layers. Supercond. Sci. Technol. 2010, 24, 015012. [Google Scholar] [CrossRef]
- Innocenti, D.; Poccia, N.; Ricci, A.; Valletta, A.; Caprara, S.; Perali, A.; Bianconi, A. Resonant and crossover phenomena in a multiband superconductor: Tuning the chemical potential near a band edge. Phys. Rev. B 2010, 82, 184528. [Google Scholar] [CrossRef]
- Kamihara, Y.; Watanabe, T.; Hirano, M.; Hosono, H. Iron-Based Layered Superconductor La[O1-xFx]FeAs(x=0.05-0.12) with Tc=26 K. J. Am. Chem. Soc. 2008, 130, 3296–3297. [Google Scholar] [CrossRef]
- Bianconi, A. Shape resonances in superstripes. Nat. Phys. 2013, 9, 536–537. [Google Scholar] [CrossRef]
- Gonnelli, R.S.; Calzolari, A.; Daghero, D.; Natale, L.; Ummarino, G.A.; Stepanov, V.A.; Ferretti, M. Evidence for pseudogap and phase-coherence gap separation by Andreev reflection experiments in Au/La2-xSrxCuO4 point-contact junctions. Eur. Phys. J. B 2001, 22, 411–414. [Google Scholar] [CrossRef][Green Version]
- Ashcroft, N. Metallic hydrogen: A high-temperature superconductor? Phys. Rev. Lett. 1968, 21, 1748. [Google Scholar] [CrossRef]
- Ashcroft, N. Hydrogen dominant metallic alloys: High temperature superconductors? Phys. Rev. Lett. 2004, 92, 187002. [Google Scholar] [CrossRef] [PubMed]
- Duan, D.; Liu, Y.; Tian, F.; Li, D.; Huang, X.; Zhao, Z.; Yu, H.; Liu, B.; Tian, W.; Cui, T. Pressure-induced metallization of dense (H2S)2H2 with high-Tc superconductivity. Sci. Rep. 2014, 4, 6968. [Google Scholar] [CrossRef]
- Drozdov, A.; Eremets, M.; Troyan, I.; Ksenofontov, V.; Shylin, S. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 2015, 525, 73–76. [Google Scholar] [CrossRef]
- Bianconi, A.; Jarlborg, T. Lifshitz transitions and zero point lattice fluctuations in sulfur hydride showing near room temperature superconductivity. Nov. Supercond. Mater. 2015, 1, 37. [Google Scholar] [CrossRef]
- Purans, J.; Menushenkov, A.P.; Besedin, S.P.; Ivanov, A.A.; Minkov, V.S.; Pudza, I.; Kuzmin, A.; Klementiev, K.V.; Pascarelli, S.; Mathon, O.; et al. Local electronic structure rearrangements and strong anharmonicity in YH3 under pressures up to 180 GPa. Nat. Commun. 2021, 12, 1765. [Google Scholar] [CrossRef]
- Gorkov, L.P.; Kresin, V.Z. Colloquium: High pressure and road to room temperature superconductivity. Rev. Mod. Phys. 2018, 90, 011001. [Google Scholar] [CrossRef]
- Pickett, W.E. Colloquium: Room temperature superconductivity: The roles of theory and materials design. Rev. Mod. Phys. 2023, 95, 021001. [Google Scholar] [CrossRef]
- Jarlborg, T.; Bianconi, A. Breakdown of the Migdal approximation at Lifshitz transitions with giant zero-point motion in the H3S superconductor. Sci. Rep. 2016, 6, 24816. [Google Scholar] [CrossRef]
- Mozaffari, S.; Sun, D.; Minkov, V.S.; Drozdov, A.P.; Knyazev, D.; Betts, J.B.; Einaga, M.; Shimizu, K.; Eremets, M.I.; Balicas, L.; et al. Superconducting phase diagram of H3S under high magnetic fields. Nat. Commun. 2019, 10, 2522. [Google Scholar] [CrossRef]
- Eremets, M.I. Communication in “Superconductivity in superhydrides. New developments”. In Proceedings of the SUPERSTRIPES 2023 Conference, Ischia, Italy, 25 June–1 July 2023. [Google Scholar]
- Ummarino, G.A.; Tortello, M.; Daghero, D.; Gonnelli, R.S. Three-band s± Eliashberg theory and the superconducting gaps of iron pnictides. Phys. Rev. B 2009, 80, 172503. [Google Scholar] [CrossRef]
- Ghigo, G.; Gozzelino, G.A.U.L.; Tamegai, T. Penetration depth of Ba1-xKxFe2As2 single crystals explained within a multiband Eliashberg s± approach. Phys. Rev. B 2017, 96, 014501. [Google Scholar] [CrossRef]
- Torsello, D.; Ummarino, G.A.; Gozzelino, L.; Tamegai, T.; Ghigo, G. Comprehensive Eliashberg analysis of microwave conductivity and penetration depth of K-, Co-, and P-substituted BaFe2As2. Phys. Rev. B 2019, 99, 134518. [Google Scholar] [CrossRef]
- Ummarino, G.A.; Gonnelli, R.S. Breakdown of Migdal’s theorem and intensity of electron-phonon coupling in high-Tc superconductors. Phys. Rev. B 1997, 56, R14279. [Google Scholar] [CrossRef]
- Daghero, D.; Calzolari, A.; Delaude, D.; Gonnelli, R.S.; Tortello, M.; Ummarino, G.A.; Stepanov, V.A.; Zhigadlo, N.D.; Karpinski, J.; Putti, M. Point-contact study of the role of non-magnetic impurities and disorder in the superconductivity of MgB2. Phys. C 2007, 460–462, 975–976. [Google Scholar] [CrossRef]
- Villa-Cortés, S.; De la Peña-Seaman, O. Effect of van Hove singularity on the isotope effect and critical temperature of H3S hydride superconductor as a function of pressure. J. Phys. Chem. Solids 2022, 161, 110451. [Google Scholar] [CrossRef]
- Cappelluti, E.; Grimaldi, C.; Pietronero, L.; Strassler, S.; Ummarino, G.A. Superconductivity of Rb3C60: Breakdown of the Migdal-Eliashberg theory. Eur. Phys. J. B 2001, 21, 383–391. [Google Scholar] [CrossRef][Green Version]
- Ummarino, G.A.; Gonnelli, R.S. Possible explanation of electric-field-doped C60 phenomenology in the framework of Eliashberg theory. Phys. Rev. B 2002, 66, 104514. [Google Scholar] [CrossRef]
- Mansor, M.; Carbotte, J.P. Upper critical field in two-band superconductivity. Phys. Rev. B 2005, 72, 024538. [Google Scholar] [CrossRef]
- Ummarino, G.A.; Tortello, M.; Daghero, D.; Gonnelli, R.S. Predictions of multiband s±strong-coupling Eliashberg theory compared to experimental data in iron pnictides. J. Supercond. Nov. Magn. 2011, 24, 247–253. [Google Scholar] [CrossRef]
- Mazziotti, M.V.; Raimondi, R.; Valletta, A.; Campi, G.; Bianconi, A. Spin–orbit coupling controlling the superconducting dome of artificial superlattices of quantum wells. J. Appl. Phys. 2022, 132, 193908. [Google Scholar] [CrossRef]
- Mazziotti, M.V.; Jarlborg, T.; Bianconi, A.; Valletta, Q. Room temperature superconductivity dome at a Fano resonance in superlattices of wires. Europhys. Lett. 2021, 134, 17001. [Google Scholar] [CrossRef]
- Vittorini-Orgeas, A.; Bianconi, A. From Majorana theory of atomic autoionization to Feshbach resonances in high temperature superconductors. J. Supercond. Nov. Magn. 2009, 22, 215–221. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ummarino, G.A.; Bianconi, A. Multiband Superconductivity in High-Pressure Sulfur Hydrides. Condens. Matter 2023, 8, 69. https://doi.org/10.3390/condmat8030069
Ummarino GA, Bianconi A. Multiband Superconductivity in High-Pressure Sulfur Hydrides. Condensed Matter. 2023; 8(3):69. https://doi.org/10.3390/condmat8030069
Chicago/Turabian StyleUmmarino, Giovanni Alberto, and Antonio Bianconi. 2023. "Multiband Superconductivity in High-Pressure Sulfur Hydrides" Condensed Matter 8, no. 3: 69. https://doi.org/10.3390/condmat8030069
APA StyleUmmarino, G. A., & Bianconi, A. (2023). Multiband Superconductivity in High-Pressure Sulfur Hydrides. Condensed Matter, 8(3), 69. https://doi.org/10.3390/condmat8030069






