Superconducting Diode Effect in Topological Hybrid Structures
Abstract
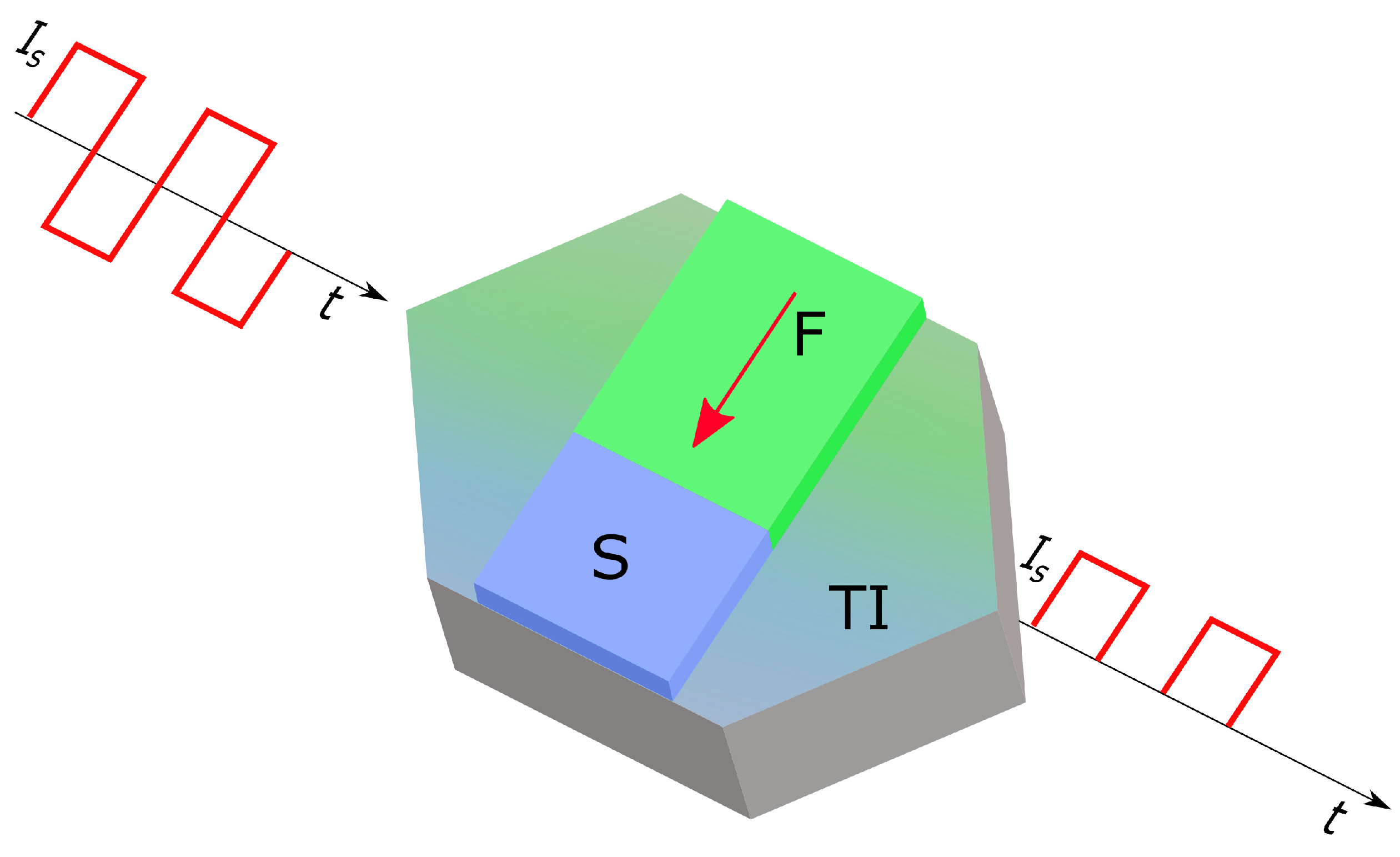
1. Introduction
2. Materials and Methods
2.1. Nonlinear Usadel Equations
2.2. Linear Usadel Equations
Single-Mode Approximation
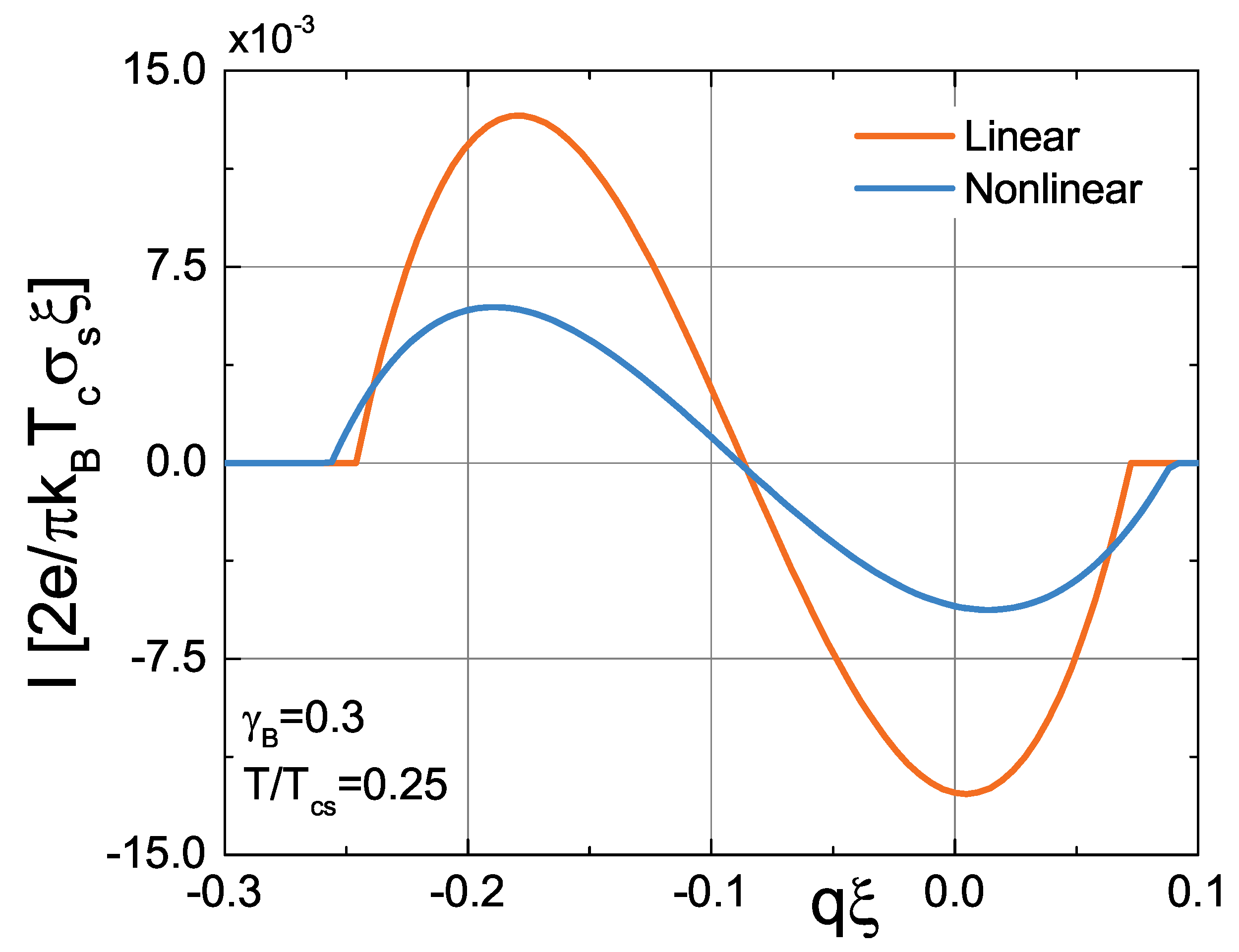
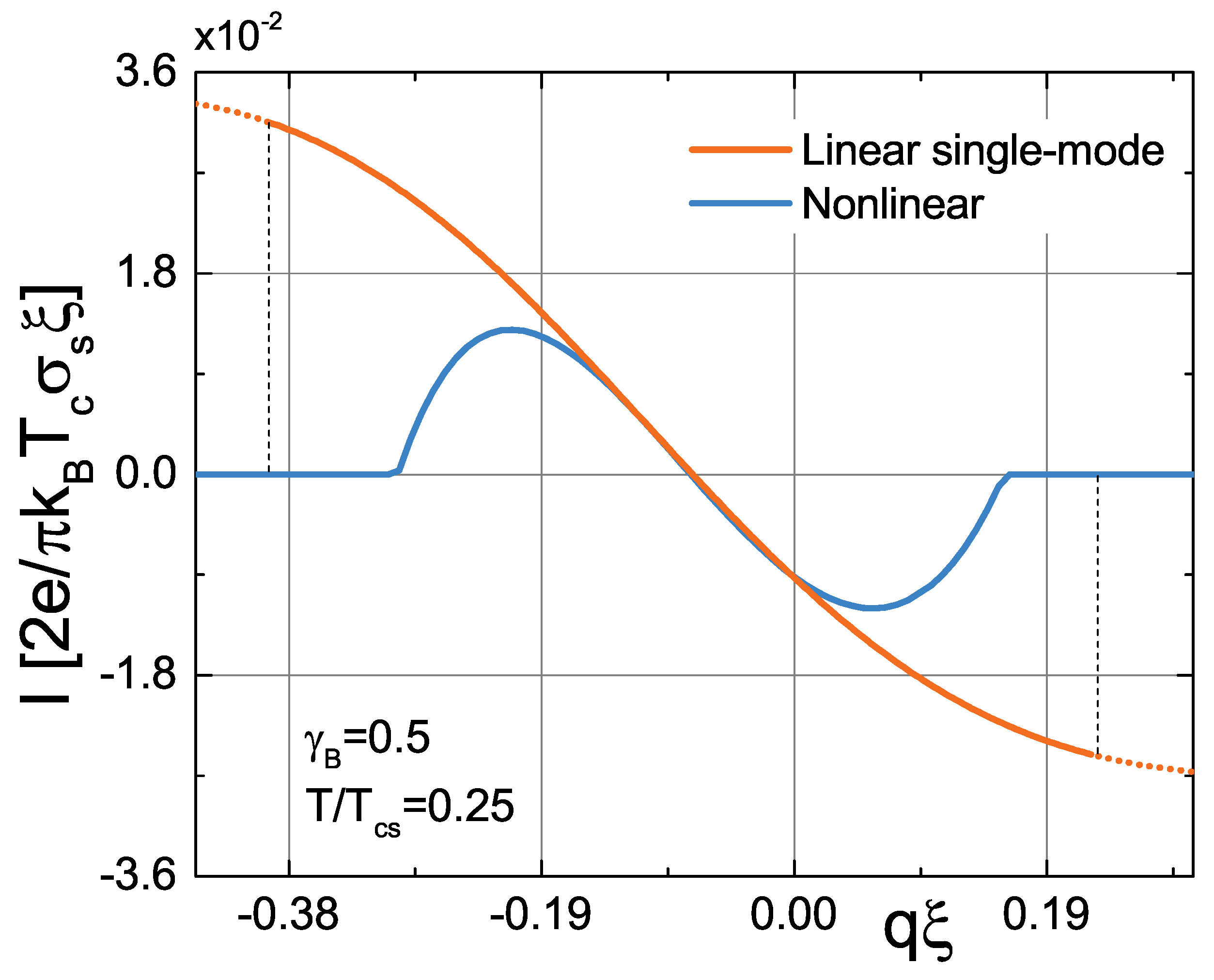
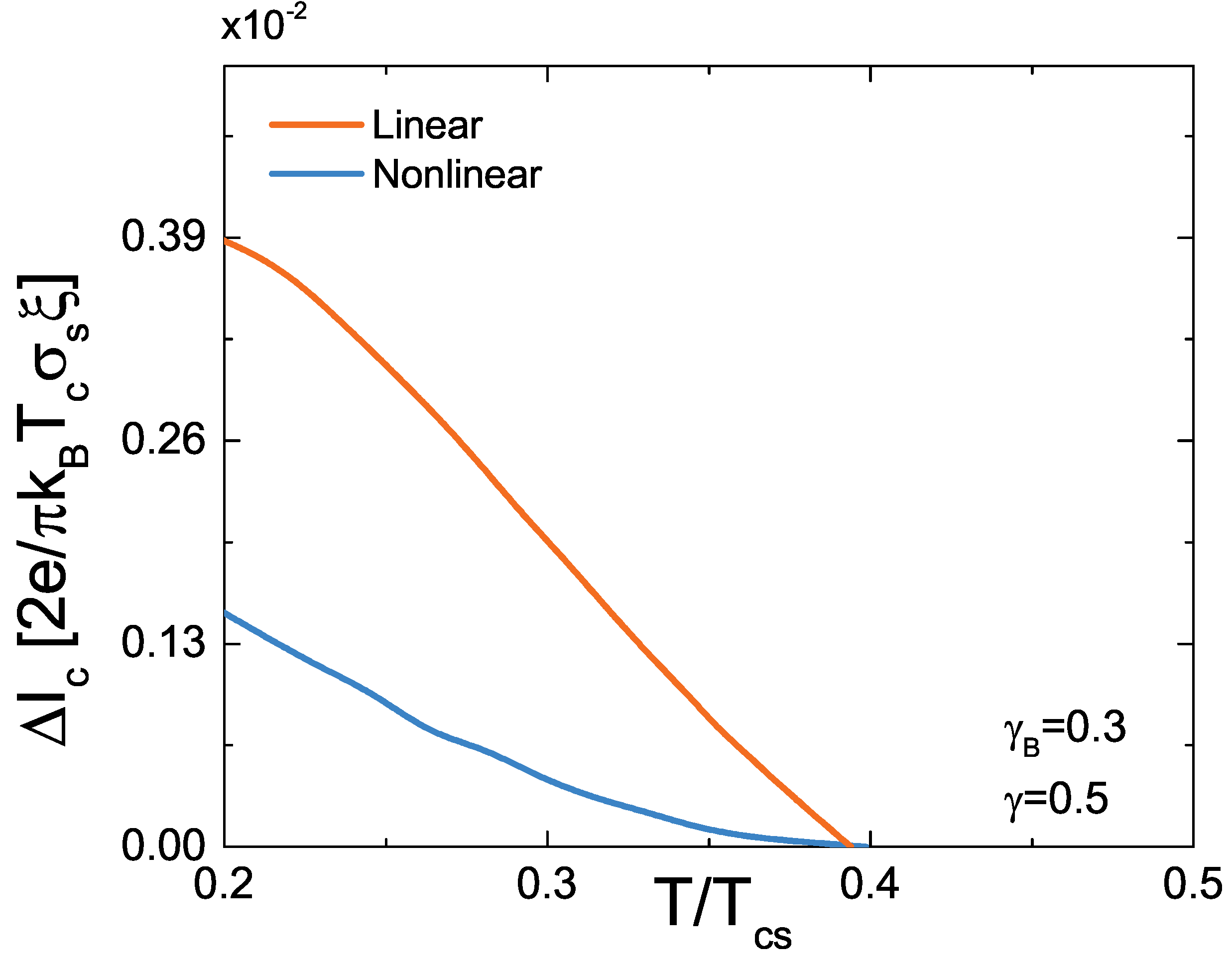
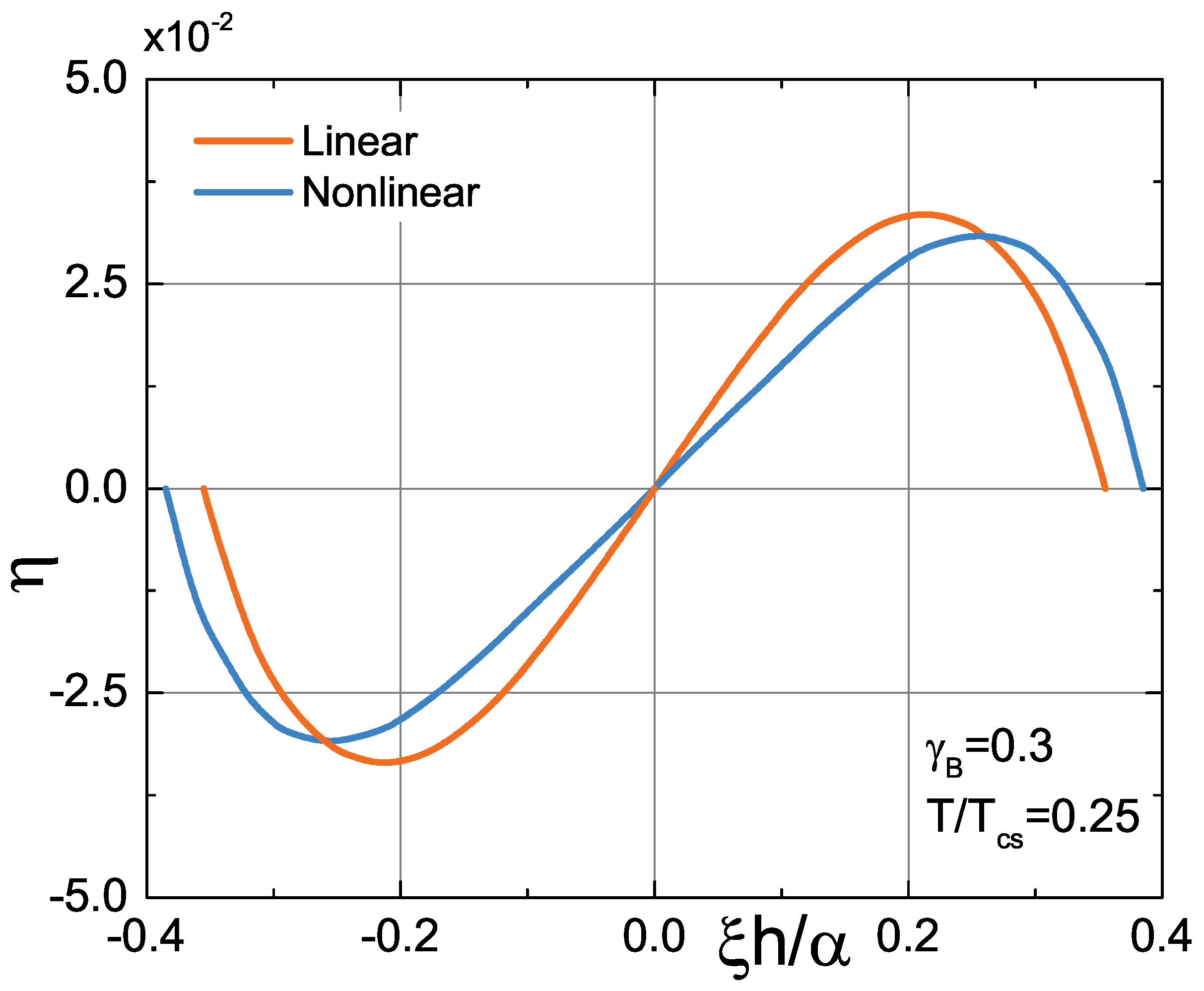
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SDE | Superconducting diode effect |
| SOC | Spin–orbit coupling |
| S | Superconductor |
| F | Ferromagnetic material |
| TI | Topological insulator |
References
- Buzdin, A.I. Proximity effects in superconductor-ferromagnet heterostructures. Rev. Mod. Phys. 2005, 77, 935–976. [Google Scholar] [CrossRef]
- Golubov, A.A.; Kupriyanov, M.Y.; Il’ichev, E. The current-phase relation in Josephson junctions. Rev. Mod. Phys. 2004, 76, 411–469. [Google Scholar] [CrossRef]
- Bergeret, F.S.; Volkov, A.F.; Efetov, K.B. Odd triplet superconductivity and related phenomena in superconductor-ferromagnet structures. Rev. Mod. Phys. 2005, 77, 1321–1373. [Google Scholar] [CrossRef]
- Demler, E.A.; Arnold, G.B.; Beasley, M.R. Superconducting proximity effects in magnetic metals. Phys. Rev. B 1997, 55, 15174–15182. [Google Scholar] [CrossRef]
- Ozaeta, A.; Vasenko, A.S.; Hekking, F.W.J.; Bergeret, F.S. Andreev current enhancement and subgap conductance of superconducting SFN hybrid structures in the presence of a small spin-splitting magnetic field. Phys. Rev. B 2012, 86, 060509. [Google Scholar] [CrossRef]
- Bergeret, F.S.; Tokatly, I.V. Singlet-Triplet Conversion and the Long-Range Proximity Effect in Superconductor-Ferromagnet Structures with Generic Spin Dependent Fields. Phys. Rev. Lett. 2013, 110, 117003. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L. Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Phys. Rev. Lett. 2008, 100, 096407. [Google Scholar] [CrossRef]
- Stanescu, T.D.; Sau, J.D.; Lutchyn, R.M.; Das Sarma, S. Proximity effect at the superconductor–topological insulator interface. Phys. Rev. B 2010, 81, 241310. [Google Scholar] [CrossRef]
- Black-Schaffer, A.M. Self-consistent superconducting proximity effect at the quantum spin Hall edge. Phys. Rev. B 2011, 83, 060504. [Google Scholar] [CrossRef]
- Yano, R.; Hirose, H.T.; Tsumura, K.; Yamamoto, S.; Koyanagi, M.; Kanou, M.; Kashiwaya, H.; Sasagawa, T.; Kashiwaya, S. Proximity-Induced Superconducting States of Magnetically Doped 3D Topological Insulators with High Bulk Insulation. Condens. Matter 2019, 4, 9. [Google Scholar] [CrossRef]
- Romano, P.; Polcari, A.; Cirillo, C.; Attanasio, C. Drag Voltages in a Superconductor/Insulator/Ferromagnet Trilayer. Materials 2021, 14, 7575. [Google Scholar] [CrossRef] [PubMed]
- Soloviev, I.I.; Klenov, N.V.; Bakurskiy, S.V.; Kupriyanov, M.Y.; Gudkov, A.L.; Sidorenko, A.S. Beyond Moore’s technologies: Operation principles of a superconductor alternative. Beilstein J. Nanotechnol. 2017, 8, 2689–2710. [Google Scholar] [CrossRef] [PubMed]
- Chernodub, M.N.; Garaud, J.; Kharzeev, D.E. Chiral Magnetic Josephson Junction as a Base for Low-Noise Superconducting Qubits. Universe 2022, 8, 657. [Google Scholar] [CrossRef]
- Soloviev, I.I.; Schegolev, A.E.; Klenov, N.V.; Bakurskiy, S.V.; Kupriyanov, M.Y.; Tereshonok, M.V.; Shadrin, A.V.; Stolyarov, V.S.; Golubov, A.A. Adiabatic superconducting artificial neural network: Basic cells. J. Appl. Phys. 2018, 124, 152113. [Google Scholar] [CrossRef]
- Gordeeva, A.V.; Pankratov, A.L.; Pugach, N.G.; Vasenko, A.S.; Zbrozhek, V.O.; Blagodatkin, A.V.; Pimanov, D.A.; Kuzmin, L.S. Record electron self-cooling in cold-electron bolometers with a hybrid superconductor-ferromagnetic nanoabsorber and traps. Sci. Rep. 2020, 10, 21961. [Google Scholar] [CrossRef]
- Ozaeta, A.; Vasenko, A.S.; Hekking, F.W.J.; Bergeret, F.S. Electron cooling in diffusive normal metal–superconductor tunnel junctions with a spin-valve ferromagnetic interlayer. Phys. Rev. B 2012, 85, 174518. [Google Scholar] [CrossRef]
- Kawabata, S.; Ozaeta, A.; Vasenko, A.S.; Hekking, F.W.; Bergeret, F.S. Efficient electron refrigeration using superconductor/spin-filter devices. Appl. Phys. Lett. 2013, 103, 032602. [Google Scholar] [CrossRef]
- Neilo, A.; Bakurskiy, S.; Klenov, N.; Soloviev, I.; Kupriyanov, M. Superconducting Valve Exploiting Interplay between Spin-Orbit and Exchange Interactions. Nanomaterials 2022, 12, 4426. [Google Scholar] [CrossRef] [PubMed]
- Nadeem, M.; Fuhrer, M.S.; Wang, X. Superconducting Diode Effect–Fundamental Concepts, Material Aspects, and Device Prospects. arXiv 2023, arXiv:2301.13564. [Google Scholar]
- Houzet, M.; Meyer, J.S. Quasiclassical theory of disordered Rashba superconductors. Phys. Rev. B 2015, 92, 014509. [Google Scholar] [CrossRef]
- Ando, F.; Miyasaka, Y.; Li, T.; Ishizuka, J.; Arakawa, T.; Shiota, Y.; Moriyama, T.; Yanase, Y.; Ono, T. Observation of superconducting diode effect. Nature 2020, 584, 373–376. [Google Scholar] [CrossRef] [PubMed]
- Bauriedl, L.; Bäuml, C.; Fuchs, L.; Baumgartner, C.; Paulik, N.; Bauer, J.M.; Lin, K.Q.; Lupton, J.M.; Taniguchi, T.; Watanabe, K.; et al. Supercurrent diode effect and magnetochiral anisotropy in few-layer NbSe2. Nat. Commun. 2022, 13, 4266. [Google Scholar] [CrossRef] [PubMed]
- Shin, J.; Son, S.; Yun, J.; Park, G.; Zhang, K.; Shin, Y.J.; Park, J.G.; Kim, D. Magnetic proximity-induced superconducting diode effect and infinite magnetoresistance in van der waals heterostructure. arXiv 2021, arXiv:2111.05627. [Google Scholar]
- Trahms, M.; Melischek, L.; Steiner, J.F.; Mahendru, B.; Tamir, I.; Bogdanoff, N.; Peters, O.; Reecht, G.; Winkelmann, C.B.; von Oppen, F.; et al. Diode effect in Josephson junctions with a single magnetic atom. arXiv 2022, arXiv:2212.04432. [Google Scholar] [CrossRef]
- Chahid, S.; Teknowijoyo, S.; Mowgood, I.; Gulian, A. High-frequency diode effect in superconducting Nb3Sn microbridges. Phys. Rev. B 2023, 107, 054506. [Google Scholar] [CrossRef]
- Chahid, S.; Teknowijoyo, S.; Gulian, A. Quadristor: A novel device for superconducting electronics. arXiv 2022, arXiv:2211.13340. [Google Scholar]
- Suri, D.; Kamra, A.; Meier, T.N.G.; Kronseder, M.; Belzig, W.; Back, C.H.; Strunk, C. Non-reciprocity of vortex-limited critical current in conventional superconducting micro-bridges. Appl. Phys. Lett. 2022, 121, 102601. [Google Scholar] [CrossRef]
- Daido, A.; Ikeda, Y.; Yanase, Y. Intrinsic Superconducting Diode Effect. Phys. Rev. Lett. 2022, 128, 037001. [Google Scholar] [CrossRef]
- He, J.J.; Tanaka, Y.; Nagaosa, N. A phenomenological theory of superconductor diodes. New J. Phys. 2022, 24, 053014. [Google Scholar] [CrossRef]
- Yuan, N.F.Q.; Fu, L. Supercurrent diode effect and finite-momentum superconductors. Proc. Natl. Acad. Sci. USA 2022, 119, e2119548119. [Google Scholar] [CrossRef]
- Scammell, H.D.; Li, J.I.A.; Scheurer, M.S. Theory of zero-field superconducting diode effect in twisted trilayer graphene. 2D Mater. 2022, 9, 025027. [Google Scholar] [CrossRef]
- Ilić, S.; Bergeret, F.S. Theory of the Supercurrent Diode Effect in Rashba Superconductors with Arbitrary Disorder. Phys. Rev. Lett. 2022, 128, 177001. [Google Scholar] [CrossRef]
- Devizorova, Z.; Putilov, A.V.; Chaykin, I.; Mironov, S.; Buzdin, A.I. Phase transitions in superconductor/ferromagnet bilayer driven by spontaneous supercurrents. Phys. Rev. B 2021, 103, 064504. [Google Scholar] [CrossRef]
- de Picoli, T.; Blood, Z.; Lyanda-Geller, Y.; Väyrynen, J.I. Superconducting diode effect in quasi-one-dimensional systems. arXiv 2023, arXiv:2302.04277. [Google Scholar]
- Grein, R.; Eschrig, M.; Metalidis, G.; Schön, G. Spin-Dependent Cooper Pair Phase and Pure Spin Supercurrents in Strongly Polarized Ferromagnets. Phys. Rev. Lett. 2009, 102, 227005. [Google Scholar] [CrossRef] [PubMed]
- Lu, B.; Ikegaya, S.; Burset, P.; Tanaka, Y.; Nagaosa, N. Tunable Josephson diode effect on the surface of topological insulators. arXiv 2023, arXiv:2211.10572. [Google Scholar]
- Kokkeler, T.H.; Golubov, A.A.; Bergeret, F.S. Field-free anomalous junction and superconducting diode effect in spin-split superconductor/topological insulator junctions. Phys. Rev. B 2022, 106, 214504. [Google Scholar] [CrossRef]
- Karabassov, T.; Bobkova, I.V.; Golubov, A.A.; Vasenko, A.S. Hybrid helical state and superconducting diode effect in superconductor/ferromagnet/topological insulator heterostructures. Phys. Rev. B 2022, 106, 224509. [Google Scholar] [CrossRef]
- Bobkova, I.V.; Barash, Y.S. Effects of spin-orbit interaction on superconductor-ferromagnet heterostructures: Spontaneous electric and spin surface currents. J. Exp. Theor. Phys. Lett. 2004, 80, 494–499. [Google Scholar] [CrossRef]
- Mironov, S.; Buzdin, A. Spontaneous Currents in Superconducting Systems with Strong Spin-Orbit Coupling. Phys. Rev. Lett. 2017, 118, 077001. [Google Scholar] [CrossRef]
- Pershoguba, S.S.; Björnson, K.; Black-Schaffer, A.M.; Balatsky, A.V. Currents Induced by Magnetic Impurities in Superconductors with Spin-Orbit Coupling. Phys. Rev. Lett. 2015, 115, 116602. [Google Scholar] [CrossRef] [PubMed]
- Mal’shukov, A.G. Fraunhofer oscillations of the critical current at a varying Zeeman field in a spin-orbit coupled Josephson junction. Phys. Rev. B 2020, 102, 134509. [Google Scholar] [CrossRef]
- Mal’shukov, A.G. Spontaneous generation of vortices by a nonuniform Zeeman field in a two-dimensional Rashba-coupled superconductor. Phys. Rev. B 2020, 102, 144503. [Google Scholar] [CrossRef]
- Mal’shukov, A.G. Supercurrent vortices and Majorana zero modes induced by an in-plane Zeeman field on the surface of a three-dimensional topological insulator. Phys. Rev. B 2020, 101, 134514. [Google Scholar] [CrossRef]
- Qi, X.L.; Li, R.; Zang, J.; Zhang, S.C. Inducing a Magnetic Monopole with Topological Surface States. Science 2009, 323, 1184–1187. [Google Scholar] [CrossRef]
- Tanaka, Y.; Yokoyama, T.; Nagaosa, N. Manipulation of the Majorana Fermion, Andreev Reflection, and Josephson Current on Topological Insulators. Phys. Rev. Lett. 2009, 103, 107002. [Google Scholar] [CrossRef]
- Maiellaro, A.; Citro, R. Topological Edge States of a Majorana BBH Model. Condens. Matter 2021, 6, 15. [Google Scholar] [CrossRef]
- Mazziotti, M.V.; Scopigno, N.; Grilli, M.; Caprara, S. Majorana Fermions in One-Dimensional Structures at LaAlO3/SrTiO3 Oxide Interfaces. Condens. Matter 2018, 3, 37. [Google Scholar] [CrossRef]
- Maiellaro, A.; Illuminati, F.; Citro, R. Topological Phases of an Interacting Majorana Benalcazar–Bernevig–Hughes Model. Condens. Matter 2022, 7, 26. [Google Scholar] [CrossRef]
- Karabassov, T.; Golubov, A.A.; Silkin, V.M.; Stolyarov, V.S.; Vasenko, A.S. Reentrant superconductivity in proximity to a topological insulator. Phys. Rev. B 2021, 103, 224508. [Google Scholar] [CrossRef]
- Legg, H.F.; Loss, D.; Klinovaja, J. Superconducting diode effect due to magnetochiral anisotropy in topological insulators and Rashba nanowires. Phys. Rev. B 2022, 106, 104501. [Google Scholar] [CrossRef]
- Davydova, M.; Prembabu, S.; Fu, L. Universal Josephson diode effect. Sci. Adv. 2022, 8, 309. [Google Scholar] [CrossRef]
- Vasenko, A.S.; Hekking, F.W. Nonequilibrium electron cooling by NIS tunnel junctions. J. Low Temp. Phys. 2009, 154, 221–232. [Google Scholar] [CrossRef]
- Arutyunov, K.Y.; Auraneva, H.P.; Vasenko, A.S. Spatially resolved measurement of nonequilibrium quasiparticle relaxation in superconducting Al. Phys. Rev. B 2011, 83, 104509. [Google Scholar] [CrossRef]
- Arutyunov, K.Y.; Chernyaev, S.A.; Karabassov, T.; Lvov, D.S.; Stolyarov, V.S.; Vasenko, A.S. Relaxation of nonequilibrium quasiparticles in mesoscopic size superconductors. J. Phys. Condens. Matter 2018, 30, 343001. [Google Scholar] [CrossRef]
- Zyuzin, A.; Alidoust, M.; Loss, D. Josephson junction through a disordered topological insulator with helical magnetization. Phys. Rev. B 2016, 93, 214502. [Google Scholar] [CrossRef]
- Bobkova, I.V.; Bobkov, A.M. Electrically controllable spin filtering based on superconducting helical states. Phys. Rev. B 2017, 96, 224505. [Google Scholar] [CrossRef]
- Belzig, W.; Wilhelm, F.K.; Bruder, C.; Schön, G.; Zaikin, A.D. Quasiclassical Green’s function approach to mesoscopic superconductivity. Superlattices Microstruct. 1999, 25, 1251–1288. [Google Scholar] [CrossRef]
- Kuprianov, M.Y.; Lukichev, V.F. Influence of boundary transparency on the critical current of “dirty” SS’S structures. J. Exp. Theor. Phys. Lett. 1988, 67, 1163. [Google Scholar]
- Bezuglyi, E.V.; Vasenko, A.S.; Shumeiko, V.S.; Wendin, G. Nonequilibrium effects in tunnel Josephson junctions. Phys. Rev. B 2005, 72, 014501. [Google Scholar] [CrossRef]
- Bezuglyi, E.V.; Vasenko, A.S.; Bratus, E.N.; Shumeiko, V.S.; Wendin, G. Subgap current in superconducting tunnel junctions with diffusive electrodes. Phys. Rev. B 2006, 73, 220506. [Google Scholar] [CrossRef]
- Usadel, K.D. Generalized Diffusion Equation for Superconducting Alloys. Phys. Rev. Lett. 1970, 25, 507–509. [Google Scholar] [CrossRef]
- Fominov, Y.V.; Chtchelkatchev, N.M.; Golubov, A.A. Nonmonotonic critical temperature in superconductor/ferromagnet bilayers. Phys. Rev. B 2002, 66, 014507. [Google Scholar] [CrossRef]
- Karabassov, T.; Stolyarov, V.S.; Golubov, A.A.; Silkin, V.M.; Bayazitov, V.M.; Lvov, B.G.; Vasenko, A.S. Competitive 0 and π states in S/F/S trilayers: Multimode approach. Phys. Rev. B 2019, 100, 104502. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karabassov, T.; Amirov, E.S.; Bobkova, I.V.; Golubov, A.A.; Kazakova, E.A.; Vasenko, A.S. Superconducting Diode Effect in Topological Hybrid Structures. Condens. Matter 2023, 8, 36. https://doi.org/10.3390/condmat8020036
Karabassov T, Amirov ES, Bobkova IV, Golubov AA, Kazakova EA, Vasenko AS. Superconducting Diode Effect in Topological Hybrid Structures. Condensed Matter. 2023; 8(2):36. https://doi.org/10.3390/condmat8020036
Chicago/Turabian StyleKarabassov, Tairzhan, Emir S. Amirov, Irina V. Bobkova, Alexander A. Golubov, Elena A. Kazakova, and Andrey S. Vasenko. 2023. "Superconducting Diode Effect in Topological Hybrid Structures" Condensed Matter 8, no. 2: 36. https://doi.org/10.3390/condmat8020036
APA StyleKarabassov, T., Amirov, E. S., Bobkova, I. V., Golubov, A. A., Kazakova, E. A., & Vasenko, A. S. (2023). Superconducting Diode Effect in Topological Hybrid Structures. Condensed Matter, 8(2), 36. https://doi.org/10.3390/condmat8020036








