1. Introduction
A peculiar feature of hole-doped cuprates is that in the same range of (in-plane) doping and temperature some quantities have a Fermi liquid (FL)-type behaviour and others exhibit a clearly non-Fermi liquid (NFL) behaviour.
Let us mention some examples in two regions of the phase diagram.
In the “pseudogap phase” (see, e.g., [
1]), i.e., roughly in the underdoped low-temperature region, ARPES experiments prove the existence of gapless Fermi arcs (see, e.g., [
2] and references therein) and the Fermi liquid paradigm would suggest a metallic resistivity with a temperature dependence
, with
for standard FL, and more generally greater than 1. Instead, the in-plane resistivity exhibits a metal-insulator crossover (see, e.g., [
3]) and, if suitably normalized, a universal behaviour [
4] which appears hardly compatible with an explanation of the crossover in terms of disorder localization.
In the so-called “strange metal phase” [
1], i.e., roughly for moderate dopings and temperatures, the uniform spin susceptibility at large
T almost approaches a constant behaviour [
5], as expected for a Fermi liquid. In the same range of parameters, the spin-lattice relaxation time of the Cu sites,
, involving the spin susceptibility at the antiferromagnetic wave vector, is such that
never approaches the Fermi liquid constant behaviour, growing up instead linearly in
T [
6].
We propose that such dichotomic FL versus NFL behaviours of physical quantities in hole-doped cuprates can be explained in terms of the FL* fractionalized Fermi liquid concept, introduced in [
7,
8] and briefly recalled below, within a description of the low-energy physics of the cuprates in terms of the
t-
-
J model for the Cu sites. Of course, it is known that this model is insufficient to explain some phenomena appearing in the cuprates, such as charge density waves and fluctuations (see, e.g., [
9]), and a more complete description is needed including doubly occupied sites, oxigen, phonons and disorder. However, apparently these phenomena are qualitatively irrelevant for the issue of the present paper, where we briefly discuss the above-mentioned dichotomy for the spin susceptibility.
An FL* is an exotic fractionalized Fermi liquid which has conventional excitations, either electron-like or hole-like as in the hole-doped cuprates, near a Fermi surface satisfying a generalization of Luttinger theorem, together with fractionalized excitations emerging from a topological order, in particular holons
charged spinless and spinons
neutral of spin½, interacting via gauge fields
. The electron or hole is a bound state or resonance arising from holon–spinon binding generated by the gauge attraction. There have been several proposals of an FL* nature of the “pseudogap phase” [
10,
11] (and references therein), but to our knowledge not of the “strange metal phase” as claimed here.
The proposed FL* interpretation of the above-cited FL versus NFL dichotomies is as follows: if some physical response is dominated by the hole excitations (spinon–holon interaction), then its behaviour is close to that of a Fermi liquid; if instead it is dominated by a spinon–spinon (and possibly also holon–holon) interaction, then it has a clear non-Fermi liquid character.
In this paper, we show that indeed an interpretation of the above quoted dichotomy for the spin susceptibility can be achieved according to this line of thought.
2. Emergence of FL* Structure in the t-t′-J Model
In the description of the low-energy physics of the cuprates in terms of a two-dimensional (2D)
t-
-
J model, the sites correspond to the Cu sites of a CuO plane in the cuprates and the Zhang-Rice singlets to the empty sites. The Hamiltonian is given by
where
denotes next-nearest-neighbor sites and
the spin index which is assumed to be summed up in the following if repeated.
denotes the Gutzwiller projection implementing the no-double occupation and describing the Mott physics of the system. It can be tackled with a spin-charge decomposition of the hole field
where the holon
h is a spinless fermion, so that by the Pauli principle the no-double occupation is implemented, and the spinon
s is a boson, satisfying in each site the constraint
.
However, for the
t-
J model in 1D, the above statistics of holon and spinon are not able to reproduce the critical exponents obtained in the exact solution by means of Bethe ansatz or conformal field theory techniques [
12,
13]. To reproduce such exponents, both the holon and the spinon should be semions (see e.g., [
14]), i.e., an equal time exchange of their fields introduces a factor
, the sign depending on their order on the time 0 real line, instead of the +1 factor for boson and −1 factor for fermion fields. In 1D, this change of statistics can be obtained by a generalized Jordan–Wigner transformation dressing the fermionic holon by a “charge string” with coefficient ½ (with respect to standard Jordan–Wigner) and the bosonic spinon by a “spin ½ string” [
15,
16].
To obtain the same change of statistics in the 2D model, one adds a charge ½ flux,
, to the spinless fermion
h and an
spin ½ flux,
, to the spin ½ boson
s. The gradient of such fluxes is the potential of a vortex (similar to Laughlin vortices in the fractional quantum Hall effect) modifying the statistics of the holon and spinon, converting them into semions as in 1D, still keeping the hole
c fermionic [
17,
18]. These fluxes do not modify the dynamics, and the statistics changes of
and
compensate each other, thus providing an exact rewriting of the model. This is rigorously proved in the
t-
J model in the previous references using the euclidean path integral approach, where the introduction of the charge and spin fluxes is implemented by minimally coupling the fermions of the
t-
J model to Chern–Simons gauge fields. The proof is based on the representation of partition and correlation functions in terms of quantum mechanical paths of the fermions, where the Chern–Simons gauge fields appear in phase factors associated to the fermion worldlines. Since the Chern–Simons gauge theory is topological, the only effect of the
and
gauge fields is the introduction of phase factors,
i for
and
for
, for each undercrossing and the opposite factors for each overcrossing of the fermion worldlines. Therefore, the two contributions cancel in every crossing among each other, thus providing an exact rewriting of the model. The crucial ingredients for such rewriting are the existence of a global
charge and
spin symmetries of the model, allowing the gauging by Chern–Simons gauge fields and, for lattice models, the no-double occupation constraint, forbidding finite intersections in the worldlines of fermions, so that the crossings are well defined. Therefore, this procedure can be applied to any model with the above features and in particular the extension to the
t-
-
J model considered here is straightforward. As a bonus, the additional
degree of freedom for
s turns out to be more efficient in optimizing both
t and
J terms in the mean field, with respect to the standard abelian slave-boson treatment, as in 1D.
The spin-charge decomposition of the hole in terms of spinon and holon brings up an emergent local
slave-particle gauge symmetry, whose parameter we denote by
:
,
. In the large-scale continuum limit, this local gauge-invariance can be made manifest with the introduction of a gauge field
transforming as
. Such slave-particle gauge fields generate an attraction between the spinon and holon giving rise to a hole resonance at low energy. Analogously, an attraction between a spinon and antispinon gives rise to a magnon resonance. Furthermore, this gauge interaction introduces a new scale into the theory: the Reizer momentum [
19]. In fact, the dynamic of the transverse mode of the gauge field is dominated by the contribution of the gapless holons, and their Fermi surface (FS) produces an anomalous skin effect, with the momentum scale being given by the Reizer momentum
, where
is the (average, in our approximation) holon Fermi momentum. As a consequence of the
T-dependence of the Reizer momentum, the hole and the magnon resonances have a strongly
T-dependent life time, leading to a behaviour of these excitations that is less coherent than in a standard Fermi liquid. In particular, in the “strange metal phase” it behaves as
. To take into account the effect of gauge fluctuations beyond perturbation theory as a very rough approximation, we apply a kind of eikonal resummation. This resummation is obtained by treating first
as an external field, expanding the correlation function in terms of quantum mechanical paths of spinons and, for the hole, also of holons, then integrating out the leading transverse component of
to obtain an interaction between paths, controlled by the Reizer momentum. The interaction is then treated in the eikonal approximation. Finally, a Fourier transform is performed to obtain the retarded correlation function, treating the short scales via a multiplicative scale-renormalization, assuming as UV cutoff the Reizer momentum, see [
18] and references therein.
Let us turn to the effects generated by spin and charge fluxes.
Neglecting the spinon fluctuations in the spin flux one obtains , with , denoting the Pauli matrices. Physically then attaches antiferromagnetic (AF) spin vortices at the holon positions with opposite chirality in the two Néel sublattices. These vortices are in the subgroup of the spin group complementary to the two-sphere of spin directions, therefore they do not modify the AF background, but still, as discussed below, they have a physical dual role.
In the large scale continuum limit, the interaction of the AF vortices with the spinons is described by the term
with
representing the coupling of the large-scale spinon action, where
corresponds to in-plane doping in the cuprates.
Then, on one hand, a quenched average, denoted
, of
in (
2) yields a mass term
providing a gap
to the originally gapless spinon of the
sigma model describing the low energy of the undoped system, thus generating a phase transition from a long-range AF order to a short-range one.
On the other hand, averaging
in (
2) produces a term
, where
is the 2D lattice laplacian. This term describes at large scales a 2D Coulomb attraction between holons in different Néel sublattices due to a Kosterlitz–Thouless interaction between the AF spin-vortices [
20]. As a consequence at the BKT temperature
, there is the formation of a finite density of incoherent holon pairs, the corresponding order parameter
being obtained by solving a BCS-like gap equation. Its doping dependence turns out to be of the form
where
and
in units of
J. The spin degrees of freedom are still unpaired above a lower crossover spin-pairing temperature (with a dome structure in the phase diagram, above the superconducting dome [
21]).
In our approximation, we keep the modulus of
(up to its
d-structure) constant near the Fermi surface, but its phase is strongly fluctuating, since the charge pairs are not condensed. The field describing the phase fluctuations of the pairs has a gap, denoted by
, decreasing with
T, that modifies the standard BCS form of self-energy near the hole Fermi surface [
22] to
where
is the
d-wave holon pair order parameter,
the holon dispersion and
the scattering rate of the hole without charge pairing. This d-wave charge-pairing produces a reduction of the hole spectral weight away from diagonals in the Brillouin zone giving rise to what one may call a high pseudogap phenomenon. Qualitatively, it has some analogy to the one advocated by Uemura [
23], and in fact the pairing temperature has a somewhat similar doping dependence.
The charge-flux companion of the spin flux is given by
and it has also a double role.
On one hand, the uniform term corresponding to 1 in (
5) produces a
flux per plaquette at low
in a region that we identify as low pseudogap (PG); such
lattice is screened by spinon fluctuations above a crossover temperature, denoted
, and the region above can be identified as the “strange metal phase” (SM).
The
flux produces small hole Fermi surfaces near
with linear dispersion and a reduced spectral weight in the outer boundary, giving rise for the holes to a phenomenology of Fermi arcs for strong underdoping. The destruction of the
lattice in SM allows the recovery of a large “ tight-binding” hole FS, but still with a suppression of the spectral weight away from the diagonal below
(where in this approach holons have two small nodal Fermi surfaces and a small antinodal one due to folding), induced by the charge pairing [
22].
On the other hand, the non-uniform term in (
5) (which is analogous to the Jordan–Wigner “charge string” in 1D) acts by modifying the exchange statistics of holons, turning them into semions, and also changing their occupation statistics, giving to them Haldane 1/2 statistics [
24,
25] (as in 1D), so that the area of the FS of semionic spinless holons is equal to the area of the FS of spin ½ fermions [
26].
From the above description, one can see that we have all the ingredients for an FL*: holons, spinons and holes. In this approach in PG we have a
topological order, as suggested in somewhat different frameworks by several authors [
10,
11] and a generalized Luttinger theorem proves that the area of the four hole FS pockets is given by
. Additionally, in SM a generalized Luttinger theorem proves that the area of the FS of the holes is given by
. This has been shown [
27] using topological arguments of the kind considered in [
8], starting from an insulator at half-filling in PG and from the fully occupied band in SM. Hence, both in PG and in SM we have an FL* in our approach to the
t-
-
J model.
3. FL* Solution of FL vs. NFL Dichotomy in the Spin Susceptibility in SM
The relation between spinons s, holons h and the electron spin at the site j is given by , and the low-energy continuum limit of is described by a magnon field , behaving as a spinon–antispinon resonance. From the above formula, it follows that the spinon’s contribution to the spin susceptibility is peaked at the AF wavevector .
In SM at , the hole/electron contribution is subleading because there is no nesting of the FS. Therefore, through the magnon resonance, the spinon’s contribution to the spin susceptibility at is dominating.
The spin-lattice relaxation time
of Cu sites is known to be controlled by the spin susceptibility at
(see, e.g., [
28]). The spinon dependence can explain its NFL-like behaviour, with
growing linearly with
T at high temperatures, instead of approaching a constant behaviour expected for a standard Fermi liquid.
More concretely, the calculation is performed using the formula
where
is the spin susceptibility and
is the hyperfine field which for the Cu sites is peaked around
, thus probing the AF spin fluctuations. We can use this fact and the representation of the spin in terms of spinons to approximate the above formula. We treat in mean field the term
in
and use the relevant Kubo formula obtaining
The right hand side of Equation (
7) is then treated with the techniques and approximations sketched in the previous section and discussed in [
18], with the
q-integration cutoff by the Reizer momentum and considering
arising from the
t-
-
J model. In our approach, the physics of
is dominated by the dissipation proportional to
of the gauge fluctuations binding the spinon and antispinon in a magnon resonance together with the scale set by the Reizer momentum, producing for
a large-
T behaviour linear in
T with coefficient
, where
is the diamagnetic susceptibility of the holons with “large Fermi surface”.
is an effective hole doping corresponding to the holon FS which is slightly smaller than the hole Fermi surface; numerically, for values of
adopted for LSCO, one finds
(modification essentially irrelevant not considered in [
18]).
It turns out that the above coefficient of the
T behaviour for intermediate dopings is almost doping-independent, as observed also in the slope of the experimental data of
in LSCO [
6]. As a side remark, we notice that with the same formalism a linear
T contribution to the in-plane resistivity is reproduced in SM, but with the slope decreasing with doping, as in the experiments [
18]. In the above calculation of
, the upward shift with doping of the experimental curves is not reproduced, but one can conjecture that it might arise from a contribution of weak antiferromagnetism of the hole resonance. Notice that, as in the experimental data, there is no effect of the high pseudogap, which in our theoretical framework is naturally explained by the fact that spinons are not affected by the charge pairing responsible for the high pseudogap.
In the uniform spin susceptibility in SM, the effect of the spinons is instead negligible, precisely because the spectral weight due to spinons is peaked at . Therefore the uniform susceptibility is dominated by the hole resonance and, taking into account the effect of the high pseudogap causing its suppression for low T, it is more FL-like.
The calculation is performed using the standard procedure for FL, but taking into account the anomalous gauge-induced dissipation and the charge pairing. In fact, contrary to
, the uniform susceptibility feels the effect of the high pseudogap, because the charge pairing of holons is also reflected in the holes, as shown in the contribution to the hole self-energy given in (
4).
More in detail, in the calculation the doping dependence of the order parameter at
is given by solving numerically the BCS gap equation mentioned in the previous section (as in [
20]). The extension of the order parameter to finite temperature is achieved using a standard d-wave BCS approximate formula [
29]:
The scale of the holon pairing temperature
is fixed by identifying it in two doping values with the experimental high-pseudogap temperature in LSCO. This gives a reasonable result because the doping dependence of
derived from the BCS gap equation is approximately the one found experimentally in [
5] for the high pseudogap. For the mass of the phase of the charge pairs,
, we use an approximate ansatz of the kind suggested in [
30], setting the pair condensation temperature to 0 (since holon pairs by themselves never condense in our approach):
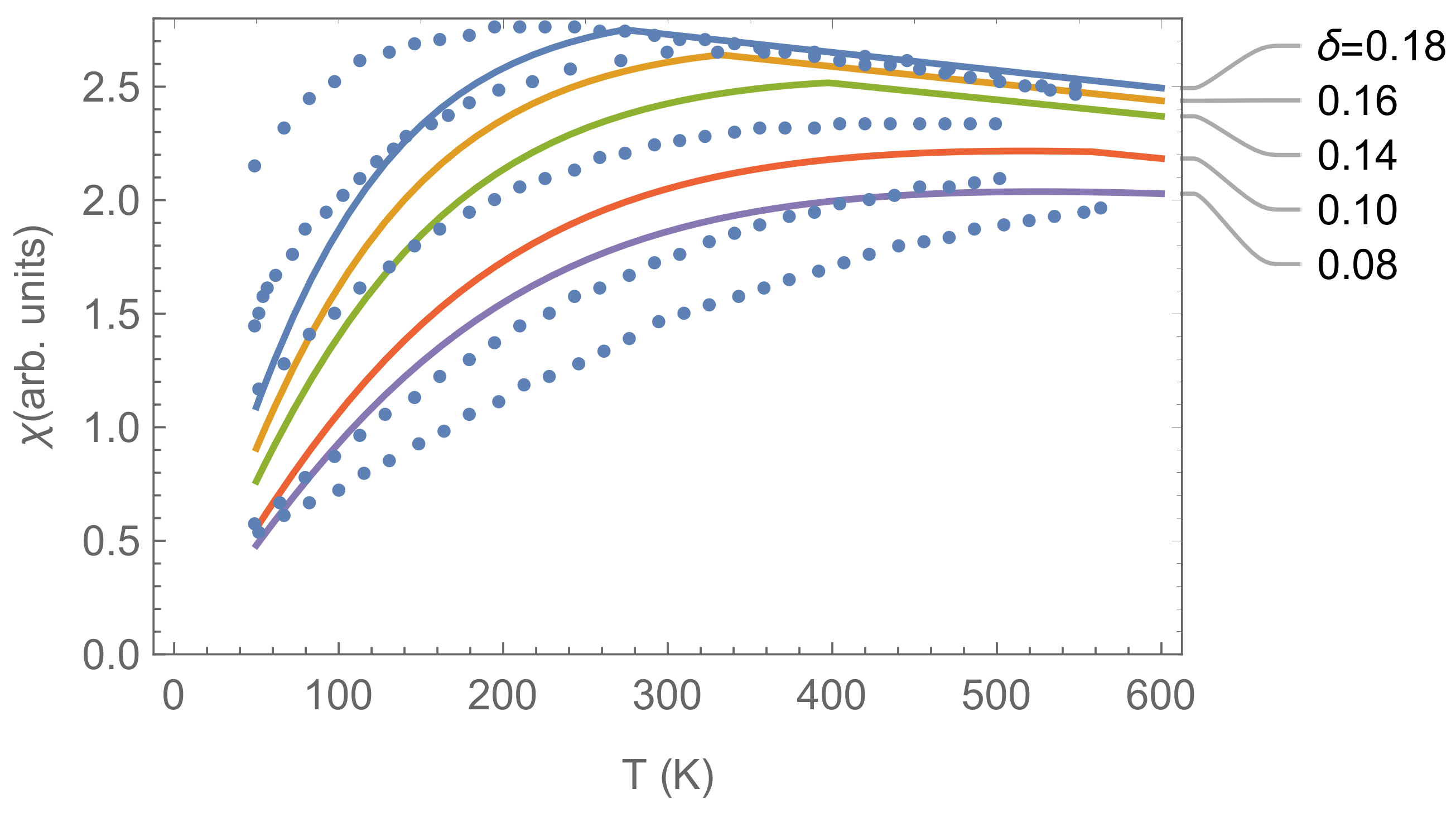
The result for the temperature dependence of the uniform spin susceptibility with the above approximate calculation is qualitatively consistent with experimental data for LSCO at intermediate dopings. Decreasing the temperature, it exhibits for moderate
a slow increase up to the pairing temperature
, instead of a constant behaviour of a standard Fermi liquid, due to the enhanced scattering rate of the electron generated by the gauge fluctuations. Then, it falls rapidly due to the high-pseudogap phenomenon generated by charge pairing. If above
one assumes a renormalization of the scattering rate of the hole with respect to that of the magnon proportional to the square of the ratio between the holon and spinon velocity (∼
), the calculated behaviour also agrees qualitatively in doping dependence with the experimental data (see
Figure 1), in spite of the big approximations made. Let us remark that within such approximations, the doping and temperature dependences are completely determined by the theory only up to the scales involved, which have been optimized for one doping and then never changed.