Low-Lying Collective Excitations of Superconductors and Charged Superfluids

Abstract

We investigate theoretically the momentum-dependent frequency and damping of low-lying collective excitations of superconductors and charged superfluids in the BCS–BEC crossover regime. The study is based on the Gaussian pair-and-density fluctuation method for the propagator of Gaussian fluctuations of the pair and density fields. Eigenfrequencies and damping rates are determined in a mutually consistent nonperturbative way as complex poles of the fluctuation propagator. Particular attention is paid to new features with respect to preceding theoretical studies, which were devoted to collective excitations of superconductors in the far BCS regime. We find that at a sufficiently strong coupling, new branches of collective excitations appear, which manifest different behavior as functions of the momentum and the temperature.

1. Introduction

Superconductors and fermionic superfluids exhibit a rich variety of collective excitations, which are provided by the density and pair field response. The majority of known superconductors are realized at high concentrations of electrons such that the plasma energy is large with respect to the gap, $\hslash {\omega }_p\gg \Delta$. Under this condition, the response of superconductors and charged superfluids in the frequency range $\omega \sim {\omega }_p$ is dominated by the plasma branch of collective excitations [1]. At lower frequencies, namely in the range of the pair-breaking threshold, other collective excitations can be observable in superconductors and charged superfluid systems, e.g., pair-breaking Higgs modes [2] and gapless Carlson–Goldman modes [3]. The low-lying collective excitations can be resolved experimentally in both neutral and charged Fermi superfluids using different methods, such as Bragg spectroscopy [4], spatially resolved interferometry [5], and pump-THz probe spectroscopy [6].

The low-lying collective excitations are well studied theoretically for superconductors [2,7] in the weak-coupling BCS regime. Recent progress in a realization of the BCS–BEC crossover regime in superconductors makes the treatment of collective excitations in the whole crossover range timely and relevant.

We consider collective excitations as small Gaussian fluctuations on the top of a uniform mean-field solution for the pair and density fields. This formalism is equivalent to the random phase approximation (RPA) [8]. Using these methods, collective excitations in charged superfluids have been investigated [9,10], being concentrated on the case of relatively small plasma frequencies, which can be in resonance with the pair-breaking threshold. The present study is devoted to the other regime, when the plasma frequency is large with respect to the gap, which is relevant for existing superconductors. For $\hslash {\omega }_p\gg \Delta$, the plasma branch of the response is only slightly affected by the difference between the BCS–BEC crossover and the far BCS regime. Therefore, the paper is particularly focused on the dispersion and damping of low-lying collective excitations.

2. Gaussian Pair-and-Density Fluctuation Method

The present treatment follows the theoretical scheme which is represented in detail in Ref. [10]. Therefore, we only briefly describe the main steps of the derivation. It exploits the partition function of a gas of fermions with the spin projection $\sigma =\pm 1/2$, which is a path integral over anticommuting Grassmann fields $\left\{{\overline{\psi }}_{\sigma },{\psi }_{\sigma }\right\}$,

$$\mathcal{Z}=\int e^{-S}D\left. [\overline{\psi },\psi \right]$$

(1)

with the action functional

$$\begin{array}{cc}\hfill S& ={\int }_0^{\beta }d\tau \int d\mathbf{r}\left. [\sum _{\sigma =\uparrow ,\downarrow }{\overline{\psi }}_{\sigma }\left(\frac{\partial }{\partial \tau }+H-\mu \right){\psi }_{\sigma }+g{\overline{\psi }}_{\uparrow }{\overline{\psi }}_{\downarrow }{\psi }_{\downarrow }{\psi }_{\uparrow }\right]\hfill \\ \hfill & +\frac{1}{2}{\int }_0^{\beta }d\tau \int d\mathbf{r}\int d{\mathbf{r}}^{\prime }\frac{e^2}{4\pi {ϵ}_0\epsilon \left|{\mathbf{r}}^{\prime }-\mathbf{r}\right|}\sum _{\sigma ,{\sigma }^{\prime }}{\overline{\psi }}_{\sigma }\left(\mathbf{r}\right){\overline{\psi }}_{{\sigma }^{\prime }}\left({\mathbf{r}}^{\prime }\right){\psi }_{{\sigma }^{\prime }}\left({\mathbf{r}}^{\prime }\right){\psi }_{\sigma }\left(\mathbf{r}\right).\hfill \end{array}$$

(2)

The interparticle interaction in (2) is a sum of the attractive contact potential with the coupling constant $g<0$ and the repulsive Coulomb potential, in which ${ϵ}_0$ is the permittivity of free space and $\epsilon$ is the high-frequency dielectric constant of a medium. Additionally, $\beta =\hslash /k_{B}T$ is the inverse temperature, and $\mu$ is the chemical potential. We use the set of units with $\hslash =1$, the particle mass $m=1/2$, and the particle density n such that the Fermi wave vector of free fermions in 3D is $k_F\equiv {\left(3{\pi }^{2}n\right)}^{1/3}=1$. Consequently, the free-particle Fermi energy $E_F$ in these units is $E_F=1$.

Next, we obtain the effective bosonic action through standard steps as described in detail in Ref. [10]. First, we introduce the auxiliary bosonic fields: the pair field $\left. [\overline{\mathsf{\Psi }},\mathsf{\Psi }\right]$ and the density field $\left. [\mathsf{\Phi }\right]$. Second, the Hubbard–Stratonovich shift of bosonic variables allows us to perform the path integration over fermionic variables analytically exactly. This results in the effective bosonic action

$$S_{eff}=-tr\left. [ln\left(-{\mathbb{G}}^{-1}\right)\right]+{\int }_0^{\beta }d\tau \int d\mathbf{r}\left(-\frac{1}{g}\overline{\mathsf{\Psi }}\mathsf{\Psi }+\frac{1}{8\pi }{\left(\nabla \mathsf{\Phi }\right)}^2\right).$$

(3)

with the inverse Nambu matrix

$$-{\mathbb{G}}^{-1}=\left(\begin{array}{cc}\frac{\partial }{\partial \tau }+H-\mu +i\sqrt{{\alpha }_0}\mathsf{\Phi }& -\mathsf{\Psi }\\ -\overline{\mathsf{\Psi }}& \frac{\partial }{\partial \tau }-H+\mu -i\sqrt{{\alpha }_0}\mathsf{\Phi }\end{array}\right).$$

(4)

Here, ${\alpha }_0$ is the dimensionless coupling strength for the Coulomb interaction,

$${\alpha }_0\equiv \frac{e^2}{4\pi {ϵ}_0\epsilon \hslash }\sqrt{\frac{2m}{E_F}}.$$

(5)

The relation between ${\alpha }_0$ and the bare plasma frequency ${\omega }_p=\sqrt{e^{2}n/{ϵ}_0\epsilon m}$ in the chosen units is given by ${\omega }_p=\sqrt{\left(8/3\pi \right){\alpha }_0}$.

The expansion of the effective bosonic action (3) up to the quadratic order in powers of fluctuations of the pair and density fields about the mean-field solution leads to the Gaussian pair-and-density fluctuation (GPDF) action. We approximate the mean-field solution by uniform values, neglecting exchange scattering contributions [9]. Consequently, the gap equation remains the same as for a neutral superfluid:

$${\int }_{k<K_0}\frac{d\mathbf{k}}{{\left(2\pi \right)}^3}\left(\frac{1}{2E_{\mathbf{k}}}tanh\left(\frac{\beta E_{\mathbf{k}}}{2}\right)-\frac{1}{2k^2}\right)+\frac{1}{8\pi a_s}=0,$$

(6)

where $E_{\mathbf{k}}=\sqrt{{\xi }_{\mathbf{k}}^2+{\Delta }^2}$ is the pair excitation energy, ${\xi }_{\mathbf{k}}=k^2-\mu$ is the free-fermion energy, and $a_s$ is the s-wave scattering length coming from the renormalization of the coupling constant [11]:

$$\frac{1}{g}=\frac{1}{8\pi a_s}-{\int }_{k<K_0}\frac{d\mathbf{k}}{{\left(2\pi \right)}^3}\frac{1}{2k^2},$$

(7)

with the ultraviolet cutoff $K_0$. In the case of the model contact interaction, $g\to 0$ and, correspondingly, the cutoff is set to $K_0\to \infty$, keeping the integral in Equation (6) convergent.

The resulting GPDF action is a quadratic form of the modulus $\left({\lambda }_{\mathbf{q},m}\right)$ and phase $\left({\theta }_{\mathbf{q},m}\right)$ fluctuations of the pair field and the density fluctuations ${\mathsf{\Phi }}_{\mathbf{q},m}$:

$$\begin{array}{cc}\hfill S_{GPDF}& =\frac{1}{2}\sum _{\mathbf{q},m}\left(\begin{array}{ccc}{\lambda }_{-\mathbf{q},-m}& {\theta }_{-\mathbf{q},-m}& {\mathsf{\Phi }}_{-\mathbf{q},-m}\end{array}\right)\hfill \\ \hfill & \times \left(\begin{array}{ccc}{K}_{1,1}& K_{1,2}& K_{1,3}\\ -K_{1,2}& K_{2,2}& K_{2,3}\\ K_{1,3}& -K_{2,3}& K_{3,3}\end{array}\right)\left(\begin{array}{c}{\lambda }_{\mathbf{q},m}\\ {\theta }_{\mathbf{q},m}\\ {\mathsf{\Phi }}_{\mathbf{q},m}\end{array}\right).\hfill \end{array}$$

(8)

Here, $\mathbf{q}$ is the momentum, and m is the Matsubara index of the Fourier representation of the bosonic fields. The coefficients $K_{i,j}$ constitute the matrix of the inverse GPDF propagator. They are explicitly given by (for details, see [9,10,12]):

$$\begin{array}{cc}\hfill K_{1,1}\left(\mathbf{q},i{\mathsf{\Omega }}_m\right)& =-\frac{1}{8\pi a_s}+\int \frac{d\mathbf{k}}{{\left(2\pi \right)}^3}\left\{\frac{1}{2k^2}+\frac{tanh\left(\beta E_{\mathbf{k}}/2\right)}{4E_{\mathbf{k}}{E}_{\mathbf{k}+\mathbf{q}}}\right.\hfill \\ \hfill & \times [\left({\xi }_{\mathbf{k}}{\xi }_{\mathbf{k}+\mathbf{q}}+E_{\mathbf{k}}{E}_{\mathbf{k}+\mathbf{q}}-{\Delta }^2\right)\left(\frac{1}{i{\mathsf{\Omega }}_m-E_{\mathbf{k}}-E_{\mathbf{k}+\mathbf{q}}}-\frac{1}{i{\mathsf{\Omega }}_m+E_{\mathbf{k}}+E_{\mathbf{k}+\mathbf{q}}}\right)\hfill \\ \hfill & \left.\left.+\left({\xi }_{\mathbf{k}}{\xi }_{\mathbf{k}+\mathbf{q}}-E_{\mathbf{k}}{E}_{\mathbf{k}+\mathbf{q}}-{\Delta }^2\right)\left(\frac{1}{i{\mathsf{\Omega }}_m-E_{\mathbf{k}+\mathbf{q}}+E_{\mathbf{k}}}-\frac{1}{i{\mathsf{\Omega }}_m-E_{\mathbf{k}}+E_{\mathbf{k}+\mathbf{q}}}\right)\right]\right\},\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill K_{2,2}\left(\mathbf{q},i{\mathsf{\Omega }}_m\right)& =-\frac{1}{8\pi a_s}+\int \frac{d\mathbf{k}}{{\left(2\pi \right)}^3}\left\{\frac{1}{2k^2}+\frac{tanh\left(\beta E_{\mathbf{k}}/2\right)}{4E_{\mathbf{k}}{E}_{\mathbf{k}+\mathbf{q}}}\right.\hfill \\ \hfill & \times [\left({\xi }_{\mathbf{k}}{\xi }_{\mathbf{k}+\mathbf{q}}+E_{\mathbf{k}}{E}_{\mathbf{k}+\mathbf{q}}+{\Delta }^2\right)\left(\frac{1}{i{\mathsf{\Omega }}_m-E_{\mathbf{k}}-E_{\mathbf{k}+\mathbf{q}}}-\frac{1}{i{\mathsf{\Omega }}_m+E_{\mathbf{k}}+E_{\mathbf{k}+\mathbf{q}}}\right)\hfill \\ \hfill & \left.\left.+\left({\xi }_{\mathbf{k}}{\xi }_{\mathbf{k}+\mathbf{q}}-E_{\mathbf{k}}{E}_{\mathbf{k}+\mathbf{q}}+{\Delta }^2\right)\left(\frac{1}{i{\mathsf{\Omega }}_m-E_{\mathbf{k}+\mathbf{q}}+E_{\mathbf{k}}}-\frac{1}{i{\mathsf{\Omega }}_m-E_{\mathbf{k}}+E_{\mathbf{k}+\mathbf{q}}}\right)\right]\right\},\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill K_{1,2}\left(\mathbf{q},i{\mathsf{\Omega }}_m\right)& =i\int \frac{d\mathbf{k}}{{\left(2\pi \right)}^3}\frac{tanh\left(\beta E_{\mathbf{k}}/2\right)}{4E_{\mathbf{k}}{E}_{\mathbf{k}+\mathbf{q}}}\hfill \\ \hfill & \times [\left({\xi }_{\mathbf{k}}{E}_{\mathbf{k}+\mathbf{q}}+E_{\mathbf{k}}{\xi }_{\mathbf{k}+\mathbf{q}}\right)\left(\frac{1}{i{\mathsf{\Omega }}_m-E_{\mathbf{k}}-E_{\mathbf{k}+\mathbf{q}}}+\frac{1}{i{\mathsf{\Omega }}_m+E_{\mathbf{k}}+E_{\mathbf{k}+\mathbf{q}}}\right)\hfill \\ \hfill & \left.+\left({\xi }_{\mathbf{k}}{E}_{\mathbf{k}+\mathbf{q}}-E_{\mathbf{k}}{\xi }_{\mathbf{k}+\mathbf{q}}\right)\left(\frac{1}{i{\mathsf{\Omega }}_m-E_{\mathbf{k}+\mathbf{q}}+E_{\mathbf{k}}}+\frac{1}{i{\mathsf{\Omega }}_m-E_{\mathbf{k}}+E_{\mathbf{k}+\mathbf{q}}}\right)\right],\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill K_{1,3}\left(\mathbf{q},i{\mathsf{\Omega }}_m\right)& =-i\sqrt{2{\alpha }_0}\Delta \int \frac{d\mathbf{k}}{{\left(2\pi \right)}^3}\frac{tanh\left(\beta E_{\mathbf{k}}/2\right)}{4E_{\mathbf{k}}{E}_{\mathbf{k}+\mathbf{q}}}\left({\xi }_{\mathbf{k}}+{\xi }_{\mathbf{k}+\mathbf{q}}\right)\hfill \\ \hfill & \times \left(\frac{1}{i{\mathsf{\Omega }}_m-E_{\mathbf{k}}-E_{\mathbf{k}+\mathbf{q}}}-\frac{1}{i{\mathsf{\Omega }}_m+E_{\mathbf{k}}+E_{\mathbf{k}+\mathbf{q}}}\right)\hfill \\ \hfill & \left.+\frac{1}{i{\mathsf{\Omega }}_m+E_{\mathbf{k}}-E_{\mathbf{k}+\mathbf{q}}}-\frac{1}{i{\mathsf{\Omega }}_m-E_{\mathbf{k}}+E_{\mathbf{k}+\mathbf{q}}}\right),\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill K_{2,3}\left(\mathbf{q},i{\mathsf{\Omega }}_m\right)& =-\sqrt{2{\alpha }_0}\Delta \int \frac{d\mathbf{k}}{{\left(2\pi \right)}^3}\frac{tanh\left(\beta E_{\mathbf{k}}/2\right)}{4E_{\mathbf{k}}{E}_{\mathbf{k}+\mathbf{q}}}\hfill \\ \hfill & \times [\left(E_{\mathbf{k}+\mathbf{q}}+E_{\mathbf{k}}\right)\left(\frac{1}{i{\mathsf{\Omega }}_m-E_{\mathbf{k}}-E_{\mathbf{k}+\mathbf{q}}}+\frac{1}{i{\mathsf{\Omega }}_m+E_{\mathbf{k}}+E_{\mathbf{k}+\mathbf{q}}}\right)\hfill \\ \hfill & \left.+\left(E_{\mathbf{k}+\mathbf{q}}-E_{\mathbf{k}}\right)\left(\frac{1}{i{\mathsf{\Omega }}_m+E_{\mathbf{k}}-E_{\mathbf{k}+\mathbf{q}}}+\frac{1}{i{\mathsf{\Omega }}_m-E_{\mathbf{k}}+E_{\mathbf{k}+\mathbf{q}}}\right)\right],\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill K_{3,3}\left(\mathbf{q},i{\mathsf{\Omega }}_m\right)& =\frac{q^2}{4\pi }-{\alpha }_0\int \frac{d\mathbf{k}}{{\left(2\pi \right)}^3}\frac{tanh\left(\beta E_{\mathbf{k}}/2\right)}{2E_{\mathbf{k}}{E}_{\mathbf{k}+\mathbf{q}}}\hfill \\ \hfill & \times \left(\frac{E_{\mathbf{k}}{E}_{\mathbf{k}+\mathbf{q}}-{\xi }_{\mathbf{k}}{\xi }_{\mathbf{k}+\mathbf{q}}+{\Delta }^2}{i{\mathsf{\Omega }}_m-E_{\mathbf{k}}-E_{\mathbf{k}+\mathbf{q}}}+\frac{E_{\mathbf{k}}{E}_{\mathbf{k}+\mathbf{q}}+{\xi }_{\mathbf{k}}{\xi }_{\mathbf{k}+\mathbf{q}}-{\Delta }^2}{i{\mathsf{\Omega }}_m-E_{\mathbf{k}}+E_{\mathbf{k}+\mathbf{q}}}\right.\hfill \\ \hfill & \left.-\frac{E_{\mathbf{k}}{E}_{\mathbf{k}+\mathbf{q}}+{\xi }_{\mathbf{k}}{\xi }_{\mathbf{k}+\mathbf{q}}-{\Delta }^2}{i{\mathsf{\Omega }}_m+E_{\mathbf{k}}-E_{\mathbf{k}+\mathbf{q}}}-\frac{E_{\mathbf{k}}{E}_{\mathbf{k}+\mathbf{q}}-{\xi }_{\mathbf{k}}{\xi }_{\mathbf{k}+\mathbf{q}}+{\Delta }^2}{i{\mathsf{\Omega }}_m+E_{\mathbf{k}}+E_{\mathbf{k}+\mathbf{q}}}\right).\hfill \end{array}$$

(14)

The other matrix elements can be written down using the symmetry relations,

$$\begin{array}{cc}\hfill K_{2,1}\left(\mathbf{q},i{\mathsf{\Omega }}_m\right)& =-K_{1,2}\left(\mathbf{q},i{\mathsf{\Omega }}_m\right),\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill K_{3,1}\left(\mathbf{q},i{\mathsf{\Omega }}_m\right)& =K_{1,3}\left(\mathbf{q},i{\mathsf{\Omega }}_m\right),\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill K_{3,2}\left(\mathbf{q},i{\mathsf{\Omega }}_m\right)& =-K_{2,3}\left(\mathbf{q},i{\mathsf{\Omega }}_m\right)\hfill \end{array}$$

(17)

As the matrix elements of the inverse GPDF propagator $K_{1,3}$ and $K_{2,3}$ are proportional to the gap $\Delta$, the pair and density fields become decoupled at $T=T_c$. For lower temperatures, however, this coupling can influence the spectra of collective modes. Moreover, as shown below, even in a relatively close vicinity of the transition temperature, at $T=0.99T_c$, the coupling of the pair and density fields leads to clearly observable consequences, such as an appearance of new collective modes.

Frequencies and damping factors of collective excitations are determined in a mutually consistent way through roots of the determinant of the inverse GPDF propagator for the complex frequency argument $z=\omega +i\gamma$,

$$det\mathbb{K}\left(z\right)=0,$$

(18)

or, in other words, as complex poles of the GPDF propagator. In order to get these poles, the propagator is analytically continued through the branch cut at the real axis (for more details, see Ref. [10]). This method is well established and widely used, particularly for Green’s functions [13], for the dielectric function [14], for collective excitations of ultracold Fermi gases [15,16].

The matrix elements $K_{j,k}\left(\mathbf{q},z\right)$ contain several angular points at the branch cut. The analytic continuation is therefore possible through several intervals between these points, as analyzed in detail in Ref. [16]. Different intervals can reveal different branches of collective excitations.

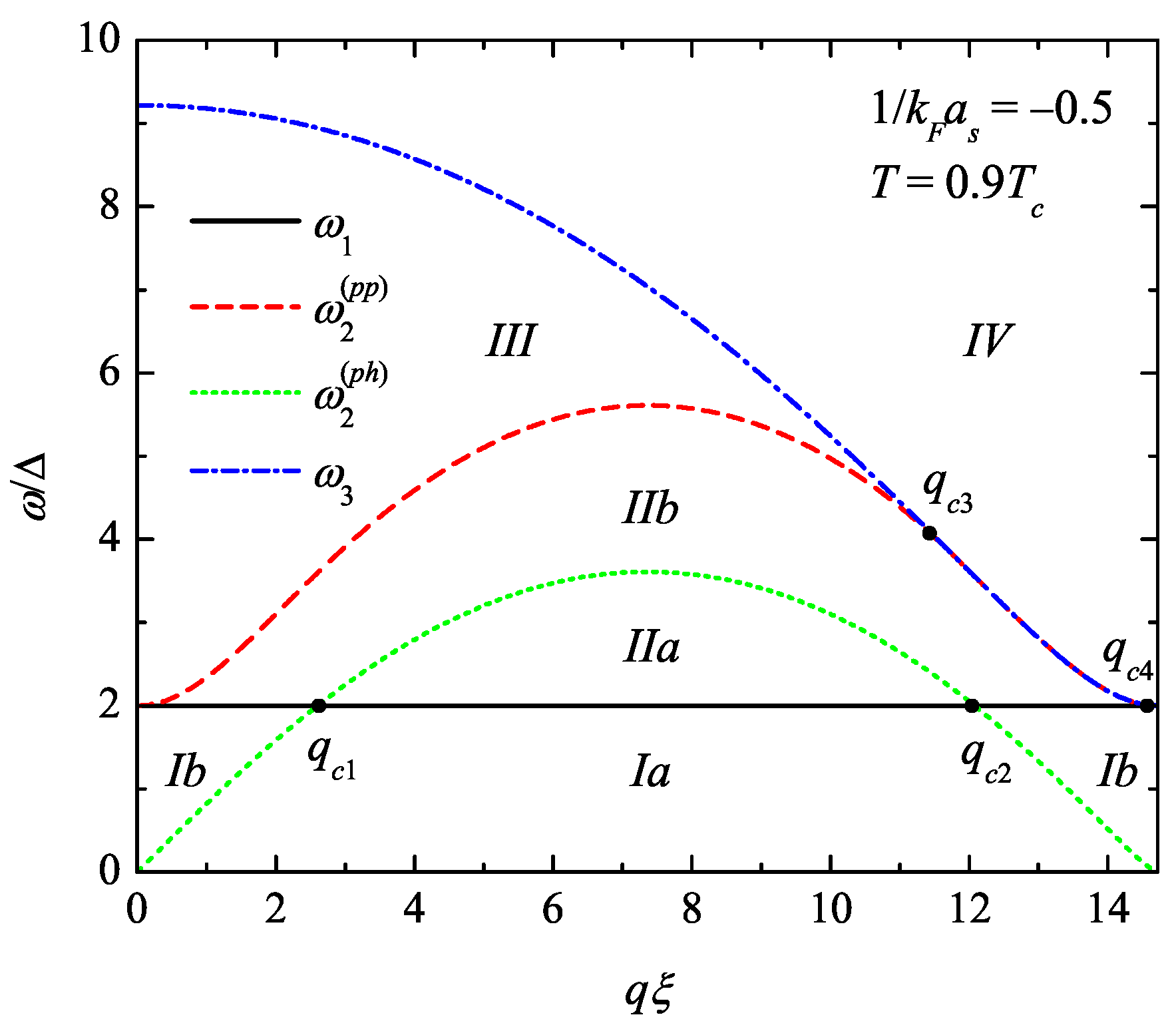
Bounds of intervals for the analytic continuation shown in Figure 1 (and considered in detail in Ref. [16]) influence both the analytic solutions of the dispersion equation and the spectral weight functions, where they are explicitly manifested as shown below. In the figure, the frequency ${\omega }_1$ is the pair-breaking continuum edge. The frequencies ${\omega }_2^{\left(pp\right)}$ and ${\omega }_2^{\left(ph\right)}$ correspond to bounds of channels for the particle–particle and particle–hole scattering processes, respectively, and ${\omega }_3=2\sqrt{{\left(\mu -q^2/4\right)}^2+{\Delta }^2}$ is the energy of the BCS pair $E_{\mathbf{k}-\mathbf{q}/2}+E_{\mathbf{k}+\mathbf{q}/2}$ at zero fermion momentum $\mathbf{k}$. The set of these bounds is determined by a change in the configuration of the resonant wave vectors for any of the two resonance conditions, $\omega =E_{\mathbf{k}-\mathbf{q}/2}+E_{\mathbf{k}+\mathbf{q}/2}$ for the particle–particle scattering channel and $\omega =\left|E_{\mathbf{k}-\mathbf{q}/2}-E_{\mathbf{k}+\mathbf{q}/2}\right|$ for the particle–hole channel. The values $q_{cj}$ indicate bounds of intervals of momentum where different branches of collective excitations can exist.

For completeness, we can also compute spectral weight functions for the phase–phase and modulus–modulus correlation functions of the pair field and for the density–density correlation function. In the general form, they are reported in Ref. [10]. Here, we approximate them assuming the limit ${\omega }_p\to \infty$ for the plasma frequency. This approximation is relevant for low-lying collective excitations, and reads

$$\begin{array}{cc}\hfill \underset{{\alpha }_0\to \infty }{lim}{\chi }_{\lambda \lambda }\left(\mathbf{q},\omega \right)& =\frac{1}{\pi }Im\frac{K_{2,2}\left(\mathbf{q},\omega +i{0}^{+}\right){\tilde{K}}_{3,3}\left(\mathbf{q},\omega +i{0}^{+}\right)+{\tilde{K}}_{2,3}^2\left(\mathbf{q},\omega +i{0}^{+}\right)}{det\tilde{\mathbb{K}}\left(\mathbf{q},\omega +i{0}^{+}\right)},\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill \underset{{\alpha }_0\to \infty }{lim}{\chi }_{\theta \theta }\left(\mathbf{q},\omega \right)& =\frac{1}{\pi }Im\frac{K_{1,1}\left(\mathbf{q},\omega +i{0}^{+}\right){\tilde{K}}_{3,3}\left(\mathbf{q},\omega +i{0}^{+}\right)-{\tilde{K}}_{1,3}^2\left(\mathbf{q},\omega +i{0}^{+}\right)}{det\tilde{\mathbb{K}}\left(\mathbf{q},\omega +i{0}^{+}\right)},\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill \underset{{\alpha }_0\to \infty }{lim}{\chi }_{\rho \rho }\left(\mathbf{q},\omega \right)& =-\frac{q^4}{16{\pi }^3}Im\left(\frac{det{\mathbb{K}}_{GPF}\left(\mathbf{q},\omega +i{0}^{+}\right)}{det\tilde{\mathbb{K}}\left(\mathbf{q},\omega +i{0}^{+}\right)}\right),\hfill \end{array}$$

(21)

with the rescaled matrix elements and the determinant

$${\tilde{K}}_{1,3}=\frac{1}{\sqrt{{\alpha }_0}}{K}_{1,3},{\tilde{K}}_{2,3}=\frac{1}{\sqrt{{\alpha }_0}}{K}_{2,3},{\tilde{K}}_{3,3}=\frac{1}{{\alpha }_0}\left(K_{3,3}-\frac{q^2}{4\pi }\right),$$

(22)

$$det\tilde{\mathbb{K}}=\underset{{\alpha }_0\to \infty }{lim}\left(\frac{1}{{\alpha }_0}det\mathbb{K}\right),$$

(23)

which tend to finite and nonzero limiting values when ${\alpha }_0\to +\infty$.

In the limit of large ${\omega }_p$, the contribution of the low-lying collective excitations in the density–density spectral weight is extremely small. Moreover, in this limit, the contribution of the density oscillations to the low-lying excitations must be relatively small. Therefore, we use the pair–field spectral weight functions in the subsequent numeric results. The phase–phase and modulus–modulus spectral weight functions are useful to clarify the physical sense of different modes and to see whether they are provided by oscillations of the modulus or the phase of the pair field. Thus, the spectrum of collective excitations is determined below in two complementary ways, (1) as peaks of spectral weight functions, and (2) finding a solution for complex poles of the GPDF propagator analytically continued to the lower half-plane of the complex frequency.

The random-phase and Gaussian fluctuation approximations are well substantiated and widely used in the whole BCS–BEC crossover, as long as we stay under the assumption that collective excitations are small (harmonic) oscillations about the uniform background. The special case when higher-order terms in the power of fluctuations are important is considered in Ref. [17]. The other reason for a quantitative inaccuracy of the present approach can follow from the mean-field results for the uniform gap and the chemical potential. This does not influence the qualitative behavior of collective excitations as discussed in Refs. [15,16].

3. Spectra of Collective Excitations

There is a significant difference between the behavior of collective excitations in neutral and charged fermionic superfluids in the frequency range of the order of the pair-breaking threshold. In a neutral superfluid Fermi gas, there exists the gapless (Anderson–Bogoliubov, Goldstone) collective excitation branch provided by the phase response of the pair field, and the gapped (pair-breaking, Higgs) branch constituted by the modulus response. The Anderson–Bogoliubov mode turns to the gapped plasma mode due to the Coulomb interaction, and the Goldstone phase mode is thus suppressed [8]. When the temperature rises, approaching the vicinity of the transition temperature $T_c$, a gapless mode appears again due to the presence of the normal fraction, as described by Carlson and Goldman [3].

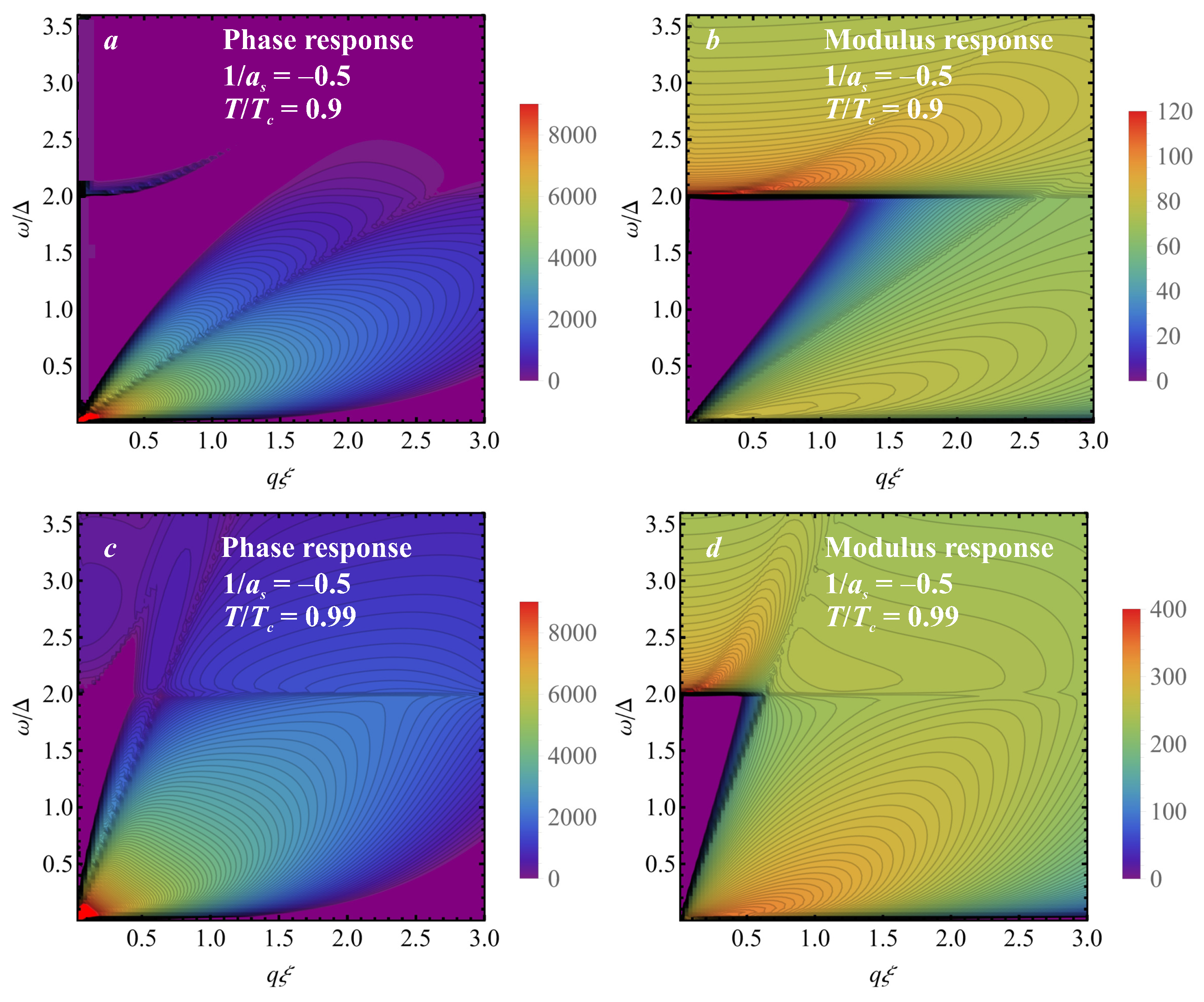
In the BCS–BEC crossover, the strong coupling is favorable for the manifestation of the gapless collective excitation branch with respect to that in the far BCS regime. This extended range of survival for gapless excitations is revealed in the contour plots of the spectral weight functions for the phase and modulus response of a charged superfluid in Figure 2. In the far BCS limit [7], the gapless mode disappears below $T/T_c\approx 0.9$, while it is rather strongly expressed at that temperature even in the moderate BCS case with $1/k_F{a}_s=-0.5$, and moreover at higher coupling strengths. The logarithmic scale is used for the better visibility of the whole spectrum. Additionally, we partly clipped the plot range for the spectral weights of the phase response in Figure 2a,c. The clipping areas are shown in red.

Comparing the phase and modulus spectral weight functions to each other, it can be seen that gapless collective excitations in the BCS–BEC crossover appear in both phase and modulus spectral weight functions such that they are provided by both the modulus and phase response as distinct from the far BCS limit $1/a_s\to -\infty$ [7], where they are constituted by phase excitations only. The spectral weight functions show the existence of more than one gapless branch. One of them contains a significant contribution of amplitude excitations, with an increasing relative weight when T approaches $T_c$, as can be seen from Figure 2b,d. The other gapless branches are not visible in the modulus spectral weight functions. Consequently, they can be attributed to the phase response. We can see a splitting of these collective excitations to the branches above and below the particle–hole angular point frequency ${\omega }_2^{\left(ph\right)}$, which is revealed as a kink in the contour plots.

The pair-breaking collective excitation branch is less affected by the Coulomb interaction and exists both in superconductors and in neutral Fermi superfluids. The pair-breaking Higgs modes do not contain a sufficiently resolvable phase component and, therefore, are not visible in the spectral weight functions for the phase response (Figure 2a,c). They are provided by amplitude oscillations in both neutral and charged superfluids.

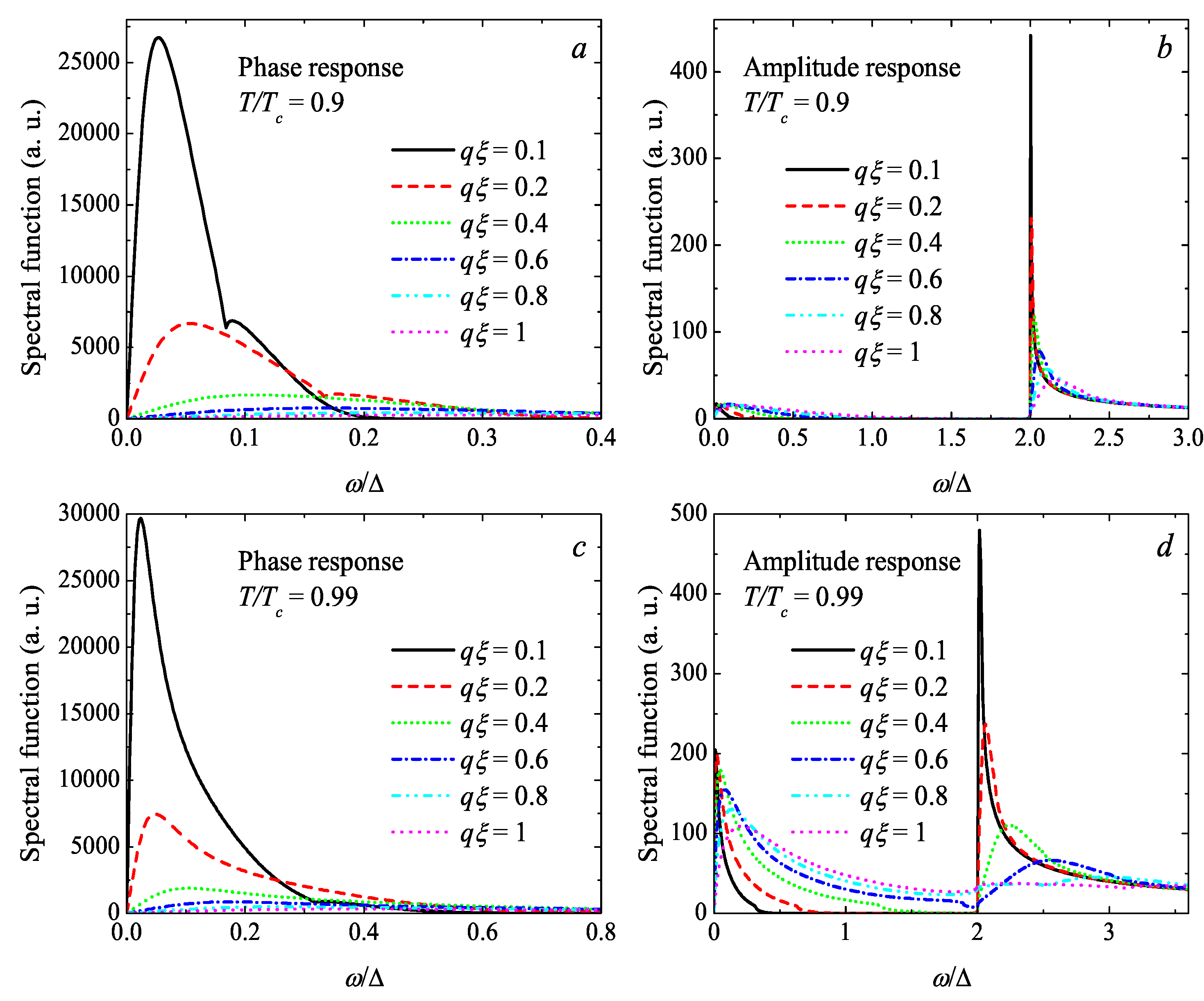
The one-dimensional slices of the spectral weight functions at selected values of the pair field momentum q shown in Figure 3 give us even more transparent picture of the behavior of different collective excitation branches. The kink in the spectral weight functions of the phase response manifested in Figure 3a,c at $\omega ={\omega }_2^{\left(ph\right)}$ apparently indicates the existence of two gapless modes related to phase excitations. They are not well resolved from each other because in the temperature range where gapless modes exist they exhibit significant damping. Consequently, the two peaks in Figure 3a,c substantially overlap.

According to the spectral weight functions in comparison with the results of Ref. [16], the gapless mode splits to more branches in charged superfluids/superconductors than in neutral superfluids. It is not a priori clear whether or not this splitting is accompanied by an appearance of more than one complex poles in the analytic solution. Below, we show that the splitting is indeed consistent with the behavior of the poles of the propagator.

The spectral weight functions for the amplitude response in Figure 3b,d show peaks attributed to the gapped Higgs modes and gapless modes. The Higgs mode frequencies are pinned to the pair-breaking continuum edge and tend to $2\Delta$ at the small momentum. Their behavior in charged superfluids is only slightly influenced by plasma oscillations at ${\omega }_p\gg \Delta$, contrary to the case of small plasma frequencies considered in Ref. [10], where Higgs and plasma modes can be in resonance.

Besides the Higgs modes, the amplitude response exhibits the lowest-energy gapless excitation branch, which shows a distinctive dissipative behavior. Its response magnitude increases when moving close toward $T_c$.

Next, we analyze complex eigenfrequencies given by roots of the dispersion Equation (18). The solution based on the analytic continuation of the GPDF propagator exhibits more complex poles in the BCS–BEC crossover with respect to the far BCS limit, in accordance with the spectral weight functions shown in Figure 2. Only a part of them are really physically significant, namely those that have relatively small damping rates, because in general, complex poles of Green’s functions can be convincingly attributed to elementary excitations only at sufficiently small damping [18]. 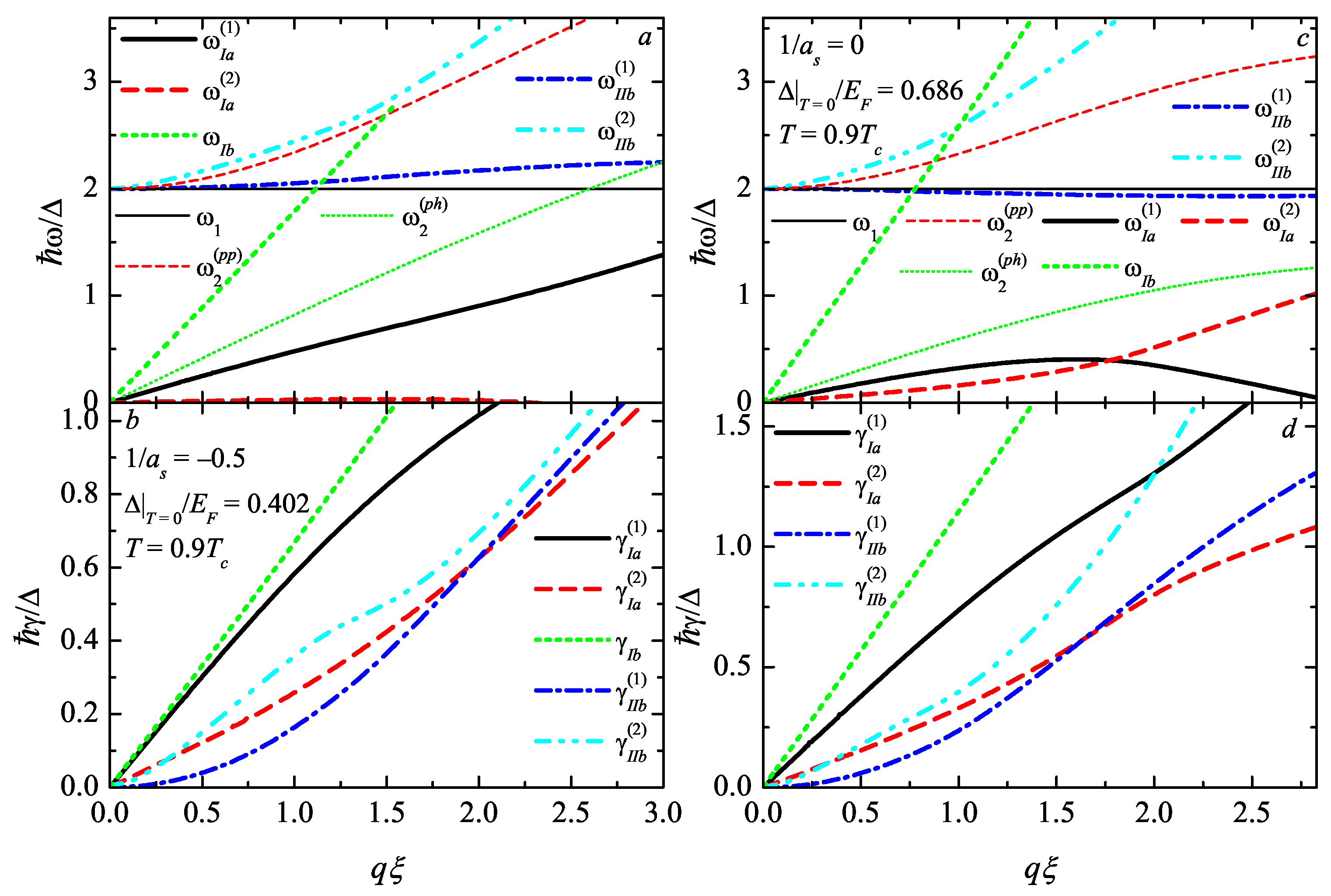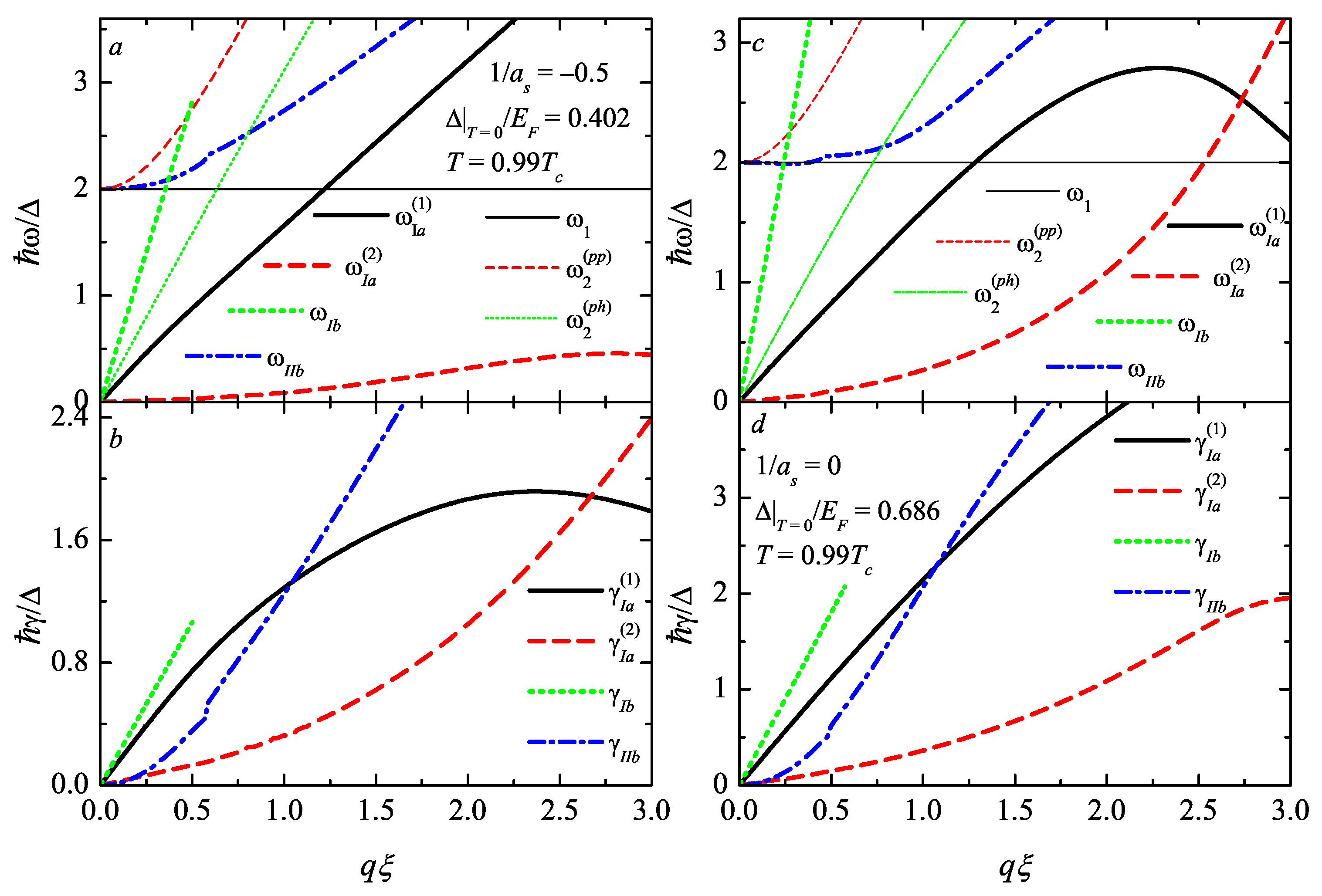Figure 4 shows the momentum dependence of eigenfrequencies and damping factors in the moderate BCS regime for $T=0.9T_c$ and for two values of the inverse scattering length, $1/k_F{a}_s=-0.5$, which corresponds to Figure 2, and the unitarity regime with $1/k_F{a}_s=0$.

Even at small damping, the mutually consistent calculation of eigenfrequencies and damping factors is more rigorous than the perturbation approach, where the eigenfrequency is determined for the zero damping, and the damping rate is then calculated within the lowest-order perturbation theory. The perturbation approach can give solutions such as an upper mode at $\omega \approx 2\Delta$ for phase excitations, which may be unphysical, as mentioned in Ref. [7].

We show in Figure 4 the most representative (with non-negligible spectral weights) branches of gapless collective excitations. These roots of the dispersion Equation (18) are generated by the analytic continuation of the GPDF propagator through the intervals $Ia$ and $Ib$ from Figure 1. In agreement with the spectral weight functions, we can see three of the most representative complex poles with the eigenfrequencies $\left({\omega }_{Ia}^{\left(1\right)},{\omega }_{Ia}^{\left(2\right)}\right)<{\omega }_2^{\left(ph\right)}$ and ${\omega }_{Ib}>{\omega }_2^{\left(ph\right)}$. The latter pole does not exist in the solution for neutral superfluids [16]. Therefore, the appearance of this gapless mode is provided by the interaction of the phase and plasma collective excitations. These two upper-frequency gapless modes have the sound-like (linear) dispersion at the small momentum. This looks like the splitting of the phononic-like Carlson0-Goldman branch to two phononic-like collective excitation modes. Figure 4a demonstrates an example of the upper-frequency gapless mode pole $z_{Ia}^{\left(2\right)}$ existing in the restricted area of momentum $q<q_{1c}$, as follows from the scheme of intervals for the analytic continuation (Figure 1).

The lower-frequency gapless branch with the eigenfrequency ${\omega }_{Ia}^{\left(2\right)}$ is an analog of the second gapless mode in neutral Fermi superfluids [19]. It exists at T sufficiently close to the transition temperature and disappears at some temperature below $T_c$, which depends on the inverse scattering length, and decreases when rising the coupling strength. As can be seen from Figure 1, this second mode is close to disappearance at $T=0.9T_c$ and $1/a_s=-0.5$, but it is non-vanishing at $1/a_s=0$ with the same relative temperature. Moreover, at unitarity, we can see the crossing of the solutions ${\omega }_{Ia}^{\left(1\right)}$ and ${\omega }_{Ia}^{\left(2\right)}$ at $q\xi \approx 1.6$. Thus, at a larger momentum, ${\omega }_{Ia}^{\left(2\right)}$ becomes the upper gapless mode of the two. This crossing of frequencies is accompanied by the avoided crossing of the damping factors so that complex roots are not crossed. This behavior of complex eigenfrequencies is qualitatively the same as that for neutral Fermi superfluids, discussed in Refs. [16,19].

The pair-breaking collective excitation branch in the BCS–BEC crossover and at $T\ne 0$ splits to two branches ${\omega }_{IIb}^{\left(1\right)}$ and ${\omega }_{IIb}^{\left(2\right)}$, similarly to the pair-breaking mode in a neutral fermionic superfluid [16]. The first solution ${\omega }_{IIb}^{\left(1\right)}$ dominates at a small momentum with respect to ${\omega }_{IIb}^{\left(2\right)}$ due to a smaller damping. It exhibits a negative dispersion approaching a minimum at some finite q. This behavior has an analog with the negative dispersion of the plasma mode [9] found when the plasma frequency is low and comparable with the gap.

The gapless mode frequencies ${\omega }_{Ia}^{\left(1\right)}$ and ${\omega }_{Ib}$ expand to the continuum when T is close to $T_c$, as shown in Figure 5, similarly to the phononic-like mode in a neutral superfluid [16]. This mode frequency demonstrates an avoided crossing with the frequency of the pair-breaking mode frequency ${\omega }_{IIb}$ above the threshold, accompanied by the crossing of their damping factors. The other gapless mode $z_{Ib}$ exhibits crossing with the Higgs mode for frequencies but no crossing for damping factors. The two gapless branches ${\omega }_{Ia}^{\left(1\right)}$ and ${\omega }_{Ia}^{\left(2\right)}$ manifest the crossing in the BCS regime at $1/k_F{a}_s=-0.5$, which is changed to the avoided crossing at a strong coupling with $1/k_F{a}_s=0$. Correspondingly, the damping factors ${\gamma }_{Ia}^{\left(1\right)}$ and ${\gamma }_{Ia}^{\left(2\right)}$ are crossed in the BCS regime and exhibit an avoided crossing at unitarity. The aforesaid behavior of complex poles is qualitatively similar to that found for collective excitations in a neutral superfluid, where they behave as particles interacting with each other via a repulsive potential.

Comparing the solutions of the dispersion Equation (18) with the peaks of the spectral weight functions in Figure 2, it can be seen that the gapless modes with the frequencies ${\omega }_{Ia}^{\left(1\right)}$ and ${\omega }_{Ib}$ are related to the phase response because there are no visible fingerprints of these modes in the modulus spectral weight functions. The other gapless mode ${\omega }_{Ia}^{\left(2\right)}$ is distinctively manifested in the spectral weight functions of the modulus response, and consequently contains a significant part of the amplitude oscillations. When the temperature shifts toward $T_c$, the relative weight of this (lowest energy at small q) gapless mode in the modulus response increases with respect to the relative weight of the Higgs mode, while the relative weights of the gapless modes in the phase response vary only slightly.

The dispersion of the gapless mode ${\omega }_{Ia}^{\left(2\right)}$ is linear at a sufficiently small momentum. When the momentum increases further, we can observe a range of q, where ${\omega }_{Ia}^{\left(2\right)}\left(q\right)$ is a convex function. When T approaches a vicinity of $T_c$, the interval of linearity gradually shrinks so that the gapless branch ${\omega }_{Ia}^{\left(2\right)}$ apparently tends to the mode with a quadratic dispersion, similarly to the analogous mode in a neutral superfluid [11,16].

In general, the real part of a complex pole is interpreted as the eigenfrequency of the collective mode, and the imaginary part determines the damping factor, which is the inverse lifetime of the mode. This physical picture is adequate at relatively small damping factors, when complex poles are well-determined quasiparticle excitations. For stronger damping, this understanding gradually becomes rather conventional. Nevertheless, we can observe this about collective excitations even when damping is not small, just describing the obtained complex poles as they appear.

The broadening of collective excitations hardly can be subdivided into the quantum and thermal parts precisely. Within the GPDF/RPA methods, they come together in the matrix elements. The broadening of collective modes at $T=0$ is of course only quantum, and it is nonzero only for the nonzero momentum. At zero temperature, the gapless modes do not survive in charged superfluids. Therefore, the purely quantum broadening of Carlson–Goldman excitations hardly can be observed. As we can see from the obtained results in the figures, the broadening of all modes increases when rising the temperature.

4. Conclusions

We considered collective excitations in superconductors and charged Fermi superfluids in the case when the plasma frequency substantially exceeds the gap and pair-breaking threshold, focusing on the low-lying collective modes with energies of the order of the superconducting/superfluid gap. Within the present study, we find several low-lying collective modes existing in a charged superfluid/superconductor. The pair-breaking Higgs branch of collective excitations survives both in neutral and charged superfluid systems. It is relatively slightly influenced by the Coulomb interaction, except for the case of resonance of the plasma excitation branch with the pair-breaking threshold considered in Refs. [9,10]. In the BCS–BEC crossover, we found more than one pair-breaking collective excitation branch.

When the temperature rises toward $T_c$, gapless collective excitation branches can appear in the BCS–BEC crossover. The physical origin of these modes is the presence of a normal fluid fraction when T is sufficiently close to $T_c$, the same reason as for Carlson–Goldman excitations [3]. There can appear several gapless modes, distinct from a single mode in the far BCS limit. At the small momentum, one of the gapless modes with a linear dispersion can be attributed to the Carlson–Goldman collective mode as in Ref. [7]. The other gapless excitation branch, which has a lower energy at small momentum, contains a resolvable part of the modulus response. Despite the amplitude contribution to this mode, it is quite different from the pair-breaking Higgs modes, which are gapped and pinned to the pair-breaking threshold. When T approaches $T_c$, this mode exhibits a quadratic dispersion and is analogous to the excitation branch for a neutral Fermi superfluid described in Ref. [11]. Finally, the other gapless mode, which is sound-like at a small momentum, appears in the BCS–BEC crossover for charged superfluids, being new with respect to the previously considered neutral superfluids.

The spectral weight function for the phase response reveals the gapless modes but does not contain a resolvable contribution of the Higgs modes. On the contrary, the modulus response is dominated by the Higgs modes and the second gapless mode without a visible fingerprint of the Carlson–Goldman branch, which remains, therefore, a phase mode both in the BCS and crossover regimes.

The evolution of low-lying collective excitation spectra as functions of the interaction strength and on the temperature can reveal a resonant interaction of different modes, particularly their avoided crossing. Additionally, multiple branches of gapless and pair-breaking excitations can be observable. Because the collective excitations analyzed in the present work are common for superconductors and charged superfluid systems, they are an example of a bridge between the physics of superconductors and condensed quantum gases, and can thus represent a particular interest for both theoretical and experimental investigations.