Abstract
The non-trivial topology of electronic bands in Weyl semimetals originates from band inversion due to strong spin–orbit coupling. The Weyl semimetals have pairs of Weyl gap-less nodes in the bulk Brillouin zone. The tungsten ditelluride WTe2 likely belongs to type II Weyl semimetals. Doping WTe2 with magnetic ions could induce magnetic ordering in this crystal, which provides prospects for practical applications. We studied the magnetic properties of the iron-doped single crystals Fe0.03W0.97Te2, annealed and unannealed, in comparison with the undoped WTe2. Measurements of the dc magnetization were carried out from 1.8 to 400 K. We revealed pronounced ferromagnetic ordering that was affected by annealing. Anomalies associated with antiferromagnetism and paramagnetism were also found. The magnetic order was suppressed by a field of 60 kOe. The rise in susceptibility with increasing temperature was observed at high temperatures in all samples and was treated using a model developed for Weyl semimetals. The Curie–Weiss law fit at 60 kOe showed that the effective magnetic moment was close to that of Fe2+. Metamagnetism was demonstrated for the unannealed doped WTe2 crystal. The data for the heat capacity of the iron-doped sample agreed with results for the undoped WTe2.
1. Introduction
Weyl semimetals (WSM) are three-dimensional topological materials [1,2,3]. The non-trivial topology of electronic bands in WSM originates from band inversion due to strong spin–orbit coupling. This is related to the violation of the time-reversal symmetry (T-symmetry) [4,5,6] or the lattice inversion symmetry (P-symmetry) [7,8,9,10] and is associated with the existence of pairs of gap-less Weyl points with opposite chirality in the bulk Brillouin zone of WSM. The surface Brillouin zone comprises the Fermi arcs, which connect the projections of the Weyl nodes [1]. It was suggested that the non-centrosymmetric tungsten and molybdenum ditellurides, WTe2 and MoTe2, the mixed ditellurides MoxW1−xTe2 [11,12,13,14,15,16,17,18,19] and the Heusler alloy LaAlGe [20] belong to type II WSM. While the attribution of WTe2 to WSM raised doubts [21], recent studies agreed with its non-trivial topological nature [17,22,23,24]. The electron and hole bands in type II WSM have touching points and form tilted Weyl cones with a finite density of states at nodes [25], whereas the Fermi surface in type I WSM shrinks to zero at the Weyl points. In addition, the Lorentz invariance in type II WSM is broken because of tilted Weyl cones. The pairs of Weyl points in WSM can be considered as Dirac points separated owing to breaking symmetry [1,2]. The tungsten ditelluride was well known before it was attributed to WSM as a good thermoelectric material [26]. WTe2 also showed the temperature-driven Lifshitz transition [27], the non-saturated magnetoresistance probably related to the hole and electron compensation [28,29], and anisotropic non-linear magnetoresistance [30]. Recently, a metallic ferroelectricity was experimentally confirmed in WTe2 [31]. It was shown in [32] that the stacking order and symmetry in WTe2 can be drastically affected by special optical excitation. Great interest was caused by the behavior of WTe2 monolayers, which demonstrated a strain-induced transition into a topological phase [33], the properties of an excitonic insulator [34], and an anomalous Hall effect in the heterostructure with a ferromagnetic insulator [35].
Doping the topological materials remarkably influences their behavior. For instance, the magnetic ordering emerges in the Bi2Se3 topological insulator doped with chromium ions, which allows observing the anomalous quantum Hall effect in the internal fields [36]. Coexistence of several types of magnetic orders was found for the Cr-doped Bi2Se3 in [37]. Doping the Bi0.97−xSb0.03 topological insulators with magnetic Ni and Fe ions was found in [38] to affect the magnetoresistance. In addition, the metamagnetic hysteretic behavior was observed in [37], which differed from hysteresis loops considered for the antiferromagnetic topological materials [39,40]. Strong effects of doping were observed in topological semimetals. Doping with S and Ir ions led to the pronounced enhancement of superconductivity in a MoTe2 single crystal [41,42]. Theoretical studies showed that doping with magnetic ions can produce a topological phase transition from a Dirac to a Weyl semimetal [43]. The experimental evidence was obtained for the Mn-doped Dirac semimetal VAl3 [44]. As a result of doping the Weyl semimetallic state coexisted with the Kondo effect. Ni doping was shown to reduce the rise of the resistance with increasing magnetic field in WTe2 [45], which agrees with general effect of the disorder on the magnetoresistance [46]. However, the magnetoresistance was found to be increased by p doping in WTe2 likely due to better carrier compensation [47]. The potassium intercalation in WTe2 induced superconductivity below 2.6 K [48]. The impact of Fe doping on the WTe2 transport properties was recently reported in [49,50]. Substituting Fe for Te induced the metal–insulator transition and changes in the transport. Magnetic ordering was recently found only in the crystalline chromium-doped WTe2 [51]. The temperature dependence of magnetization was measured at a field of 1 kOe. Ferromagnetism was noticed below room temperature. The findings for doped topological materials open new possibilities for tuning electronic properties, which can be of great importance for applications [52,53,54,55]. However, more various doped WSM should be studied to outline the prospective trends.
Here, we present results of magnetic studies of the iron-doped single crystals Fe0.03W0.97Te2, which were compared with the data for the non-doped single-crystalline WTe2. Detailed measurements show ferromagnetic ordering with the phase transition above room temperature at low magnetic fields. Strong anisotropy of magnetic properties is observed. The impact of annealing is seen. Ferromagnetism coexists with paramagnetic behavior, as well as with additional anomalies at low temperatures. Metamagnetism is demonstrated, which is characterized by hysteresis loops typical for the itinerant nature.
2. Sample and Experiment
The tungsten ditelluride WTe2 (TD) single crystal and its iron-doped Fe0.03W0.97Te2 counterpart were grown by the chemical vapor transport method with iodine as the transport agent. The process of the crystal growth was carried out in an evacuated quartz-glass ampoule over three weeks [56]. Plates for magnetic measurements were split from the grown ingots perpendicular to the crystalline c axis. One plate of the iron-doped tungsten ditelluride before measurements was annealed at T = 1183 K for two hours followed by water quenching while another plate was studied as it was grown. The annealed and unannealed iron-doped tungsten ditelluride were denoted as FeTDa and FeTD, respectively. The weights of the FeTD, FeTDa, and TD samples were 3.96, 6.32, and 23.53 mg, respectively. The undoped WTe2 was not annealed. The layered WTe2 crystal has an orthorhombic, non-centrosymmetric Td lattice structure (space group Pmn21) [57]. The structure of WTe2 keeps stable with changing temperature [58,59].
The X-ray diffraction carried out at room temperature confirmed that both the doped and undoped samples belonged to the Td symmetry and were single crystalline. The X-ray diffraction spectra for the undoped and doped WTe2 are shown in Supplemented Materials, Figure S1. The tiny differences in the X-ray peaks between the doped and undoped samples can be caused by some disorder induced by doping. The Td lattice consists of Te–W–Te triple atom layers bounded by weak van der Waals interactions, while the intralayer bonds are covalent. The triple layers are stacked up along the c-axis. The unit cell comprises four formula units. Iron ions substitute for tungsten. An example is shown in Figure 1a.
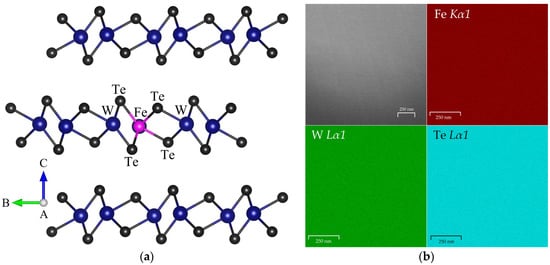
Figure 1.
(a) Crystalline lattice of WTe2. An example is shown of iron substitution for tungsten. (b) The element mapping images of the FeTD.
The nominal composition was close to that obtained by Tescan Mira SEM equipped with Oxford Instruments INCA x-act EDS spectroscope and electron backscatter diffraction (see Figure S2 in Supplemented Materials). The elemental mapping obtained for FeTD and FeTDa confirmed that Fe doping was homogeneous without iron agglomeration (Figure 1b). This suggests that the magnetic properties reported in the present work do not appear because of segregated magnetic phases.
Dc magnetization M was measured using a Quantum Design MPMS SQUID magnetometer (SQUID VSM). The temperature range of measurements was from 1.8 to 400 K. The magnetic field changed up to 70 kOe. The temperature dependence of M was monitored under the ZFC and FCC protocols at warming after cooling in zero field and subsequent cooling in fields. The bias magnetic field was oriented either along or perpendicularly to the crystalline c-axis. The M(H) isotherms were also obtained at cycling field. The heat capacity was measured on a Quantum Design Physical Property Measurement Systems PPMS-9 + Ever-Cool-II using the built-in procedure at temperatures from 1.9 to 300 K in fields from 0 to 1 kOe. A magnetic field was applied along the c-axis.
3. Results and Discussion
Figure 2 shows the temperature dependences of susceptibility for the FeTD sample at a magnetic field of 100 Oe in two sample orientations and . Pronounced bifurcations of the ZFC and FCC curves can be seen below 300 K, which evidence the emergence of the ferromagnetic ordering. The ferromagnetic phase transition temperature decreases down to approximately 170 and 20 K with increasing magnetic field to 1 and 10 kOe, respectively (Figure 2a). In contrast, the ferromagnetic transitions did not shift noticeably and remained below room temperature in the Cr-doped WTe2 [51] when the magnetic field increased from 0 to 1 kOe.
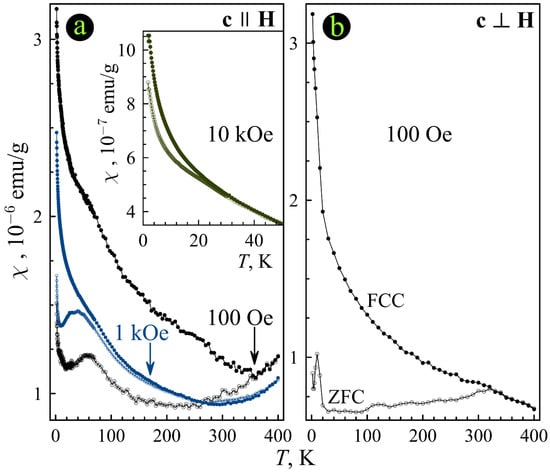
Figure 2.
Temperature dependences of the dc susceptibility for FeTD at two orientations obtained in magnetic fields shown in the panels. Open and closed symbols are ZFC and FCC.
At the field 60 kOe, the ferromagnetic transition shifts below the lower limit of our measurements as the ZFC and FCC susceptibilities run close to each other. At the fields 100 Oe and 1 kOe, we can see humps on the ZFC curves for the orientation (Figure 2a), which demonstrate the second, low-temperature, ferromagnetic transition. This transition moves to low temperatures when magnetic field increases from 100 Oe to 1 kOe. The similar humps are not seen for another sample orientation. Instead, a ZFC susceptibility peak appears neat 10 K. The magnetic anomalies associated with the second ferromagnetic transition are not observed at the fields 10 and 60 kOe (Figure 3) due to a reduction in its temperature. Figure 2 shows a remarkable rise of both ZFC and FC susceptibilities with decreasing temperature below 10 K. Such behavior likely corresponds to the paramagnetic contribution, which becomes noticeable at low temperatures on the background of ferromagnetism. The magnetic susceptibilities at 60 kOe anomalously rise from approximately 250 to 400 K. The rise is weaker for the sample orientation. For the orientation, the similar rise of the susceptibility can be also seen at lower fields (Figure 2a).
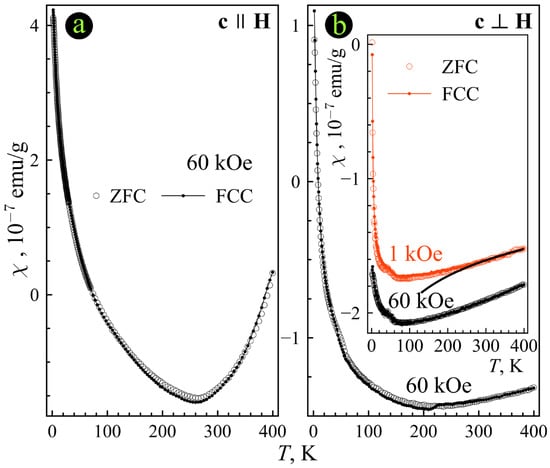
Figure 3.
Temperature dependences of the dc susceptibility for FeTD at 60 kOe. The inset in the panel b shows the dc susceptibility for the undoped TD. The solid line is the fitting curve described in the text. The sample orientations and magnetic fields are indicated in the panels. Open and closed symbols are ZFC and FCC.
The inset in Figure 3b shows the temperature dependences of the ZFC and FCC susceptibilities for the undoped TD plate at 1 and 60 kOe. The ZFC and FCC curves coincide within the whole temperature range of our experiments in agreement with the non-magnetic nature of this WSM.
The susceptibilities are noticeably smaller than the relevant values in the doped FeTD and are negative confirming its diamagnetic properties [60]. Weak paramagnetism below 60 K might be caused by small amount of magnetic impurities or defects. However, we should emphasize the rise of susceptibility above 60 K, which is similar to the behavior of in the iron-doped FeTD sample.
The magnetization isotherms M(H) for FeTD in two orientations and at several temperatures are shown in Figure 4a,b, respectively. The hysteresis loop obtained at 5 K in the orientation is typical for metamagnetism [61]. The descending and ascending branches of the hysteresis loop merge with the virgin magnetization and with each other at the origin H = 0, M = 0. The hysteresis loops obtained at 15 K in the orientation (Figure 4a) and at 2 K in the orientation (Figure 4b) represent both the ferromagnetic and metamagnetic features. The magnetization isotherms in Figure 4a,b are far from saturation at a field of 70 kOe.
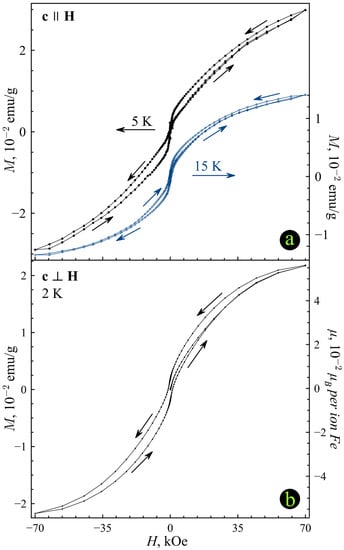
Figure 4.
(a) Magnetization isotherms for FeTD in the orientation. (b) Magnetization isotherms for FeTD in the cH orientation at 2 K. The arrows show the directions of field changes.
Temperature dependences of susceptibility for the annealed FeTDa single crystal are shown in Figure 5 at the sample orientation . Ferromagnetic ordering with the phase transition above 400 K at 100 Oe is evidenced by strong bifurcation of the ZFC and FCC curves. This ordering is not seen in the whole temperature range of our experiments at the magnetic field 60 kOe. Other magnetization anomalies associated with phase transitions appear on the temperature dependences at fields 100 Oe and 1 and 10 kOe below room temperature; however, they are completely smoothed down at 60 kOe. Note the pronounced rise in the susceptibility at low temperatures. In 60 kOe the behavior of susceptibility is described by the Curie law within a limited temperature range from 125 to 265 K (see the inset to Figure 5b). In this range the susceptibility follows the relationship , where the Weiss temperature , the Curie–Weiss constant and the temperature-independent diamagnetic contribution . The Curie–Weiss constant allows evaluating the effective magnetic moment of Fe ions: , where kB is the Boltzmann constant, N is the number of the iron ions per gram, is the Bohr magneton. This gives , which is close to the effective moment of Fe2+ [62].
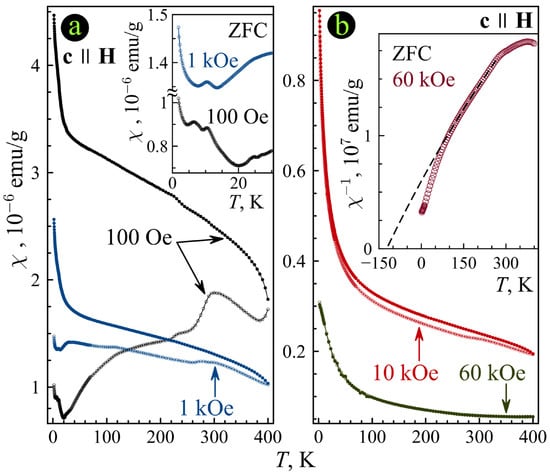
Figure 5.
Temperature dependences of the dc susceptibility for FeTDa in the orientation at different fields indicated in the panels. The inset in the panel (a) shows the scaled susceptibility. The inset in the panel (b) shows the inversed susceptibility . Open and closed symbols are ZFC and FCC.
The magnetization isotherms M(H) for FeTDa in the orientation are shown in Figure 6. The hysteresis loops are observed from 2 to 320 K (see the lower inset in Figure 6). The temperature dependence of coercitivity HC calculated from the loops is presented in the upper inset to Figure 6.
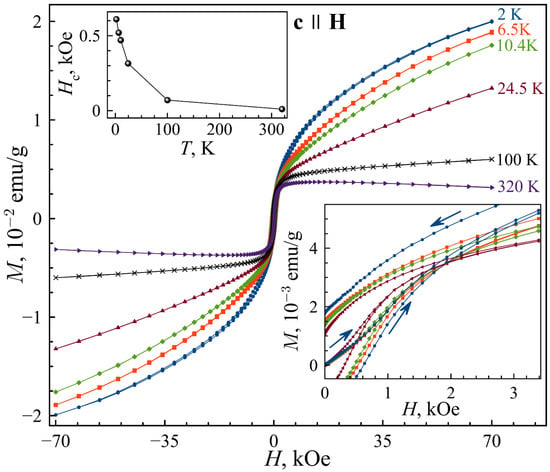
Figure 6.
Magnetization isotherms for FeTDa in the orientation at temperatures indicated in the panel. The upper inset shows the temperature dependence of the coercitivity . The lower inset shows the central parts of the isotherms. The arrows show the directions of field changes.
The heat capacity C of FeTD in zero magnetic field is shown in Figure 7. Measurements were also carried out at 0.5 and 1 kOe. The variations of versus obtained in different magnetic fields are shown in the inset in Figure 7. The plot in the inset demonstrates the validity of the relationship at low temperatures below 5 K, which describes the contribution of the electron and phonon systems [62]. Here, the Sommerfeld constant and the phonon coefficient . The Debye temperature can be found using the coefficient : = 161 K. The calculated values of the Sommerfeld constant and Debye temperature agree well with the studies of the WTe2 single crystal in [63]. Note, that the application of the magnetic field does not noticeably affect the heat capacity in the iron-doped sample.
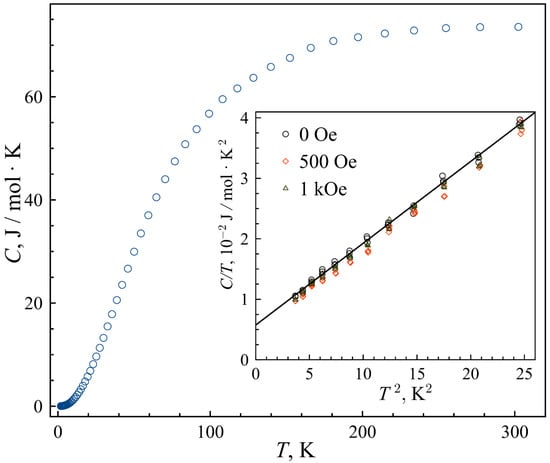
Figure 7.
Temperature dependence of the heat capacity C(T) for FeTD at zero magnetic field. The inset shows the plots at fields 0 and 500 Oe and 1 kOe.
The magnetic properties of the undopped WTe2 crystals were studied long before the discovery of their non-trivial topology [60]. The susceptibility of TD at room temperature was shown to be negative and equal to −1.5 × 10−7 emu/g. This consists of the Pauli paramagnetism (~2.2 × 10−7 emu/g) and greater diamagnetic contribution of the and ions. The total susceptibility found in [60] agrees rather well with the results obtained here at the field 1 kOe and presented in the inset to Figure 3b. The continuous increase in the susceptibility above the minimum near 85 K at increasing temperature, which is not related to magnetic ordering, is likely similar to the behavior of susceptibility in some other topological materials. Minima on the temperature dependences of susceptibility were observed in single crystals of type I WSM TaAs [64], NbP and TaP [65], as well as in graphene [66]. Such behavior was not observed, however, for the undoped and Cr-doped WTe2 at zero field and a field of 1 kOe in [51]. A theoretical treatment developed in [65] predicts for the particular case of WSM the logarithmic dependence for the susceptibility at low field and high enough temperatures. Here, is the temperature-independent coefficient and is the temperature-independent contribution. Approximation with this relationship of the susceptibility in TD at 1 kOe is shown in the inset in Figure 3b. The agreement between the theory and experiment is excellent above 250 K for and . The similar model can be used to treat the anomalous rises of susceptibility at high temperatures in the iron-doped crystals. Note that no susceptibility rise is seen in Figure 2b for FeTD up to 400 K. We can suggest that for this particular case, the susceptibility minimum and further rise are moved above the upper temperature limit of our measurements.
The iron-doped crystals, both unannealed and annealed, show the ferromagnetic ordering as can be seen from pronounced bifurcations of the ZFC and FCC curves in contrast to the undoped TD. Annealing of the doped crystals strengthened the ferromagnetismism and shifted the transition to high temperatures (Figure 2 and Figure 5). Weak magnetic anomalies below room temperature, which became more noticeable after annealing, can emerge due to antiferromagnetic correlations or charge density waves. The similar numerous magnetization maxima were observed in [67,68] on studying the magnetic and transport properties of the antiferromagnetic GdTe3 with Van der Waals structure and for frustrated antiferromagnetic with spin-glass phases [69,70]. The emergence of the Kondo effect, which coexisted with the Weyl semimetallic state, was suggested on the base of transport measurements for the Mn-doped VAl3 in [44]. The Kondo effect also can influence the low-temperature magnetism in our samples. The additional low-temperature anomalies on the temperature dependences of susceptibility were not obtained in the Cr-doped WTe2 in [51]. The nature of magnetic ordering in doped Weyl semimetals is related to the RKKY and to the Dzyaloshinskii–Moriya interactions [71,72,73].
The very interesting metamagnetic phenomenon was observed for the unannealed FeTD crystal at 5 K in the cH orientation. Metamagnetism demonstrates itself as a pronounced rise of magnetization in applied magnetic fields. The common metamagnetic phenomenon is observed due to the magnetic field-induced spin reorientation in antiferromagnets [61] and is associated with opening the hysteresis loops at a threshold field. Some recent studies reported this type of metamagnetism in topological antiferromagnets [39,40] as was mentioned in Introduction. Another type of metamagnetism emerges in conductors and is caused by charge carriers [74,75]. The hysteresis loops shown in Figure 4 are similar to the isotherms observed due to such itinerant metamagnetism. The itinerant metamagnetism was also observed in the doped topological insulator [37]. Note that the itinerant metamagnetism can be related to the changes in the Fermi surface topology [76,77]. The metamagnetism in the doped FeTD sample weakens with increasing temperature (Figure 4a) and in other crystal orientation at magnetic field (Figure 4b). Annealing suppresses completely the metamagnetism in the FeTDa sample (Figure 6).
4. Conclusions
Studies of the magnetic properties of the undoped WTe2 single crystal revealed the rise in susceptibility with increasing temperature above 80 K, which was treated using a model developed for type I Weyl semimetals. The similar anomalous rises in susceptibility were found for the iron-doped samples, both annealed and unannealed, at high enough temperatures. The paramagnetic contribution to susceptibility likely due to growth defects was observed at low temperatures in the undoped and doped crystals. The dc magnetization measurements showed the strong bifurcation of the ZFC and FCC curves in the doped samples. This demonstrated the ferromagnetic ordering that was affected by annealing. Anomalies associated with antiferromagnetism were also found. The magnetic order was suppressed by a magnetic field of 60 kOe. We also observed the anisotropy of the magnetic behavior of the doped samples. The itinerant metamagnetism was demonstrated for the unannealed doped WTe2 crystal at low temperatures for the cH orientation. At higher temperatures and another crystal orientation, the metamagnetism weakened and was masked by ferromagnetic ordering. A magnetic field did not affect the heat capacity of the iron-doped sample, which coincided with the heat capacity of the undoped WTe2.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/condmat8010006/s1, Figure S1: Comparison of X-ray diffraction (XRD) patterns for (a) WTe2 and (b) Fe doped WTe2, respectively. The patterns correspond to the crystal plane (001). The inset shows scaled diffraction peaks; Figure S2: Area EDS spectrum and table for the atomic and weight percentage of the elements.
Author Contributions
Conceptualization, A.S.K., E.V.C., M.K.L. and L.-J.C.; methodology, A.S.K., M.V.L. and E.V.S.; validation, E.V.C.; formal analysis, A.S.K. and E.V.C.; investigation, A.S.K., E.B.M. and M.V.L.; resources, S.V.N., A.N.P. and V.V.M.; data curation, A.S.K.; writing—original draft preparation, A.S.K.; writing—review and editing, E.V.C.; supervision, E.V.C. and L.-J.C.; funding acquisition, E.V.C., V.V.M., M.K.L. and L.-J.C.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by RFBR, grant 19-57-52001. The crystal growing was carried out within the state assignment of Ministry of Science and Higher Education of the Russian Federation (theme “Spin”, No. 122021000036-3), supported in part by the scholarship of the President of the Russian Federation to young scientists and graduate students (A.N. Perevalova, SP-2705.2022.1).
Data Availability Statement
Not applicable.
Acknowledgments
Measurements were carried out using the equipment of the Research park of St. Petersburg State University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Armitage, N.P.; Mele, E.J.; Vishwanath, A. Weyl and Dirac Semimetals in Three-Dimensional Solids. Rev. Mod. Phys. 2018, 90, 015001. [Google Scholar] [CrossRef]
- Lv, B.Q.; Qian, T.; Ding, H. Experimental Perspective on Three-Dimensional Topological Semimetals. Rev. Mod. Phys. 2021, 93, 025002. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, X. Berry phase in quantum oscillations of topological materials. Adv. Phys. X 2022, 7, 2064230. [Google Scholar] [CrossRef]
- Wan, X.; Turner, A.M.; Vishwanath, A.; Savrasov, S.Y. Topological Semimetal and Fermi-Arc Surface States in the Electronic Structure of Pyrochlore Iridates. Phys. Rev. B 2011, 83, 205101. [Google Scholar] [CrossRef]
- Xu, G.; Weng, H.; Wang, Z.; Dai, X.; Fang, Z. Chern Semimetal and the Quantized Anomalous Hall Effect in HgCr2Se4. Phys. Rev. Lett. 2011, 107, 186806. [Google Scholar] [CrossRef]
- Wang, Z.; Vergniory, M.G.; Kushwaha, S.; Hirschberger, M.; Chulkov, E.V.; Ernst, A.; Ong, N.P.; Cava, R.J.; Bernevig, B.A. Time-Reversal-Breaking Weyl Fermions in Magnetic Heusler Alloys. Phys. Rev. Lett. 2016, 117, 236401. [Google Scholar] [CrossRef]
- Xu, S.-Y.; Belopolski, I.; Alidoust, N.; Neupane, M.; Bian, G.; Zhang, C.; Sankar, R.; Chang, G.; Yuan, Z.; Lee, C.-C.; et al. Discovery of a Weyl Fermion Semimetal and Topological Fermi Arcs. Science 2015, 349, 613–617. [Google Scholar] [CrossRef]
- Lv, B.Q.; Weng, H.M.; Fu, B.B.; Wang, X.P.; Miao, H.; Ma, J.; Richard, P.; Huang, X.C.; Zhao, L.X.; Chen, G.F.; et al. Experimental Discovery of Weyl Semimetal TaAs. Phys. Rev. X 2015, 5, 031013. [Google Scholar] [CrossRef]
- Weng, H.; Fang, C.; Fang, Z.; Bernevig, B.A.; Dai, X. Weyl Semimetal Phase in Noncentrosymmetric Transition-Metal Monophosphides. Phys. Rev. X 2015, 5, 011029. [Google Scholar] [CrossRef]
- Huang, S.-M.; Xu, S.-Y.; Belopolski, I.; Lee, C.-C.; Chang, G.; Wang, B.; Alidoust, N.; Bian, G.; Neupane, M.; Zhang, C.; et al. A Weyl Fermion Semimetal with Surface Fermi Arcs in the Transition Metal Monopnictide TaAs Class. Nat. Commun. 2015, 6, 7373. [Google Scholar] [CrossRef]
- Deng, K.; Wan, G.; Deng, P.; Zhang, K.; Ding, S.; Wang, E.; Yan, M.; Huang, H.; Zhang, H.; Xu, Z.; et al. Experimental Observation of Topological Fermi Arcs in Type-II Weyl Semimetal MoTe2. Nature Phys. 2016, 12, 1105–1110. [Google Scholar] [CrossRef]
- Huang, L.; McCormick, T.M.; Ochi, M.; Zhao, Z.; Suzuki, M.-T.; Arita, R.; Wu, Y.; Mou, D.; Cao, H.; Yan, J.; et al. Spectroscopic Evidence for a Type II Weyl Semimetallic State in MoTe2. Nature Mater. 2016, 15, 1155–1160. [Google Scholar] [CrossRef] [PubMed]
- Liang, A.; Huang, J.; Nie, S.; Ding, Y.; Gao, Q.; Hu, C.; He, S.; Zhang, Y.; Wang, C.; Shen, B.; et al. Electronic Evidence for Type II Weyl Semimetal State in MoTe2. arXiv 2016, arXiv:1604.01706. [Google Scholar] [CrossRef]
- Tamai, A.; Wu, Q.S.; Cucchi, I.; Bruno, F.Y.; Riccò, S.; Kim, T.K.; Hoesch, M.; Barreteau, C.; Giannini, E.; Besnard, C.; et al. Fermi Arcs and Their Topological Character in the Candidate Type-II Weyl Semimetal MoTe2. Phys. Rev. X 2016, 6, 031021. [Google Scholar] [CrossRef]
- Jiang, J.; Liu, Z.K.; Sun, Y.; Yang, H.F.; Rajamathi, C.R.; Qi, Y.P.; Yang, L.X.; Chen, C.; Peng, H.; Hwang, C.-C.; et al. Signature of Type-II Weyl Semimetal Phase in MoTe2. Nat. Commun. 2017, 8, 13973. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.; Huang, J.; Nie, S.; Liu, G.; Liang, A.; Zhang, Y.; Shen, B.; Liu, J.; Hu, C.; et al. Observation of Fermi Arc and Its Connection with Bulk States in the Candidate Type-II Weyl Semimetal WTe2. Phys. Rev. B 2016, 94, 241119. [Google Scholar] [CrossRef]
- Lin, C.-L.; Kawakami, N.; Arafune, R.; Minamitani, E.; Takagi, N. Scanning Tunneling Spectroscopy Studies of Topological Materials. J. Phys. Condens. Matter 2020, 32, 243001. [Google Scholar] [CrossRef]
- Belopolski, I.; Sanchez, D.S.; Ishida, Y.; Pan, X.; Yu, P.; Xu, S.-Y.; Chang, G.; Chang, T.-R.; Zheng, H.; Alidoust, N.; et al. Discovery of a New Type of Topological Weyl Fermion Semimetal State in MoxW1−xTe2. Nat. Commun. 2016, 7, 13643. [Google Scholar] [CrossRef]
- Belopolski, I.; Xu, S.-Y.; Ishida, Y.; Pan, X.; Yu, P.; Sanchez, D.S.; Zheng, H.; Neupane, M.; Alidoust, N.; Chang, G.; et al. Fermi Arc Electronic Structure and Chern Numbers in the Type-II Weyl Semimetal Candidate MoxW1−xTe2. Phys. Rev. B 2016, 94, 085127. [Google Scholar] [CrossRef]
- Xu, S.-Y.; Alidoust, N.; Chang, G.; Lu, H.; Singh, B.; Belopolski, I.; Sanchez, D.S.; Zhang, X.; Bian, G.; Zheng, H.; et al. Discovery of Lorentz-Violating Type II Weyl Fermions in LaAlGe. Sci. Adv. 2017, 3, e1603266. [Google Scholar] [CrossRef]
- Bruno, F.Y.; Tamai, A.; Wu, Q.S.; Cucchi, I.; Barreteau, C.; de la Torre, A.; McKeown Walker, S.; Riccò, S.; Wang, Z.; Kim, T.K.; et al. Observation of Large Topologically Trivial Fermi Arcs in the Candidate Type-II Weyl Semimetal WTe2. Phys. Rev. B 2016, 94, 121112. [Google Scholar] [CrossRef]
- Li, P.; Wen, Y.; He, X.; Zhang, Q.; Xia, C.; Yu, Z.-M.; Yang, S.A.; Zhu, Z.; Alshareef, H.N.; Zhang, X.-X. Evidence for Topological Type-II Weyl Semimetal WTe2. Nat. Commun. 2017, 8, 2150. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.J.; Gong, J.X.; Liang, D.D.; Ge, M.; Wang, J.R.; Zhu, W.K. Planar Hall Effect in Type-II Weyl Semimetal WTe2. arXiv 2018, arXiv:1801.05929. [Google Scholar] [CrossRef]
- Antonenko, A.O.; Charnaya, E.V.; Pirozerskii, A.L.; Nefedov, D.Y.; Lee, M.K.; Chang, L.J.; Haase, J.; Naumov, S.V.; Domozhirova, A.N.; Marchenkov, V.V. 125Te Spin-Lattice Relaxation in a Candidate to Weyl Semimetals WTe2. Results Phys. 2021, 21, 103793. [Google Scholar] [CrossRef]
- Soluyanov, A.A.; Gresch, D.; Wang, Z.; Wu, Q.; Troyer, M.; Dai, X.; Bernevig, B.A. Type-II Weyl Semimetals. Nature 2015, 527, 495–498. [Google Scholar] [CrossRef] [PubMed]
- Kabashima, S. Electrical Properties of Tungsten-Ditelluride WTe2. J. Phys. Soc. Jpn. 1966, 21, 945–948. [Google Scholar] [CrossRef]
- Wu, Y.; Jo, N.H.; Ochi, M.; Huang, L.; Mou, D.; Bud’ko, S.L.; Canfield, P.C.; Trivedi, N.; Arita, R.; Kaminski, A. Temperature-Induced Lifshitz Transition in WTe2. Phys. Rev. Lett. 2015, 115, 166602. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.N.; Xiong, J.; Flynn, S.; Tao, J.; Gibson, Q.D.; Schoop, L.M.; Liang, T.; Haldolaarachchige, N.; Hirschberger, M.; Ong, N.P.; et al. Large, Non-Saturating Magnetoresistance in WTe2. Nature 2014, 514, 205–208. [Google Scholar] [CrossRef]
- Pirozerskii, A.L.; Charnaya, E.V.; Lee, M.K.; Chang, L.-J.; Naumov, S.V.; Domozhirova, A.N.; Marchenkov, V.V. Magnetoresistance and Quantum Oscillations in WTe2 Semimetal. Phys. Solid State 2022, 64, 80–84. [Google Scholar] [CrossRef]
- He, P.; Hsu, C.-H.; Shi, S.; Cai, K.; Wang, J.; Wang, Q.; Eda, G.; Lin, H.; Pereira, V.M.; Yang, H. Nonlinear magnetotransport shaped by Fermi surface topology and convexity. Nat. Commun. 2019, 10, 1290. [Google Scholar] [CrossRef]
- Fei, Z.; Zhao, W.; Palomaki, T.A.; Sun, B.; Miller, M.K.; Zhao, Z.; Yan, J.; Xu, X.; Cobden, D.H. Ferroelectric Switching of a Two-Dimensional Metal. Nature 2018, 560, 336–339. [Google Scholar] [CrossRef] [PubMed]
- Ji, S.; Grånäs, O.; Weissenriede, J. Manipulation of Stacking Order in Td-WTe2 by Ultrafast Optical Excitation. ACS Nano 2021, 15, 8826–8835. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Hu, M.; Qin, J.; Xia, B.; Liu, C.; Wang, S.; Guan, D.; Li, Y.; Zheng, H.; Liu, J.; et al. Strain Tunable Semimetal–Topological-Insulator Transition in Monolayer 1T′−WTe2. Phys. Rev. Lett. 2020, 125, 046801. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.; Wang, P.; Chiu, C.L.; Song, Z.; Yu, G.; Jäck, B.; Lei, S.; Klemenz, S.; Cevallos, F.A.; Onyszczak, M.; et al. Evidence for a monolayer excitonic insulator. Nat. Phys. 2022, 18, 87–93. [Google Scholar] [CrossRef]
- Li, J.; Rashetnia, M.; Lohmann, M.; Koo, J.; Xu, Y.; Zhang, X.; Watanabe, K.; Taniguchi, T.; Jia, S.; Chen, X.; et al. Proximity-magnetized quantum spin Hall insulator: Monolayer 1 T’ WTe2/Cr2Ge2Te6. Nat. Commun. 2022, 13, 5134. [Google Scholar] [CrossRef]
- Chang, C.-Z.; Zhang, J.; Feng, X.; Shen, J.; Zhang, Z.; Guo, M.; Li, K.; Ou, Y.; Wei, P.; Wang, L.-L.; et al. Experimental Observation of the Quantum Anomalous Hall Effect in a Magnetic Topological Insulator. Science 2013, 340, 167–170. [Google Scholar] [CrossRef]
- Khachatryan, A.S.; Charnaya, E.V.; Shevchenko, E.V.; Likholetova, M.V.; Lee, M.K.; Chang, L.J.; Naumov, S.V.; Domozhirova, A.N.; Marchenkov, V.V. Coexistence of Magnetic States and Metamagnetism in the Bi2-xCrxSe3 Topological Insulators. EPL 2021, 134, 47002. [Google Scholar] [CrossRef]
- Maurya, V.K.; Patidar, M.M.; Dhaka, A.; Rawat, R.; Ganesan, V.; Dhaka, R.S. Magnetotransport and Berry phase in magnetically doped Bi0.97−xSb0.03 single crystals. Phys. Rev. B 2020, 102, 144412. [Google Scholar] [CrossRef]
- Tan, A.; Labracherie, V.; Kunchur, N.; Wolter, A.U.B.; Cornejo, J.; Dufouleur, J.; Büchner, B.; Isaeva, A.; Giraud, R. Metamagnetism of Weakly Coupled Antiferromagnetic Topological Insulators. Phys. Rev. Lett. 2020, 124, 197201. [Google Scholar] [CrossRef]
- Lei, C.; Heinonen, O.; MacDonald, A.H.; McQueeney, R.J. Metamagnetism of Few-Layer Topological Antiferromagnets. Phys. Rev. Mater. 2021, 5, 064201. [Google Scholar] [CrossRef]
- Chen, F.C.; Luo, X.; Xiao, R.C.; Lu, W.J.; Zhang, B.H.; Yang, H.X.; Li, J.Q.; Pei, Q.L.; Shao, D.F.; Zhang, R.R.; et al. Superconductivity enhancement in the S-doped Weyl semimetal candidate MoTe2. Appl. Phys. Lett. 2016, 108, 162601. [Google Scholar] [CrossRef]
- Mandal1, M.; Patra, C.; Kataria, A.; Suvodeep, P.; Saha, S.; Singh, R.P. Superconductivity in doped Weyl semimetal Mo0.9Ir0.1Te2 with broken inversion symmetry. Supercond. Sci. Technol. 2022, 35, 025011. [Google Scholar] [CrossRef]
- Deng, M.-X.; Luo, W.; Wang, R.-Q.; Sheng, L.; Xing, D.Y. Weyl semimetal induced from a Dirac semimetal by magnetic doping. Phys. Rev. B 2017, 96, 155141. [Google Scholar] [CrossRef]
- Lee, K.-Y.; Yun, J.-H.; Kim, J.H.; Salawu, Y.A.; Kim, H.-J.; Lee, J.J.; Lee, H.; Rhyee, J.-S. Coexistence of Kondo Effect and Weyl Semimetallic States in Mn-Doped MnxVAl3 Compounds. Mater. Today Phys. 2022, 26, 100732. [Google Scholar] [CrossRef]
- Singh, A.; Sasmal, S.; Iyer, K.K.; Thamizhavel, A.; Maiti, K. Evolution of Extremely Large Magnetoresistance in a Weyl Semimetal, WTe2 with Ni-Doping. Phys. Rev. Mater. 2022, 6, 124202. [Google Scholar] [CrossRef]
- Kumar, N.; Guin, S.N.; Manna, K.; Shekhar, C.; Felser, C. Topological Quantum Materials from the Viewpoint of Chemistry. Chem. Rev. 2021, 121, 2780–2815. [Google Scholar] [CrossRef]
- Lin, E.-C.; Lin, Y.-T.; Chou, C.-T.; Chen, C.-A.; Wu, Y.-J.; Chen, P.-H.; Lee, S.-F.; Chang, C.-S.; Chen, Y.-F.; Lee, Y.-H. Enhanced Magnetoresistance of Doped WTe2 Single Crystals. ACS Appl. Electron. Mater. 2022, 4, 4540–4546. [Google Scholar] [CrossRef]
- Zhu, L.; Li, Q.-Y.; Lv, Y.; Li, S.; Zhu, X.-Y.; Jia, Z.-Y.; Chen, Y.B.; Wen, J.; Li, S.-C. Superconductivity in Potassium-intercalated Td-WTe2. Nano Lett. 2018, 18, 6585–6590. [Google Scholar] [CrossRef] [PubMed]
- Basnet, R.; Pandey, K.; Acharya, G.; Nabi, M.R.U.; Wegner, A.; Hu, J. Transport Properties of Fe-doped type-II Weyl semimetal WTe2. Bull. Am. Phys. Soc. 2021, 66, 1. Available online: https://meetings.aps.org/Meeting/MAR21/Session/E51.6 (accessed on 16 March 2021).
- Basnet, R.; Pandey, K.; Acharya, G.; Nabi, M.R.U.; Wegner, A.; Stephenson, C.B.; Bishop, S.; Hu, J. Metal-insulator transition in Fe-doped type-II Weyl semimetal WTe2. Bull. Am. Phys. Soc. 2022, 67, 3. Available online: https://meetings.aps.org/Meeting/MAR22/Session/Q70.11 (accessed on 16 March 2022).
- Yang, L.; Wu, H.; Zhang, L.; Zhang, W.; Li, L.; Kawakami, T.; Sugawara, K.; Sato, T.; Zhang, G.; Gao, P.; et al. Highly Tunable Near-Room Temperature Ferromagnetism in Cr-Doped Layered Td-WTe2. Adv. Funct. Mater. 2021, 31, 2008116. [Google Scholar] [CrossRef]
- Kohno, H. Spintronics with Weyl Semimetal. JPSJ News Comments 2021, 18, 13. [Google Scholar] [CrossRef]
- Yang, S.A. Dirac and Weyl Materials: Fundamental Aspects and Some Spintronics Applications. SPIN 2016, 06, 1640003. [Google Scholar] [CrossRef]
- Rubel, M.H.K.; Hossain, M.K. Crystal Structures and Properties of Nanomagnetic Materials. In Fundamentals of Low Dimensional Magnets, 1st ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2022; Chapter 10. [Google Scholar] [CrossRef]
- Anik, M.I.; Hossain, M.K.; Hossain, I.; Mahfuz, A.M.U.B.; Rahman, M.T.; Ahmed, I. Recent progress of magnetic nanoparticles in biomedical applications: A review. Nano Select 2021, 2, 1146–1186. [Google Scholar] [CrossRef]
- Perevalova, A.N.; Naumov, S.V.; Podgornykh, S.M.; Chistyakov, V.V.; Marchenkova, E.B.; Fominykh, B.M.; Marchenkov, V.V. Kinetic Properties of a Topological Semimetal WTe2 Single Crystal. Phys. Met. Metallogr. 2022, 123, 1061–1067. [Google Scholar] [CrossRef]
- Brown, B.E. The Crystal Structures of WTe2 and High-Temperature MoTe2. Acta Cryst. 1966, 20, 268–274. [Google Scholar] [CrossRef]
- Kang, D.; Zhou, Y.; Yi, W.; Yang, C.; Guo, J.; Shi, Y.; Zhang, S.; Wang, Z.; Zhang, C.; Jiang, S.; et al. Superconductivity Emerging from a Suppressed Large Magnetoresistant State in Tungsten Ditelluride. Nat. Commun. 2015, 6, 7804. [Google Scholar] [CrossRef]
- Pan, X.-C.; Chen, X.; Liu, H.; Feng, Y.; Wei, Z.; Zhou, Y.; Chi, Z.; Pi, L.; Yen, F.; Song, F.; et al. Pressure-Driven Dome-Shaped Superconductivity and Electronic Structural Evolution in Tungsten Ditelluride. Nat. Commun. 2015, 6, 7805. [Google Scholar] [CrossRef]
- Mar, A.; Jobic, S.; Ibers, J.A. Metal-Metal vs. Tellurium-Tellurium Bonding in WTe2 and Its Ternary Variants TaIrTe4 and NbIrTe4. J. Am. Chem. Soc. 1992, 114, 8963–8971. [Google Scholar] [CrossRef]
- Stryjewski, E.; Giordano, N. Metamagnetism. Adv. Phys. 1977, 26, 487–650. [Google Scholar] [CrossRef]
- Quinn, J.J.; Yi, K.-S. Solid State Physics: Principles and Modern Applications; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-540-92230-8. [Google Scholar]
- Callanan, J.E.; Hope, G.A.; Weir, R.D.; Westrum, E.F. Thermodynamic Properties of Tungsten Ditelluride (WTe2) I. The Preparation and Low temperature Heat Capacity at Temperatures from 6 K to 326 K. J. Chem. Thermodyn. 1992, 24, 627–638. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Guo, L.; Chen, X.; Yuan, Y.; Liu, F.; Prucnal, S.; Helm, M.; Zhou, S. Intrinsic Diamagnetism in the Weyl Semimetal TaAs. J. Magn. Magn. Mater. 2016, 408, 73–76. [Google Scholar] [CrossRef]
- Leahy, I.A.; Lin, Y.-P.; Siegfried, P.E.; Treglia, A.C.; Song, J.C.W.; Nandkishore, R.M.; Lee, M. Nonsaturating Large Magnetoresistance in Semimetals. Proc. Natl. Acad. Sci. USA 2018, 115, 10570–10575. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Chen, L.; Meng, S.; Guo, L.; Huang, J.; Liu, Y.; Wang, W.; Chen, X. Field and Temperature Dependence of Intrinsic Diamagnetism in Graphene: Theory and Experiment. Phys. Rev. B 2015, 91, 094429. [Google Scholar] [CrossRef]
- Lei, S.; Lin, J.; Jia, Y.; Gray, M.; Topp, A.; Farahi, G.; Klemenz, S.; Gao, T.; Rodolakis, F.; McChesney, J.L.; et al. High Mobility in a van Der Waals Layered Antiferromagnetic Metal. Sci. Adv. 2020, 6, eaay6407. [Google Scholar] [CrossRef]
- Guo, Q.; Bao, D.; Zhao, L.J.; Ebisu, S. Novel Magnetic Behavior of Antiferromagnetic GdTe3 Induced by Magnetic Field. Phys. B Condens. 2021, 617, 413153. [Google Scholar] [CrossRef]
- Pakhira, S.; Mazumdar, C.; Ranganathan, R.; Giri, S.; Avdeev, M. Large Magnetic Cooling Power Involving Frustrated Antiferromagnetic Spin-Glass State in R2NiSi3 (R = Gd, Er). Phys. Rev. B 2016, 94, 104414. [Google Scholar] [CrossRef]
- Pal, S.; Kumar, K.; Banerjee, A. Memorylike Response of the Magnetic Glass. Phys. Rev. B 2021, 103, 144434. [Google Scholar] [CrossRef]
- Wang, S.-X.; Chang, H.-R.; Zhou, J. RKKY Interaction in Three-Dimensional Electron Gases with Linear Spin-Orbit Coupling. Phys. Rev. B 2017, 96, 115204. [Google Scholar] [CrossRef]
- Araki, Y.; Nomura, K. Spin Textures and Spin-Wave Excitations in Doped Dirac-Weyl Semimetals. Phys. Rev. B 2016, 93, 094438. [Google Scholar] [CrossRef]
- Hosseini, M.V.; Askari, M. Ruderman-Kittel-Kasuya-Yosida Interaction in Weyl Semimetals. Phys. Rev. B 2015, 92, 224435. [Google Scholar] [CrossRef]
- Levitin, R.Z.; Markosyan, A.S. Itinerant Metamagnetism. Sov. Phys. Usp. 1988, 21, 730. [Google Scholar] [CrossRef]
- Leithe-Jasper, A.; Schnelle, W.; Rosner, H.; Baenitz, M.; Rabis, A.; Gippius, A.A.; Morozova, E.N.; Borrmann, H.; Burkhardt, U.; Ramlau, R.; et al. Weak Itinerant Ferromagnetism and Electronic and Crystal Structures of Alkali-Metal Iron Antimonides: NaFe4Sb12 and KFe4Sb12. Phys. Rev. B 2004, 70, 214418. [Google Scholar] [CrossRef]
- Yamaji, Y.; Misawa, T.; Imada, M. Quantum Metamagnetic Transitions Induced by Changes in Fermi-Surface Topology: Applications to a Weak Itinerant-Electron Ferromagnet ZrZn2. J. Phys. Soc. Jpn. 2007, 76, 063702. [Google Scholar] [CrossRef][Green Version]
- Chen, W.; James, A.D.N.; Dugdale, S.B. Local Electron Correlation Effects on the Fermiology of the Weak Itinerant Ferromagnet ZrZn2. Electron. Struct. 2022, 4, 045002. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).