Charge–Phase Duality and Cotunneling of Fluxons in SQUID-like Nanorings

Abstract

Employing charge–flux duality for Josephson junctions and superconducting nanowires, we predict a novel effect of fluxon cotunneling in SQUID-like nanorings. This process is strictly dual to that of Cooper pair cotunneling in superconducting transistors formed by a pairs of Josephson tunnel junctions connected in series. Cooper pair cotunneling is known to lift Coulomb blockade in these structures at low temperatures. Likewise, fluxon cotunneling may eliminate the magnetic blockade of superconducting phase fluctuations in SQUID-like nanorings, driving them into an insulating state.

1. Introduction

Recent technological progress made in the miniaturization of superconducting circuits and devices has led to a large number of new interesting effects [1]. Among these devices, superconducting circuits with ultrasmall tunnel junctions [2] and superconducting nanowires/nanorings [3,4] attract a lot of attention in the community, demonstrating the non-trivial interplay occurring between quantum coherent phenomena and dissipative effects.

A fundamentally important property of the above structures is the so-called charge–phase (or charge–flux) duality. This property was initially discovered for ultrasmall Josephson junctions [5,6,7], implying that under a certain transformation for the junction parameters, the quantum dynamics of Cooper pairs (with the charge $2e$) in such systems is identical to that of magnetic flux quanta ${\mathsf{\Phi }}_0=\pi /e$. Later on, the same duality arguments were extended to superconducting nanowires [8,9]. In particular, charge–flux duality allows us to establish and understand a profound relationship between the superconducting and insulating behavior of these systems.

Manifestations and implications of the charge–flux duality in Josephson junctions and superconducting nanowires were observed in a variety of experiments. These observations include the coherent tunneling of magnetic flux quanta through superconducting nanowires [10], Coulomb blockade and Bloch steps [11,12,13,14], as well as the coexistence of the local superconductivity and global localization of Cooper pairs [15]. These and other observations open new horizons for applications of such systems in modern nanoelectronics, metrology, and information technology. For instance, operations of duality-based single-charge transistor [16] and charge quantum interference devices [17] have been demonstrated. Superconducting junctions and nanowires have also been proposed to serve as central elements of both charge- and flux-based qubits [18,19,20], as well as for creating an electric current standard [13,14,21].

In this work, we further extend the duality arguments explicitly involving the effect of cotunneling. The importance of the cotunneling of single electrons in systems of coupled normal tunnel junctions in the Coulomb blockade regime was pointed out by Averin and Nazarov [22,23]. At low temperatures, the sequential tunneling of electrons across different tunnel barriers involves intermediate states with substantially higher energies and, hence, yields a vanishing contribution to the system conductance $\propto exp(-E_C/T)$, where $E_C$ is some characteristic charging energy. In this case, cotunneling—i.e., the (almost) simultaneous tunneling of electrons across different barriers—may lift the Coulomb blockade and dominate the system conductance, as it does not cause any extra charging in the course of tunneling. Golubev and Zaikin [24] demonstrated that charge fluctuations in a chain of N normal tunnel junctions are dominated by the process of electron cotunneling, which generates the power–law $I-V$ curve in the form $I\sim V^{2N-1+1/2g_s}$ (where $g_s$ is the dimensionless conductance of the external leads), in agreement with earlier experimental findings [25,26]. The significance of electron cotunneling for current fluctuations was also emphasized in [27,28], where the super-Poissonian behavior of shot noise in chains of tunnel-coupled quantum dots was demonstrated in the Coulomb blockade regime. Cooper pair cotunneling in the superconducting single charge transistor was also discussed theoretically [29] and realized in a number of experiments [30,31].

In all the above examples, one essentially deals only with the cotunneling of discrete charges—single electrons or Cooper pairs. Below, we predict and analyze a novel effect of flux cotunneling. We will demonstrate that this effect may crucially influence the low-temperature properties of SQUID-like nanorings, turning their superconducting behavior into an insulating one.

2. Results

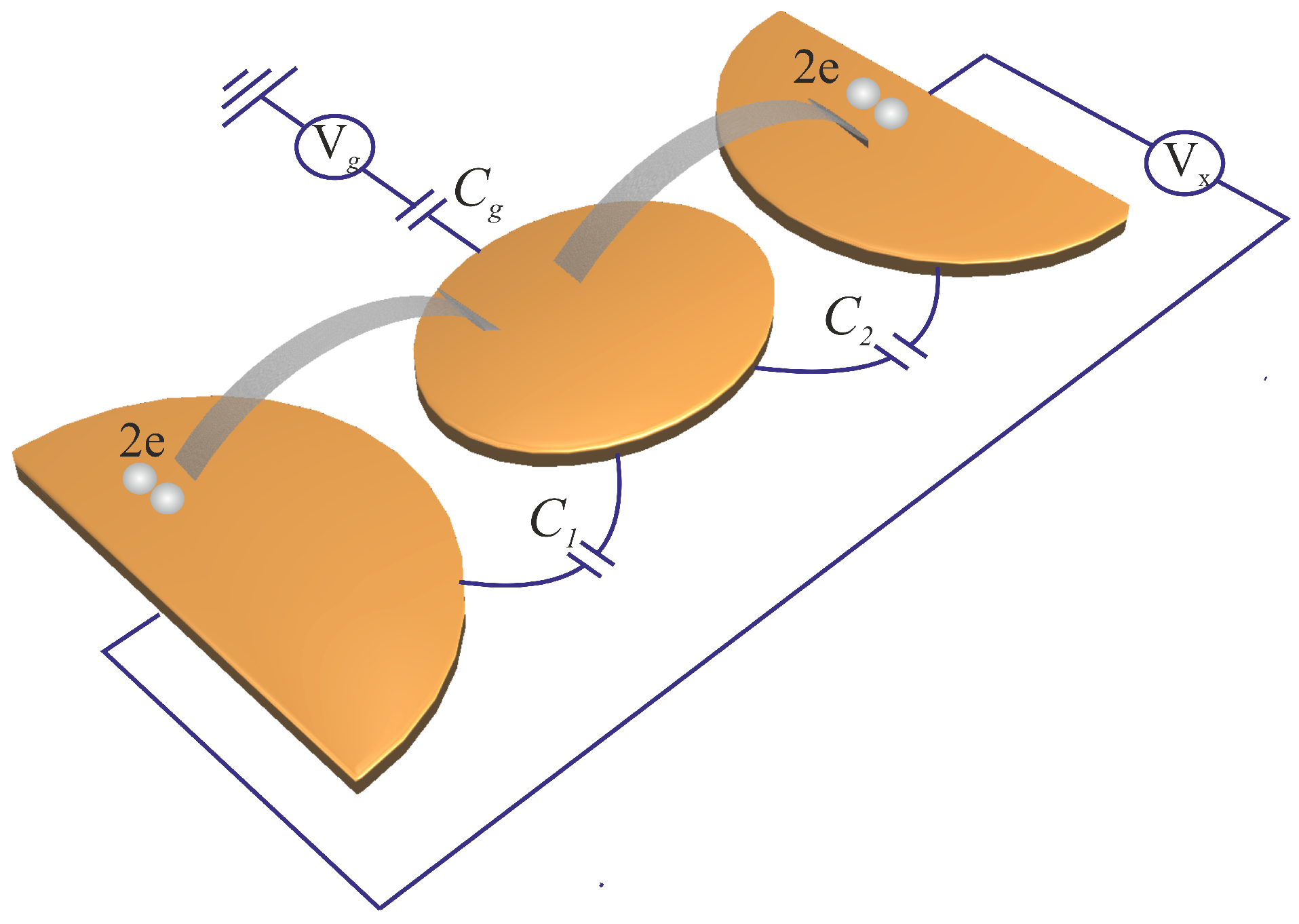
We begin our analysis by considering the system displayed in Figure 1. This system represents a Copper pair transistor, which consists of three superconducting islands connected in series via tunnel junctions with capacitances of $C_1$ and $C_2$ and Josephson coupling energies of $E_{J1}$ and $E_{J2}$. The charge of the central island is controlled by the gate voltage $V_g$ via gate capacitance $C_g$. We will also assume that the superconducting phase difference for the two outer islands is externally kept equal to ${\phi }_0$ and does not fluctuate in time. This phase may either stay constant (provided an externally applied voltage $V_x$ is equal to zero) or depend linearly on time according to the Josephson relation ${\dot{\phi }}_0=2e{V}_x$.

Figure 1. Cooper pair transistor.

The Hamiltonian of our Cooper pair transistor reads

$${\widehat{H}}_{CPT}=E_C{(\widehat{q}-q_g)}^2-\sum _{n=1,2}{E}_{Jn}cos\left(\widehat{\phi }-{(-1)}^n\frac{{\phi }_0}{2}\right),$$

(1)

where the first term on the right-hand side accounts for the charging energy of the system (with $E_C=2e^2/(C_1+C_2+C_g)$) being the charging energy for a Cooper pair) and the last term describes the Josephson coupling energies of two tunnel junctions. Here, we introduced the (dimensionless) charge operator for the central island $\widehat{q}\equiv \widehat{Q}/2e$ and the gate charge $q_g=V_g{C}_g/2e$ normalized to that of a Cooper pair $2e$. The operator $\widehat{\phi }$ corresponds to the superconducting phase of the central island being canonically conjugate to that of the charge $\widehat{q}$—i.e., these two operators obey the commutation relation $[\widehat{q},\widehat{\phi }]=-i$.

Consider the limit of low temperatures and high charging energies $T,E_{J1,2}\ll E_C$. In this case, for $q_g$, not very close to the values $\pm 1/2,\pm 3/2,\cdots$, the sequential tunneling of Cooper pairs in both Josephson junctions is strongly suppressed because each tunneling event of a Cooper pair to/from the central island increases the system energy by a large amount $\sim E_C$, thus being energetically unfavorable. Hence, one could naively conclude that in this regime charge transfer across CPT would be impossible due to Coulomb blockade of Cooper pairs, and the system would behave as an insulator.

This conclusion, however, turns out to be premature due to the presence of Cooper pair cotunneling, which dominates the charge transfer across CPT in the above “Coulomb blockade” regime. According to this mechanism, Cooper pairs may tunnel across two junctions (see Figure 1) almost simultaneously, keeping the system charging energy unchanged except for a short time interval $\delta t\sim 1/E_C$.

Merely for pedagogical purposes, we now present a detailed calculation of the ground state energy $E_0(q_g,{\phi }_0)$ of CPT perturbatively in $E_{J1,2}$. In doing so, we will closely follow the analysis [2] (see, e.g., Section 3.3.5 of that work). The grand partition function of our system can be represented as a path integral over all possible charge configurations of the central island $q\left(\tau \right)$ in the form

$${\mathcal{Z}}_{q_g}=\sum _{p=-\infty }^{\infty }\tilde{\mathcal{Z}}(q_g+p),$$

(2)

where

$$\begin{array}{c}\tilde{\mathcal{Z}}\left(q_g\right)={\int }_{q_g}^{q_g}\mathcal{D}q\left(\tau \right)\sum _{n,m=0}^{\infty }\frac{1}{n!m!}\left(\frac{E_{J1}^n{E}_{J2}^m}{2^{n+m}}\right){\int }_0^{1/T}d{\tau }_1...{\int }_0^{1/T}d{\tau }_n{\int }_0^{1/T}d{\tau }_1^{\prime }...{\int }_0^{1/T}d{\tau }_m^{\prime }\hfill \\ \hfill \times \sum _{{ϵ}_j=\pm 1,{\nu }_k=\pm 1}exp\left[\frac{i{\phi }_0}{2}\left(\sum _{j=1}^n{ϵ}_j+\sum _{k=1}^m{\nu }_k\right)\right]\delta (\dot{q}\left(\tau \right)-{\dot{q}}_{n,m}\left(\tau \right))exp\left(-E_C{\int }_0^{1/T}d\tau q^2\left(\tau \right)\right)\end{array}$$

(3)

and

$$q_{n,m}\left(\tau \right)=\sum _{j=1}^n{ϵ}_j\theta (\tau -{\tau }_j)-\sum _{k=1}^m{\nu }_k\theta (\tau -{\tau }_k^{\prime }).$$

(4)

All charge trajectories $q\left(\tau \right)$ start and end at a value of the gate charge $q_g$, implying that the sum in Equation (3) runs only over positive and negative unity charges ${ϵ}_j$ and ${\nu }_k$, obeying the neutrality condition

$$\sum _{j=1}^n{ϵ}_j-\sum _{k=1}^m{\nu }_k=0.$$

(5)

These trajectories describe charge jumps corresponding to tunneling events of Cooper pairs across the first and second junctions, respectively, at $\tau ={\tau }_j$ and $\tau ={\tau }_k^{\prime }$.

In the limit $E_{J1,2}\ll E_C$, we can proceed perturbatively in the Josephson coupling energies $E_{J1,2}$. In this case, the main charge configurations are those in the second order in such energies corresponding to two tunneling events of Cooper pairs (see Figure 1), either across one of the junctions ($\propto E_{J1}^2$ or $\propto E_{J2}^2$) or across both of them ($\propto E_{J1}{E}_{J2}$). The first class of trajectories can be safely disregarded, as it plays no significant role except for an immediate vicinity of the gate charge values $q_g=\pm 1/2$, where the charge states $q=q_g$ and $q=q_g\mp 1$ become degenerate. Taking into account the remaining trajectories describing two successive tunneling events across the first and the second Josephson junctions, in the limit $T\to 0$ we obtain

$$\tilde{\mathcal{Z}}\left(q_g\right)\sim exp[-E_0(q_g,{\phi }_0)/T],$$

(6)

where the ground state energy has the form

$$\begin{array}{c}{E}_0(q_g,{\phi }_0)\simeq E_C{q}_g^2-\frac{E_{J1}{E}_{J2}}{2}{e}^{-E_C{q}_g^2/T}cos{\phi }_0{\int }_0^{1/T}d\tau \sum _{\pm }{e}^{-E_C(1\pm 2q_g)\tau }\hfill \\ \hfill =E_C{q}_g^2-\frac{E_{J1}{E}_{J2}cos{\phi }_0}{E_C(1-4q_g^2)},\left|q_g\right|<\frac{1}{2}.\end{array}$$

(7)

Taking the derivative of $E_0$ (7) with respect to ${\phi }_0$, one immediately arrives at the cotunneling contribution to the supercurrent $I_S$ flowing across CPT in the form

$$I_S=I_{C}sin{\phi }_0,I_C=\frac{2e{E}_{J1}{E}_{J2}}{E_C(1-4q_g^2)},\left|q_g\right|<\frac{1}{2}.$$

(8)

Thus, even in the “Coulomb blockade” regime $E_C\gg T,E_{J1,2}$, the system of Figure 1 actually behaves as a superconductor rather than as an insulator due to the effect of Cooper pair cotunneling.

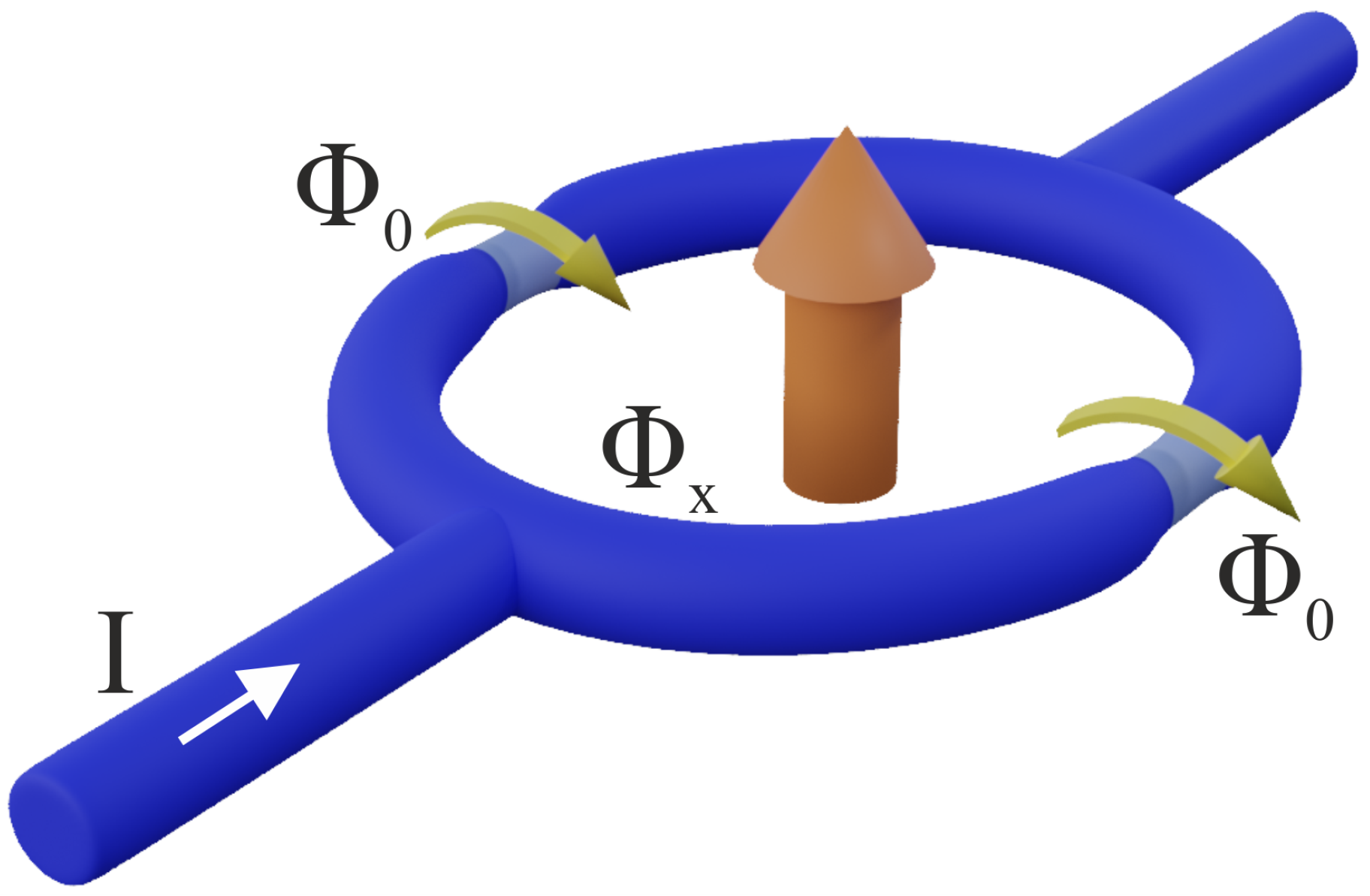
Let us now turn to a somewhat different structure displayed in Figure 2. This structure represents a SQUID-like nanoring formed by thicker superconducting wires containing two weak links, which can be either Josephson junctions (again with coupling energies $E_{J1,2}$ and charging energies $E_{C1,2}$) or, alternatively, segments of ultranarrow superconducting wires of lengths $L_{1,2}$ and normal state resistances $R_{1,2}$. In the first case, we will assume the condition $E_{Ji}>E_{Ci}$ ($i=1,2$) to be fulfilled, while in the second one an analogous condition reads $R_i/L_i<R_q/{\xi }_i$, where $R_q=2\pi /e^2\simeq 25.8$ k$\mathsf{\Omega }$ is the quantum resistance unit and ${\xi }_i$ is the superconducting coherence length for the i-th wire. The ring has inductance $\mathcal{L}$ and is pierced by external magnetic flux ${\mathsf{\Phi }}_x$. It can also be biased by an external current I, as shown in the Figure 2.

Figure 2. SQUID-like nanoring.

Under the above conditions, most important fluctuations of the superconducting phase across both weak links are instantons [1,2] or quantum phase slips (QPS), which are the same [1,3,4]. Physically, each QPS event describes the process of quantum tunneling of the phase difference across a weak link by $\delta \phi =\pm 2\pi$ accompanied by the voltage pulse $\delta V=\dot{\phi }/2e$, which, in turn, implies the tunneling of one magnetic flux quantum ${\mathsf{\Phi }}_0\equiv \pi /e=\int \left|V\left(t\right)\right|dt$ between the outer and inner parts of the ring, as is schematically indicated in Figure 2.

In our further analysis, we will essentially employ phase-charge duality arguments. Slightly generalizing the results [4,9], one can write the Hamiltonian of our SQUID-like nanoring in the form

$${\widehat{H}}_{SR}=E_{\mathcal{L}}{(\widehat{\varphi }-{\varphi }_x)}^2-\sum _{n=1,2}{\gamma }_{n}cos\left(\widehat{\chi }-{(-1)}^n\frac{{\chi }_0}{2}\right),$$

(9)

where the first term is responsible for the magnetic energy of the ring, while the second one takes care of QPS effects in both superconducting weak links. Here, we introduced the magnetic flux operator (normalized to the flux quantum ${\mathsf{\Phi }}_0$) $\widehat{\varphi }=\widehat{\mathsf{\Phi }}/{\mathsf{\Phi }}_0$ and defined the magnetic energy for a flux quantum $E_{\mathcal{L}}={\mathsf{\Phi }}_0^2/2\mathcal{L}$, as well as the dimensionless magnetic flux ${\varphi }_x={\mathsf{\Phi }}_x/{\mathsf{\Phi }}_0$. The operator $\widehat{\chi }/{\mathsf{\Phi }}_0$ controls the charge flowing around the ring. The value ${\chi }_0/{\mathsf{\Phi }}_0$ is set by the charge Q that has passed across the structure up to some moment of time. It can either stay constant, provided an external current I is turned off, or depends linearly on time, obeying the equation ${\dot{\chi }}_0={\mathsf{\Phi }}_{0}I$. As before, the flux and charge are canonically conjugate operators obeying the commutation relations $[\widehat{\varphi },\widehat{\chi }]=-i$.

The quantities ${\gamma }_{1,2}$ represent QPS amplitudes for two weak links. For the problem in question, they take the standard form ${\gamma }_i=B_{i}exp(-A_i)$, where $A_i\sim \sqrt{E_{Ji}/E_{Ci}}$, $B_i\sim E_{Ji}^{3/4}{E}_{Ci}^{1/4}$ in the case of Josephson junctions [2] and $A_i\sim (R_q/R_i)(L_i/\xi )$, $B_i\sim A_i{\mathsf{\Delta }}_i(L_i/\xi )$ in the case of superconducting nanowires [32], with ${\mathsf{\Delta }}_i$ being the mean field value of the superconducting order parameter in the corresponding nanowire.

One can easily observe that the two Hamiltonians (1) and (9) are exactly dual to each other under the transformation

$$\widehat{q}\leftrightarrow \widehat{\varphi },\widehat{\phi }\leftrightarrow \widehat{\chi },E_C\leftrightarrow E_{\mathcal{L}},E_{Jn}\leftrightarrow {\gamma }_n,{\phi }_0\leftrightarrow {\chi }_0.$$

(10)

Hence, all physical properties of the systems displayed in Figure 1 and Figure 2 are dual to each other and one can immediately translate the results derived for CPT to the SQUID-like nanoring of Figure 2 without any extra calculation.

In the absence of quantum phase slips, the structure should sustain a non-vanishing supercurrent and, hence, remain superconducting. By contrast, proliferating quantum phase slips in each of the weak links (the process dual to sequential tunneling of Cooper pairs) destroy the superconductivity and turn these weak links insulating at $T\to 0$ [2]. On the other hand, in the limit $T,{\gamma }_{1,2}\ll E_{\mathcal{L}}$ and for ${\varphi }_x$ outside an immediate vicinity of the points $|{\varphi }_x|=1/2,3/2,\cdots$, the sequential quantum tunneling of single fluxons in each of the wires is essentially prohibited, as it takes too much energy to change the magnetic flux inside the ring. Such a magnetic blockade is a complete dual analogue of the Coulomb blockade in CPT. This blockade would restore the superconducting properties of our system.

Analogously to the previous example, this magnetic blockade is, however, lifted due to flux cotunneling: Two fluxons (see Figure 2) can tunnel through both superconducting nanowires (almost) simultaneously, thus keeping the magnetic energy of the ring unchanged. Making use of a similar analysis to that employed above (2), (3) and (7) together with the duality property (10) and proceeding perturbatively in ${\gamma }_{1,2}$, we immediately arrive at the ground state energy for the superconducting nanoring in the form

$$E_0({\varphi }_x,{\chi }_0)\simeq E_{\mathcal{L}}{\varphi }_x^2-\frac{{\gamma }_1{\gamma }_{2}cos{\chi }_0}{E_{\mathcal{L}}(1-4{\varphi }_x^2)},\left|{\varphi }_x\right|<\frac{1}{2}.$$

(11)

Outside the interval $|{\varphi }_x|<1/2$, this expression should be periodically continued in ${\varphi }_x$ with the period equal to unity. Here, however, we are merely interested in the contribution to $E_0$, which depends on the parameter ${\chi }_0$ and defines the lowest Brillouin zone of our device. Taking the derivative of $E_0({\varphi }_x,{\chi }_0)$ with respect to ${\chi }_0$ and keeping in mind the relation ${\chi }_0={\mathsf{\Phi }}_{0}Q$ from Equation (11), we immediately reconstruct the voltage value corresponding to the charge Q placed across our SQUID-like ring

$$V=V_{C}sin\frac{\pi Q}{e},V_C=\frac{{\mathsf{\Phi }}_0{\gamma }_1{\gamma }_2}{E_{\mathcal{L}}(1-4{\varphi }_x^2)},\left|{\varphi }_x\right|<\frac{1}{2}.$$

(12)

Equation (12) represents the main result of this work. This result implies that flux cotunneling restores the insulating regime in our superconducting nanoring: At $T\to 0$ and for ${\gamma }_{1,2}\ll E_{\mathcal{L}}$, no dc current will flow across the device, provided the voltage V does not exceed the critical value $V_C$ (12). As soon as the regime $V=V_C$ is reached, the charge Q starts increasing with time as $Q=It$, and Equation (12) describes Bloch oscillations of the voltage (with period $I/2e$) dual to the Josephson oscillations of the supercurrent $I_S$ (8) in CPT.

In order to complete our analysis, let us present a rough order-of-magnitude estimate for the maximum value of the critical voltage $V_C$ (12). In the case of Josephson junctions, this value is reached at the border of applicability of our theory—i.e., at $E_{Ji}\sim E_{Ci}$. Then, for (almost) identical junctions with $E_{Ji}=I_C/2e$, we have ${\gamma }_1\simeq {\gamma }_2\lesssim I_C/e$. For the case of diffusive metallic wires with the diameter of order superconducting coherence length $\xi$, the kinetic inductance strongly exceeds the geometric one, in which case we have [9] $E_{\mathcal{L}}\sim g_{\xi }\mathsf{\Delta }\xi /r$, where $\mathsf{\Delta }$ and $\xi$ are, respectively, the order parameter and the coherence length of a superconductor forming the ring, $g_{\xi }$ is the dimensionless conductance of a ring segment of length $\xi$, and r is the ring radius. Combining these estimates with Equation (12) and employing the Ambegaokar–Baratoff formula $I_c=g_N\mathsf{\Delta }/2$ (where $g_N$ is the normal state dimensionless junction conductance), we obtain

$$e{V}_C\lesssim \frac{g_N^2}{g_{\xi }}\frac{r}{\xi }\frac{\mathsf{\Delta }}{1-4{\varphi }_x^2}.$$

(13)

If we set, e.g., $g_N\sim 0.1$, $g_{\xi }\sim 10÷100$ and $r/\xi \sim 10÷100$, we immediately arrive at the order-of-magnitude estimate for the maximum value $e{V}_C$ reaching up to ∼$0.1\mathsf{\Delta }$. Although in most cases one can expect $e{V}_C$ to be smaller, nevertheless the effect of Coulomb blockade induced by the cotunneling of fluxons should still remain in the measurable range and could be easily detected in modern experiments.

3. Discussion

In this work, we employed the charge–flux duality property for Josephson junctions and superconducting nanowires, extending it to explicitly account for the effect of cotunneling. Provided two Josephson junctions are connected in series—thus forming a Cooper pair transistor (Figure 1)—the cotunneling of Cooper pairs may play a dominant role at low temperatures, turning the Coulomb blockade regime into a superconducting one.

On the other hand, when connecting superconducting weak links in parallel in the form of a SQUID-like nanoring (Figure 2), one may realize a regime of cotunneling of fluxons strictly dual to that of Cooper pairs. At low enough temperatures, the cotunneling of fluxons—in contrast to its dual counterpart—may turn the behavior of such structures from superconducting to insulating. In a way, one can argue that at low T, a SQUID-like nanoring can behave as a superconductor, provided the sequential tunneling of flux quanta through weak links is suppressed, as this costs too much energy $\sim E_{\mathcal{L}}\gg T$. This regime can be called a magnetic blockade of superconducting phase fluctuations. Fluxon cotunneling lifts this magnetic blockade, thereby destroying superconductivity and restoring the insulating regime.

For the sake of simplicity, in the above analysis we did not include the effect of dissipation that may arise, e.g., due to the presence of an external circuit. Note that, for instance, in the case of the Ohmic impedance of the external circuit—similarly to the case of single Josephson junctions [2,5,6,7]—the duality property remains applicable; it embraces both the sequential tunneling and cotunneling of Cooper pairs and fluxons and yields an even richer physical picture that includes— among other features—a dissipation-diven quantum phase transition (the so-called Schmid phase transition [2]). This issue, however, is beyond the scope of the present paper.