Q-Balls in the Pseudogap Phase of Superconducting HgBa2CuO4+y
Abstract
1. Introduction
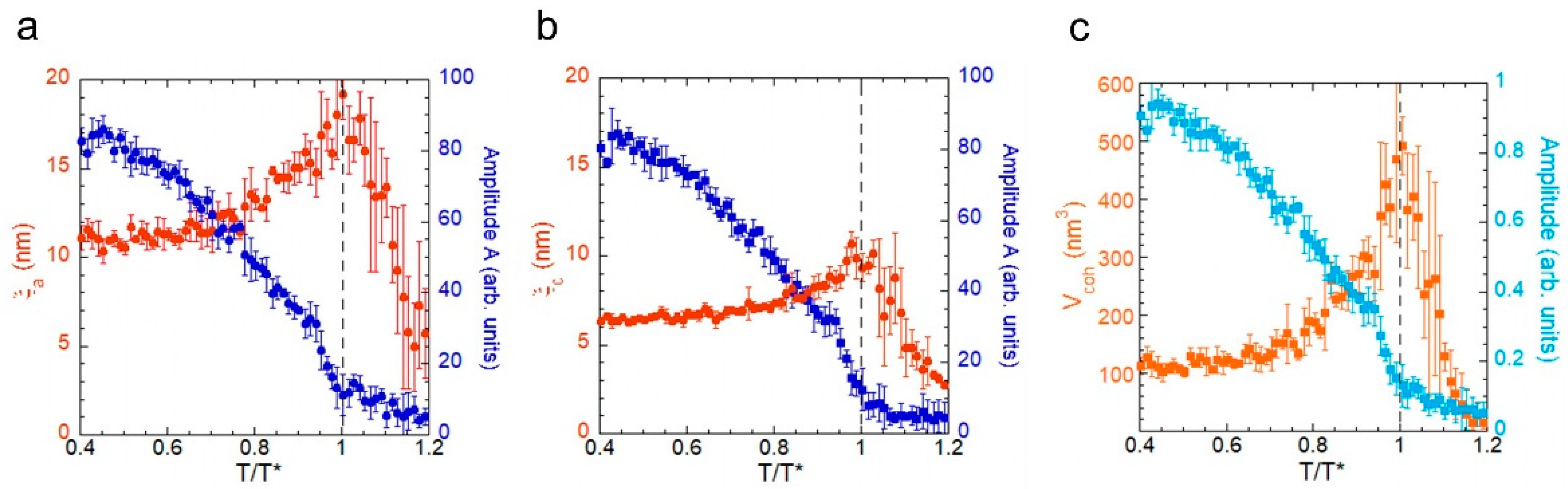
2. Results and Discussion
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mukhin, S. Euclidean Q-balls of fluctuating sdw/cdw in the ‘nested’ hubbard model of high-Tc superconductors as the origin of pseudogap and superconducting behaviors. Condens. Matter 2022, 7, 31. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A.; Poccia, N.; Barba, L.; Arrighetti, G.; Innocenti, D.; Karpinski, J.; Zhigadlo, N.D.; Kazakov, S.M.; Burghammer, M.; et al. Inhomogeneity of charge-density-wave order and quenched disorder in a high-Tc superconductor. Nature 2015, 525, 359–362. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, A. Superstripes. Int. J. Mod. Phys. B 2000, 14, 3289–3297. [Google Scholar] [CrossRef]
- Bianconi, A. Shape resonances in superstripes. Nat. Phys. 2013, 9, 536–537. [Google Scholar] [CrossRef]
- Bednorz, J.G.; Müller, K.A. Perovskite-type oxides—The new approach to high-Tc superconductivity. Rev. Mod. Phys. 1988, 60, 585. [Google Scholar] [CrossRef]
- Egami, T. Alex and the origin of high-temperature superconductivity. In High-Tc Copper Oxide Superconductors and Related Novel Materials; Springer: Cham, Switzerland, 2017; pp. 35–46. [Google Scholar]
- Kronig, R.D.L. Zur theorie der feinstruktur in den röntgenabsorptionsspektren. Z. Phys. 1931, 70, 317–323. [Google Scholar] [CrossRef]
- Kronig, R.D.L. Zur theorie der feinstruktur in den Röntgenabsorptionsspektren. II. Z. Phys. 1932, 75, 191–210. [Google Scholar] [CrossRef]
- Bianconi, A. On the Fermi liquid coupled with a generalized Wigner polaronic CDW giving high Tc superconductivity. Solid State Commun. 1994, 91, 1–5. [Google Scholar] [CrossRef]
- Bianconi, A.; Missori, M.; Oyanagi, H.; Yamaguchi, H.; Ha, D.H.; Nishiara, Y.; Della Longa, S. The measurement of the polaron size in the metallic phase of cuprate superconductors. EPL Europhys. Lett. 1995, 31, 411. [Google Scholar] [CrossRef]
- Bianconi, A.; Saini, N.L.; Lanzara, A.; Missori, M.; Rossetti, T.; Oyanagi, H.; Yamaguchi, H.; Oka, K.; Ito, T. Determination of the local lattice distortions in the CuO2 plane of La1.85Sr0.15CuO4. Phys. Rev. Lett. 1996, 76, 3412. [Google Scholar] [CrossRef]
- Zhao, G.M.; Conder, K.; Keller, H.; Müller, K.A. Oxygen isotope effects in: Evidence for polaronic charge carriers and their condensation. J. Phys. Condens. Matter 1998, 10, 9055. [Google Scholar] [CrossRef]
- Lanzara, A.; Zhao, G.M.; Saini, N.L.; Bianconi, A.; Conder, K.; Keller, H.; Müller, K.A. Oxygen-isotope shift of the charge-stripe ordering temperature in La2−xSrxCuO4 from x-ray absorption spectroscopy. J. Phys. Condens. Matter 1999, 11, L541. [Google Scholar] [CrossRef]
- Bendele, M.; Von Rohr, F.; Guguchia, Z.; Pomjakushina, E.; Conder, K.; Bianconi, A.; Simon, A.; Bussman-Holder, A.; Keller, H. Evidence for strong lattice effects as revealed from huge unconventional oxygen isotope effects on the pseudogap temperature in La2−xSrxCuO4. Phys. Rev. B 2017, 95, 014514. [Google Scholar] [CrossRef]
- Della Longa, S.; Soldatov, A.; Pompa, M.; Bianconi, A. Atomic and electronic structure probed by X-ray absorption spectroscopy: Full multiple scattering analysis with the G4XANES package. Comput. Mater. Sci. 1995, 4, 199–210. [Google Scholar] [CrossRef]
- Bianconi, A.; Bauer, R.S. Evidence of SiO at the Si-oxide interface by surface soft X-ray absorption near edge spectroscopy. Surf. Sci. 1980, 99, 76–86. [Google Scholar] [CrossRef]
- Bianconi, A. Multiplet splitting of final-state configurations in x-ray-absorption spectrum of metal VO2: Effect of core-hole-screening, electron correlation, and metal-insulator transition. Phys. Rev. B 1982, 26, 2741. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Zhou, J.S.; Bersuker, G.I. Thermoelectric Power and normal state of the high-Tc copper oxides. In Proceedings of the International Workshop on Anharmonic-Properties of High-Tc cuprates, Bled, Slovenia, 1–6 September 1994. [Google Scholar]
- Zhou, J.S.; Bersuker, G.I.; Goodenough, J.B. Non-adiabatic electron-lattice interactions in the copper-oxide superconductors. J. Supercond. 1995, 8, 541–544. [Google Scholar] [CrossRef]
- Bersuker, G.I.; Goodenough, J.B. Large low-symmetry polarons of the high-Tc copper oxides: Formation, mobility and ordering. Phys. C Supercond. 1997, 274, 267–285. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Zhou, J.S. Vibronic states in La2−xBaxCuO4. J. Supercond. 1997, 10, 309–314. [Google Scholar] [CrossRef]
- Zhou, J.S.; Goodenough, J.B. Electron-lattice coupling and stripe formation in La2−xBaxCuO4. Phys. Rev. B 1997, 56, 6288. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Zhou, J.S. New forms of phase segregation. Nature 1997, 386, 229–230. [Google Scholar] [CrossRef]
- Kremer, R.K.; Hizhnyakov, V.; Sigmund, E.; Simon, A.; Müller, K.A. Electronic phase separation in La-cuprates. Z. Phys. B Condens. Matter 1993, 91, 169–174. [Google Scholar] [CrossRef]
- Muller, K.A.; Benedek, G. (Eds.) Phase Separation in cuprate superconductors. In Proceedings of the Workshop Phase Separation in Cuprate Superconductors Held in Erice, Erice, Italy, 6–9 May 1992; World Scientific: Singapore, 1993. [Google Scholar]
- Sigmund, E.; Müller, K.A. (Eds.) Phase Separation in Cuprate Superconductors. In Proceedings of the Second International Workshop on “Phase Separation in Cuprate Superconductors”, Cottbus, Germany, 4–10 September 1993; Springer Science Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Müller, K.A.; Zhao, G.M.; Conder, K.; Keller, H. The ratio of small polarons to free carriers in derived from susceptibility measurements. J. Phys. Condens. Matter 1998, 10, L291. [Google Scholar] [CrossRef]
- Bianconi, A.; Valletta, A.; Perali, A.; Saini, N.L. Superconductivity of a striped phase at the atomic limit. Phys. C Supercond. 1998, 296, 269–280. [Google Scholar] [CrossRef]
- Bauer, E.; Paul, C.; Berger, S.; Majumdar, S.; Michor, H.; Giovannini, M.; Saccone, A.; Bianconi, A. Thermal conductivity of superconducting MgB2. J. Phys. Condens. Matter 2001, 13, L487. [Google Scholar] [CrossRef]
- Kusmartsev, F.V.; Di Castro, D.; Bianconi, G.; Bianconi, A. Transformation of strings into an inhomogeneous phase of stripes and itinerant carriers. Phys. Lett. A 2000, 275, 118–123. [Google Scholar] [CrossRef]
- Kusmartsev, F.V. Electron strings in oxides. In Phase Transitions and Self-Organization in Electronic and Molecular Networks; Springer: Boston, MA, USA, 2002. [Google Scholar]
- Kusmartsev, F.V.; Saarela, M. Dipolar clusters and ferroelectricity in high Tc superconductors. Int. J. Mod. Phys. B 2015, 29, 1542002. [Google Scholar] [CrossRef]
- Saarela, M.; Kusmartsev, F.V. Phase transitions to dipolar clusters and charge density waves in high Tc superconductors. Phys. C Supercond. Appl. 2017, 533, 9–19. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Zhou, J.S. Enhanced thermoelectric power and stripes in cuprate superconductors. In Stripes and Related Phenomena; Springer: Boston, MA, USA, 2002; pp. 199–209. [Google Scholar]
- Yan, J.Q.; Zhou, J.S.; Goodenough, J.B. Thermal conductivity in the stripe-ordered phase of cuprates and nickelates. Phys. Rev. B 2003, 68, 104520. [Google Scholar] [CrossRef]
- Goodenough, J.B. Ordering of bond length fluctuations in the copper-oxide superconductors. EPL Europhys. Lett. 2002, 57, 550. [Google Scholar] [CrossRef]
- Shengelaya, A.; Bruun, M.; Kochelaev, B.I.; Safina, A.; Conder, K.; Müller, K.A. Microscopic Phase Separation and two type of quasiparticles in lightly doped La2−xSrxCuO4 observed by electron paramagnetic resonance. In Symmetry and Heterogeneity in High Temperature Superconductors; Springer: Dordrecht, The Netherlands, 2006; pp. 105–116. [Google Scholar]
- Müller, K.A. Electron paramagnetic resonance and high temperature superconductivity. J. Supercond. Nov. Magn. 2006, 19, 53–57. [Google Scholar] [CrossRef]
- Campi, G.; Cappelluti, E.; Proffen, T.; Qiu, X.; Bozin, E.S.; Billinge, S.J.L.; Agrestini, S.; Saini, N.L.; Bianconi, A. Study of temperature dependent atomic correlations in MgB2. Eur. Phys. J. B-Condens. Matter Complex Syst. 2006, 52, 15–21. [Google Scholar] [CrossRef]
- Shengelaya, A.; Müller, K.A. The intrinsic heterogeneity of superconductivity in the cuprates. EPL Europhys. Lett. 2015, 109, 27001. [Google Scholar] [CrossRef]
- Müller, K.A. Essential heterogeneities in hole-doped cuprate superconductors. In Intrinsic Multiscale Structure and Dynamics in Complex Electronic Oxides; World Scientific: Singapore, 2003; pp. 1–5. [Google Scholar]
- Müller, K.A.; Bussmann-Holder, A. (Eds.) Superconductivity in Complex Systems; Springer: Berlin/Heidelberg, Germany, 2005; Volume 114. [Google Scholar]
- Deutscher, G.; de Gennes, P.G. A spatial interpretation of emerging superconductivity in lightly doped cuprates. Comptes Rendus Phys. 2007, 8, 937–941. [Google Scholar] [CrossRef]
- Keller, H.; Bussmann-Holder, A.; Müller, K.A. Jahn–Teller physics and high-Tc superconductivity. Mater. Today 2008, 11, 38–46. [Google Scholar] [CrossRef]
- Müller, K.A. The unique properties of superconductivity in cuprates. J. Supercond. Nov. Magn. 2014, 27, 2163–2179. [Google Scholar] [CrossRef]
- Müller, K.A. The polaronic basis for high-temperature superconductivity. J. Supercond. Nov. Magn. 2017, 30, 3007–3018. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Keller, H.; Bishop, A.R.; Simon, A.; Müller, K.A. Polaron coherence as origin of the pseudogap phase in high temperature superconducting cuprates. J. Supercond. Nov. Magn. 2008, 21, 353–357. [Google Scholar] [CrossRef]
- Barišić, N.; Sunko, D.K. High-Tc cuprates: A story of two electronic subsystems. J. Supercond. Nov. Magn. 2022, 35, 1781–1799. [Google Scholar] [CrossRef]
- Krockenberger, Y.; Ikeda, A.; Yamamoto, H. Atomic stripe formation in infinite-layer cuprates. ACS Omega 2021, 6, 21884–21891. [Google Scholar] [CrossRef]
- Conradson, S.D.; Geballe, T.H.; Gauzzi, A.; Karppinen, M.; Jin, C.; Baldinozzi, G.; Li, W.; Cao, L.; Gilioli, E.; Jiang, J.M.; et al. Local lattice distortions and dynamics in extremely overdoped superconducting YSr2Cu2.75Mo0.25O7.54. Proc. Natl. Acad. Sci. USA 2020, 117, 4559–4564. [Google Scholar] [CrossRef] [PubMed]
- Velasco, V.; Neto, M.B.S.; Perali, A.; Wimberger, S.; Bishop, A.R.; Conradson, S.D. Kuramoto synchronization of quantum tunneling polarons for describing the dynamic structure in cuprate superconductors. Phys. Rev. B 2022, 105, 174305. [Google Scholar] [CrossRef]
- Velasco, V.; Silva Neto, M.B.; Perali, A.; Wimberger, S.; Bishop, A.R.; Conradson, S.D. Evolution of Charge-Lattice Dynamics across the Kuramoto Synchronization Phase Diagram of Quantum Tunneling Polarons in Cuprate Superconductors. Condens. Matter 2021, 6, 52. [Google Scholar] [CrossRef]
- Menushenkov, A.P.; Klementev, K.V. Extended x-ray absorption fine-structure indication of a double-well potential for oxygen vibration in Ba1−xKxBiO3. J. Phys. Condens. Matter 2000, 12, 3767. [Google Scholar] [CrossRef]
- Menushenkov, A.P.; Kuznetsov, A.V.; Klementiev, K.V.; Kagan, M.Y. Fermi-Bose mixture in Ba (K) BiO3 superconducting oxide. J. Supercond. Nov. Magn. 2016, 29, 701–705. [Google Scholar] [CrossRef]
- Giraldo-Gallo, P.; Zhang, Y.; Parra, C.; Manoharan, H.C.; Beasley, M.R.; Geballe, T.H.; Kramer, M.J.; Fisher, I.R. Stripe-like nanoscale structural phase separation in superconducting BaPb1−xBixO3. Nat. Commun. 2015, 6, 8231. [Google Scholar] [CrossRef]
- Bianconi, A.; Jarlborg, T. Lifshitz transitions and zero point lattice fluctuations in sulfur hydride showing near room temperature superconductivity. Nov. Supercond. Mater. 2015, 1, 37–49. [Google Scholar] [CrossRef]
- Popčević, P.; Pelc, D.; Tang, Y.; Velebit, K.; Anderson, Z.; Nagarajan, V.; Yu, G.; Požek, M.; Baričić, N.; Greven, M. Percolative nature of the direct-current paraconductivity in cuprate superconductors. NPJ Quantum Mater. 2018, 3, 42. [Google Scholar] [CrossRef]
- Pelc, D.; Spieker, R.J.; Anderson, Z.W.; Krogstad, M.J.; Biniskos, N.; Bielinski, N.G.; Yu, B.; Sasagawa, T.; Chauviere, L.; Dosanjh, P.; et al. Unconventional short-range structural fluctuations in cuprate superconductors. Sci. Rep. 2022, 12, 20483. [Google Scholar] [CrossRef]
- Caprara, S.; Di Castro, C.; Seibold, G.; Grilli, M. Dynamical charge density waves rule the phase diagram of cuprates. Phys. Rev. B 2017, 95, 224511. [Google Scholar] [CrossRef]
- Arpaia, R.; Caprara, S.; Fumagalli, R.; De Vecchi, G.; Peng, Y.Y.; Andersson, E.; Betto, D.; De Luca, G.M.; Brookes, N.B.; Lombardi, F.; et al. Dynamical charge density fluctuations pervading the phase diagram of a Cu-based high-Tc superconductor. Science 2019, 365, 906–910. [Google Scholar] [CrossRef] [PubMed]
- Wen, J.J.; Huang, H.; Lee, S.J.; Jang, H.; Knight, J.; Lee, Y.S.; Fujita, M.; Suzuki, K.M.; Asano, S.; Kivelson, S.A.; et al. Observation of two types of charge-density-wave orders in superconducting La2−xSrxCuO4. Nat. Commun. 2019, 10, 3269. [Google Scholar] [CrossRef] [PubMed]
- Miao, H.; Fumagalli, R.; Rossi, M.; Lorenzana, J.; Seibold, G.; Yakhou-Harris, F.; Kummer, K.; Brookes, N.B.; Gu, G.D.; Braicovich, L.; et al. Formation of incommensurate charge density waves in cuprates. Phys. Rev. X 2019, 9, 031042. [Google Scholar] [CrossRef]
- Cremin, K.A.; Zhang, J.; Homes, C.C.; Gu, G.D.; Sun, Z.; Fogler, M.M.; Millis, A.J.; Basov, D.N.; Averitt, R.D. Photoenhanced metastable c-axis electrodynamics in stripe-ordered cuprate La1.885Ba0.115CuO4. Proc. Natl. Acad. Sci. USA 2019, 116, 19875–19879. [Google Scholar] [CrossRef] [PubMed]
- Yu, G.; Xia, D.D.; Pelc, D.; He, R.H.; Kaneko, N.H.; Sasagawa, T.; Li, Y.; Zhao, X.; Barišić, N.; Shekhter, A.; et al. Universal precursor of superconductivity in the cuprates. Phys. Rev. B 2019, 99, 214502. [Google Scholar] [CrossRef]
- Pelc, D.; Popčević, P.; Požek, M.; Greven, M.; Barišić, N. Unusual behavior of cuprates explained by heterogeneous charge localization. Sci. Adv. 2019, 5, eaau4538. [Google Scholar] [CrossRef]
- Caprara, S. The ancient romans’ route to charge density waves in cuprates. Condens. Matter 2019, 4, 60. [Google Scholar] [CrossRef]
- Lin, J.Q.; Miao, H.; Mazzone, D.G.; Gu, G.D.; Nag, A.; Walters, A.C.; García-Fernández, M.; Barbour, A.; Pelliciari, J.; Jarrige, I.; et al. Strongly correlated charge density wave in La2−xSrxCuO4 evidenced by doping-dependent phonon anomaly. Phys. Rev. Lett. 2020, 124, 207005. [Google Scholar] [CrossRef]
- Chen, X.M.; Mazzoli, C.; Cao, Y.; Thampy, V.; Barbour, A.M.; Hu, W.; Lu, M.; Assefa, T.A.; Miao, H.; Fabbris, G.; et al. Charge density wave memory in a cuprate superconductor. Nat. Commun. 2019, 10, 1435. [Google Scholar] [CrossRef] [PubMed]
- Yu, B.; Tabis, W.; Bialo, I.; Yakhou, F.; Brookes, B.; Anderson, Z.; Tang, Y.; Yu, G.; Greven, M. Unusual dynamic charge correlations in simple-tetragonal HgBa2CuO4+δ. Phys. Rev. X 2020, 10, 021059. [Google Scholar] [CrossRef]
- Seibold, G.; Arpaia, R.; Peng, Y.Y.; Fumagalli, R.; Braicovich, L.; Di Castro, C.; Grilli, M.; Ghiringhelli, G.C.; Caprara, S. Strange metal behaviour from charge density fluctuations in cuprates. Commun. Phys. 2021, 4, 7. [Google Scholar] [CrossRef]
- Miao, H.; Fabbris, G.; Koch, R.J.; Mazzone, D.G.; Nelson, C.S.; Acevedo-Esteves, R.; Gu, G.D.; Li, Y.; Yilimaz, T.; Kaznatcheev, K.; et al. Charge density waves in cuprate superconductors beyond the critical doping. NPJ Quantum Mater. 2021, 6, 31. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A.; Joseph, B.; Mishra, S.K.; Muller, L.; Zozulya, A.; Nugroho, A.A.; Roy, S.; Sprung, M.; Ricci, A. Nanoscale inhomogeneity of charge density waves dynamics in La2−xSrxNiO4. Sci. Rep. 2022, 12, 15964. [Google Scholar] [CrossRef] [PubMed]
- Croft, T.; Lester, C.J.; Senn, M.S.; Bombardi, A.; Hayden, S.M. Charge density wave fluctuations in La2−xSrxCuO4 and their competition with superconductivity. Phys. Rev. B 2014, 89, 224513. [Google Scholar] [CrossRef]
- Forgan, E.; Blackburn, E.; Holmes, A.; Briffa, A.K.R.; Chang, J.; Bouchenoire, L.; Brown, S.D.; Liang, R.; Bonn, D.; Hardy, W.N.; et al. The microscopic structure of charge density waves in underdoped YBa2Cu3O6.54 revealed by X-ray diffraction. Nat. Commun. 2015, 6, 10064. [Google Scholar] [CrossRef]
- Putilin, S.; Antipov, E.; Chmaissem, O.; Marezio, M.J.N. Superconductivity at 94 K in HgBa2Cu04+δ. Nature 1993, 362, 226–228. [Google Scholar] [CrossRef]
- Karpinski, J.; Meijer, G.I.; Schwer, H.; Molinski, R.; Kopnin, E.; Conder, K.; Angst, M.; Jun, J.; Kazakov, S.; Wisniewski, A.; et al. High-pressure synthesis, crystal growth, phase diagrams, structural and magnetic properties of Y2Ba4CunO2n+x, HgBa2 Can−1 CunO2n+2+x and quasi-one-dimensional cuprates. Supercond. Sci. Technol. 1999, 12, R153–R181. [Google Scholar] [CrossRef]
- Legros, A.; Loret, B.; Forget, A.; Bonnaillie, P.; Collin, G.; Thuéry, P.; Sacuto, A.; Colson, D. Crystal growth and doping control of HgBa2CuO4+δ, the model compound for high-Tc superconductors. Mater. Res. Bull. 2019, 118, 110479. [Google Scholar] [CrossRef]
- Bordet, P.; Duc, F.; LeFloch, S.; Capponi, J.J.; Alexandre, E.; Rosa-Nunes, M.; Putilin, S.; Antipov, E.V. Single crystal X-ray diffraction study of the HgBa2CuO4+δ superconducting compound. Phys. C Supercond. 1996, 271, 189–196. [Google Scholar] [CrossRef]
- Balagurov, A.M.; Sheptyakov, D.V.; Aksenov, V.L.; Antipov, E.V.; Putilin, S.N.; Radaelli, P.G.; Marezio, M. Structure of HgBa2CuO4+δ (0.06 < δ < 0.19) at ambient and high pressure. Phys. Rev. B 1999, 59, 7209–7215. [Google Scholar] [CrossRef]
- Auvray, N.; Loret, B.; Chibani, S.; Grasset, R.; Guarnelli, Y.; Parisiades, P.; Forget, A.; Colson, D.; Cazayous, M.; Gallais, Y.; et al. Exploration of Hg-based cuprate superconductors by Raman spectroscopy under hydrostatic pressure. Phys. Rev. B 2021, 103, 19513. [Google Scholar] [CrossRef]
- Izquierdo, M.; Megtert, S.; Colson, D.; Honkimäki, V.; Forget, A.; Raffy, H.; Comès, R. One dimensional ordering of doping oxygen in superconductors evidenced by x-ray diffuse scattering. J. Phys. Chem. Solids 2011, 72, 545–548. [Google Scholar] [CrossRef]
- Izquierdo, M.; Freitas, D.C.; Colson, D.; Garbarino, G.; Forget, A.; Raffy, H.; Itié, J.-P.; Ravy, S.; Fertey, P.; Núñez-Regueiro, M. Charge order and suppression of superconductivity in HgBa2CuO4+d at high pressures. Condens. Matter 2021, 6, 25. [Google Scholar] [CrossRef]
- Barbiellini, B.; Jarlborg, T. Electron and positron states in HgBa2CuO4. Phys. Rev. B 1994, 50, 3239. [Google Scholar] [CrossRef] [PubMed]
- Ambrosch-Draxl, C.; Sherman, E.Y. Inhomogeneity effects in oxygen-doped HgBa2CuO4. Phys. Rev. B 2006, 74, 024503. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, J.; Yan, J.; Che, X.-J.; Struzhkin, V.; Tabis, W.; Barisic, N.; Chan, M.K.; Dorow, C.; Zhao, X.; et al. Strain derivatives of Tc in HgBa2CuO4+δ: The CuO2 plane alone is not enough. Phys. Rev. B 2014, 89, 024515. [Google Scholar] [CrossRef]
- Ohgoe, T.; Hirayama, M.; Misawa, T.; Ido, K.; Yamaji, Y.; Imada, M. Ab initio study of superconductivity and inhomogeneity in a Hg-based cuprate superconductor. Phys. Rev. B 2020, 101, 045124. [Google Scholar] [CrossRef]
- Tabis, W.; Yu, B.; Bialo, I.; Bluschke, M.; Kolodziej, T.; Kozlowski, A.; Blackburn, E.; Sen, K.; Forgan, E.M.; Zimmermann, M.; et al. Synchrotron x-ray scattering study of charge-density-wave order in HgBa2CuO4+δ. Phys. Rev. B 2017, 96, 134510. [Google Scholar] [CrossRef]
- Clougherty, D.P.; Foell, C.A. Vector polarons in a degenerate electron system. Phys. Rev. B 2004, 70, 052301. [Google Scholar] [CrossRef]
- Clougherty, D.P. Jahn-Teller solitons, structural phase transitions, and phase separation. Phys. Rev. Lett. 2006, 96, 045703. [Google Scholar] [CrossRef]
- Mukhin, S. Possible manifestation of Q-ball mechanism of high Tc superconductivity in X-ray diffraction. Condens. Matter 2022, 8, 16. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campi, G.; Barba, L.; Zhigadlo, N.D.; Ivanov, A.A.; Menushenkov, A.P.; Bianconi, A. Q-Balls in the Pseudogap Phase of Superconducting HgBa2CuO4+y. Condens. Matter 2023, 8, 15. https://doi.org/10.3390/condmat8010015
Campi G, Barba L, Zhigadlo ND, Ivanov AA, Menushenkov AP, Bianconi A. Q-Balls in the Pseudogap Phase of Superconducting HgBa2CuO4+y. Condensed Matter. 2023; 8(1):15. https://doi.org/10.3390/condmat8010015
Chicago/Turabian StyleCampi, Gaetano, Luisa Barba, Nikolai D. Zhigadlo, Andrey A. Ivanov, Alexey P. Menushenkov, and Antonio Bianconi. 2023. "Q-Balls in the Pseudogap Phase of Superconducting HgBa2CuO4+y" Condensed Matter 8, no. 1: 15. https://doi.org/10.3390/condmat8010015
APA StyleCampi, G., Barba, L., Zhigadlo, N. D., Ivanov, A. A., Menushenkov, A. P., & Bianconi, A. (2023). Q-Balls in the Pseudogap Phase of Superconducting HgBa2CuO4+y. Condensed Matter, 8(1), 15. https://doi.org/10.3390/condmat8010015







