Breakdown of Adiabatic Superconductivity in Ca-Doped h-BN Monolayer

Abstract

In the present paper, we report the breakdown of the adiabatic picture of superconductivity in a calcium-doped hexagonal boron nitride (Ca-h-BN) monolayer and discuss its implications for the selected properties of this phase. In particular, it is shown that the shallow conduction band of the Ca-h-BN superconductor potentially cause a violation of the adiabatic Migdal’s theorem. As a result, the pivotal parameters that describe the superconducting state in Ca-h-BN are found to be notably influenced by the non-adiabatic effects. This finding is described here within the vertex-corrected Eliashberg formalism that predicts a strong reduction of the order parameter, superconducting transition temperature and superconducting gap in comparison to the estimates obtained in the framework of the adiabatic theory. The observed trends are in agreement with the recent results on superconductivity in hexagonal monolayers and confirm that the non-adiabatic effects have to be taken into account during the design of such future low-dimensional superconductors.

1. Introduction

Recently, the calcium-doped hexagonal boron nitride (Ca-h-BN) monolayer joined the family of hypothetical two-dimensional (2D) superconductors characterized by the hexagonal structure and conventional pairing mechanism [1]. This group of 2D superconductors gained increasing attention over the last years, after the theoretical prediction of phonon-mediated superconductivity in lithium-decorated graphene (LiC${}_6$) [2] that was later partially confirmed within the experiment [3]. In other words, the LiC${}_6$ material promised a perspective on scaled-down phonon-mediated superconductors with novel applications, so that e further research in this direction became naturally desirable [2,3]. Currently, the low-dimensional conventional superconducting phase is suggested to exist not only in the Ca-h-BN and LiC${}_6$ monolayers but also in many other sibling materials such as the hole-doped fully hydrogenated graphene (known also as graphane) [4], strained silicene [5], phosphorene [6] or the electron/hole-doped graphene [7]. However, among them, the discussed Ca-h-BN monolayer is particularly interesting as it exhibits relatively high critical temperature values, offers an experimentally feasible structure and develops the idea of using modified insulators as superconducting materials [1]. In what follows, this material is fundamentally different from many other representatives of the 2D hexagonal superconductors. For example, in contrast to h-BN, the calcium doping does not lead to a superconducting state in graphene, as caused by different behavior of the low-energy phonon modes between these two materials [1,2].

In addition to the above features of Ca-h-BN, it is also important to observe that this material is characterized by the shallow conduction band [1]. This is similar to what can be found in other 2D hexagonal materials [8] but also in bismuthates [9] or in fullerides and fullerenes [10,11,12,13]. Here, however, we additionally note that the electronic energy scale in Ca-h-BN is comparable to the phononic one, meaning that the adiabatic Migdal’s theorem [14] potentially breaks down in the discussed case. This scenario is well-known and was originally described by Pietronero et al. in their milestone works on non-adiabatic superconductivity [15,16]. In detail, we can parametrize the electron and phonon scales by the Fermi ($E_F$) and Debye’s (${\omega }_D$) energies, respectively, and next calculate the adiabatic ratio ${\omega }_D/E_F$. For the Ca-h-BN superconductor, these energies can be directly extracted from the results presented in [1], i.e., the $E_F$ can be interpreted as a conduction half-bandwidth (similarly to in [17]) while ${\omega }_D$ is taken as the highest phonon frequency of the electron–phonon spectral function (see [18,19] for more information). In what follows, ${\omega }_D/E_F\simeq 0.1$ for Ca-h-BN [1] and is clearly non-negligible in contrast to adiabatic Migdal’s theorem [14] where ${\omega }_D/E_F\simeq 0$. This is to say, the calculated ratio suggests that the non-adiabatic effects may have an influence on the superconducting phase in the Ca-h-BN material. Note that the magnitude of this impact is subject to change according to the above definition of the adiabatic ratio. For example, external factors such as doping or strain can lead to substantial variations of this ratio value (see [8] for a brief discussion of adiabatic ratios in selected 2D hexagonal superconductors under the influence of various external factors).

Herein, to verify the above statement, we characterize the Ca-h-BN superconductor within the adiabatic and non-adiabatic theoretical approaches of choice, and later compare their predictions of the most important superconducting parameters. In particular, this analysis is conducted here in the framework of the Eliashberg equations [20,21] by assuming the Migdal’s approximation and the first-order vertex corrections to the electron–phonon interaction for the adiabatic and non-adiabatic cases, respectively. The latter modification follows the work of Freericks et al. [22] and is introduced within the perturbation theory since the nonadiabaticity in Ca-h-BN seems not to be related to the Fermi liquid picture breakdown. In this manner, we calculate and compare theoretical predictions for the order parameter and later on for the critical transition temperature as well as the superconducting gap. This list of observables is additionally supplemented here by the ratio for the order parameter, characteristic of the Bardeen–Cooper–Schrieffer (BCS) theory [23,24].

The present article is organized as follows: in Section 2 we present a comprehensive introduction to the employed theoretical model; next, in Section 3, we present and describe the most important results of our analysis. Finally, the manuscript is summarized with our conclusions and perspectives.

2. Theoretical Model

To perform the analysis of the Ca-h-BN superconductor, we used the following formulation of the Eliashberg equations for the order parameter function (${\varphi }_n=\varphi \left(i{\omega }_n\right)$) and the wave function renormalization factor ($Z_n=Z\left(i{\omega }_n\right)$) [22] in terms of the n-th Matsubara frequency (${\omega }_n=\pi k_{B}T\left(2n+1\right)$):

$${\varphi }_n=\pi k_{B}T\sum _{m=-M}^M\frac{K_{n,m}-{\mu }_m^{*}}{\sqrt{{\omega }_m^2{Z}_m^2+{\varphi }_m^2}}{\varphi }_m-V_{\varphi },$$

(1)

$$Z_n=1+\frac{\pi k_{B}T}{{\omega }_n}\sum _{m=-M}^M\frac{K_{n,m}}{\sqrt{{\omega }_m^2{Z}_m^2+{\varphi }_m^2}}{\omega }_m{Z}_m-V_Z,$$

(2)

where:

$$K_{n,m}=2{\int }_0^{{\omega }_D}d\omega \frac{\omega }{{\omega }^2+4{\pi }^2{\left(k_{B}T\right)}^2{\left(n-m\right)}^2}{\alpha }^{2}F\left(\omega \right),$$

(3)

is the electron–phonon pairing kernel that depends on the phonon energy given by $\omega$ and the electron–phonon spectral function (known also a the Eliashberg function) written as:

$${\alpha }^{2}F\left(\omega \right)=\frac{1}{2\pi \rho \left(E_F\right)}\sum _{\mathbf{q}\nu }\delta (\omega -{\omega }_{\mathbf{q}\nu })\frac{{\gamma }_{\mathbf{q}\nu }}{{\omega }_{\mathbf{q}\nu }},$$

(4)

with $\alpha$ being the average electron–phonon coupling, $F\left(\omega \right)$ representing the phonon density of states, $\rho \left(E_F\right)$ denoting the electron density of states at the Fermi level, and ${\gamma }_{\mathbf{q}\nu }$ standing for the phonon linewidth at given phonon energy ${\omega }_{\mathbf{q}\nu }$. Note that in the present analysis we assume the form of the ${\alpha }^{2}F\left(\omega \right)$ function after [1], where this function was calculated by using the ab initio methods. Hence, the Eliashberg function provides a direct relation to the considered Ca-h-BN superconductor within the employed equations by containing the unique information about the system as described by Equation (4). In this context ${\mu }_n^{*}={\mu }^{*}\theta \left({\omega }_c-\left|{\omega }_n\right|\right)$ is the Coulomb pseudopotential (parameter describing magnitude of the depairing Coulomb interactions), where $\theta$ gives the Heaviside function and ${\omega }_c$ is the cut-off frequency. Moreover, the $V_{\varphi }$ and $V_Z$ are the first-order vertex correction terms to the electron–phonon interaction written as:

$$\begin{array}{ccc}\hfill V_{\varphi }& =& \frac{{\pi }^3{\left(k_{B}T\right)}^2}{4E_F}\hfill \\ \hfill & \times & \sum _{m=-M}^M\sum _{m^{\prime }=-M}^M\frac{K_{n,m}{K}_{n,m^{\prime }}}{\sqrt{\left({\omega }_m^2{Z}_m^2+{\varphi }_m^2\right)\left({\omega }_{m^{\prime }}^2{Z}_{m^{\prime }}^2+{\varphi }_{m^{\prime }}^2\right)\left({\omega }_{-n+m+m^{\prime }}^2{Z}_{-n+m+m^{\prime }}^2+{\varphi }_{-n+m+m^{\prime }}^2\right)}}\hfill \\ & \times & \left({\varphi }_m{\varphi }_{m^{\prime }}{\varphi }_{-n+m+m^{\prime }}+2{\varphi }_m{\omega }_{m^{\prime }}{Z}_{m^{\prime }}{\omega }_{-n+m+m^{\prime }}{Z}_{-n+m+m^{\prime }}-{\omega }_m{Z}_m{\omega }_{m^{\prime }}{Z}_{m^{\prime }}{\varphi }_{-n+m+m^{\prime }}\right),\hfill \end{array}$$

(5)

and

$$\begin{array}{ccc}\hfill V_Z& =& \frac{{\pi }^3{\left(k_{B}T\right)}^2}{4E_F{\omega }_n}\hfill \\ \hfill & \times & \sum _{m=-M}^M\sum _{m^{\prime }=-M}^M\frac{K_{n,m}{K}_{n,m^{\prime }}}{\sqrt{\left({\omega }_m^2{Z}_m^2+{\varphi }_m^2\right)\left({\omega }_{m^{\prime }}^2{Z}_{m^{\prime }}^2+{\varphi }_{m^{\prime }}^2\right)\left({\omega }_{-n+m+m^{\prime }}^2{Z}_{-n+m+m^{\prime }}^2+{\varphi }_{-n+m+m^{\prime }}^2\right)}}\hfill \\ & \times & \left({\omega }_m{Z}_m{\omega }_{m^{\prime }}{Z}_{m^{\prime }}{\omega }_{-n+m+m^{\prime }}{Z}_{-n+m+m^{\prime }}+2{\omega }_m{Z}_m{\varphi }_{m^{\prime }}{\varphi }_{-n+m+m^{\prime }}-{\varphi }_m{\varphi }_{m^{\prime }}{\omega }_{-n+m+m^{\prime }}{Z}_{-n+m+m^{\prime }}\right).\hfill \end{array}$$

(6)

In the present work, Equations (1) and (2) are called the non-adiabatic Eliashberg formalism (N-E). On the other hand, when terms (5) and (6) are neglected we refer to the obtained set of equations as the adiabatic Eliashberg approach (A-E). Note that both sets are given here within the isotropic approximation according to the character of the Eliashberg function adopted from [1]. Such approximation can be introduced here because the Fermi surfaces originating from the interlayer states (pivotal for superconductivity in Ca-h-BN) resemble circular pockets for the discussed superconductor [1]. As a result, the k-momentum dependence can be neglected in the present equations.

To this end, Equations (1) and (2) are solved here numerically by using the in-house developed computational packages. The details of the numerical procedures can be found in [18] in the case of the adiabatic formulation and in [8,22] for the non-adiabatic approach.

3. Results and Discussion

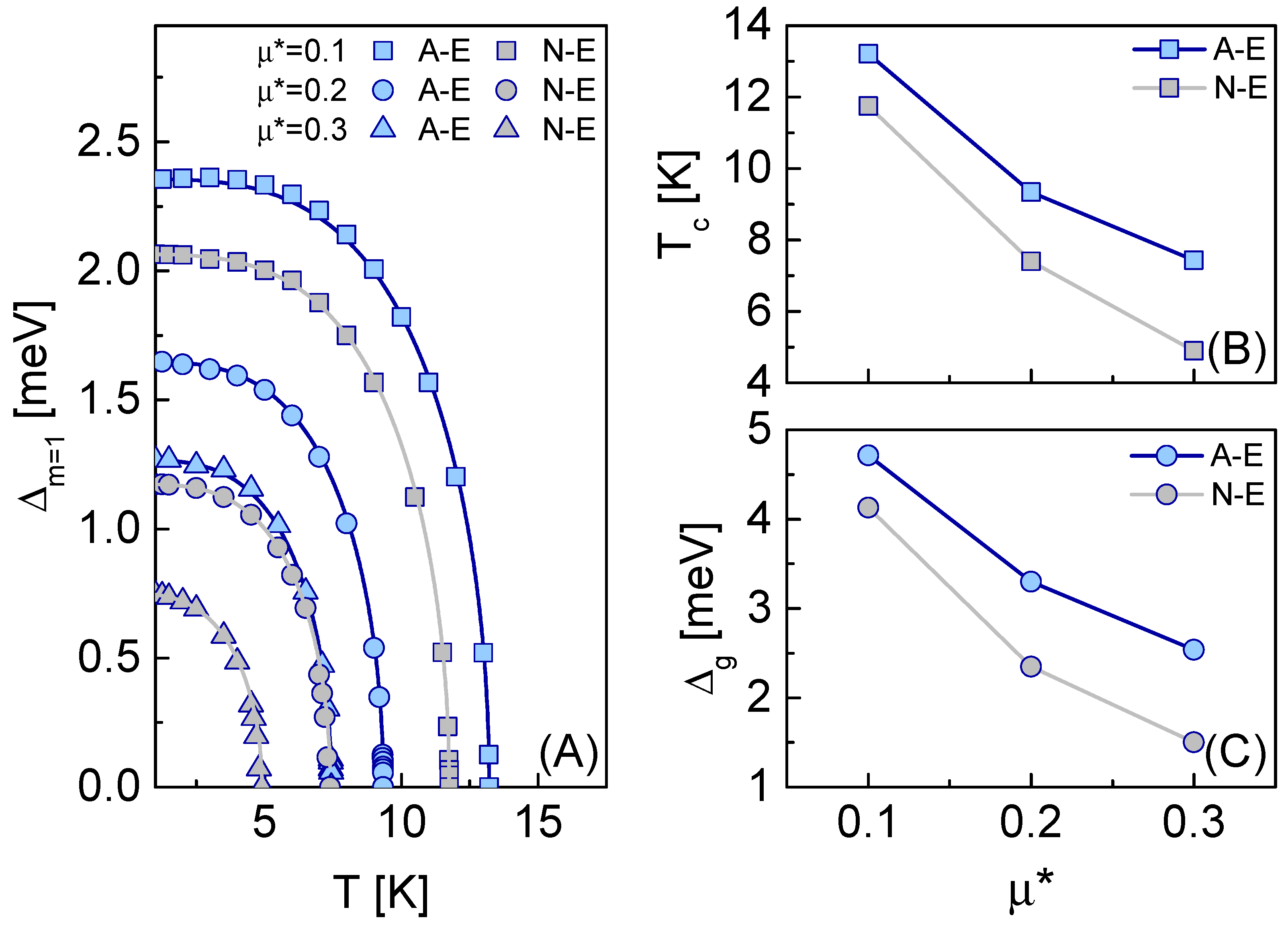
The main results of our theoretical computations are depicted in Figure 1. Therein, the symbols mark the exact numerical solutions of the Eliashberg equations, whereas lines should be considered as a guide for the eye. In detail, Figure 1A presents direct solutions of the Eliashberg equations in the adiabatic (blue symbols) and non-adiabatic (grey symbols) regime as a temperature dependence of the order parameter (${\mathsf{\Delta }}_{m=1}\left(T\right)={\varphi }_{m=1}/Z_{m=1}$) for the selected values of the Coulomb pseudopotential. Note that the exact value of $\mu$* is unknown due the the fact that there are no experimental estimates of the $T_C$ for the Ca-h-BN superconductor. In other words, $\mu$* cannot be currently used as a fitting parameter to match predictions of the Eliashberg equations with the experimental estimates. This is due to the fact that Equation (1) depends simultaneously on $\mu$* and T. Therefore, various values of Coulomb pseudopotential are considered here in order to cover the entirety of the potential superconducting phase in Ca-h-BN, i.e., $\mu$* = 0.1 is the conventional choice that corresponds to the low/moderate magnitude of the depairing correlations according to [21,25], while $\mu$* = 0.3 can be viewed as an extreme case of the strong depairing Coulomb interaction [26]. In this manner, $\mu$* = 0.2 is the intermediate level that supplements our sampling of the superconducting phase. In this context, future comparisons of the results, presented here with the experimental measurements, as well as predictions for other hypothetical 2D superconductors, should be possible.

In relation to the above, the results presented in Figure 1A show all the major features that can be expected in terms of the phonon-mediated superconducting phase. Specifically, for each considered case, the ${\mathsf{\Delta }}_{m=1}\left(T\right)$ function has a plateau at lower temperatures and becomes a decreasing function as the temperature increases. Nonetheless, central to our analysis is the comparison between the results obtained within the adiabatic and non-adiabatic regimes. It can be observed that at each $\mu$* level, the inclusion of the vertex corrections leads to the lower ${\mathsf{\Delta }}_{m=1}\left(T\right)$ values when comparing to the adiabatic case. Moreover, by inspecting Figure 1 (A) more closely, the reduction of the ${\mathsf{\Delta }}_{m=1}\left(T\right)$ function appears to be stronger for higher $\mu$* values. This observation is crucial as it shows that non-adiabatic effects strongly influence the superconducting state in Ca-h-BN, as suggested before by the non-negligible value of the adiabatic ratio for the discussed material. It also shows the correlation between the magnitude of the non-adiabatic effects and the strength of the Coulomb depairing interaction.

The above findings can be further investigated and reinforced by analyzing other pivotal parameters of the superconducting state based on Figure 1A. Herein, of special interest are the parameters and related effects that can be later observed in the experiment [27]. In particular, from the results given in Figure 1A, we can first extract the critical temperature ($T_C$) value that marks the metal-superconductor phase transition. This temperature value is obtained by using the following relation: ${\mathsf{\Delta }}_{m=1}\left(T_C\right)=0$. Such critical temperatures for the selected Coulomb pseudopotential values are given in Figure 1B. As previously, the results are presented here for the adiabatic and non-adiabatic cases. The solutions in Figure 1B once again show the divergence between values obtained in the framework of the adiabatic and non-adiabatic approaches. In particular, the non-adiabatic effects clearly suppress the superconducting state by lowering the $T_C$ value at each considered $\mu$* level and the suppression is stronger as the Coulomb pseudopotential becomes higher; strictly speaking, the $T_C\in 〈13.2,7.4〉$ K for the adiabatic case and $T_C\in 〈11.8,4.9〉$ K in the non-adiabatic regime. As a result, we observe that the percentage difference between the adiabatic and non-adiabatic predictions rises from 11.2% to 40.7% when ${\mu }^{*}$ increases from 0.1 to 0.3. The discussed results also allow us to note that, even for the strong depairing Coulomb correlations (${\mu }^{*}=0.3$), the superconducting state is not suppressed (the $T_C$ values are still non-negligible). We argue that this is due to the fact that Ca-h-BN is characterized by the relatively high electron–phonon coupling constant ($\lambda >1$) [1].

Similar observations can be made by employing the straightforward relation for the superconducting gap: ${\mathsf{\Delta }}_g=2{\mathsf{\Delta }}_{m=1}\left(0\right)$. The computed values of this property are shown in Figure 1C for the adiabatic and non-adiabatic regimes by considering selected Coulomb pseudopotential values. We observe that the superconducting gap is notably higher in the adiabatic case when comparing to the non-adiabatic one. From the theoretical standpoint, this is an expected behavior, since materials with higher gap values should present more enhanced superconducting properties than their narrow-gap counterparts [21]; in detail, ${\mathsf{\Delta }}_g\in 〈4.7,2.5〉$ meV and ${\mathsf{\Delta }}_g\in 〈4.1,1.5〉$ meV for the adiabatic and non-adiabatic approaches. This gives us discrepancies in terms of the percentage difference at the level of 13.6% and 50% for $\mu$* = 0.1 and $\mu$* = 0.3, respectively.

The results obtained for the ${\mathsf{\Delta }}_g$ may also be used to determine the characteristic ratio for the superconducting gap given as: $R_{\mathsf{\Delta }}\equiv {\mathsf{\Delta }}_g/k_B{T}_C$. This ratio is familiar in the BCS microscopic theory of superconductivity [23,24] and may be yet another observable for future comparisons with the experiment [27]. In the present analysis, we obtain $R_{\mathsf{\Delta }}\in 〈4.14,3.96〉$ within the adiabatic formalism and $R_{\mathsf{\Delta }}\in 〈4.08,3.55〉$ by using the non-adiabatic approach. While the behavior of the $R_{\mathsf{\Delta }}$ is similar to the already discussed ${\mathsf{\Delta }}_g$ behavior, the computed values point to the additional aspects hitherto not discussed in the present study. By referring to the BCS theory again, we know that the conventional superconductors described within this theory should exhibit a universal value of the discussed ratio equal to 3.53 [23,24]. In what follows, one can easily observe that the predictions of the present analysis exceed those of the BCS theory, no matter if we consider the adiabatic or the non-adiabatic case. According to the Eliashberg formalism, this means that strong-coupling and retardation effects play an important role in the superconductivity of the Ca-h-BN, an aspect that was already discussed in detail for the adiabatic regime in [28]. However, the present analysis also shows that there is a strong interplay between nonadiabaticity and not only the Coulomb interaction but also the aforementioned strong-coupling and retardation effects.

4. Summary and Conclusions

In the present study, we have discussed the superconducting phase in the monolayer Ca-h-BN. Our attention was paid to the role of potential non-adiabatic effects, as suggested by the non-negligible value of the adiabatic ratio. To provide the most comprehensive and complementary analysis, we have employed the Eliashberg equations formalism in the adiabatic and non-adiabatic regimes. By using this formalism it was possible for us to investigate the pivotal superconducting properties of the discussed material, such as the critical temperature ($T_C$) and the superconducting gap (${\mathsf{\Delta }}_g$).

Our findings are summarized in

Table 1. The superconducting properties of the Ca-h-BN monolayer: the critical temperature $T_C$, the superconducting gap $\left({\mathsf{\Delta }}_g\right)$ and the characteristic ratio $R_{\mathsf{\Delta }}$. Results are presented for the adiabatic (A-E) and non-adiabatic (N-E) regimes.

${\mathit{\mu }}^{*}$	${\mathit{T}}_{\mathit{C}}$ [K]	${\mathit{T}}_{\mathit{C}}$ [K]	${\mathbf{\Delta }}_{\mathit{g}}$ [meV]	${\mathbf{\Delta }}_{\mathit{g}}$ [meV]	${\mathit{R}}_{\mathbf{\Delta }}$	${\mathit{R}}_{\mathbf{\Delta }}$
	(A-E)	(N-E)	(A-E)	(N-E)	(A-E)	(N-E)
0.1	13.2	11.8	4.7	4.1	4.14	4.08
0.2	9.3	7.4	3.3	2.3	4.10	3.68
0.3	7.4	4.9	2.5	1.5	3.96	3.55

in terms of the numerical values as calculated within the adiabatic and non-adiabatic Eliashberg formalism. Based on the obtained results, we observe that non-adiabatic effects strongly influence the superconducting phase in the Ca-h-BN material, meaning that the adiabatic Migdal’s theorem breaks down in the considered case. The observed influence is clearly negative as the non-adiabatic formalism suggests lower values for every analyzed superconducting property, compared to the case of the adiabatic model. The decrease caused by the nonadiabaticity varies from ∼11% up to even ∼50% in terms of the percentage difference, depending on the considered property and the strength of the Coulomb interaction. The reason the nonadiabaticity suppresses the superconducting phase in Ca-h-BN can be argued to be related to the sign of the vertex corrections to the electron–phonon interaction, included in the framework of the non-adiabatic Eliashberg formalism [15,29]. This is to say, the vertex corrections of a given order may enter the Eliashberg equations with a specific sign, meaning that they contribute to the suppression or enhancement of the superconducting state depending on this sign. This should be considered as a qualitative argument since the order-dependent contribution of the vertex corrections is a nontrivial problem. Nonetheless, we note that our finding is in qualitative agreement with previous studies on non-adiabatic superconductivity in two-dimensional materials such as the LiC${}_6$ [8] or the electron-doped graphene [30].

In addition to the above, we observe notable interplay between the non-adiabatic effects and depairing correlations as well as the strong-coupling and retardation effects. The first two appear to complement each other and cause suppression of the superconducting state. On the other hand, the two former enhance the superconductivity in comparison to the predictions of the BCS theory given in [1]. Specifically, this observation can be parametrized by inspecting the $T_C$ value, which appears to be up to 7% higher in terms of the percentage difference for ${\mu }^{*}=0.1$, when calculated within the adiabatic Eliashberg formalism in comparison to the BCS-like McMillan–Allen–Dynes formula used in [1]. This naturally follows our other finding, which says that the characteristic ratio for the superconducting gap notably exceeds the universal BCS value of 3.53 [23,24] (see Table 1). It is also observed that, along with the stronger depairing correlations, the role of the non-adiabatic effects increases.

In summary, the superconducting phase in Ca-h-BN seems to have phenomenology that is more complex than previously thought. The obtained results still suggest that the analyzed state is caused by the strong-coupling between electrons and phonons but with an equally strong influence of the non-adiabatic effects. They also suggest potential routes for the future design of two-dimensional superconductors, where even more attention should be paid to the reduction of the Coulomb interactions because of their interplay with the negative non-adiabatic effects. As a consequence, the presented predictions can serve as a reference point for future theoretical and experimental investigations aimed at the superconducting properties of the Ca-h-BN monolayer. They not only show what can be expected in terms of the character of the superconducting phase in Ca-h-BN but also motivate further studies on potentially easy-to-realize 2D conventional superconductors. To this end, we note that the presented analysis can be extended even further by considering the impact of the high-order vertex corrections on the superconducting state in terms of their sign and absolute contribution. As we noted earlier, this is, however, a nontrivial problem for future investigations and the instructive preliminary discussion of these aspects can be found in [22].