Innovative Analytical Method for X-ray Imaging and Space-Resolved Spectroscopy of ECR Plasmas
Abstract
1. Introduction
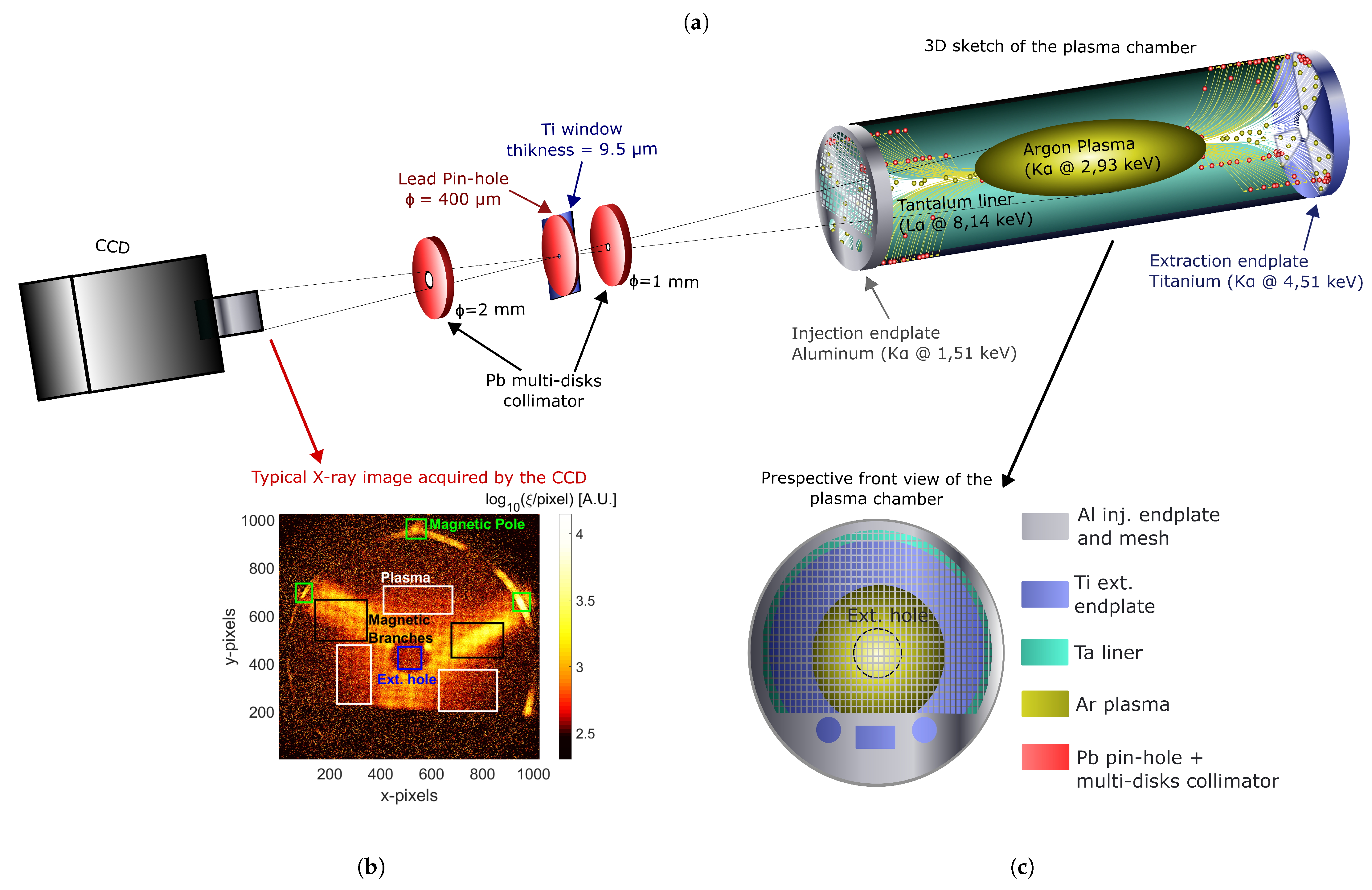
2. The Experimental Setup
3. X-ray Spectrally-Resolved Imaging Algorithm
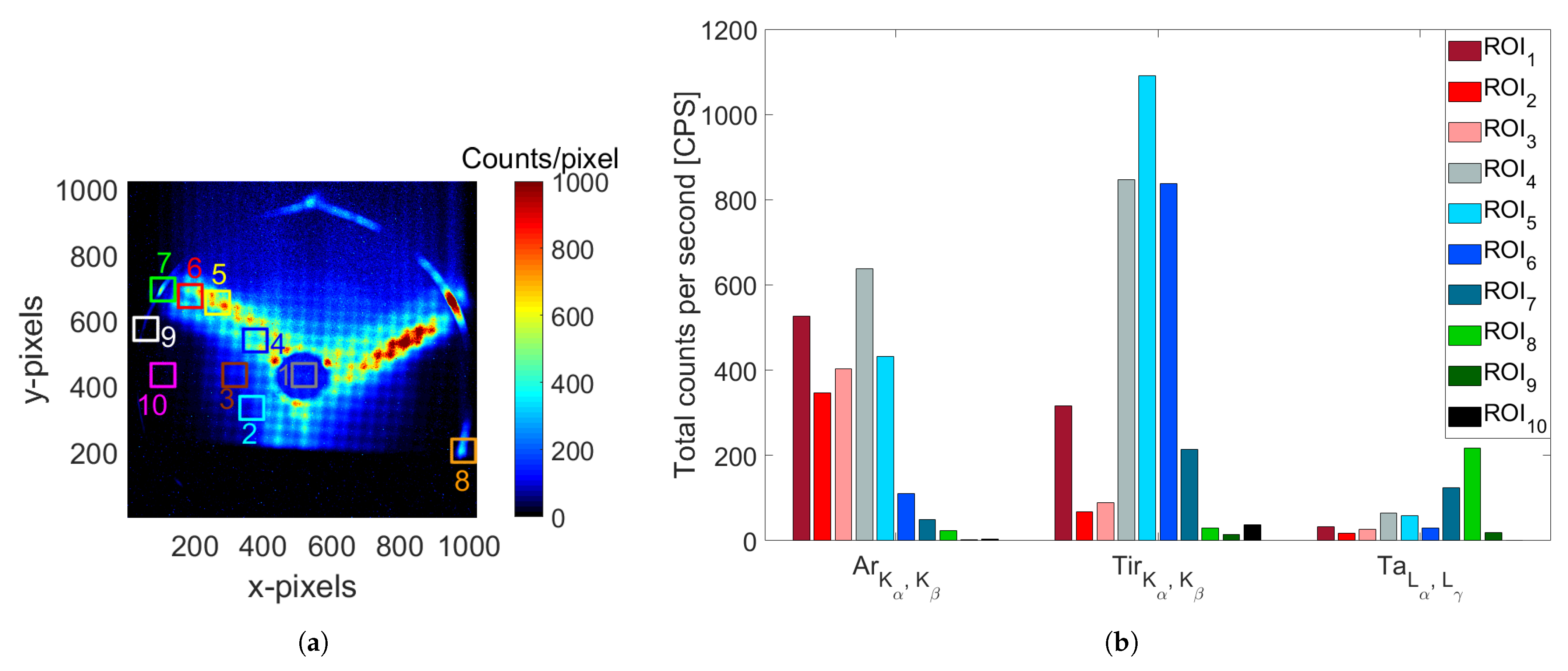
- White rectangles, enclosing the regions where the X-rays come from the plasma region (i.e., there are no perspective interceptions with the chamber endplates beyond them);
- Black squares, highlighting the so-called “magnetic branches”, i.e., the bremsstrahlung-produced X-rays and X-ray fluorescence coming from extraction endplate, due to electrons escaping axially (shown in yellow in the pictorial view of Figure 1a);
- Bright green squares, indicating the regions where the magnetic field lines intercept the lateral walls of the plasma chamber (the ones depicted in red in Figure 1a).
- (I)
- Grouping process (Gr-p);
- (II)
- Energy calibration and event counting normalization;
- (III)
- Energy filtering process;
- (IV)
- High Dynamical Range (HDR) imaging and spectroscopy;
- (V)
- Readout Noise (RON) removal (RON-r).
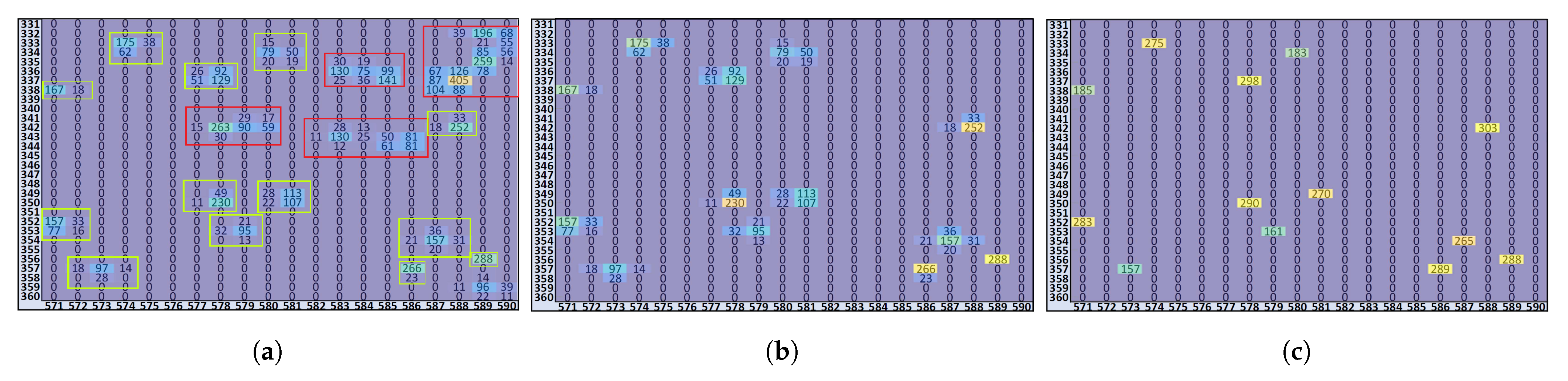
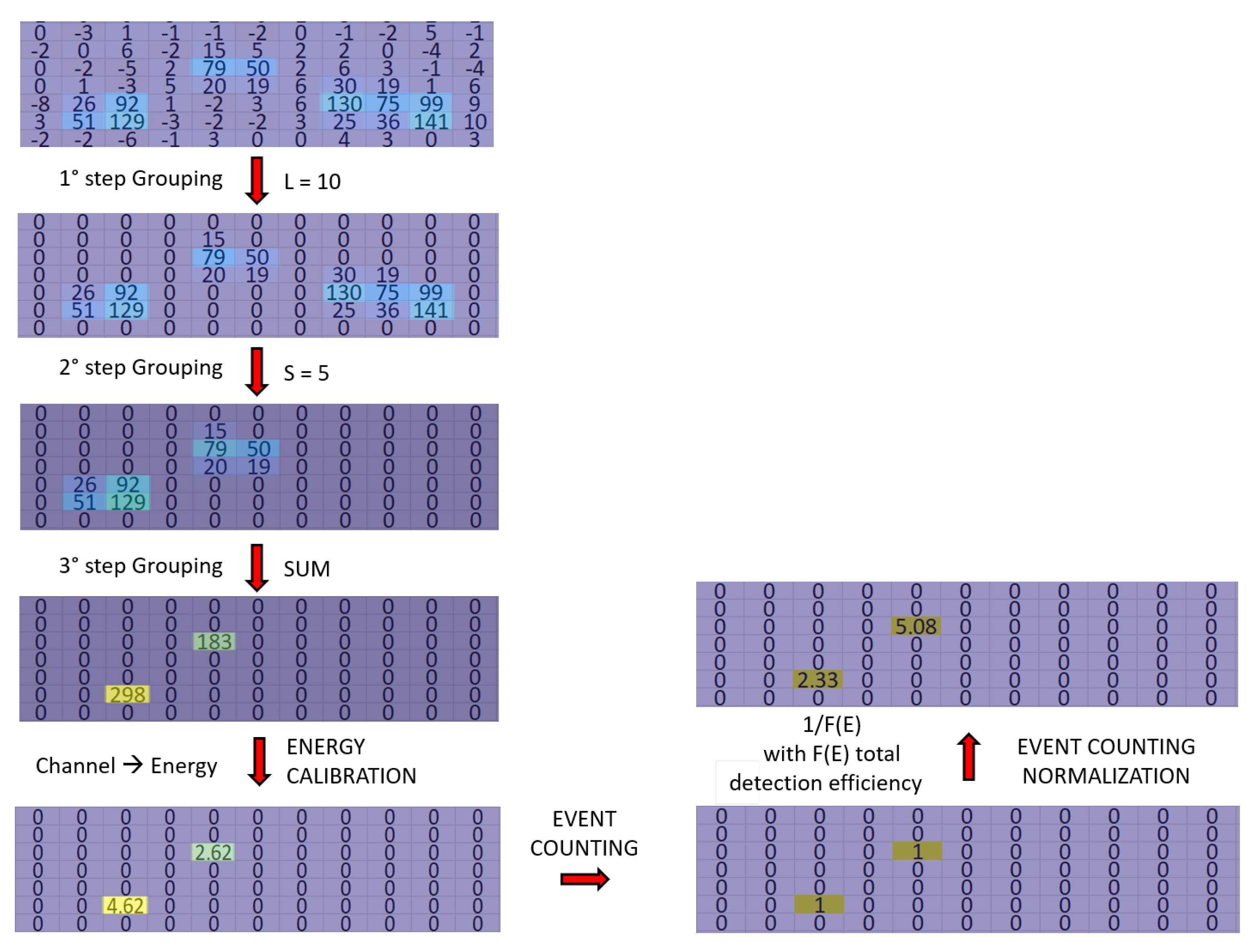
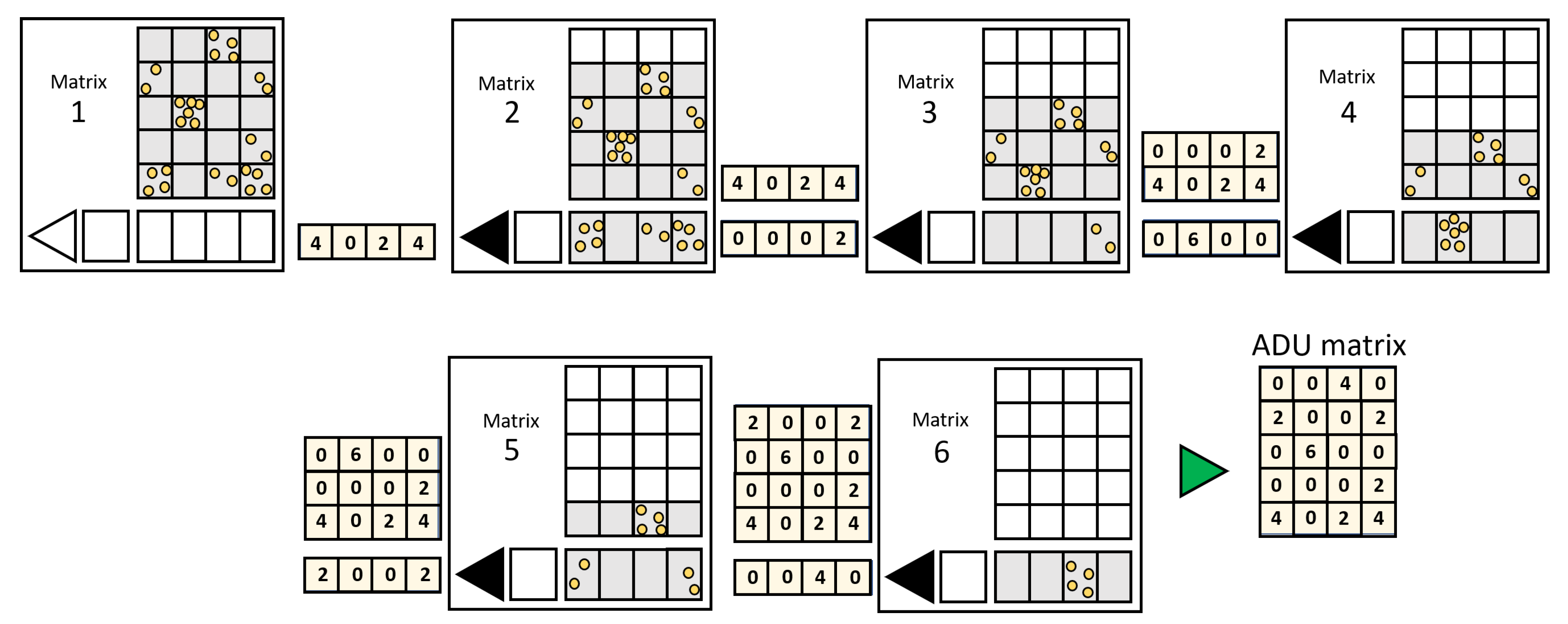
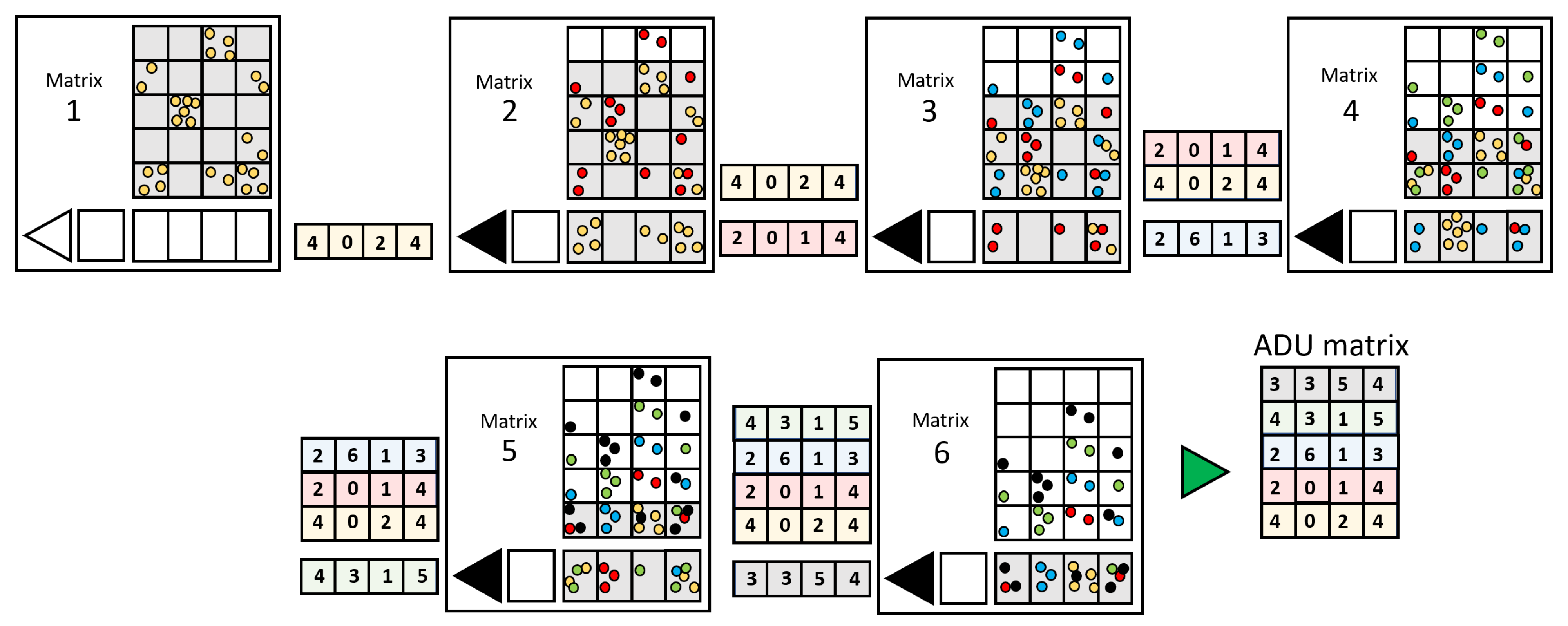
3.1. The Grouping Process
- STEP-1:
- Considering a given image-frame J, all pixels with an ADU < L are “turned off”; then, for a given J frame, neighboring pixels of an illuminated pixel at coordinates are checked. In case there are no charges in the surrounding pixels, the event is considered to be purely a single photon and is associated with three coordinates , with E being the energy associated with the photon (determined as in Section 3.2). This is shown in Figure 2a;
- STEP-2:
- When a group of active neighboring pixels (a cluster) is identified, the algorithm tries to distinguish single from multiple-events:
- (a)
- Single photon-event clusters are typically characterized by a single, clear maximum: for these, in STEP-3, described below, we see that the code associates the integrated total charge to a single photon energy, whose coordinate corresponds to the maximum;
- (b)
- Clusters associated with multiple-hit events (showing different relative maxima in a big-size cluster) are filtered out from SPhC images. However, the algorithm stores the information anyway, labelling them spurious events (in SPhC images, their value is set at zero);
- STEP-3:
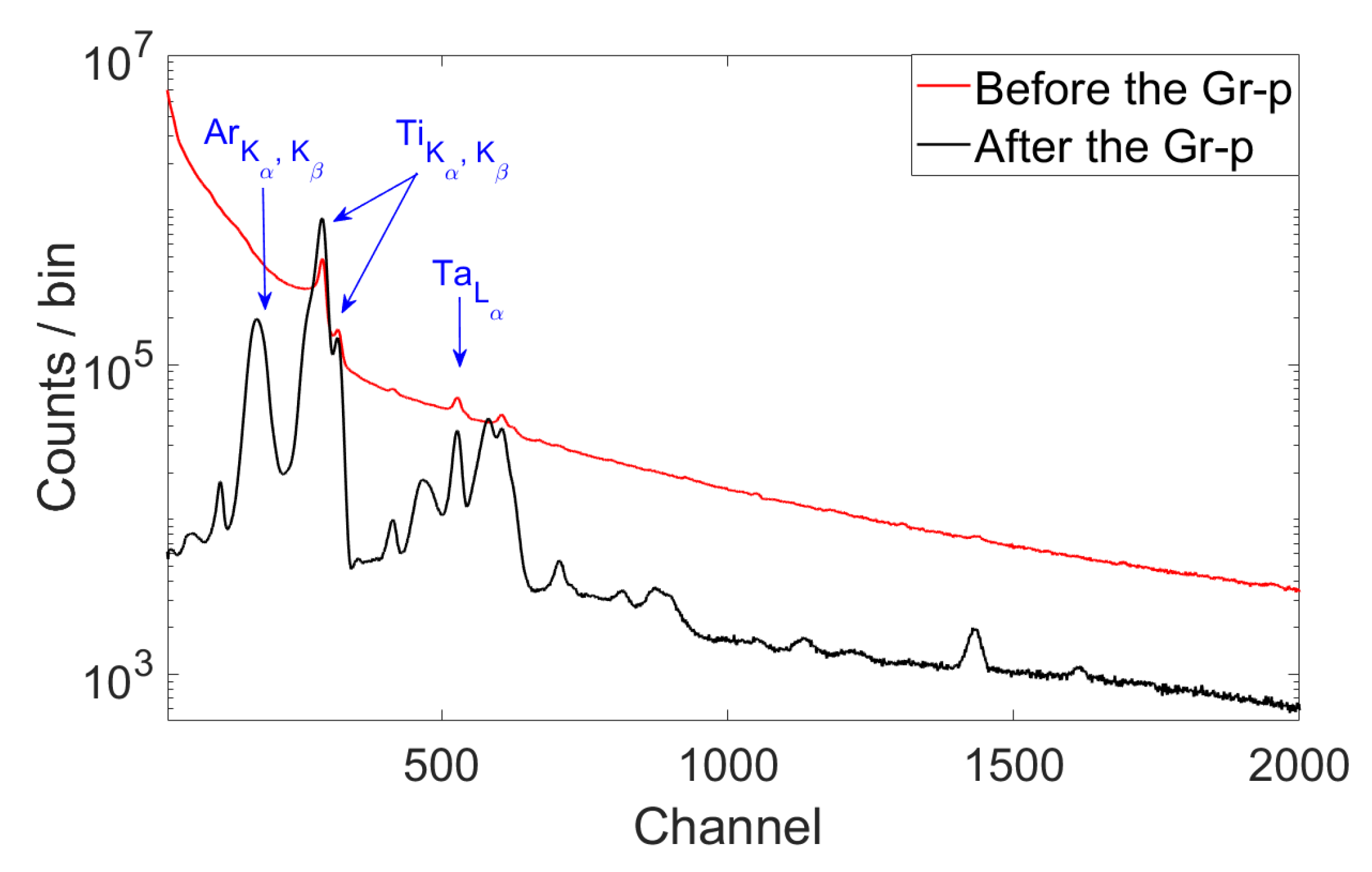
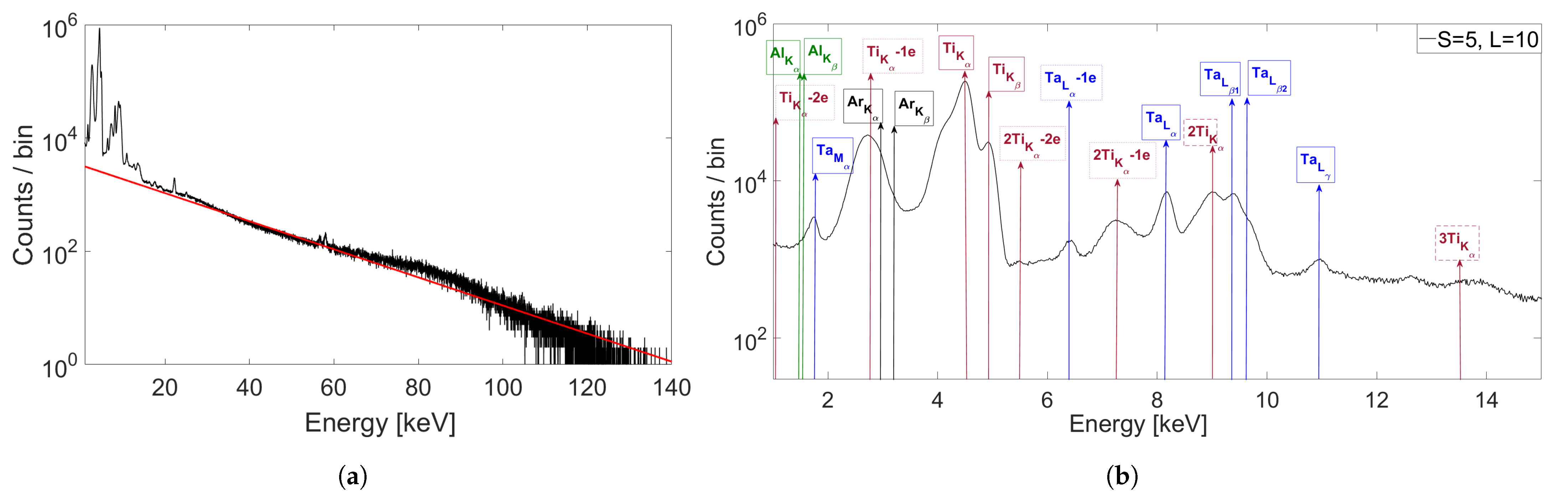
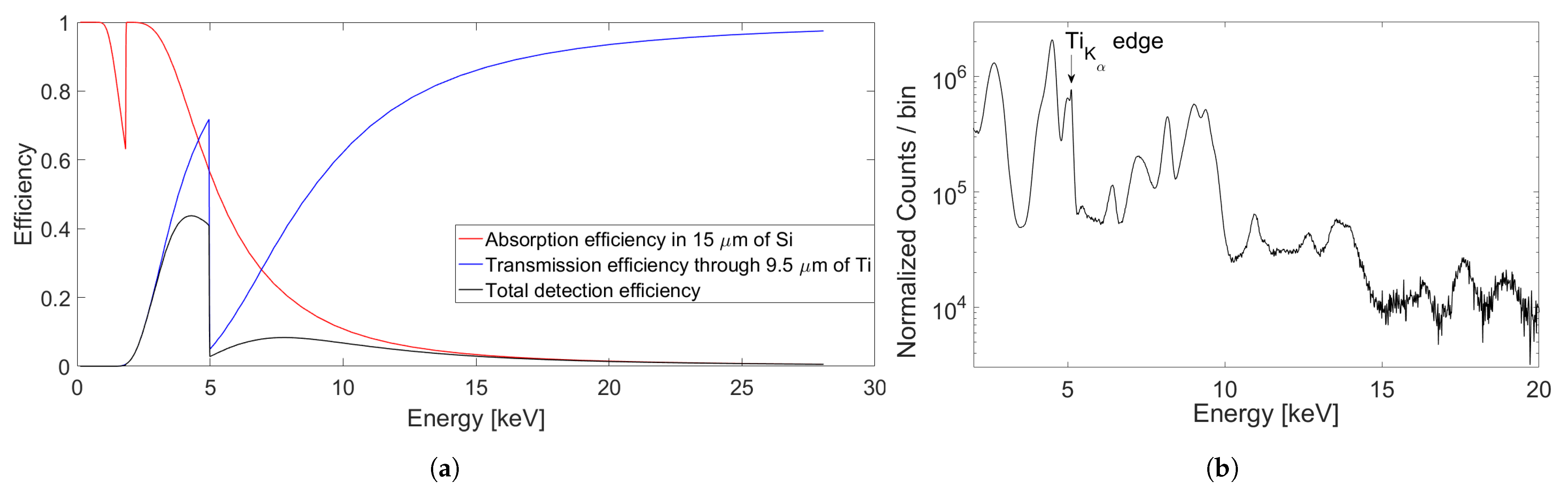
3.2. Energy Calibration and Counting Normalization
Optimization of the Algorithm
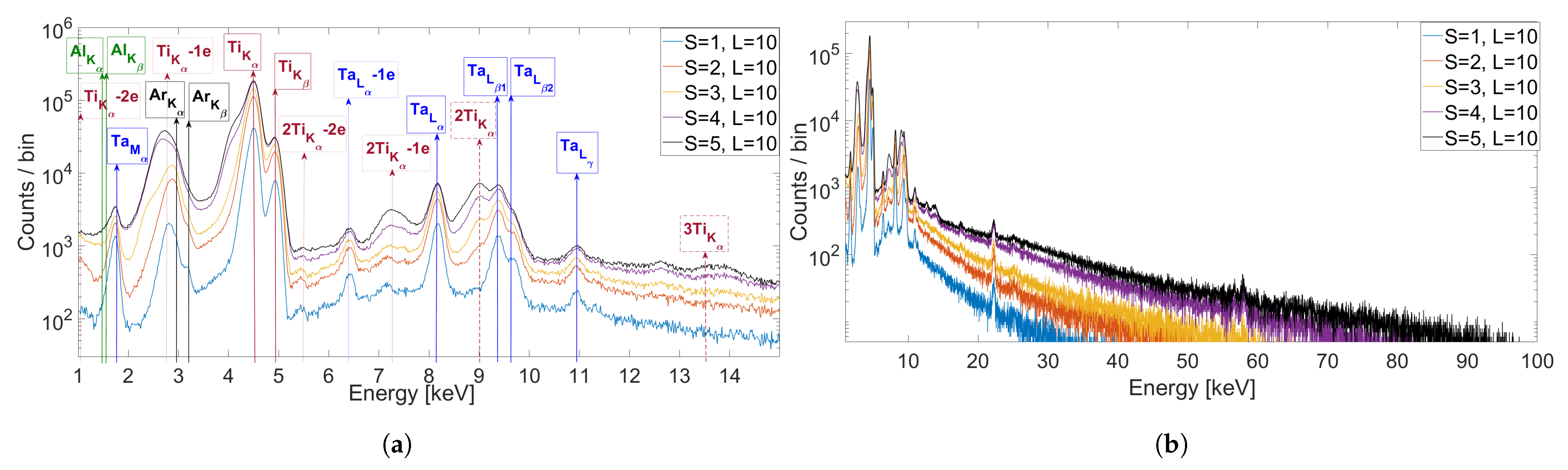
- (a)
- The ratio for ;
- (b)
- The ratio for ;
- (c)
- The total for ;
- (a)
- The escape peak intensity vs. the main peak intensity is almost independent of L and S;
- (b)
- The dimer peak intensity dramatically increases with respect to the main peak when increasing the cluster size;
- (c)
- The intensity of the spectral components (e.g., ) increases with S.
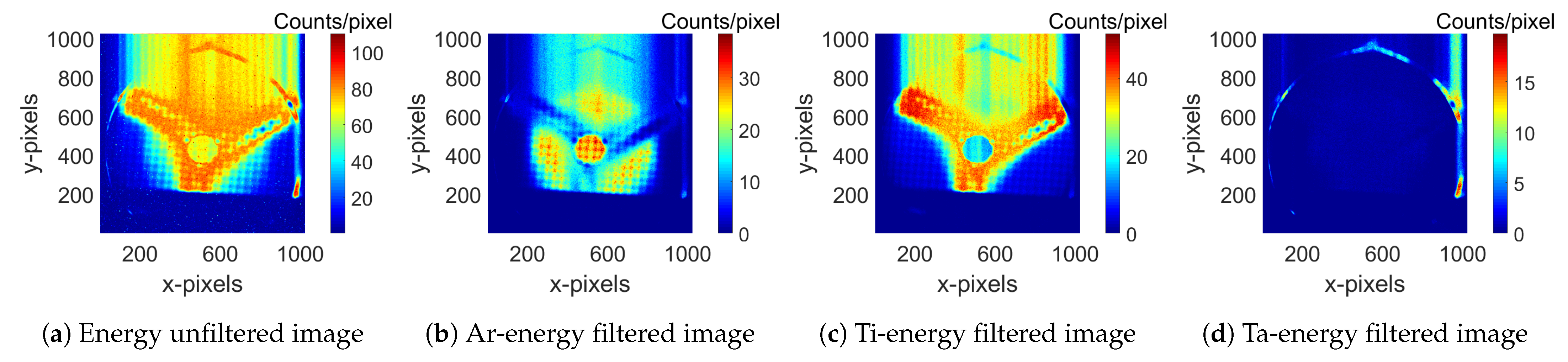
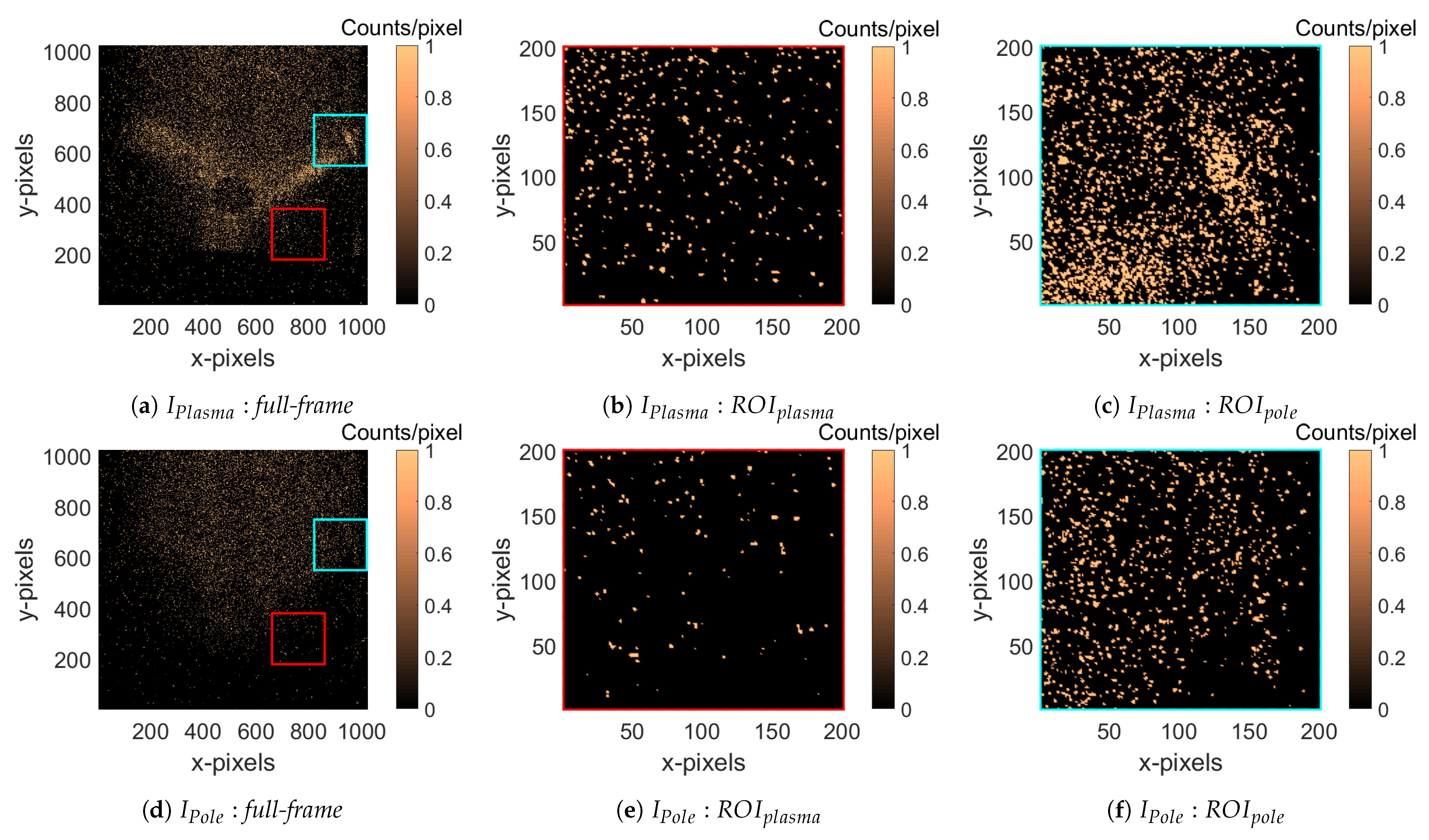
3.3. Energy Filtered Images
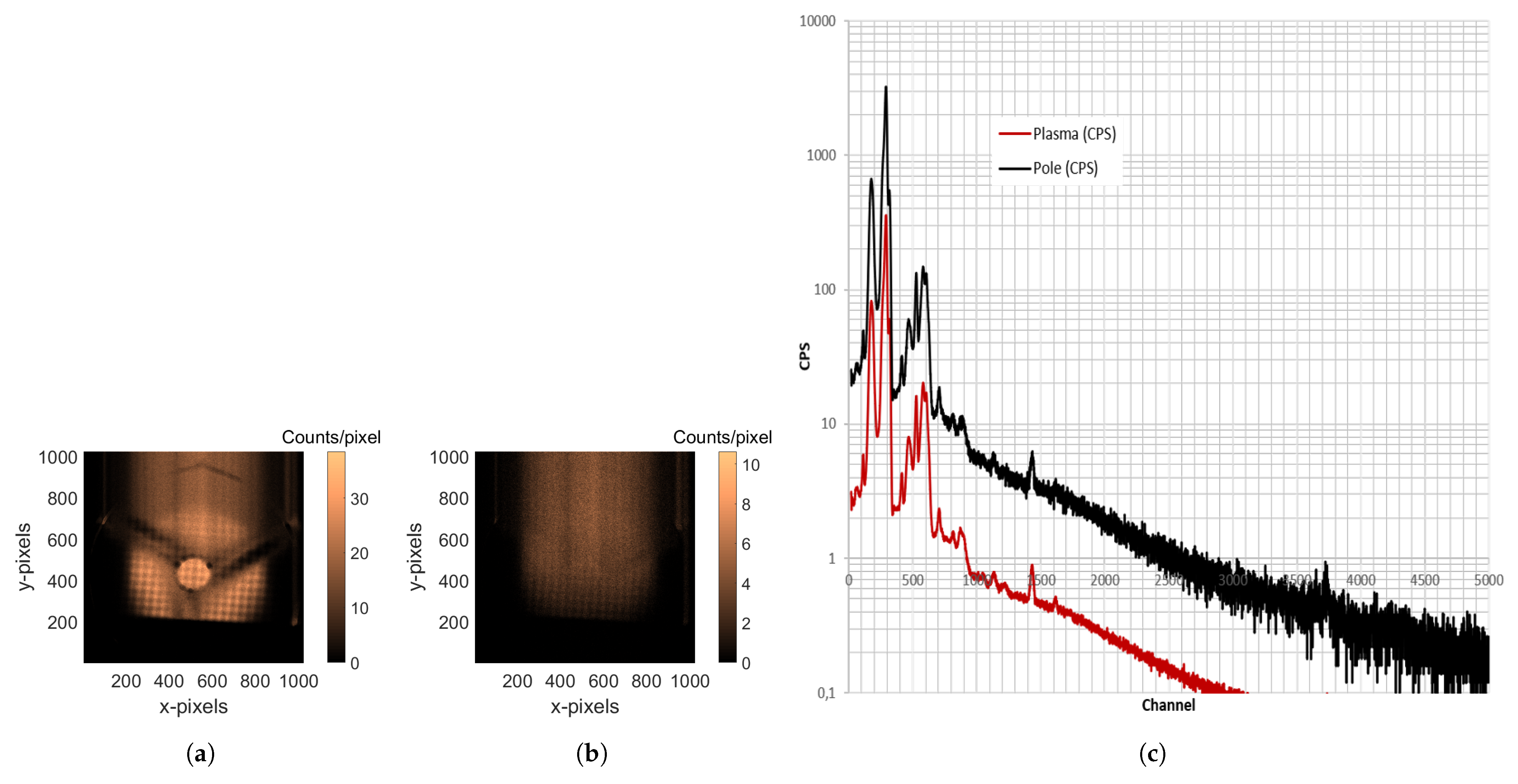
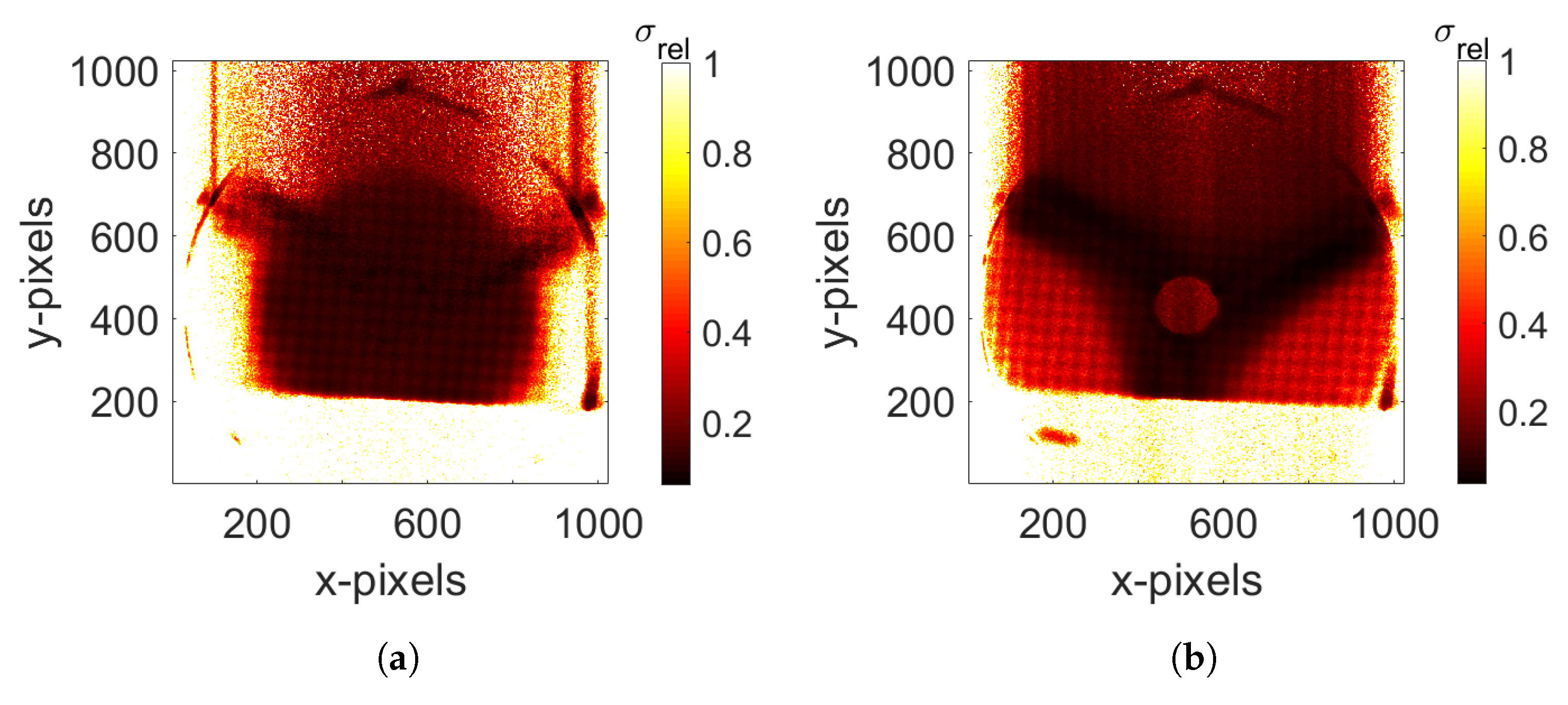
3.4. High Dynamical Range (HDR) Imaging and Spectroscopy
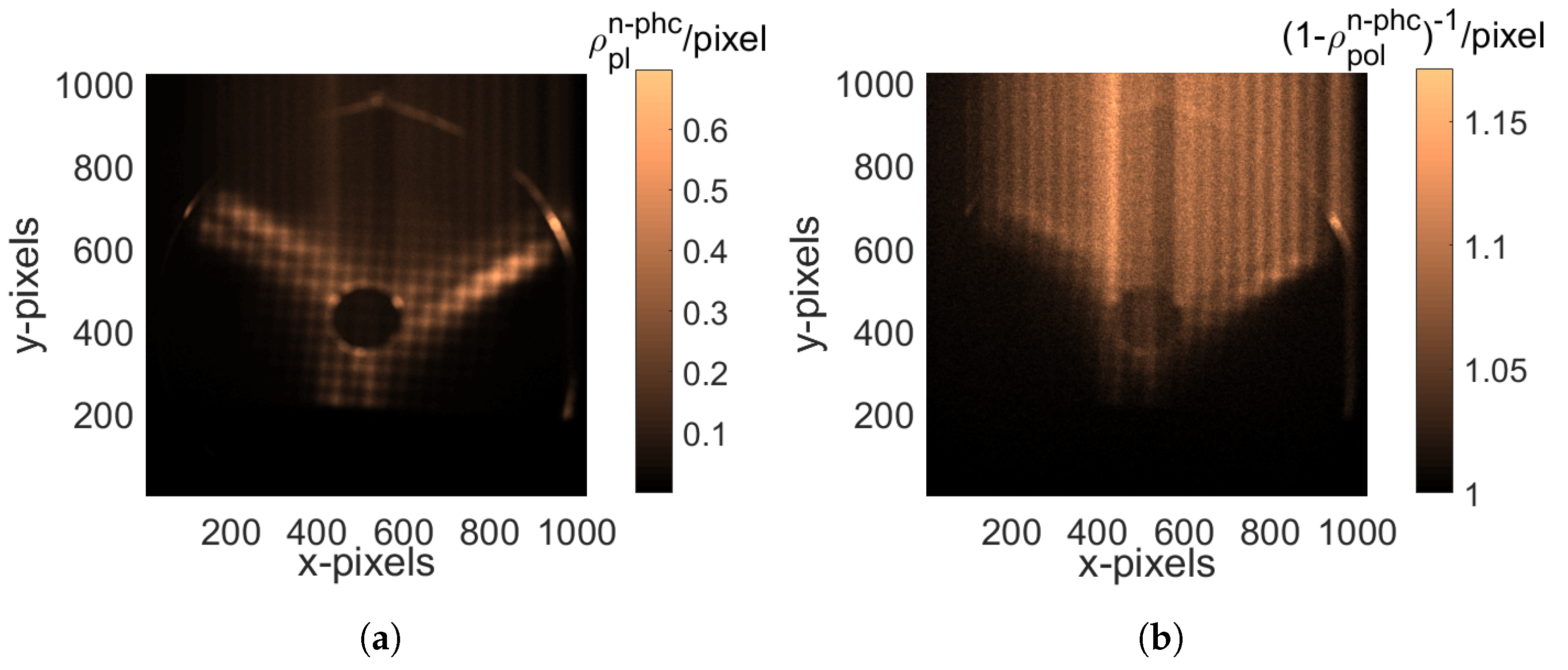
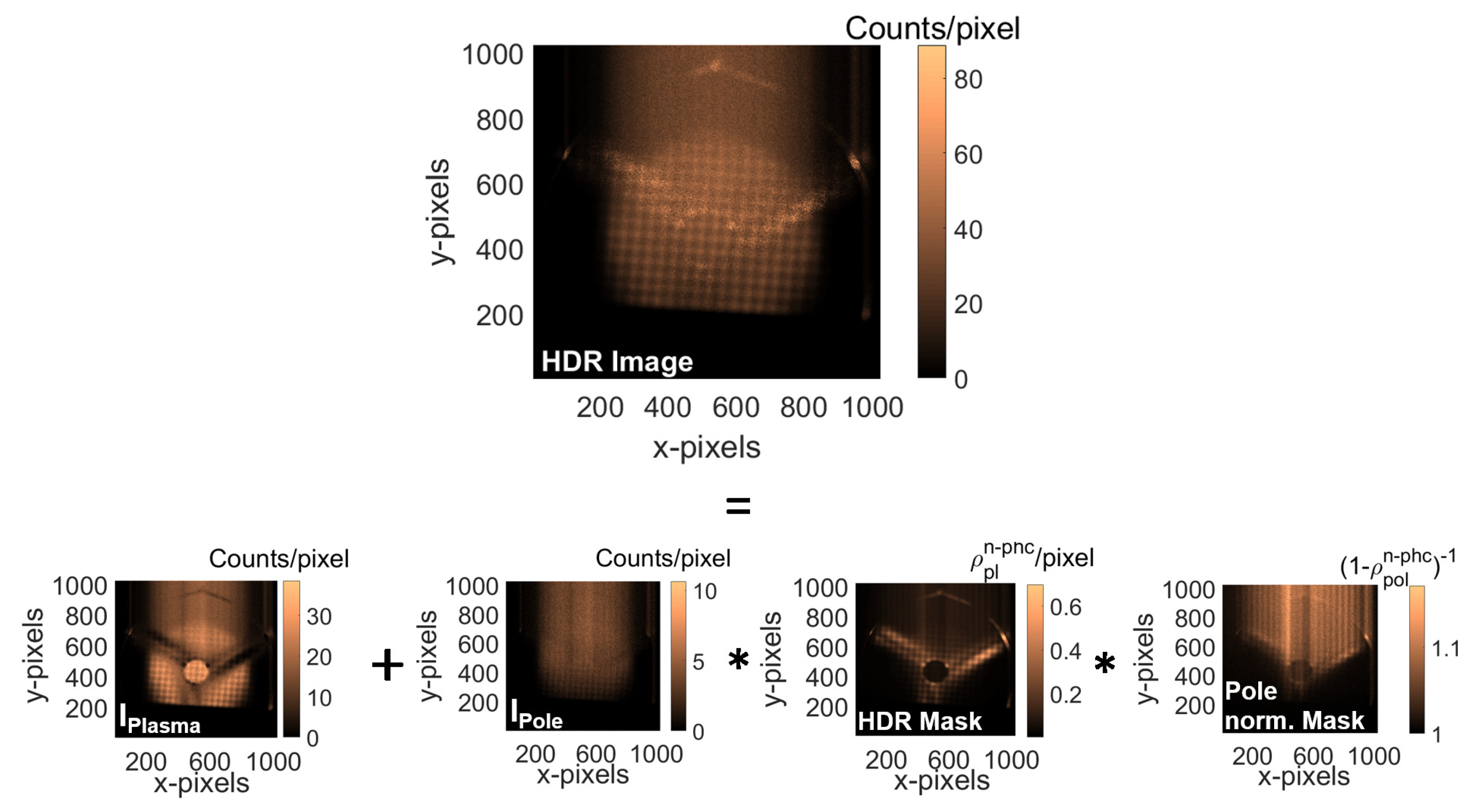
- HDR Mask: This mask shows those pixels which were not photon-counted on images. It consists of a digital (0–1) array, where a position evaluated as 1 corresponds to those pixels that are part of a cluster larger than the S parameter, for each image frame. The sum of those images, divided by , gives the desired HDR Mask, where each number corresponds to the probability normalized to 1 of a given pixel to be not photon-counted, as shown in Figure 12a.
- Pole normalization Mask generation from frames: Even the frames are not always photon-counted; therefore, the counts are under-represented and the missing information is spatially dependent. Using the not-photon-counted matrix (NPhC) obtained from the images (), a normalization matrix was obtained (shown in the Figure 12b): Normalization matrix = 1/(1 − NPhC/1000).
- HDR image = + HDR maskPole normalization mask. Of course, was normalized for and . The HDR image is shown in the Figure 13.
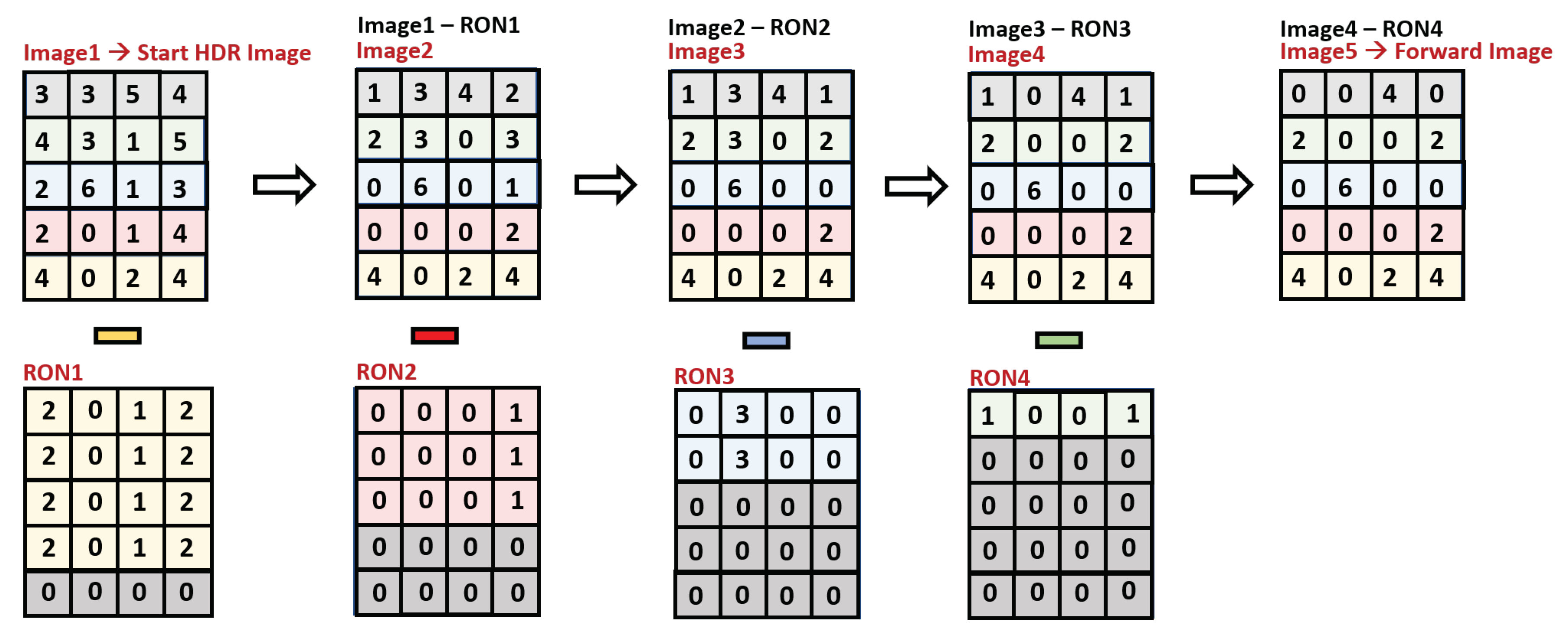
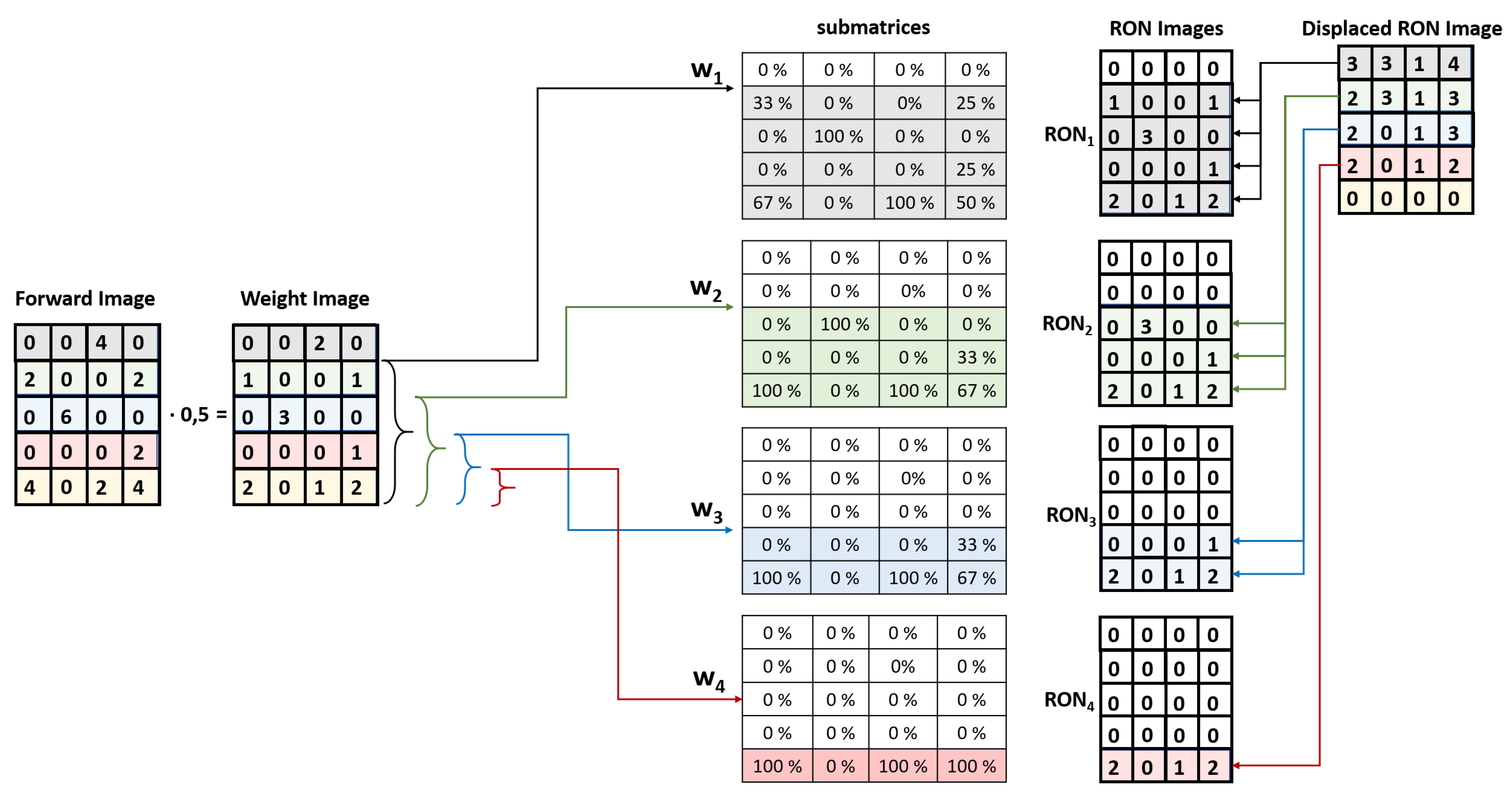
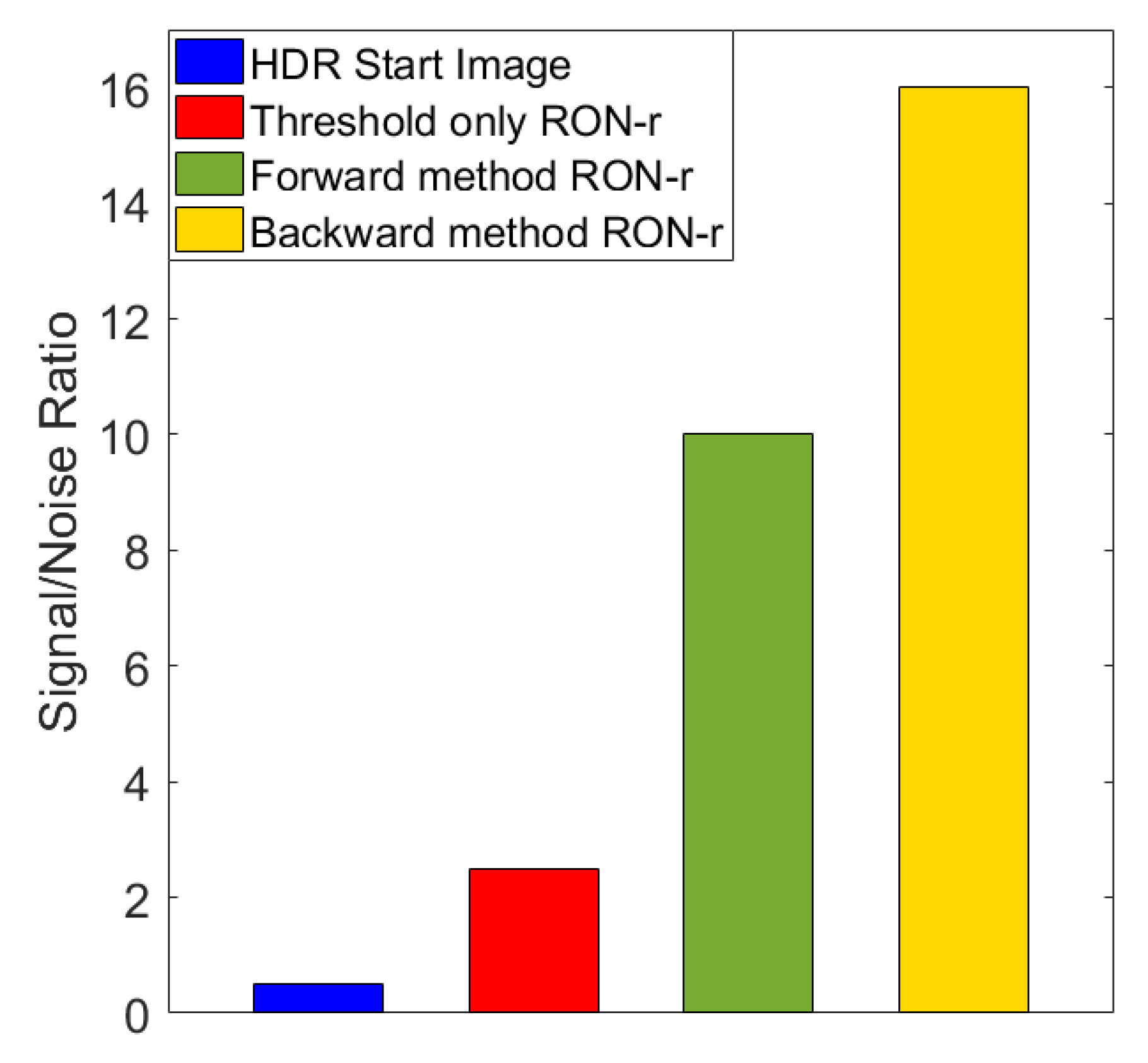
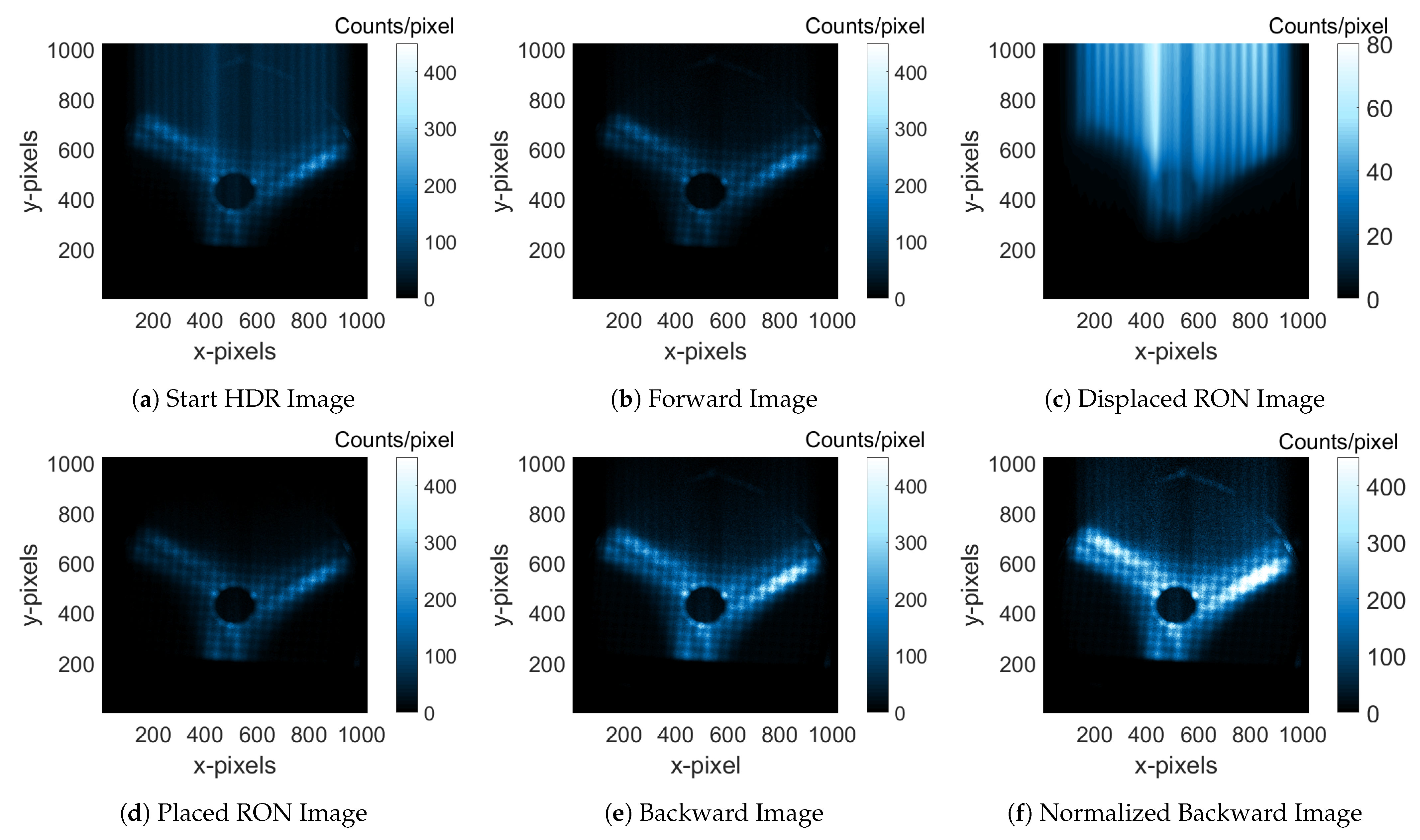
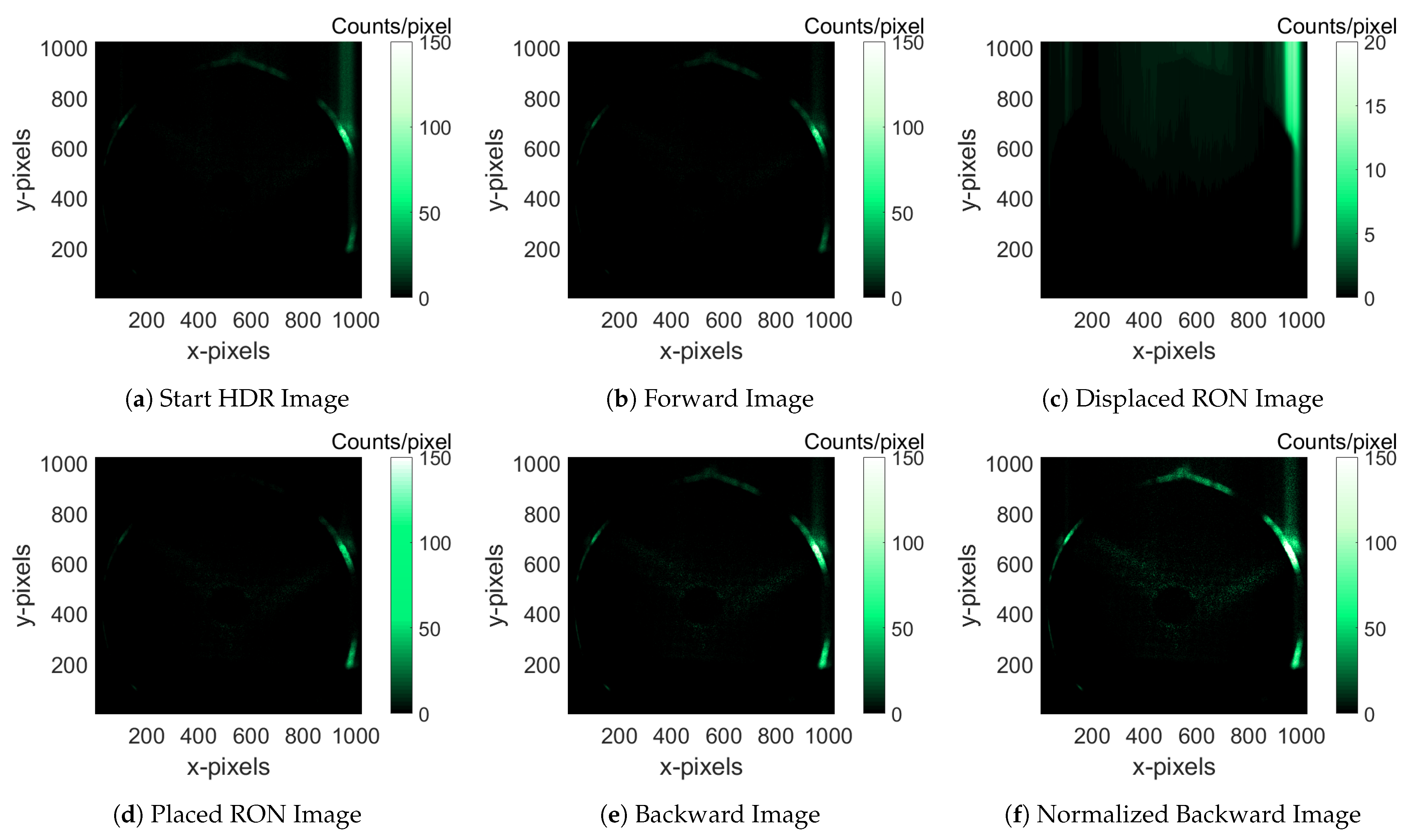
3.5. The Readout Noise (RON) Removal Algorithm
3.5.1. Step-1: The Forward Method
3.5.2. II Step: The Backward Method
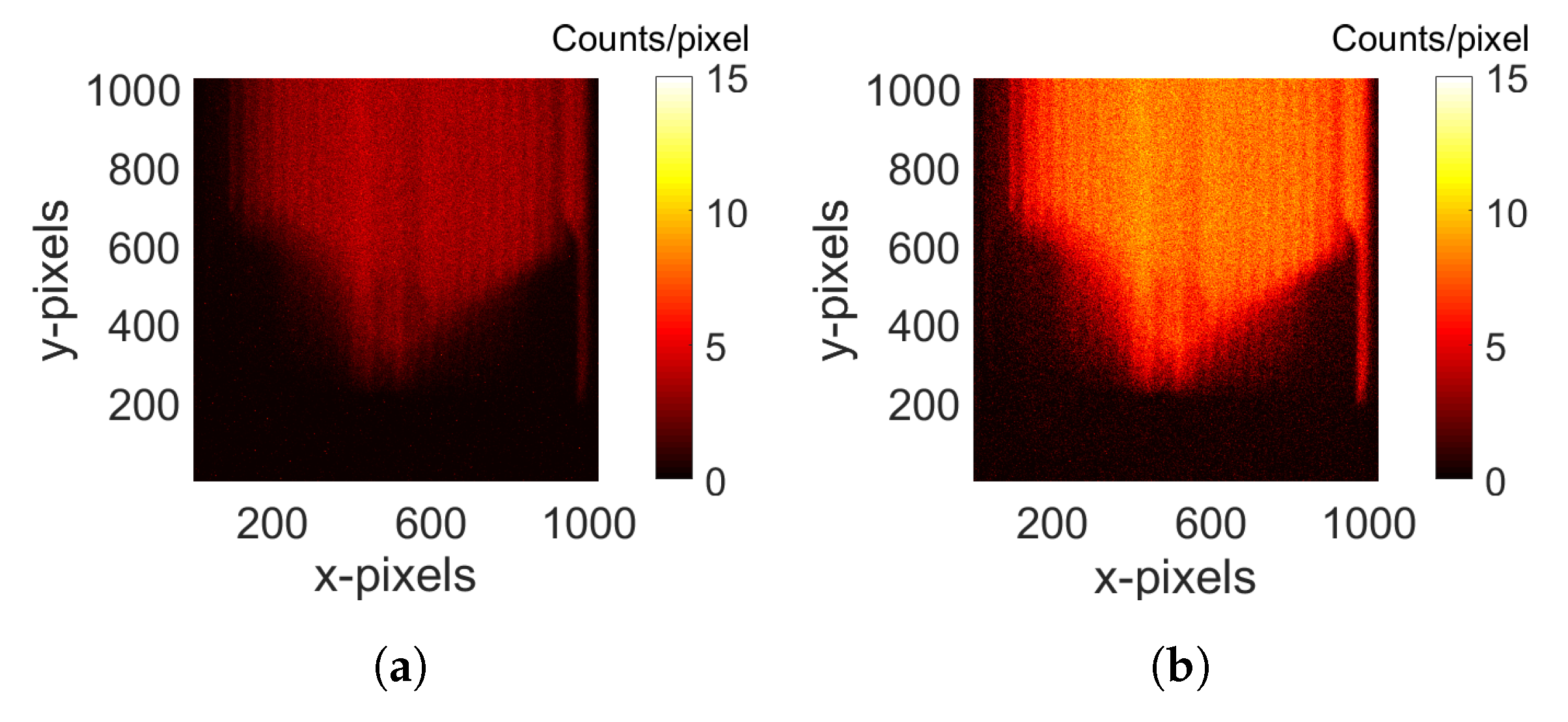
- First, 200 image frames acquired setting the lowest possible in the driver (s) were used to estimate the BGN threshold. The sum of the 200 event-counted frames is shown in Figure 22a, which was normalized for the frames number, and the level, pixel-by-pixel, was considered the BGN threshold (Figure 22b).
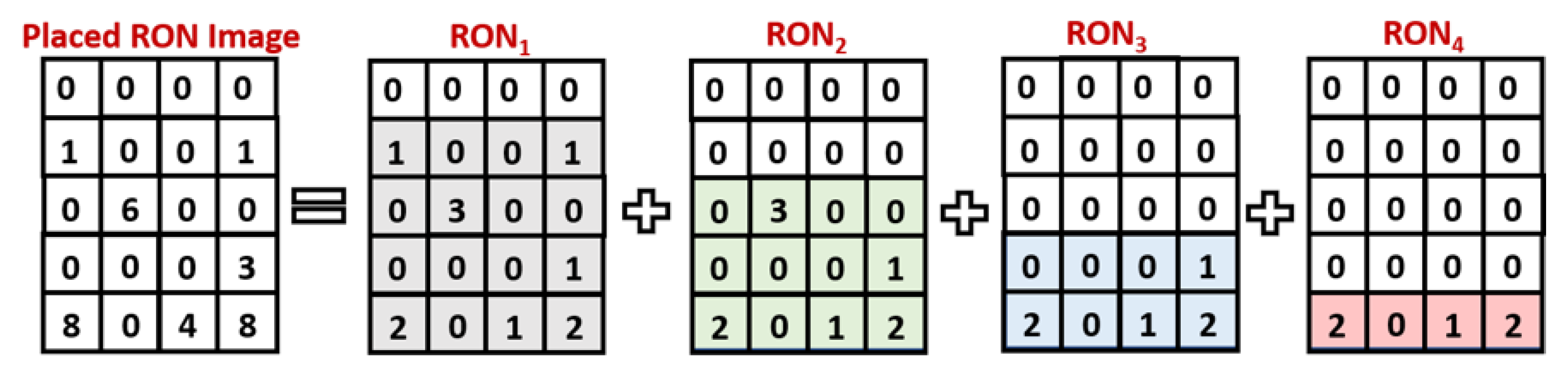
- Setting the BGN threshold in the Forward Image, the Weight Image was obtained and used to estimate the Placed RON Image (Figure 23d). It contains the same RON charge as was collected in the Displaced RON image, but placed in the correct positions.
- The sum of the Forward Image and of the Placed RON Image gives the so-called “Backward Image”, shown in Figure 23e, which contains the whole charges (collected during the measurement time + RON time) in the correct pixel-positions.
- For the data collected during the RO, the effective is pixel-position-dependent; therefore, the Backward Image was also properly time-normalized. The final post-processed image is called the “Normalized Backward Image” and is shown in Figure 23f.
4. Plasma Analysis: A Short Overview
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Naselli, E.; Mascali, D.; Biri, S.; Caliri, C.; Castro, G.; Celona, L.; Cosentino, L.G.; Galatà, A.; Gammino, S.; Giarrusso, M.; et al. Multidiagnostics setups for magnetoplasmas devoted to astrophysics and nuclear astrophysics research in compact traps. J. Instrum. 2019, 14, C10008. [Google Scholar] [CrossRef]
- Biri, S.; Pálinkás, J.; Perduk, Z.; Rácz, R.; Caliri, C.; Castro, G.; Celona, L.; Gammino, S.; Mascali, D.; Mazzaglia, M.; et al. Multi diagnostic setup at the Atomki-ECRIS to investigate the two-close-frequency heating phenomena. J. Instrum. 2018, 13, C11016. [Google Scholar] [CrossRef]
- Mascali, D.; Musumarra, A.; Leone, F.; Romano, F.P.; Galatà, A.; Gammino, S.; Massimi, C. PANDORA, a new facility for interdisciplinary in-plasma physics. Eur. Phys. J. A 2017, 53, 145. [Google Scholar] [CrossRef]
- Mascali, D.; Busso, M.; Mengoni, A.; Amaducci, S.; Castro, G.; Celona, L.; Cosentino, L.G.; Cristallo, S.; Finocchiaro, P.; Galatà, A.; et al. The PANDORA project: An experimental setup for measuring in-plasma β-decays of astrophysical interest. EPJ Web Conf. 2020, 227, 01013. [Google Scholar] [CrossRef]
- Nebem, D.; Fogleman, J.; Isherwood, B.; Leitner, D.; Machicoane, G.; Renteria, S.; Stetson, J.; Tobos, L. X-ray investigation on the Superconducting Source for Ions (SuSI). J. Instrum. 2019, 14, C02008. [Google Scholar] [CrossRef]
- Li, J.B.; Li, L.X.; Li, L.B.; Guo, J.W.; Hitz, D.; Lu, W.; Feng, J.C.; Zhang, W.H.; Zhang, X.Z.; Zhao, H.Y.; et al. Influence of electron cyclotron resonance ion source parameters on high energy electrons. Rev. Sci. Instrum. 2020, 91, 083302. [Google Scholar] [CrossRef]
- Benitez, J.; Lineis, C.; Phair, L.; Todd, D.; Xie, D. Dependence of the Bremsstrahlung Spectral Temperature in Minimum-B Electron Cyclotron Resonance Ion Sources. IEEE Trans. Plasma Sci. 2017, 45, 7. [Google Scholar] [CrossRef]
- Isherwood, B.; Machicoane, G. Measurement of the energy distribution of electrons escaping confinement from an electron cyclotron resonance ion source. Rev. Sci. Instrum. 2020, 91, 025104. [Google Scholar] [CrossRef] [PubMed]
- Ropponen, T.; Tarvainen, O.; Toivanen, V.; Peura, P.; Jones, P.; Kalvas, T.; Koivisto, H.; Noland, J.; Leitner, D. The effect of rf pulse pattern on bremsstrahlung and ion current time evolution of an ECRIS. Rev. Sci. Instrum. 2010, 81, 02A302. [Google Scholar] [CrossRef]
- Mascali, D.; Celona, L.; Maimone, F.; Maeder, J.; Castro, G.; Romano, F.P.; Musumarra, A.; Altana, C.; Caliri, C.; Torrisi, G.; et al. X-ray spectroscopy of warm and hot electron components in the CAPRICE source plasma at EIS testbench at GSI. Rev. Sci. Instrum. 2014, 85, 02A956. [Google Scholar] [CrossRef]
- Miracoli, R.; Castro, G.; Celona, L.; Gammino, S.; Mascali, D.; Mazzaglia, M.; Naselli, E.; Torrisi, G. Characterization of ECR plasma by means of radial and axial X-ray diagnostics. J. Instrum. 2019, 14, C01016. [Google Scholar] [CrossRef]
- Mascali, D.; Castro, G.; Altana, C.; Caliri, C.; Mazzaglia, M.; Romano, F.P.; Leone, F.; Musumarra, A.; Naselli, E.; Reitano, R.; et al. Electromagnetic diagnostics of ECR-Ion Sources plasmas: Optical/X-ray imaging and spectroscopy. J. Instrum. 2017, 12, C12047. [Google Scholar] [CrossRef]
- Gumberidze, A.; Trassinelli, M.; Adrouche, N.; Szabo, C.I.; Indelicato, P.; Haranger, F.; Isac, J.-M.I.; Lamour, E.; Le Bigot, E.-O.; Mérot, J.; et al. Electronic temperatures, densities, and plasma X-ray emission of a 14.5 GHz electron-cyclotron resonance ion source. Rev. Sci. Instrum. 2010, 81, 033303. [Google Scholar] [CrossRef] [PubMed]
- Biri, S.; Valek, A.; Suta, T.; Takács, E.; Szabó, C.; Hudson, L.T.; Radics, B.; Imrek, J.; Juhász, B.; Pálinkás, J. Imaging of ECR plasmas with a pinhole X-ray camera. Rev. Sci. Instrum. 2004, 75, 1420. [Google Scholar] [CrossRef]
- Takács, E.; Radics, B.; Szabó, C.I.; Biri, S.; Hudson, L.T.; Imreka, J.; Juhászc, B.; Suta, T.; Valek, A.; Pálinkás, J. Spatially resolved X-ray spectroscopy of an ECR plasma—Indication for evaporative cooling. Nucl. Instrum. Meth. B 2005, 235, 120–125. [Google Scholar] [CrossRef]
- Rácz, R.; Biri, S.; Pálinkás, J.; Mascali, D.; Castro, G.; Caliri, C.; Romano, F.P.; Gammino, S. X-ray pinhole camera setups used in the Atomki ECR Laboratory for plasma diagnostics. Rev. Sci. Instrum. 2016, 87, 02A741. [Google Scholar] [CrossRef]
- Mascali, D.; Castro, G.; Biri, S.; Rácz, R.; Pálinkás, J.; Caliri, C.; Celona, L.; Neri, L.; Romano, F.P.; Torrisi, G.; et al. Electron cyclotron resonance ion source plasma characterization by X-ray spectroscopy and X-ray imaging. Rev. Sci. Instrum. 2016, 87, 02A510. [Google Scholar] [CrossRef]
- Rácz, R.; Mascali, D.; Biri, S.; Caliri, C.; Castro, G.; Galatà, A.; Gammino, S.; Neri, L.; Pálinkás, J.; Romano, F.P.; et al. Electron cyclotron resonance ion source plasma characterization by energy dispersive X-ray imaging. Plasma Sources Sci. Technol. 2017, 26, 075011. [Google Scholar] [CrossRef]
- Romano, F.P.; Caliri, C.; Cosentino, L.; Gammino, S.; Giuntini, L.; Mascali, D.; Neri, L.; Pappalardo, L.; Rizzo, F.; Taccetti, F. Macro and Micro Full Field X-Ray Fluorescence with an X-Ray Pinhole Camera Presenting High Energy and High Spatial Resolution. Anal. Chem. 2014, 86, 21. [Google Scholar] [CrossRef]
- Jones, B.; Deeney, C.; Pirela, A.; Meyer, C.; Petmecky, D.; Gard, P.; Clark, R.; David, J. Design of a multilayer mirror monochromatic X-ray imager for the Z accelerator. Rev. Sci. Instrum. 2004, 75, 4029. [Google Scholar] [CrossRef]
- McPherson, L.A.; Ampleford, D.J.; Coverdale, C.A.; Argo, J.W.; Owen, A.C.; Jaramillo, D.M. High energy X-ray pinhole imaging at the Z facility. Rev. Sci. Instrum. 2016, 87, 063502. [Google Scholar] [CrossRef]
- Bachmann, B.; Hilsabeck, T.; Fieldet, J.; Masters, N.; Reed, C.; Pardini, T.; Rygg, J.R.; Alexander, N.; Benedetti, L.R.; Döppner, T.; et al. Resolving hot spot microstructure using X-ray penumbral imaging. Rev. Sci. Instrum. 2016, 87, 11E201. [Google Scholar] [CrossRef] [PubMed]
- Sasaya, T.; Sunaguchi, N.; Hyodo, K.; Zeniya, T.; Yuasa, T. Multi-pinhole fluorescent X-ray computed tomography for molecular imaging. Sci. Rep. 2017, 7, 5742. [Google Scholar] [CrossRef]
- Pacella, D.; Leigheb, M.; Bellazzini, R.; Brez, A.; Finkenthal, M.; Stutman, D.; Kaita, R.; Sabbagh, S.A. Soft X-ray tangential imaging of the NSTX core plasma by means of an MPGD pinhole camera. Plasma Phys. Control. Fusion 2004, 46, 1075. [Google Scholar] [CrossRef][Green Version]
- Jang, S.; Lee, S.G.; Lim, C.H.; Kim, H.O.; Kim, S.Y.; Lee, S.H.; Hong, J.; Jang, J.; Jeon, T.; Moon, M.K.M.; et al. Preliminary result of an advanced tangential X-ray pinhole camera system with a duplex MWPC on KSTAR plasma. Curr. Appl. Phys. 2013, 13, 5. [Google Scholar] [CrossRef]
- Song, I.; Jang, J.; Jeon, T.; Pacella, D.; Claps, G.; Murtas, F.; Lee, S.H.; Choe, W. Tomographic 2-D X-ray imaging of toroidal fusion plasma using a tangential pinhole camera with gas electron multiplier detector. Curr. Appl. Phys. 2016, 16, 10. [Google Scholar] [CrossRef]
- Pablant, N.A.; Delgado-Aparicio, L.; Bitter, M.; Brandstetter, S.; Eikenberry, E.; Ellis, R.; Hill, K.W.; Hofer, P.; Schneebeli, M. Novel energy resolving X-ray pinhole camera on Alcator C-Mod. Rev. Sci. Instrum. 2012, 83, 10E526. [Google Scholar] [CrossRef]
- Biri, S.; Rácz, R.; Perduk, Z.; Pálinkás, J.; Naselli, E.; Mazzaglia, M.; Torrisi, G.; Castro, G.; Celona, L.; Gammino, S.; et al. Innovative experimental setup for X-ray imaging to study energetic magnetized plasmas. J. Instrum. 2021, 16, P03003. [Google Scholar] [CrossRef]
- Skalyga, V.; Izotov, I.; Kalvas, T.; Koivisto, H.; Komppula, J.; Kronholm, R.; Laulainen, J.; Mansfeld, D.; Tarvainen, O. Suppression of cyclotron instability in Electron Cyclotron Resonance ion sources by two-frequency heating. Phys. Plasma 2015, 22, 083509. [Google Scholar] [CrossRef]
- Shalashov, A.G.; Viktorov, M.; Mansfeld, D.A.; Golubev, S.V. Kinetic instabilities in a mirror-confined plasma sustained by high-power microwave radiation. Phys. Plasma 2017, 24, 032111. [Google Scholar] [CrossRef]
- Naselli, E.; Biri, S.; Celona, L.; Galatà, A.; Gammino, S.; Mazzaglia, M.; Rácz, R.; Torrisi, G.; Mascali, D. High-resolution X-ray imaging as a powerful diagnostics tool to investigate in-plasma nuclear β-decays. Il Nuovo Cimento C 2021, 44, 64. [Google Scholar]
- Mascali, D.; Naselli, E.; Rácz, R.; Biri, S.; Celona, L.; Galatá, A.; Gammino, S.; Mazzaglia, M.; Torrisi, G. Experimental study of single vs. two-close-frequency heating impact on confinement and losses dynamics in ECR Ion Sources plasmas by means of X-ray spectroscopy and imaging. Plasma Phys. Control. Fusion 2021. [Google Scholar] [CrossRef]
- Rácz, R.; Biri, S.; Perduk, Z.; Pálinkás, J.; Mascali, D.; Mazzaglia, M.; Naselli, E.; Torrisi, G.; Castro, G.; Celona, L.; et al. Effect of the two-close-frequency heating to the extracted ion beam and to the X-ray flux emitted by the ECR plasma. J. Instrum. 2018, 13, C12012. [Google Scholar] [CrossRef]
- Naselli, E.; Mascali, D.; Mazzaglia, M.; Biri, S.; Rácz, R.; Pálinkás, J.; Perduk, Z.; Galatá, A.; Castro, G.; Celona, L.; et al. Impact of the two-close-frequency heating on ECR Ion Sources plasmas radio emission and stability. Plasma Source Sci. Technol. 2019, 28, 8. [Google Scholar] [CrossRef]
- Ryohei, T.; Koretaka, Y.; Jun, K.; Hussain, A. Artificial peaks in energy dispersive X-ray spectra: Sum peaks, escape peaks, and diffraction peaks. X-ray Spectrom. 2016, 46, 5–11. [Google Scholar]
- Kang, S.X.; Sun, X.; Ju, X.; Huang, Y.Y.; Yao, K.; Wu, Z.Q.; Xian, D.C. Measurement and calculation of escape peak intensities in synchrotron radiation X-ray fluorescence analysis. Nucl. Instrum. Methods Phys. Res. B 2002, 192, 4. [Google Scholar] [CrossRef]
- Karydas, A.G.; Paradellis, T. A study of silicon escape peaks for X-ray detectors with various crystal dimensions. AIP Conf. Proc. 1999, 475, 858. [Google Scholar]
- NIST National Institute of Standards and Technology. X-ray Form Factor, Attenuation and Scattering Tables. Available online: https://physics.nist.gov/PhysRefData/FFast/html/form.html (accessed on 1 September 2020).
- Naselli, E.; Rácz, R.; Biri, S.; Mazzaglia, M.; Galatà, A.; Celona, L.; Gammino, S.; Torrisi, G.; Mascali, D. Quantitative analysis of an ECR Ar plasma structure by energy dispersive X-ray spectroscopy at high spatial resolution. J. Instrum. accepted.
- Mishra, B.; Pidatella, A.; Biri, S.; Galatà, A.; Naselli, E.; Rácz, R.; Torrisi, G.; Mascali, D. A novel numerical tool to study electron energy distribution functions of spatially anisotropic and non-homogeneous ECR plasmas. Phys. Plasmas 2021, 28, 102509. [Google Scholar] [CrossRef]

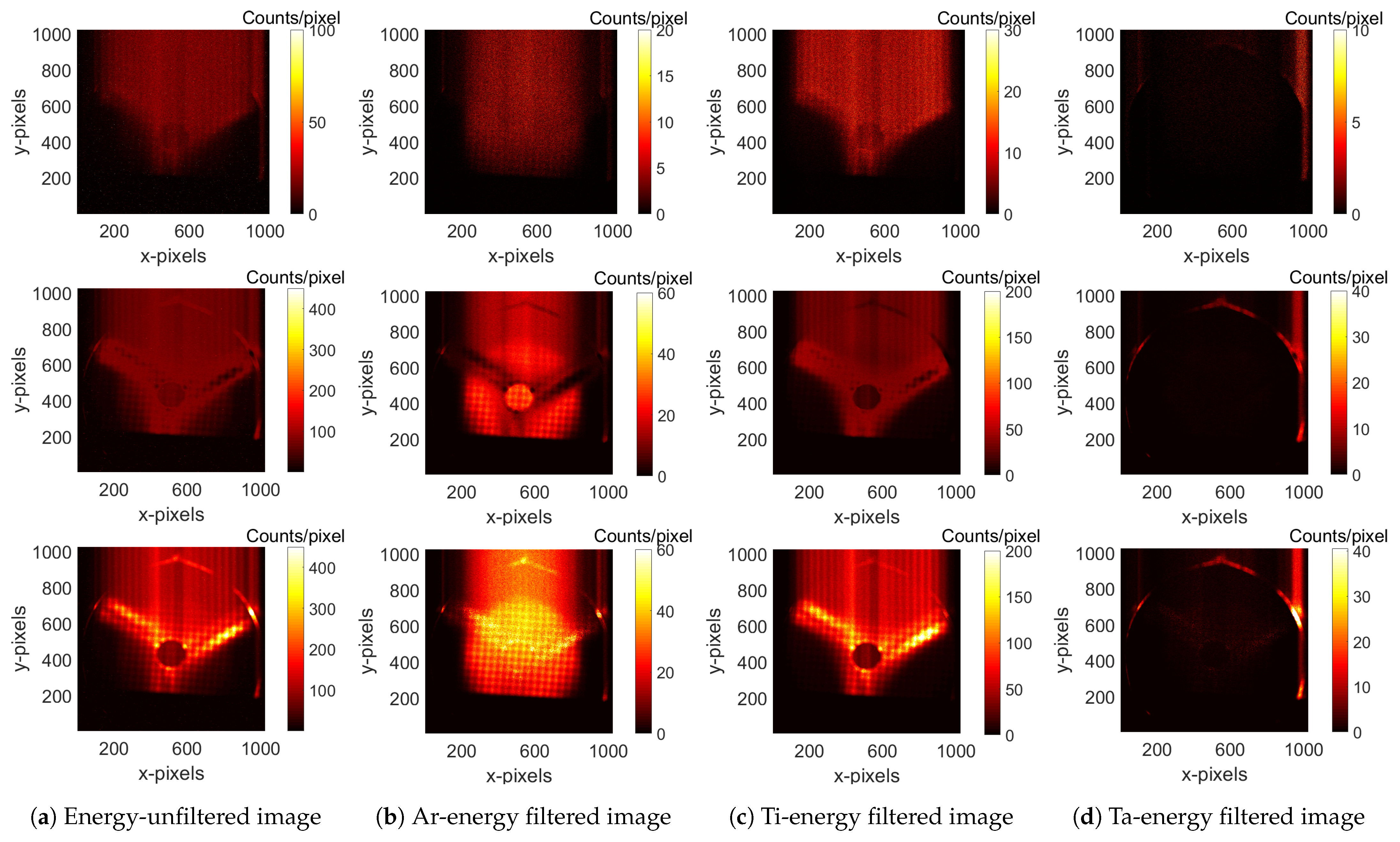



| 290 | 318 | 527 | 705 | |
| (a) | ||
| (b) | keV and keV | |
| (c) | keV and keV | |
| (d) | keV |
| Acquisition | [s] | N° Frames |
|---|---|---|
| 0.5 | 4200 | |
| 0.05 | 1000 |
| Name and Description of the Image | Total Counts | |
|---|---|---|
| (a) | Start HDR Image: | 1.49 |
| HDR Image with Readout Noise | ||
| (b) | Forward Image: | 0.74 |
| Original Image without the Readout Noise removed by means of the forward method | ||
| (c) | Displaced Readout-Noise Image: | 0.75 |
| Subtraction between the Original Image and the Forward Image | ||
| (d) | Placed Readout-Noise Image: | 0.75 |
| Displaced Readout-Noise Image with photons placed in the correct position by the backward method | ||
| (e) | Backward Image: | 1.49 |
| Sum pixel-by-pixel of the Forward Image and the Placed Readout-Noise Image | ||
| (f) | Normalized Backward Image: | 2.27 |
| Time normalized Backward Image | ||
| (g) | Background Image: | 0.16 |
| Mean image of 200 image-frames acquired setting an exposure time ∼ readout time | ||
| (h) | Threshold Image: | 0.42 |
| Square root of the Background (and Normalized) Image pixel-by-pixel | ||
| (i) | Weighing Image: | 0.72 |
| Forward Image filter out all events lower than the threshold pixel-by-pixel taken in the Threshold Image |
| Not-Filtered | Ar-Filtered | Ti-Filtered | Ta-Filtered | |
|---|---|---|---|---|
| [Counts ] | [Counts ] | [Counts ] | [Counts ] | |
| ROI 1 | 6.5050.008 | 3.8870.006 | 1.8600.004 | 0.4190.001 |
| ROI 2 | 6.0040.008 | 3.3640.006 | 1.9750.004 | 0.7110.001 |
| ROI 3 | 6.8700.008 | 3.3110.006 | 2.7670.005 | 0.7830.001 |
| ROI 4 | 21.4070.015 | 4.1530.006 | 10.3920.010 | 1.8220.001 |
| ROI 5 | 25.9320.016 | 2.3640.005 | 14.4450.012 | 1.7290.001 |
| ROI 6 | 18.2030.014 | 0.9030.003 | 11.4570.011 | 0.7250.001 |
| ROI 7 | 6.2400.008 | 0.6230.003 | 2.3740.005 | 5.0170.002 |
| ROI 8 | 4.4460.007 | 0.5200.002 | 0.3310.002 | 9.6600.003 |
| ROI 9 | 0.8040.003 | 0.0380.001 | 0.1860.001 | 0.8190.001 |
| ROI 10 | 0.8050.003 | 0.0340.001 | 0.4840.002 | 0.0320.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naselli, E.; Rácz, R.; Biri, S.; Mazzaglia, M.; Celona, L.; Gammino, S.; Torrisi, G.; Perduk, Z.; Galatà, A.; Mascali, D. Innovative Analytical Method for X-ray Imaging and Space-Resolved Spectroscopy of ECR Plasmas. Condens. Matter 2022, 7, 5. https://doi.org/10.3390/condmat7010005
Naselli E, Rácz R, Biri S, Mazzaglia M, Celona L, Gammino S, Torrisi G, Perduk Z, Galatà A, Mascali D. Innovative Analytical Method for X-ray Imaging and Space-Resolved Spectroscopy of ECR Plasmas. Condensed Matter. 2022; 7(1):5. https://doi.org/10.3390/condmat7010005
Chicago/Turabian StyleNaselli, Eugenia, Richard Rácz, Sandor Biri, Maria Mazzaglia, Luigi Celona, Santo Gammino, Giuseppe Torrisi, Zoltan Perduk, Alessio Galatà, and David Mascali. 2022. "Innovative Analytical Method for X-ray Imaging and Space-Resolved Spectroscopy of ECR Plasmas" Condensed Matter 7, no. 1: 5. https://doi.org/10.3390/condmat7010005
APA StyleNaselli, E., Rácz, R., Biri, S., Mazzaglia, M., Celona, L., Gammino, S., Torrisi, G., Perduk, Z., Galatà, A., & Mascali, D. (2022). Innovative Analytical Method for X-ray Imaging and Space-Resolved Spectroscopy of ECR Plasmas. Condensed Matter, 7(1), 5. https://doi.org/10.3390/condmat7010005






