Magnetic Compton Scattering Study of Li-Rich Battery Materials
Abstract
:1. Introduction
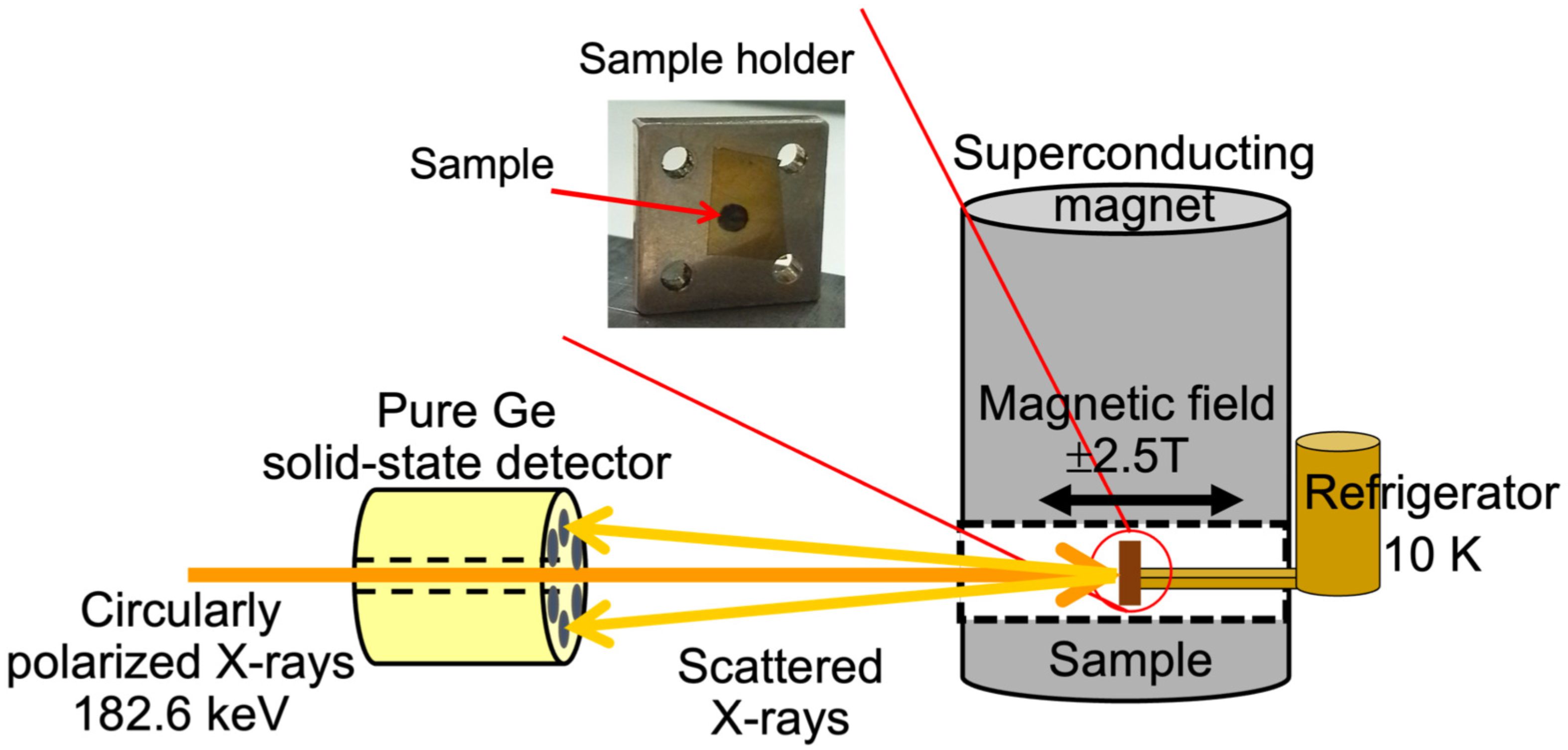
2. Materials and Methods
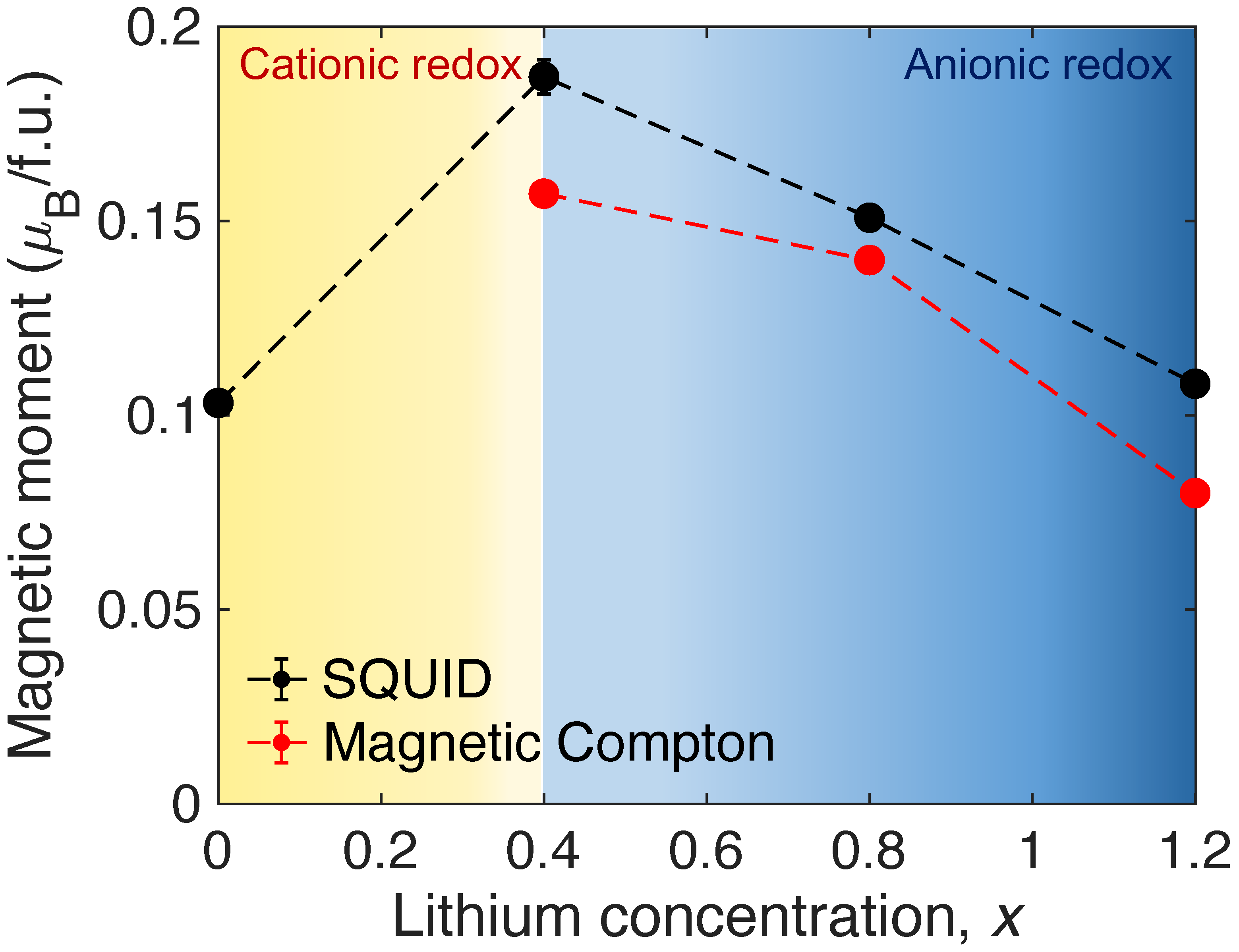
3. Results and Discussions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Assat, G.; Tarascon, J.M. Fundamental understanding and practical challenges of anionic redox activity in Li-ion batteries. Nat. Energy 2018, 3, 373–386. [Google Scholar] [CrossRef]
- Okubo, M.; Yamada, A. Molecular orbital principles of oxygen-redox battery electrodes. ACS Appl. Mater. Interfaces 2017, 9, 36463–36472. [Google Scholar] [CrossRef]
- Hafiz, H.; Suzuki, K.; Barbiellini, B.; Tsuji, N.; Yabuuchi, N.; Yamamoto, K.; Orikasa, Y.; Uchimoto, Y.; Sakurai, Y.; Sakurai, H.; et al. Tomographic reconstruction of oxygen orbitals in lithium-rich battery materials. Nature 2021, 594, 213–216. [Google Scholar] [CrossRef] [PubMed]
- Barbiellini, B.; Suzuki, K.; Orikasa, Y.; Kaprzyk, S.; Itou, M.; Yamamoto, K.; Wang, Y.J.; Hafiz, H.; Yamada, R.; Uchimoto, Y.; et al. Identifying a descriptor for d-orbital delocalization in cathodes of Li batteries based on x-ray Compton scattering. Appl. Phys. Lett. 2016, 109, 073102. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, K.; Barbiellini, B.; Orikasa, Y.; Go, N.; Sakurai, H.; Kaprzyk, S.; Itou, M.; Yamamoto, K.; Uchimoto, Y.; Wang, Y.J.; et al. Extracting the Redox Orbitals in Li Battery Materials with High-Resolution X-Ray Compton Scattering Spectroscopy. Phys. Rev. Lett. 2015, 114, 087401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hafiz, H.; Suzuki, K.; Barbiellini, B.; Orikasa, Y.; Kaprzyk, S.; Tsuji, N.; Yamamoto, K.; Terasaka, A.; Hoshi, K.; Uchimoto, Y.; et al. Identification of ferrimagnetic orbitals preventing spinel degradation by charge ordering in LixMn2O4. Phys. Rev. B 2019, 100, 205104. [Google Scholar] [CrossRef] [Green Version]
- Hafiz, H.; Suzuki, K.; Barbiellini, B.; Orikasa, Y.; Callewaert, V.; Kaprzyk, S.; Itou, M.; Yamamoto, K.; Yamada, R.; Uchimoto, Y.; et al. Visualizing redox orbitals and their potentials in advanced lithium-ion battery materials using high-resolution X-ray Compton scattering. Sci. Adv. 2017, 3, e1700971. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, K.; Suzuki, S.; Otsuka, Y.; Tsuji, N.; Jalkanen, K.; Koskinen, J.; Hoshi, K.; Honkanen, A.P.; Hafiz, H.; Sakurai, Y.; et al. Redox oscillations in 18650-type lithium-ion cell revealed by in operando Compton scattering imaging. Appl. Phys. Lett. 2021, 118, 161902. [Google Scholar] [CrossRef]
- Naylor, A.J.; Makkos, E.; Maibach, J.; Guerrini, N.; Sobkowiak, A.; Björklund, E.; Lozano, J.G.; Menon, A.S.; Younesi, R.; Roberts, M.R.; et al. Depth-dependent oxygen redox activity in lithium-rich layered oxide cathodes. J. Mater. Chem. A 2019, 7, 25355–25368. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Liu, T.; Bi, X.; Chen, Z.; Amine, K.; Zhong, C.; Lu, J. Cationic and anionic redox in lithium-ion based batteries. Chem. Soc. Rev. 2020, 49, 1688–1705. [Google Scholar] [CrossRef]
- Xu, J.; Sun, M.; Qiao, R.; Renfrew, S.E.; Ma, L.; Wu, T.; Hwang, S.; Nordlund, D.; Su, D.; Amine, K.; et al. Elucidating anionic oxygen activity in lithium-rich layered oxides. Nat. Commun. 2018, 9, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Chernova, N.A.; Nolis, G.M.; Omenya, F.O.; Zhou, H.; Li, Z.; Whittingham, M.S. What can we learn about battery materials from their magnetic properties? J. Mater. Chem. 2011, 21, 9865–9875. [Google Scholar] [CrossRef]
- Zhang, Q.; Luo, X.; Wang, L.; Zhang, L.; Khalid, B.; Gong, J.; Wu, H. Lithium-ion battery cycling for magnetism control. Nano Lett. 2016, 16, 583–587. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wei, G.; Wei, L.; Wang, D.; Chen, Y.; Tian, Y.; Yan, S.; Mei, L.; Jiao, J. Reversible control of the magnetization of spinel ferrites based electrodes by lithium-ion migration. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koizumi, A.; Miyaki, S.; Kakutani, Y.; Koizumi, H.; Hiraoka, N.; Makoshi, K.; Sakai, N.; Hirota, K.; Murakami, Y. Study of the e g Orbitals in the Bilayer Manganite La 2- 2 x Sr 1+ 2 x Mn 2 O 7 by Using Magnetic Compton-Profile Measurement. Phys. Rev. Lett. 2001, 86, 5589. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Montano, P.; Mitchell, J.; Barbiellini, B.; Mijnarends, P.; Kaprzyk, S.; Bansil, A. Temperature-dependent orbital degree of freedom of a bilayer manganite by magnetic Compton scattering. Phys. Rev. Lett. 2004, 93, 207206. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yabuuchi, N.; Nakayama, M.; Takeuchi, M.; Komaba, S.; Hashimoto, Y.; Mukai, T.; Shiiba, H.; Sato, K.; Kobayashi, Y.; Nakao, A.; et al. Origin of stabilization and destabilization in solid-state redox reaction of oxide ions for lithium-ion batteries. Nat. Commun. 2016, 7, 1–10. [Google Scholar] [CrossRef]
- Sakurai, Y. High-energy inelastic-scattering beamline for electron momentum density study. J. Synchrotron Radiat. 1998, 5, 208–214. [Google Scholar] [CrossRef] [Green Version]
- Kakutani, Y.; Kubo, Y.; Koizumi, A.; Sakai, N.; BL, A. Magnetic Compton profiles of fcc-Ni, fcc-Fe50Ni50 and hcp-Co. J. Phys. Soc. Jpn. 2003, 72, 599–606. [Google Scholar] [CrossRef]
- Cooper, M.J.; Mijnarends, P.; Mijnarends, P.E.; Shiotani, N.; Sakai, N.; Bansil, A. X-ray Compton scattering; Oxford University Press on Demand: Oxford, UK, 2004. [Google Scholar]
- Bansil, A. Coherent-potential and average t-matrix approximations for disordered muffin-tin alloys. I. Formalism. Phys. Rev. B 1979, 20, 4025. [Google Scholar] [CrossRef]
- Bansil, A. Coherent-potential and average t-matrix approximations for disordered muffin-tin alloys. II. Application to realistic system. Phys. Rev. B 1979, 20, 4035. [Google Scholar] [CrossRef]
- Bansil, A.; Kaprzyk, S. First-principles treatment of disorder effects in complex alloys: A study of BaxK1-xBiO3 and BaPb1-xBixO3. Phys. Rev. B 1991, 43, 10335. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Biggs, F.; Mendelsohn, L.; Mann, J. Hartree-Fock Compton profiles for the elements. At. Data Nucl. Data Tables 1975, 16, 201–309. [Google Scholar] [CrossRef]
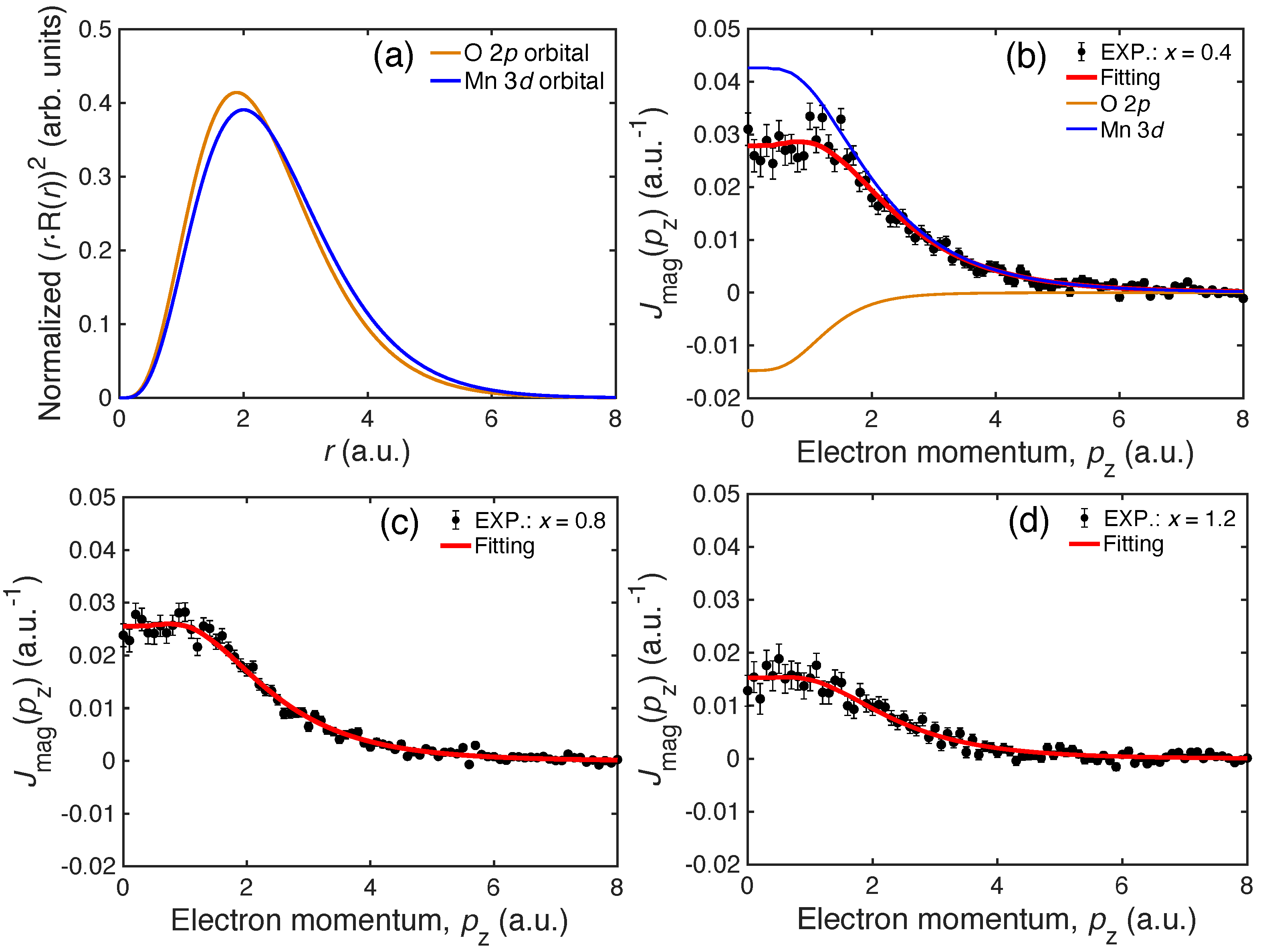
| Lithium Concentration | Spin Magnetic Moment | O 2p | Mn 3d |
|---|---|---|---|
| 0.4 | 0.157 ± 0.002 | 0.027 | 0.184 |
| 0.8 | 0.140 ± 0.002 | 0.022 | 0.162 |
| 1.2 | 0.080 ± 0.002 | 0.010 | 0.090 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suzuki, K.; Otsuka, Y.; Hoshi, K.; Sakurai, H.; Tsuji, N.; Yamamoto, K.; Yabuuchi, N.; Hafiz, H.; Orikasa, Y.; Uchimoto, Y.; et al. Magnetic Compton Scattering Study of Li-Rich Battery Materials. Condens. Matter 2022, 7, 4. https://doi.org/10.3390/condmat7010004
Suzuki K, Otsuka Y, Hoshi K, Sakurai H, Tsuji N, Yamamoto K, Yabuuchi N, Hafiz H, Orikasa Y, Uchimoto Y, et al. Magnetic Compton Scattering Study of Li-Rich Battery Materials. Condensed Matter. 2022; 7(1):4. https://doi.org/10.3390/condmat7010004
Chicago/Turabian StyleSuzuki, Kosuke, Yuji Otsuka, Kazushi Hoshi, Hiroshi Sakurai, Naruki Tsuji, Kentaro Yamamoto, Naoaki Yabuuchi, Hasnain Hafiz, Yuki Orikasa, Yoshiharu Uchimoto, and et al. 2022. "Magnetic Compton Scattering Study of Li-Rich Battery Materials" Condensed Matter 7, no. 1: 4. https://doi.org/10.3390/condmat7010004
APA StyleSuzuki, K., Otsuka, Y., Hoshi, K., Sakurai, H., Tsuji, N., Yamamoto, K., Yabuuchi, N., Hafiz, H., Orikasa, Y., Uchimoto, Y., Sakurai, Y., Viswanathan, V., Bansil, A., & Barbiellini, B. (2022). Magnetic Compton Scattering Study of Li-Rich Battery Materials. Condensed Matter, 7(1), 4. https://doi.org/10.3390/condmat7010004








