Abstract
A finite element method (FEM) was employed to investigate the interaction of borophene nanoplatelets (BNPs) and graphene nanoplatelets (GNPs) on the mechanical properties of Poly(3,4-ethylene dioxythiophene):poly(styrene sulfonate) PEDOT:PSS film. A 3D random distribution of the inclusion into the PEDOT:PSS matrix was constructed by developing a 145 × 145 × 145 representative volume element (RVE) with a 4% volume fraction of BNPs and GNPs. In comparison to the pristine PEDOT:PSS, the calculated effective elastic moduli of the BNP-PEDOT:PSS and GNP-PEDOT:PSS nanocomposites exhibited 9.6% and 10.2% improvement, respectively. The predicted FE results were validated by calculating the elastic moduli of the nanocomposites using a modified Halpine-Tsai (H-T) model. The reinforcing effect of the inclusion into the PEDOT:PSS film offers a promising electrode with improved mechanical stability. Consequently, this intriguing result makes the BNP/PEDOT:PSS nanocomposite highly promising for further investigation and application in cutting-edge devices such as touchscreen, thermoelectric, light-emitting diode, electrochemical, photodiode, sensor, solar cell, and electrostatic devices.
1. Introduction
The growing market for wearable, flexible, and portable electronics has paved the way for a slew of new wearable applications including smart apparel, stretchable thermoelectric electrodes, biomedical implants, and flexible pseudocapacitive nanocomposites for energy storage [1]. Fabrication of conductive electrodes with desired mechanical characteristics is the key to endowing advanced materials with such capabilities. In the place of rigid metallic oxides, conductive polymers (CPs) such as PEDOT:PSS have emerged as the most promising flexible electrode materials; they play a critical role in groundbreaking devices as transparent electrodes, hole transport layers, interconnectors, electroactive layers, or motion-sensing conductors [2]. Because of its exceptional flexibility, ease of manufacture, high electrical conductivity, and outstanding optical transparency, PEDOT:PSS is widely employed for practical applications such as energy conversion and storage devices [3,4]. However, PEDOT:PSS film has significant drawbacks, such as excessive acidity, inhomogeneous electrical characteristics, hygroscopicity, the low elastic modulus of ~2.7 GPa, and the little strain (ε) and break of ~5%, all of which contribute to its limited endurance [1,5,6].
To address this limitation, PEDOT:PSS is usually reinforced with inorganic nanomaterials such as graphene, MXenes (e.g., Ti3C2TX), gold nanoparticles (AuNPs), tin oxide (SnO2), molybdenum diselenide (MoSe2), and hexamethylene diisocyanate (HDI)-functionalized GO (HDI-GO) [3,4,7,8,9,10,11]. Among these nanomaterials, two-dimensional (2D) materials are at the frontier of innovation in materials science. In the recent decade, 2D structures, as the most dynamic systems, have been discovered to exhibit innovative, distinctive, and exotic behaviors [12]. They have a high degree of flexibility in the face of out-of-plane deformation, making them ideal for the fabrication of flexible nanodevices.
Several researchers have looked at the possibilities of PEDOT:PSS supplemented with graphene. In rechargeable lithium-ion and sodium-ion batteries, graphene and its derivatives are widely employed as electrode materials. Due to its great mechanical qualities, remarkable thermal and electrical capabilities, and high specific area, it is a one-of-a-kind material. Additionally, it has been employed as a filler in sophisticated nanocomposites for a variety of uses, including electronics, supercapacitor electrodes, sensors, and structural composites [4,7,13,14,15].
Consequently, Syed et al. recently demonstrated the effect of GNPs incorporation on the mechanical behavior of PEDOT:PSS. Owing to the excellent dispersion of GNPs with poly(acrylic acid) (PAA) in PEDOT-PSS, the nanocomposites have improved its mechanical characteristics. The Young’s modulus and tensile strength of PEDOT:PSS increases from 2.4 ± 0.2 GPa and 55 ± 2.5 MPa to 4.6 ± 0.2 GPa and 78 ± 2.5 MPa, respectively [16]. Díez-Pascual, on the other hand, investigated the mechanical properties of a SnO2 reinforced PEDOT:PSS nanocomposite. The Young’s modulus of pristine PEDOT:PSS employed increased up to 120% with the addition of SnO2. This is attributed to the combination of a random and homogeneous dispersion within the matrix and a very high interfacial adhesion resulting from multiple hydrogen bonds [3].
Borophene, on the other hand, is a 2D nanostructural material for flexible nanoelectronics that has recently received a lot of interest since it shows an incredible diversity of structural phases due to complicated bonding patterns [17]. It has a lower mass density than other 2D materials because boron is lighter than most elements. This opens the exciting option of employing borophene as a reinforcing component in composite construction. In comparison to GNPs, which has an elastic modulus of around 1 TPa and a thickness of roughly 0.34 nm, borophene has an in-plane elastic modulus of 586.2 GPa and 1372.4 GPa [18,19].
However, experimenting on nanocomposites, like experiments in most fields of study, is time-consuming, expensive, needs precise execution. As a result, analytical and computational approaches to predicting composite mechanical behavior are appealing. Many analytical approaches may be used to better understand the physical behavior of materials at the atomic and subatomic levels, such as estimating the elastic modulus of a two-phase composite. The most common of these models, such as the Moriee-Tanaka (M-T) and Halpine-Tsai (H-T) models, have been proven to be in good agreement with experimental data [20,21,22,23].
Therefore, the elastic moduli of a 4% volume fraction () of BNP and GNP packed PEDOT:PSS nanocomposites are predicted and compared using a finite element model established in this paper. Digimat software [24] is employed for the construction of the Representative Volume Elements (RVE) for the nanocomposites and for simulating the mechanical behavior of the material. The predicted moduli for the nanocomposites are validated with a modified Halpine-Tsai (H-T) model and compared to the experimental result.
2. Finite Element Model
In this study, the modeling approach for the 2-phase composite uses either BNP or GNP platelets to reinforce the PEDOT:PSS matrix. To reduce the computational cost, BNP is assumed to be transversely isotropic whereas GNP is taken to be isotropic, and both are represented with circular platelets. The shear modulus of BNPs is calculated from Equation (1). The aspect ratio and thickness of the nanosheets chosen for this calculation are 0.01 and 0.29 nm, respectively, which translate to a platelet diameter of 29 nm. Based on this, the density of BNP employed in the modeling was estimated from its mass density of 7.73 × 10−7 kg/m2 [18]. A preliminary FE calculation determined a 4% volume fraction as the percolation threshold for the effective reinforcement of PEDOT:PSS with BNP that was in good agreement with the theoretical calculation. Digimat software [24] was then employed to construct the realistic (stochastic) Representative Volume Elements (RVE) of a 4% volume fraction of BNP/PEDOT:PSS and GNP/PEDOT:PSS nanocomposites. An RVE is the minimum volume of microstructure with the general properties of the entire microstructure, such as morphology, dimension, volume fraction, and phase randomization, over which specialized attributes are modeled [25]. It should be large enough to encompass the fundamental microstructural properties, but small enough that the stress and strain levels may be roughly regarded homogenous throughout the RVE [26]. The RVE is considered to be in equilibrium, with a suitable total deformation. Based on this, the software automatically generated an RVE of 145 × 145 × 145 nm3 with 639 BNP and 639 GNP inclusions for the respective composites. To arrange the inclusions one after another in the RVE, Digimat-FE employs random placement algorithms. Therefore, the inclusions are randomly distributed in 3D within the matrix and voxel-based meshing was used to mesh the matrix and reinforcement components. The interface between the PEDOT:PSS and the inclusions was considered to be fully bonded, resulting in total load transmission. According to the data in Table 1, all relevant variables for an elastic analysis were entered into the models.
where , , and represent the transverse shear modulus, transverse elastic modulus, and transverse Poisson ratio of BNP, respectively.

Table 1.
Material properties of the matrix (PEDOT:PSS) and inclusion (BNP).
For validation, we employed a modified version of the H-T theoretical technique (Equations (2)–(4)) to estimate the elastic modulus of our model to assess the FEM findings. This method considered the aspect ratio and volume fraction variables, which are important parameters to consider when evaluating the mechanical characteristics of randomly distributed 2D nanosheet reinforced composites [20].
where, , , and are the moduli for the nanocomposite, matrix, and fillers, respectively, is the aspect ratio of the BNP and GNP platelets, is the thickness of the platelet, and is the diameter.
3. Result and Discussion
The mechanical characteristics of BNP and GNP-reinforced composites are studied using a finite element model in this work. The features of the RVE model of the PEDOT:PSS matrix and the inclusions are shown in Figure 1, having the dimension of 145 × 145 × 145 nm3. In addition, the elastic result of the nanocomposites is summarized in Table 2. Whereas Table 3 tabulates the effective moduli of the nanocomposites calculated using FEM and H-T methods. As a function of the characteristics of the inclusions and matrix, as well as the filler content of the inclusions, the effective elastic moduli (Equations (5) and (6)) of the filled nanocomposite material (i.e., effective bulk moduli and effective shear moduli ), are calculated:
where is the shear moduli of the nanocomposites, is the bulk moduli of the nanocomposites, f is the volume fraction of inclusions, and subscript m and f are the matrix and inclusions, respectively [26].

Figure 1.
RVE details of PEDOT:PSS film, GNPs, and BNPs.

Table 2.
Elastic properties of BNP/PEDOT:PSS and GNP/PEDOT:PSS nanocomposites.

Table 3.
The calculated effective moduli for the nanocomposite using FEM and H-T methods.
The average Young’s modulus, Poisson’s ratio, and shear modulus of BNP/PEDOT:PSS nanocomposites are predicted to be ~3 GPa, ~0.32, and ~1.1 GPa, respectively. For the GNP/PEDOT:PSS nanocomposite, the average Young’s modulus, Poisson’s ratio, and shear modulus are ~3 GPa, ~0.32, and ~1.1 GPa, respectively. The global densities of the composites are 1.12 g/cm3 and 0.88 g/cm3 for the BNP/PEDOT:PSS and GNP/PEDOT:PSS nanocomposites, respectively.
In comparison to pristine PEDOT:PSS with a maximum elastic modulus of 2.7 GPa, the incorporation of BNPs and GNPs translates to a 9.6% and 10.2% enhancement in moduli. The improvement in mechanical property is attributable to the homogeneous random dispersion of the BNPs and GNPs in the PEDOT:PSS matrix. Moreover, the platelet morphology of the inclusions is another noteworthy structural property that improves the composites’ Young’s modulus. The calculated elastic moduli for the nanocomposites from the H-T model are ~3 GPa and ~3 GPa for BNP/PEDOT:PSS and GNP/PEDOT:PSS nanocomposites, respectively, which are in excellent agreement with the FEM prediction. The experimental result of Young’s modulus for GNP/PEDOT:PSS reported in the literature is 4.6 GPa [16]. This result showed a significant difference from the FEM and H-T findings. The discrepancy between the experimental and theoretical results is mainly due to the incorporation of additional reinforcement with PAA which resulted in ~54% enhancement to the modulus of pristine PEDOT:PSS matrix. Moreover, PEDOT:PSS and PAA benefit from hydrogen bonding which promotes strong bonding between the matrix and the reinforcer.
The equivalent von Mises stress and maximum primary total strain distribution of the nanocomposites are shown in Figure 2. The portion of the PEDOT:PSS film where two inclusions come near to one another experiences the most strain, resulting in greater stiffness. Meanwhile, the stiff inclusions embedded in the softer matrix carry the most stress. Figure 3 shows the findings of the Digimat-FE stress-strain prediction in the RVE of the BNP/PEDOT:PSS and GNP/PEDOT:PSS nanocomposites. The nanocomposites exhibit similar responses which are linear and conform to the elastic range of material’s behavior.
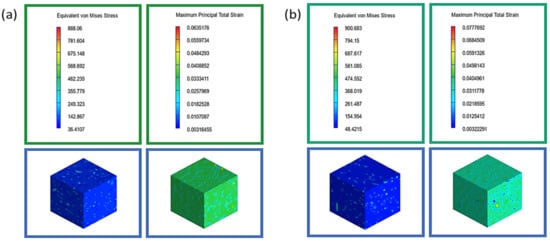
Figure 2.
Stress and strain distribution of the (a) BNP/PEDOT:PSS nanocomposites and (b) GNP/PEDOT:PSS nanocomposites.
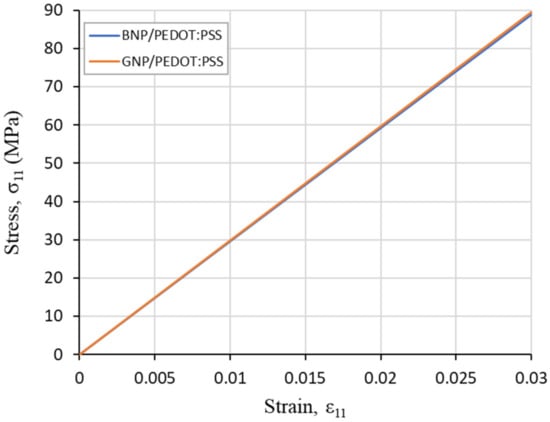
Figure 3.
FE prediction of stress-strain relation of BNP/PEDOT:PSS and GNP/PEDOT:PSS nanocomposites.
4. Conclusions
We introduce borophene and graphene sheets as reinforcing materials for PEDOT:PSS in this work. Both resulting nanocomposites have an increased elastic modulus of 9.6% and 10.2% in their mechanical properties, respectively. BNP and GNP are feasible additives to PEDOT:PSS to improve its mechanical durability. The modeling method used in this study might be useful for the FEM investigation of BNP and GNP fillers in PEDOT:PSS composites. Furthermore, the FEM and H-T conclusions were shown to be in great agreement with theoretical approaches. The stress-strain curves predicted from the RVE models of the nanocomposites show elastic response based on the assumed critical strain of 0.03.
Author Contributions
The manuscript was written through the contributions of all authors. G.J.A., O.C.A., E.R.S., Y.H., and S.S.R. framed, organized, edited, and corrected the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
National Research Foundation of South Africa (Grant No.: 116083/138768); Department of Science and Innovation (Grant No.: C6ACH35); Council for Scientific and Industrial Research of South Africa (Grant No: 086ADMI).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
GBJ would like to thank the National Research Foundation (Grant Number: 116083/) of South Africa and Adekoya Clara Chinyele for financial support. SSR would like to thank the Department of Science and Innovation (Grant No: C6ACH35) and the Council for Scientific and Industrial Research (Grant No: 086ADMI) of South Africa for financial support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kim, N.; Lienemann, S.; Petsagkourakis, I.; Mengistie, D.A.; Kee, S.; Ederth, T.; Gueskine, V.; Leclère, P.; Lazzaroni, R.; Crispin, X.; et al. Elastic conducting polymer composites in thermoelectric modules. Nat. Commun. 2020, 11, 1424. [Google Scholar] [CrossRef] [Green Version]
- Fan, X.; Nie, W.; Tsai, H.; Wang, N.; Huang, H.; Cheng, Y.; Wen, R.; Ma, L.; Yan, F.; Xia, Y. PEDOT:PSS for Flexible and Stretchable Electronics: Modifications, Strategies, and Applications. Adv. Sci. 2019, 6, 1900813. [Google Scholar] [CrossRef] [Green Version]
- Díez-Pascual, A.M. Environmentally Friendly Synthesis of Poly(3,4-Ethylenedioxythiophene):Poly(Styrene Sulfonate)/SnO2 Nanocomposites. Polymers 2021, 13, 2445. [Google Scholar] [CrossRef] [PubMed]
- Adekoya, G.J.; Sadiku, R.E.; Ray, S.S. Nanocomposites of PEDOT:PSS with Graphene and its Derivatives for Flexible Electronic Applications: A Review. Macromol. Mater. Eng. 2021, 306, 2000716. [Google Scholar] [CrossRef]
- Lang, U.; Dual, J. Mechanical Properties of the Intrinsically Conductive Polymer Poly(3,4-Ethylenedioxythiophene) Poly(Styrenesulfonate) (PEDOT/PSS). Key Eng. Mater. 2007, 345–346, 1189–1192. [Google Scholar] [CrossRef]
- Qu, J.; Ouyang, L.; Kuo, C.-C.; Martin, D.C. Stiffness, strength and adhesion characterization of electrochemically deposited conjugated polymer films. Acta Biomater. 2016, 31, 114–121. [Google Scholar] [CrossRef] [Green Version]
- Adekoya, G.J.; Adekoya, O.C.; Sadiku, R.E.; Ray, S.S. Structure-property relationship and nascent applications of thermoelectric PEDOT:PSS/carbon composites: A review. Compos. Commun. 2021, 27, 100890. [Google Scholar] [CrossRef]
- Novak, T.G.; Shin, H.; Kim, J.; Kim, K.; Azam, A.; Nguyen, C.V.; Park, S.H.; Song, J.Y.; Jeon, S. Low-Cost Black Phosphorus Nanofillers for Improved Thermoelectric Performance in PEDOT:PSS Composite Films. ACS Appl. Mater. Interfaces 2018, 10, 17957–17962. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, J.A.L.; Capilla, R.P.; Díez-Pascual, A.M. High-Performance PEDOT:PSS/Hexamethylene Diisocyanate-Functionalized Graphene Oxide Nanocomposites: Preparation and Properties. Polymers 2018, 10, 1169. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hou, C.; Yu, H. Modifying the nanostructures of PEDOT:PSS/Ti3C2TX composite hole transport layers for highly efficient polymer solar cells. J. Mater. Chem. C 2020, 8, 4169–4180. [Google Scholar] [CrossRef]
- Li, X.; Liu, C.; Wang, T.; Wang, W.; Wang, X.; Jiang, Q.; Jiang, F.; Xu, J. Preparation of 2D MoSe2/PEDOT:PSS composite and its thermoelectric properties. Mater. Res. Express 2017, 4, 116410. [Google Scholar] [CrossRef]
- Khoa, D.Q.; Hieu, N.N.; Hoi, B.D. Enhanced anisotropic electrical conductivity of perturbed monolayer β12-borophene. Phys. Chem. Chem. Phys. 2020, 22, 286–294. [Google Scholar] [CrossRef]
- Vázquez de Parga, A.L.; Calleja, F.; Norris, A. Electronic Structure of Organic Films on Graphene, in Encyclopedia of Interfacial Chemistry; Wandelt, K., Ed.; Elsevier: Oxford, UK, 2018; pp. 45–49. [Google Scholar]
- Dasari, B.; Naher, S. Graphene Materials for Batteries, in Encyclopedia of Smart Materials; Olabi, A.-G., Ed.; Elsevier: Oxford, UK, 2022; pp. 69–84. [Google Scholar]
- Banerjee, S.; Lee, J.H.; Kuila, T.; Kim, N.H. 7-Synthesis of Graphene-Based Polymeric Nanocomposites, in Fillers and Reinforcements for Advanced Nanocomposites; Dong, Y., Umer, R., Lau, A.K.-T., Eds.; Woodhead Publishing: Sawston, UK, 2015; pp. 133–155. [Google Scholar]
- Khasim, S.; Badi, N.; Pasha, A.; Al-Ghamdi, S.A.; Dhananjaya, N.; Pratibha, S. Fabrication and Testing of Ultra-Long Life Anode Material Using PEDOT-PSS/Graphene Nanoplatelet Composite for Flexible Li-ion Batteries. Int. J. Electrochem. Sci. 2021, 16, 210227. [Google Scholar] [CrossRef]
- Ayodhya, D.; Veerabhadram, G. A brief review on synthesis, properties and lithium-ion battery applications of borophene. FlatChem 2020, 19, 100150. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, Y.; Penev, E.S.; Yakobson, B.I. Elasticity, Flexibility, and Ideal Strength of Borophenes. Adv. Funct. Mater. 2017, 27, 1605059. [Google Scholar] [CrossRef] [Green Version]
- Arabha, S.; Akbarzadeh, A.; Rajabpour, A. Engineered porous borophene with tunable anisotropic properties. Compos. Part B Eng. 2020, 200, 108260. [Google Scholar] [CrossRef]
- Ali, D.; Sen, S. Finite element analysis of the effect of boron nitride nanotubes in beta tricalcium phosphate and hydroxyapatite elastic modulus using the RVE model. Compos. Part B Eng. 2016, 90, 336–340. [Google Scholar] [CrossRef]
- Chandra, Y.; Adhikari, S.; Flores, E.S.; Figiel, L. Advances in finite element modelling of graphene and associated nanostructures. Mater. Sci. Eng. R Rep. 2020, 140, 100544. [Google Scholar] [CrossRef]
- Xiao, W.; Zhai, X.; Ma, P.; Fan, T.; Li, X. Numerical study on the thermal behavior of graphene nanoplatelets/epoxy composites. Results Phys. 2018, 9, 673–679. [Google Scholar] [CrossRef]
- Hassanzadeh-Aghdam, M.K.; Jamali, J. A new form of a Halpin–Tsai micromechanical model for characterizing the mechanical properties of carbon nanotube-reinforced polymer nanocomposites. Bull. Mater. Sci. 2019, 42, 117. [Google Scholar] [CrossRef] [Green Version]
- e-Xstream. Digimat—A Nonlinear Multi-Scale Material Modeling Platform. In Mscsoftware; Hexagon, Ed.; e-Xstream: Luxembourg, 2017. [Google Scholar]
- Amirmaleki, M.; Samei, J.; Green, D.E.; van Riemsdijk, I.; Stewart, L. 3D micromechanical modeling of dual phase steels using the representative volume element method. Mech. Mater. 2016, 101, 27–39. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Ryzińska, G.; Biglar, M.; Gromada, M. Modelling of multilayer actuator layers by homogenisation technique using Digimat software. Ceram. Int. 2017, 43, 3259–3266. [Google Scholar] [CrossRef]
- Lenz, A.; Kariis, H.; Pohl, A.; Persson, P.; Ojamäe, L. The electronic structure and reflectivity of PEDOT:PSS from density functional theory. Chem. Phys. 2011, 384, 44–51. [Google Scholar] [CrossRef] [Green Version]
- Kyaw, A.K.K.; Yemata, T.A.; Wang, X.; Lim, S.L.; Chin, W.S.; Hippalgaonkar, K.; Xu, J. Enhanced Thermoelectric Performance of PEDOT:PSS Films by Sequential Post-Treatment with Formamide. Macromol. Mater. Eng. 2018, 303, 1700429. [Google Scholar] [CrossRef]
- Elmarakbi, A.; Azoti, W.; Serry, M. Multiscale modelling of hybrid glass fibres reinforced graphene platelets polyamide PA6 matrix composites for crashworthiness applications. Appl. Mater. Today 2017, 6, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Mannix, A.J.; Zhou, X.-F.; Kiraly, B.; Wood, J.D.; Alducin, D.; Myers, B.D.; Liu, X.; Fisher, B.L.; Santiago, U.; Guest, J.R.; et al. Synthesis of borophenes: Anisotropic, two-dimensional boron polymorphs. Science 2015, 350, 1513. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385. [Google Scholar] [CrossRef] [PubMed]
- Greco, F.; Zucca, A.; Taccola, S.; Menciassi, A.; Fujie, T.; Haniuda, H.; Takeoka, S.; Dario, P.; Mattoli, V. Ultra-thin conductive free-standing PEDOT/PSS nanofilms. Soft Matter 2011, 7, 10642–10650. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.; Jang, Y.; Oh, J.; Jung, J. A silver-nanoparticle-embedded activated-carbon–PEDOT:PSS composite conductor for enhancing electrical conductivity of a gas sensor module. Dig. J. Nanomater. Biostruct. 2018, 13, 527–534. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).