Planar Cu and O NMR and the Pseudogap of Cuprate Superconductors
Abstract
:1. Introduction
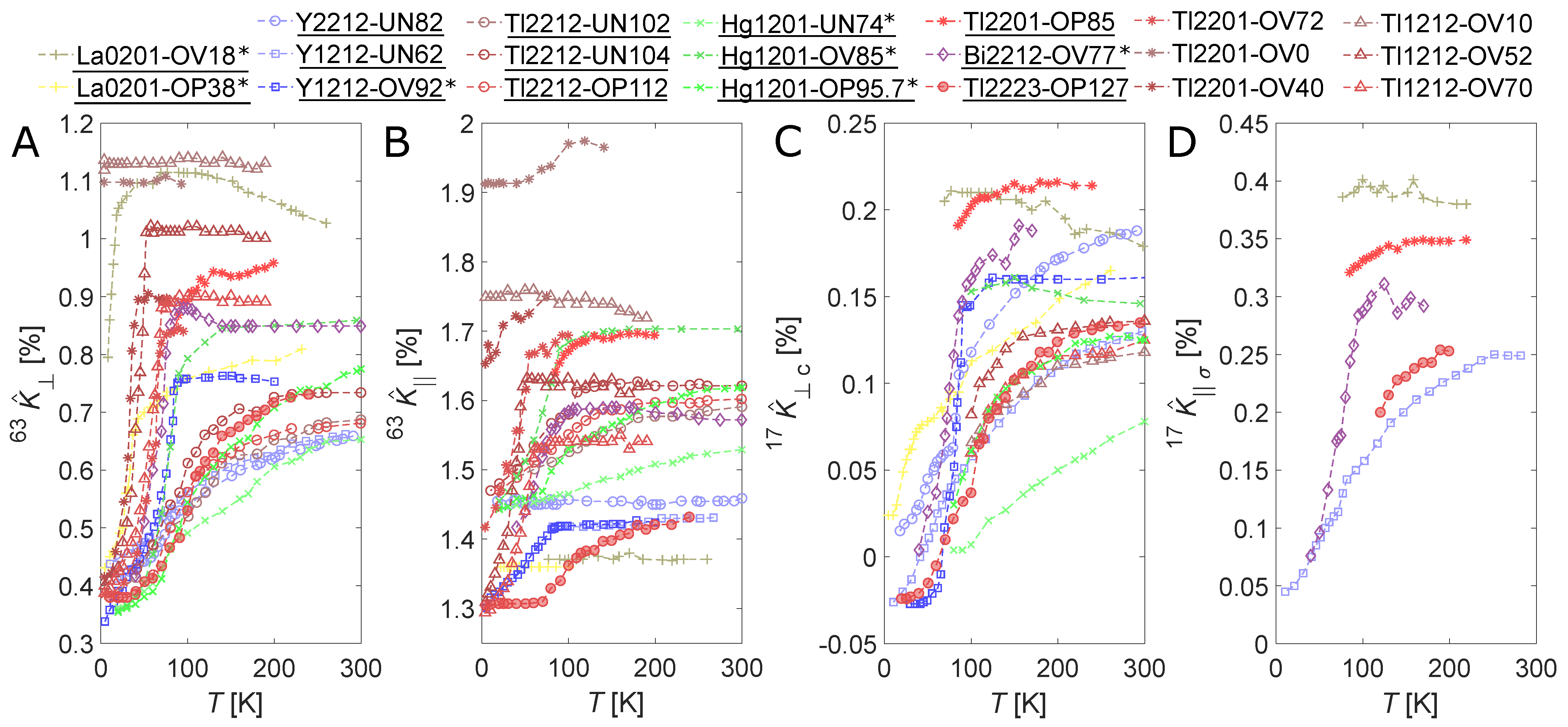
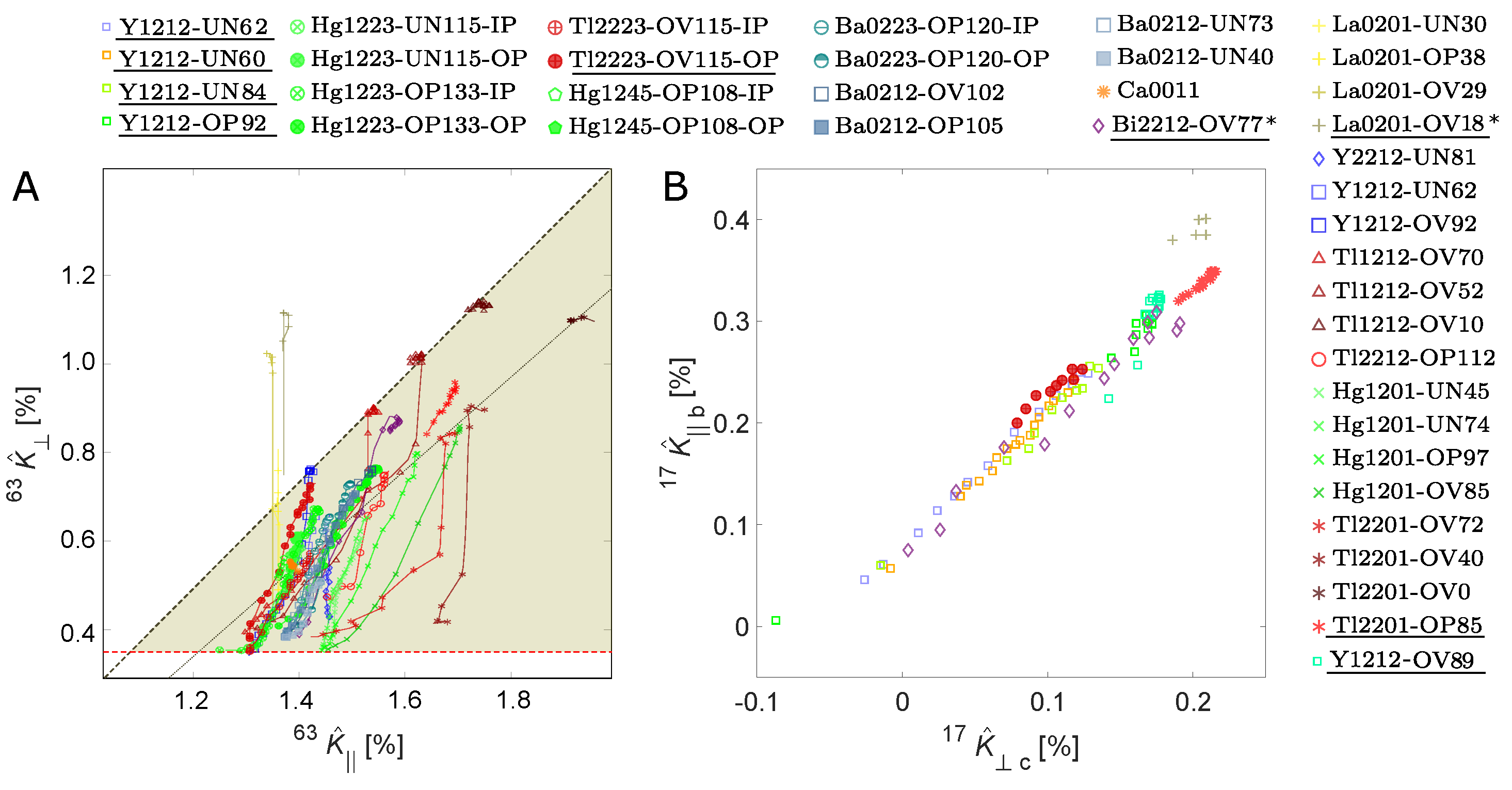
2. Planar Cu and O Magnetic Shifts
2.1. Overview
2.2. Single Spin Component Picture
2.3. Hyperfine Coefficients and Orbital Shifts
2.4. Two Spin Components
2.5. Discussion of Cu and O Shifts
3. Planar Cu and O Nuclear Relaxation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Literature Data
| System | Label | Ref. |
|---|---|---|
| LaSrCuO | La0201 | [27,28] |
| BiSrCaCuO | Bi2221 | [29,30] |
| YBaCuO | Y1212 | [23,31,32] |
| YBaCuO | Y2212 | [24] |
| TlBaCuO | Tl2201 | [33,34] |
| TlSrCaCuO | Tl2212 | [35] |
| TlBaCaCuO | Tl2212 | [36] |
| TlBaCaCuO | Tl2223 | [37] |
| HgBaCuO | Hg1201 | [5,38] |
| HgBaCaCuO | Hg1223 | [39,40] |
| HgBaCaCuO | Hg1245 | [41] |
| BaCaCuO(F,O) | Ba2212 | [42] |
| BaCaCuO(F,O) | Ba0223 | [42] |
| CaSrCuO | Ca0011 | [43] |
References
- Bednorz, J.G.; Müller, K.A. Possible High Tc Superconductivity in the Ba-La-Cu-O System. Z. Phys. B Condens. Matter 1986, 193, 189–193. [Google Scholar] [CrossRef]
- Slichter, C.P. Magnetic Resonance Studies of High Temperature Superconductors. In Handbook of High-Temperature Superconductivity; Schrieffer, J.R., Brooks, J.S., Eds.; Springer: New York, NY, USA, 2007; pp. 215–256. [Google Scholar] [CrossRef]
- Haase, J.; Slichter, C.P.; Williams, G.V.M. Evidence for two electronic components in high-temperature superconductivity from NMR. J. Phys. Condens. Matter 2009, 21, 455702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haase, J.; Rybicki, D.; Slichter, C.P.; Greven, M.; Yu, G.; Li, Y.; Zhao, X. Two-component uniform spin susceptibility of superconducting HgBa2CuO4+ single crystals measured using 63Cu and 199Hg nuclear magnetic resonance. Phys. Rev. B 2012, 85, 104517. [Google Scholar] [CrossRef] [Green Version]
- Rybicki, D.; Kohlrautz, J.; Haase, J.; Greven, M.; Zhao, X.; Chan, M.K.; Dorow, C.J.; Veit, M.J. Electronic spin susceptibilities and superconductivity in HgBa2CuO4+δ from nuclear magnetic resonance. Phys. Rev. B 2015, 92, 081115. [Google Scholar] [CrossRef] [Green Version]
- Nachtigal, J.; Avramovska, M.; Erb, A.; Pavićević, D.; Guehne, R.; Haase, J. Temperature-Independent Cuprate Pseudogap from Planar Oxygen NMR. Condens. Matter 2020, 5, 66. [Google Scholar] [CrossRef]
- Avramovska, M.; Nachtigal, J.; Haase, J. Temperature independent pseudogap from 17O and 89Y NMR and the single component picture. J. Supercond. Nov. Magn. 2022, in press.
- Loram, J.W.; Mirza, K.A.; Cooper, J.R.; Tallon, J.L. Specific heat evidence on the normal state pseudogap. J. Phys. Chem. Solids 1998, 59, 2091–2094. [Google Scholar] [CrossRef]
- Tallon, J.L.; Loram, J.W. Field-dependent specific heat of the canonical underdoped cuprate superconductor YBa2Cu4O8. Sci. Rep. 2020, 10, 22288. [Google Scholar] [CrossRef]
- Jurkutat, M.; Rybicki, D.; Sushkov, O.P.; Williams, G.V.M.; Erb, A.; Haase, J. Distribution of electrons and holes in cuprate superconductors as determined from 17O and 63Cu nuclear magnetic resonance. Phys. Rev. B 2014, 90, 140504. [Google Scholar] [CrossRef] [Green Version]
- Haase, J.; Jurkutat, M.; Kohlrautz, J. Contrasting Phenomenology of NMR Shifts in Cuprate Superconductors. Condens. Matter 2017, 2, 16. [Google Scholar] [CrossRef] [Green Version]
- Avramovska, M.; Pavićević, D.; Haase, J. Properties of the Electronic Fluid of Superconducting Cuprates from 63Cu NMR Shift and Relaxation. J. Supercond. Nov. Magn. 2019, 32, 3761–3776. [Google Scholar] [CrossRef] [Green Version]
- Jurkutat, M.; Avramovska, M.; Williams, G.V.M.; Dernbach, D.; Pavićević, D.; Haase, J. Phenomenology of 63Cu Nuclear Relaxation in Cuprate Superconductors. J. Supercond. Nov. Magn. 2019, 32, 3369–3376. [Google Scholar] [CrossRef] [Green Version]
- Pennington, C.H.; Durand, D.J.; Slichter, C.P.; Rice, J.P.; Bukowski, E.D.; Ginsberg, D.M. Static and dynamic Cu NMR tensors of YBa2Cu3O7−δ. Phys. Rev. B 1989, 39, 2902–2905. [Google Scholar] [CrossRef] [PubMed]
- Renold, S.; Heine, T.; Weber, J.; Meier, P.F. Nuclear magnetic resonance chemical shifts and paramagnetic field modifications in La2CuO4. Phys. Rev. B 2003, 67, 24501. [Google Scholar] [CrossRef]
- Hüsser, P.; Suter, H.U.; Stoll, E.P.; Meier, P.F. First-principles calculations of hyperfine interactions in La2CuO4. Phys. Rev. B 2000, 61, 1567–1579. [Google Scholar] [CrossRef] [Green Version]
- Mila, F.; Rice, T.M. Analysis of magnetic resonance experiments in YBa2Cu3O7. Phys. C Supercond. 1989, 157, 561–570. [Google Scholar] [CrossRef]
- Pavićević, D.; Avramovska, M.; Haase, J. Unconventional 17O and 63Cu NMR shift components in cuprate superconductors. Mod. Phys. Lett. B 2020, 34, 2040047. [Google Scholar] [CrossRef]
- Varma, C.M. Theory of the pseudogap state of the cuprates. Phys. Rev. B 2006, 73, 155113–155117. [Google Scholar] [CrossRef] [Green Version]
- Avramovska, M.; Pavićević, D.; Haase, J. NMR Shift and Relaxation and the Electronic Spin of Superconducting Cuprates. J. Supercond. Nov. Magn. 2020, 33, 2621–2628. [Google Scholar] [CrossRef] [Green Version]
- Reichardt, S.; Jurkutat, M.; Guehne, R.; Kohlrautz, J.; Erb, A.; Haase, J. Bulk Charge Ordering in the CuO2 Plane of the Cuprate Superconductor YBa2Cu3O6.9 by High-Pressure NMR. Condens. Matter 2018, 3, 23. [Google Scholar] [CrossRef] [Green Version]
- Haase, J. Charge density variation in YBa2Cu3O6+y. Phys. Rev. Lett. 2003, 91, 189701. [Google Scholar] [CrossRef] [PubMed]
- Takigawa, M.; Reyes, A.P.; Hammel, P.C.; Thompson, J.D.; Heffner, R.H.; Fisk, Z.; Ott, K.C. Cu and O NMR studies of the magnetic properties of YBa2Cu3O6.63 (Tc = 62 K). Phys. Rev. B 1991, 43, 247–257. [Google Scholar] [CrossRef] [PubMed]
- Bankay, M.; Mali, M.; Roos, J.; Brinkmann, D. Single-spin fluid, spin gap, and d-wave pairing in YBa2Cu4O8: A NMR and NQR study. Phys. Rev. B 1994, 50, 6416–6425. [Google Scholar] [CrossRef] [PubMed]
- Thurber, K.R.; Hunt, A.W.; Imai, T.; Chou, F.C.; Lee, Y.S. 17O NMR Study of Undoped and Lightly Hole Doped CuO2 Planes. Phys. Rev. Lett. 1997, 79, 171–174. [Google Scholar] [CrossRef]
- Singer, P.M.; Imai, T.; Chou, F.C.; Hirota, K.; Takaba, M.; Kakeshita, T.; Eisaki, H.; Uchida, S. 17O NMR study of the inhomogeneous electronic state in La2-xSrxCuO4 crystals. Phys. Rev. B 2005, 72, 014537. [Google Scholar] [CrossRef]
- Ohsugi, S.; Kitaoka, Y.; Ishida, K.; Zheng, G.q.; Asayama, K. Cu NMR and NQR Studies of High-Tc Superconductor La2-xSrxCuO4. J. Phys. Soc. Jpn. 1994, 63, 700. [Google Scholar] [CrossRef]
- Zheng, G.Q.; Kuse, T.; Kitaoka, Y.; Ishida, K.; Ohsugi, S.; Asayama, K.; Yamada, Y. 17O NMR study of La2-xSrxCuO4 in the lightly and heavily doped regions. Phys. C Supercond. 1993, 208, 339–346. [Google Scholar] [CrossRef]
- Crocker, J.; Dioguardi, A.P.; apRoberts Warren, N.; Shockley, A.C.; Grafe, H.J.; Xu, Z.; Wen, J.; Gu, G.; Curro, N.J. NMR studies of pseudogap and electronic inhomogeneity in Bi2Sr2CaCu2O8+δ. Phys. Rev. B 2011, 84, 224502. [Google Scholar] [CrossRef] [Green Version]
- Walstedt, R.; Bell, R.; Mitzi, D. Nuclear relaxation behavior of the superconducting cuprates: Bi2 Sr2CaCu2O8. Phys. Rev. B 1991, 44, 7760. [Google Scholar] [CrossRef]
- Horvatić, M.; Berthier, Y.; Butaud, P.; Kitaoka, Y.; Ségransan, P.; Berthier, C.; Katayama-Yoshida, H.; Okabe, Y.; Takahashi, T. 17O NMR study of YBa2Cu3O7-δ (Tc = 92 K). Phys. C Superond. 1989, 159, 689–696. [Google Scholar] [CrossRef]
- Takigawa, M.; Hammel, P.C.; Heffner, R.H.; Fisk, Z. Spin susceptibility in superconducting YBa2Cu3O7 from 63Cu Knight shift. Phys. Rev. B 1989, 39, 7371–7374. [Google Scholar] [CrossRef] [PubMed]
- Kambe, S.; Yasuoka, H.; Hayashi, A.; Ueda, Y. NMR study of the spin dynamics in Tl2Ba2CuOy (Tc = 85 K). Phys. Rev. B 1993, 47, 2825. [Google Scholar] [CrossRef] [PubMed]
- Fujiwara, K.; Kitaoka, Y.; Ishida, K.; Asayama, K.; Shimakawa, Y.; Manako, T.; Kubo, Y. NMR and NQR studies of superconductivity in heavily doped Tl2Ba2CuO6+y with a single CuO2 plane. Phys. C Supercond. 1991, 184, 207–219. [Google Scholar] [CrossRef]
- Magishi, K.; Kitaoka, Y.; Zheng, G.q.; Asayama, K.; Kondo, T.; Shimakawa, Y.; Manako, T.; Kubo, Y. Magnetic excitation and superconductivity in overdoped TlSr2CaCu2O7-δ: A 63Cu NMR study. Phys. Rev. B 1996, 54, 10131–10142. [Google Scholar] [CrossRef]
- Gerashchenko, A.P.; Piskunov, Y.V.; Mikhalev, K.; Ananyev, A.; Okuluva, K.; Verkhovskii, S.; Yakubovskii, A.; Shustov, L.; Trokiner, A. The 63Cu and 17O NMR studies of spin susceptibility in differently doped Tl2Ba2CaCu2O8−δ compounds. Physica C 1999, 328, 163–176. [Google Scholar] [CrossRef]
- Zheng, G.Q.; Kitaoka, Y.; Asayama, K.; Hamada, K.; Yamauchi, H.; Tanaka, S. NMR study of local hole distribution, spin fluctuation and superconductivity in Tl2Ba2Ca2Cu3O10. Phys. C Supercond. 1996, 260, 197–210. [Google Scholar] [CrossRef]
- Bobroff, J.; Alloul, H.; Mendels, P.; Viallet, V.; Marucco, J.F.; Colson, D. 17O NMR Evidence for a Pseudogap in the Monolayer HgBa2CuO4+δ. Phys. Rev. Lett. 1997, 78, 3757. [Google Scholar] [CrossRef]
- Magishi, K.; Kitaoka, Y.; Zheng, G.q.; Asayama, K.; Tokiwa, K.; Iyo, A.; Ihara, H. Spin Correlation in High-Tc Cuprate HgBa2Ca2Cu3O8+δ with Tc=133K. An Origin of Tc-Enhancement Evidenced by 63Cu-NMR Study. J. Phys. Soc. Jpn. 1995, 64, 4561–4565. [Google Scholar] [CrossRef]
- Julien, M.H.; Carretta, P.; Horvatić, M.; Berthier, C.; Berthier, Y.; Ségransan, P.; Carrington, A.; Colson, D. Spin Gap in HgBa2Ca2Cu3O8+δ Single Crystals from 63Cu NMR. Phys. Rev. Lett. 1996, 76, 4238–4241. [Google Scholar] [CrossRef]
- Kotegawa, H.; Tokunaga, Y.; Araki, Y.; Zheng, G.q.; Kitaoka, Y.; Tokiwa, K.; Ito, K.; Watanabe, T.; Iyo, A.; Tanaka, Y.; et al. Coexistence of superconductivity and antiferromagnetism in multilayered high-Tc superconductor HgBa2Ca4Cu5Oy: Cu-NMR study. Phys. Rev. B 2004, 69, 014501. [Google Scholar] [CrossRef] [Green Version]
- Shimizu, S.; Iwai, S.; Tabata, S.i.; Mukuda, H.; Kitaoka, Y.; Shirage, P.M.; Kito, H.; Iyo, A. Planar CuO2 hole density in high-Tc cuprates determined by NMR Knight shift: Cu63 NMR on bilayered Ba2CaCu2O4(F,O)2 and three-layered Ba2Ca2Cu3O6(F,O)2. Phys. Rev. B 2011, 83, 144523. [Google Scholar] [CrossRef] [Green Version]
- Pozzi, R.; Mali, M.; Matsumura, M.; Raffa, F.; Roos, J.; Brinkmann, D. Paramagnetic phase of the infinite-layer antiferromagnet Ca0.85Sr0.15CuO2 as seen by Cu NMR. Phys. Rev. B 1997, 56, 759–765. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avramovska, M.; Nachtigal, J.; Tsankov, S.; Haase, J. Planar Cu and O NMR and the Pseudogap of Cuprate Superconductors. Condens. Matter 2022, 7, 21. https://doi.org/10.3390/condmat7010021
Avramovska M, Nachtigal J, Tsankov S, Haase J. Planar Cu and O NMR and the Pseudogap of Cuprate Superconductors. Condensed Matter. 2022; 7(1):21. https://doi.org/10.3390/condmat7010021
Chicago/Turabian StyleAvramovska, Marija, Jakob Nachtigal, Stefan Tsankov, and Jürgen Haase. 2022. "Planar Cu and O NMR and the Pseudogap of Cuprate Superconductors" Condensed Matter 7, no. 1: 21. https://doi.org/10.3390/condmat7010021
APA StyleAvramovska, M., Nachtigal, J., Tsankov, S., & Haase, J. (2022). Planar Cu and O NMR and the Pseudogap of Cuprate Superconductors. Condensed Matter, 7(1), 21. https://doi.org/10.3390/condmat7010021






