1. Introduction
X-Ray Absorption spectroscopy (XAS) is a powerful tool to investigate both the electronic and geometrical structure around to a well-defined absorbing atom belonging to any type of material, from biological samples to condensed matter. XAS spectroscopy is based on the measurement of absorption coefficient
μ(E) as a function of energy, where
μ(E) can be written as
μ(E) = n
a σ(E), where n
a is the density of the absorbing medium. The quantity
σ(E) is the total absorption cross section for the excitation of an electron from the core level (typically s and p orbitals) to continuum states. This can be calculated on the basis of the so-called Fermi “golden rule”:
where
α is the fine structure constant,
is the initial core level, and
is the final state in the continuum part of the spectrum [
1]. The dipole approximation for the matter-light coupling is enough for most of the systems, mainly for the K-edges of the elements. The total absorption cross section can be calculated on the basis of multiple scattering (MS) theory which is a method to calculate from first principle the electronic structure of polyatomic molecules and solids. This method avoids many of the difficulties of the standard methods of quantum chemistry and band theory, leading to an accurate description of the wave function in molecules and solids of considerable stereo-chemical complexity. This method works in the real space without the need of any spatial symmetry and translation invariance. This last point is particularly relevant in the calculation of XAS spectra because the presence of the core-hole in the final state breaks any translational invariance. Using this method, one can calculate both bound states and the continuum part of molecular wave function. The MS theory normally uses the so-called “muffin-tin” (MT) approximation for the shape of the potential of the cluster of atoms used in the calculation [
2].
The low energy part of the XAS spectrum, typically from the rising edge up to a few hundreds of eV, is called the XANES (X-ray absorption near-edge structure) region and is extremely rich of electronic and structural information. Oxidation state, overall symmetry, distances, and angles between atomic species around absorbing site can be derived from this part of the spectrum. An almost complete quantitative recovery of the geometrical structure within 6–7 Å from the absorber can be normally achieved from the XANES spectrum [
3]. Some years ago, Benfatto and Della Longa proposed in the literature a new method, called MXAN, to derive structural information from the XANES energy region of the spectrum based on the full MS theory, i.e., the absorption cross section is calculated without any series expansion [
4]. Since then, the MXAN method has been successfully used for the analyses of many known and unknown systems, leading to a structural determination having a precision comparable to that of diffraction or modern EXAFS analysis. The possibility to perform quantitative XANES analysis to obtain a structural determination of an unknown compound can be relevant in many scientific fields, such as extra-dilute systems, biological systems where the low S/N ratio and the weak scattering power of the light elements limits the
k-range of the available experimental data, materials under extreme conditions, and, recently, the analysis of time-depended data coming from metastable systems living few pico-seconds or even less.
Currently, in modern synchrotron light machines, the so-called 3rd generation machines, it is possible to carry out pump-probe type of experiments by taking advantage the native pulsed X-ray timing structure to probe species in solution on the sub-100 picosecond (ps) timescale. The use of the X-ray-laser slicing technique allows reduction of the timescale to some picosecond, which becomes few femtoseconds in the last free electron laser facilities. The pump-probe technique involves excitation of the sample with a short laser pulse, followed by a variable time delay, after which the sample is probed with a short X-ray pulse [
5]. The XAS signal is generally measured simultaneously in both transmission and fluorescence modes. In this way, it is possible to follow the structural and electronic dynamics in a wide variety of metal based molecular species ranging from metal-proteins to transition metal ions, where a change from low spin (LS) to high spin (HS) states is observed.
Recently, the MXAN code has been modified to allow the fitting of difference spectra, i.e., signals from the difference of two XANES data sets [
6]. It is, thus, possible to analyze differential transient XAS data, which consist of the difference between the transmission spectra of an unexcited and a laser-excited sample. This approach greatly increases the sensitivity of the data to small changes and, at the same time, reduces the influence of systematic errors in the experiment and in the calculation. In this way, it is possible to analyze in detail spectra related to atomic configurations having lifetimes of a few picoseconds, or even less.
The introduction of a metal ion into an octahedral field causes its d-orbitals to separate into the well-known e
g and t
2g orbitals by the ligand-field interaction. The size of the 10Dq splitting determines whether the system is in a LS or HS configuration and a transition between these two states can subsequently be induced using changes in temperature, pressure, or, exposure to short pulses of visible light [
7]. The Fe(II)-tris-bipyridine ([Fe(bpy)
3]
2+) is a prototypically example of a spin-cross-over (SCO) system where the transition between LS and HS configuration can be induced by visible light. In the ground state, the [Fe(bpy)
3]
2+ complex is in a
1A
1 low-spin (S = 0) configuration with an average bond length between Fe and the six N atoms of the bipyridine rings of about 2.0 Å. Photoexcitation with visible light creates an electronic metal-to-ligand charge transfer (MLCT) state, which rapidly decays to a metastable
5T
2 high-spin state (S = 2) with unitary quantum yield. In the HS configuration, the population of the antibonding e
g orbitals produces an average increase of the Fe-N distances of about 0.2 Å [
8]. The HS state is reached in about 120 fs, although the system continues to oscillate around the equilibrium position for approximately 1 ps [
9]. At room temperature, this state relaxes in a non-radiative way to the LS ground state in about 0.6 ns [
10]. This value is quite low considering that the back transition HS to LS implies a spin variation of ΔS = 2.
In literature, several studies were devoted to the theoretical predictions of the molecular structure of the [Fe(bpy)
3]
2+ complex at Density Functional Theory (DFT) level, often substituting the iron atom with chemically similar metals, or adopting Time Dependent (TD-DFT) methods, to directly compute the XAS spectra. Nonetheless, all the theoretical and computational approaches adopted relied on the assumption that both LS and HS-spin states belonged to D
3 molecular symmetry. This theoretical assumption on the symmetry of complex molecular geometry well fit [
8] the experimental XANES spectra for the LS state, giving rise to a geometry in excellent agreement with the crystallographic data [
11,
12]. The fit of the XANES difference spectrum of the HS state produces a result that, at its best, has an error, quantified by the R
sq function (see below for details), significantly higher than those normally obtained with the MXAN procedure. This may indicate the need to refine the structural details of the HS state geometry, relaxing the assumption that the D
3 symmetry is preserved even in the HS state.
The present computational study was inspired by the recent results we obtained using Quantum Mechanical (QM) methods carried out using gaussian basis sets and cross-validation by direct comparison with experimental evidence. In fact, we have recently published [
13] a revision of the minimum energy structures of the LS and HS states of the complex [Fe(bpy)
3]
2+ which confirms, for the singlet state (LS), the symmetric structure belonging to the D
3 group of symmetry, while, for the transient quintet state, we have discovered a non-symmetric structure (C
1) which, hypothesized by QM calculations based on density functional using a PBE/6-311+G** method, has been further confirmed by the analysis of XANES spectra, validating the distorted structure, and by ultrafast spectroscopic experiments assigning the Fe-N stretching frequencies observed experimentally with an asymmetrical environment around the central Fe
2+ atom of the complex. These results and the most recent experimental evidence [
14] confirm that the structure of this complex tends to be extremely flexible, particularly in the HS state; consequently, an accurate description of its possible electronic states is far more complex than the minimum energy state of singlet. Nevertheless, experimental techniques capable of snapshotting vibronic dynamics at very short time pulses [
15,
16] have made it possible to identify viable electronic states due to non-Franck-Condon excitations, such as transient triplet states, and possible pathways of non-radiative decay towards the transient spin quintet state. The question, therefore, remains open to identify the intermediate Metal to Ligand Charge Transfer (MLCT) state (e.g., see Ref. [
8]) which, in the light of the latest works, appears to be less and less due to a vertical transition of Franck-Condon type but, rather, the result of a complex mix of coupled electronic and vibrational states that suddenly decay towards the transient state of quintet.
In the light of this evidence, therefore, it seems necessary that the theoretical-computational treatment of electronic states and the complex framework of geometries at play in describing the [Fe(bpy)
3]
2+ complex must consider its dynamic nature, where a static vision should be replaced by a time-dependent simulation or, at least, different molecular structures should be identified as contributing to the molecular properties as a whole. Following these guidelines, in this work, we present a first step toward the dynamical study of this intriguing molecular system by setting up a computational procedure using plane wave Self-Consistent Field (SCF) codes (Quantum ESPRESSO–PWscf [
16]) to characterize the Potential Energy Surface (PES) of the singlet and quintet spin states of [Fe(bpy)
3]
2+. Here, for the first time, we used a plane wave QM code to model this chemical system with respect to the most and widely used codes in the literature (e.g., see Refs. [
17,
18]), which are based on gaussian basis set functions. The idea is to benchmark this approach by validating the stationary points of the PES using PWscf, thus paving the route to a future use this extremely efficient computational method to eventually identify Intrinsic Reaction Coordinates among the various stable geometries from LS to HS, and, hopefully, to study the dynamical behavior of this complex by Bohr-Oppenheimer ab-initio molecular dynamics.
The resulting stationary points identified by PWscf calculations have been fully characterized and their geometries and electronic properties were compared with ab-initio fits of XANES absorption spectra of the transient state, as better described below. In this regard, in
Section 2, we discuss the results of this work, while, in
Section 3 we report the Material and Methods used, and, finally, we leave to
Section 4 the conclusions and follow-up on possible developments on the study of this intriguing molecular system.
2. Materials and Methods
The MXAN software procedure employs the full MS approach within the muffin-tin approximation for the shape of the potential to calculate the XANES part of the X-ray absorption cross section. The total charge density needed to calculate the whole potential is obtained as the superposition of the charge density of each single atomic species obtained through a self-consistent Dirac Hartree-Fock procedure. The muffin-tin approximation (MT) is used to shape the whole potential, and the multiple scattering (MS) equations are solved within the so-called “extended continuum” scheme. In this way, the outer sphere of the standard MT approach can be eliminated [
2], and the interstitial potential can no longer be calculated according to the standard way but must be imposed from the outside. The MT radii of each sphere surrounding all the atoms in the cluster are chosen according the Norman criterion, with some percentage of overlapping between contiguous spheres. This percentage and the interstitial potential are considered free parameter of the theory to be optimized during the fitting procedure [
6].
The MXAN procedure works in the space of energies and optimizes structural and non-structural parameters by minimizing the function
where
is the number of independent parameters,
is the number of data points,
and
are the theoretical and experimental values of the absorption, respectively,
is the estimated error in each point of the experimental data set, and
is a statistical weight, that, in our case, is equal to 1 [
4,
6]. The new version of the program also has the possibility to optimize the two non-structural parameters present in the theory, namely the muffin-tin radii and the interstitial potential. This is of particular importance in this case, where the fits have been performed using an external fixed geometrical structure derived from quantum mechanical calculations.
When there is the need to compare several fits with very close error
values, it is useful to introduce the following function:
again
and
are the theoretical and experimental absorption spectrum, and, to follow the behavior of its integral as a function of energy, in this way, it is possible to discriminate between the various fits to choose the best one.
All plane-wave calculations are performed in gas phase using the PW-SCF module in Quantum ESPRESSO suite V6.7 [
18]. The electronic structure is evaluated within the DFT framework by using the Perdew-Burke-Ernzerhof (PBE) functional for exchange and correlation energy [
19]. We adopt a plane-wave pseudopotentials (PP’s) expansion [
20,
21] using ultrasoft Vanderbilt PP’s for all atoms [
22], and Martins-Troullier PP [
23] for Fe atoms. Heavy atom pseudopotentials are generated (see pseudopotentials library in Ref. [
22]) by scalar relativistic calculations. We use energy cut-offs of 80 and 410 Rydberg to truncate the plane-waves expansion of the pseudo wave functions and of the augmented charge density, respectively. The molecular system in a box is subject to Periodic Boundary Conditions (PBC), and our supercell includes a vacuum region of 15 Å to avoid spurious interactions with its images. The Brillouin zone was previously sampled by (2*2*1) Monkhorst and Pack points [
24], and production calculations were performed at Gamma points. Open-shell systems (e.g., quintet,
5T
1 state) were treated using unrestricted DFT (PBE) calculations. Spin states reported from calculation (S
tot= 0 and S
tot = 2 for LS and HS, respectively) were computed with an error below 0.1% after annihilation with negligible spin contamination. The molecular geometries were fully re-optimized with PWscf, with conditions described so far, from the minimum energy stationary points calculated at PBE/6-311+G** level of computations we found, recently [
13], using gaussian basis sets.
3. Discussion
The geometrical structures derived with quantum mechanical calculations were used to fit the XANES data of both LS and HS spin states. This is achieved through the MXAN procedure, where the fits are carried out only on non-structural parameters; in other words, the geometrical structure was kept fixed to the one derived through the PWscf code, while the overlapping percentage and the interstitial potential were made to vary to reach the best fit condition; see previous section and Ref. [
6] for details.
In a previous work [
13], we reported the results of a similar analysis, where the geometries used are those obtained through the PBE functional; for brevity, we do not report them here in detail. We just want to remember that the PBE functional generates a geometric structure for the HS state that produces an XANES spectrum that is in better agreement with the experimental data than those produced with other types of functional that generate geometries that preserve the D
3 symmetry typical of the LS state.
We started the work on PWscf by optimizing the molecular geometries of the LS (belonging to D
3 symmetry group) and HS (no symmetry, C
1) states of the [Fe(bpy)
3]
2+ complex, starting from the global minimum structures we calculated at the PBE/6-311+G** level of computations [
13]. Although it is known in the literature that the SCF solution on plane waves can only apply relatively well to molecular systems, rather than periodic crystalline systems, the results of minimization using the same density functional (PBE) with relativistic correction [
18,
19] have shown an excellent agreement with the geometries previously proposed. PWscf calculation confirmed the energy stability observed in the literature and at QM/PBE, being the LS the ground state of the system and the HS the closest excited state. Looking at
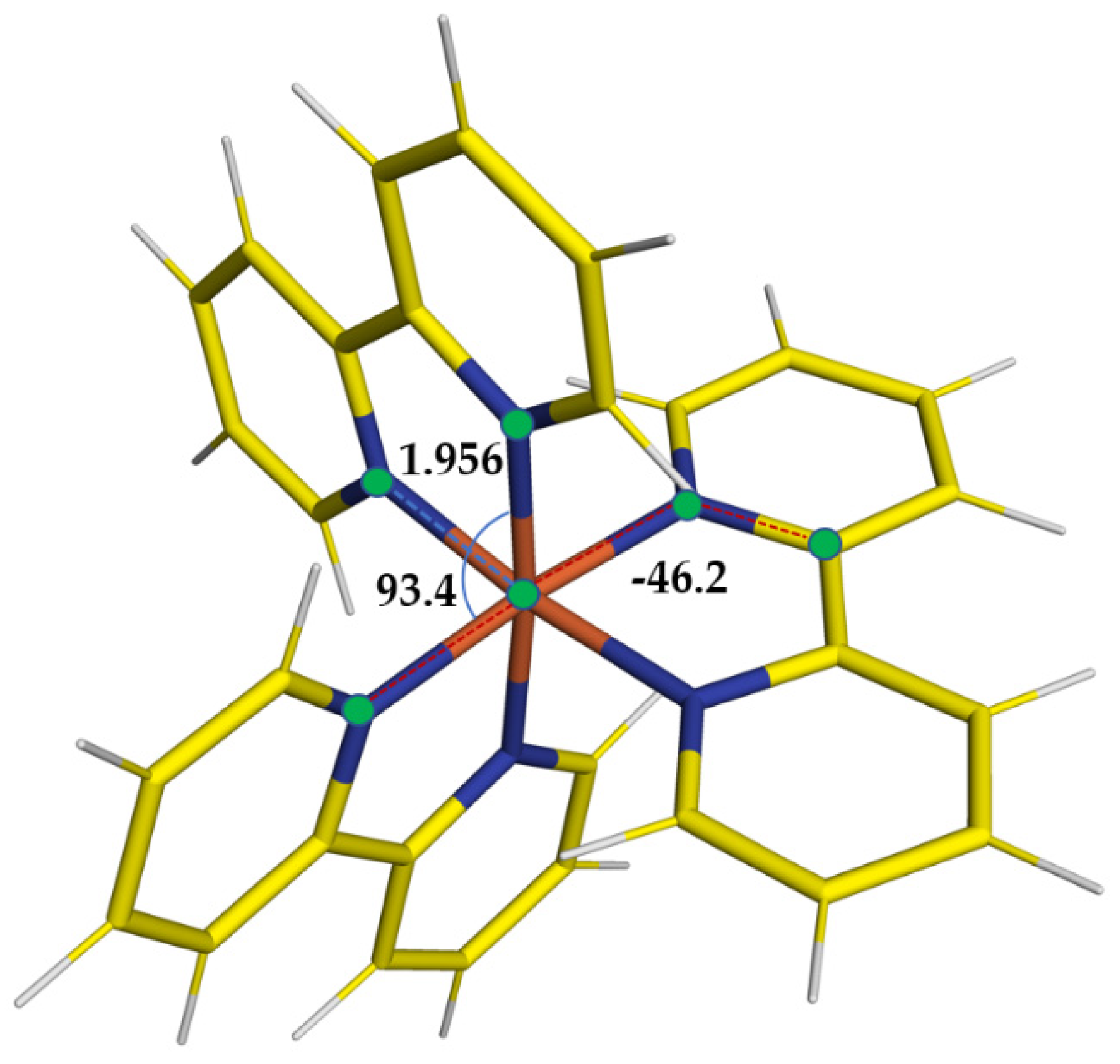
Figure 1 and
Table 1, where we are reporting the most relevant structural parameters of the LS and HS geometries of the complex, it is noted that, even at the PWscf level, the transient state results are distorted, and albeit far from a D
3 symmetry (confirmed instead for the LS state), the PWscf structures are slightly more compact than those obtained with gaussian basis sets.
The drift from D
3 symmetry of HS state may also be appreciated by looking at
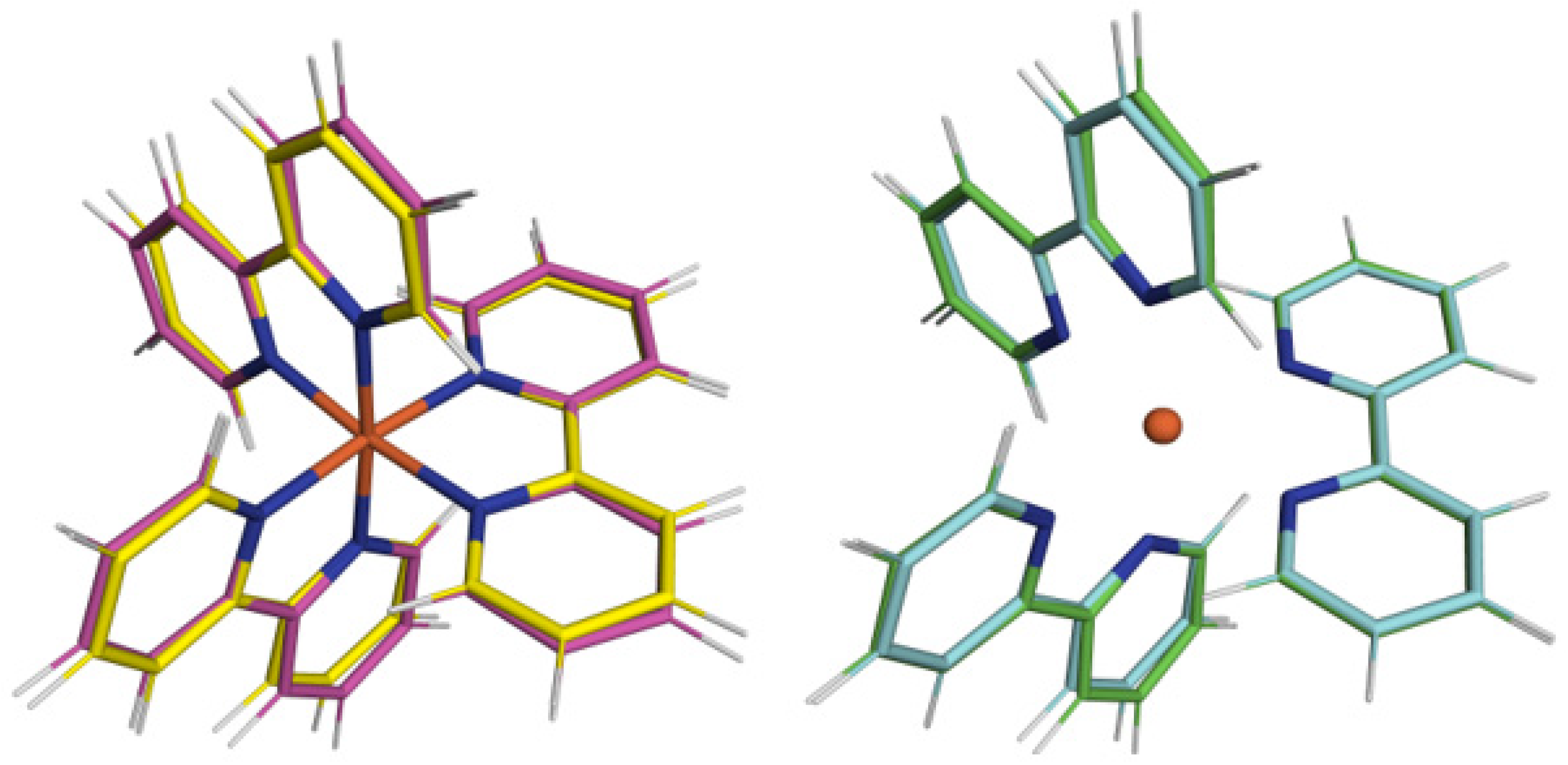
Figure 2, where we are reporting the superposition of its geometry after alignment with the one of the ground LS state, where it is visually evident that passing from the former to the latter increases the Fe-N distances by about 10%, but a consistent change in in-plane angles of bipyridil groups is also observed.
Once again, looking at the same figure, comparing the molecular structures obtained by calculations based on gaussian with those on plane wave bases set, we may appreciate an overall excellent agreement between the two sets of calculations. In fact, the calculation of
RMSD, Root Mean Square Deviation, defined as
using the euclidean distance
δ between the same two atoms of a couple of geometries, which, calculated in Å, gives almost similar values for the LS/HS structures being 0.276 Å for the calculation performed with gaussian b.s. and 0.283 Å for the present calculation. A further analysis of the
RMSD on geometries involved may confirm the consistency of the PWscf calculations with respect to the QM ones carried out at the PBE/6-311+G** level of computation. To this end, if one measures the
RMSD between the LS molecular structures obtained at PWscf after alignment with respect to the one at the QM level of computation, one observes a value of 0.191 Å, while, for the HS, we have 0.053 Å. This result, also reported in
Figure 3, shows that the PWscf LS geometry has the more significant drift from the QM one taken as reference, but, as a whole, the structural picture remains unaltered.
As a last analysis, we would highlight the relative stabilities of HS with respect the ground LS state ΔΕ
Q/S = E(HS) − E(LS) (ΔE
Q/S in kcal/mol) among the various computations in literature and the present work, as reported in
Table 2.
As can be seen in the table, our previous QM [
13] calculations overestimate the ΔE
Q/S by more than 50%, while those of the reference [
18] underestimate, by more than 200%, the experimental data reported in the literature [
17]. This is a well-known effect of the various gaussian basis DFT functionals which, while offering high-quality stationary point geometries with respect to experimental structures and related observables, the calculated energies are strongly dependent on the weights of the electronic exchange component of the functional itself [
17]. Nevertheless, the version of the PBE implemented in PWscf V6.7 gives a ΔE
Q/S of 17.6 kcal/mol, which is in excellent agreement with the highest relative energy value reported in the literature, which is equal to 17.2 kcal/mol.
The laser-pump X-ray-probe experiments were performed at the micro-XAS beam line of the Swiss Light Source. Details of the experimental strategy are described elsewhere [
25]. Briefly, an intense 400 nm pulse of a time width of 10 ps pulse width with a variable repetition rate up to 8 MHz excites an aqueous solution of 1–25 mM of [Fe(byp)
3]
2+. An about 85 ps monochromatic tunable hard X-ray pulse probes the system by X-ray absorption spectroscopy as a function of the adjustable pump-probe time delay. The detected signal is the difference X-ray absorption spectrum between the HS and LS states. All spectra are obtained at iron K-edge.
Here, we compare the fits obtained with the geometries related to the stationary points found with the PWscf method with the experimental data of LS and HS transient data and also with calculations obtained using the PBE/6-311+G** QM geometry.
In
Figure 4A, we report the comparison between the experimental data (blue points) of LS with the fit (red line) done using the PWscf geometry. Although the quality of the fit is slightly worse than that obtained with PBE/QM geometry, the agreement with the experimental data remains quite good throughout the energy range of the experimental data. The R
sq value is 3.94, compared with 3.18 obtained with the PBE/QM geometry. This is confirmed by the integral of the function
defined in the previous section and shown in
Figure 4B. For PWscf geometry, it is always larger (red line) than the one corresponding to the PBE case (blue line) in the whole energy range. This mainly stems from the difference in the Fe-N distance, which is shorter by about 0.02 Å than the value with PBE/QM.
The same type of comparison is made for transient HS data. In
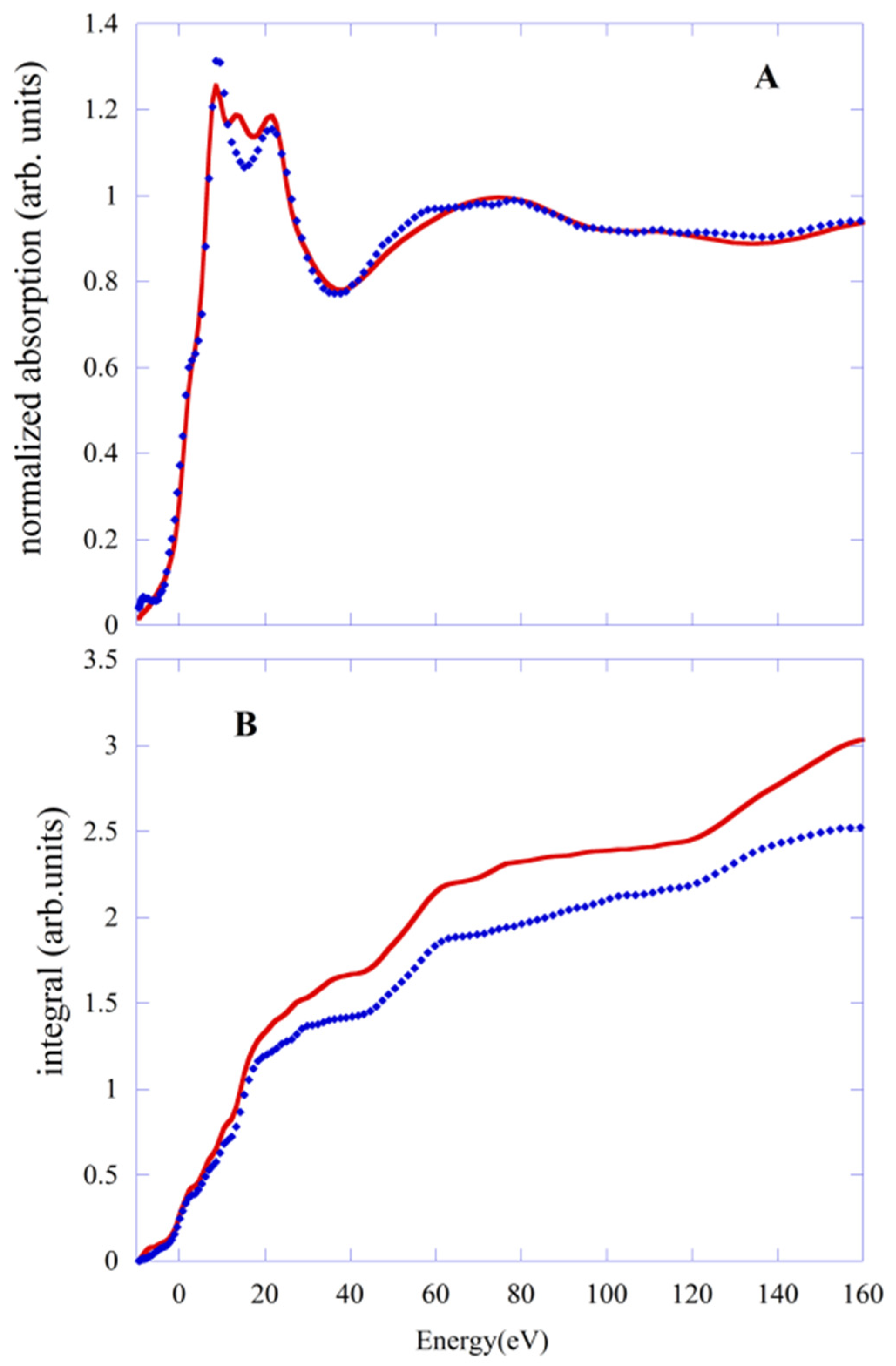
Figure 5A, we compare the experimental data (blue points) with fits obtained with PBE/QM (red line) and the PWscf geometries.The value of R
sq is 1.38 and 2.0, respectively. The behavior of the integral of
f(
E) functions (
Figure 5B) confirms this finding. Again, a shortening of the Fe-N distances of about 0.04 Å and the substantial recovery of the octahedral symmetry of the first shell are the reason for the worsening of the fit obtained with the PWscf structure.