Micromagnetic Simulation of Round Ferromagnetic Nanodots with Varying Roughness and Symmetry
Abstract
1. Introduction
2. Materials and Methods
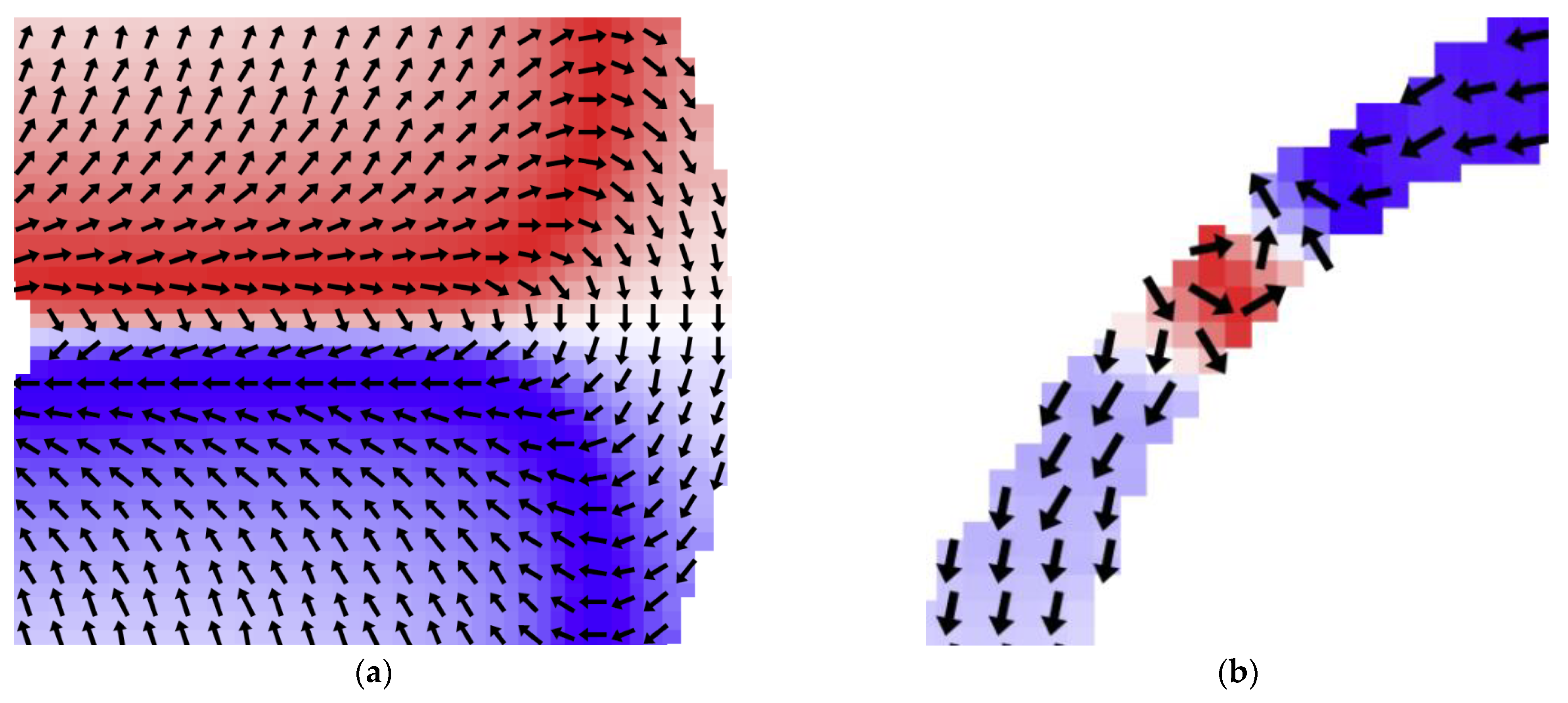
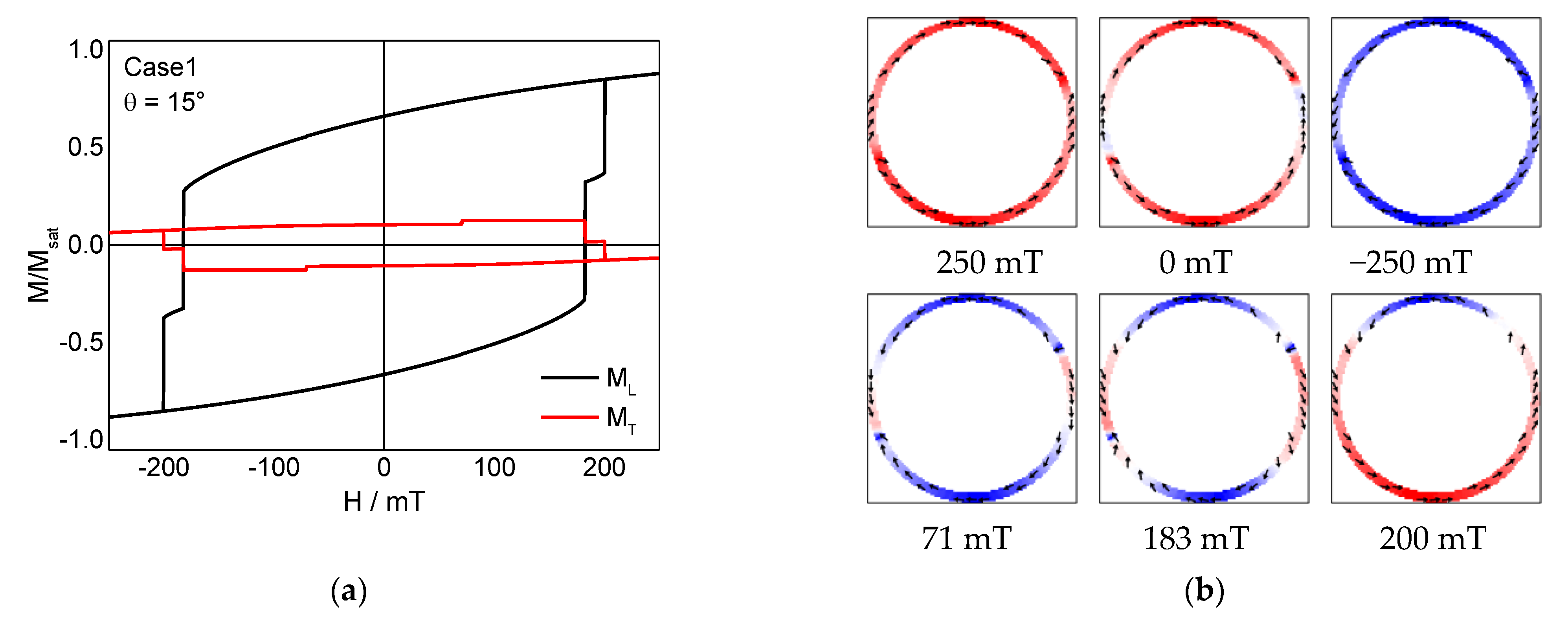
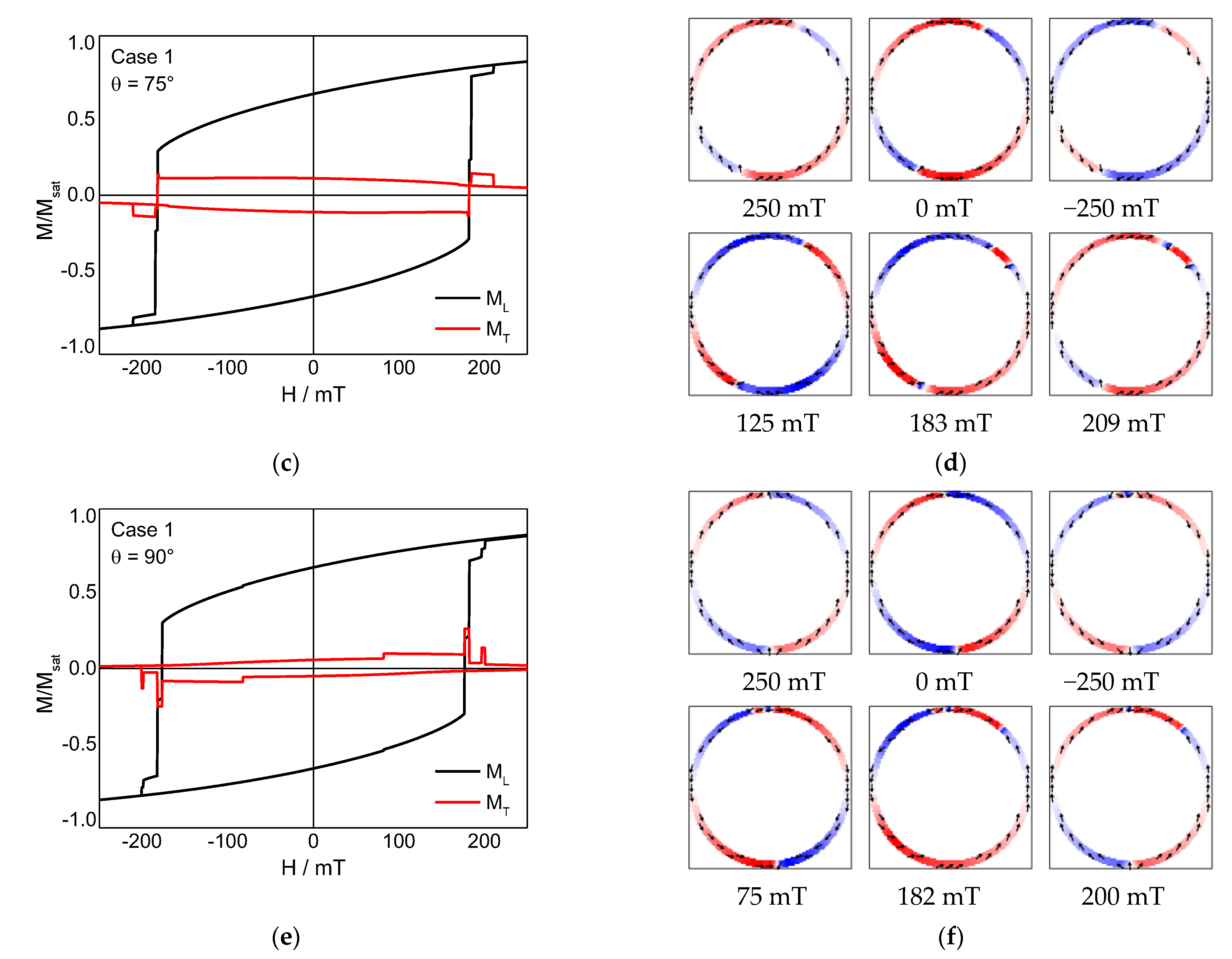
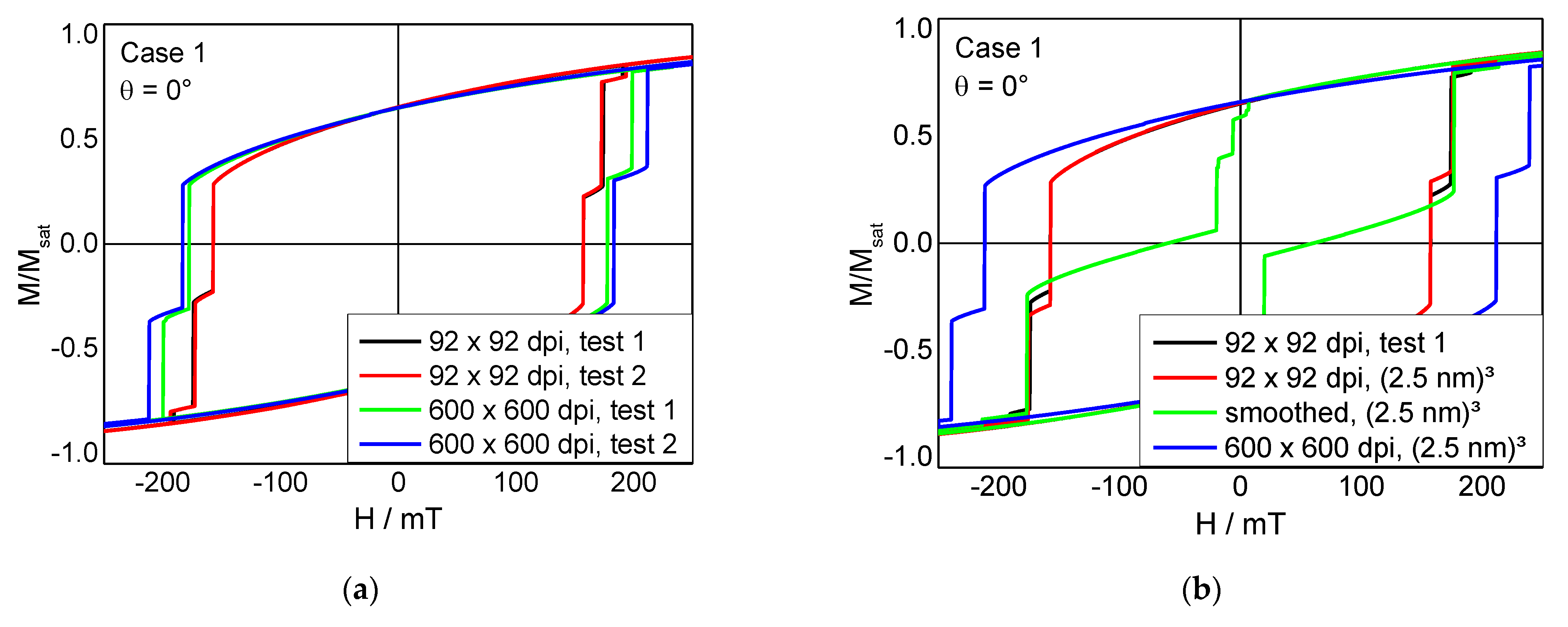
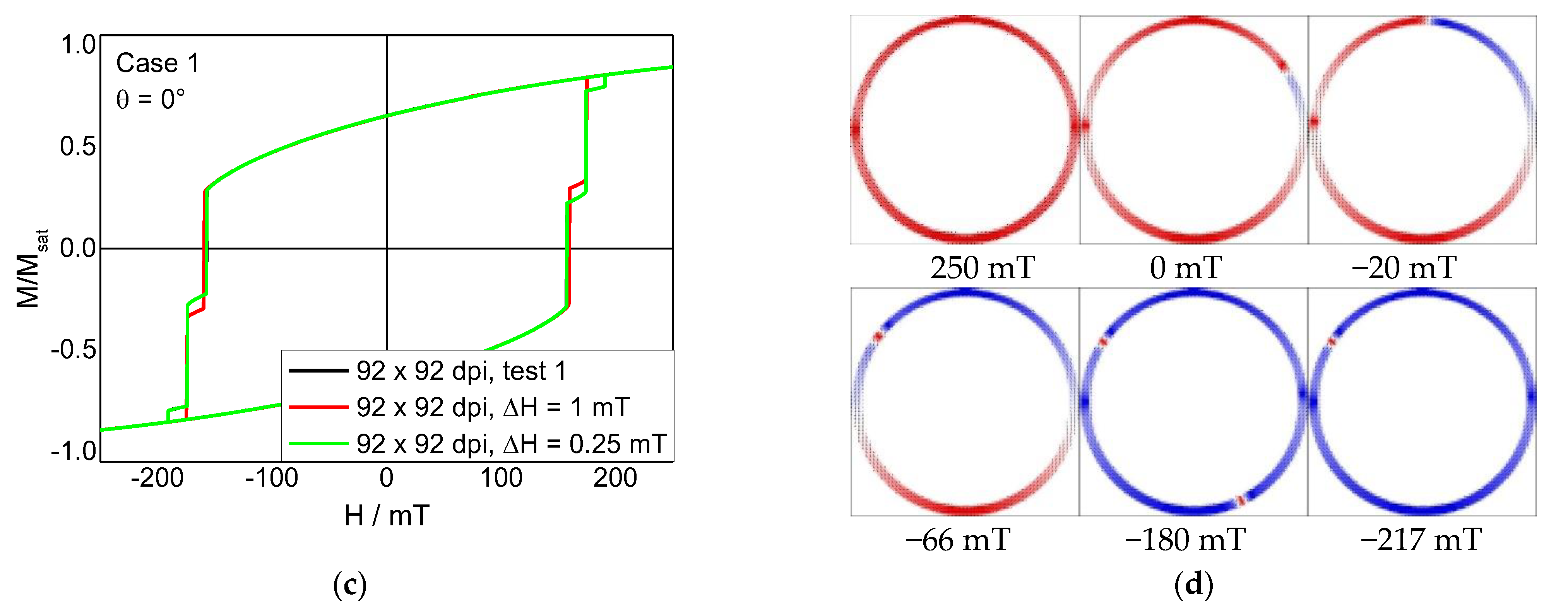
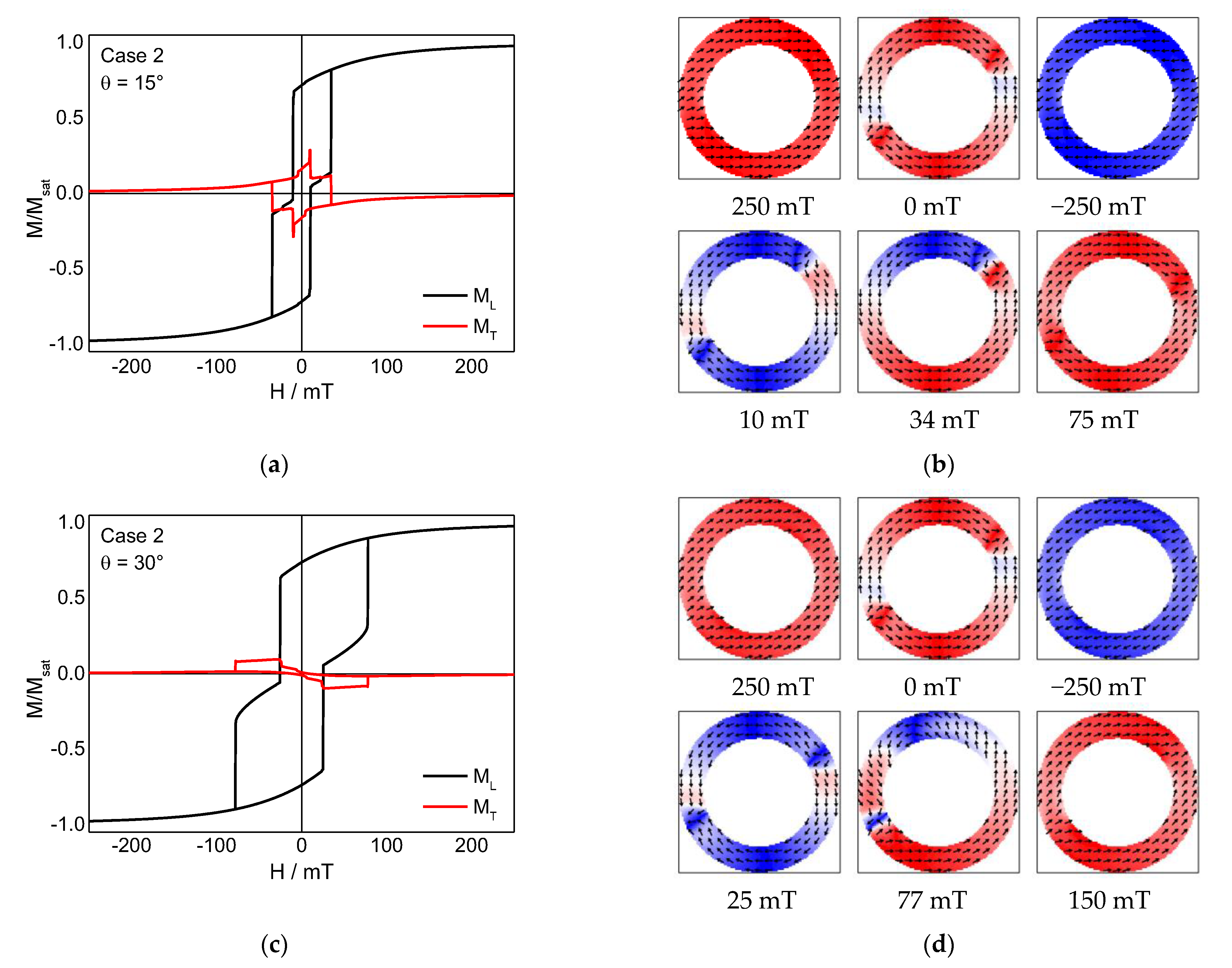
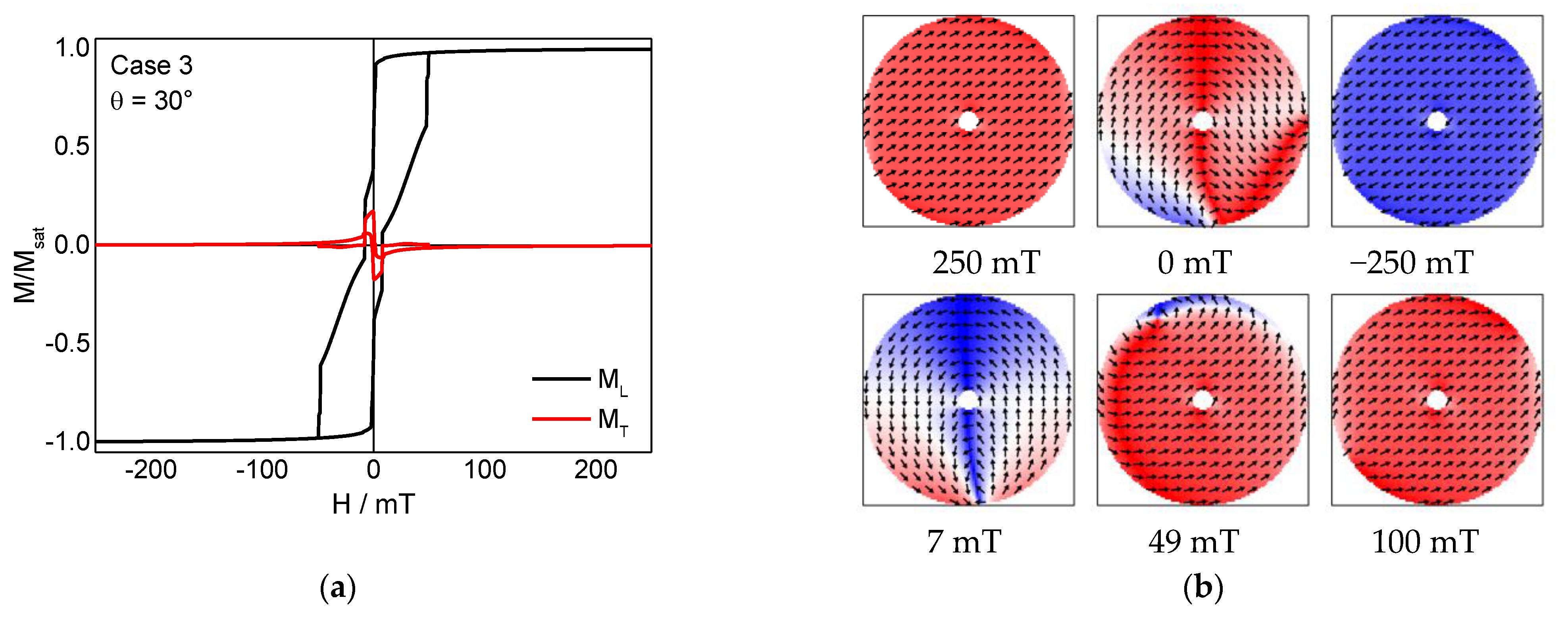
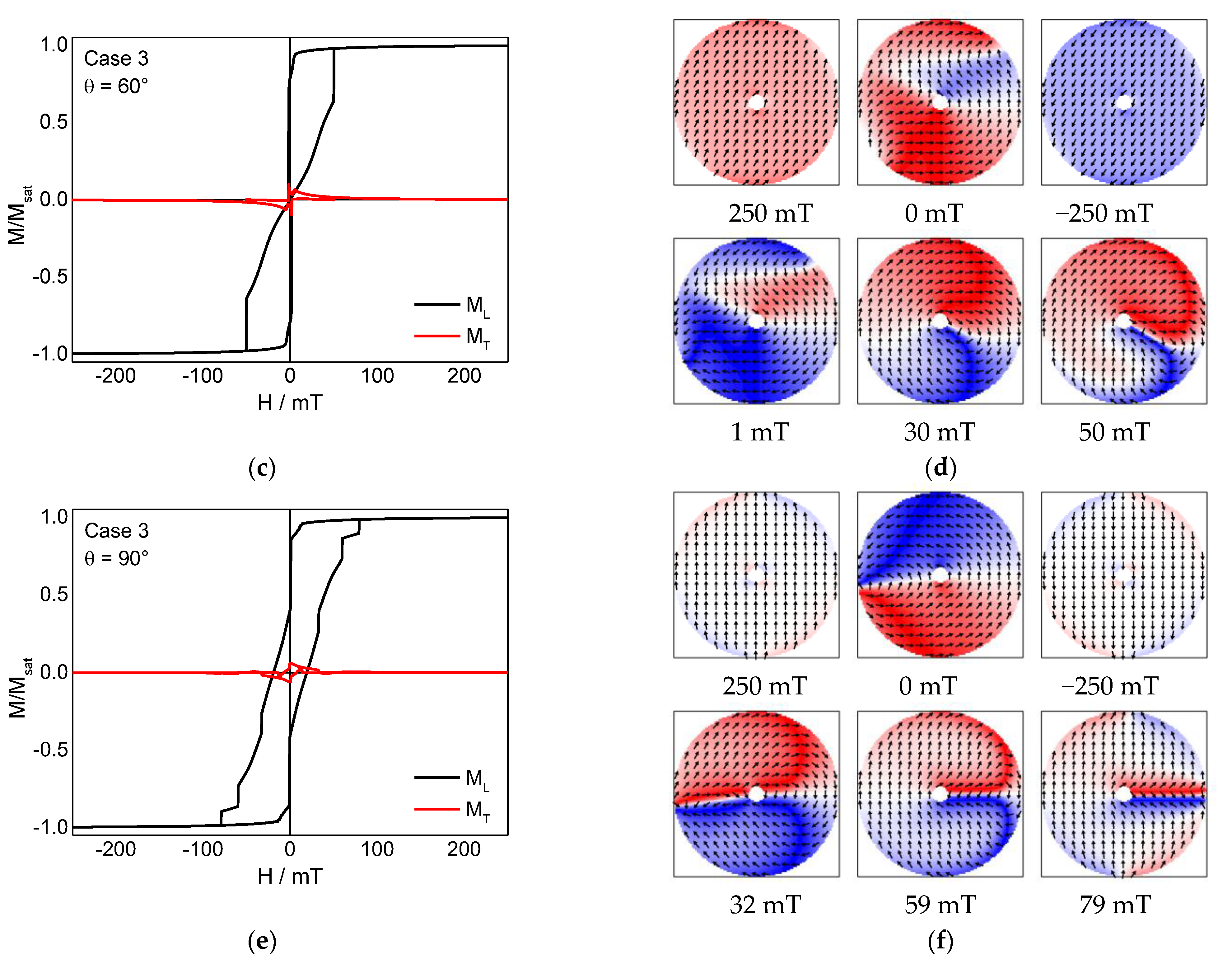
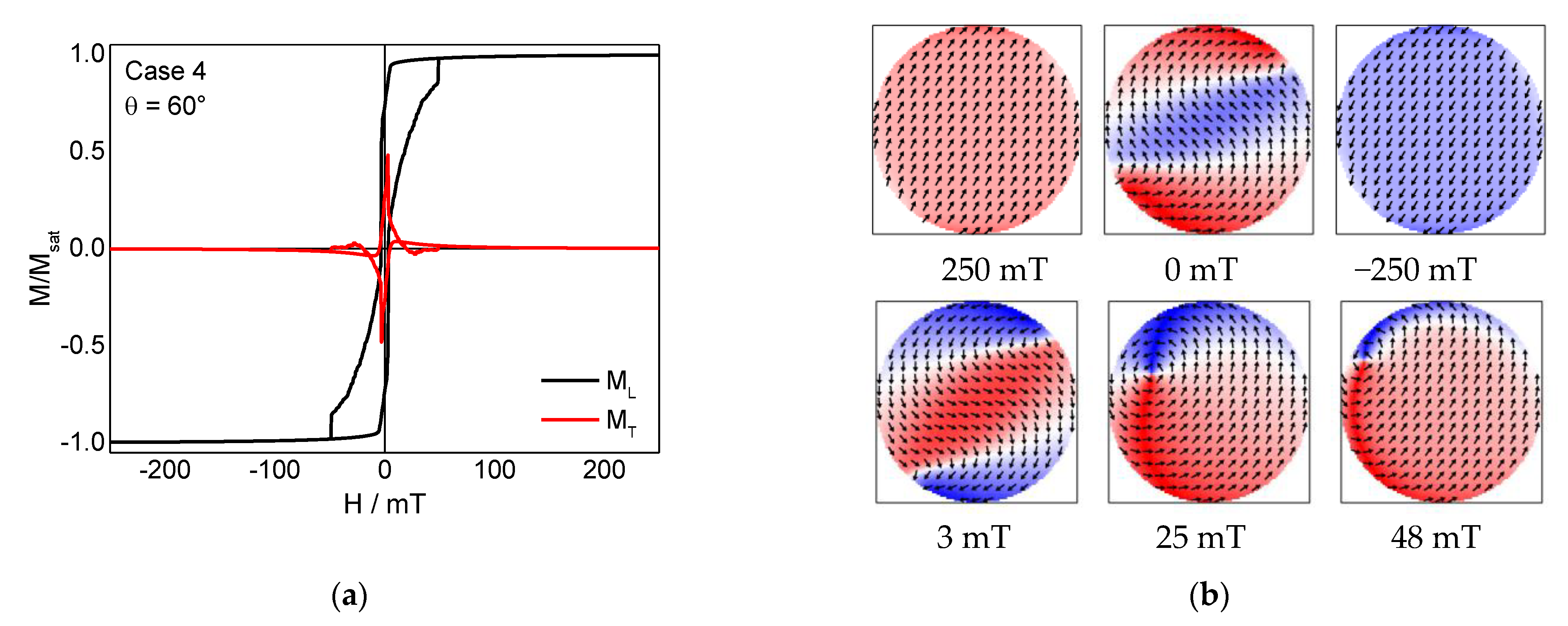
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wachowiak, A.; Wiebe, J.; Bode, M.; Pietzsch, O.; Morgenstern, M.; Wiesendanger, R. Direct observation of internal spin structure of magnetic vortex cores. Science 2002, 298, 577–580. [Google Scholar] [CrossRef]
- Guslienko, K.Y.; Aranda, G.R.; Gonzalez, J.M. Topological gauge field in nanomagnets: Spin-wave excitations over a slowly moving magnetization background. Phys. Rev. B 2010, 81, 014414. [Google Scholar] [CrossRef]
- Mejía-López, J.; Altbir, D.; Romero, A.H.; Batlle, X.; Roshchin, I.V.; Li, C.-P.; Ivan, S.K. Vortex state and effect of anisotropy in sub-100-nm magnetic nanodots. J. Appl. Phys. 2006, 100, 104319. [Google Scholar] [CrossRef]
- Noske, M.; Stoll, H.; Fähnle, M.; Gangwar, A.; Woltersdorf, G.; Slavin, A.; Weigand, M.; Dieterle, G.; Förster, J.; Back, C.H.; et al. Three-dimensional character of the magnetization dynamics in magnetic vortex structures: Hybridization of flexure gyromodes with spin waves. Phys. Rev. Lett. 2016, 117, 037208. [Google Scholar] [CrossRef] [PubMed]
- Weigand, M.; van Waeyenberge, B.; Vansteenkiste, A.; Curcic, M.; Sackmann, V.; Stoll, H.; Tyliszczak, T.; Kaznatcheev, K.; Bertwistle, D.; Woltersdorf, G.; et al. Vortex core switching by coherent excitation with single in-plane magnetic field pulses. Phys. Rev. Lett. 2009, 102, 077201. [Google Scholar] [CrossRef] [PubMed]
- Gaididei, Y.; Kravchuk, V.P.; Sheka, D.D.; Mertens, F.G. Multiple vortex-antivortex pair generation in magnetic nanodots. Phys. Rev. B 2010, 81, 094431. [Google Scholar] [CrossRef]
- Otxoa, R.M.; Petit-Watelot, S.; Manfrini, M.; Radu, I.P.; Thean, A.; Kim, J.-V.; Devolder, T. Dynamic influence of vortex-antivortex pairs in magnetic vortex oscillators. J. Magn. Magn. Mater. 2015, 394, 292–298. [Google Scholar] [CrossRef]
- Ehrmann, A.; Blachowicz, T. Influence of tilted fields on magnetization reversal in Fe nanodots. In Proceedings of the IEEE 8th International Conference on Nanomaterials: Applications & Properties, Sumy, Ukraine, 9–11 November 2020. [Google Scholar]
- Li, J.Q.; Wang, Y.; Cao, J.F.; Meng, X.G.; Zhu, F.Y.; Tai, R.Z. Fast control of the polarity of the magnetic vortex for a pair of magnetic nanodots. J. Magn. Magn. Mater. 2021, 529, 167841. [Google Scholar] [CrossRef]
- Buess, M.; Knowles, T.P.J.; Höllinger, R.; Haug, T.; Krey, U.; Weiss, D.; Pescia, D.; Scheinfein, M.R.; Back, C.H. Excitations with negative dispersion in a spin vortex. Phys. Rev. B 2005, 71, 104415. [Google Scholar] [CrossRef]
- Blachowicz, T.; Ehrmann, A.; Steblinski, P.; Palka, J. Directional-dependent coercivities and magnetization reversal mechanisms in fourfold ferromagnetic systems of varying sizes. J. Appl. Phys. 2013, 113, 013901. [Google Scholar] [CrossRef]
- Janutka, A.; Gawronski, P. Spin-transfer-driven dynamics of magnetic vortices and antivortices in dots with crystalline cubic anisotropy. IEEE Trans. Magn. 2017, 53, 4300706. [Google Scholar] [CrossRef]
- Pylypovskyi, O.V.; Sheka, D.D.; Kravchuk, V.P.; Gaididei, Y. Effects of surface anisotropy on magnetic vortex core. J. Magn. Magn. Mater. 2014, 361, 201–205. [Google Scholar] [CrossRef][Green Version]
- Sudsom, D.; Ehrmann, A. Micromagnetic simulations of Fe and Ni nanodot arrays surrounded by magnetic or non-magnetic matrices. Nanomater. 2021, 11, 349. [Google Scholar] [CrossRef]
- Sudsom, D.; Juhász Junger, I.; Döpke, C.; Blachowicz, T.; Hahn, L.; Ehrmann, A. Micromagnetic simulation of vortex development in magnetic bi-material bow-tie structures. Condens. Matter 2020, 5, 5. [Google Scholar] [CrossRef]
- Sellarajan, B.; Saravanan, P.; Ghosh, S.K.; Nagaraja, H.S.; Barshilia, H.C.; Chowdhury, P. Shape induced magnetic vortex state in hexagonal ordered CoFe nanodot arrays using ultrathin alumina shadow mask. J. Magn. Magn. Mater. 2018, 451, 51–56. [Google Scholar] [CrossRef]
- Prejbeanu, I.L.; Natali, M.; Buda, L.D.; Ebels, U.; Lebib, A.; Chen, Y.; Ounadjela, K. In-plane reversal mechanism in circular Co dots. J. Appl. Phys. 2002, 91, 7343–7345. [Google Scholar] [CrossRef]
- Vavassori, P.; Zaluzec, N.; Metlushko, V.; Novosad, V.; Ilic, B.; Grimsditch, M. Magnetization reversal via single and bouble vortex states in submicron Permalloy ellipses. Phys. Rev. B 2004, 69, 214404. [Google Scholar] [CrossRef]
- Prosandeev, S.; Bellaiche, L. Controlling double vortex states in low-dimensional dipolar systems. Phys. Rev. Lett. 2008, 101, 097203. [Google Scholar] [CrossRef]
- Ehrmann, A.; Blachowicz, T. Vortex and double-vortex nucleation during magnetization reversal in Fe nanodots of different dimensions. J. Magn. Magn. Mater. 2019, 475, 727–733. [Google Scholar] [CrossRef]
- Zhang, W.; Haas, S. Phase Diagram of Magnetization Reversal Processes in Nanorings. Phys. Rev. B 2010, 81, 064433. [Google Scholar] [CrossRef]
- Yoo, Y.G.; Kläui, M.; Vaz, C.A.F.; Heyderman, L.J.; Bland, J.A.C. Switching field phase diagram of Co nanoring magnets. Appl. Phys. Lett. 2003, 82, 2470–2472. [Google Scholar] [CrossRef]
- Vaz, C.A.F.; Hayward, T.J.; Llandro, J.; Schackert, F.; Morecroft, D.; Bland, J.A.C.; Kläui, M.; Laufenberg, M.; Backes, D.; Rüdiger, U.; et al. Ferromagnetic nanorings. J. Phys. Condens. Matter 2007, 19, 255207. [Google Scholar] [CrossRef]
- Park, M.H.; Hong, Y.K.; Choi, B.C.; Donahue, M.J.; Han, H.; Gee, S.H. Vortex head-to-head domain walls and their formation in onion-state ring elements. Phys. Rev. B 2006, 73, 094424. [Google Scholar] [CrossRef]
- Muscas, G.; Menniti, M.; Brucas, R.; Jönsson, P.E. Mesoscale Magnetic Rings: Complex magnetization reversal uncovered by FORC. J. Magn. Magn. Mater. 2020, 502, 166559. [Google Scholar] [CrossRef]
- Fernandez, E.; Tu, K.-H.; Ho, P.; Ross, C.A. Thermal stability of L10-FePt nanodots patterned by self-assembled block copolymer lithography. Nanotechnology 2018, 29, 465301. [Google Scholar] [CrossRef]
- Bryan, M.T.; Atkinson, D.; Cowburn, R.P. Experimental study of the influence of edge roughness on magnetization switching in Permalloy nanostructures. Appl. Phys. Lett. 2004, 85, 3510. [Google Scholar] [CrossRef]
- Zhu, F.Q.; Shang, Z.; Monet, D.; Chien, C.L. Large enhancement of coercivity of magnetic Co/Pt nanodots with perpendicular anisotropy. J. Appl. Phys. 2007, 101, 09J101. [Google Scholar] [CrossRef]
- Li, X.; Leung, C.W.; Chiu, C.-C.; Lin, K.-W.; Chan, M.S.; Zhou, Y.; Pong, P.W.T. Reduced magnetic coercivity and switching field in NiFeCuMo/Ru/NiFeCuMo synthetic-ferrimagnetic nanodots. Appl. Surf. Sci. 2017, 410, 479–484. [Google Scholar] [CrossRef]
- Madami, M.; Gubbiotti, G.; Tacchi, S.; Carlotti, G. Magnetization dynamics of single-domain nanodots and minimum energy dissipation during either irreversible or reversible switching. J. Phys. D. Appl. Phys. 2017, 50, 453002. [Google Scholar] [CrossRef]
- Tu, K.-H.; Bai, W.B.; Liontos, G.; Ntetsikas, K.; Avgeropoulos, A.; Ross, C.A. Universal pattern transfer methods for metal nanostructures by block copolymer lithography. Nanotechnology 2015, 26, 375301. [Google Scholar] [CrossRef]
- Donahue, M.J.; Porter, D.G. OOMMF User’s Guide; Version 1.0; Interagency Report NISTIR 6376; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1999. [Google Scholar]
- Gilbert, T.L. A phenomenological theory of damping in ferromagnetic materials. IEEE Trans. Magn. 2004, 40, 3443–3449. [Google Scholar] [CrossRef]
- Leliaert, J.; Dvornik, M.; Mulkers, J.; de Clercq, J.; Milosevic, M.V.; van Waeyenberge, B. Fast micromagnetic simulations on GPU – recent advances made with mumax3. J. Phys. D Appl. Phys. 2018, 51, 123002. [Google Scholar] [CrossRef]
- Kneller, E.F.; Hawig, R. The exchange-spring magnet: A new material principle for permanent magnets. IEEE Trans. Magn. 1991, 27, 3588–3560. [Google Scholar] [CrossRef]
- Ehrmann, A.; Blachowicz, T. Asymmetric hysteresis loops in Co thin films. Condens. Matter. 2020, 5, 71. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steinmetz, P.; Ehrmann, A. Micromagnetic Simulation of Round Ferromagnetic Nanodots with Varying Roughness and Symmetry. Condens. Matter 2021, 6, 19. https://doi.org/10.3390/condmat6020019
Steinmetz P, Ehrmann A. Micromagnetic Simulation of Round Ferromagnetic Nanodots with Varying Roughness and Symmetry. Condensed Matter. 2021; 6(2):19. https://doi.org/10.3390/condmat6020019
Chicago/Turabian StyleSteinmetz, Pia, and Andrea Ehrmann. 2021. "Micromagnetic Simulation of Round Ferromagnetic Nanodots with Varying Roughness and Symmetry" Condensed Matter 6, no. 2: 19. https://doi.org/10.3390/condmat6020019
APA StyleSteinmetz, P., & Ehrmann, A. (2021). Micromagnetic Simulation of Round Ferromagnetic Nanodots with Varying Roughness and Symmetry. Condensed Matter, 6(2), 19. https://doi.org/10.3390/condmat6020019