Revival of Charge Density Waves and Charge Density Fluctuations in Cuprate High-Temperature Superconductors

Abstract

I present here a short memory of my scientific contacts with K.A. Müller starting from the Interlaken Conference (1988), Erice (1992 and 1993), and Cottbus (1994) on the initial studies on phase separation (PS) and charge inhomogeneity in cuprates carried out against the view of the majority of the scientific community at that time. Going over the years and passing through the charge density wave (CDW) instability of the correlated Fermi liquid (FL) and to the consequences of charge density fluctuations (CDFs), I end with a presentation of my current research activity on CDWs and the related two-dimensional charge density fluctuations (2D-CDFs). A scenario follows of the physics of cuprates, which includes the solution of the decades-long problem of the strange metal (SM) state.

1. Introduction

My scientific familiarity with Alex Müller goes back to the 1970s when I was involved in the research on critical phenomena. His contributions to this field could not be overlooked by any researcher active in the field.

His research was fundamental in bringing the static and dynamical behavior of structural phase transition and ferroelectrics within the mainstream of critical phenomena [1].

Again, in the 1970s, he together with Harry Thomas presented a theory of structural phase transitions in which the lowering of symmetry comes from the Jahn–Teller effect of the ionic constituents [2]. That paper, in addition to showing the versatile nature and the usual deep understanding of the physics by Alex, is also the paper to which he was often referring when discussing his approach in searching high-temperature superconductivity.

In 1986, his discovery with J. G. Bednorz [3] of high critical temperature superconductors (HTSCs) in barium-doped lanthanum copper oxides with the critical temperature T_C in the thirty Kelvin range realized the chimera of experimental physicists for decades. Their paper was quickly followed by the discovery of various families of cuprate superconductors, with critical temperature values well above the liquefaction temperature of nitrogen.

At the time, I was studying with C. Castellani another important problem in condensed matter—the generalization to correlated electrons of the metal–insulator transition resulting from the Anderson localization due to disorder. The problematic of interacting disordered electronic systems was still a very hot topic, but it was overshadowed by the new problematic of HTSCs. The importance of electron correlation for the study of these materials became immediately apparent, in particular under the input offered by P.W. Anderson [4]. Those who, like us, had been working on strongly correlated electron systems, could not escape the temptation to work on this new type of superconductor. Then, my adventure on HTSCs started and my friendly relations with Alex became direct and deeper.

It will be apparent how much our scientific community is indebted to Alex and how much our research activity in this field, mine in particular, was inspired and supported by him. I therefore consider it my duty and pleasure to dedicate this work to him. My aim is to retrace the line we followed over the years in Rome to produce a scenario of the physics of cuprates, for a recent review see [5]. I proceed through the years to end up with two recent contributions [6,7] produced with S. Caprara, M. Grilli and G. Seibold in a collaboration with the experimental group of the Politecnico of Milano on resonant X-ray scattering (RXS) (G. Ghiringhelli, L. Braicovich, R. Arpaia, among others) in which charge density fluctuations (CDFs) are thoroughly investigated leading to a deeper understanding of the physics of these systems. I have no claim of completeness; I only follow my line of reasoning for which no one else is responsible even though I am deeply indebted to Alex Müller for his continuous support in the first fifteen years of my research activity in this field and to all my collaborators throughout the years.

2. Results

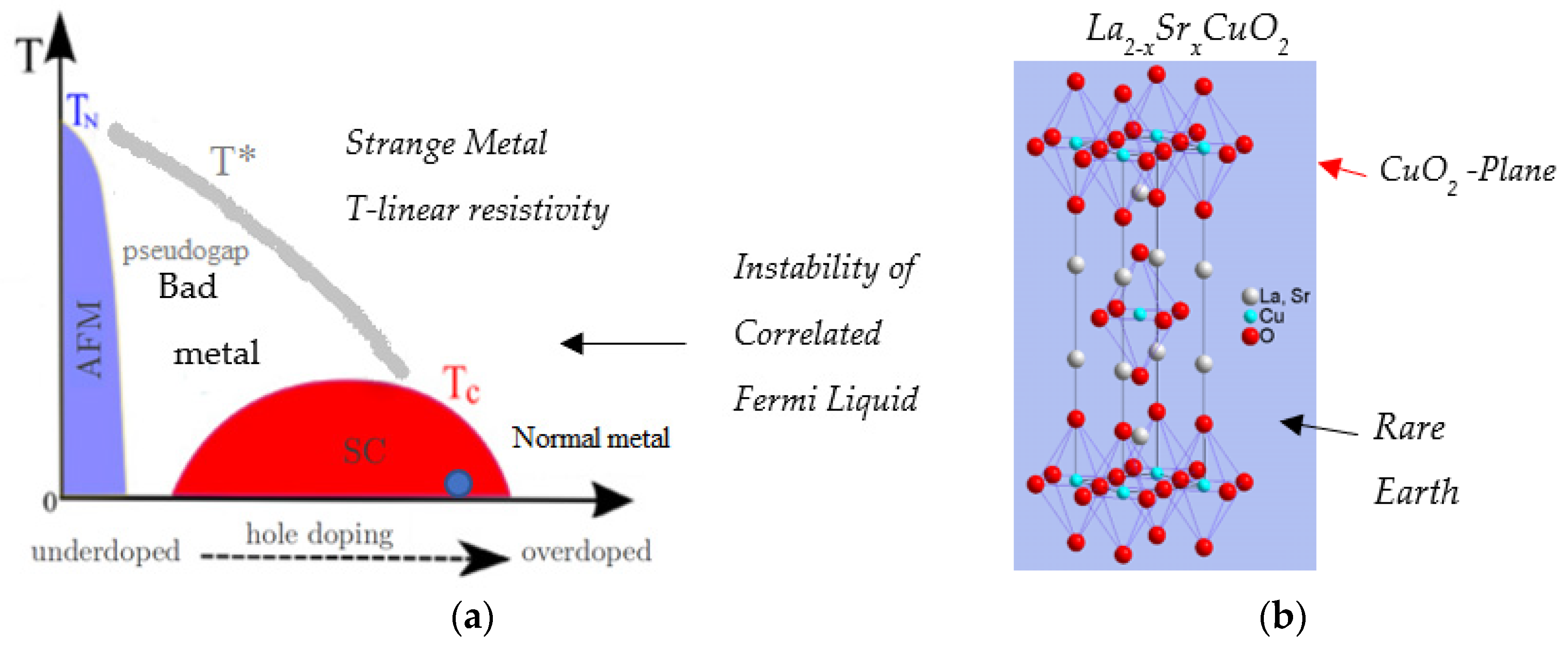
2.1. General Properties

Let me recall the general properties of the cuprates by referring to their generic phase diagram (Figure 1a). All these materials are made up of copper–oxygen planes (CuO₂), a quasi-bidimensional structure intercalated with layers of rare earth (lanthanum, yttrium, barium, etc., depending on the various families of cuprates, Figure 1b). In their stoichiometric composition (e.g., La₂CuO₄), these materials are antiferromagnetic (AF) Mott insulators, despite the fact that they have one hole per CuO₂ unit cell in the copper–oxygen plane and should have been metals. Hence, there is the need for a strong correlation between charge carriers, holes in this case.

Figure 1. (a) Generic phase diagram of cuprates of temperature T vs. doping p. Blue region: antiferromagnetic (AF) phase. Red region: superconductive phase. T* smeared gray line: pseudogap line. (b) Structure of cuprates, e.g., La_2−xSr_xCuO₂ (LSCO).

Upon substitution of the rare earth with heterovalent dopants (e.g., strontium replacing lanthanum in LSCO), the number of holes increases in the CuO₂ plane and the system becomes a metal, albeit a bad metal. Nevertheless, the system becomes a superconductor, with d-wave symmetry, when the temperature is lowered below a dome-shaped doping-dependent critical temperature T_C(p) (red region in Figure 1a). T_C reaches a maximum at the so-called optimal doping and decreases by lowering p in the underdoped region or increasing p in the so-called overdoped region, where the system is well described by the normal Fermi liquid (FL) theory. On the contrary, the metallic phase in the underdoped region and above optimal doping is not in line with ordinary metals and the predictions of the normal Fermi liquid theory. In the metal phase, a strong anisotropy is measured in the electrical conductivity that, in the CuO₂ plane, exceeds the transversal conductivity by orders of magnitude. Moreover, the resistance displays a linear in T dependence (strange metal) over a wide range of temperatures above the doping-dependent pseudogap line T*(p) [8]. T*(p) decreases with p and merges with T_C around optimal doping. Below T*(p), a pseudogap is formed with an even stronger violation of Fermi liquid (FL) behavior (Figure 1). The pseudogap formation is apparently connected [9] with the suppression of quasiparticle (QP) states at the Fermi surface (FS) along the so-called antinodal (0,0)–(0.5,0) direction, as shown in Figure 9, and the consequent formation of Fermi arcs in the nodal region.

In classic superconductors, the necessary attraction for the formation of electron pairs is mediated by phonons, as indicated by the so-called isotope effect, whereby the critical temperature for the onset of superconductivity depends on the isotopic mass of the lattice ion. As a further anomaly of these systems, the isotope effect is either absent or anomalous, for example, having a strong effect on T* [10].

An international debate thus ensued among theoretical physicists about whether a strongly correlated hole (or electron) system, with an occupation of approximately one hole per lattice site of a quasi-two-dimensional system, can become a superconductor, what the new paired state would be, and by what mechanisms it might be formed. At the same time, another, perhaps even more stimulating theoretical problem, presented itself—understanding the anomalous metallic phase to which the superconductivity was linked. I embarked upon this twofold adventure together with the condensed matter theory group of Rome.

2.2. Phase Separation—Spin and Charge Order

The question we asked ourselves was how could a system, whose interaction between charges is strongly repulsive, generate the pairing between charges in general without referring to special symmetry conditions to reduce the repulsion? We then referred to the phase separation (PS), as it occurs in simple fluids. In cuprates, the separation occurs between charge-rich metallic regions and charge-poor zones. The strong local repulsion between charge carriers reduces their mobility and favors the possibility of phase separation. Theoretically, all of the models with strong local repulsion that were introduced to represent the copper–oxygen planes showed PS in charge-rich regions and in charge-poor regions (see, e.g., [11]). Besides the PS in various other models, we found that whenever PS is present, pairing then occurs in a nearby region of phase space, thus enforcing a possible connection between the two phenomena [12,13,14]. Charge inhomogeneity appeared to be a bridge that connects the low doping region (in the presence of strong repulsion necessary for an insulating antiferromagnet), the intermediate doping region (with a special attraction for superconductivity), up to a correlated FL at higher doping. Long-range Coulomb interaction, however, forbids the macroscopic phase separation. The system chooses a compromise and segregates charge on a shorter scale, while keeping charge neutrality at a large distance giving rise to the so-called frustrated phase separation [14,15,16].

Emery and Kivelson [15,16] achieved the frustrated PS concept starting from the low doping region near the antiferromagnetic insulating phase, in which the few present charges are expelled from the antiferromagnetic substrate and align in stripes. Spin fluctuations are dominating in this case.

Coming instead from the high doping region, correlated FL in the presence of long-range Coulomb interaction undergoes to a Pomeranchuk instability towards a charge density wave (CDW) state with finite modulation vector q_c [17]. This instability occurs along a line of temperature as a function of doping T_CDW(p), ending at T = 0 in a quantum critical point (QCP) nearby optimal doping. In this case, charge fluctuations are prominent.

Both charge and spin modes may act as mediators of pairing [18,19].

Experimentally, spin and charge order have been observed in two different forms:

-

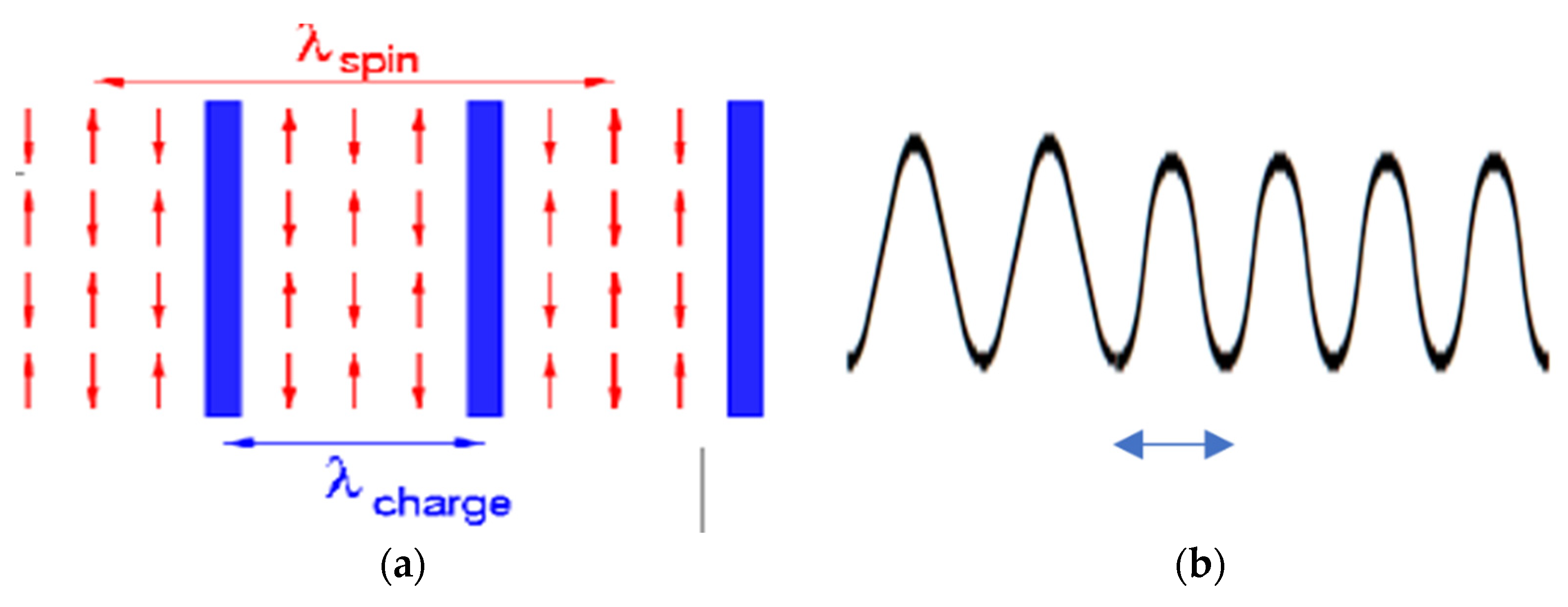
Stripes with strong interplay between charge and spin degrees of freedom (Figure 2a) observed in the LSCO family by neutron scattering since 1995 [20]. Charge and spin incommensurate modulation vectors q_c = 2π/λ_c and q_s = 2π/λ_s are strictly related (q_s = q_c/2) one to another and align along the Cu-O bond.

Figure 2. (a) Stripes: charge and spin modulation vectors q_c and q_s are connected. (b) The different modulation of charge density waves (CDWs) with respect to stripes is shown. In this case, CDWs and SDWs evolve independently one from another (see, e.g., [21,22]).

However, both spin and charge modulation were observed simultaneously in co-doped LSCO only (e.g., La_1.48Nd_0.4Sr_0.12CuO₄); otherwise, there was no detection of charge modulation (only spin).

-

Charge Density Wave (Figure 2b). Charge and spin degrees of freedom evolve independently one from another [21,22]. CDWs, foreseen since 1995 [17], were until 2011 elusive, contrasted, and confirmed only indirectly. Due to the improvement of resonant X-ray scattering (RXS), CDWs are now ubiquitously observed (see, e.g., [21,22,23,24,25,26,27,28]) in cuprate families, and most investigated among the orders competing with SC in countless papers following the pioneering paper on YBCO by Ghiringhelli et al. [23].

As shown in Figure 3, (i) energy-integrated CDW peaks are along the Cu-O bond, (0.31,0) and (0,031) in CuO₂ planes; (ii) the width decreases by lowering T and the correlation length increases but remains finite (less than 16a lattice constant), so that the fluctuating CDWs tend to become critical but never succeed, and for this reason they were called Quasi-Critical dynamical fluctuating CDWs (QC-CDWs); and (iii) the QC-CDW peak is increasing by lowering T down to Tc, while it is decreasing for T < T_C, i.e., the incipient CDW phase transition is preempted by the SC transition.

Figure 3. Adapted from [23]. Energy-integrated resonant X-ray scattering (RXS) for underdoped YBa2Cu3O6.6 (T_c = 61 K) as a function of the in-plane momentum vector at various temperatures. The arrows indicate the increasing or decreasing of the peak by lowering the temperature above or below T_c, respectively.

The QC-CDW onset line T_QC-CDW(p) starts around optimal doping and initially follows the pseudogap line T*(p) (see Figure 4).

Figure 4. Adapted from [21,22]. Phase diagram T vs. doping for YBCO. Red line: Quasi-Critical-CDW T_QCCDW. Black line: pseudogap T*. Black dashed line: superconductive critical temperature. Blue region below the superconductive dome: sketched 3D long-range CDW in the presence of high magnetic field. The two blue dots: 3D extrapolated quantum critical points (QCPs). Red dot: the extrapolated QCP of the QC-CDW.

In the presence of a sufficiently high magnetic field to suppress superconductivity, a static 3D transition is unveiled (blue region in Figure 4), mainly in YBCO, by NMR [29,30], quantum-oscillation, negative Hall, and FS reconstruction [31,32,33,34,35,36,37,38], and finally by thermodynamic 3D transition by pulsed ultrasound [39]. Zero field QC-CDW and 3D long-range charge order with two QCPs (p_c’ < p_c ≠ p_c⁰ ≈ p*) have the same in-plane incommensurate vector q_c, suggesting a common origin.

3. A Digression for Alex Müller and My Memories

Actually, the community was and has been for decades strongly against the idea of phase separation and of non-uniform charge in general. Most researchers were referring to spin fluctuations due to the vicinity of the AF-QCP in the low-doped Mott insulator [4,19,40,41,42,43]. Charge order has been at most considered as a byproduct of spin order. For instance, at the first big international conference on HTSCs of 1988 held in Interlaken, following my remark on the possible interconnection between different charge density values that could coexist in these materials [44], P.W. Anderson argued that “simple calculations” show it to be impossible. Alex Müller, instead, trusted us from the beginning, and gave a strong support to the community that was inquiring about charge inhomogeneity in cuprates. He organized several conferences on PS (see, e.g., Erice in 1992 (Figure 5 and Figure 6) and Cottbus in 1993).

Figure 5. Erice, 6–12 May 1992, Workshop on Phase Separation in cuprate Superconductors.

Figure 6. Erice, July 1995. E. Sigmund, C. Di Castro, and G. Benedek with K.A. Müller in the center, looking at a gift for him, a book on rare cars, one of his hobbies.

In the proceedings [45,46], our work carried out in Rome, the one by Emery and Kivelson, and the one by Sigmund, Hiznyakov, and Seibold on PS of that early period were summarized. A comprehensive presentation of the experimental situation was also given. The task of keeping the members of this community linked was carried out also by the three editors of this volume, in particular by Antonio Bianconi with the Superstripes organization. Alex often recalled the scientific contributions of Annette Bussman-Holder, Hugo Keller, and Antonio Bianconi (see, e.g., the distorted octahedrons of Antonio that, according to Alex, can be assigned to Jahn–Teller polarons, whereas the undistorted ones are located within a metallic cluster or stripe [47]).

The idea of charge inhomogeneity corresponds, at least in part, to the idea of strong polarization that guided Müller in his discovery of high-temperature superconductivity.

I have been corresponding with Alex extensively on the subject, for many years. I presented the “elogio” on the occasion of his Laurea Honoris Causa in Rome in November 1990 (Figure 7). Furthermore, I was later called (1997) to Cottbus for the equivalent ceremony.

Figure 7. K.A. Müller. Laurea Honoris Causa, Rome 1990.

In Cottbus, we experienced an episode that is unusual for meetings among physicists. After the ceremony, the neo-laureate with his wife as well as my wife and myself were taken to a party in a villa–castle located in the outskirts of Cottbus. We were proceeding in a Mercedes along a highway, when the car stopped; we then got into a seventeenth century-like chariot with the coachmen in “livrea” (livery). Cars were speeding around us, and we finally arrived in the villa, where we were received by a string quartet playing classical-style music, organized for Alex by the noble family who had recently repossessed the villa.

4. Correlated Fermi Liquid and CDW Fluctuations

4.1. Correlated Fermi Liquid Instability Producing a Charge Density Wave State

Let us see how the scenario presented in Section 2 arises from our old and new stories.

The proposal of a CDW instability in cuprates is quite old [17] and it is based on the mechanism of frustrated phase separation discussed above.

At high doping, as it has been already mentioned, strong correlations weaken the metallic character of the system giving rise to a correlated FL with a substantial enhancement of the QP mass m* and a sizable repulsive residual interaction. The presence of weak or moderate additional attraction due to phonons reduces this residual interaction and may provide a mechanism that induces an electronic PS with charge segregation on a large scale, i.e., a diverging compressibility $\kappa$, the static density-density response function at q = 0:

$$\mathsf{\kappa }=\underset{q\to 0}{\lim }{\chi }_{\rho \rho }(q,\omega =0)=\underset{q\to 0}{\lim }<\rho (q,\omega =0)\rho (-q,\omega =0)>\to \infty$$

(1)

The FL expression of the compressibility κ in terms of the static Γ_q and dynamic Γ_ω scattering amplitudes is as follows:

$$\kappa =2N(0)/(1+2N(0){\mathsf{\Gamma }}_{\omega })=2N(0)(1-2N(0){\mathsf{\Gamma }}_q)\to \infty as q\to 0$$

(2)

From equation (2), the Pomeranchuk condition for the instability of the FL reads as follows:

$$2N(0){\mathsf{\Gamma }}_{\omega }=-1,{\mathsf{\Gamma }}_q\to -\infty$$

(3)

The static scattering amplitude diverges at q = 0.

With a long-range Coulomb interaction, it would cost too much in energy to fully segregate the charge and the system phase separates on a shorter scale. The Fermi liquid instability coming from the overdoped region occurs at finite modulation vector q = q_c leading to an incommensurate charge density wave state with wavelength ${\lambda }_c=2\pi /q_c$. q_c is not related to nesting but is determined by the balance between PS tendency and Coulomb energy cost [17].

A strong scattering increase has been indeed measured in YBCO at optimal doping [48], as it is required by Equation (3) but this time at a finite q.

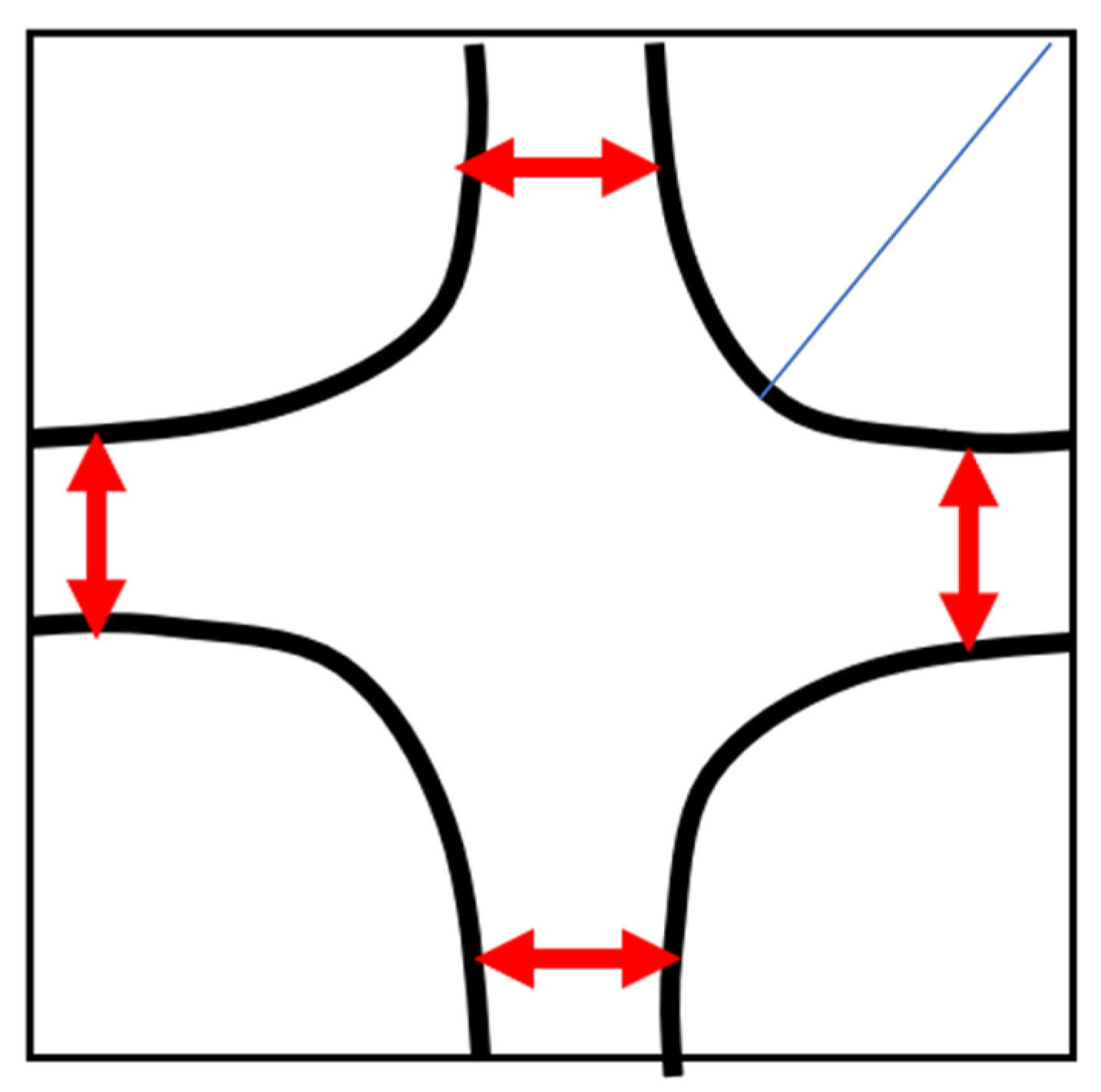
4.2. Theoretical Realization

The general ideas of the previous section are implemented within a correlated FL theory described by a Hubbard–Holstein model with large local repulsion and a long-range Coulomb interaction V_c(q). The values of the hopping parameters are derived from the quasiparticle band. Slave Boson technique was used to implement the condition of no double occupancy [17,49,50] with the result that strong correlation severely reduces the kinetic homogenizing term. This technical procedure was indeed shown [51] to produce a correlated FL with a quasiparticle dispersion having a reduced hopping and a residual density–density interaction V(q) between the quasiparticles:

$$V(q)=V_c(q)+U(q)-\lambda$$

(4)

where U(q) is the short-range residual repulsion stemming from the large repulsion of the one-band Hubbard model and λ is the coupling of the Holstein e-ph interaction leading to the thermodynamic PS in the absence of V_c. In the FL, V(q) is screened in the random phase approximation via the polarization due to the repeated particle–hole virtual processes of the Lindhard polarization bubble Π(q, ω):

$$V_{scr}=\frac{V(q)}{1+\mathsf{\Pi }(q,\omega )V(q)}.$$

(5)

The effects of strong correlations are contained in the form of V(q) and in the QP effective mass entering Π(q, ω). The dressed dynamical density–density correlation function ${\chi }_{\rho \rho }=\frac{\mathsf{\Pi }}{1+\mathsf{\Pi }(q,\omega )V(q)}$ has the same denominator of V_scr.

Within the present approximation, the FL instability condition (Equation (2)) towards the CDW is given by the vanishing of the denominator in Equation (5) at a finite modulation vector q = q_c, eventually marking a mean-field critical line as a function of doping p, $T_{CDW}^0(p)$ as it is sketched in Figure 8:

$$1+\mathsf{\Pi }(q,\omega )V(q)=0$$

(6)

Figure 8. Courtesy of M. Grilli. Sketch of the instability condition of FL to form CDW. Dotted line: Coulomb interaction. Dashed line: residual repulsive interaction. Red line: sum of the two. Black line: red line shifted by the attraction $\lambda$. Blue line: inverse Lindhard polarization bubble. The FL instability condition is also shown.

U(q) is less repulsive and the hopping largest along the Cu-O direction ((0.5,0) and (0,0.5)). Mean-field CDW instability of FL and modulation vector q_c are therefore in this direction and determine the hot regions of the Fermi surface (shown in Figure 9) where CDW fluctuations (CDFs) mediate strong scattering between Fermi quasiparticles and suppress quasiparticle states, forming the so-called Fermi arcs. We consider this as the beginning of the formation of a pseudogap (see also [9]); we then let the mean-field CDW critical line start at T = 0 at the same doping p* of the extrapolated pseudogap line.

Figure 9. Red arrows: modulation vectors q_c of CDFs connecting two branches of the quasiparticle Fermi surface (FS) in the antinodal regions of the FS. Blue line: nodal direction.

The formation of gaped electron states near the antinodal regions suggests a pseudogap with d-wave symmetry as the superconductive gap [9]. The analysis of the superconductive transition in the presence of a doping-dependent normal state pseudogap with d-wave symmetry [52] accounts for a doping-dependent superconductive critical temperature T_c(p) and a T_c − T* bifurcation near optimum doping, within a d-Density-Wave scheme a year before a more known proposal appeared [53].

Expanding in q-q_c and ω around the mean-field critical line $T_{CDW}^0(p)$:

$${\chi }_{\rho \rho }^{-1}\propto D^{-1}\equiv m_0+\nu {(q-q_c)}^2-i\omega \gamma ,m_0=\nu {({\xi }_{CDW}^0)}^{-2}\propto T-T_{CDW}^0$$

(7)

where D in field theory is named the “propagator” of the fluctuation and m₀ is its “bare” mass.

Essentially, Equation (7) represents a time-dependent Landau–Ginzburg (TDLG) equation in the Gaussian approximation:

$$\frac{\partial \phi (x,t)}{\partial t}={\gamma }^{-1}\frac{\delta H\left\{\phi \right\}}{\delta \phi }, H\left\{\phi \right\}=\frac{1}{2}{{\displaystyle \int }}^{}dx[m_0{\left|\phi \right|}^2+\nu {\left|\nabla \phi \right|}^2],$$

(7’)

where $\phi$ is the CDW field (or fluctuation mode) and $\gamma$ is the coefficient of the Landau damping term $i\omega$.

From an inspection of Equation (7), it is natural to define a characteristic energy for each q:

$${\omega }_{ch}(q)=\frac{m_0}{\gamma }+\frac{\nu {(q-q_c)}^2}{\gamma }~{\tau }_q^{-1}$$

(8)

which is minimum at q = q_c and its inverse defines the relaxation time ${\tau }_q$ of the fluctuation mode ${\phi }_q$ to its equilibrium zero value.

4.3. Correction to Mean Field Due to Fluctuations

In systems with quasi-2D layered structures such as cuprates fluctuations reduce strongly the mean-field critical temperature. The first correction to m₀ due to fluctuations was calculated [54] in the mode–mode coupling of the CDFs, as shown diagrammatically in Figure 10. The loop of the fluctuation mode in the second diagram is a constant in momentum and gives a correction $\delta m$ to the mean field m₀.

Figure 10. First correction to the CDF propagator at first order in the coupling u (blue dot). The blue dashed loop in the second diagram is the Hartree self-energy term, constant in q, and gives the first correction to m₀.

In the same paper [54], stimulated by discussion with Alex Müller, the anomalous isotope effect in cuprates [10] was also considered. Even though phonons do not directly pair the fermionic quasiparticles, they nevertheless act indirectly on various quantities as T* and have a doping-dependent effect on T_c.

The expressions of the full mass m in terms of the corrected T_CDW and of the corrected correlation length ${\xi }_{CDW}$ derived by the loop integral, shown in Figure 10, are as follows:

$$m(T)=m_0+u\delta m\propto T-T_{CDW}(p), \mathrm{m}=\nu {\xi }_{CDW}^{-2}$$

(9)

m(T) must therefore vanish at criticality. m should replace m₀ in the Equation (8) of ${\omega }_{ch}$.

There are three cases according to the value of the loop integration.

-

In two dimensions (2D), the density of states N(ω) is constant and δm is ln-divergent. It is then impossible to satisfy the criticality condition of vanishing m(T) and there is no transition at finite T, as in general for a continuous symmetry. A quantum critical point and charge order are possible only at T = 0. In 2D and finite T, dynamical charge fluctuations (CDFs) only can be present.

-

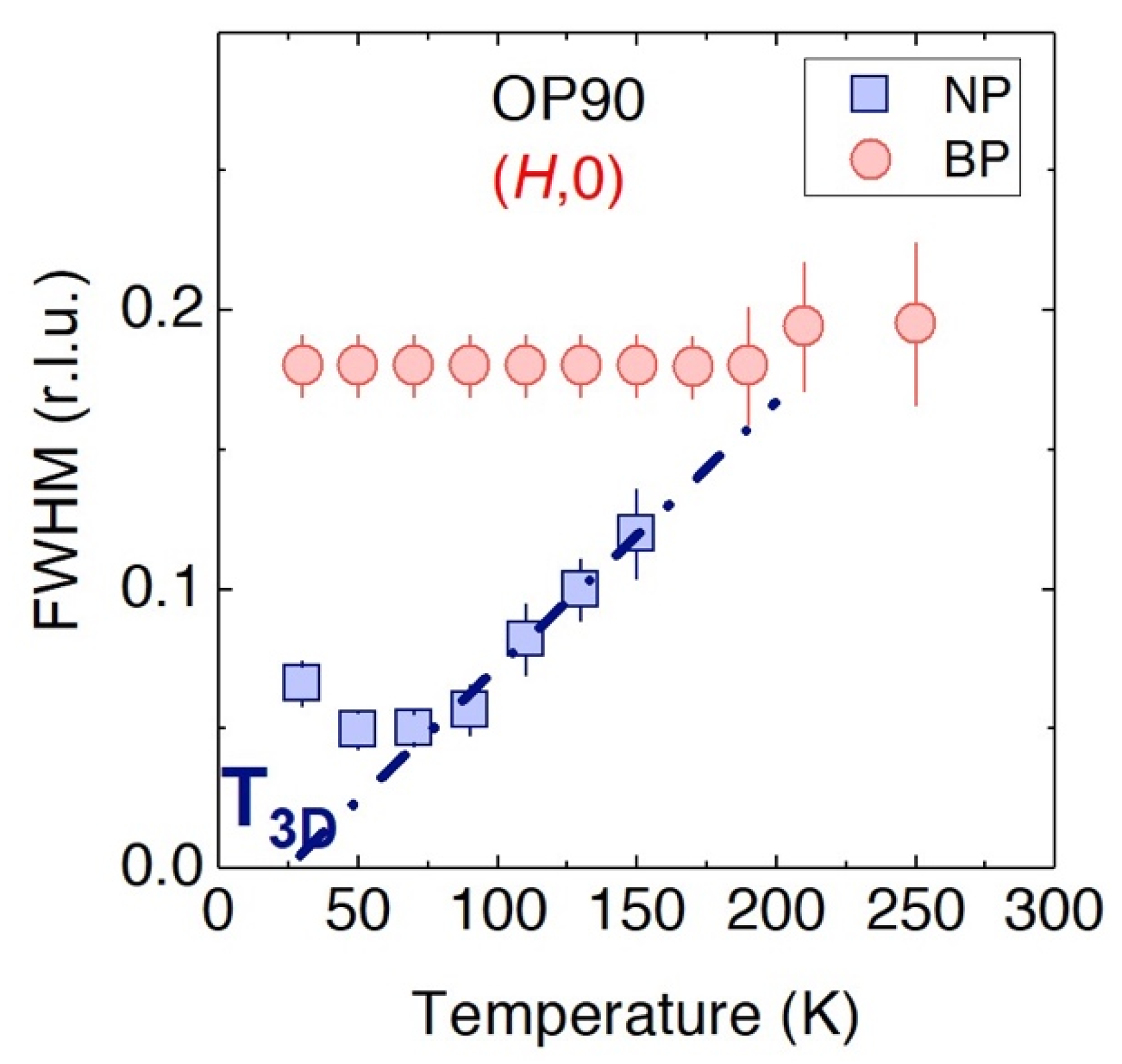
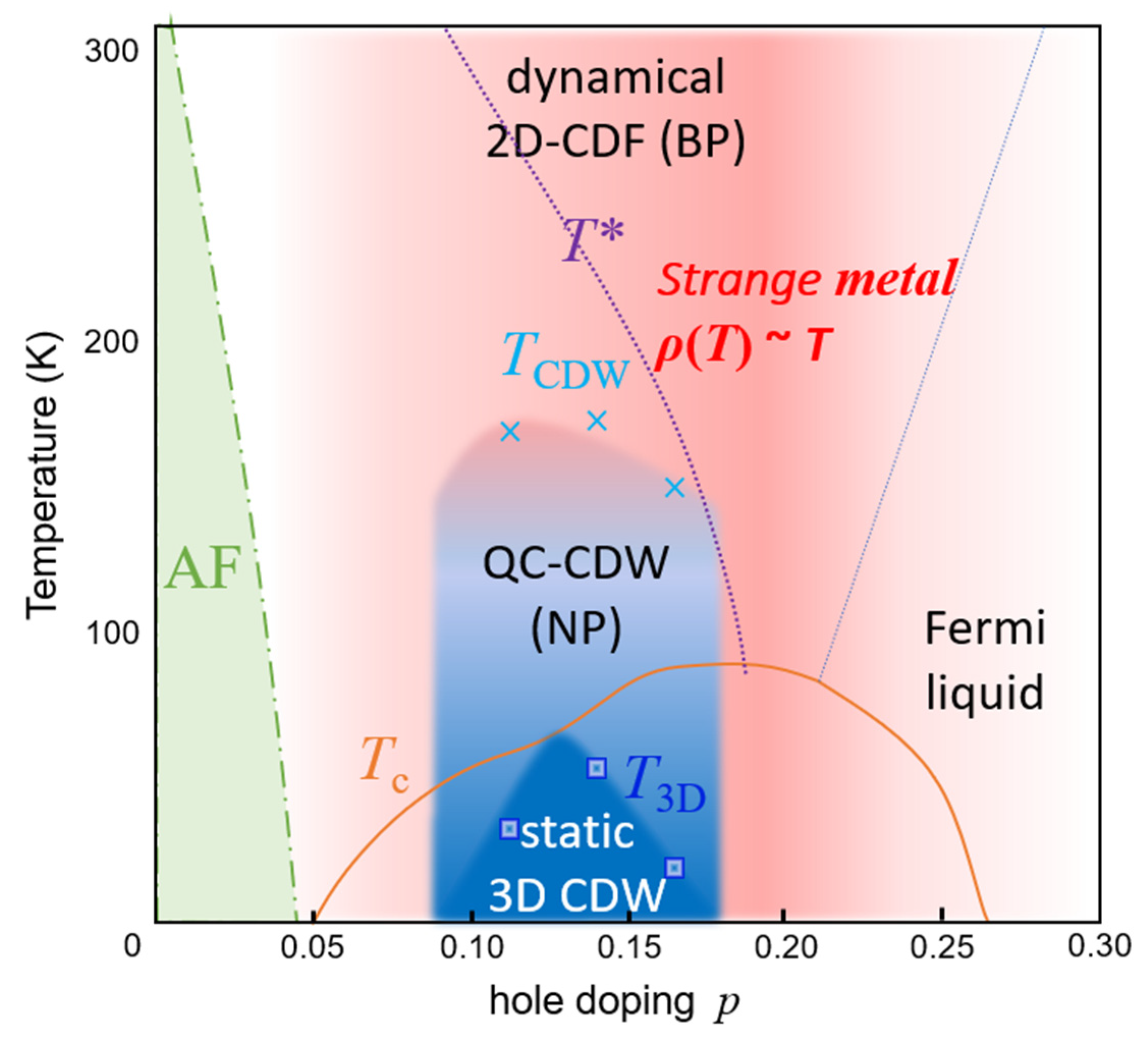
The drastic role of fluctuations can be reduced by cutting their long-range effect in the loop integral with an infrared cut-off ${\omega }_{min}$ (possibly of the order of ${\omega }_{ch}(q_c)=\frac{m}{\gamma }=\frac{\nu }{\gamma }{\xi }_{CDW}^{-2})$ to simulate the quasi-2D structure of cuprates. Lowering T at fixed doping gives rise to a quasi-critical dynamical CDW (QC-CDW), which can be observed with sensitive experiments like RXS.

-

In three dimension (3D), N(ω) vanishes as ω goes to zero and makes δm finite also at finite T. By lowering T further, the QC-CDW may cross over to a long-range 3D-CDW, which is however hidden by superconductivity.

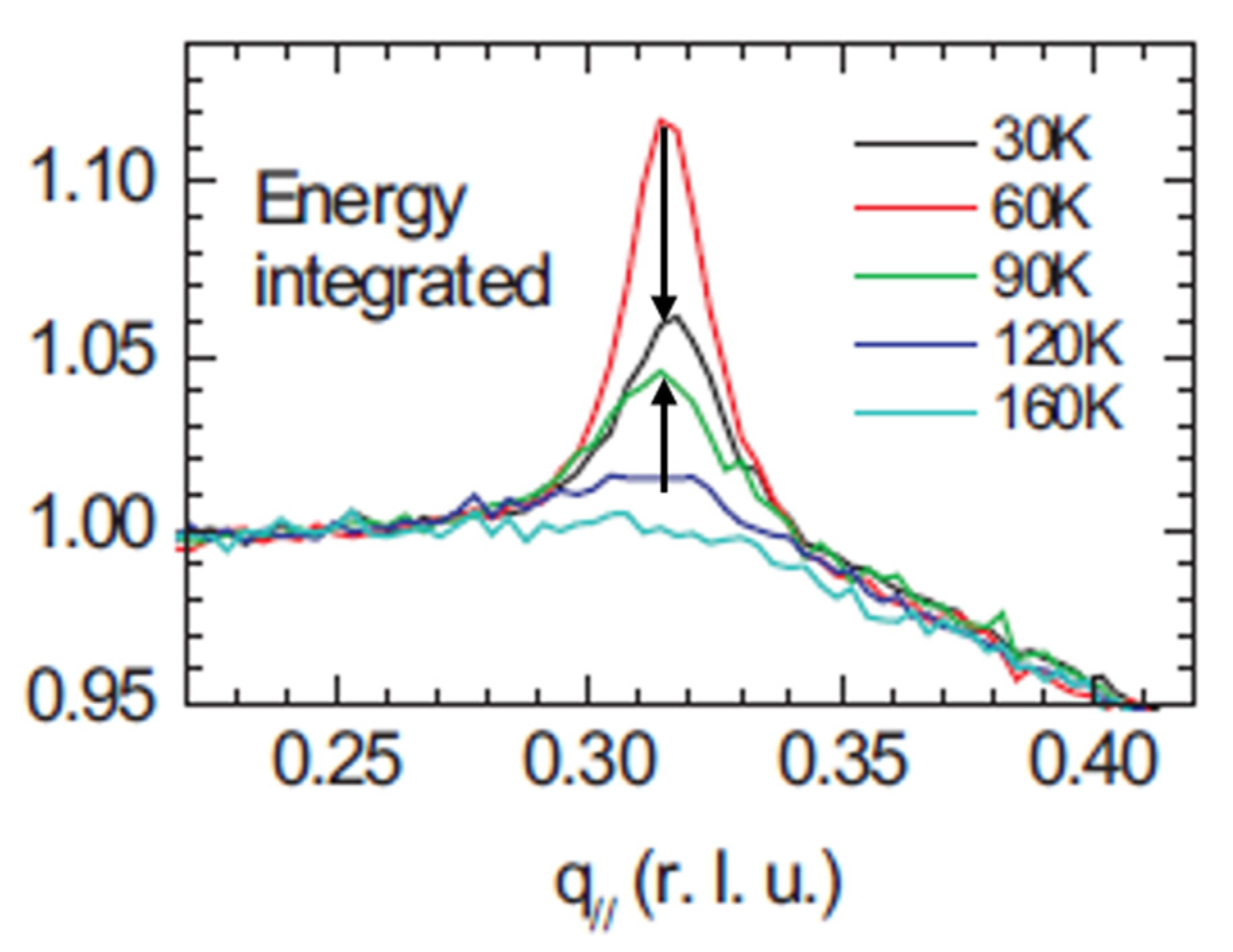
4.4. Experimental Observation of the Scenario Presented Above

RXS experiments may test directly the dissipative part of the density–density dynamical response and can therefore be analyzed within the theoretical scenario presented above. In this case, the RXS intensity I_RXS is proportional to the $Im{\chi }_{\varrho \varrho }$∝ ImD, times the occupancy CDFs given by the Bose function b($\omega$/T) as follows:

$$I_{RXS}=AImD(q,\omega )b(\frac{\omega }{T})~\mathrm{Ab}(\frac{\omega }{T})\frac{\omega /\gamma }{{({\omega }_{ch})}^2+{(\omega )}^2},$$

(10)

where A is a constant and the characteristic frequency ${\omega }_{ch}$ is specified by Equation (8) with m instead of m₀.

If ${\omega }_{ch}(q_c)$ never vanishes, its finite value determines the dynamical nature of the fluctuations that do not become critical. This is visualized in the experiment by a shift of the peak of high-resolution experiments. In Equation (10), $b(\frac{\omega }{T})$ can be classically approximated as $T/\omega$ and a T-factor appears in I_RXS, if $k_{B}T>{\omega }_{ch}(q_c)$.

A thorough RXS analysis in (Y, Nd)Ba₂Cu₃O_7-(YBCO, NBCO) at various doping values (0.11–0.19) and temperatures 20 < T < 270 K was performed in [6].

After subtracting the background, the experimental results for the density–density part of the response can be summarized as follows:

At high T, the energy integrated RXS quasi-elastic intensity can be fitted by assuming a single profile. At lower T instead, two peaks are necessary. One peak (NP) has a narrow width at half maximum (FWHM ~ ξ⁻¹). The other, instead, is very broad with very short correlation length (BP).

In the underdoped YBCO sample at p = 0.14, the two peaks are centered at slightly different values of q. Both values, however, are around 0.3 r.l.u., a value proper of the modulation vector of CDW in the YBCO family at this doping. Moreover, the two vectors become equal ($q_c^{NP}=q_c^{BP}$ = 0. 32 r.l.u.) at optimal doping p=017. Both peaks are therefore related to the same phenomenon of CDW.

The NP has the following properties: (i) a dome-shaped onset temperature as a function of doping T_QC-CDW(p) as shown in Figure 4; (ii) the peak narrows and the correlation length increases as T decreases down to T_c; and (iii) this ordering competes with superconductivity as T_c is reached (see Figure 11).

Figure 11. From [6]. Width vs. T in (H,0) scan of energy integrated quasi-elastic peaks for the optimally doped YBCO sample: NP (blue squares) and BP (red dots). The extrapolation of the NP width, marked by a dash-dotted line, tends to zero at the hypothetical T_3D and towards the BP width at higher T.

The NP presents all the characteristics of the quasi-critical dynamical CDW discussed above for the quasi-2D layered structure.

By extrapolating to zero the linear in T dependence of NP-FWHM before the competition with SC is reached, the long-range 3D onset temperature T_3D(p) was determined at which NP-FWHM would vanish and ξ_CDW would diverge in the absence of superconductivity (Figure 11). The values determined in this way are in good agreement with the values detected in the presence of a strong magnetic field.

The new feature of the experiments is the very broad BP (FWHM~ξ⁻¹~0.16–0.18 r.l.u.), by now observed in many other families [55,56,57,58,59,60]. It has many peculiar properties (Figure 11), as follows: (i) it is present up to the highest measured T well above T*(p); (ii) the width (FWHM) and the correlation length are almost constant in T; the corresponding charge fluctuations are then non-critical and do not show any tendency to become critical at any finite T; and (iii) the characteristic energy ${\omega }_{ch}$ has been measured by fitting the dynamical high-resolution spectra on the OP90 (and UD60) samples at T = 90 K, 150 K, 250 K and q = q_c. At T = 150 K and 250 K, only the BP is present (no NP), $\omega$_ch ≈ 15 meV of the order of T* showing the dynamical nature of the fluctuations of the BP, which can be considered as the 2D dynamical charge fluctuations (CDFs) non-critical at any finite T.

At the lower temperature, T = 90, the NP is also present and ω_ch has a finite but smaller value, reinforcing the idea of the quasi-critical nature of the CDW of the NP.

The extrapolation of NP-FWHM from T > T_C to higher T (Figure 11) suggests that the NP emerges from the BP. It is not clear at the moment whether the two kinds of excitation coexist or are spatially separated, giving rise to an inhomogeneous landscape, as found in [61].

As a first conclusion, we can say that the three cases envisaged by the theory in Section 4.3. were found in the experiments with a continuous evolution from pure 2D dynamical CDFs at high T and all doping, to a coexistence with quasi-critical CDWs below T_QC-CDW, to the static 3D CDW hindered by superconductivity and measured in a high magnetic field.

4.5. Strange Metallic Behavior Above T*

The very broad spectrum (BP) of CDFs allows us [7] to approach the old standing problem of strange metal (SM) of cuprates, in particular the anomalous linear in T resistivity ρ(T)$~T$ from T > T* up to the highest attained temperatures. One of the prerequisites identified in the marginal FL phenomenological theory [62] to reproduce the strange metal is the presence of a strong isotropic scattering channel for the Fermi quasiparticles with all states on the Fermi surface nearly equally affected. This was accomplished by assuming 2D-CDFs of the BP as mediators of scattering among the Fermi QPs. The width of the CDFs is such that a Fermi QP of one branch of the FS can always find a CDF that scatters it onto another region of FS. The scattering among the Fermi quasiparticles is then almost uniform along the entire Fermi surface.

I refer to the original article for the explicit calculation of the following quantities for an optimally doped (Tc = 93 K) NBCO sample and an overdoped (Tc = 83 K) YBCO sample: (i) the fermion self-energy, i.e., how the Fermi QPs are dressed by CDFs, using the same set of parameters that was obtained by fitting the BP response; (ii) the zero frequency quasiparticle scattering rate along the Fermi surface from the imaginary part of the self-energy; and (iii) finally, the resistivity within the standard Boltzmann equation approach using the calculated scattering. In both cases, the strange metal requirements are satisfied and linearity in T of the resistivity for T > T* is quantitatively matched.

I only consider here the following heuristic simple argument. Since the scattering is almost uniform over the entire Fermi surface, the scattering integral in the Boltzmann equation can be well approximated with an effective scattering time of a single scattering event. Its inverse then determines the effective characteristic frequency of the process, which depends on the characteristic frequency of the scatterers given by Equation (8) at q = q_c. In analogy with a disordered electron system, the full inverse scattering time must be proportional to the one of the single event multiplied by the population of the scatterers, i.e., the Bose function. As long as $kT>\hslash {\omega }_{ch}$, the semiclassical approximation of $b(\frac{\omega }{T})$ is valid and a linear T dependence is introduced:

$$\frac{\hslash }{\tau }=a\left(\upsilon ,\xi ,\dots \right)kT$$

(11)

where a is a dimensionless doping-dependent function of the parameters of the theory. In the present argument a can be considered as a fitting parameter, independent from T since the BP correlation length does not depend on T in any relevant way (Figure 11).

5. Conclusions

The following Figure 12 gives a graphic representation of the scenario described above.

Figure 12. Adapted from [6]. CDW in the phase diagram T vs. doping p of YBCO. The green zone is the antiferromagnetic phase. The reddish zone represents the 2D charge density dynamical fluctuations associated with the BP (actually the experiments in [6] were performed for 0.11 < p < 0.19). In the cone above optimal doping (between T* and the Fermi liquid), CDFs produce the strange metal and the linear in T resistivity. Light blue zone: the quasi-critical CDWs associated with the NP. Dark blue zone: the static 3D long-range order hidden in the absence of a magnetic field by the superconductive dome.

The phase diagram visualizes the continuous evolution from a pure 2D dynamical CDF at high T and all doping, to a coexistence with quasi-critical CDWs below T_QC-CDW, to the static 3D-CDW hindered by superconductivity and measured in a high magnetic field.

Finally, the dynamical CDFs (BP), characterized by the same parameters used to fit RXS experiments, were chosen as mediators of isotropic scattering among Fermi quasiparticles and provide an understanding of the long-standing problem of strange metallic state, matching the resistivity data, in the whole range from room temperature down to T* [7].

Some open problems deserve further investigation:

In Section 4.4., it was already mentioned that the present knowledge of the relation between the quasi-critical CDW (NP) and the dynamical CDF (BP) does not allow to distinguish between a spatial separation or a coexistence of the two.

At temperatures T < T*, the role on scattering of the pseudogap state and of other intertwined incipient orders (CDWs, Cooper pairing, etc.) must be clarified.

Investigation is also required to see whether CDFs with a reduced value of ω_ch can also account for the so-called Planckian or better for the linear behavior observed at low temperatures and special doping in the presence of high magnetic fields to suppress superconductivity (see, e.g., [63]).