Abstract
In 1986 Bednorz and Műller discovered high temperature superconductivity in copper oxides by chemically doping holes into La2CuO4 (LCO), the antiferromagnetic insulator. Despite intense experimental and theoretical research during the past 34 years, no general consensus on the electronic-spin structures and the origin of pseudogap has been obtained. In this circumstance, we performed a first-principles calculation of underdoped cuprate superconductors La2-xSrxCuO4 (LSCO) within the meta-generalized gradient approximation of the density functional theory. Our calculations clarify first the important role of the anti Jahn-Teller (JT) effect, the backward deformation against the JT distortion in La2CuO4 by doping extra holes. The resulting electronic structure agrees with the two-component theory provided by the tight-binding model of Kamimura and Suwa (K-S), which has been also used to elucidate the d-wave superconductivity. Our first-principles calculation thus justifies the K-S model and demonstrates advanced understanding of cuprates. For example, the remarkable feature of our calculations is the appearance of the spin-polarized band with a nearly flat-band character, showing the peaky nature in the density of states at the Fermi level.
1. Prologue by Hiroshi Kamimura
In 1987, Georg Bednorz and Alex Műller received the Nobel Prize in Physics for “their discovery of new superconducting materials”. In 1988, the Steering Committee of NEC Symposium on Fundamental Approaches to the New Material Phases decided to choose “Mechanism of High Temperature Superconductivity” as the subject of the second NEC Symposium. This Symposium was held in Hakone, near Mt. Fuji, Japan on 24–27 October 1988. Alex was chosen as a plenary speaker, and I was the Symposium chairperson. The Symposium’s group photo is shown in Figure 1.

Figure 1.
Symposium’s group photo in the front of the Hakone Kanko Hotel.
In 2005, we organized the International Workshop on Electronic Structure and Lattice Effects in Cuprates on October 27 and 28 in the National Institute of Advanced Industrial Science and Technology (AIST) in Tsukuba. Alex was a plenary speaker, and a number of Alex’s friends, companions, colleagues, and former students attended this Workshop (see Figure 2).

Figure 2.
International Workshop’s group photo in the front of the Conference Hall in AIST.
On 27–28 March 2006, the International Symposium in Honor of J.G. Bednorz and K.A. Műller was held in University of Zurich, celebrating their discovery of cuprate superconductors 20 years ago. From Japan, six HTSC researchers, Yoichi Ando, Masatoshi Arai, Yoshiteru Maeno, Hiroyuki Oyanagi, Masaki Takashige, and Hiroshi Kamimura were invited. The group photo is shown below in Figure 3.

Figure 3.
International Symposium’ group photo. The front row: From the left, Prof. Hugo Keller, Prof. Alex Műller, Dr. Georg Bednorz, Prof. Hiroshi Kamimura.
2. Introduction
By the discovery of high-temperature superconductivity (HTSC) in cuprates by Bednorz and Műller [1,2], it is well known that cuprate superconductors are different from ordinary metallic superconductors in the production process of carriers. Cuprates are ionic crystals. The carriers in La2CuO4, an antiferromagnetic insulator [3], are produced from doping chemical elements or making oxygen deficiencies, for example, by replacing 3+ cations (La3+) by 2+ ones (Sr2+) in La2-xSrx CuO4 (LSCO). Thus, the electronic structures of cuprate superconductors may vary drastically upon doping holes [4].
In this circumstance, we pay attention to the experimental facts that a CuO6 octahedron in a parent material La2CuO4 is deformed into an elongated shape (tetragonal) due to the Jahn–Teller (JT) theorem for an orbitally doubly degenerate state of a Cu2+ ion [1,5]. When extra holes are doped, the apical O2− ions in elongated CuO6 octahedrons in LCO tend to approach toward Cu2+ ions to gain the attractive electrostatic energy [6]. This backward deformation against the JT deformations is called the anti-JT effect [7,8]. As a result, the energy separation between the two JT-split levels becomes smaller, i.e., pseudo-degenerate. This anti-JT effect in cuprates was supported experimentally by the neutron scattering [9] and the polarization-dependent spectroscopy [10,11].
Under these circumstances, there are two views concerning the electronic structures of LSCO. One view is based on the single-component theory in which only orbitals extended in a CuO2 plane are considered. Since a doped hole moves within a CuO2 plane, this model is irrelevant to the anti-JT effect. A typical model to take this view is the t-J model [12,13].
An alternative view is based on the two-component theory initiated by the Kamimura–Suwa (K–S) model [14,15], in which the two kinds of molecular orbitals (MOs) of each CuO6 octahedron parallel and perpendicular to a CuO2 plane are considered. Those MOs are |a*1g> antibonding and |b1g> bonding orbitals, as shown in Figure 4. In this figure, the schematic MO levels, b1g bonding, a*1g antibonding, and b*1g antibonding orbitals, and the hole configurations in Hund’s coupling multiplet 3B1g and spin-singlet multiplet 1A1g are shown. On the left side of the figure, a hole occupying a*1g orbital (red arrow) aligns its spin in parallel to the up spin of a localized hole occupying the b*1g orbital (green arrow) to form 3B1g, owing to the Hund’s coupling exchange interaction with the coupling constant, Ka1g (−2 eV) [16].
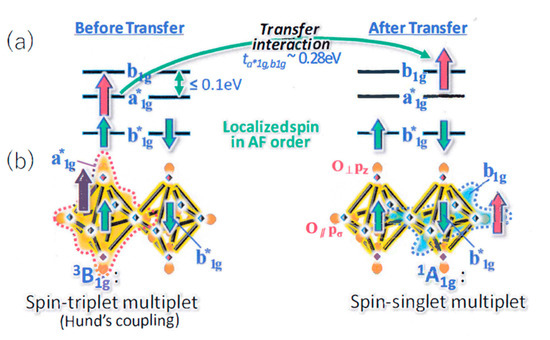
Figure 4.
The K–S model: the coexistence of a metallic state and the AF order. In this figure, (a) the transfer (a long curved arrow) of a doped hole (red arrows) from 3B1g to 1A1g without destroying the AF order is shown, and (b) the spatial extension of a*1g MO (left side) and b1g MO (right side) are shown, where O// and O┴ represent in-plane and apical oxygen, respectively.
On the other hand, on the right side of the figure, a hole occupying the b1g level (up red arrow) forms a spin-singlet (SS) multiplet with the down spin of a localized hole occupying the b*1g level (green arrow), 1A1g, owing to the larger exchange coupling Kb1g (= 4 eV) [16]. The key-feature of the K–S model is the coexistence of a metallic state and the AF order.
The above two types of exchange interaction, the Hund’s coupling spin-triplet and the spin-singlet (SS), can be described by the scalar product of the spin of the localized |b*1g > hole,, and that of the itinerant |a*1g> or |b1g> hole, or , at each CuO6 site, i, yielding the Hamiltonian interaction
This Hamiltonian interaction constitutes the K–S Hamiltonian to describe the K–S model, in which the localized spins form an AF order [14,15]. The whole K–S Hamiltonian is shown below.
where εm (m = a1g*, or b1g) represents the one-electron energy of the a*1g or b1g MO states, C†imσ and Cimσ are the creation and annihilation operators of a doped hole in the m-type MO with spin σ in the i-th CuO6 octahedron, respectively, tmn is the transfer integral of a doped hole between the m- and n- type MOs of neighboring CuO6 octahedrons, J the superexchange interacrion (as regards the details of the K–S Hamiltonian, see Ref. [17]).
3. First-Principles Calculations
In order to decide whether the one-component t–J model or the two-component K–S model is suitable to describe the electronic-spin state of cuprates, Kamimura et al. [18] recently performed the first-principles non-empirical calculation. In their calculations, the first-principle method of the constrained-and-appropriately normed (SCAN) density functional was adopted to calculate a non-rigid electronic-spin energy bands of LCO and LSCO, following Furness et al. [19]. Kohn-Sham density functional theory (DFT) is a widely-used electronic structure theory for materials as well as condensed matters. This SCAN method is more useful for the electronic-spin structures of diversely-bonded materials (including covalent, metallic, ionic, Jahn-Teller deformed bonds, cuprates consisting of CuO6 octahedrons and CuO5 pyramids).
The purpose of this contribution is to show how the first-principles SCAN calculations agree with the K–S model in the tight binding form. In the first-principles calculations, a unique method was adopted—that is, to investigate the electronic states of LSCO by calculating both the energy bands in k-space and the wavefunctions in r-space simultaneously. For this purpose, we calculated not only the non-rigid energy band and the density of states (DOS) in k-space but also the partial DOS (PDOS) which gives information on MOs in a CuO6 octahedron in r-space. Here PDOS means the density of states projected to the wavefunctions, or orbitals.
4. Calculated Results
4.1. La2CuO4 (LCO): Antiferromagnetic (AF) Insulator
The La2CuO4 (LCO) transforms from the high temperature tetragonal phase (HTT) into the low temperature orthorhombic phase (LTO) when temperature decreases. The calculated results on the crystal structure explains the Jahn–Teller distortion of an elongated octahedron. The calculated Cu magnetic moment, 0.510 μB, is in agreement with the observed values of 0.50 μB [20,21]. This means that the DFT-SCAN method [18,19] treats the spin-fluctuation effect properly. The calculated result shows that LCO is the antiferromagnetic insulator.
4.2. La2-xSrx CuO4 (LSCO)
In order to calculate the non-rigid energy bands for LSCO with AF order [22], the 2√2 × 2√2 supercell is adopted, in which there are two CuO2 planes and each CuO2 plane includes eight CuO6 octahedrons. The Brillouin zone (BZ) for this 2√2 × 2√2 supercell is shown in Figure 5. In this supercell, we cannot discuss the stability of stripe phases which were recently reported by Zhang et al. for YBCO systems [23].
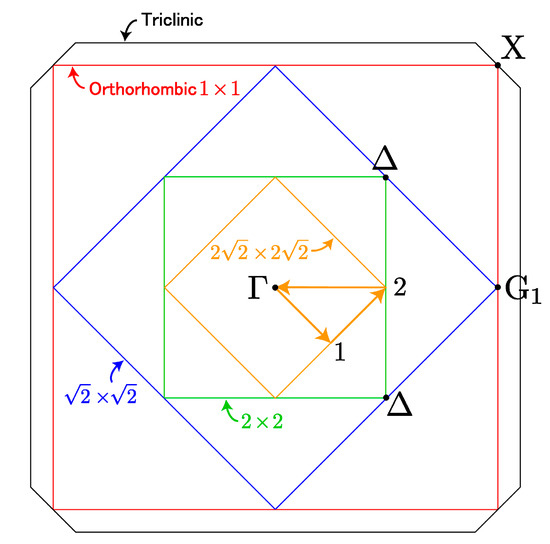
Figure 5.
The Brillouin zone (BZ) for the 2√2 × 2√2 supercell. Inside the BZ, a special triangle root starting form Γ is shown, where the special points 1 and 2 are used later in Figure 10.
Here we show that the key points obtained from the first-principles calculations for LSCO agree with those of the K–S model shown in Figure 4. In particular, it is shown that the Hund’s coupling spin-triplet in the K–S model agrees with the appearance of a spin-polarized band in cuprates.
4.3. A Metallic Phase with x = 0.125 (the Underdoped Regime)
In this case, Sr is substituted for one La in each CuO2 plane in the supercell, leading to x = 0.125. The calculated Cu and apical O shortest distance in a CuO6 octahedron in LSCO is 2.216 Å, which is considerably smaller than 2.448 Å in LCO. This shrinkage of the Cu and apical O distance by doping holes indicates that the anti-JT effect really occurs in LSCO. This result also supports the K–S model.
Although the calculated magnetization at each Cu site suggests the existence of AF order, the calculated value at each site takes a different value. For example, among the calculated values of the magnetization at each Cu site in Figure 6, the absolute value at Cu4 site shows the maximum value of 0.643 μB, which is considerably larger than the magnetization at a Cu site in LCO, 0.510 μB. Here we discuss the origin of the high value of magnetization, 0.643 μB in LSCO with x = 0.125.
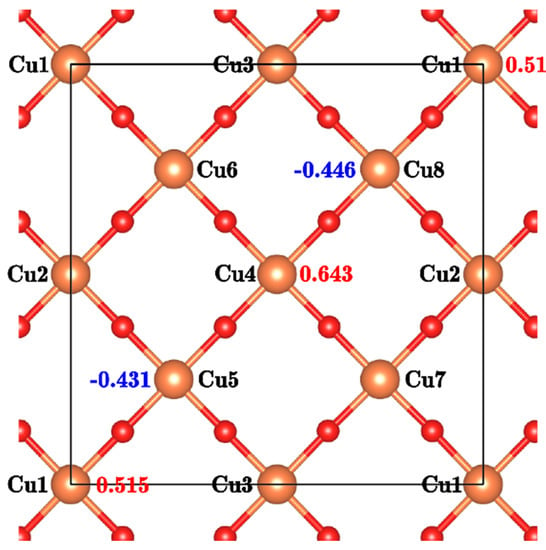
Figure 6.
The calculated magnetization at each Cu site in La2−xSrx CuO4 (LSCO) with x = 0.125.
In order to obtain information on the wavefunctions in a CuO6 octahedron, the PDOS (partial density of states) of dz2 orbital and its ligand O pz orbitals in a CuO6 octahedron at the Cu4 site is calculated. The calculated results are shown in Figure 7. Using these orbitals in a CuO6 octahedron at the Cu4 site, an antibonding |a*1g> MO is constructed, in order to investigate a relation between the |a*1g> orbital in the energy band and the antibonding |a*1g> MO in the K–S model in Figure 4, where Cu in CuO6 octahedron is assigned to Cu4.
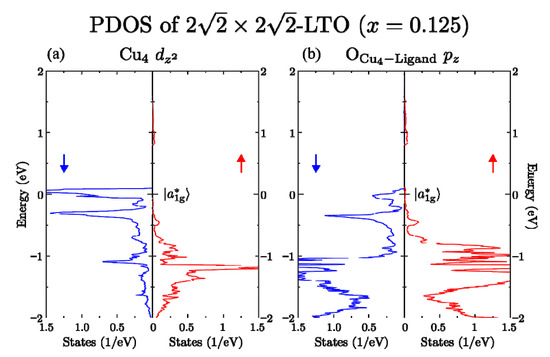
Figure 7.
Calculated partial density of states (PDOS) of orbitals in CuO6 at Cu4 site: energy 0 is EF. (a) PDOS of Cu-dz2 orbital; (b) PDOS of ligand apical O-pz orbital.
4.4. The Close Relation between a Spin-Polarized Band in the First Principles Calculations and Hund’s Coupling Spin Triplet in the K–S Model
4.4.1. The Appearance of a Spin-Polarized Band in Cuprates
Another remarkable feature of the highest hole band is the spin polarization at the Cu4 site (Figure 7). The difference in the highest states between up-spin and down-spin bands is considered as the “ferromagnetic band splitting” discussed by Slater [24], and Connolly [25]. Indeed, according to the criterion for the occurrence of a spin-polarized band in LSCO derived in the paper [18], the Hund’s coupling exchange interaction in Equation (1) may cause a spin-polarized band when , where K(x) = │Ka*1g (x)│and the density of states at EF. The magnitude of K(x) is 2.0 eV for LCO (x = 0) and is larger in LSCO because of the anti-JT effect. Figure 7 shows that much larger than 1.5 states/eV. Thus, the condition for the appearance of the spin-polarized band is satisfied. We also notice that the PDOS of the highest down-spin Cu4 dz2 hole band in Figure 7a, i.e., the spin-polarized band, shows a “peaky” nature due to the existence of a nearly-flat highest hole band, which originates from the JT and the anti-JT deformations. In fact, the effective mass of a hole carrier in this band is six times heavier than the free electron mass. Thus, we consider that this hole carrier is a “Jahn-Teller polaron”, proposed by Alex [26,27,28]. We expect that the peaky nature may be observed for underdoped LSCO by performing an STM or STS measurement
4.4.2. Relation between the Cu4 dz2 Band and the Hund’s Coupling Spin-Triplet in the K–S Model
Now, in order to investigate whether a doped hole in the Cu4 dz2 band(|a*1g> MO) forms the Hund’s coupling spin-triplet 3B1g with a localized spin at the same Cu4 site, we calculated the PDOS of Cu4 dx2-y2 and ligand O-px, py orbitals in x-y plane, which form the antibonding |b*1g> MO and the bonding |b1g> MO in a CuO6 octahedron. The calculated results are shown in Figure 8. The Cu4 dx2-y2 orbital and the ligand O-px, py orbitals that appear in the energy region of 1 to 2eV above EF in Figure 8 form the antibonding |b*1g> MO. This MO is occupied by the localized holes with down spins. Since both spins of the localized holes in |b*1g > MO and of the doped holes in the Cu4 dz2 band (|a*1g > MO) take the same direction, down spins, the total magnetization at the Cu4 site becomes the maximum value of 0.643μB. Thus, one can conclude that the Hund’s coupling between a localized hole in |b*1g > MO and a doped hole in the Cu4 dz2 band (|a*1g > MO) plays an important role in LSCO with x = 0.125 in the first-principles calculations.
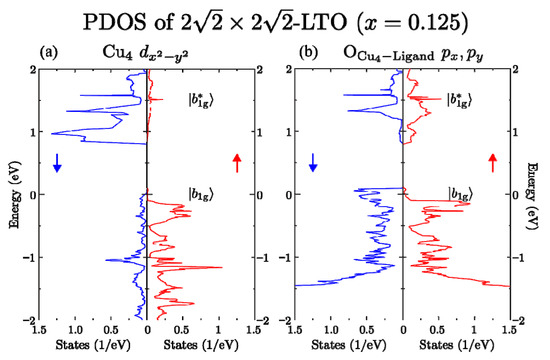
Figure 8.
Calculated PDOS of orbitals in CuO6 at Cu4 site: Energy 0 is EF. (a) PDOS of Cu-dx2-dy2 orbital; (b) PDOS of ligand in-plane-O px, py orbitals.
4.4.3. Itinerancy of a Hole in the Cu4 dz2 Band
The present first-principle calculations also show how a doped hole in the Cu4 dz2 band (|a*1g> MO) itinerates in LSCO in the underdoped regime.
Let us pay attention to the hopping of a doped hole with down spin from a Cu4 site to a neighboring Cu8 site in the AF order, whose magnetization, −0.446μB, is opposite to that at the Cu4 site, +0.643 μB. We calculated the PDOS of Cu-dx2-y2 orbital and ligand O-px, py orbitals in the x–y plane at the neighboring Cu8 site, as shown in Figure 9. In this figure, we find that these orbitals form bonding b1g and antibonding b*1g MOs in a CuO6 octahedron at the Cu8 site. The |b*1g> MO with Cu-dx2-y2 (a localized hole) appears in the energy region of 1 to 2 eV above EF (red color) in Figure 9a while the |b1g> MO (a doped hole) appears just above EF. By comparing the calculated results of the spin-direction of a localized hole in Figure 9a (red color) with that in Figure 8a (blue color), we notice that the localized spins at the Cu8 site are directed upwards, while those at the Cu4 site are opposite in the spin directions. Thus, we conclude that the AF order is not destroyed during the itinerancy of a doped hole in LSCO.
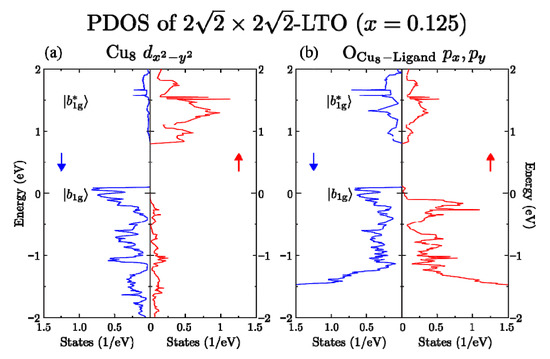
Figure 9.
Calculated PDOS of orbitals in CuO6 at Cu8 site: (a) PDOS of Cu-dx2-dy2 orbital; (b) PDOS of ligand in-plane-O px, py orbitals. Energy 0 is EF.
Furthermore, when a hole with down spin in the Cu4 dz2 band (|a*1g > MO) at the Cu4 site hops into a neighboring Cu8 site in the AF order, the first-principles calculation shows that this hole enters an empty |b1g > MO just above EF at the Cu8 site, taking a spin antiparallel configuration (the spin-singlet) with the localized hole in |b*1g > MO at the same site (see Figure 9).
4.4.4. Good Agreement between the First-Principles SCAN Calculations and the K–S Model in the Tight-Binding Form
Summarizing the itinerancy of a doped hole from Cu4 dz2 orbital to Cu8 dx2-y2 orbital, the spin-state of the doped hole changes from the Hund’ coupling spin-triplet with the localized spin at Cu4 site to the spin-singlet with the localized spin at Cu8 site.
This itinerancy of a doped hole in the first-principles SCAN calculations is strikingly consistent with the K–S model. In the K–S model (see Figure 4), when a doped hole with up spin enters a Cu site with a up localized spin in b*1g MO, it occupies an a*1g MO to align its spin in parallel with the up spin of a localized hole in the b*1g MO to form 3B1g, owing to the Hund’s coupling exchange interaction, and owing to the transfer interactions, hops to the b1g MO of a neighboring Cu site in the AF order taking antiparallel spin configuration with the localized spin. By repeating this transfer process, a doped hole itinerates in LSCO without destroying the AF order. We call this doped hole a “KS particle”.
Thus, we understand that the first-principle SCAN calculation is in good agreement with the K–S model in the tight-binding form [14,15]. Namely, in LSCO a doped hole itinerates by taking the Hund’s coupling and the spin-singlet states alternately without destroying the AF order.
4.5. Construction of Fermi Surfaces of LSCO with x = 0.125
Based on the present first-principle SCAN calculated results for x = 0.125, we construct a Fermi surface (FS) in the underdoped LSCO. In doing so, we would like to point out one problem in our supercell model. In the supercell, a size of a unit cell is wider than that of an ordinal LSCO crystal with the LTO phase. As seen in BZs for various supercell-models in Figure 5, the BZ of a supercell is obtained by folding that of a regular crystal, as shown in Figure 5. As a result, in the case of 2√2 × 2√2 model, the symmetry points Γ(0, 0), X(π,π), G1(π, 0), and Δ(π/2, π/2) gather at Γ. Thus, one may have a difficulty in assigning each calculated energy band to either of symmetry points Γ, X, G1, and Δ.
As an example, we show the calculated energy bands and DOS of LSCO with x = 0.125 in Figure 10. In this figure one may notice that there are two hole-bands above EF, and that the DOS of the second highest hole-band is very large and peaky shape. Since the peaky shape of DOS is originated from the spin-polarized band |a*1g > in Figure 7 and the spin-polarized band appears at G1(π, 0) in k space, we assign this hole band to a symmetry point G1(π, 0). On the other hand, we also pay attention to a doped hole in the highest hole-band (|b1g>) and a localized hole in the band (|b*1g>) in the energy 1 to 2 eV above EF in Figure 8b. These holes form an SS (spin-singlet) particle (see Figure 4), and contribute to the formation of Fermi arcs at the Δ point in BZ.
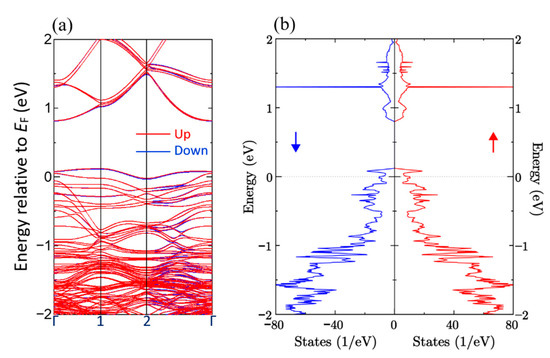
Figure 10.
Spin-dependent Non-rigid energy bands and DOS of LSCO with x = 0.125. EF is energy zero. (a) Energy bands. (b) DOS
Based on the above-mentioned results of the first-principles calculations, we construct the Fermi surface of LSCO with x = 0.125. The feature of the thus-obtained Fermi surface (FS) of LSCO with x = 0.125 in the underdoped regime is the coexistence of Fermi pockets (G1 points) and Fermi arcs (Δ points), and the KS particles occupy the Fermi pockets while the SS particles occupy the Fermi arcs, as shown in Figure 11. This feature seems consistent with the experimental results of angle-resolved photoemission spectroscopy (ARPES) for LSCO with x = 0.15 by Yoshida et al. [29].
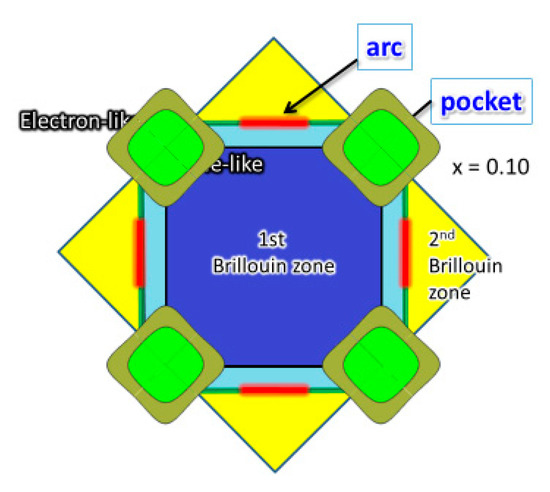
Figure 11.
Fermi surface of LSCO with x = 0.10 (the underdoped regime).
5. Final Remarks
The feature of the obtained Fermi surface (FS) of LSCO with x = 0.125 in the underdoped regime mentioned in Section 4.5 is the coexistence of Fermi pockets (G1 points) and Fermi arcs (Δ points), and the KS particles occupy the Fermi pockets while the SS particles occupy the Fermi arcs. We find that the FS for the underdoped LSCO (Figure 10) is similar to that of the K–S model [14,15], which is shown in Figure 11. This feature is likely to be consistent with the experimental results of angle-resolved photoemission spectroscopy (ARPES) for LSCO with x = 0.15 by Yoshida et al. [27]. Here, the wavefunctions of a KS particle with up and down spins, Ψk,↑(r) and Ψk,↓(r), have the unique phase relation [30],
where a is a vector connecting Cu atoms along the Cu-O-Cu line.
Ψk,↓(r) = exp (i k·a) Ψk,↑(r),
Thus, the KS particles on the Fermi pockets around G1(π, 0) points contribute to the d-wave superconductivity in the phonon mechanism below Tc [30,31,32,33] (see also [4]).
6. Conclusions
In the present paper, we have shown that the K–S model is consistent with the first-principle method of the constrained-and-appropriately normed (SCAN) density functional. Furthermore, the Fermi-surfaces of LSCO in the underdoped region obtained from the first-principle SCAN density functional method coincide with those derived from the K–S model semi-empirically, so that one may consider that the theory of d-wave superconductivity developed by the K–S model [30] is justified by the first-principles theory.
Author Contributions
All authors contributed extensively to the work presented in this paper. M.A. carried out the DFT-SCAN computations. H.K., M.A. K.S., O.S., K.I. developed the non-rigid energy-band theory of correlated electrons in cuprates, especially the spin-dependent band theory, and compared with the K–S model in the tight binding form. S.M. developed the d-wave superconductivity based on the K–S model, H.S. and J.-S.T. compared theoretical results with experiments on STM, STS, interlayer tunneling experiments in cuprates. H.K. mainly wrote the manuscript. All authors discussed the results and commented on the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
At this happy occasion of dedicating the present paper to Alex, I, Hiroshi kamimura, sincerely thank Alex for guiding me to our research on cuprates of the Jahn-Teller materials. We would like to thank Atsushi Fujimori, Kazuyoshi Yamada, Setsuo Mitsuda for their valuable discussion on experimental results. This work was supported by Tokyo University of Science. The computation was carried out in part using the computer resource offered under the category of General Projects by Research Institute for Information Technology, Kyushu University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bednorz, J.G.; Müller, K.A. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z. Phys. B 1986, 64, 189–193. [Google Scholar]
- Bednorz, J.G.; Müller, K.A. Perovskite-type oxides-the new approach to high- Tc superconductivity. Rev. Mod. Phys. 1988, 60, 585. [Google Scholar] [CrossRef]
- Anderson, P.W. Resonating valence bond state in La2CuO4 and superconductivity. Science 1987, 235, 1196–1198. [Google Scholar] [CrossRef] [PubMed]
- Kamimura, H.; Sugino, O.; Tsai, J.S.; Ushio, H. Jahn-Teller-effect induced superconductivity in copper oxides: Theoretical developments. In High-Tc Copper Oxide Superconductors and Related Novel Materials, Dedicated to Prof. K.A. Müller on the Occasion of his 90th Birthday; Bussmann-Holder, A., Keller, H., Bianconi, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Sugano, S.; Tanabe, Y.; Kamimura, H. Multiplets of Transition Metal U., and Ions in Crystals; Chapter X; Academic Press: Cambridge, MA, USA, 1970. [Google Scholar]
- Shima, N.; Shiraishi, K.; Nakayama, T.; Oshiyama, A.; Kamimura, H. Electronic structures of doped (La(1-x)Srx)2CuO4.in tetragonal phase. In Proceedings of the 1st International Conference on Electronic Materials Tokyo, June 1988: New Materials and New Physical Phenomena for Electronics of the 21st Century, Shigaku-Kaikan, Tokyo, Japan, 13–15 June 1988; Sugano, T., Chang, R.P.H., Kamimura, H., Hayashi, I., Kamiya, T., Eds.; Material Research Society: Pittsburgh, PA, USA, 1989; pp. 51–54. [Google Scholar]
- Anisimov, V.L.; Ezhov, S.Y.; Rice, T.H. Singlet and triplet hole-doped configuration in La2Cu0.5Li0.5O4. Phys. Rev. B 1997, 55, 12829–12832. [Google Scholar] [CrossRef]
- Kamimura, H.; Matsuno, S.; Mizokawa, T.; Sasaoka, K.; Shiraishi, K.; Ushio, H. On the important role of the anti-Jahn-Teller effect in underdoped cuprate superconductors. J. Phys. Conf. Ser. 2013, 428, 012043. [Google Scholar] [CrossRef]
- Egami, T.; Toby, B.H.; Billinge, S.J.L.; Janot, C.; Jorgensen, J.D.; Hinks, D.G.; Subramanian, M.A.; Crawford, M.K.; Farneth, W.E.; McCarron, E.M. Local structural anomaly at Tc observed by neutron scattering. 389. In High Temperature Superconductivity; Ashkenazi, J., Barnes, J., Vezzoli, G.C., Klein, B.M., Eds.; Springer Science + Business Media, LLC.: New York, NY, USA, 1991. [Google Scholar]
- Chen, C.T.; Tjeng, L.H.; Kwo, H.; Kao, L.; Rudolf, P.; Sette, P.; Fleming, R.M. Out-of-plane orbital characteristics of intrinsic and doped holes in La2−xSrxCuO4. Phys. Rev. Lett. 1992, 68, 2543–2546. [Google Scholar] [CrossRef] [PubMed]
- Pellegrin, E.; Nücker, N.; Fink, J.; Molodtsov, S.L.; Gutierre, A.; Navas, E.; Sterebel, O.; Hu, Z.; Domke, M.; Kaindl, G.; et al. Greene, Orbital character of states at the Fermi level in La2−xSrxCuO4 and R2−xCexCuO4 (R = Nd2Sm). Phys. Rev. B 1993, 47, 3354–3367. [Google Scholar] [CrossRef]
- Zhang, F.C.; Rice, T.M. Effective Hamiltonian for the superconducting Cu oxides. Phys. Rev. B 1988, 37, 3759–3761. [Google Scholar] [CrossRef]
- Norman, M.R.; Kanigel, A.; Randeria, M.; Chtterjee, M.; Campuzano, J.C. Modeling the Fermi arc in underdoped cuprates. Phys. Rev. B 2007, 76, 174501. [Google Scholar] [CrossRef]
- Kamimura, H.; Suwa, Y. New theoretical view for high temperature superconductivity. J. Phys. Soc. Jpn. 1993, 62, 3368–3371. [Google Scholar] [CrossRef]
- Kamimura, H.; Hamada, T.; Ushio, H. Theoretical exploration of electronic structure in cuprates from electronic entropy. Phys. Rev. B 2002, 66, 054504. [Google Scholar] [CrossRef]
- Kamimura, H.; Eto, M. 1A1g to 3B1g Conversion at the onset of superconductivity in La2−xSrxCuO4 due to the apical oxygen effect. J. Phys. Soc. Jpn. 1990, 59, 3053–3056. [Google Scholar] [CrossRef]
- Kamimura, H.; Ushio, H.; Matusno, S.; Hamada, T. Theory of Copper Oxide Superconductors; Chapter 8.3; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Kamimura, H.; Sugino, O.; Shiraishi, K.; Araidai, M.; Tsai, J.S.; Sakata, H.; Ishida, K.; Matsuno, S. A First-Principles Non-Rigid Band Theory of Correlated Electrons in Copper Oxide Superconductors. 2020; In Preparation. [Google Scholar]
- Furness, J.W.; Zhang, Y.; Lane, C.; Buda, I.G.; Barbielini, B.; Markiewicz, R.S.; Bansil, A.; Sun, J. An accurate first-principles treatment of doping-dependent electronic structure of high-temperature cuprate superconductors. Commun. Phys. 2018, 1, 11. [Google Scholar] [CrossRef]
- Vaknin, D.; Sinha, S.K.; Moncton, D.E.; Johnson, D.C.; Newsam, J.; Safinya, C.R.; King, H. Antiferromagnetism in La2CuO4-γ. Phys. Rev. Lett. 1996, 77, 723–726. [Google Scholar]
- Freltoft, T.; Shirane, G.; Mitsuda, S.; Remeika, J.P.; Cooper, A.S. Magnetic form factor of Cu in La2CuO4. Phys. Rev. B 1988, 37, 137. [Google Scholar] [CrossRef] [PubMed]
- Yamada, K.; Lee, C.H.; Wada, J.; Kurahashi, K.; Kimura, H.; Endoh, Y.; Hosoya, S.; Shirane, G.; Birgeneau, R.J.; Kastner, M.A. Spatial modulation of low-frequency spin-fluctuation in hole-doped La2CuO4. J. Supercond. 1997, 10, 343. [Google Scholar] [CrossRef]
- Zhang, Y.; Lane, C.; Furness, J.W.; Barbiellini, B.; Perdew, J.P.; Markiewicz, R.S.; Bansil, A.; Suna, J. Competing stripe and magnetic phases in the cuprates from first principles. Proc. Nat. Acad. Sci. USA 2020, 117, 68. [Google Scholar] [CrossRef]
- Slater, J.C. The Ferromagnetism of Nickel. Phys. Rev. 1936, 49, 537. [Google Scholar] [CrossRef]
- Connolly, J.W. Energy bands in ferromagnetic nickel. Phys. Rev. 1967, 159, 415. [Google Scholar] [CrossRef]
- Műller, K.A. Large, small, and especially jahn-teller polarons. J. Supercond. 1999, 12, 3. [Google Scholar] [CrossRef]
- Shengelaya, A.; Zhao, G.M.; Keller, H.; Műller, K.A. EPR evidence of Jahn-Teller polaron formation in La1-xCaxMnO3+y. Phys. Rev. Lett. 1996, 77, 5296. [Google Scholar] [CrossRef]
- Lanzara, A.; Saini, N.L.; Brunelnelli, M.; Natali, F.; Bianconi, A.; Radaelli, P.G.; Cheong, S.W. Crossover from large to small polarons across the metal-insulator transition in manganites. Phys. Rev. Lett. 1998, 81, 878. [Google Scholar] [CrossRef]
- Yoshida, T.; Zhou, X.J.; Tanaka, K.; Yang, W.L.; Hussain, Z.; Shen, Z.-X.; Fujimori, A.; Sahrakorpi, S.; Lindroos, M.; Markiewicz, R.S.; et al. Systematic doping evolution off underlying Fermi surface of La2−xSrxCuO4. Phys. Rev. B 2006, 74, 224510. [Google Scholar] [CrossRef]
- Kamimura, H.; Matsuno, S.; Suwa, Y.; Ushio, H. Occurrence of d-wave pairing in the phonon-mediated mechanism of high temperature superconductivity in cuprates. Phys. Rev. Lett. 1996, 77, 723. [Google Scholar] [CrossRef] [PubMed]
- Tsuei, C.C.; Kirtley, J.R. Pairing symmetry in cuprate superconductors. Rev. Mod. Phys. 2000, 72, 969–1016. [Google Scholar] [CrossRef]
- Takagi, H.; Ido, T.; Ishibashi, S.; Uota, M.; Uchida, S.; Tokura, Y. Superconductor-to-nonsuperconductor transition in (La1-xSrx)2CuO4 as investigated by transport and magnetic measurements. Phys. Rev. B 1989, 40, 2254. [Google Scholar] [CrossRef] [PubMed]
- Kamimura, H.; Ushio, H. On the Interplay of Jahn-Teller Physics and Mott Physics leading to the occurrence of Fermi pockets without pseudogap hypothesis and d-wave high Tc superconductivity in underdoped cuprate superconductivity. J. Supercond. Nov. Magn. 2012, 25, 677. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).