Evolution of Spin-Orbital Entanglement with Increasing Ising Spin-Orbit Coupling
Abstract
1. Introduction
2. The Model and Basic Questions
3. Methods
3.1. Entanglement Entropy and Correlation Functions
3.2. Effective Hamiltonian in the Large Limit
4. Results and Discussion
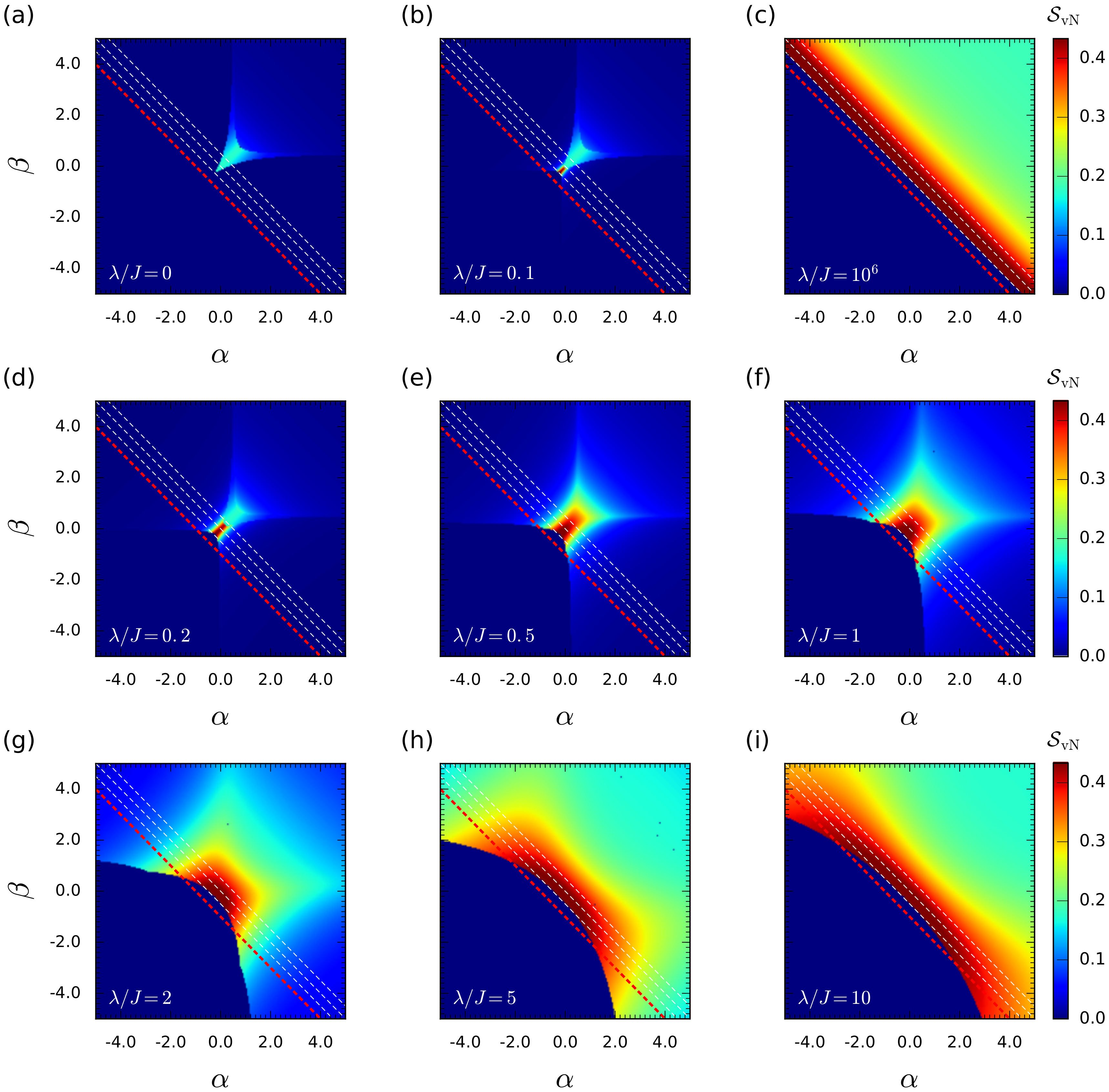
4.1. Gradual Evolution of Spin-Orbital Entanglement with Increasing Ising Spin-Orbit Coupling
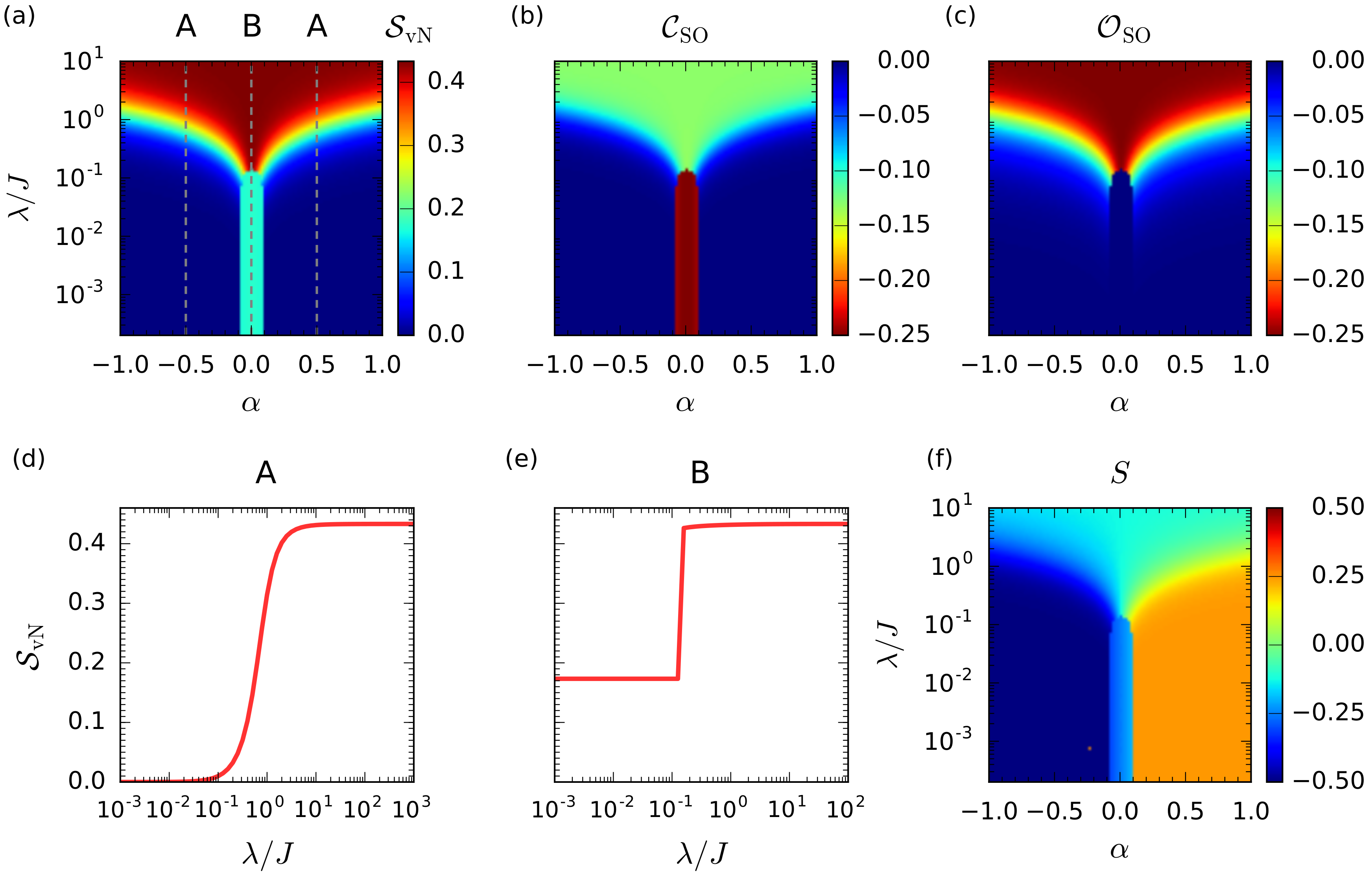
4.2. Entanglement Evolution for the Quantum Phases along the Line
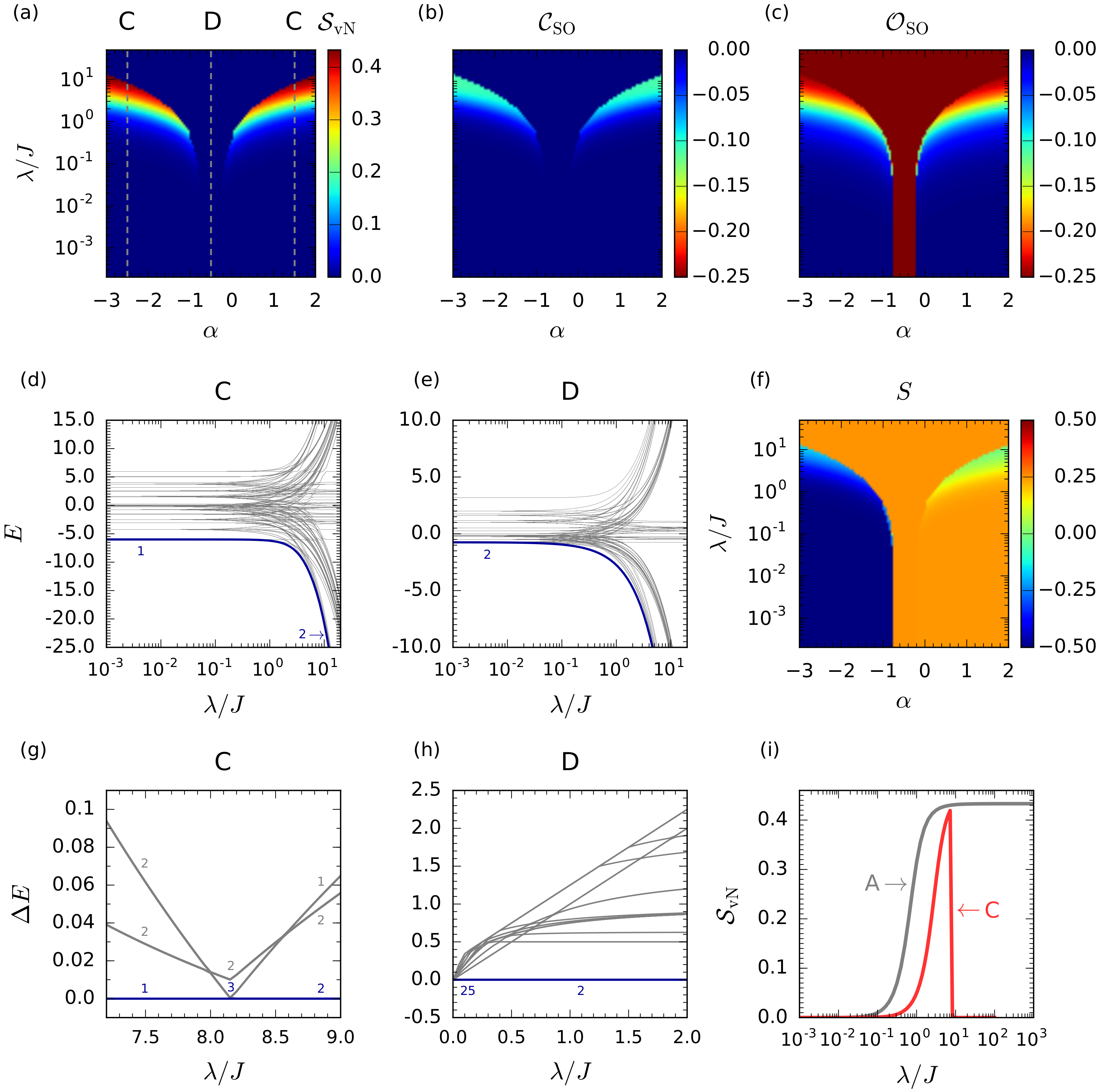
4.3. Entanglement Evolution for the Quantum Phases along the Line
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gotfryd, D.; Pärschke, E.M.; Chaloupka, J.; Oleś, A.M.; Wohlfeld, K. How spin-orbital entanglement depends on the spin-orbit coupling in a Mott insulator. Phys. Rev. Res. 2020, 2, 013353. [Google Scholar] [CrossRef]
- Bentsson, I.; Zyczkowski, K. Geometry of Quantum States: An Introduction to Quantum Entanglement; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Oleś, A.M.; Horsch, P.; Feiner, L.F.; Khaliullin, G. Spin-Orbital Entanglement and Violation of the Goodenough-Kanamori Rules. Phys. Rev. Lett. 2006, 96, 147205. [Google Scholar] [CrossRef] [PubMed]
- Kugel, K.I.; Khomskii, D.I. Jahn-Teller Effect and Magnetism: Transition Metal Compounds. Usp. Fiz. Nauk 1982, 25, 621–664. [Google Scholar] [CrossRef]
- Feiner, L.F.; Oleś, A.M.; Zaanen, J. Quantum Melting of Magnetic Order due to Orbital Fluctuations. Phys. Rev. Lett. 1997, 78, 2799–2802. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Z.D.; Li, Y.Q.; Zhang, F.C. Spin-orbital entanglement and quantum phase transitions in a spin-orbital chain with SU(2)×SU(2) symmetry. Phys. Rev. B 2007, 75, 195113. [Google Scholar] [CrossRef]
- Brzezicki, W.; Dziarmaga, J.; Oleś, A.M. Noncollinear Magnetic Order Stabilized by Entangled Spin-Orbital Fluctuations. Phys. Rev. Lett. 2012, 109, 237201. [Google Scholar] [CrossRef]
- You, W.-L.; Horsch, P.; Oleś, A.M. Entanglement driven Phase Transitions in Spin-Orbital Models. New J. Phys. 2015, 17, 083009. [Google Scholar] [CrossRef]
- Snamina, M.; Oleś, A.M. Magnon Dressing by Orbital Excitations in Ferromagnetic Planes of K2CuF4 and LaMnO3. New J. Phys. 2019, 21, 023018. [Google Scholar] [CrossRef]
- Jackeli, G.; Khaliullin, G. Mott Insulators in the Strong Spin-Orbit Coupling Limit: From Heisenberg to a Quantum Compass and Kitaev Models. Phys. Rev. Lett. 2009, 102, 017205. [Google Scholar] [CrossRef]
- Khaliullin, G.; Maekawa, S. Orbital Liquid in Three-Dimensional Mott Insulator: LaTiO3. Phys. Rev. Lett. 2000, 85, 3950–3953. [Google Scholar] [CrossRef]
- Normand, B.; Oleś, A.M. Frustration and Entanglement in the t2g Spin–Orbital Model on a Triangular Lattice: Valence–Bond and Generalized Liquid States. Phys. Rev. B 2008, 78, 094427. [Google Scholar] [CrossRef]
- Normand, B. Multicolored quantum dimer models, resonating valence-bond states, color visons, and the triangular-lattice t2g spin-orbital system. Phys. Rev. B 2011, 83, 064413. [Google Scholar] [CrossRef]
- Chaloupka, J.; Oleś, A.M. Spin-Orbital Resonating Valence-Bond Liquid on a Triangular Lattice: Evidence from Finite Cluster Diagonalization. Phys. Rev. B 2011, 83, 094406. [Google Scholar] [CrossRef]
- Brzezicki, W.; Dziarmaga, J.; Oleś, A.M. Topological Order in an Entangled SU(2)⊗XY Spin-Orbital Ring. Phys. Rev. Lett. 2014, 112, 117204. [Google Scholar] [CrossRef] [PubMed]
- Chaloupka, J.; Khaliullin, G. Orbital Order and Possible Superconductivity in LaNiO3/LaMO3 Superlattices. Phys. Rev. Lett. 2008, 100, 016404. [Google Scholar] [CrossRef]
- Miyasaka, S.; Okimoto, Y.; Tokura, Y. Anisotropy of Mott-Hubbard Gap Transitions due to Spin and Orbital Ordering in LaVO3 and YVO3. J. Phys. Soc. Jpn. 2002, 71, 2086–2089. [Google Scholar] [CrossRef]
- Khaliullin, G.; Horsch, P.; Oleś, A.M. Theory of Optical Spectral Weights in Mott Insulators with Orbital Degrees of Freedom. Phys. Rev. B 2004, 70, 195103. [Google Scholar] [CrossRef]
- Kovaleva, N.N.; Oleś, A.M.; Balbashov, A.M.; Maljuk, A.; Argyriou, D.N.; Khaliullin, G.; Keimer, B. Low-energy Mott-Hubbard excitations in LaMnO3 probed by optical ellipsometry. Phys. Rev. B 2010, 81, 235130. [Google Scholar] [CrossRef]
- Laurita, N.J.; Deisenhofer, J.; Pan, L.-D.; Morris, C.M.; Schmidt, M.; Johnsson, M.; Tsurkan, V.; Loidl, A.; Armitage, N.P. Singlet-Triplet Excitations and Long-Range Entanglement in the Spin-Orbital Liquid Candidate FeSc2S4. Phys. Rev. Lett. 2015, 114, 207201. [Google Scholar] [CrossRef]
- Man, H.Y.; Halim, M.; Sawa, H.; Hagiwara, M.; Wakabayashi, Y.; Nakatsuji, S. Spin-orbital entangled liquid state in the copper oxide Ba3CuSb2O9. J. Phys. Condens. Matter 2018, 30, 443002. [Google Scholar] [CrossRef]
- Becker, M.; Hermanns, M.; Bauer, B.; Garst, M.; Trebst, S. Spin-orbit physics of j = 1/2 Mott insulators on the triangular lattice. Phys. Rev. B 2015, 91, 155133. [Google Scholar] [CrossRef]
- Hermanns, M.; Kimchi, I.; Knolle, J. Physics of the Kitaev Model: Fractionalization, Dynamic Correlations, and Material Connections. Ann. Rev. Cond. Mat. Phys. 2018, 9, 17–33. [Google Scholar] [CrossRef]
- Rusnačko, J.; Gotfryd, D.; Chaloupka, J. Kitaev-like Honeycomb Magnets: Global Phase Behavior and Emerging Effective Models. Phys. Rev. B 2019, 99, 064425. [Google Scholar] [CrossRef]
- Natori, W.M.H.; Knolle, J. Dynamics of a Two-Dimensional Quantum Spin-Orbital Liquid: Spectroscopic Signatures of Fermionic Magnons. Phys. Rev. Lett. 2020, 125, 067201. [Google Scholar] [CrossRef]
- Takagi, H.; Takayama, T.; Jackeli, G.; Khaliullin, G.; Nagler, S.E. Concept and realization of Kitaev quantum spin liquids. Nat. Rev. Phys. 2019, 1, 264–280. [Google Scholar] [CrossRef]
- Ulrich, C.; Khaliullin, G.; Sirker, J.; Reehuis, M.; Ohl, M.; Miyasaka, S.; Tokura, Y.; Keimer, B. Magnetic Neutron Scattering Study of YVO3: Evidence for an Orbital Peierls State. Phys. Rev. Lett. 2003, 91, 257202. [Google Scholar] [CrossRef]
- Sirker, J.; Herzog, A.; Oleś, A.M.; Horsch, P. Thermally Activated Peierls Dimerization in Ferromagnetic Spin Chains. Phys. Rev. Lett. 2008, 101, 157204. [Google Scholar] [CrossRef]
- Horsch, P.; Oleś, A.M.; Feiner, L.F.; Khaliullin, G. Evolution of Spin-Orbital-Lattice Coupling in the RVO3 Perovskites. Phys. Rev. Lett. 2008, 100, 167205. [Google Scholar] [CrossRef]
- Fujioka, J.; Yasue, T.; Miyasaka, S.; Yamasaki, Y.; Arima, T.; Sagayama, H.; Inami, T.; Ishii, K.; Tokura, Y. Critical competition between two distinct orbital-spin ordered states in perovskite vanadates. Phys. Rev. B 2010, 82, 144425. [Google Scholar] [CrossRef]
- Yan, J.-Q.; Tian, W.; Cao, H.B.; Chi, S.; Ye, F.; Llobet, A.; Puretzky, A.; Chen, Q.; Ma, J.; Ren, Y.; et al. Lattice distortion in the spin-orbital entangled state in RVO3 perovskites. Phys. Rev. B 2019, 100, 184423. [Google Scholar] [CrossRef]
- Chen, C.C.; van Veenendaal, M.; Devereaux, T.P.; Wohlfeld, K. Fractionalization, entanglement, and separation: Understanding the collective excitations in a spin-orbital chain. Phys. Rev. B 2015, 91, 165102. [Google Scholar] [CrossRef]
- Ronquillo, D.C.; Vengal, A.; Trivedi, N. Signatures of magnetic-field-driven quantum phase transitions in the entanglement entropy and spin dynamics of the Kitaev honeycomb model. Phys. Rev. B 2019, 99, 140413. [Google Scholar] [CrossRef]
- Daghofer, M.; Oleś, A.M.; von der Linden, W. Orbital Polarons versus Itinerant eg Electrons in Doped Manganites. Phys. Rev. B 2004, 70, 184430. [Google Scholar] [CrossRef]
- Avella, A.; Oleś, A.M.; Horsch, P. Defect-Induced Orbital Polarization and Collapse of Orbital Order in Doped Vanadium Perovskites. Phys. Rev. Lett. 2019, 122, 127206. [Google Scholar] [CrossRef]
- Yaji, K.; Kuroda, K.; Toyohisa, S.; Harasawa, A.; Ishida, Y.; Watanabe, S.; Chen, C.T.; Kobayashi, K.; Komori, F.; Shin, S. Spin-dependent quantum interference in photoemission process from spin-orbit coupled states. Nat. Commun. 2017, 8, 14588. [Google Scholar] [CrossRef]
- Oleś, A.M. Fingerprints of Spin-Orbital Entanglement in Transition Metal Oxides. J. Phys. Condens. Matter 2012, 24, 313201. [Google Scholar] [CrossRef]
- Brzezicki, W. Spin, orbital and topological order in models of strongly correlated electrons. J. Phys. Condens Matter 2020, 32, 023001. [Google Scholar] [CrossRef]
- Witczak-Krempa, W.; Chen, G.; Kim, Y.B.; Balents, L. Correlated Quantum Phenomena in the Strong Spin-Orbit Regime. Ann. Rev. Cond. Mat. Phys. 2014, 5, 58–82. [Google Scholar] [CrossRef]
- Bianconi, A. Superstripes and complexity in High-Temperature Superconductors. J. Supercond. Nov. Magn. 2014, 27, 909–912. [Google Scholar] [CrossRef]
- Keimer, B.; Kivelson, S.A.; Norman, M.R.; Uchida, S.; Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 2015, 518, 179–186. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A. High-Temperature Superconductivity in a Hyperbolic Geometry of Complex Matter from Nanoscale to Mesoscopic Scale. J. Supercond. Nov. Magn. 2016, 29, 627–631. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Kohler, J.; Simon, A.; Whangbo, M.-H.; Bianconi, A.; Perali, A. The Road Map toward Room-Temperature Superconductivity: Manipulating Different Pairing Channels in Systems Composed of Multiple Electronic Components. Condens. Matter 2017, 2, 24. [Google Scholar] [CrossRef]
- Bianconi, A. Lifshitz Transitions in Multi-band Hubbard Models for Topological Superconductivity in Complex Quantum Matter. J. Supercond. Novel Magn. 2018, 31, 603–610. [Google Scholar] [CrossRef]
- Khomskii, D.I. Transition Metal Compounds; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Pati, S.K.; Singh, R.R.P.; Khomskii, D.I. Alternating Spin and Orbital Dimerization and Spin-Gap Formation in Coupled Spin-Orbital Systems. Phys. Rev. Lett. 1998, 81, 5406–5409. [Google Scholar] [CrossRef]
- Itoi, C.; Qin, S.; Affleck, I. Phase diagram of a one-dimensional spin-orbital model. Phys. Rev. B 2000, 61, 6747. [Google Scholar] [CrossRef]
- Lundgren, R.; Chua, V.; Fiete, G.A. Entanglement entropy and spectra of the one-dimensional Kugel–Khomskii model. Phys. Rev. B 2012, 86, 224422. [Google Scholar] [CrossRef]
- Kugel, K.I.; Khomskii, D.I.; Sboychakov, A.O.; Streltsov, S.V. Spin-orbital interaction for face-sharing octahedra: Realization of a highly symmetric SU(4) model. Phys. Rev. B 2015, 91, 155125. [Google Scholar] [CrossRef]
- Valiulin, V.E.; Mikheyenkov, A.V.; Kugel, K.I.; Barabanov, A.F. Thermodynamics of Symmetric Spin-Orbital Model: One- and Two-Dimensional Cases. JETP Lett. 2019, 109, 546–551. [Google Scholar] [CrossRef]
- Horsch, P.; Khaliullin, G.; Oleś, A.M. Dimerization versus Orbital Moment Ordering in a Mott Insulator YVO3. Phys. Rev. Lett. 2003, 91, 257203. [Google Scholar] [CrossRef]
- Solovyev, V.I. Spin-orbital superexchange physics emerging from interacting oxygen molecules in KO2. New J. Phys. 2008, 10, 013035. [Google Scholar] [CrossRef]
- Veenstra, C.N.; Zhu, Z.-H.; Raichle, M.; Ludbrook, B.M.; Nicolaou, A.; Slomski, B.; Landolt, G.; Kittaka, S.; Maeno, Y.; Dil, J.H.; et al. Spin-Orbital Entanglement and the Breakdown of Singlets and Triplets in Sr2RuO4 Revealed by Spin- and Angle-Resolved Photoemission Spectroscopy. Phys. Rev. Lett. 2014, 112, 127002. [Google Scholar] [CrossRef] [PubMed]
- Bahr, S.; Alfonsov, A.; Jackeli, G.; Khaliullin, G.; Matsumoto, A.; Takayama, T.; Takagi, H.; Büchner, B.; Kataev, V. Low-energy magnetic excitations in the spin-orbital Mott insulator Sr2IrO4. Phys. Rev. B 2014, 89, 180401(R). [Google Scholar] [CrossRef]
- Zhang, G.; Gorelov, E.; Sarvestani, E.; Pavarini, E. Fermi Surface of Sr2RuO4: Spin-Orbit and Anisotropic Coulomb Interaction Effects. Phys. Rev. Lett. 2016, 116, 106402. [Google Scholar] [CrossRef]
- Oleś, A.M.; Wohlfeld, K.; Khaliullin, G. Orbital Symmetry and Orbital Excitations in High-Tc Superconductors. Condens. Matter 2019, 4, 46. [Google Scholar] [CrossRef]
- Khaliullin, G. Excitonic Magnetism in Van Vleck-type d4 Mott Insulators. Phys. Rev. Lett. 2013, 111, 197201. [Google Scholar] [CrossRef]
- Souliou, S.-M.; Chaloupka, J.; Khaliullin, G.; Ryu, G.; Jain, A.; Kim, B.J.; Le Tacon, M.; Keimer, B. Raman scattering from Higgs mode oscillations in the two-dimensional antiferromagnet Ca2RuO4. Phys. Rev. Lett. 2017, 119, 067201. [Google Scholar] [CrossRef] [PubMed]
- Svoboda, C.; Randeria, M.; Trivedi, N. Effective magnetic interactions in spin-orbit coupled d4 Mott insulators. Phys. Rev. B 2017, 95, 014409. [Google Scholar] [CrossRef]
- Li, F.-Y.; Chan, G. Spin-orbital entanglement in d8 Mott insulators: Possible excitonic magnetism in diamond lattice antiferromagnets. Phys. Rev. B 2019, 100, 045103. [Google Scholar] [CrossRef]
- Chaloupka, J.; Khaliullin, G. Highly frustrated magnetism in relativistic d4 Mott insulators: Bosonic analog of the Kitaev honeycomb model. Phys. Rev. B 2019, 100, 224413. [Google Scholar] [CrossRef]
- Pärschke, E.M.; Wohlfeld, K.; Foyevtsova, K.; van den Brink, J. Correlation induced electron-hole asymmetry in quasi- two-dimensional iridates. Nat. Commun. 2017, 8, 686. [Google Scholar] [CrossRef] [PubMed]
- Kim, C.H.; Baidya, S.; Cho, H.; Gapontsev, V.V.; Streltsov, S.V.; Khomskii, D.I.; Park, J.-G.; Go, A.; Jin, H. Theoretical evidence of spin-orbital-entangled Jeff=12 state in the 3d transition metal oxide CuAl2O4. Phys. Rev. B 2019, 100, 161104. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gotfryd, D.; Pärschke, E.; Wohlfeld, K.; Oleś, A.M. Evolution of Spin-Orbital Entanglement with Increasing Ising Spin-Orbit Coupling. Condens. Matter 2020, 5, 53. https://doi.org/10.3390/condmat5030053
Gotfryd D, Pärschke E, Wohlfeld K, Oleś AM. Evolution of Spin-Orbital Entanglement with Increasing Ising Spin-Orbit Coupling. Condensed Matter. 2020; 5(3):53. https://doi.org/10.3390/condmat5030053
Chicago/Turabian StyleGotfryd, Dorota, Ekaterina Pärschke, Krzysztof Wohlfeld, and Andrzej M. Oleś. 2020. "Evolution of Spin-Orbital Entanglement with Increasing Ising Spin-Orbit Coupling" Condensed Matter 5, no. 3: 53. https://doi.org/10.3390/condmat5030053
APA StyleGotfryd, D., Pärschke, E., Wohlfeld, K., & Oleś, A. M. (2020). Evolution of Spin-Orbital Entanglement with Increasing Ising Spin-Orbit Coupling. Condensed Matter, 5(3), 53. https://doi.org/10.3390/condmat5030053






