Superfluid Properties of Superconductors with Disorder at the Nanoscale: A Random Impedance Model

Abstract

Some two-dimensional superconductors like, e.g., LaAlO${}_3$/SrTiO${}_3$ heterostructures or thin films of transition metal dichalcogenides, display peculiar properties that can be understood in terms of electron inhomogeneity at the nanoscale. In this framework, unusual features of the metal-superconductor transition have been interpreted as due to percolative effects within a network of superconducting regions embedded in a metallic matrix. In this work we use a mean-field-like effective medium approach to investigate the superconducting phase below the critical temperature $T_c$ at which the resistivity vanishes. Specifically, we consider the finite frequency impedance of the system to extract the dissipative part of the conductance and the superfluid stiffness in the superconducting state. Intriguing effects arise from the metallic character of the embedding matrix: upon decreasing the temperature below $T_c$ proximity effects may rapidly increase the superfluid stiffness. Then, a rather fragile superconducting state, living on a filamentary network just below $T_c$, can be substantially consolidated by additional superconducting regions induced by proximity effect in the interstitial metallic regions. This mean-field prediction should call for further theoretical analyses and trigger experimental investigations of the superconducting properties of the above systems.

1. Introduction

In recent years, a growing interest in the study of two-dimensional (2D) electron systems has been registered [1]. The new experimental achievements have indeed paved the way for the study of new ideal 2D systems ranging from monolayer graphene, to transition metal dichalcogenides (TMD), or SrTiO${}_3$-based oxide interfaces like LaAlO${}_3$/SrTiO${}_3$. Quite interestingly, the experimental measurements carried out on these compounds have revealed unexpected physical characteristics. Among the open and more controversial issues, there is the emergence of a low-temperature metallic state, called quantum metal: by decreasing the temperature, the resistivity undergoes a superconductivity-driven drop, but it does not vanish and reaches a plateau saturating at a finite value down to the lowest accessible temperatures [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. Even when no low-temperature saturation of the resistance is observed, the resistance curves $R\left(T\right)$ show a peculiar behavior as a function of the temperature T. Under certain conditions, as it can be an applied magnetic field (for graphene) or an ionic-liquid gating (for TMD), the superconducting transition appears to be very broad, i.e., much broader than one would expected by taking into account only standard superconductive fluctuations [17,18]. 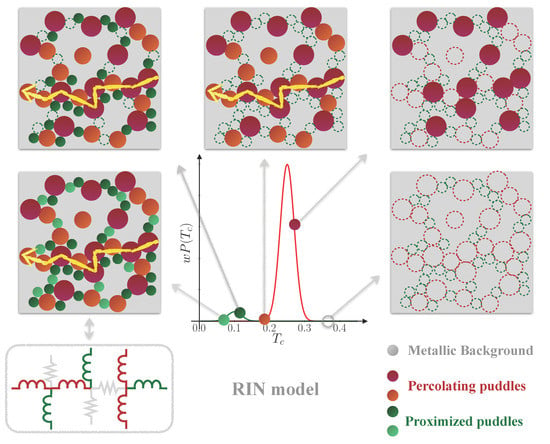At the same time, $R\left(T\right)$ displays a tailish shape with a very slow vanishing in the low-temperature regime. This behavior also occurs in the absence of magnetic fields and therefore it can hardly be interpreted in terms of standard vortex dissipation. So far, these anomalous features have been successfully reproduced considering the presence of an electron inhomogeneity [19,20,21,22,23,24]. For instance, it has been shown [24] that most of the phenomenology of TMD can be captured by considering superconducting puddles with random critical temperature $T_c$, embedded in a metallic matrrix. Lowering the temperature, one would indeed observe a downturn of the resistance, due to the progressive nucleation of superconducting puddles, followed by a low-temperature saturation, if the overall fraction of superconducting puddles is not large enough to give rise to a percolating superconducting path. In this perspective, the enigmatic quantum metal finds a simpler mundane explanation as a non-percolating randomly distributed superconducting network embedded in a metallic matrix. The $R\left(T\right)$ tailish behavior in the low-temperature regime seems to be a consequence of the filamentary character of the superconducting network connecting the puddles, with a weak long-distance connectivity [20].

Therefore, the above peculiar transport properties of the normal state of several 2D superconductors have been interpreted in terms of randomly distributed nano-sized superconducting regions embedded in a normal metallic matrix. This scenario has been successfully described by means of a 2D random resistor network (RRN) model [19,20,21,22,24]. The question then naturally arises whenever the same inhomogeneous state induces unusual properties in the superconducting state and whether their interpretation can rest on the same theoretical scenario and modeling. In particular, properties specifically related to the superconducting phase, like, e.g., the optical conductivity $\sigma \left(\omega \right)$ and the superfluid stiffness $J_s$, should reflect the inhomogeneous character of these 2D superconductors. Indeed, this seems to be the case in LaAlO${}_3$/SrTiO${}_3$, where an anomalous behavior of the superfluid stiffness has been measured at low temperature by gate-induced variations of the electron density [25].

In the present work, we present a first theoretical investigation of the temperature dependence of $\sigma \left(\omega \right)$ and $J_s$ at finite frequencies in the range of a few GHz, for an inhomogeneous electron state mixing metallic and superconducting regions. Specifically, we will study a spatially uncorrelated inhomogeneous system, investigating the changes in superfluid stiffness and in dissipation due to the broadening of the superconducting regions induced by proximity effects in the embedding metallic matrix. To this purpose, we will thus consider a random impedance network (RIN) at finite frequency, solving the model within the effective medium theory (EMT) [26,27]. Although this approach neglects the spatial structure of the inhomogeneity, which has been essential to capture the low-temperature tail of $R\left(T\right)$, it still provides very useful insights in the temperature dependence of $\sigma \left(\omega \right)$ and $J_s$. In particular, one should remember that the matrix embedding the superconducting cluster has a metallic character (this is a major difference with respect to, e.g., granular superconducting systems). Therefore when the temperature T is lowered, it can partially become superconducting by proximity effects. Then, upon lowering the temperature, the filamentary structure of the superconducting network can become thicker because of proximization processes. Therefore, by introducing a second class of superconducting bonds, which enter into play at lower temperature as a result of proximization processes, one can find some new qualitative features as the reduction (or, conversely, the increase) of the zero-temperature value of the dissipative (real) part of the optical conductivity or a two-step trend of the superfluid stiffness, closely reminiscent of features in the superfluid stiffness recently observed in LaAlO${}_3$/SrTiO${}_3$ heterostructures [28].

The paper is organized as follows. In Section 2, we will briefly review the RRN model in the EMT approximation. In Section 3, we will introduce the RIN model and in Section 4, we will comment on the results obtained solving the EMT equations. Finally, in Section 5 we will discuss the main conclusions of this study and some perspectives.

2. The RRN Model

In previous works (see, e.g., Ref. [24]), the presence of an electron nanoscale inhomogeneity in 2D superconductors was inferred, and the system was described, at a coarse-grained level, as a 2D random resistor network (RRN). This network is realized as a 2D square lattice, with random resistors located on all bonds of the lattice. A critical temperature $T_c^i$ is assigned to each resistor $R^i$ according to a given probability distribution. By lowering the external temperature T, the resistors will then switch off to their superconducting state ($R^i=0$) as soon as the condition $T\le T_c^i$ is verified:

$$R^i=\left\{\begin{array}{cc}{R}_N,\hfill & ifT>T_c^i,\hfill \\ 0,\hfill & ifT\le T_c^i,\hfill \end{array}\right.$$

(1)

where $R_N$ is the experimental resistance per square of the 2D material in the high-temperature regime. In order to model the inhomogeneities, two different kind of resistors are considered: a first kind of metallic (m) resistors, that will maintain their finite resistance $R^i=R_N$ down to $T=0$ K, i.e., with local critical temperature $T_c^i\le 0$, and a second kind of resistors that will instead become superconducting (s) at a finite $T_c^i$, randomly distributed across the sample. Since it was previously shown that different distributions give rise to qualitatively similar physical properties [20], for the sake of definiteness and simplicity, the probability density distributions of the local critical temperatures $T_c^i$ for the superconducting fraction is taken as Gaussian

$$P_s\left(T_c^i\right)=\frac{w_s}{\sqrt{2\pi }{\sigma }_s}exp\left[-\frac{{(T_c^i-{\mu }_{c,s})}^2}{2{\sigma }_s^2}\right]$$

(2)

where the subscript s indicates that this distribution refers to the superconducting fraction. The total weight of the distribution corresponds to the maximum fraction $w_s$ that can become superconducting. A fraction $w_m=1-w_s$ of the system will always stay metallic, down to $T=0$ K.

In the simplest case of the EMT approximation [27], the effective resistance per square of the 2D system $R_{em}$ is given by the solution of the following self-consistent equation [26]

$$\sum _{j=m.s}{\tilde{w}}_j\left(T\right)\frac{R_j-R_{em}}{R_j+R_{em}}=0$$

(3)

where ${\tilde{w}}_s\left(T\right)={\int }_T^{+\infty }\mathrm{d}{T}_c{P}_s\left(T_c\right)$, unlike the constant parameter $w_s$, is a function of the temperature, and represents the fraction of superconducting bonds at a temperature T [evidently, $0\le {\tilde{w}}_s\left(T\right)\le w_s$], while ${\tilde{w}}_m\left(T\right)=1-{\tilde{w}}_s\left(T\right)$ is the metallic fraction at the same temperature (see Appendix A for details). Since $R_m=R_N$ and $R_s=0$, the solution of Equation (3) can be found analytically [21,27] and takes the form:

$$\frac{R_{em}\left(T\right)}{R_N}=\theta \left[w_s\mathrm{erf}\left(\frac{T-{\mu }_{c,s}}{\sqrt{2}{\sigma }_s}\right)+1-w_s\right],$$

where $\theta (·)$ is the Heaviside step function and erf $(·)$ is the error function. The Gaussian distribution, Equation (2), sets the broadening of the transition and the downturn of $R_{em}$, and reproduces the tail at low temperatures. Most importantly, the parameter $w_s$ rules the percolation of the superconducting cluster. 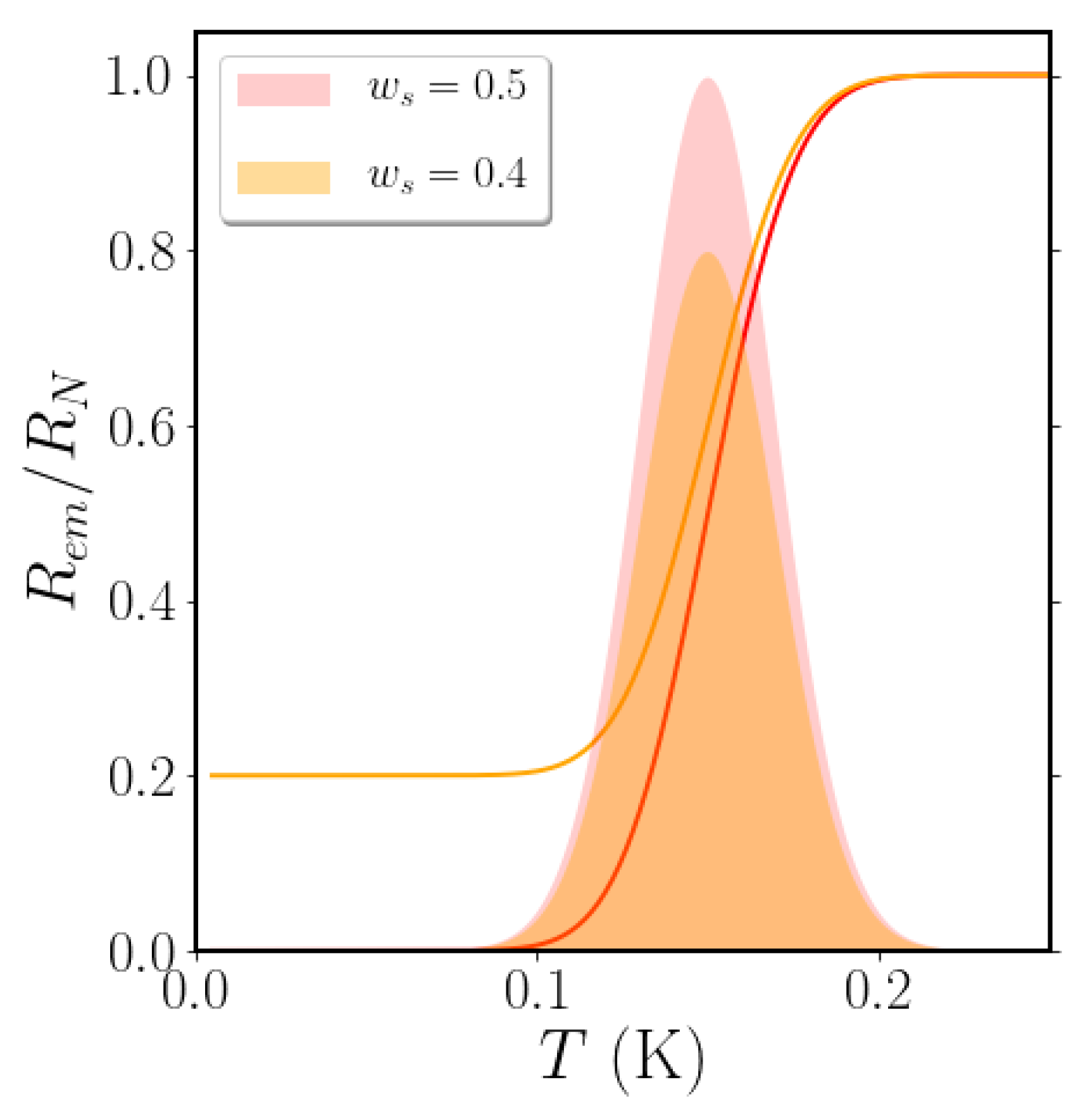Being $w^p\equiv 0.5$ the percolation (hence, the superscript p) threshold for a homogeneous distribution of superconducting puddles, for each $w_s<w^p$ the effective resistance will saturate to a finite value in the limit $T\to 0$ K (orange curve and yellow shaded area in Figure 1).

In what follows, for the sake of definiteness, we will devote our analysis to the weakly percolating case and fix $w_s=0.5$, i.e., the minimum value of the superconducting fraction needed to have a percolating superconducting cluster in the EMT approximation. For this particular choice (red curve and pink shaded area in Figure 1), the decrease of $R_{em}$ will correspond, qualitatively, to the decrease of the left-side of the Gaussian distribution: once the first resistors are switched off, $R_{em}$ starts to decrease, vanishing when half of the resistors become superconducting.

Despite the fact that the EMT neglects all spatial structures, still it can give important insights about the main ingredients at play, like for instance the appearance of the zero-temperature metallic state as a result of the lack of percolation.

However, the RRN model as it is presented here is apt to describe the phenomenology of transport measurements above the critical temperature $T_c$, defined as the percolating temperature corresponding to $R\left(T_c\right)=0$. What remain unsolved are the properties below $T_c$. To have access to quantities such as the optical conductivity in the superconducting state or the superfluid stiffness, the model has to be extended to consider finite frequencies $\omega$. The local resistors must hence be replaced by complex impedances, so that the resulting model may be dubbed as RIN model.

3. The RIN Model

In the RIN model, the conditions for the local resistors in Equation (1) translate into conditions for the local impedances $z_i$ at finite frequency $\omega$:

$$z^i=\left\{\begin{array}{cc}{R}_N+\mathrm{i}\omega L^i,\hfill & ifT>T_c^i,\hfill \\ \mathrm{i}\omega L^i,\hfill & ifT\le T_c^i,\hfill \end{array}\right.$$

the local inductance $L^i$ being the new ingredient at play: it rules the purely reactive AC electromagnetic response of a superconducting puddle below its local critical temperature. In analogy with the RRN model presented in the previous section, we consider the value of $L^i$ as a real constant, possibly different for the different components of the system. Of course, one can think of improving the model, using more sophisticated relations for the local inductances, i.e., taking for instance a temperature and/or frequency dependent (complex) inductance $L^i(T,\omega )$, to account for finite-frequency dissipation processes inside the superconducting puddles. This extension of the model is of course mandatory if one is to explore, e.g., the regime of frequencies higher than the superconducting gap. For this reason, here we limit our analysis to low (sub-gap) frequencies.

Having in mind SrTiO${}_3$-based oxide interfaces, for the sake of definiteness, the numerical values of the parameters will be taken as typical of (or plausible for) these systems [21,25]. We recall that in this work resistances and inductances (and hence, impedances) are measured per square, for any given 2D system.

In analogy with the RRN case, one can proceed by solving the correspondent EMT equation

$$\sum _{j=m,s}{\tilde{w}}_j\left(T\right)\frac{z_j-z_{em}}{z_j+z_{em}}=0$$

(4)

where $z_{em}$ is the effective impedance of the network, the index $j=m,s$ labels the different components of the inhomogeneous system, and ${\tilde{w}}_j\left(T\right)$ is the weight of the corresponding component at a temperature T, as defined in the previous section (see also Appendix A). By means of Equation (4), one has direct access to the effective conductance of the system at $T<T_c$, $g_{em}(T,\omega )=z_{em}^{-1}(T,\omega )$. As a consequence, also the effective optical conductivity ${\sigma }_{em}(T,\omega )=\mathrm{Re}\left[g_{em}(T,\omega )\right]\equiv g_{em}^{\prime }(T,\omega )$ and the superfluid stiffness ${\displaystyle J_s\left(T\right)\propto -\underset{\omega \to 0}{lim}\omega g_{em}^{″}(T,\omega )}$, where $g_{em}^{″}(T,\omega )\equiv \mathrm{Im}\left[g_{em}(T,\omega )\right]$, can be obtained. In practice, if the experiment is carried out at a constant low frequency [25], one can directly take $J_s\left(T\right)\propto -g_{em}^{″}(T,\omega \approx 0)$, i.e., one can directly read the behavior of the superfluid stiffness as a function of T from the behavior of the imaginary part of the conductance.

For the sake of comparison, we recall that within a homogeneous Drude model the complex AC conductance is

$$g(T,\omega )=\frac{{\sigma }_0}{1+\mathrm{i}\omega \tau }\equiv \frac{1}{R+\mathrm{i}\omega L},$$

where ${\sigma }_0\equiv n{e}^2\tau /m$ is the DC conductivity, n is the carrier density, e is the electron charge, m is the carrier effective mass, and $\tau$ is the scattering time. Then, the resistance is $R=1/{\sigma }_0$ and the inductance is $L\equiv \tau /{\sigma }_0={\left(e^2{J}_s\right)}^{-1}$, where the superfluid stiffness is $J_s\equiv n/m$. In the superconducting state $R=0$ and the AC electromagnetic response is purely reactive.

In the present study, we want to consider the scenario proposed in Ref. [24], where, just below $T_c$, the system is characterized by the presence of superconducting filaments connecting superconducting puddles. If on the one hand, the presence of a superconducting percolating path guarantees the appearance of a global zero-resistance state, on the other hand the superconducting state remains very fragile towards an applied current [29], so one can expect a very low value of the superfluid stiffness. This low superfluid stiffness, however, can rapidly increase when the temperature is lowered and proximity effects induce superconductivity in the metallic matrix. This can induce different mechanisms leading to an increase of the superfluid stiffness. First of all, proximity effects increase the superconducting regions at the expense of the metallic matrix. This effect generically occurs irrespective of the spatial organization of the superconducting clusters. On the other hand, proximity effects can open new superconducting paths connecting the few filamentary structure of the superconducting network rapidly increasing the long-distance connectivity and strongly increasing the superconducting condensate rigidity. While the first effect does not involve the spatial structure and it can easily be described within the EMT, the second type of effects involve topological features that can be conveniently addressed by direct calculations of RIN simulations. Nevertheless, a wealth of information can still be extracted from the mean-field-like EMT approach, so that in the present study, we will model the proximity effect at EMT level. Neglecting any spatial structure, we will just consider a second superconducting component, resulting from proximization, with randomly distributed critical temperature, setting in at lower temperatures.

The three different impedances, corresponding to the three different components, are thus distributed across the system according to the corresponding fractions:

• $w_1$: the superconducting fraction percolating at $T_c$, with local critical temperatures following a Gaussian distribution with parameters (${\mu }_{c,1}$, ${\sigma }_1$);
• $w_2$: the superconducting fraction arising after proximization, with local critical temperatures following a Gaussian distribution with parameters (${\mu }_{c,2}\le {\mu }_{c,1}$, ${\sigma }_2$);
• $w_3=1-w_1-w_2$: the fraction of the residual metallic matrix, that will never undergo proximization.

In what follows, we will keep $w_1=w^p\equiv 0.5$, i.e., equal to the minimal fraction of superconducting bonds needed for the system to percolate, with the assumption of a homogeneous dispersion of the three components, implicit within the EMT. Again, having in mind SrTiO${}_3$-based oxide interfaces, for the sake of definiteness, the values characterizing the average critical temperature and the width of the distribution are taken as typical for these systems [21]. Although the EMT is just the first step towards more sophisticated studies of the RIN, we will show in the next section that it can provide valuable insights into the effect of the physical mechanisms described by our tuning parameters.

4. EMT Results

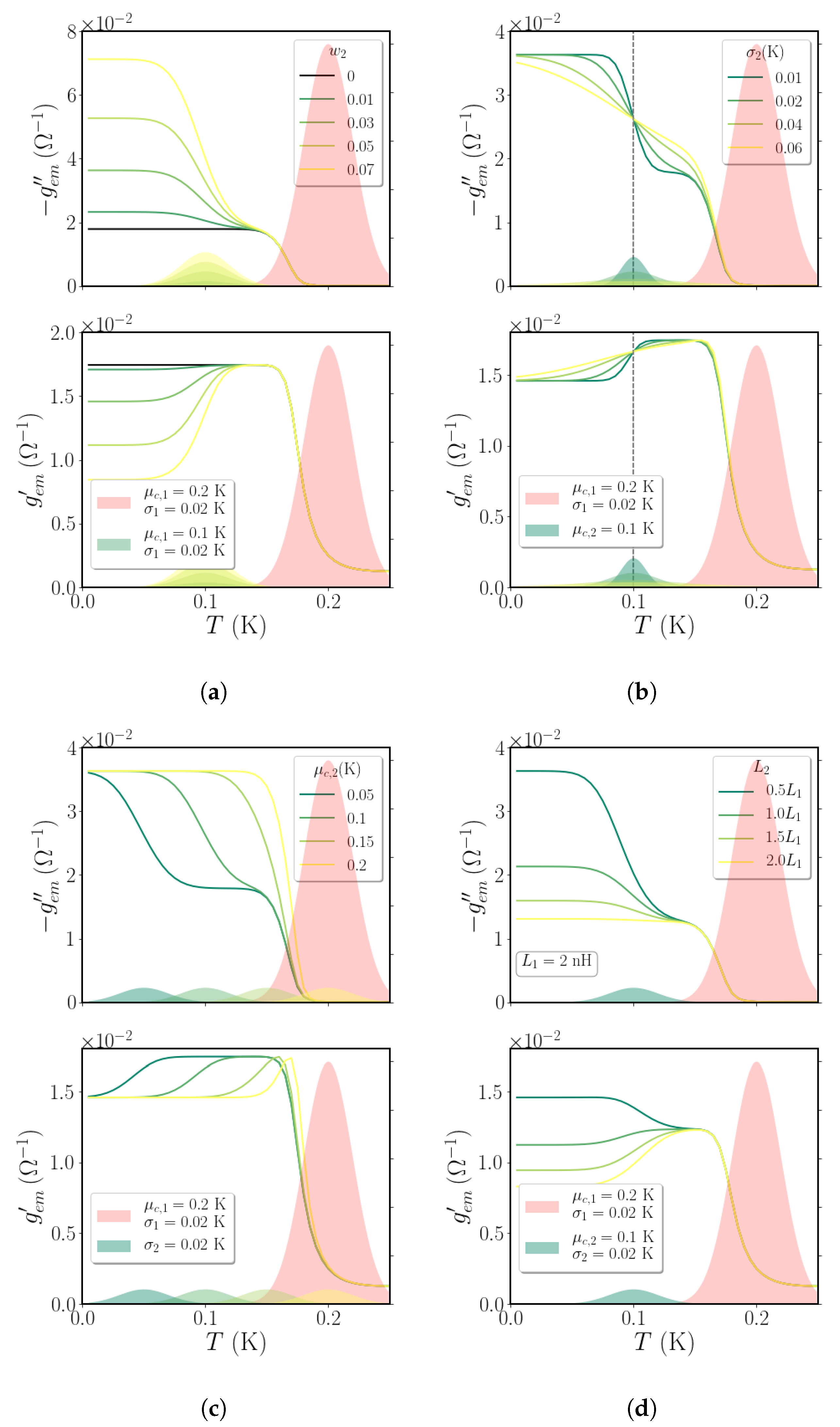
Let us discuss the results obtained by solving Equation (4) (see Appendix B for details about the analytic solution of the EMT equation for a three-component system at finite frequency). We start with the simple case treated within the RRN model. To this aim, we set $w_2=0$ so as to consider just the two kinds of resistors accounted for in the previous section: those belonging to the metallic matrix and those belonging to the percolating superconducting cluster. Having set $w_1=w^p\equiv 0.5$, the global resistance of the system will vanish as soon as all the bonds of the superconducting cluster have switched to their superconducting state (see Figure 1). On the other hand, the finite-frequency response of the system appears already above $T_c$, at $T\lesssim {\mu }_{c,1}$: as one can see from the trend of the black curves in Figure 2a, both the superfluid stiffness $J_s\propto -g_{em}^{″}$ (at a fixed low frequency) and the optical conductivity $\sigma =g_{em}^{\prime }$ start to increase above the percolating temperature, saturating to a constant value around $T_c$.

Let us now introduce the second fraction of superconducting bonds ($w_2>0$), which comes into play at lower temperatures, as a result of a proximity effect. To investigate the impact of this new superconducting fraction on the AC transport properties, we keep fixed the fraction of the first (percolating) superconducting bonds ($w_1=0.5$) as well as the Gaussian distribution of their critical temperatures (with parameters: ${\mu }_{c,1}=0.2$ K; ${\sigma }_1=0.02$ K), and we tune individually the parameters relative to the second, proximity-induced, fraction of superconducting bonds.

Let us start by fixing the Gaussian distribution with ${\mu }_{c,2}=0.1$ K and ${\sigma }_2=0.02$ K, and by tuning the fraction $w_2$ of proximized bonds. As one can see from Figure 2a, increasing the value of $w_2$ both $g_{em}^{″}$ and $g_{em}^{\prime }$ assume a two-step character, which can be smoother or more pronounced depending on the other parameters at play, with opposite trends: while $g_{em}^{″}$ registers a further growth as a consequence of a reduction of the global inductance, the optical conductivity $g_{em}^{\prime }$ sees a downturn after a sort of plateau, which will become more or less peaked depending on $({\mu }_{c,2},{\sigma }_2)$ (Figure 2b,c. We also stress that, by increasing $w_2$, the ratio between the saturation values at $T=0$ of $g_{em}^{″}$ and $g_{em}^{\prime }$ strongly increases: a fraction of just $w_2=0.07$ proximized bonds make the ratio $g_{em}^{″}\left(0\right)/g_{em}^{\prime }\left(0\right)$ 10 times bigger with respect to the case when proximization is not taken into account, and $w_2=0$.

We now set the fraction of the proximized bonds to $w_2=0.03$ and we observe the effects in changing the variance ${\sigma }_2$ and the mean value ${\mu }_{c,2}$ of the Gaussian distribution of its critical temperatures. A broader probability distribution, i.e., a larger value of ${\sigma }_2$, smoothens out the two-step character of both response functions: it broadens the downturn of $g_{em}^{\prime }$ as well as the increase of $g_{em}^{″}$ (see Figure 2b). On the other hand, the value of ${\mu }_{c,2}$ rules the temperature range at which both $g_{em}^{\prime }$ and $g_{em}^{″}$ start to increase and, quite interestingly, it corresponds to the inflection point of the two curves (see Figure 2c). In general, from Figure 2b,c, one can see that the more the two probability distributions overlap, either because of a larger ${\sigma }_2$ or because ${\mu }_{c,2}$ is taken closer to ${\mu }_{c,1}$, the more the growth of $g_{em}^{″}$ is continuous and the bump of $g_{em}^{\prime }$ peaks.

So far, we have assumed that both superconducting fractions have the same inductance value $L_1=L_2=1$ nH, while the metallic residue has $L_3=10$ nH. Finally, thus, we look at the effects of changing the relative values of $L_1$ and $L_2$ on the response of the system. Fixing $L_1=2$ nH we tune the value of $L_2$. As one can see from Figure 2d, the variations of $L_{1,2}$ correspond to tuning the magnitude in the zero-temperature limit of $g_{em}^{\prime }$ and $g_{em}^{″}$. In particular, an increase (decrease) of $L_2$ with respect to $L_1$ corresponds to a decrease (increase) of the saturation values of both the real and imaginary part of $g_{em}$. It is worth noting that, while an increase in $w_2$ acts in opposite directions in $g_{em}^{\prime }$ and $g_{em}^{″}$ (Figure 2a), the decrease of $L_1$ corresponds to an increase of both $g_{em}^{\prime }\left(0\right)$ and $g_{em}^{″}\left(0\right)$, albeit with a different magnitude. From $L_2=2L_1$ to $L_2=L_1$, the relative increase of $g_{em}^{″}\left(0\right)$ is ≈1.3 while for $g_{em}^{\prime }$ this is ≈0.5. Qualitatively, for $L_2\le L_1=1$ nH we also observe an increase of $g_{em}^{\prime }$ in the lower temperature range, while in all other cases we observe a bump and then a decrease, while lowering T.

5. Conclusions

The possibility to control superconductivity via electric or ionic-liquid gating poses new theoretical challenges and opens the way to a wealth of applications. For instance, the simultaneous presence of superconductivity and spin-orbit coupling at LaAlO${}_3$/SrTiO${}_3$ interfaces may open the way to the possible occurrence of Majorana Fermions in suitably gate-tailored nano-sized one-dimensional geometries of the two-dimensional electron gas [30,31,32]. At the same time, intrinsic [23,24] and extrinsic effects may render the superconducting state of gate-tuned superconductors inhomogeneous at the nanoscale, with the peculiarity that the superconducting regions may be surrounded by a metallic matrix. In view of future applications, like the realization of gate-tunable superconducting devices, it is then crucial to describe the electrodynamic response of these inhomogeneous systems.

This work was devoted to the description of the AC response of a superconductor with disorder at the nanoscale. Along the line of previous works [24,27], dealing with DC transport in inhomogeneous superconductors above the percolative superconducting transition, we studied the RIN model, in the EMT approximation. The RIN model was obtained as an extension of the RRN model to the domain of finite frequency. We were thus able to investigate the superconducting properties below the percolative superconducting critical temperature. In its simplest realization, where the inductance L of the superconducting regions is assumed to be real and frequency independent, our model is apt to describe the low (i.e., lower than the superconducting gap) frequency regime. An extension to higher frequencies is within the reach of our approach, but requires a description of dissipative processes within the superconducting regions, entailing a properly devised frequency dependence of the (complex) inductance L. This analysis is left for future studies, when experimental data guiding and constraining our modeling will be available.

Looking at the real and imaginary parts of the complex conductivity, which corresponds to the optical conductivity and the superfluid stiffness, respectively, we found very interesting features once a second fraction of superconducting bonds is included, which can arise at lower temperature because of a proximation process. A small fraction of superconducting proximized bonds are sufficient in order to have a non negligible increase in $g_{em}^{″}$ as compared to the case of a single superconducting component (i.e., in the absence of proximization within the metallic matrix).

This increase can be more or less abrupt, depending on the shape of the distribution of local $T_c^i$ assigned to the proximized bonds. More specifically, the increase of $g_{em}^{″}$ can be qualitatively different depending on the relative positions of the two Gaussians governing the superconducting clusters. Indeed, if the two are overlapping, either because ${\mu }_{c,1}$ and ${\mu }_{c,2}$ are close to one another or ${\sigma }_1$ and ${\sigma }_2$ are large enough, the increase in $g_{em}^{″}$ is rather smooth and it takes place via a rather continuous increase. On the contrary, when the two $T_c$ distributions are sufficiently separated, $g_{em}^{″}$ displays s a two-step character.

It is worth noting that the onset of the proximized fraction in the superconducting phase is also responsible for the decrease of the (dissipative part of the) optical conductivity, which instead saturated at a constant value (already at $T\sim T_c$) in the single-component case ($w_2=0$). The distribution $P_2\left(T_c^i\right)$ controls the width of this maximum in $g_{em}^{\prime }$ and its broadening. Finally, the tuning of the inductance values of the two superconducting fractions $L_1$ and $L_2$ has provided very interesting insights as well. Indeed, while both the saturation value of $g_{em}^{″}(T=0)$ and $g_{em}^{\prime }(T=0)$ increases with decreasing $L_2$ at fixed value of $L_1$, for $L_2/L_1<1$ the optical conductivity changes qualitatively its behavior: the decrease generating a bump observed in all other cases turns into an increase towards a higher $g_{em}^{\prime }(T=0)$ value with respect to its value in the case when proximization is neglected.

As already mentioned, despite its simplicity, the EMT approximation is quite rich and it can be a valuable guidance in the study of the exact solution of the RIN model, where spatial correlations in the system can be taken into account. Indeed, we found some interesting features coming from the proximization process and we hope to trigger the experimental interest in the finite-frequency response in the superconducting phase in 2D inhomogeneous systems. Work in this direction is underway [28].