Abstract
We investigate pairing fluctuation effects in a two band fermionic system, where a shallow band in the Bardeen–Cooper–Schrieffer–Bose–Einstein condensation (BCS-BEC) crossover regime is coupled with a weakly interacting deep band. Within a diagrammatic T matrix approach, we report how thermodynamic quantities such as the critical temperature, chemical potential, and momentum distributions undergo the crossover from the BCS to BEC regime by tuning the intraband coupling in the shallow band. We also generalize the definition of Tan’s contact to a two band system and report the two contacts for different pair-exchange couplings. The present results are compared with those obtained by the simpler Nozières–Schmitt–Rink approximation. We confirm a pronounced enhancement of the critical temperature due to the multiband configuration, as well as to the pair-exchange coupling.
1. Introduction
Superconductivity and superfluidity play a central role in modern physics. The first microscopic theory for superconductivity, namely the Bardeen–Cooper–Schrieffer (BCS) theory [1], has successfully been applied to various quantum many body systems. On the other hand, some of them, in particular so-called unconventional superconductors, involve nontrivial effects beyond the BCS theory due to their complex band structures. In this regard, a theoretical model for multi-band superconductors was developed by Suhl, Matthias, and Walker in 1959 [2]. This pioneering work is the starting point for the recent studies of multi-component superconductors [3,4]. In condensed matter systems, such superconductors have experimentally been discovered, e.g., in MgB2 [5] and iron based compounds [6]. From the theoretical viewpoint, a variety of non-trivial phenomena has been proposed (e.g., topological phase soliton [7,8], odd-frequency pairing [9], multiple Leggett mode [10], hidden criticality [11], stable Sarma phase [12], and Lifshitz transitions with resonance effects and amplification of the critical temperature [13,14]).
As another direction toward the unconventional properties of superconductors, the crossover from the weakly coupled BCS state to the Bose–Einstein condensate (BEC) of a tightly bound molecule with increasing the two body attractive interaction has extensively been discussed [15,16]. In fact, this crossover has been realized in ultracold Fermi atomic gases [17,18], and currently, various properties and fluctuation phenomena of this system have been investigated theoretically and experimentally [19,20,21]. Interestingly, recent experiments of FeSe multi-band superconductors also indicated that this electron system is in the BCS-BEC crossover regime [22,23,24].
Combining these two aspects of unconventional superconducting/superfluid properties is a promising route toward room temperature superconductivity [25,26]. One striking feature predicted in the multi-band BCS-BEC crossover is the screening of pairing fluctuations [26,27]. Since pairing fluctuations are known to lower generally the superconducting/superfluid critical temperature, this screening effect is expected to enhance the critical temperature compared to the single band counterpart. Indeed, a missing pseudogap in the multi-band FeSe superconductors in the BCS-BEC crossover has been reported in a recent experiment [28]. Since single particle spectra in a single band system in the BCS-BEC crossover regime exhibit the pseudogap originating from strong pairing fluctuations [29,30,31,32], this experimental finding supports the screening of pairing fluctuations due to the multi-band nature of the FeSe superconductor. In addition, a recent torque magnetometry measurement also supports the absence of strong pairing fluctuations in this system [33]. In contrast, other experimental works have reported superconducting fluctuation effects in FeSe multi-band superconductors [23,34,35]. In this sense, we have to establish a whole picture of this system to understand where multi-band FeSe superconductors locate in the BCS-BEC crossover regime. In addition, since the realization of the multi-band BCS-BEC crossover has been anticipated in Yb Fermi atomic gases, a systematic study is required to obtain a unified understanding of these unconventional strongly coupled systems [36,37,38,39,40,41]. Such a study could promote further interdisciplinary investigations of the BCS-BEC crossover, such as in nuclear systems and neutron stars [21,42,43].
In this work, we theoretically investigate the multi-band BCS-BEC crossover and the effects of pairing fluctuations within the framework of the many body T matrix approximation, extending our previous work [27], which was based on the Nozières–Schmitt–Rink (NSR) approximation [44]. While this extension is crucial to access dynamical quantities such as spectral functions, one has to examine also how higher fluctuation effects beyond the NSR scheme appear in thermodynamic quantities. Specifically, as first pointed out by Serene [45], the many body T matrix approximation sums all repeated scatterings of an electron by independent pair fluctuations, while omitting vertex corrections and interactions between fluctuations. The NSR approximation, as well, omits the latter, but it also misses the repeated scatterings by independent fluctuations. Considering a two band configuration, where a strongly interacting shallow band is coupled with a weakly interacting deep band through the pair-exchange couplings [46], we show the evolution of the critical temperature, momentum distribution functions, chemical potential, and occupation number densities in each band. This specific band configuration is physically motivated by FeSe superconductors, which are believed to locate in the BCS-BEC crossover regime with a strongly interacting shallow band [35] and for which the BCS-BEC crossover can be tuned by chemical doping [24]. Therefore, we systematically investigate thermodynamic quantities in the two band model by changing the interaction in the shallow band from weak to strong. In this paper, we set , and the volume is taken to be unity.
2. Hamiltonian
We start from the two band fermion model [27,47,48] described by the Hamiltonian:
where is an annihilation operator of a fermion with momentum and spin in the i band (). is the kinetic energy measured from the chemical potential . We assume parabolic band structures with a common effective mass in the momentum space as where is the energy separation between the two bands. The second term in Equation (1) is the interaction term with coupling constants and the pair annihilation operator in the i band with center of mass momentum . is a momentum cutoff, taken to be where is the Fermi momentum of the total system with the total number density n. The intraband couplings can be characterized in terms of the intraband scattering lengths as:
In this work, we define the band Fermi momentum where is the number density of each band in the absence of interactions at zero temperature, noting that . Then, we fix while is tuned from the weak coupling BCS to the strong coupling BEC regime. For convenience, we also introduce a dimensionless pair-exchange coupling (where ) and . To realize the situation where the shallow band is close to the Lifshitz transition [46], we take , corresponding to .
3. T Matrix Approximation for Two Band Systems
We examine the effects of pairing fluctuations on thermodynamic quantities by extending the many body T matrix approach to the present two band system. We define the Matsubara–Green’s function in the i band as:
where (ℓ integer) is a fermionic Matsubara frequency at temperature T. As diagrammatically drawn in Figure 1a, the self-energy contains pair-fluctuation corrections as:
where is the bare Green’s function, (l integer) is a bosonic Matsubara frequency, and:
is the many body T matrix (see also Figure 1b). Here, we have defined the matrix of coupling constants as:
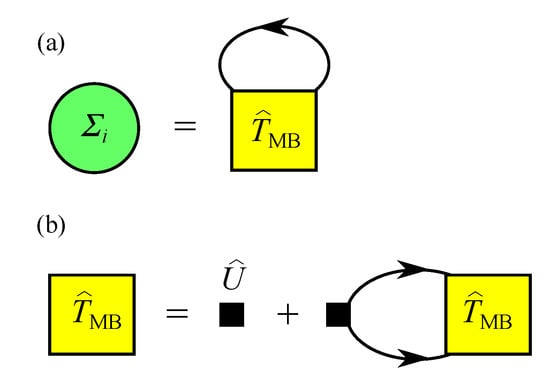
Figure 1.
Feynman diagrams of (a) the self-energy and (b) many body T matrix where single lines represent bare Green’s functions . The black box indicates the matrix of coupling constants .
The particle-particle propagator matrix is given by:
with:
where f is the Fermi function at temperature T.
Note that the particle-particle propagator matrix is diagonal because in the Hamiltonian (1), the two bands are coupled only by the Josephson interaction associated with the transfer of a pair from one band to the other one (as is usually assumed, following [2]). Off-diagonal terms would appear only in the presence of cross–pairing interaction directly coupling fermions belonging to different bands. The self-energy (4), which is obtained by applying standard Feynman rules for the perturbative expansion of the single particle Green’s function, sums up an infinite series of ladder diagrams describing the interaction of a fermion in a given band with a fluctuating pair. Mathematically, the fluctuating pair interacting with fermions belonging to the band i is described by the matrix element of the many body T matrix. Physically, it corresponds to a pair that starts and ends in a given band after having been transferred back and forth from and to the other band (as can be seen by expanding Equation (1) in powers of ).
In the following, we mention how to calculate the physical quantities of interest and the practical differences with respect to the NSR approach used in our previous work [27]. To determine the chemical potential , we numerically invert the particle number equation with:
where is the momentum distribution function in the i band, which is obtained from the Matsubara frequency summation of the dressed Green’s function with T matrix self-energy as:
The delicate frequency sum in Equation (10), with the convergence factor , is performed by adding and subtracting in the sum a non-interacting Green’s function, leading to:
where now, the sum over the frequency is absolutely convergent, and the convergence factor can be dropped.
We note that the difference between the present T matrix approach and the Nozières–Schmitt–Rink one [44,49] adopted in our previous work [27] consists in the form of used in Equation (10). Specifically, in the NSR approach, Dyson’s Equation (3) for is truncated to first order as:
while in the T matrix approach, Equation (3) is retained exactly. In the NSR approach, the fermions in a given band thus interact only once with a fluctuating pair, while the full solution of Dyson’s equation performed in the T matrix approach retains all repeated scattering of independent fluctuations. On the numerical side, a simplification introduced by the NSR approach is that the NSR particle number , with:
can also be obtained from the Equation [47]:
which with a numerical differentiation with respect to , avoids the calculation of the self-energy and the nested sums over required by Equations (4) and (13). The implementation of these nested sums is instead unavoidable in the T matrix approach. Clearly, the NSR and T matrix approaches are essentially equivalent when the self-energy corrections are small, while when this does not occur, quantitative differences are expected in their results for thermodynamic quantities, such as, e.g., the chemical potential and critical temperature . For the BCS-BEC crossover in a single band, these differences turn out to be rather moderate across the whole BCS-BEC crossover, even when the self-energy is not small [21]. We will show below that the same occurs in the two band system considered in this work.
4. Results
As a first quantity, Figure 2 shows our results for the momentum distribution functions in the two bands at three different values of the coupling strength spanning the BCS-BEC crossover. The interband coupling parameter is taken at the values (left column) and (right column), while the temperature is set at the superfluid critical temperature , as determined by Equation (15) (the results for are presented in Figure 3 below). In the weak coupling cases shown in Figure 2a,d, where , the momentum distribution in each band exhibits a clear Fermi step, rounded by finite temperature. Indeed, when , one sees from Equation (11) that is dominated by the Fermi–Dirac distribution function . At the stronger couplings and shown in Figure 2b,c,e,f, respectively, the interaction effects become progressively more important. In the shallow band, in particular, the momentum distribution clearly departs from the corresponding non-interacting distributions for both values of the pair-exchange coupling. For the deep band, instead, the effects are much weaker. This is because increasing the interaction in the shallow band affects the fermions in the deep band only indirectly, through the pair-exchange coupling . One sees indeed that the interaction effects on are more visible for the larger value of the pair-exchange coupling.
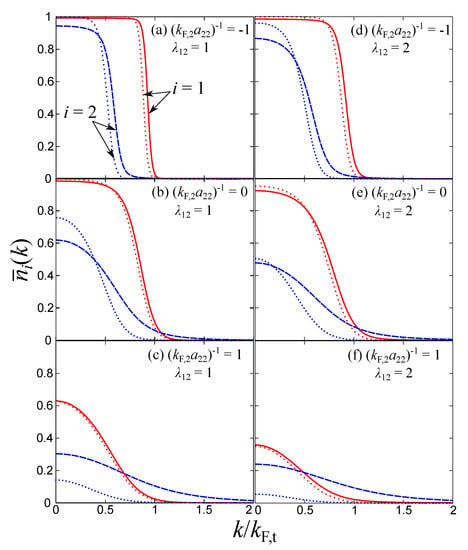
Figure 2.
Momentum distribution functions at the superfluid critical temperature identified by Equation (15). The left column corresponds to and (a) , (b) , and (c) , while the right column corresponds to and (d) , (e) , and (f) . The coupling in the deep band is fixed at . The dotted curves correspond to the free Fermi distribution functions calculated with the same chemical potential and temperature.
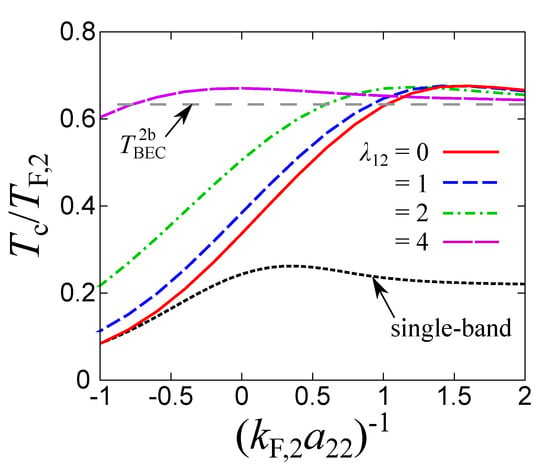
Figure 3.
Superfluid critical temperature in the Bardeen–Cooper–Schrieffer–Bose–Einstein condensation (BCS-BEC) crossover regime of the shallow band calculated for different values of the pair-exchange coupling as a function of the coupling in the shallow band. The black dotted curve represents the numerical result of the single band counterpart. The dashed line is the molecular BEC temperature when all particles in both bands form tightly bound molecules. The coupling in the deep band is fixed at .
Figure 3 shows the calculated superfluid critical temperature for various values of the pair-exchange coupling as functions of the coupling in the shallow band. The superfluid critical temperature is determined by employing the Thouless criterion, which for the present multi-band system, corresponds to the equation:
Physically, the Thouless criterion corresponds to a diverging pairing susceptibility in any of the two bands. Coming from the normal phase, it can be obtained by calculating the pairing susceptibility within linear response theory, with the many body T matrix diagrams as the central part of the corresponding two particle Green’s function (see, e.g., [50]). Coming instead from the superfluid phase, the Thouless criterion corresponds to the vanishing of the BCS gap in both bands. We stress in this respect that, as for the single band case, the differences in the value of the critical temperature compared with the BCS mean field are entirely due to the different particle number equation, which includes the effects of paring fluctuations in the T matrix approach. One can see that in the two band system is greatly enhanced in the strong coupling regime for all values of , compared to the isolated single band counterpart. For , this behavior originates from the particle transfer from the deep band to the shallow band, as a result of free energy minimization. Indeed, in the strong coupling limit, approaches the BEC temperature , where all particles in both bands form tightly bound molecules. Additionally, if one increases , the BEC limit is reached already at rather weak values of the coupling parameter . This finding can be understood as the increase of an effective intraband coupling due to the pair-exchange induced interaction as:
From Equation (16), one can see that the two body attractive interaction in the shallow band is enhanced due to the pair-exchange coupling.
The effect of the pair-exchange coupling induced intraband attraction can also be found in the evolution of the chemical potential at . Specifically, for the sake of comparison with the single band case, it is useful to consider the chemical potential referred to the bottom of the shallow band, as presented in Figure 4. One sees that by increasing the pair-exchange coupling, the BEC limit for the shallow band (corresponding roughly to ) is reached very rapidly compared with the single-band case. When the chemical potential goes further below and crosses the bottom of the lower band (corresponding to the dashed horizontal line in Figure 4), the calculated values of the chemical potential can be compared with the bound state solution of the two body Schrödinger equation:
where is the two body wave function in the i band with (and the binding energy is referred to the bottom of the lower band). After a straightforward calculation, we obtain the equation for the binding energy as:
where . In Figure 4, one can find that is indeed in good agreement with in the strong coupling regime.
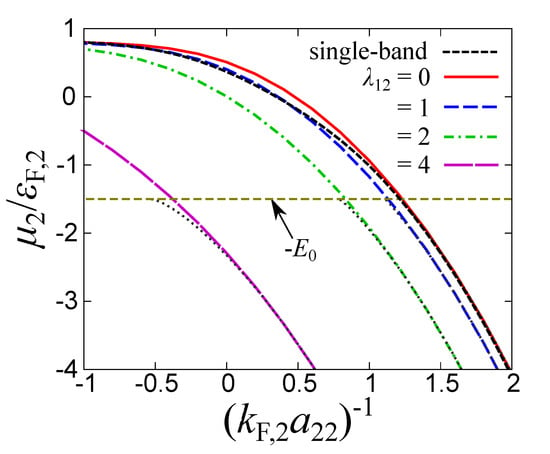
Figure 4.
Chemical potential referred to the bottom of the shallow band, at for different values of the pair-exchange coupling as a function of the coupling in the shallow band. The horizontal line corresponds to the bottom of the lower band. The dotted curves represent half of the two body binding energy in our two band configuration. The coupling in the deep band is fixed at .
To confirm our scenario for the enhancement of due to the particle transfer between bands, we also calculate the occupation number density in each band. Figure 5 shows the calculated number densities in the BCS-BEC crossover regime. In the weak coupling limit, and approach the non-interacting results and , as expected. For increasing coupling , increases because the particles in the deep band flow into the shallow band. Note that a full transfer of particles from the deep to the shallow band can be achieved even for vanishing pair-exchange coupling for sufficiently strong interaction in the shallow band. On the other hand, a finite pair-exchange coupling induces the mixing of two kinds of molecular BEC in the strong coupling regime [27]. As a result, remains finite in the strong coupling limit with finite .
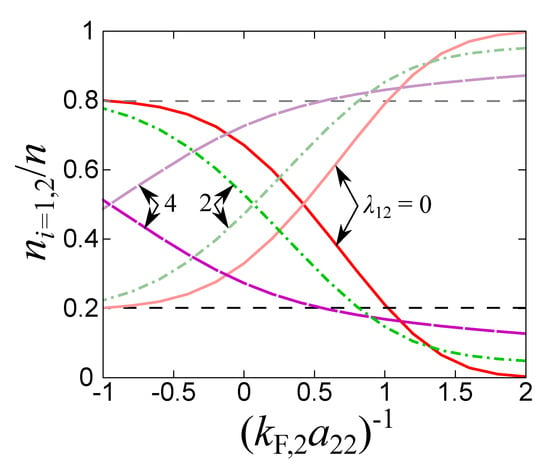
Figure 5.
Occupation number density (decreasing functions) and (increasing functions) at for different values of the pair-exchange coupling as a function of the coupling in the shallow band. The horizontal dashed lines represent (upper line) and (lower line). The coupling in the deep band is fixed at .
The T matrix approach presented in this paper can address the pair correlations from the momentum distribution functions . Figure 6 shows the calculated multiplied by at , (and , as everywhere in our paper). In the single band case, the momentum distribution function has a large momentum tail characterized by Tan’s contact C [51,52,53]. Since Tan’s contact is defined as a thermodynamic quantity conjugate to the inverse scattering length, the two band system in principle involves two contact parameters as:
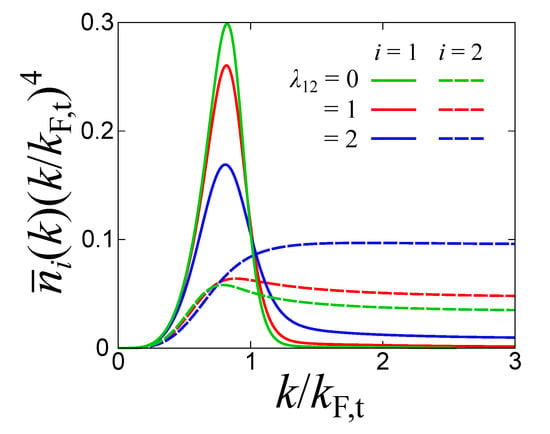
Figure 6.
Momentum distribution functions multiplied by at and . Solid (dashed) lines show the results of a deep (shallow) band. The coupling in the deep band is fixed at .
Indeed, one can find that in both bands approach constants (namely, ) in the large momentum region as in the case of single band [54]. While is small because of the weak intraband coupling , in the strongly interacting shallow band is larger. Moreover, at finite , both and increase due to the pair-exchange induced interaction given by Equation (16). Since is proportional to the molecular density in the strong coupling limit, the emergence of two finite contact parameters supports the coexistence of two kinds of molecular BEC in the present two band system.
The above results for the critical temperature, chemical potential, and particle numbers obtained with the T matrix approach thus confirm our previous findings obtained with the NSR approximation [27]. We emphasize, however, that our results presented in this paper are different from those of NSR. To make this comparison more quantitative, we report in Figure 7a the critical temperature obtained by the T matrix approach () and by the NSR approximation (). One can see that, also in the two band case, both approaches exhibit a qualitatively similar behavior along the BCS-BEC crossover. Indeed, as shown in Figure 7b, the relative difference between the critical temperature obtained by the two approaches, namely , is less than 15% in the whole crossover region. An interesting feature of Figure 7b is also the position of the maximum of . Since the expansion parameter of Dyson’s equation is , one expects the maximum to occur for intermediate couplings. This is because in weak coupling, is small due to weak interaction, while for strong coupling, it is the large and negative chemical potential contained in that makes the expansion parameter small. This expectation is confirmed by Figure 7b. In particular, for a single band, the maximum is located near the coupling strength where the chemical potential goes below the bottom of the single band (corresponding to in Figure 4). The same criterion holds also in the two band case, where now, the relevant band is the deep one (corresponding to and thus in Figure 4).
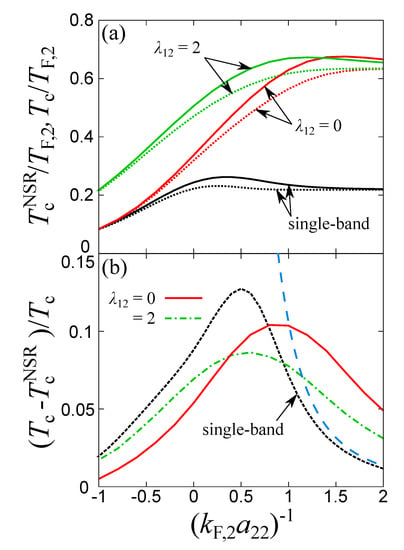
Figure 7.
(a) Critical temperatures within the T matrix approach (, full lines) and Nozières–Schmitt–Rink (NSR) approximation (, dotted lines) for different values of the coupling as a function of the coupling in the shallow band. (b) Relative difference between the two critical temperatures along the BCS-BEC crossover in the shallow band. The dashed curve is the asymptotic behavior for the single band counterpart given by Equation (20) [55]. The coupling in the deep band is fixed at .
Notice furthermore that, as one can evinces from Figure 7a, in the strong coupling limit, the T matrix approach reaches the BEC value for more slowly than the NSR approach. In the single band case, one can show indeed that for the T matrix approach, the BEC value for is reached in the strong coupling limit according to the asymptotic law [55]:
where all quantities refer to a single band, for which . A similar power law behavior is expected in the two band case, with a coefficient depending on . For the NSR approximation, on the other hand, one can easily show that the correction to vanishes exponentially in the strong coupling limit (for both the single band and two band cases). For the single band case, Equation (20) shows indeed good agreement with in the strong coupling regime (see the dashed line in Figure 7b).
5. Conclusions
We investigated the BCS-BEC crossover and the effects of pairing fluctuations for a two band system within the framework of the many body T matrix approximation. We analyzed the evolution of thermodynamic properties from BCS to BEC limits in a shallow band coupled with a weakly interacting deep band. We confirmed the finding, previously obtained with the simpler NSR approximation, of a strong enhancement of the critical temperature in the two band case compared with the single band case. Furthermore, we calculated the momentum distribution functions in each band, which exhibit a large momentum tail characterized by Tan’s contact. Generalizing Tan’s relation to the present two band model is an interesting future problem. We finally remark that the calculation of dynamic quantities (such as single particle spectral weight functions and density of states) should necessarily rely on approaches like the T matrix approximation, which do not expand Dyson’s equation. For such quantities, therefore, the NSR approach could not be used. Our analysis of thermodynamic quantities with the T matrix approach thus paves the way toward future investigations of spectral weight functions of a two band system through the BCS-BEC crossover.
Author Contributions
Conceptualization, H.T., A.P., and P.P.; methodology, H.T., A.P., and P.P., software, H.T.; investigation, H.T.; data curation, H.T.; writing, original draft, H.T.; writing, review and editing, H.T., A.P., and P.P.; visualization, H.T.; supervision, A.P. and P.P.; project administration, A.P. and P.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Japan Society for the Promotion of Science with Grant-in-Aid for JSPS fellows No. 17J03975, the grant for Scientific Research No. 18H05406, and by Italian MIUR through the PRIN 2015 program, Grant No. 2015C5SEJJ001.
Acknowledgments
We thank Yuriy Yerin for useful discussions. H.T. thanks the Physics Division at the University of Camerino for the hospitality.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175. [Google Scholar] [CrossRef]
- Suhl, H.; Matthias, B.T.; Walker, L.R. Bardeen–Cooper–Schrieffer Theory of Superconductivity in the Case of Overlapping Bands. Phys. Rev. Lett. 1959, 3, 552. [Google Scholar] [CrossRef]
- Tanaka, Y. Multicomponent superconductivity based on multiband superconductors. Supercond. Sci. Technol. 2015, 28, 034002. [Google Scholar] [CrossRef]
- Milošević, M.V.; Perali, A. Emergent phenomena in multicomponent superconductivity: An introduction to the focus issue. Supercond. Sci. Technol. 2015, 28, 060201. [Google Scholar] [CrossRef]
- Nagamatsu, J.; Nakagawa, N.; Muranaka, T.; Zenitani, Y.; Akimitsu, J. Superconductivity at 39K in magnesium diboride. Nature 2001, 410, 63–64. [Google Scholar] [CrossRef]
- Kamihara, Y.; Watanabe, T.; Hirano, M.; Hosono, H. Iron-Based Layered Superconductor La[O1−xFx]FeAs (x = 0.05–0.12) with Tc = 26 K. J. Am. Chem. Soc. 2008, 130, 3296–3297. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, Y. Soliton in Two-Band Superconductor. Phys. Rev. Lett. 2001, 88, 017002. [Google Scholar] [CrossRef] [PubMed]
- Kuplevakhsky, S.V.; Omelyanchouk, A.N.; Yerin, Y.S. Soliton states in mesoscopic two band-superconducting cylinders. Low Temp. Phys. 2011, 37, 667. [Google Scholar] [CrossRef][Green Version]
- Black-Schaffer, A.M.; Balatsky, A.V. Odd-frequency superconducting pairing in multiband superconductors. Phys. Rev. B 2013, 88, 104514. [Google Scholar] [CrossRef]
- Ota, Y.; Machida, M.; Koyama, T.; Aoki, H. Collective modes in multiband superfluids and superconductors: Multiple dynamic classes. Phys. Rev. B 2011, 83, 060507(R). [Google Scholar] [CrossRef]
- Komendová, L.; Chen, Y.; Shanenko, A.A.; Milošević, M.V.; Peeters, F.M. Two-Band Superconductors: Hidden Criticality Deep in the Superconducting State. Phys. Rev. Lett. 2012, 108, 207002. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Zhuang, P. Stable Sarma state in two band Fermi systems. Phys. Rev. B 2009, 79, 024511. [Google Scholar] [CrossRef]
- Valletta, A.; Bianconi, A.; Perali, A.; Saini, N.L. Electronic and superconducting properties of a superlattice of quantum stripes at the atomic limit. Z. Phys. B: Condens. Matter 1997, 104, 707–713. [Google Scholar] [CrossRef]
- Mazziotti, M.V.; Valletta, A.; Campi, G.; Innocenti, D.; Perali, A.; Bianconi, A. Possible Fano resonance for high-Tc multi-gap superconductivity in p-Terphenyl doped by K at the Lifshitz transition. Eur. Phys. Lett. 2017, 118, 37003. [Google Scholar] [CrossRef]
- Eagles, D.M. Possible pairing without superconductivity at low carrier concentrations in bulk and thin-film superconducting semiconductor. Phys. Rev. 1969, 186, 456. [Google Scholar] [CrossRef]
- Leggett, A.J. Diatomic molecules and Cooper pairs. In Modern Trends in the Theory of Condensed Matter; Peralski, A., Przystawa, J.A., Eds.; Springer: Berlin, Germany, 1980. [Google Scholar]
- Regal, C.A.; Greiner, M.; Jin, D.S. Observation of Resonance Condensation of Fermionic Atom Pairs. Phys. Rev. Lett. 2004, 92, 040403. [Google Scholar] [CrossRef]
- Zwierlein, M.W.; Stan, C.A.; Schunck, C.H.; Raupach, S.M.F.; Kerman, A.J.; Ketterle, W. Condensation of Pairs of Fermionic Atoms near a Feshbach Resonance. Phys. Rev. Lett. 2004, 92, 120403. [Google Scholar] [CrossRef]
- Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of ultracold atomic Fermi gases. Rev. Mod. Phys. 2008, 80, 1215. [Google Scholar] [CrossRef]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885. [Google Scholar] [CrossRef]
- Calvanese Strinati, G.; Pieri, P.; Röpke, G.; Schuck, P.; Urban, M. The BCS-BEC crossover: From ultra-cold Fermi gases to nuclear systems. Phys. Rep. 2018, 738, 1. [Google Scholar] [CrossRef]
- Kasahara, S.; Watashige, T.; Hanaguri, T.; Kohsaka, Y.; Yamashita, T.; Shimoyama, Y.; Mizukami, Y.; Endo, R.; Ikeda, H.; Aoyama, K.; et al. Field-induced superconducting phase of FeSe in the BCS-BEC cross-over. Proc. Natl. Acad. Sci. USA 2014, 111, 16309. [Google Scholar] [CrossRef] [PubMed]
- Kasahara, S.; Yamashita, T.; Shi, A.; Kobayashi, R.; Shimoyama, Y.; Watashige, T.; Ishida, K.; Terashima, T.; Wolf, T.; Hardy, F.; et al. Giant superconducting fluctuations in the compensated semimetal FeSe at the BCS-BEC crossover. Nat. Commun. 2016, 7, 12843. [Google Scholar] [CrossRef] [PubMed]
- Rinott, S.; Chashka, K.B.; Ribak, A.; Rienks Emile, D.L.; Taleb-Ibrahimi, A.; Le Fevre, P.; Bertran, F.; Randeria, M.; Kanigel, A. Tuning across the BCS-BEC crossover in the multiband superconductor Fe1+ySexTe1−x: An angle-resolved photoemission study. Sci. Adv. 2017, 3, e1602372. [Google Scholar] [CrossRef] [PubMed]
- Innocenti, D.; Poccia, N.; Ricci, A.; Valletta, A.; Caprara, S.; Perali, A.; Bianconi, A. Resonant and crossover phenomena in a multiband superconductor: Tuning the chemical potential near a band edge. Phys. Rev. B 2010, 82, 184528. [Google Scholar] [CrossRef]
- Salasnich, L.; Shanenko, A.A.; Vagov, A.; Albino Aguiar, J.; Perali, A. Screening of pair fluctuations in superconductors with coupled shallow and deep bands: A route to higher-temperature superconductivity. Phys. Rev. B 2019, 100, 064510. [Google Scholar] [CrossRef]
- Tajima, H.; Yerin, Y.; Perali, A.; Pieri, P. Enhanced critical temperature, pairing fluctuation effects, and BCS-BEC crossover in a two band Fermi gas. Phys. Rev. B 2019, 99, 180503(R). [Google Scholar] [CrossRef]
- Hanaguri, T.; Kasahara, S.; Böker, J.; Eremin, I.; Shibauchi, T.; Matsuda, Y. Quantum Vortex Core and Missing Pseudogap in the Multiband BCS-BEC Crossover Superconductor FeSe. Phys. Rev. Lett. 2019, 122, 077001. [Google Scholar] [CrossRef]
- Perali, A.; Pieri, P.; Strinati, G.C.; Castellani, C. Pseudogap and spectral function from superconducting fluctuations to the bosonic limit. Phys. Rev. B 2002, 66, 024510. [Google Scholar] [CrossRef]
- Tsuchiya, S.; Watanabe, R.; Ohashi, Y. Single-particle properties and pseudogap effects in the BCS-BEC crossover regime of an ultracold Fermi gas above Tc. Phys. Rev. A 2009, 80, 033613. [Google Scholar] [CrossRef]
- Palestini, F.; Perali, A.; Pieri, P.; Strinati, G.C. Dispersions, weights, and widths of the single-particle spectral function in the normal phase of a Fermi gas. Phys. Rev. B 2012, 85, 024517. [Google Scholar] [CrossRef]
- Marsiglio, F.; Pieri, P.; Perali, A.; Palestini, F.; Strinati, G.C. Pairing effects in the normal phase of a two-dimensional Fermi gas. Phys. Rev. B 2015, 91, 054509. [Google Scholar] [CrossRef]
- Takahashi, H.; Nabeshima, F.; Ogawa, R.; Ohmichi, E.; Ohta, H.; Maeda, A. Superconducting fluctuations in FeSe investigated by precise torque magnetometry. Phys. Rev. B 2019, 99, 060503(R). [Google Scholar] [CrossRef]
- Gati, E.; Böhmer, A.E.; Bud’ko, S.L.; Canfield, P.C. Bulk superconductivity and role of fluctuations in the iron based superconductor FeSe at high pressures. Phys. Rev. Lett. 2019, 123, 167002. [Google Scholar] [CrossRef] [PubMed]
- Lubashevsky, Y.; Lahoud, E.; Chashka, K.; Podolsky, D.; Kanigel, A. Shallow pockets and very strong coupling superconductivity in FeSexTe1−x. Nat. Phys. 2012, 8, 309–312. [Google Scholar] [CrossRef]
- Zhang, R.; Cheng, Y.; Zhai, H.; Zhang, P. Orbital Feshbach Resonance in Alkali-Earth Atoms. Phys. Rev. Lett. 2015, 115, 135301. [Google Scholar] [CrossRef]
- Pagano, G.; Mancini, M.; Cappellini, G.; Livi, L.; Sias, C.; Catani, J.; Inguscio, M.; Fallani, L. Strongly Interacting Gas of Two-Electron Fermions at an Orbital Feshbach Reonance. Phys. Rev. Lett. 2015, 115, 265301. [Google Scholar] [CrossRef]
- Höfer, M.; Riegger, L.; Scazza, F.; Hofrichter, C.; Fernandes, D.R.; Parish, M.M.; Levinsen, J.; Bloch, I.; Folling, S. Observation of an Orbital Interaction-Induced Feshbach Resonance in 173Yb. Phys. Rev. Lett. 2015, 115, 265302. [Google Scholar] [CrossRef]
- He, L.; Hu, H.; Liu, X.-J. Two-band description of resonant supefluidity in atomic Fermi gases. Phys. Rev. A 2015, 91, 023622. [Google Scholar] [CrossRef]
- He, L.; Wang, J.; Peng, S.-G.; Liu, X.-J.; Hu, H. Strongly correlated Fermi superfluid near an orbital Feshbach resonance: Stability, equation of state, and Leggett mode. Phys. Rev. A 2016, 94, 043624. [Google Scholar] [CrossRef]
- Mondal, S.; Inotani, D.; Ohashi, Y. Single-particle Excitations and Strong-Coupling Effects in the BCS-BEC Crossover Regime of a Rare-Earth Fermi Gas with an Orbital Feshbach Resonance. J. Phys. Soc. Jpn. 2018, 87, 084302. [Google Scholar] [CrossRef]
- Sedrakian, A.; Clark, J.W. Superfluidity in nuclear systems and neutron stars. Eur. Phys. Jour. A 2019, 55, 167. [Google Scholar] [CrossRef]
- Ohashi, Y.; Tajima, H.; van Wyk, P. BCS-BEC crossover in cold atomic and in nuclear systems. Progr. Part. Nucl. Phys. 2019. [Google Scholar] [CrossRef]
- Nozières, P.; Schmitt-Rink, S. Bose condensation in an attractive fermion gas: From weak to strong coupling superconductivity. J. Low Temp. Phys. 1985, 59, 195–211. [Google Scholar] [CrossRef]
- Serene, J.W. Stability of two-dimensional Fermi liquids against pair fluctuations with large total momentum. Phys. Rev. B 1989, 40, 10873. [Google Scholar] [CrossRef] [PubMed]
- Wolf, S.; Vagov, A.; Shanenko, A.A.; Axt, V.M.; Perali, A.; Albino Aguiar, J. BCS-BEC crossover induced by a shallow band: Pushing standard superconductivity types apart. Phys. Rev. B 2017, 95, 094521. [Google Scholar] [CrossRef]
- Iskin, M.; Sá de Melo, C.A.R. Two-band superfluidity from the BCS to the BEC limit. Phys. Rev. B 2006, 74, 144517. [Google Scholar] [CrossRef]
- Yerin, Y.; Tajima, H.; Pieri, P.; Perali, A. Coexistence of giant Cooper pairs with a bosonic condensate and anomalous behavior of energy gaps in the BCS-BEC crossover of a two band superfluid Fermi gas. Phys. Rev. B 2019, 100, 104528. [Google Scholar] [CrossRef]
- Sá de Melo, C.A.R.; Randeria, M.; Engelbrecht, J.R. Crossover from BCS to Bose Superconductivity: Transition Temperature and Time-Dependent Ginzburg-Landau Theory. Phys. Rev. Lett. 1993, 71, 3202. [Google Scholar] [CrossRef]
- Pekker, D.; Babadi, M.; Sensarma, R.; Zinner, N.; Pollet, L.; Zwierlein, M.W.; Demler, E. Competition between Pairing and Ferromagnetic Instabilities in Ultracold Fermi Gases near Feshbach Resonances. Phys. Rev. Lett. 2011, 106, 05402. [Google Scholar] [CrossRef]
- Tan, S. Energetics of a strongly correlated Fermi gas. Ann. Phys. 2008, 323, 2952. [Google Scholar] [CrossRef]
- Tan, S. Large momentum part of a strongly correlated Fermi gas. Ann. Phys. 2008, 323, 2971. [Google Scholar] [CrossRef]
- Tan, S. Generalized virial theorem and pressure relation for a strongly correlated Fermi gas. Ann. Phys. 2008, 323, 2987. [Google Scholar] [CrossRef]
- Palestini, F.; Perali, A.; Pieri, P.; Strinati, G.C. Temperature and coupling dependence of the universal contact intensity for an ultracold Fermi gas. Phys. Rev. A 2010, 82, 021605(R). [Google Scholar] [CrossRef]
- Pini, M.; Pieri, P.; Strinati, G.C. Fermi gas throughout the BCS-BEC crossover: Comparative study of t matrix approaches with various degrees of self-consistency. Phys. Rev. B 2019, 99, 094502. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).