Mössbauer Spectroscopy of Triphylite (LiFePO4) at Low Temperatures
Abstract
:1. Introduction
2. Experimental and Computational Methods
3. Results and Discussion
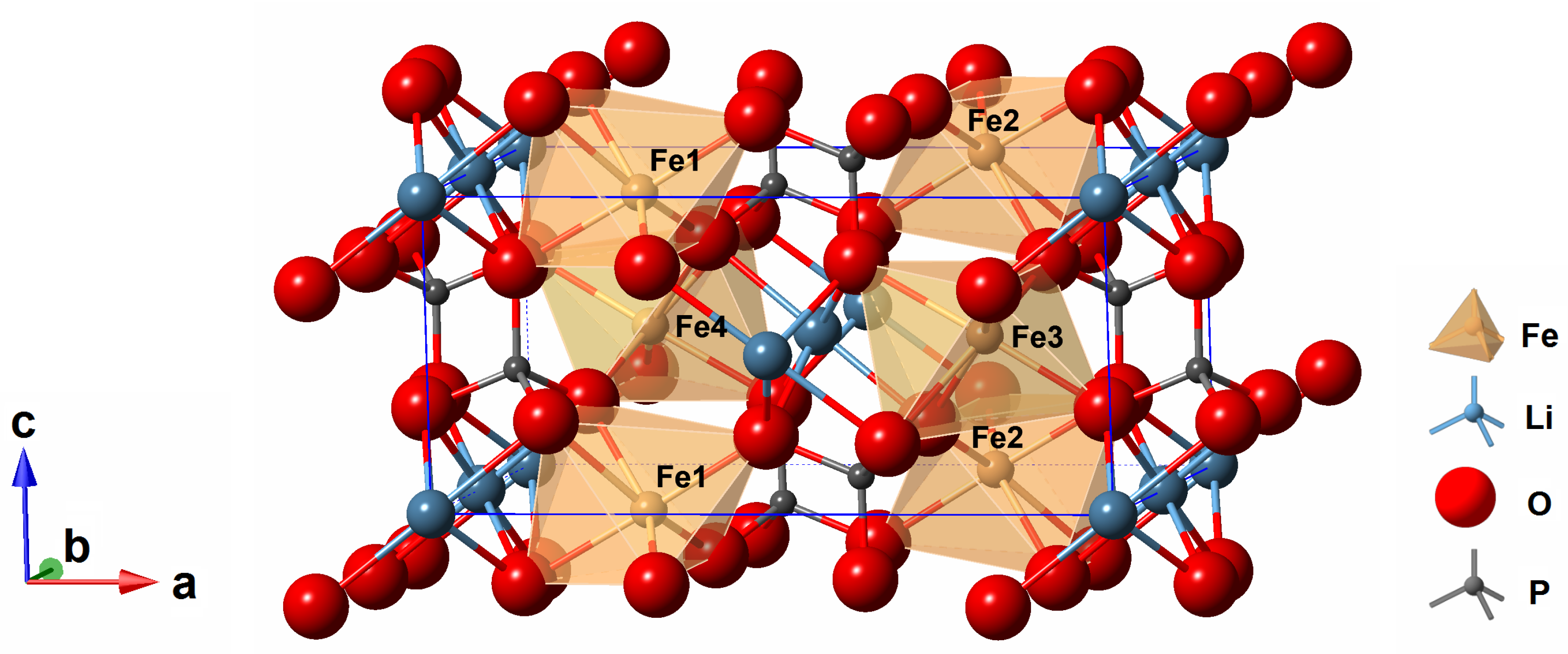
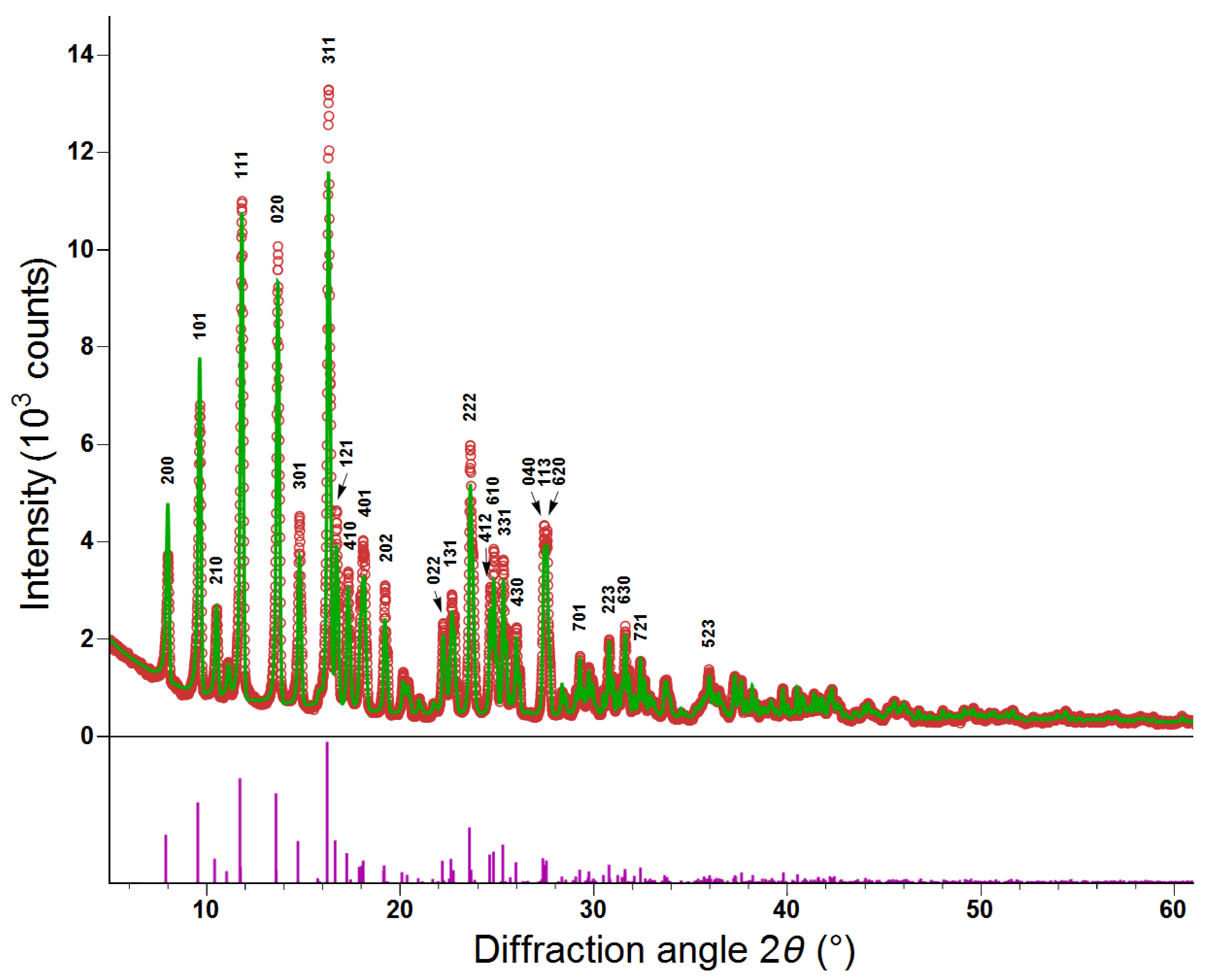
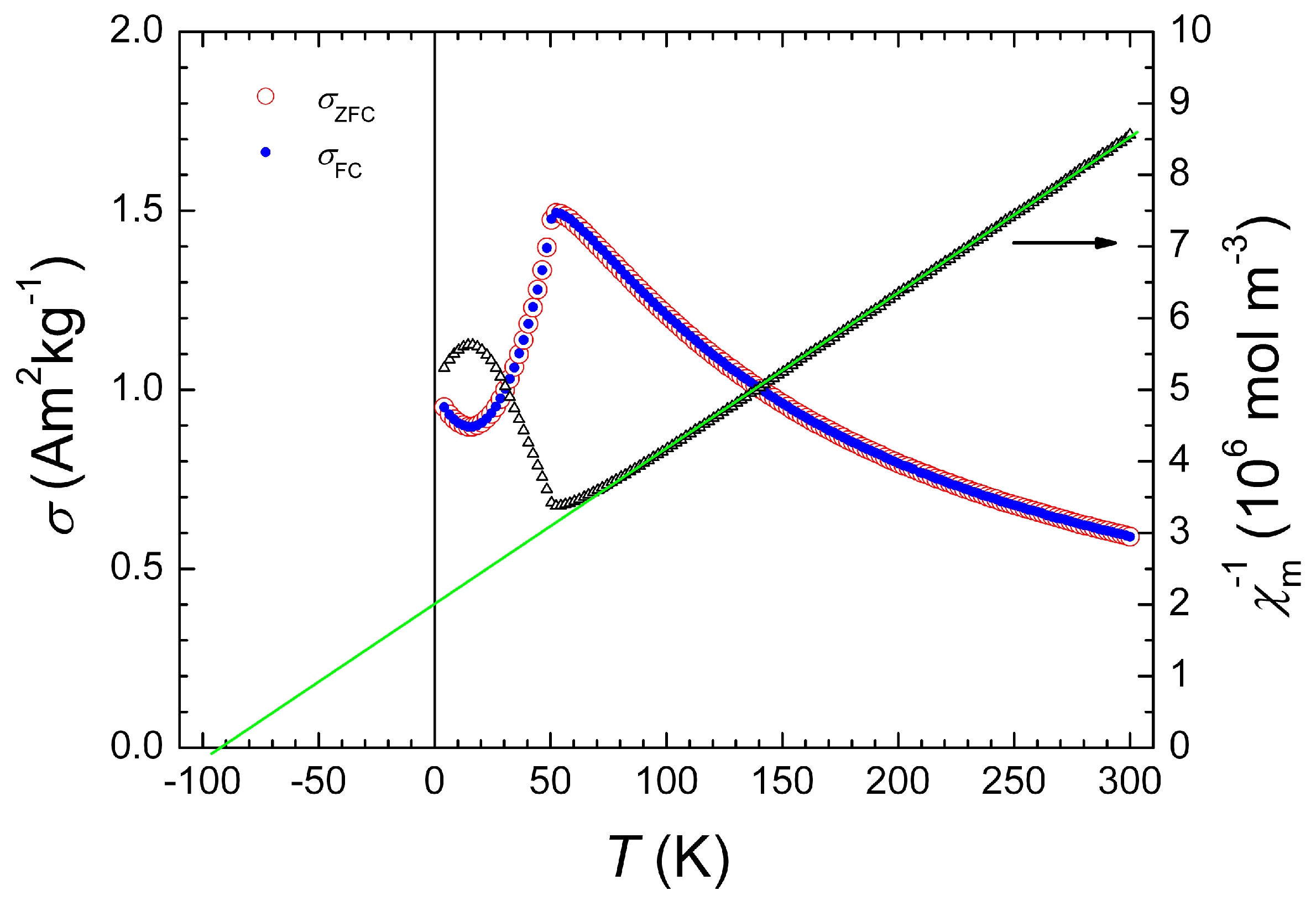
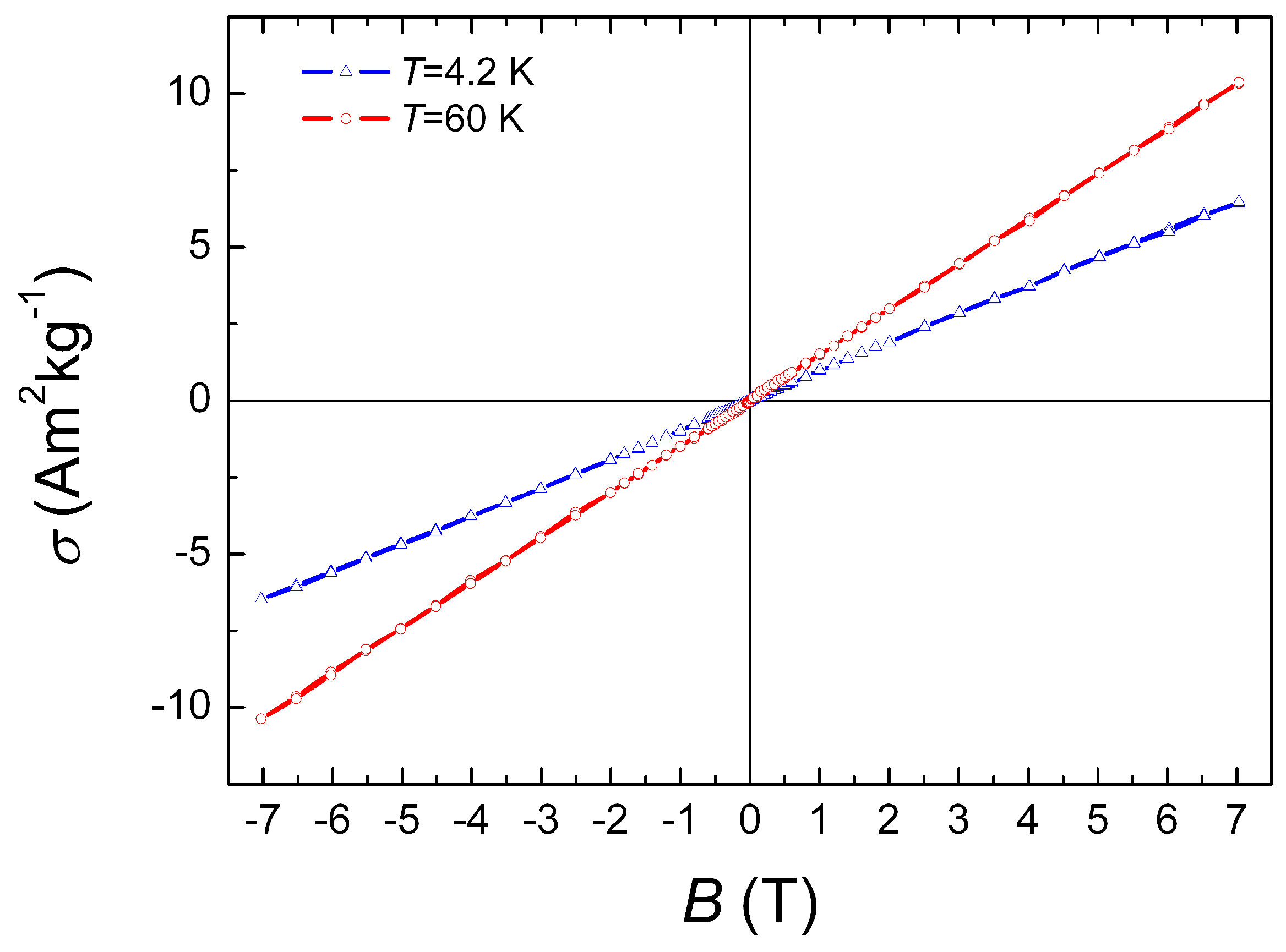
3.1. Structural and Magnetic Measurements
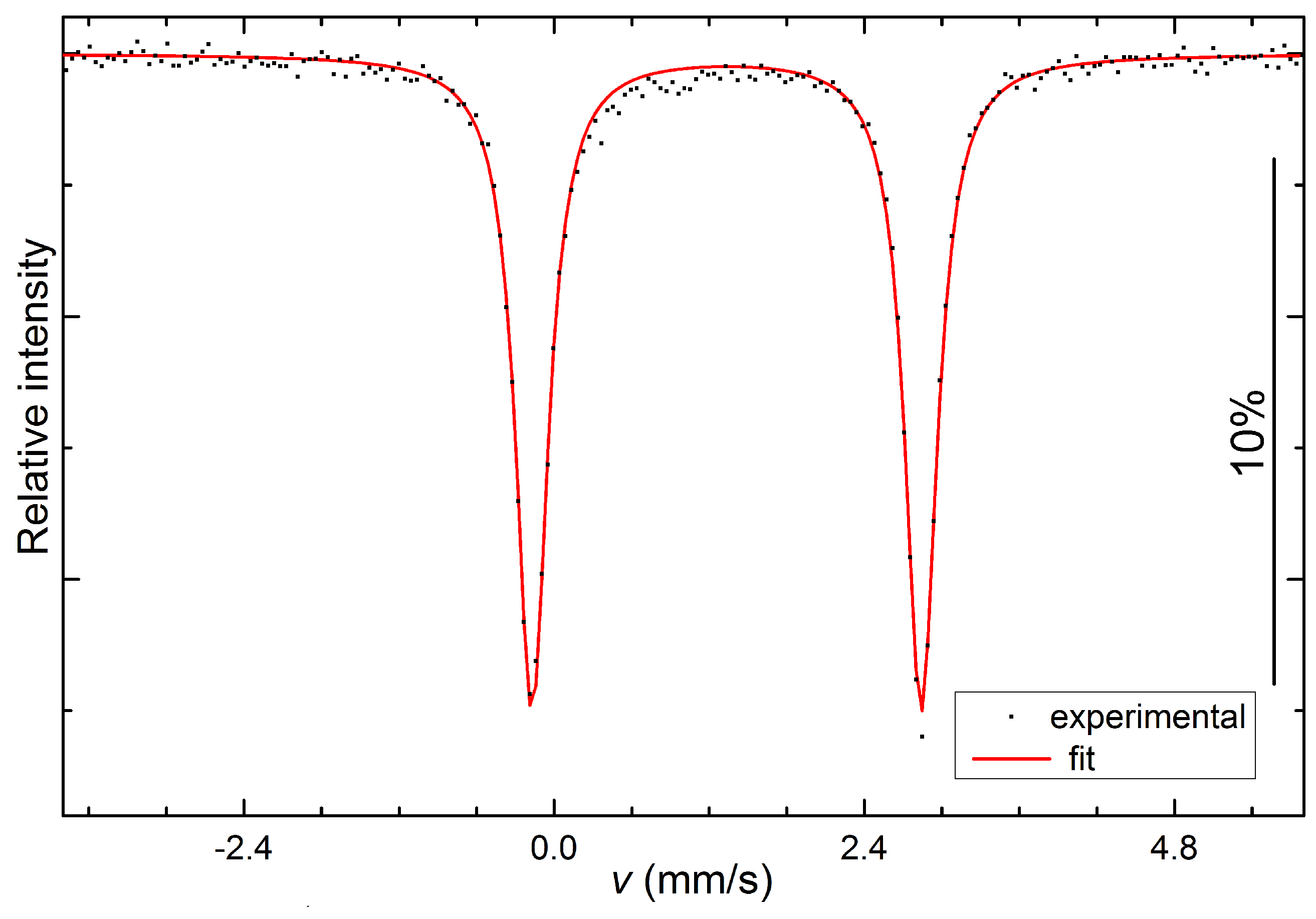
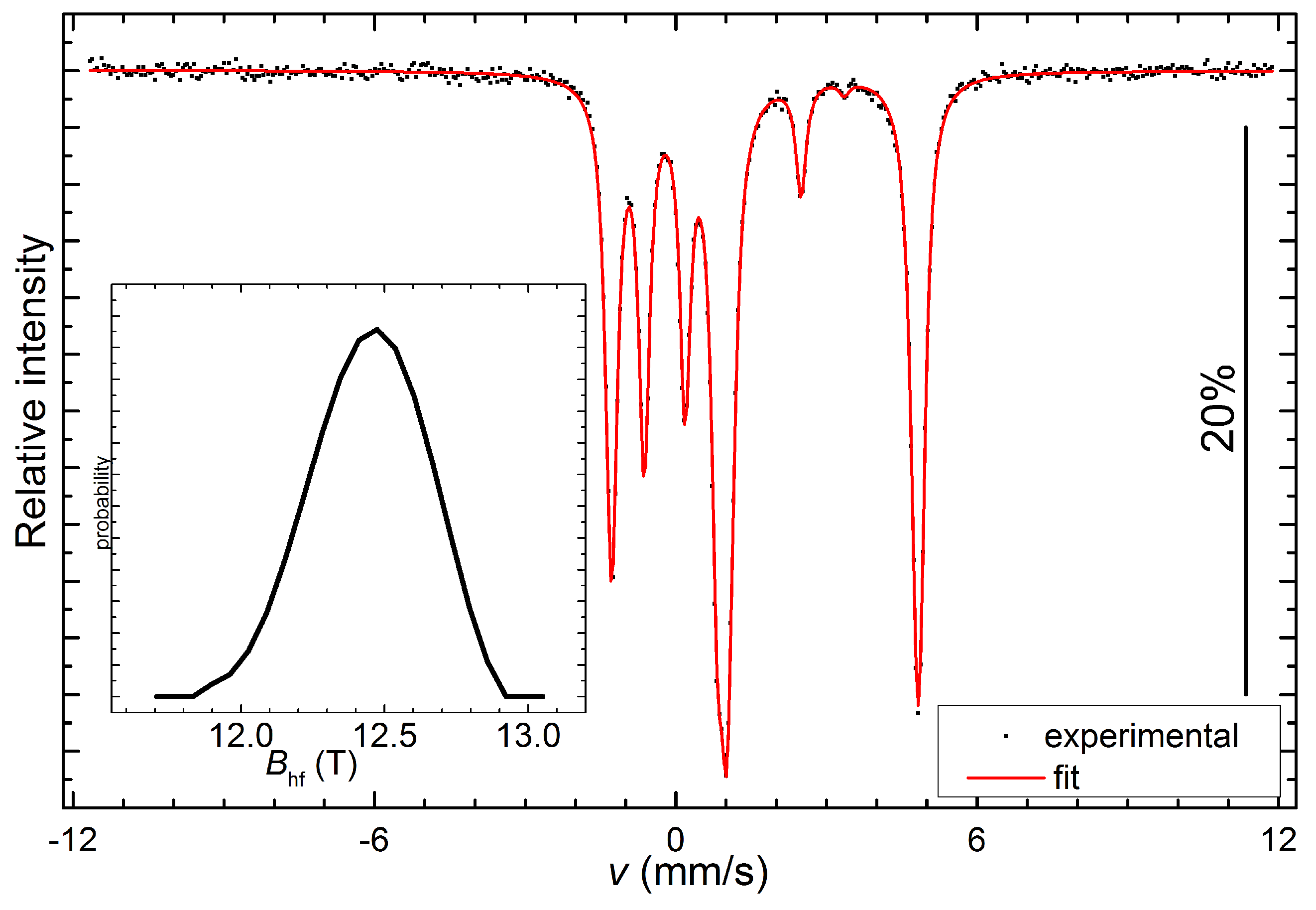
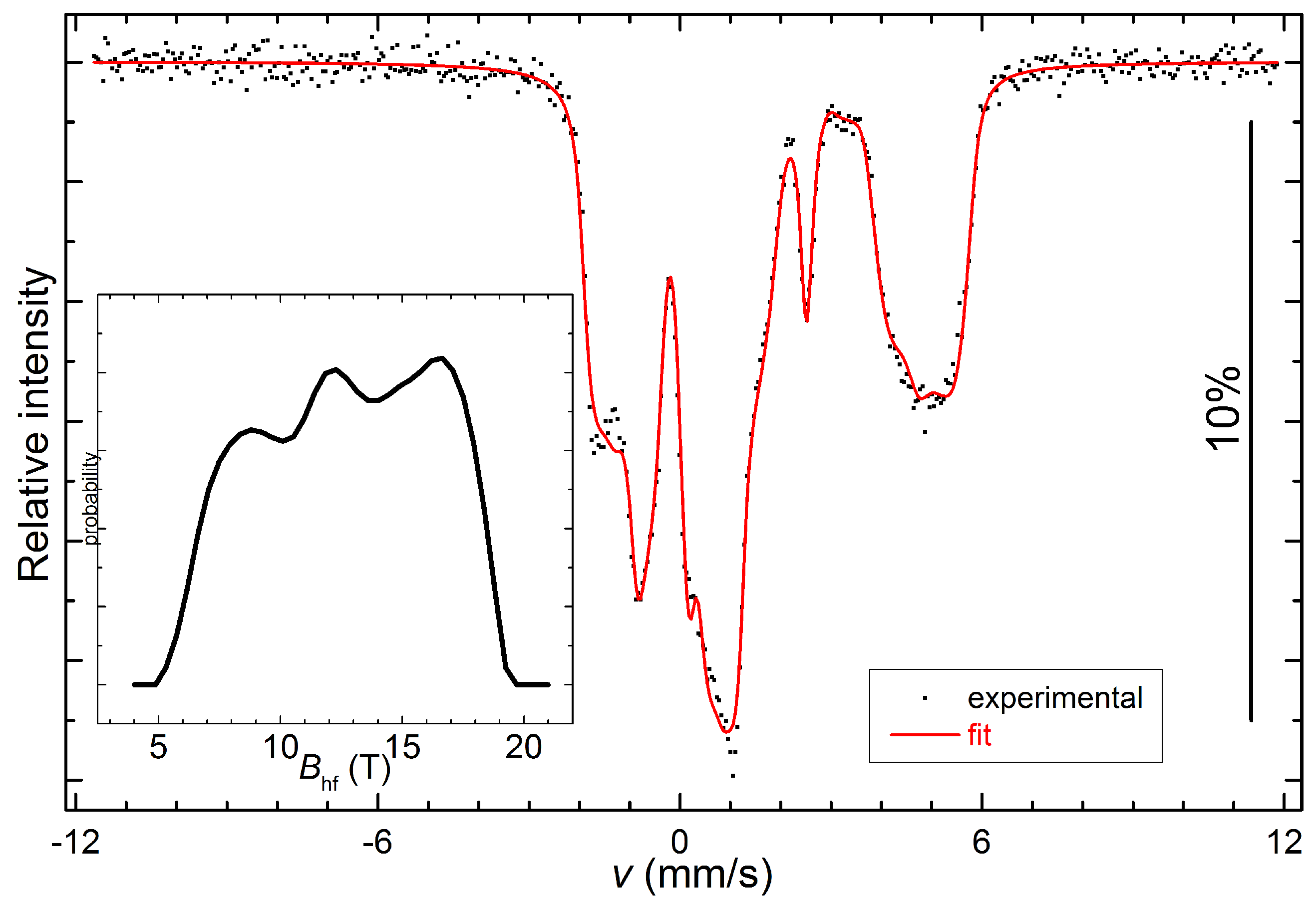
3.2. Mössbauer Spectroscopy of LiFePO
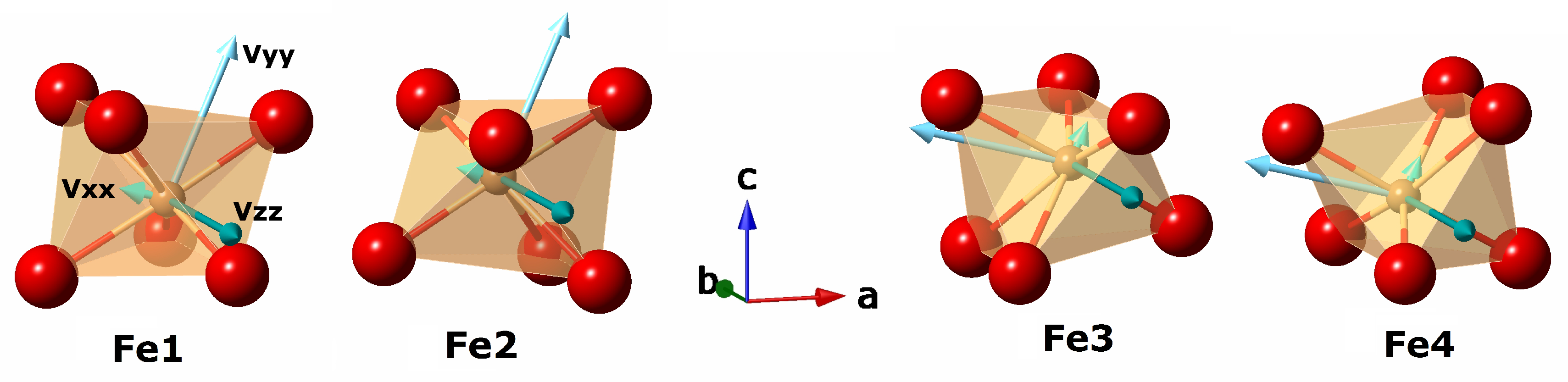
3.3. Theoretical Exploration of Magnetism and Hyperfine Interactions
4. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References and Notes
- Padhi, A.K.; Nanjundaswamy, K.S.; Goodenough, J.B. Phospho-olivines as Positive-Electrode Materials for Rechargeable Lithium Batteries. J. Electrochem. Soc. 1997, 144, 1188–1194. [Google Scholar] [CrossRef]
- Mauger, A.; Julien, C.M. Olivine Positive Electrodes for Li-Ion Batteries: Status and Perspectives. Batteries 2018, 4, 39. [Google Scholar] [CrossRef]
- Streltsov, V.A.; Belokoneva, E.L.; Tsirelson, V.G.; Hansen, N.K. Multipole analysis of the electron density in triphylite, LiFePO4, using X-ray diffraction data. Acta Cryst. B 1993, 49, 147–153. [Google Scholar] [CrossRef]
- Liu, C.; Neale, Z.G.; Cao, G. Understanding electrochemical potentials of cathode materials in rechargeable batteries. Mater. Today 2016, 19, 109–123. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.J.; Barbiellini, B.; Hafiz, H.; Basak, S.; Liu, J.; Richardson, T.; Shu, G.; Chou, F.; Weng, T.C.; et al. Why LiFePO4 is a safe battery electrode: Coulomb repulsion induced electron-state reshuffling upon lithiation. Phys. Chem. Chem. Phys. 2015, 17, 26369–26377. [Google Scholar] [CrossRef] [PubMed]
- Kuriplach, J.; Pulkkinen, A.; Barbiellini, B. First principles study of the impact of grain boundary formation in the cathode material LiFePO4. Condens. Matter 2019, 4, 80. [Google Scholar] [CrossRef]
- Lachal, M.; Bouchet, R.; Boulineau, A.; Surblé, S.; Rossignol, C.; Alloin, F.; Obbade, S. Remarkable impact of grains boundaries on the chemical delithiation kinetics of LiFePO4. Solid State Ion. 2017, 300, 187–194. [Google Scholar] [CrossRef]
- Jena, A.; Nanda, B.R.K. Unconventional magnetism and band gap formation in LiFePO4: Consequence of polyanion induced non-planarity. Sci. Rep. 2016, 6, 19573. [Google Scholar] [CrossRef]
- Santoro, R.P.; Newnham, R.E. Antiferromagnetism in LiFePO4. Acta Cryst. 1967, 22, 344–347. [Google Scholar] [CrossRef]
- Rousse, G.; Rodriguez-Carvajal, J.; Patoux, S.; Masquelier, C. Magnetic structures of the triphylite LiFePO4 and of its delithiated form FePO4. Chem. Mater. 2003, 15, 4082–4090. [Google Scholar] [CrossRef]
- Li, J.; Garlea, V.O.; Zarestky, J.L.; Vaknin, D. Spin-waves in antiferromagnetic single-crystal LiFePO4. Phys. Rev. B 2006, 73, 024410. [Google Scholar] [CrossRef]
- Liang, G.; Park, K.; Li, J.; Benson, R.E.; Vaknin, D.; Markert, J.T.; Croft, M.C. Anisotropy in magnetic properties and electronic structure of single-crystal LiFePO4. Phys. Rev. B 2008, 77, 064414. [Google Scholar] [CrossRef]
- Toft-Petersen, R.; Reehuis, M.; Jensen, T.B.S.; Andersen, N.H.; Li, J.; Le, M.D.; Laver, M.; Niedermayer, C.; Klemke, B.; Lefmann, K.; et al. Anomalous magnetic structure and spin dynamics in magnetoelectric LiFePO4. Phys. Rev. B 2015, 92, 024404. [Google Scholar] [CrossRef]
- Werner, J.; Sauerland, S.; Koo, C.; Neef, C.; Pollithy, A.; Skourski, Y.; Klingeler, R. High magnetic field phase diagram and failure of the magnetic Grüneisen scaling in LiFePO4. Phys. Rev. B 2019, 99, 214432. [Google Scholar] [CrossRef]
- Gütlich, P.; Bill, E.; Trautwein, A.X. Mössbauer Spectroscopy and Transition Metal Chemistry. Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Van Alboom, A.; De Grave, E.; Wohlfahrt-Mehrens, M. Temperature dependence of the Fe2+ Mössbauer parameters in triphylite (LiFePO4). Am. Mineral. 2011, 96, 408–416. [Google Scholar] [CrossRef]
- Rhee, C.H.; Lee, I.K.; Moon, S.J.; Kim, S.J.; Kim, C.S. Neutron diffraction and Mössbauer studies of LiFePO4. J. Korean Phys. Soc. 2011, 58, 472–475. [Google Scholar] [CrossRef]
- El Khalifi, M.; Lippens, P.E. First-principles investigation of the 57Fe Mössbauer parameters of LiFePO4 and FePO4. J. Phys. Chem. C 2016, 120, 28375–28389. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Matěj, Z.; Kužel, R.; Nichtová, L. XRD total pattern fitting applied to study of microstructure of TiO2 films. Powder Diffr. 2010, 25, 125–131. [Google Scholar] [CrossRef]
- Klencsár, Z.; Kuzmann, E.; Vértes, A. User-friendly software for Mössbauer spectrum analysis. J. Radioanal. Nucl. Chem. 1996, 210, 105–118. [Google Scholar] [CrossRef]
- Dufek, P.; Blaha, P.; Schwarz, K. Determination of the nuclear quadrupole moment of 57Fe. Phys. Rev. Lett. 1995, 75, 3545–3548. [Google Scholar] [CrossRef] [PubMed]
- Hamelet, S.; Gibot, P.; Casas-Cabanas, M.; Bonnin, D.; Grey, C.P.; Cabana, J.; Leriche, J.B.; Rodriguez-Carvajal, J.; Courty, M.; Levasseur, S.; et al. The effects of moderate thermal treatments under air on LiFePO4-based nano powders. J. Mater. Chem. 2009, 19, 3979–3991. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Madsen, G.K.H.; Kvasnicka, D.; Luitz, J.; Laskowski, R.; Tran, F.; Marks, L.D. WIEN2k, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties; Karlheinz Schwarz, Technische Universität Wien: Wien, Austria, 2001; ISBN 3-9501031-1-2. [Google Scholar]
- Singh, D. Ground-state properties of lanthanum: Treatment of extended-core states. Phys. Rev. B 1991, 43, 6388–6392. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, K.; Blaha, P.; Madsen, G.K.H. Electronic structure calculations of solids using the WIEN2k package for material sciences. Comp. Phys. Commun. 2002, 147, 71–76. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Kuneš, J.; Novák, P.; Schmid, R.; Blaha, P.; Schwarz, K. Electronic structure of fcc Th: Spin-orbit calculation with 6p1/2 local orbital extension. Phys. Rev. B 2001, 64, 153102. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Herzig, P. First-principles calculation of the electric field gradient of Li3N. Phys. Rev. Lett. 1985, 54, 1192–1195. [Google Scholar] [CrossRef]
- Singh, D.J.; Schwarz, K.; Blaha, P. Electric-field gradients in YBa2Cu3O7: Discrepancy between experimental and local-density-approximation charge distributions. Phys. Rev. B 1992, 46, 5849–5852. [Google Scholar] [CrossRef]
- Blügel, S.; Akai, H.; Zeller, R.; Dederichs, P.H. Hyperfine fields of 3d and 4d impurities in nickel. Phys. Rev. B 1987, 35, 3271–3283. [Google Scholar] [CrossRef]
- Novák, P. Calculation of Hyperfine Field in WIEN2k; Technical Report; Technische Universität Wien: Wien, Austria, 2006; Available online: http://www.wien2k.at/reg_user/textbooks/Bhf_3.pdf (accessed on 16 October 2019).
- Geller, S.; Durand, J.L. Refinement of the structure of LiMnPO4. Acta Cryst. 1960, 13, 325–331. [Google Scholar] [CrossRef]
- Herle, P.S.; Ellis, B.; Coombs, N.; Nazar, L.F. Nano-network electronic conduction in iron and nickel olivine phosphates. Nat. Mater. 2004, 3, 147–152. [Google Scholar] [CrossRef] [PubMed]
- Sugiyama, J.; Nozaki, H.; Harada, M.; Kamazawa, K.; Ofer, O.; Månsson, M.; Brewer, J.H.; Ansaldo, E.J.; Chow, K.H.; Ikedo, Y.; et al. Magnetic and diffusive nature of LiFePO4 investigated by muon spin rotation and relaxation. Phys. Rev. B 2011, 84, 054430. [Google Scholar] [CrossRef]
- Menil, F. Systematic trends of the 57Fe Mössbauer isomer shifts in (FeOn) and (FeFn) polyhedra. Evidence of a new correlation between the isomer shift and the inductive effect of the competing bond T-X (→ Fe) (where X is O or F and T any element with a formal positive charge). J. Phys. Chem. Solids 1985, 46, 763–789. [Google Scholar] [CrossRef]
- Kündig, W. Evaluation of Mössbauer spectra for 57Fe. Nucl. Instrum. Methods 1967, 48, 219–228. [Google Scholar] [CrossRef]
- Cococcioni, M.; Marzari, N. Energetics and cathode voltages of LiMPO4 olivines (M = Fe, Mn) from extended Hubbard functionals. Phys. Rev. Mater. 2019, 3, 033801. [Google Scholar] [CrossRef]
- Sobolev, A.V.; Presniakov, I.A.; Gippius, A.A.; Chernyavskii, I.V.; Schaedler, M.; Buettgen, N.; Ibragimov, S.A.; Morozov, I.V.; Shevelkov, A.V. Helical magnetic structure and hyperfine interactions in FeP studied by 57Fe Mössbauer spectroscopy and 31P NMR. J. Alloys Compd. 2016, 675, 277–285. [Google Scholar] [CrossRef]
- These angles obviously differ from the polar (θ) and azimuthal (φ) introduced in the context of MS spectral parameters.
- Kara, M.; Kurki-Suonio, K. Symmetrized multipole analysis of orientational distributions. Acta Cryst. A 1981, 37, 201–210. [Google Scholar] [CrossRef]
| Spectrum Type | T | I | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (K) | (T) | (T) | (mm/s) | (mm/s) | (%) | (mm/s) | (10 V/m) | () | () | (T) | ||
| D | 60 | 0 | – | 1.33(2) | 3.01(2) | 100 | 0.30(1) | – | – | – | – | – |
| O | 4.2 | 0 | 12.4(2) | 1.35(2) | 3.05(2) | 100 | 0.29(1) | 16.7 | 0.77(1) | 0 | 0 | ∼0.3 |
| O | 4.2 | 6 | 12.7(2) | 1.35(2) | 3.04(2) | 100 | 0.29(1) | 16.7 | 0.78(1) | ∼143 | ∼13 | ∼6 |
| Order | (meV) | (10 V/m) | (T) | |
|---|---|---|---|---|
| AF1 | 35.9 | 14.2 | 0.61 | 32.7 |
| AF2 | 00.0 | 14.1 | 0.63 | 32.8 |
| AF3 | 65.1 | 13.1 | 0.55 | 31.4 |
| MM | (meV) | (10 V/m) | () | (T) | |
|---|---|---|---|---|---|
| [100] | 4.55 | 14.0 | 0.65 | 0.08 | 30.5 |
| [010] | 0.00 | 14.1 | 0.63 | 0.11 | 11.7 |
| [001] | 9.19 | 14.1 | 0.62 | 0.03 | 43.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kmječ, T.; Kohout, J.; Dopita, M.; Veverka, M.; Kuriplach, J. Mössbauer Spectroscopy of Triphylite (LiFePO4) at Low Temperatures. Condens. Matter 2019, 4, 86. https://doi.org/10.3390/condmat4040086
Kmječ T, Kohout J, Dopita M, Veverka M, Kuriplach J. Mössbauer Spectroscopy of Triphylite (LiFePO4) at Low Temperatures. Condensed Matter. 2019; 4(4):86. https://doi.org/10.3390/condmat4040086
Chicago/Turabian StyleKmječ, Tomáš, Jaroslav Kohout, Milan Dopita, Miroslav Veverka, and Jan Kuriplach. 2019. "Mössbauer Spectroscopy of Triphylite (LiFePO4) at Low Temperatures" Condensed Matter 4, no. 4: 86. https://doi.org/10.3390/condmat4040086
APA StyleKmječ, T., Kohout, J., Dopita, M., Veverka, M., & Kuriplach, J. (2019). Mössbauer Spectroscopy of Triphylite (LiFePO4) at Low Temperatures. Condensed Matter, 4(4), 86. https://doi.org/10.3390/condmat4040086





