Classifying Induced Superconductivity in Atomically Thin Dirac-Cone Materials
Abstract
1. Introduction
2. Models Description
- Two-fluid Gorter-Casimir (GC) model [97,98], as follows:where φ0 = 2.06810−15 Wb is flux quantum and ξi (0) is the ground state in-plane coherence length of the i--band. This model is widely used for single-band superconductors ranging from 3D near-room-temperature superconducting hydrides [4,7,8,9,99,100] to 2D superconductors [88,89,95,101].
- Jones-Hulm-Chandrasekhar (JHC) model [102], as follows:
3. Results
3.1. Planar Sn/SLG/Sn Array
3.2. Planar Nb/BiSbTeSe2-Nanoribbon/Nb Junctions
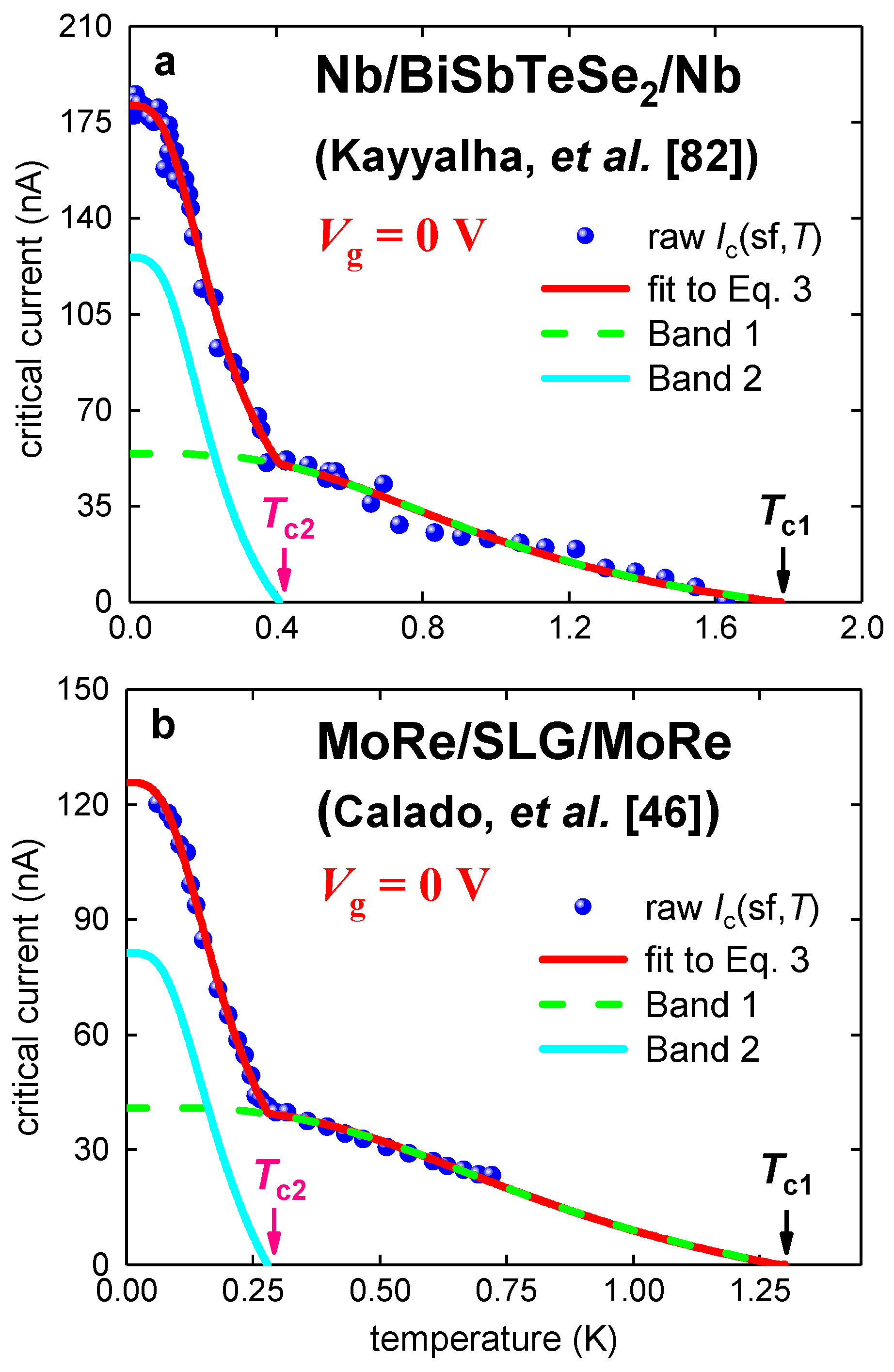
3.2.1. Nb/BiSbTeSe2-Nanoribbon/Nb Junctions
3.2.2. Nb/BiSbTeSe2-Nanoribbon/Nb Junction
3.3. Planar MoRe/SLG/MoRe Junction
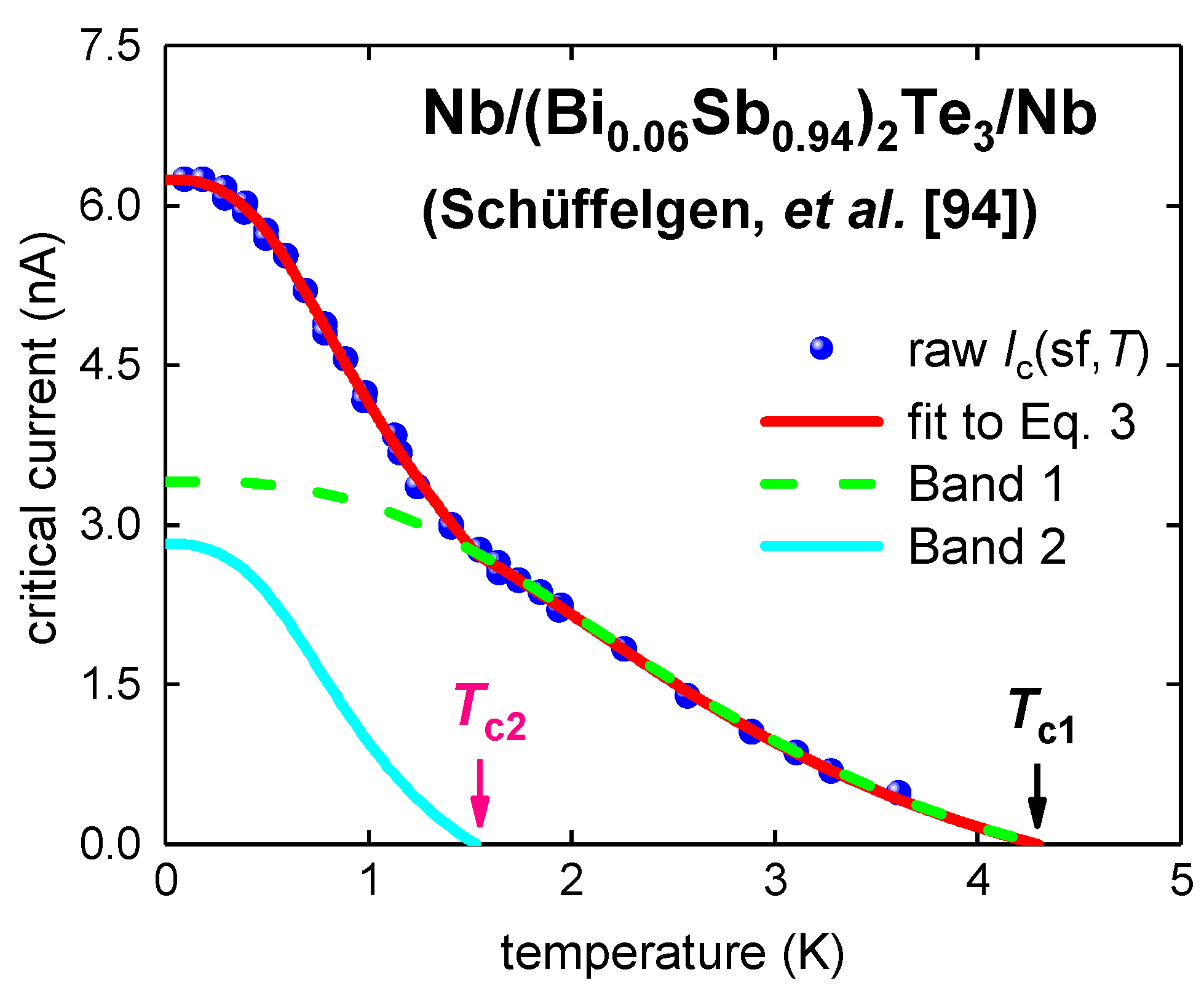
3.4. Planar Nb/(Bi0.06Sb0.94)2Te3-Nanoribbon/Nb Junction
4. Discussion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Hirsch, J.E.; Maple, M.B.; Marsiglio, F. Superconducting materials classes: Introduction and overview. Physica C 2015, 514, 1–8. [Google Scholar] [CrossRef]
- Uemura, Y.J.; Luke, G.M.; Sternlieb, B.J.; Brewer, J.H.; Carolan, J.F.; Hardy, W.N.; Kadono, R.; Kempton, J.R.; Kiefl, R.F.; Kreitzman, S.R. Universal correlations between Tc and (carrier density over effective mass) in high-Tc cuprate. Phys. Rev. Lett. 1989, 62, 2317–2320. [Google Scholar] [CrossRef] [PubMed]
- Uemura, Y.J. Condensation, excitation, pairing, and superfluid density in high-Tc superconductors: The magnetic resonance mode as a roton analogue and a possible spin-mediated pairing. J. Phys. Condens. Matter 2004, 16, S4515–S4540. [Google Scholar] [CrossRef]
- Drozdov, A.P.; Eremets, M.I.; Troyan, I.A.; Ksenofontov, V.; Shylin, S.I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 2015, 525, 73–76. [Google Scholar] [CrossRef] [PubMed]
- Somayazulu, M.; Ahart, M.; Mishra, A.K.; Geballe, Z.M.; Baldini, M.; Meng, Y.; Struzhkin, V.V.; Hemley, R.J. Evidence for superconductivity above 260 K in lanthanum superhydride at megabar pressures. Phys. Rev. Lett. 2019, 122, 027001. [Google Scholar] [CrossRef] [PubMed]
- Mozaffari, S.; Sun, D.; Minkov, V.S.; Drozdov, A.P.; Knyazev, D.; Betts, J.B.; Einaga, M.; Shimizu, K.; Eremets, M.I.; Balicas, L. Superconducting phase-diagram of H3S under high magnetic fields. Nat. Commun. 2019, 10, 2522. [Google Scholar] [CrossRef] [PubMed]
- Drozdov, A.P.; Kong, P.P.; Minkov, V.S.; Besedin, S.P.; Kuzovnikov, M.A.; Mozaffari, S.; Balicas, L.; Balakirev, F.F.; Graf, D.E.; Prakapenka, V.B. Superconductivity at 250 K in lanthanum hydride under high pressures. Nature 2019, 569, 528–531. [Google Scholar] [CrossRef] [PubMed]
- Talantsev, E.F. Classifying superconductivity in compressed H3S. Mod. Phys. Lett. B 2019, 33, 1950195. [Google Scholar] [CrossRef]
- Talantsev, E.F. Classifying hydrogen-rich superconductors. Mater. Res. Express 2019, 6, 106002. [Google Scholar] [CrossRef]
- Hardy, W.N.; Bonn, D.A.; Morgan, D.C.; Liang, R.; Zhang, K. Precision measurements of the temperature dependence of l in YBa2Cu3O6.95: Strong evidence for nodes in the gap function. Phys. Rev. Lett. 1993, 70, 3999–4002. [Google Scholar] [CrossRef]
- Bednorz, J.G.; Mueller, K.A. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z. Phys. B 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Won, H.; Maki, K. d-wave superconductor as a model of high-Tc superconductors. Phys. Rev. B 1994, 49, 1397–1402. [Google Scholar] [CrossRef] [PubMed]
- Hirsch, J.E. Hole superconductivity. Phys. Lett. A 1989, 134, 451–455. [Google Scholar] [CrossRef]
- Bianconi, A. On the possibility of new high Tc superconductors by producing metal heterostructures as in cuprate perovskites. Solid State Commun. 1994, 89, 933–936. [Google Scholar] [CrossRef]
- Bouquet, F.; Wang, Y.; Fisher, R.A.; Hinks, D.G.; Jorgensen, J.D.; Junod, A.; Phillips, N.E. Phenomenological two-gap model for the specific heat of MgB2. Europhys. Lett. 2001, 56, 856–862. [Google Scholar] [CrossRef]
- Bauer, E.; Paul, C.H.; Berger, S.T.; Majumdar, S.; Michor, H.; Giovannini, M.; Saccone, A.; Bianconi, A. Thermal conductivity of superconducting MgB2. J. Phys. Condens. Matter 2001, 13, L487–L494. [Google Scholar] [CrossRef][Green Version]
- Carrington, A.; Manzano, F. Magnetic penetration depth of MgB2. Physica C 2003, 385, 205–214. [Google Scholar] [CrossRef]
- Agrestini, S.; Metallo, C.; Filippi, M.; Simonelli, L.; Campi, G.; Sanipoli, C.; Liarokapis, E.; De Negri, S.; Giovannini, M.; Saccone, A. Substitution of Sc for Mg in MgB2: Effects on transition temperature and Kohn anomaly. Phys. Rev. B 2004, 70, 134514. [Google Scholar] [CrossRef]
- Mazin, I.I.; Singh, D.J.; Johannes, M.D.; Du, M.H. Unconventional superconductivity with a sign reversal in the order parameter of LaFeAsO1−xFx. Phys. Rev. Lett. 2008, 101, 057003. [Google Scholar] [CrossRef]
- Kuroki, K.; Onari, S.; Arita, R.; Usui, H.; Tanaka, Y.; Kontani, H.; Aoki, H. Unconventional pairing originating from the disconnected Fermi surfaces of superconducting LaFeAsO1−xFx. Phys. Rev. Lett. 2008, 101, 087004. [Google Scholar] [CrossRef] [PubMed]
- Innocenti, D.; Caprara, S.; Poccia, N.; Ricci, A.; Valletta, A.; Bianconi, A. Shape resonance for the anisotropic superconducting gaps near a Lifshitz transition: The effect of electron hopping between layers. Supercond. Sci. Technol. 2011, 24, 015012. [Google Scholar] [CrossRef]
- Bianconi, A.; Innocenti, D.; Valletta, A.; Perali, A. Shape resonances in superconducting gaps in a 2DEG at oxide-oxide interface. J. Phys. Conf. Ser. 2014, 529, 012007. [Google Scholar] [CrossRef]
- Hosono, H.; Tanabe, K.; Takayama-Muromachi, E.; Kageyama, H.; Yamanaka, S.; Kumakura, H.; Nohara, M.; Hiramatsu, H.; Fujitsu, S. Exploration of new superconductors and functional materials, and fabrication of superconducting tapes and wires of iron pnictides. Sci. Technol. Adv. Mater. 2015, 16, 033503. [Google Scholar] [CrossRef] [PubMed]
- Hosono, H.; Kuroki, K. Iron-based superconductors: Current status of materials and pairing mechanism. Physica C 2015, 514, 399–422. [Google Scholar] [CrossRef]
- Bianconi, A.; Jarlborg, T. Superconductivity above the lowest Earth temperature in pressurized sulfur hydride. EPL (Europhys. Lett.) 2015, 112, 37001. [Google Scholar] [CrossRef]
- Hirsch, J.E.; Marsiglio, F. Hole superconductivity in H2S and other sulfides under high pressure. Physica C 2015, 511, 45–49. [Google Scholar] [CrossRef][Green Version]
- Souza, T.X.R.; Marsiglio, F. Systematic study of the superconducting critical temperature in two- and three-dimensional tight-binding models: A possible scenario for superconducting H3S. Phys. Rev. B 2016, 94, 184509. [Google Scholar] [CrossRef]
- Harshman, D.R.; Fiory, A.T. Compressed H3S: Inter-sublattice Coulomb coupling in a high-Tc superconductor. J. Phys. Condens. Matter 2017, 29, 445702. [Google Scholar] [CrossRef]
- Bang, Y.; Stewart, G.R. Superconducting properties of the s±-wave state: Fe-based superconductors. J. Phys. Condens. Matter 2017, 29, 123003. [Google Scholar] [CrossRef]
- Kaplan, D.; Imry, Y. High-temperature superconductivity using a model of hydrogen bonds. Proc. Natl. Acad. Sci. USA 2018, 115, 5709–5713. [Google Scholar] [CrossRef]
- Moskvin, A.S.; Panov, Y.D. Topological structures in unconventional scenario for 2D cuprates. J. Supercond. Nov. Magn. 2019, 32, 61–84. [Google Scholar] [CrossRef]
- Ye, J.T.; Zhang, Y.J.; Akashi, R.; Bahramy, M.S.; Arita, R.; Iwasa, Y. Superconducting dome in a gate-tuned band insulator. Science 2012, 338, 1193–1196. [Google Scholar] [CrossRef] [PubMed]
- Qian, T.; Wang, X.-P.; Jin, W.-C.; Zhang, P.; Richard, P.; Xu, G.; Dai, X.; Fang, Z.; Guo, J.-G.; Chen, X.-L. Absence of a holelike Fermi surface for the iron-based K0.8Fe1.7Se2 superconductor revealed by angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 2011, 106, 187001. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, K.; Cho, K.; Shibauchi, T.; Kasahara, S.; Mizukami, Y.; Katsumata, R.; Tsuruhara, Y.; Terashima, T.; Ikeda, H.; Tanatar, M.A. A sharp peak of the zero-temperature penetration depth at optimal composition in BaFe2(As1–xPx)2. Science 2012, 336, 1554–1557. [Google Scholar] [CrossRef] [PubMed]
- Shang, T.; Philippe, J.; Verezhak, J.A.T.; Guguchia, Z.; Zhao, J.Z.; Chang, L.-J.; Lee, M.K.; Gawryluk, D.J.; Pomjakushina, E.; Shi, M. Nodeless superconductivity and preserved time-reversal symmetry in the noncentrosymmetric Mo3P superconductor. Phys. Rev. B 2019, 99, 184513. [Google Scholar] [CrossRef]
- Holm, R.; Meissner, W. Messungen mit Hilfe von flüssigem Helium. XIII. Kontaktwiderstand zwischen Supraleitern und Nichtsupraleitern (Measurements using liquid helium. XIII. Contact resistance between superconductors and non-superconductors). Z. Phys. 1932, 74, 715–735. [Google Scholar] [CrossRef]
- Natterer, F.D.; Ha, J.; Baek, H.; Zhang, D.; Cullen, W.G.; Zhitenev, N.B.; Kuk, Y.; Stroscio, J.A. Scanning tunneling spectroscopy of proximity superconductivity in epitaxial multilayer graphene. Phys. Rev. B 2016, 93, 045406. [Google Scholar] [CrossRef]
- Kim, H.; Miyata, Y.; Hasegawa, Y. Superconducting proximity effect on a Rashba-split Pb/Ge(111)-√3 × √3 surface. Supercond. Sci. Technol. 2016, 29, 084006. [Google Scholar] [CrossRef]
- Ambegaokar, V.; Baratoff, A. Tunneling between superconductors. Phys. Rev. Lett. 1963, 10, 486–489. [Google Scholar] [CrossRef]
- Ambegaokar, V.; Baratoff, A. Errata: Tunneling between superconductors. Phys. Rev. Lett. 1963, 11, 104. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Lee, G.H.; Kim, S.; Jhi, S.-H.; Lee, H.-J. Ultimately short ballistic vertical graphene Josephson junctions. Nat. Commun. 2015, 6, 6181. [Google Scholar] [CrossRef] [PubMed]
- Liao, M.; Zang, Y.; Guan, Z.; Li, H.; Gong, Y.; Zhu, K.; Hu, X.-P.; Zhang, D.; Xu, Y.; Wang, Y.-Y. Superconductivity in few-layer stanene. Nat. Phys. 2018, 14, 344–348. [Google Scholar] [CrossRef]
- Heersche, H.B.; Jarillo-Herrero, P.; Oostinga, J.B.; Vandersypen, L.M.K.; Morpurgo, A.F. Bipolar supercurrent in graphene. Nature 2007, 446, 56–59. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Skachko, I.; Andrei, E.Y. Josephson current and multiple Andreev reflections in graphene SNS junctions. Phys. Rev. B 2008, 77, 184507. [Google Scholar] [CrossRef]
- Calado, V.E.; Goswami, S.; Nanda, G.; Diez, M.; Akhmerov, A.R.; Watanabe, K.; Taniguchi, T.; Klapwijk, T.M.; Vandersypen, L.M.K. Ballistic Josephson junctions in edge-contacted graphene. Nat. Nanotechnol. 2015, 10, 761–764. [Google Scholar] [CrossRef] [PubMed]
- Ben Shalom, M.; Zhu, M.J.; Fal’ko, V.I.; Mishchenko, A.; Kretinin, A.V.; Novoselov, K.S.; Woods, C.R.; Watanabe, K.; Taniguchi, T.; Geim, A.K. Quantum oscillations of the critical current and high-field superconducting proximity in ballistic graphene. Nat. Phys. 2016, 12, 318–322. [Google Scholar] [CrossRef]
- Amet, F.; Ke, C.T.; Borzenets, I.V.; Wang, J.; Watanabe, K.; Taniguchi, T.; Deacon, R.S.; Yamamoto, M.; Bomze, Y.; Tarucha, S. Supercurrent in the quantum Hall regime. Science 2016, 352, 966–969. [Google Scholar] [CrossRef] [PubMed]
- Borzenets, I.V.; Amet, F.; Ke, C.T.; Draelos, A.W.; Wei, M.T.; Seredinski, A.; Watanabe, K.; Taniguchi, T.; Bomze, Y.; Yamamoto, M. Ballistic graphene Josephson junctions from the short to the long junction regimes. Phys. Rev. Lett. 2016, 117, 237002. [Google Scholar] [CrossRef] [PubMed]
- Island, J.O.; Steele, G.A.; van der Zant, H.S.J.; Castellanos-Gomez, A. Thickness dependent interlayer transport in vertical MoS2 Josephson. 2D Mater. 2016, 3, 031002. [Google Scholar] [CrossRef]
- Zhu, M.J.; Kretinin, A.V.; Thompson, M.D.; Bandurin, D.A.; Hu, S.; Yu, G.L.; Birkbeck, J.; Mishchenko, A.; Vera-Marun, I.J.; Watanabe, K. Edge currents shunt the insulating bulk in gapped graphene. Nat. Commun. 2017, 8, 14552. [Google Scholar] [CrossRef] [PubMed]
- Veldhorst, M.; Snelder, M.; Hoek, M.; Gang, T.; Guduru, V.K.; Wang, X.L.; Zeitler, U.; Van Der Wiel, W.G.; Golubov, A.A.; Hilgenkamp, H. Josephson supercurrent through a topological insulator surface state. Nat. Mater. 2012, 11, 417–421. [Google Scholar] [CrossRef] [PubMed]
- Kurter, C.; Finck, A.D.K.; Hor, Y.S.; Van Harlingen, D.J. Evidence for an anomalous current–phase relation in topological insulator Josephson junctions. Nat. Commun. 2015, 6, 7130. [Google Scholar] [CrossRef] [PubMed]
- Nanda, G.; Aguilera-Servin, J.L.; Rakyta, P.; Kormányos, A.; Kleiner, R.; Koelle, D.; Watanabe, K.; Taniguchi, T.; Vandersypen, L.M.K.; Goswami, S. Current-phase relation of ballistic graphene Josephson junctions. Nano Lett. 2017, 17, 3396–3401. [Google Scholar] [CrossRef] [PubMed]
- Yankowitz, M.; Chen, S.; Polshyn, H.; Watanabe, K.; Taniguchi, T.; Graf, D.; Young, A.F.; Dean, C.R. Tuning superconductivity in twisted bilayer graphene. Science 2019, 363, 1059–1064. [Google Scholar] [CrossRef] [PubMed]
- Lucignano, P.; Alfè, D.; Cataudella, V.; Ninno, D.; Cantele, G. The crucial role of atomic corrugation on the flat bands and energy gaps of twisted bilayer graphene at the “magic angle” θ∼1.08°. Phys. Rev. B 2019, 99, 195419. [Google Scholar] [CrossRef]
- Giubileo, F.; Romeo, F.; Di Bartolomeo, A.; Mizuguchi, Y.; Romano, P. Probing unconventional pairing in LaO0.5F0.5BiS2 layered superconductor by point contact spectroscopy. J. Phys. Chem. Solids 2018, 118, 192–199. [Google Scholar] [CrossRef]
- Kizilaslan, O.; Truccato, M.; Simsek, Y.; Aksan, M.A.; Koval, Y.; Müller, P. Interlayer tunneling spectroscopy of mixed-phase BSCCO superconducting whiskers. Supercond. Sci. Technol. 2016, 29, 065013. [Google Scholar] [CrossRef]
- Fête, A.; Rossi, L.; Augieri, A.; Senatore, C. Ionic liquid gating of ultra-thin YBa2Cu3O7-x films. Appl. Phys. Lett. 2016, 109, 192601. [Google Scholar] [CrossRef]
- Mueller, P.; Koval, Y.; Lazareva, Y.; Steiner, C.; Wurmehl, S.; Buechner, B.; Stuerzer, T.; Johrendt, D. C-axis transport of pnictide superconductors. Phys. Status Solidi B 2017, 254, 1600157. [Google Scholar] [CrossRef]
- Fête, A.; Senatore, C. Strong improvement of the transport characteristics of YBa2Cu3O7−x grain boundaries using ionic liquid gating. Sci. Rep. 2017, 8, 17703. [Google Scholar] [CrossRef] [PubMed]
- Paradiso, N.; Nguyen, A.-T.; Kloss, K.E.; Strunk, C. Phase slip lines in superconducting few-layer NbSe2 crystals. 2D Mater. 2019, 6, 025039. [Google Scholar] [CrossRef]
- Wu, Y.; Xiao, H.; Li, Q.; Li, X.; Li, Z.; Mu, G.; Jiang, D.; Hu, T.; Xie, X.M. The transport properties in graphene/single-unit-cell cuprates van der Waals heterostructure. Supercond. Sci. Technol. 2019, 32, 085007. [Google Scholar] [CrossRef]
- Guo, J.G.; Chen, X.; Jia, X.Y.; Zhang, Q.H.; Liu, N.; Lei, H.C.; Li, S.Y.; Gu, L.; Jin, S.F.; Chen, X.L. Quasi-two-dimensional superconductivity from dimerization of atomically ordered AuTe2Se4/3 cubes. Nat. Commun. 2017, 8, 871. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Guo, C.; Song, C.; Lai, X.; Li, H.; Zhao, W.; Zhang, H.; Mu, G.; Bu, K.; Lin, T. Enhanced superconductivity in restacked TaS2 nanosheets. J. Am. Chem. Soc. 2017, 139, 4623–4626. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Pan, J.; Guo, C.; Zhang, X.; Wang, L.; Hu, T.; Mu, G.; Huang, F.; Xie, X. Unusual evolution of Bc2 and Tc with inclined fields in restacked TaS2 nanosheets. NPJ Quantum Mater. 2018, 3, 34. [Google Scholar] [CrossRef]
- Desrat, W.; Moret, M.; Briot, O.; Ngo, T.-H.; Piot, B.A.; Jabakhanji, B.; Gil, B. Superconducting Ga/GaSe layers grown by van der Waals epitaxy. Mater. Res. Express 2018, 5, 045901. [Google Scholar] [CrossRef]
- Liu, C.; Lian, C.-S.; Liao, M.-H.; Wang, Y.; Zhong, Y.; Ding, C.; Li, W.; Song, C.-L.; He, K.; Ma, X.-C. Two-dimensional superconductivity and topological states in PdTe2 thin films. Phys. Rev. Mater. 2018, 2, 094001. [Google Scholar] [CrossRef]
- Peng, J.; Yu, Z.; Wu, J.; Zhou, Y.; Guo, Y.; Li, Z.; Zhao, J.; Wu, C.; Xie, Y. Disorder enhanced superconductivity toward TaS2 monolayer. ACS Nano 2018, 12, 9461–9466. [Google Scholar] [CrossRef]
- De La Barrera, S.C.; Sinko, M.R.; Gopalan, D.P.; Sivadas, N.; Seyler, K.L.; Watanabe, K.; Taniguchi, T.; Tsen, A.W.; Xu, X.; Xiao, D. Tuning Ising superconductivity with layer and spin-orbit coupling in two-dimensional transition-metal dichalcogenides. Nat. Commun. 2018, 9, 1427. [Google Scholar] [CrossRef]
- Di Castro, D.; Balestrino, G. Superconductivity in interacting interfaces of cuprate-based heterostructures. Supercond. Sci. Technol. 2018, 31, 073001. [Google Scholar] [CrossRef]
- Wu, Y.; He, J.; Liu, J.; Xing, H.; Mao, Z.; Liu, Y. Dimensional reduction and ionic gating induced enhancement of superconductivity in atomically thin crystals of 2H-TaSe2. Nanotechnology 2019, 30, 035702. [Google Scholar] [CrossRef]
- Talantsev, E.F. Angular dependence of the upper critical field in randomly restacked 2D superconducting nanosheets. Supercond. Sci. Technol. 2019, 32, 015013. [Google Scholar] [CrossRef]
- Pankratov, O.A.; Pakhomov, S.V.; Volkov, B.A. Supersymmetry in heterojunctions: Band-inverting contact on the basis of Pb1-xSnxTe and Hg1-xCdxTe. Solid State Commun. 1987, 61, 93–96. [Google Scholar] [CrossRef]
- König, M.; Wiedmann, S.; Brüne, C.; Roth, A.; Buhmann, H.; Molenkamp, L.W.; Qi, X.-L.; Zhang, S.-C. Quantum spin Hall insulator state in HgTe quantum wells. Science 2007, 318, 766–770. [Google Scholar] [CrossRef] [PubMed]
- Charpentier, S.; Galletti, L.; Kunakova, G.; Arpaia, R.; Song, Y.; Baghdadi, R.; Wang, S.M.; Kalaboukhov, A.; Olsson, E.; Tafuri, F. Induced unconventional superconductivity on the surface states of Bi2Te3 topological insulator. Nat. Commun. 2017, 8, 2019. [Google Scholar] [CrossRef] [PubMed]
- Qu, D.-X.; Teslich, N.E.; Dai, Z.; Chapline, G.F.; Schenkel, T.; Durham, S.R.; Dubois, J. Onset of a two-dimensional superconducting phase in a topological-insulator—Normal-metal Bi1−xSbx/Pt junction fabricated by ion-beam techniques. Phys. Rev. Lett. 2018, 121, 037001. [Google Scholar] [CrossRef]
- Li, C.-Z.; Li, C.; Wang, L.-X.; Wang, S.; Liao, Z.-M.; Brinkman, A.; Yu, D.-P. Bulk and surface states carried supercurrent in ballistic Nb-Dirac semimetal Cd3As2 nanowire-Nb junctions. Phys. Rev. B 2018, 97, 115446. [Google Scholar] [CrossRef]
- Schüffelgen, P.; Schmitt, T.; Schleenvoigt, M.; Rosenbach, D.; Perla, P.; Jalil, A.R.; Mussler, G.; Lepsa, M.; Schäpers, T.; Grützmacher, D. Exploiting topological matter for Majorana physics and devices. Solid State Electron. 2019, 155, 99–104. [Google Scholar] [CrossRef]
- Kurter, C.; Finck, A.D.K.; Huemiller, E.D.; Medvedeva, J.; Weis, A.; Atkinson, J.M.; Qiu, Y.; Shen, L.; Lee, S.H.; Vojta, T. Conductance spectroscopy of exfoliated thin flakes of NbxBi2Se3. Nano Lett. 2019, 19, 38–45. [Google Scholar] [CrossRef] [PubMed]
- German, R.; Komleva, E.V.; Stein, P.; Mazurenko, V.G.; Wang, Z.; Streltsov, S.V.; Ando, Y.; Van Loosdrecht, P.H.M. Phonon mode calculations and Raman spectroscopy of the bulk-insulating topological insulator BiSbTeSe2. Phys. Rev. Mater. 2019, 3, 054204. [Google Scholar] [CrossRef]
- Kayyalha, M.; Kargarian, M.; Kazakov, A.; Miotkowski, I.; Galitski, V.M.; Yakovenko, V.M.; Rokhinson, L.P.; Chen, Y.P. Anomalous low-temperature enhancement of supercurrent in topological-insulator nanoribbon Josephson junctions: Evidence for low-energy Andreev bound states. Phys. Rev. Lett. 2019, 122, 047003. [Google Scholar] [CrossRef] [PubMed]
- Miyazaki, A.; Delsolaro, W.V. Determination of the Bardeen–Cooper–Schrieffer material parameters of the HIE-ISOLDE superconducting resonator. Supercond. Sci. Technol. 2019, 32, 025002. [Google Scholar] [CrossRef]
- Shearer, C.J.; Slattery, A.D.; Stapleton, A.J.; Shapter, J.G.; Gibson, C.T. Accurate thickness measurement of graphene. Nanotechnology 2016, 27, 125704. [Google Scholar] [CrossRef] [PubMed]
- Talantsev, E.F.; Crump, W.P.; Tallon, J.L. Two-band induced superconductivity in single-layer graphene and topological insulator bismuth selenide. Supercond. Sci. Technol. 2018, 31, 015011. [Google Scholar] [CrossRef]
- Talantsev, E.F.; Crump, W.P.; Island, J.O.; Xing, Y.; Sun, Y.; Wang, J.; Tallon, J.L. On the origin of critical temperature enhancement in atomically thin superconductors. 2D Mater. 2017, 4, 025072. [Google Scholar] [CrossRef]
- Wang, Q.-Y.; Li, Z.; Zhang, W.-H.; Zhang, Z.-C.; Zhang, J.-S.; Li, W.; Ding, H.; Ou, Y.-B.; Deng, P.; Chang, K. Interface-induced high-temperature superconductivity in single unit-cell FeSe films on SrTiO3. Chin. Phys. Lett. 2012, 29, 037402. [Google Scholar] [CrossRef]
- Zhang, W.-H.; Sun, Y.; Zhang, J.-S.; Li, F.-S.; Guo, M.-H.; Zhao, Y.-F.; Zhang, H.-M.; Peng, J.-P.; Xing, Y.; Wang, H.-C. Direct observation of high-temperature superconductivity in one-unit-cell FeSe films. Chin. Phys. Lett. 2014, 31, 017401. [Google Scholar] [CrossRef]
- Ge, J.F.; Liu, Z.-L.; Liu, C.; Gao, C.-L.; Qian, D.; Xue, Q.-K.; Liu, Y.; Jia, J.-F. Superconductivity above 100 K in single-layer FeSe films on doped SrTiO3. Nat. Mater. 2015, 14, 285–289. [Google Scholar] [CrossRef]
- Zhang, H.-M.; Sun, Y.; Li, W.; Peng, J.-P.; Song, C.-L.; Xing, Y.; Zhang, Q.; Guan, J.; Li, Z.; Zhao, Y. Detection of a superconducting phase in a two-atom layer of hexagonal Ga film grown on semiconducting GaN(0001). Phys. Rev. Lett. 2015, 114, 107003. [Google Scholar] [CrossRef]
- Xing, Y.; Zhang, H.-M.; Fu, H.-L.; Liu, H.; Sun, Y.; Peng, J.-P.; Wang, F.; Lin, X.; Ma, X.-C.; Xue, Q.-K. Quantum Griffiths singularity of superconductor-metal transition in Ga thin films. Science 2015, 350, 542–545. [Google Scholar] [CrossRef] [PubMed]
- Navarro-Moratalla, E.; Island, J.O.; Manãs-Valero, S.; Pinilla-Cienfuegos, E.; Castellanos-Gomez, A.; Quereda, J.; Rubio-Bollinger, G.; Chirolli, L.; Silva-Guillén, J.A.; Agraït, N. Enhanced superconductivity in atomically thin TaS2. Nat. Commun. 2016, 7, 11043. [Google Scholar] [CrossRef] [PubMed]
- Rhodes, D.; Yuan, N.F.; Jung, Y.; Antony, A.; Hua Wang, H.; Kim, B.; Chiu, Y.-C.; Taniguchi, T.; Watanabe, K.; Barmak, K. Enhanced superconductivity in monolayer Td-MoTe2 with tilted Ising spin texture. arXiv 2019, arXiv:1905.06508. [Google Scholar]
- Schüffelgen, P.; Rosenbach, D.; Li, C.; Schmitt, T.; Schleenvoigt, M.; Jalil, A.R.; Kölzer, J.; Wang, M.; Bennemann, B.; Parlak, U. Boosting transparency in topological Josephson junctions via stencil lithography. arXiv 2018, arXiv:1711.01665. [Google Scholar]
- Han, Z.; Allain, A.; Arjmandi-Tash, H.; Tikhonov, K.; Feigel’man, M.; Sacépé, B.; Bouchiat, V. Collapse of superconductivity in a hybrid tin-graphene Josephson junction array. Nat. Phys. 2014, 10, 380–386. [Google Scholar] [CrossRef]
- Gross, F.; Chandrasekhar, B.S.; Einzel, D.; Andres, K.; Hirschfeld, P.J.; Ott, H.R.; Beuers, J.; Fisk, Z.; Smith, J.L. Anomalous temperature dependence of the magnetic field penetration depth in superconducting UBe13. Z. Phys. B Condens. Matter 1986, 64, 175–188. [Google Scholar] [CrossRef]
- Gorter, C.J.; Casimir, H. On supraconductivity I. Physica 1934, 1, 306–320. [Google Scholar] [CrossRef]
- Poole, P.P.; Farach, H.A.; Creswick, R.J.; Prozorov, R. Superconductivity, 2nd ed.; Associated Press: London, UK, 2007; pp. 52–55. [Google Scholar]
- Talantsev, E.F.; Crump, W.P.; Storey, J.G.; Tallon, J.L. London penetration depth and thermal fluctuations in the sulphur hydride 203 K superconductor. Ann. Phys. 2017, 529, 1600390. [Google Scholar] [CrossRef]
- Mozaffari, S.; Balicas, L.; Minkov, V.S.; Knyazev, D.; Eremets, M.I.; Einaga, M.; Shimizu, K.; Sun, D.; Balakirev, F.F. Superconducting Hydride under Extreme Field and Pressure; LA-UR-18-30460; Los Alamos National Laboratory: Los Alamos, NM, USA, 2019. [Google Scholar]
- Pal, B.; Joshi, B.P.; Chakraborti, H.; Jain, A.K.; Barick, B.K.; Ghosh, K.; Bhunia, S.; Laha, A.; Dhar, S.; Gupta, K.D. Experimental evidence of a very thin superconducting layer in epitaxial indium nitride. Supercond. Sci. Technol. 2019, 32, 015009. [Google Scholar] [CrossRef]
- Jones, C.K.; Hulm, J.K.; Chandrasekhar, B.S. Upper critical field of solid solution alloys of the transition elements. Rev. Mod. Phys. 1964, 36, 74–76. [Google Scholar] [CrossRef]
- Helfand, E.; Werthamer, N.R. Temperature and purity dependence of the superconducting critical field, Hc2. II. Phys. Rev. 1966, 147, 288–294. [Google Scholar] [CrossRef]
- Werthamer, N.R.; Helfand, E.; Hohenberg, P.C. Temperature and purity dependence of the superconducting critical field, Hc2. III. Electron spin and spin-orbit effects. Phys. Rev. 1966, 147, 295–302. [Google Scholar] [CrossRef]
- Baumgartner, T.; Eisterer, M.; Weber, H.W.; Fluekiger, R.; Scheuerlein, C.; Bottura, L. Effects of neutron irradiation on pinning force scaling in state-of-the-art Nb3Sn wires. Supercond. Sci. Technol. 2014, 27, 015005. [Google Scholar] [CrossRef]
- Gor’kov, L.P. The critical supercooling field in superconductivity theory. Sov. Phys. JETP 1960, 10, 593–599. [Google Scholar]
- Suhl, H.; Matthias, B.T.; Walker, L.R. Bardeen-Cooper-Schrieffer theory of superconductivity in the case of overlapping bands. Phys. Rev. Lett. 1959, 3, 552–554. [Google Scholar] [CrossRef]
- Nagamatsu, J.; Nakagawa, N.; Muranaka, T.; Zenitani, Y.; Akimitsu, J. Superconductivity at 39 K in magnesium diboride. Nature 2001, 410, 63–64. [Google Scholar] [CrossRef]
- Kamihara, Y.; Hiramatsu, H.; Hirano, M.; Kawamura, R.; Yanagi, H.; Kamiya, T.; Hosono, H. Iron-based layered superconductor: LaOFeP. J. Am. Chem. Soc. 2006, 128, 10012–10013. [Google Scholar] [CrossRef]
- Buzea, C.; Yamashita, T. Review of the superconducting properties of MgB2. Supercond. Sci. Technol. 2001, 14, R115–R146. [Google Scholar] [CrossRef]
- Zehetmayer, M. A review of two-band superconductivity: Materials and effects on the thermodynamic and reversible mixed-state properties. Supercond. Sci. Technol. 2013, 26, 043001. [Google Scholar] [CrossRef]
- Hänisch, J.; Iida, K.; Hühne, R.; C Tarantini, C. Fe-based superconducting thin films—preparation and tuning of superconducting properties. Supercond. Sci. Technol. 2019, 32, 093001. [Google Scholar] [CrossRef]
- Shalnikov, A. Superconducting thin films. Nature 1938, 132, 74. [Google Scholar] [CrossRef]
- Cohen, R.W.; Abeles, B. Superconductivity in granular aluminum films. Phys. Rev. 1968, 168, 444–450. [Google Scholar] [CrossRef]
- Pracht, U.S.; Bachar, N.; Benfatto, L.; Deutscher, G.; Farber, E.; Dressel, M.; Scheffler, M. Enhanced Cooper pairing versus suppressed phase coherence shaping the superconducting dome in coupled aluminum nanograins. Phys. Rev. B 2016, 93, 100503(R). [Google Scholar] [CrossRef]
- Pracht, U.S.; Cea, T.; Bachar, N.; Deutscher, G.; Farber, E.; Dressel, M.; Scheffler, M.; Castellani, C.; García-García, A.M.; Benfatto, L. Optical signatures of the superconducting Goldstone mode in granular aluminum: Experiments and theory. Phys. Rev. B 2017, 96, 094514. [Google Scholar] [CrossRef]
- Eilenberger, G. Transformation of Gorkov’s equation for type II superconductors into transport-like equations. Z. Phys. 1968, 214, 195–213. [Google Scholar] [CrossRef]
- Usadel, K.D. Generalized diffusion equation for superconducting alloys. Phys. Rev. Lett. 1970, 25, 507–509. [Google Scholar] [CrossRef]
- Rusanov, A.Y.; Hesselberth, M.B.S.; Aarts, J. Depairing currents in superconducting films of Nb and amorphous MoGe. Phys. Rev. B 2004, 70, 024510. [Google Scholar] [CrossRef]
- Sasaki, S.; Segawa, K.; Ando, Y. Superconductor derived from a topological insulator heterostructure. Phys. Rev. B 2014, 90, 220504. [Google Scholar] [CrossRef]
- Andersen, L.; Wang, Z.; Lorenz, T.; Ando, Y. Nematic superconductivity in Cu1.5(PbSe)5(Bi2Se3)6. Phys. Rev. B 2018, 98, 220512(R). [Google Scholar] [CrossRef]
- Reyren, N.; Thiel, S.; Caviglia, A.D.; Fitting Kourkoutis, L.; Hammerl, G.; Richter, C.; Schneider, C.W.; Kopp, T.; Rüetschi, A.-S.; Jaccard, D. Superconducting interfaces between insulating oxides. Science 2007, 317, 1196–1199. [Google Scholar] [CrossRef]
- Gozar, A.; Logvenov, G.; Fitting Kourkoutis, L.; Bollinger, A.T.; Giannuzzi, L.A.; Muller, D.A.; Bozovic, I. High-temperature interface superconductivity between metallic and insulating copper oxides. Nature 2008, 455, 782–785. [Google Scholar] [CrossRef] [PubMed]
- Campi, G.; Bianconi, A.; Poccia, N.; Bianconi, G.; Barba, L.; Arrighetti, G.; Innocenti, D.; Karpinski, J.; Zhigadlo, N.D.; Kazakov, S.M. Inhomogeneity of charge-density-wave order and quenched disorder in a high-Tc superconductor. Nature 2015, 525, 359–362. [Google Scholar] [CrossRef] [PubMed]
- Ricci, A.; Poccia, N.; Joseph, B.; Innocenti, D.; Campi, G.; Zozulya, A.; Westermeier, F.; Schavkan, A.; Coneri, F.; Bianconi, A. Direct observation of nanoscale interface phase in the superconducting chalcogenide KxFe2−ySe2 with intrinsic phase separation. Phys. Rev. B 2015, 91, 020503. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Talantsev, E.F. Classifying Induced Superconductivity in Atomically Thin Dirac-Cone Materials. Condens. Matter 2019, 4, 83. https://doi.org/10.3390/condmat4030083
Talantsev EF. Classifying Induced Superconductivity in Atomically Thin Dirac-Cone Materials. Condensed Matter. 2019; 4(3):83. https://doi.org/10.3390/condmat4030083
Chicago/Turabian StyleTalantsev, Evgueni F. 2019. "Classifying Induced Superconductivity in Atomically Thin Dirac-Cone Materials" Condensed Matter 4, no. 3: 83. https://doi.org/10.3390/condmat4030083
APA StyleTalantsev, E. F. (2019). Classifying Induced Superconductivity in Atomically Thin Dirac-Cone Materials. Condensed Matter, 4(3), 83. https://doi.org/10.3390/condmat4030083




