Abstract
An account is given of the main steps that led the research group in Rome, to which the author belongs, to the formulation of the charge-density-wave scenario for high- superconducting cuprates. The early finding of the generic tendency of strongly correlated electron systems with short range interactions to undergo electron phase separation was subsequently contrasted with the homogenizing effect of the long-range Coulomb interaction. The two effects can find a compromise in the formation of incommensurate charge density waves. These charge density waves are inherently dynamical and are overdamped as a consequence of the possibility to decay in electron-hole pairs, yet tend to maintain a (quantum) critical character, which is mirrored in their marked momentum and frequency dependence and in their strong variation with temperature and doping. These dynamical incommensurate charge density waves act as mediators of pairing lading to high- superconductivity, and provide the scattering mechanism that produces the observed violation of the Fermi-liquid paradigm in the metallic phase.
1. Introduction
High- superconducting cuprates represent one of the most intriguing challenges of condensed matter physics [1]. Several ingredients and experimental facts contribute to create a halo of mystery around these systems. The parent compounds are antiferromagnetic insulators and all the families share the same perovskite structure based on copper-oxygen (CuO) planes intercalated with rare-earth slabs. Upon substitution with of the rare earth atoms with heterovalent dopants, charge carriers (holes or electrons, in the following, for simplicity, I discuss the hole-doped case) are introduced in the copper-oxygen planes and the system becomes a metal, although the metallic properties are anisotropic, the resistance along the copper-oxygen planes being smaller that the resistance in the direction perpendicular to them. Moreover, the resistance displays a linear temperature dependence over a very wide temperature range (except for very heavily doped samples), that is hardly reconcilable with the paradigmatic Fermi-liquid behaviour of normal metals. Superconductivity, of d-wave symmetry, occurs below a dome-shaped doping-dependent critical line , that reaches its maximum at optimal doping and declines with further doping, in the so-called overdoped region, where the metallic phase above is well described by a Fermi liquid theory. In the underdoped region, , and in a temperature range , where decreases with p and merges with near optimal doping, various phenomena apparently connected with a suppression of the density of states at the Fermi level are detected (the so-called pseudogap phenomena), that indicate an even more pronounced violation of the Fermi liquid paradigm. Along the years, the research group in Rome, to which the author belongs, (the ancient romans named in the title of this piece of work) developed a scenario that tried to identify the crucial ingredients to account for the above complicated phenomenology, in the perspective of a modification of the Fermi liquid properties while the doping is reduced, starting from the overdoped region. My aim here is to retrace the ancient romans’ route to a theory for the anomalies of the metallic state of cuprates and their possible connections with superconductivity, that relies on charge density waves [2,3,4,5].
It must be emphasized that, over more than three decades, other groups in Rome have been working in the field of high- cuprates. Their role and relevance is witnessed by the many references cited in this piece of work. It is likewise evident that many scenarios have been developed for cuprates along all those years. The focus of this piece of work is the development of the scenario developed by the research group in Rome, to which the author belongs, that is based on charge density waves, but it may be interesting to compare this scenario at least with similar scenarios. The scenario that shares more similarities with the one presented in this piece of work relies on nearly antiferromagnetic critical spin fluctuations [6,7,8,9,10], remnants of the proximity to the antiferromagnetic phase. These fluctuations have characteristic wave vectors substantially larger than those of the charge density waves, and pointing along the direction of the Brillouin zone, so a careful analysis often allows to separate their contribution to various observed quantities from the contribution of charge density waves with characteristic wave vectors along the and directions of the Brillouin zone.
This paper is organised as follows: Section 2 is devoted to illustrate the main ideas behind supporting the possible occurrence of electron phase separation in cuprates; in Section 3 the homogeneising role of Coulomb interaction is taken into account, turning electron phase separation into incommensurate charge density waves; Section 4, Section 5 and Section 6 deal with the long search of evanescent fingerprints of the charge density waves in various experimental probes, like angle resolved photoemission spectroscopy, transport, optics, Raman spectroscopy, and other indirect evidences; in Section 7 the role of resonant X-ray scattering in providing direct evidence of charge density waves is discussed; final remarks are found in Section 8.
2. The Electron Phase Separation Era
The fact that the undoped parent compounds are antiferromagnetic insulators, was immediately recognised as the consequence of the strong correlation U in the state with two holes residing on the same copper d orbital [11]. The configuration with two holes on neighbouring sites is much less costly and the energy is further lowered if the spins of the two holes are antiparallel, because virtual hopping processes are possible in this configuration, with an energy gain of the order , where t is the hopping amplitude. This is the famous superexchange mechanism. Then, in the early days of high- superconductivity, a great effort was devoted to the investigation of the properties of various single- and multi-band models for strongly correlated electrons on the CuO planes.
It became rapidly evident that a property common to all those models was a marked tendency toward electron phase separation [12,13,14,15,16]. This can be understood as the consequence of the suppression of the main mechanism that leads to a uniform electron density in normal metals, namely the kinetic energy gain when the electrons move freely across the system. Strong correlations severely reduce this energy gain so that residual attractive forces of various origin can bring the system on the verge of an instability that favours electron phase separation in hole-rich (more metallic) and hole-poor (more insulating) regions.
One possible mechanism stabilising the system against electron phase separation was found to be superconductivity [12,17], pointing to the possibility that the same attractive forces responsible for electron phase separation in the particle-hole channel, may lead to Cooper pairing in the particle-particle channel.
3. The Charge Density Wave Era
In its crude simplicity, the electron phase separation scenario discussed in the previous section misses a crucial ingredient, namely the charged character of doped holes. It is rather clear that long-range Coulomb repulsion makes charge segregation energetically very costly, so that genuine electron phase separation can only occur in systems where the countercharges that guarantee the overall charge neutrality of the system are sufficiently mobile [18].
However, the system may reach a compromise between these two opposed tendencies and produce charge segregation on short length scales. This is the so-called frustrated electron phase separation mechanism [2,3], that leads to the formation of incommensurate charge density waves, for which an increasing experimental evidence was being gathered [19,20,21]. The electron phase separation mechanism for charge density waves was shaped as an instability of the Fermi liquid by the research group in Rome, to which the author belongs [22,23,24,25,26].
The idea may be schematised as follows: in a correlated Fermi liquid one can identify three main contributions to the electron-electron interaction, , where is the long-range Coulomb repulsion, is a short-range residual repulsion that embodies the strongly-correlated nature of the parent undoped insulator, and is the residual attraction leading to electron phase separation if long-range Coulomb forces are neglected. In a Fermi liquid, screening processes are active and the electron-electron interaction is modified by the polarisation associated with virtual electron-hole pairs, leading to a screened interaction
where is the electron-hole polarisation bubble in the random phase approximation (also called Lindhard function). This is a complex function that includes damping effects resulting from the decay process involving electron-hole pairs [see below, Equation (2), and the text therby]. Within this picture, instabilities are seen as zeroes in the denominator of Equation (1). Since is minimum at small wave vectors , while diverges for and decreases at larger , if the residual attraction has no particular structure as a function of , then the denominator of Equation (1) may vanish at along a certain line in the temperature-vs.-doping phase diagram, marking the electron phase separation instability of the Fermi liquid. This is simpler to achieve if the electron bandwidth is suppressed by strong correlation effects, thereby enhancing the polarisation bubble . However, electron phase separation can be achieved only if the term is neglected. In the presence of , the instability at is strictly impeded by the divergence of the unscreened Coulomb interaction at small wave vector, but an instability may yet be achieved along a line , marking a finite wave vector instability of the Fermi liquid, at (actually, the instability occurs at a whole star of wave vectors that are equivalent under point group symmetries of the lattice). Since this wave vector is the result of the form of and , as functions of , the instability wave vector is unrelated to the periodicity of the lattice: the compromise between the tendency toward electron phase separation and Coulomb repulsion is realised as an incommensurate charge density wave.
When Equation (1) is expanded for small frequency and wave vectors close to , then the effective interaction takes the singular form
where is a constant setting the overall strength of the interaction,
in the field-theoretic language, is called the propagator of the collective excitations mediating the effective interaction (in our case, charge density waves), vanishes along the instability line , marking the divergence of the correlation length , is a constant whose order of magnitude is set by an electron energy scale (the Fermi energy ), and sets a high energy cutoff, that depends on various energy scales. For instance, if Equation (1) is derived within the Hubbard-Holstein model including the coupling to a phonon with frequency [3], then . Apart from an overall multiplicative constant, this is the same form of the dressed density-density dynamical correlation function
where the bare term is , and the result of the right-hand side is the resummation of the diagrams in Figure 1a. This is exactly the form of a dynamical Ornstein-Zernike correlator, the term representing the Landau damping due to charge density waves decaying in electron-hole pairs in the Fermi liquid state, giving an alternative but equivalent interpretation of the charge density wave propagator D in Equation (3).
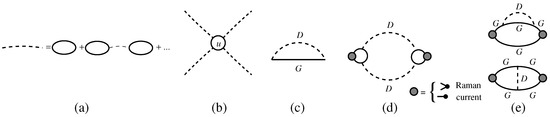
Figure 1.
Feynman diagrams describing the physical processes involving electrons (solid lines) and charge density waves (dashed lines). D and G indicate the charge density wave and electron propagator, respectively, while the thin dashed line represents the bare electron-electron interaction . (a) Propagator D of charge density waves as given by Equation (3). (b) Interaction between the dynamical charge density waves: two ingoing charge density waves are scattered into two outgoing charge density waves in a process where virtual electron excitations (solid line) are involved. (c) Electron self-energy correction due to the interaction with charge density waves. (d) Contribution to the Raman response due to processes with two dynamical charge density waves in the virtual intermediate state; the shaded circle represent a Raman or current vertex, but the diagram with the current vertex vanishes due to the neutral character of the intermediate state. (e) Self-energy (top) and vertex (bottom) corrections due to processes with electron-hole pairs in the virtual intermediate state, contributing to Raman and optical spectra.
The details of the band structure of cuprates, determining , and of the effective interaction , fix the direction of along the CuO bonds consistent with all the evidence existing at the time when the theory was developed, as well as with further evidence gathered in the subsequent years. Of course, as we stated above, the magnitude of is not related to a periodicity of the lattice, therefore the resulting charge density wave is incommensurate.
The above scenario is still rather qualitative. As a matter of fact, the loosely layered structure of cuprates makes fluctuations play an important role: the interaction between dynamical charge density wave [which can be seen as the result of corrections to Equation (1) beyond the random phase approximation] suppresses the order in a temperature region , so that charge density waves are expected to stay dynamical and fluctuating until the real instability line is reached [4]. This can be seen as the correction to the term in Equation (2),
where u is a dimensionless coupling for dynamical charge density waves (see Figure 1b, where the interaction between two ingoing and two outgoing charge density waves (broken lines) is mediated by virtually excited electrons in the medium (solid line); at low energy this interaction is a constant u) and the correlation length diverges at , marking the true instability line [4,5,27]. Further corrections dressing the vertices in the diagram of Figure 1b are expected to be small for incommensurate charge density waves [28].
The resulting instability line may be dome shaped, and completely masked underneath the superconducting dome [5]. This result is obtained, e.g., in a model where the dynamical charge density wave in the underdoped region have a different nature, the modulus of the complex charge density wave order parameter being well formed (contrary to the case of the optimally and overdoped region, where it fluctuates) while its phase fluctuates.
Of course, if a coupling to the lattice degrees of freedom is included, the maximum of will likely adjust to match a nearby nesting condition between the (doping-dependent) period of the charge density wave and the periodicity of the lattice, which in the doping region of interest may occur at .
The resulting theoretical phase diagram looks like the one sketched in Figure 2.
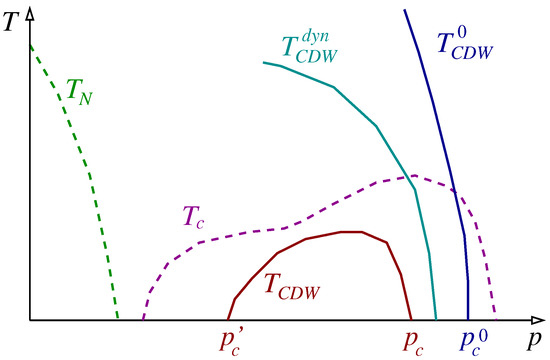
Figure 2.
Sketch of the phase diagram for charge density waves in the temperature T vs. doping p plane. For completeness, the Néel temperature below which the antiferromagnetic phase establishes (green) and the superconducting critical temperature (purple) are traced with dashed lines, according to their experimental determination. The blue line marks the temperature below which charge density waves should occur in the random phase approximation; the corresponding quantum critical point at is marked by . Below this line, one expect precursor effects of the charge density waves. Dynamical charge density waves should be observed below the cyan line , somewhat lower than the line , while true long range order would only establish below the red line , were in not for the presence of the competing superconducting phase; the two (missed) quantum critical points, that delimit the doping region in which static order would be present at , are marked with and .
4. Looking for Fingerprints: Angle Resolved Photoemission Spectroscopy
Once the possibility for a charge density wave as an instability of the Fermi liquid was assessed, the question of detecting fingerprints of this state naturally arose. Charge density waves in cuprates involve rather tiny modulations of the charge density profile, presumably because strong correlations reduce the charge density wave amplitude [29], and have a dynamical character over most of the phase diagram above [4,5,27], being therefore rather hard to observe directly (of course, one could find traces of the electron charge modulation in the accompanying lattice deformation, but here my focus is the direct observation of charge density waves), unless favourable conditions like nesting or pinning occur, and charge density waves are seen, usually in the form of charge stripes, with a highly anharmonic profile. In the early times of the detection of charge density waves in cuprates, this elusive phenomenon had to be studied mostly by means of indirect probes, apt to reveal modifications of the electron properties caused by the interaction between electrons and charge density waves.
The first fingerprints of charge density waves were looked for in angle resolved photoemission spectra [30]. The idea is to calculate the electron self-energy correction due to the interaction with dynamical charge density waves (see Figure 1c) and try to recover the various feature observed in angle resolved photoemission spectra by adjusting the parameters that characterise the dynamical charge density waves within reasonable ranges of variation, as well as entering values extracted from other experiments, see, e.g., Section 5.
Along the years, it was possible to account for the occurrence of shadow bands [30,31,32,33,34,35,36,37], to describe the peculiarities of the electron spectrum known as kinks and waterfalls [38,39,40], and the effect of a bilayer splitting [41] in systems with two CuO planes per unit cell.
It must be pointed out that angle resolved photoemission spectra of cuprates (as well as many other spectral porperties) are also affected by nearly antiferromagnetic spin density fluctuations [30,40], with their characteristic wave vector . The specificity of charge density waves is that their characteristic wave vector is along the CuO bonds, in the and directions of the Brillouin zone, and contribute with features that cannot be associated to scattering processes involving a mediator with a larger characteristic wave vector, , pointing along the diagonals of the Brillouin zone. Furthermore, charge density waves introduce lower energy scales that are appropriate to describe the kinks (while waterfalls have both contributions from charge and spin fluctuations). As it was recalled in Section 3, if Equation (1) is derived within the Hubbard-Holstein model including the coupling to a phonon with frequency [3], then the characteristic energy scale of a charge density wave turns out to be .
The role of charge density waves in the formation of the pseudogap was also investigated. The idea is that the interaction in Equation (2) is apt to gap electron states near the M points of the Brillouin zone [42,43,44]. The pseudogap temperature is interpreted in terms of a reduction of the density of states due to incipient charge density waves and, at lower temperature to the possible formation of incoherent superconducting pairs [45].
5. Looking for Fingerprints: Transport, Optics, Raman Spectroscopy
Of course, the theory provides only estimates of the order of magnitude of the various parameters characterising the charge density waves, see Equations (2) and (4), so other independent determinations of the parameters g, and , and an experimental determination of the evolution of m with temperature and doping became highly desirable.
A major breakthrough came from the idea that nearly critical dynamical charge density waves would affect the Raman response with a channel associated to the possible emission of two virtual charge density waves in the intermediate state [46] (see Figure 1d). It was soon realised that this contribution had the right form and the right symmetry properties to explain the anomalous peak observed in Raman experiment [47].
A thorough analysis of Raman spectra began [46,48,49,50,51,52,53], that enjoyed feedbacks from, and provided further inputs to, the analysis of angle resolved photoemission spectra, discussed in Section 4, allowed to extract the first reliable experimental estimates of the characteristic parameters of the charge density waves. It was confirmed that eV is an electron energy scale, while meV is a much lower energy scale. Interestingly enough, the analysis of Raman spectra confirmed the fact that charge density waves have a very weak tendency to order and stay dynamical an fluctuating over most of the accessible phase diagram above , confirming their elusive character. The parameter m, that should vanish at the charge density wave phase transition, is found to be a linear function of the temperature at sufficiently high temperature, but is always found to saturate to a small, but finite value (–10 meV) at low temperature. Extrapolation of the linear part gives an estimate of the temperature at which the charge density waves would tend to order. This temperature scale is negative (i.e., unattainable) in overdoped samples, nearly vanishing at optimal doping, thus marking the presence of a missed quantum critical point, and finite, but smaller than or comparable to in moderately underdoped samples.
A subsequent deeper analysis of Raman spectra [53,54] led to the complete characterisation of the glue function that should mediate pairing between electrons. This glue function was found to be mostly due to charge density waves in optimally an overdoped samples, whereas upon underdoping, the role of antiferromagnetic spin fluctuation increases, as it is expected, since the system is now closer to the antiferromagnetic phase. It is interesting that the strength of the two channel becomes equal around optimal doping. These spin fluctuations do contribute to the Raman spectra, but can never account for the anomalous peak via a process like the one depicted in Figure 1d, because they never become nearly critical over all the doping region where the anomalous peak is observed.
Subleading contributions to Raman spectra in channels where the intermediate state always contains an electron-hole pair (see Figure 1e), as well as contributions to optical spectra and to electron transport have provided further evidence of the presence of charge density waves [48,49,50]. These evidences being weaker than those gained by the analysis of Raman and angle resolved photoemission spectra, had mostly the role of testing the consistency of the parameters extracted thereby. It must be emphasized that also spin fluctuations do contribute to Raman spectra with subleading corrections, and this is precisely the reason why the full analysis of Raman spectra allowed to disentangle the spin and charge contribution to the glue function .
For instance, the most important contribution to Raman spectra (see Figure 1d) does not contribute to optical spectra, because of the neutral character of the dynamical charge density waves in the intermediate state, unless the conditions occur (e.g., in the presence of strong disorder) to prevent this term from vanishing [55,56]. Likewise, self-energy and vertex corrections (see Figure 1e) to the optical conductivity (and to transport) crucially depend on the cutoff as a consequence of the strong constraints imposed by charge conservation: an exact cancellation of self-energy and vertex corrections occurs, that is enforced by a Ward identity, if no retardation effect due to degrees of freedom different from the electrons themselves is present in the effective interaction . If one includes retardation effects in , e.g., due to phonons, then the charge density wave contribution to optical spectra (and transport) does not vanish [57].
6. Other Fingerprints
Yet other indirect fingerprints of the charge density waves are found in other contexts. For instance, the interplay of charge and spin degrees of freedom in the heavily underdoped region, near the antiferromagnetic state, can give rise to charge segments [58] that can be seen as the precursor (the melt [59]) of stripy charge density waves and may account for the properties of the nematic state reported in this region of the phase diagram [60,61,62,63]. Dynamical charge density waves may coexist with (or evolve into) nematic fluctuations affecting the Raman spectra [64].
An even more important context where fingerprints of the charge density waves may be detected is in the connection and interplay with superconductivity.
Since the early days of the electron phase separation era discussed in Section 2, it was found that superconductivity might stabilise the system against phase separation, indicating that the same attractive forces responsible for the instability in the particle-hole channel, could instead produce Cooper pairing in the particle-particle channel [12,17].
When the charge density wave era discussed in Section 3 began, it was likewise clear that dynamical charge density wave described by Equation (4) could mediate Cooper pairing in the particle-particle channel [65], contribute to the properties of the pseudogap state [42,43,44], explain the possible occurrence of a time-reversal-symmetry-broken superconducting state [66,67], and be possibly related to a cutoff of the damped Cooper pair fluctuations contributing to the paraconductivity above [68], within the Aslamazov-Larkin theory.
Even more interestingly, in a recent work, the possibility that in the underdoped region superconductivity and charge density waves might be different breaking of a common symmetry, led to the proposal that the occurrence of filamentary superconductivity might be promoted by disorder in a region of the phase diagram where charge order would be present in the absence of disorder. This phenomenon is related to the fact that, in order to match with the different phases of the charge order parameter in different domains induced by disorder, the order parameter must rotate to the superconducting state at the domain boundary, thus producing topologically protected filaments [69].
The fact that superconductivity and charge order compete is witnessed by the fact that once superconductivity is suppressed by a strong enough magnetic field, static charge order emerges below a dome-shaped curve [70,71] very similar to the one reported in Figure 2, that was hidden underneath the superconducting dome , at zero magnetic field. Interestingly enough, superconductivity seems to be more resilient around the two endpoints where the curve meets the axis [72]. This seems to indicate that quantum fluctuations of the competing phase act indeed as mediators of Cooper pairing in the particle-particle channel, like it happens in several heavy fermion superconductors. If this were the case, the two superconducting domes persisting around the endpoints of the curve at strong magnetic field are two-different superconducting phases, in which pairing is mediated by different quantum critical fluctuations. Upon reducing the magnetic field, the two dome expand and eventually coalesce in what appears as a single superconducting phase at zero magnetic field. The two plateaux observed, e.g., at K and K in YBCO should be the remnant of the two different superconducting phases. It must be emphasized that spin fluctuations will certainly contribute to Cooper pairing, especially in the underdoped region (see the discussion on the glue function in Section 5). However, since the quantum critical point for spin fluctuations is outside the superconducting dome and not underneath it, the quantum critical fluctuations boosting must be related with the quantum critical point(s) underneath the superconducting dome, associated to charge density waves.
It is interesting to discuss here the results of another group in Rome, led by A. Bianconi. Following the appearance of photo-induced X-ray diffraction satellites in cuprates at low temperature below 150 K, it has been shown the predicted self-organization of anisotropic polarons into striped puddles [73,74,75]. The data analysis has shown that photoinduced polarons have an anisotropic shape with a finite size of about 1 nm; it has been inferred that they are in the intermediate coupling regime and coexist with itinerant carriers in the doping range between 0.06 and 0.21 holes per Cu site. From these experimental results, it was deduced that the intermediate polarons show internal fluctuations which generate an anisotropic polaron-polaron van Der Waals attraction giving a fluid-like behavior exhibiting a complex phase separation. They have proposed a phase diagram formally similar to the gas-to-liquid-liquid transition in supercooled water, where the anisotropy interaction generates a novel intermediate liquid phase between the standard gas and liquid phases [76,77,78].
The intermediate phase has been identified with the 1/8 polaronic generalized Wigner charge density wave phase. In this scenario, it was proposed that the superconducting phase is determined by the complex filamentary network of interface pathways which could be mapped by an hyperbolic geometry [79].
7. The Resonant X-Ray Scattering Era
An exciting new era begun when resonant X-ray scattering experiment were gradually refined to reach the accuracy and sensitivity needed to directly probe charge density waves [80,81,82,83]. In a rather short lapse of time, what that far had only been seen in few experiments and under peculiar conditions, became ubiquitous and charge density waves were now finally seen, beyond any shadow of doubt, in all family of cuprates. They may even re-enter in the overdoped region, in those families of cuprates where the van Hove singularity in the electron spectrum is known to play a role [84], and may indeed enhance the polarisation bubble in Equation (1) if the doping brings the van Hove singularity sufficiently close to the Fermi level, promoting the reappearance of charge density waves to the right of in Figure 2.
The most important fact, here, is that resonant X-ray scattering processes may excite a single charge density wave in the intermediate channel, so that the absorption spectrum is directly proportional to the dressed density-density dynamical correlation function in Equation (4). Then, for the first time, experimental data may give direct access to the parameters characterizing the charge density waves
After the phase diagram sketched in Figure 2 had been published [5], purely based on theoretical calculations, with the parameters characterising the charge density waves extracted from the various indirect evidences discussed in Section 4, Section 5 and Section 6, a thorough analysis was carried out in YBCO and NBCO at various dopings and temperatures. The analysis not only confirmed the theoretical phase diagram, but also provided values for and , and allowed to trace the evolution of m with varying the temperature, in very good agreement with all previous indirect estimates [85].
Surprisingly, beyond the dynamical charge density wave, whose intensity decreases with the temperature and becomes unobservable at some , very robust and nearly temperature independent charge density fluctuations, characterised by correlation lengths much shorter that those of the charge density waves, were found to pervade the phase diagram up to the highest temperature reached in the experiment. It is not clear at the moment, whether the two kind of excitations coexist or are spatially separated (giving rise to an inhomogeneous landscape, see, e.g., [86]), but it is quite evident that charge density waves compete with (and are weakened by) superconductivity, whereas the much broader charge density fluctuations are apparently ataraxic, hardly disturbed by anything, included superconductivity, with whom they seem to peacefully coexist.
It might be speculated that the broad charge density fluctuations may be remnant of the re-entrant charge density waves due to the proximity to a van Hove singularity, whenever the singularity is not close enough to the Fermi level and only produces broad resonances in the dressed density-density dynamical correlation function in Equation (4). This hypothesis is presently under scrutiny.
8. Concluding Remarks
Despite the fact that the pace of convergence between an old theory and the experiment significantly accelerated in the resonant X-ray scattering era discussed in Section 7, many major challenges await ahead.
Open questions regard crucial aspects, like: i) the fate of charge density waves in the heavily underdoped region of the phase diagram and their interplay with the spin degrees of freedom when approaching the antiferromagnetic phase (see Reference [58]); ii) the role of charge density waves in the marginal Fermi liquid behaviour observed in the anomalous metallic phase above around optimal doping, in the formation of the pseudogap, and in the reconstruction of the Fermi surface once (nearly) static order sets in; iii) the role of disorder and inhomogeneity, of the charged dopants residing away, but not too far, from the CuO planes, of commensuration effects when charge density waves are coupled to the lattice, and of lattice strain; iv) the interplay between charge density waves and superconductivity, both as static and as fluctuating orders, including the possibility that quantum critical fluctuations of the charge density wave static order act as mediators of Cooper pairing in the particle-particle channel.
Very recently [87], the marginal Fermi liquid behaviour seems to have found an explanation based on the ubiquitous presence of the broad and nearly temperature independent charge fluctuations observed in resonant X-ray scattering experiments. How this new scenario is accommodated in the attempt to explain marginal-Fermi-liquid-like features of the Raman spectra by means of the narrower dynamical charge density waves, is a further question to be clarified.
As a final remark, although it must be admitted that often different scientist move along very different routes, the various pathways do cross several times. After a while, one always realises that Science is indeed a collective endeavour, and the contributions of other researchers, that appeared obscure at a first glance, become clearer and clearer as time goes by, making every theory, included the one highlighted in this piece of work, the result of ideas that were piecemeal triggered by all other ideas, all experimental findings.
Funding
S.C. acknowledge financial support from Sapienza Università di Roma, Project n. RM11715C642E8370.
Acknowledgments
The author is indebted with L. Benfatto, A. Bianconi, C. Castellani, C. Di Castro, M. Grilli, J. Lesueur, B. Leridon, J. Lorenzana, A. Perali, and G. Seibold, for so many insightful discussions and long-lasting collaboration along all these years of the exciting high- challenge, and with an almost endless list of colleagues and coauthors, whose contribution to this research permeates every single line of it.
Conflicts of Interest
The author declares no conflict of interest.
References
- Plakida, N. High-Temperature Cuprate Superconductors - Experiment, Theory, and Applications; Springer Series in Solid-State Sciences; Springer: Berlin/Heidelberg, Germany, 2010; Volume 166. [Google Scholar]
- Raimondi, R.; Castellani, C.; Grilli, M.; Bang, Y.; Kotliar, G. Charge collective modes and dynamic pairing in the three-band Hubbard model. II. Strong-coupling limit. Phys. Rev. B 1993, 47, 3331. [Google Scholar] [CrossRef] [PubMed]
- Castellani, C.; Di Castro, C.; Grilli, M. Singular Quasiparticle Scattering in the Proximity of Charge Instabilities. Phys. Rev. Lett. 1995, 75, 4650. [Google Scholar] [CrossRef] [PubMed]
- Andergassen, S.; Caprara, S.; Di Castro, C.; Grilli, M. Anomalous isotopic effect near the charge-ordering quantum criticality. Phys. Rev. Lett. 2001, 87, 056401. [Google Scholar] [CrossRef] [PubMed]
- Caprara, S.; Di Castro, C.; Seibold, G.; Grilli, M. Dynamical charge density waves rule the phase diagram of cuprates. Phys. Rev. B 2017, 95, 224511. [Google Scholar] [CrossRef]
- Sachdev, S.; Ye, J. Universal quantum-critical dynamics of two-dimensional antiferromagnets. Phys. Rev. Lett. 1992, 69, 2411. [Google Scholar] [CrossRef]
- Monthoux, P.; Balatsky, A.V.; Pines, D. Weak-coupling theory of high-temperature superconductivity in the antiferromagnetically correlated copper oxides. Phys. Rev. B 1992, 46, 14803. [Google Scholar] [CrossRef]
- Sokol, A.; Pines, D. Toward a unified magnetic phase diagram of the cuprate superconductors. Phys. Rev. Lett. 1993, 71, 2813. [Google Scholar] [CrossRef] [PubMed]
- Monthoux, P.; Pines, D. Nearly antiferromagnetic Fermi-liquid description of magnetic scaling and spin-gap behavior. Phys. Rev. B 1994, 50, 16015. [Google Scholar] [CrossRef]
- Abanov, A.; Chubukov, A.; Schmalian, J. Quantum-critical theory of the spin-fermion model and its application to cuprates: Normal state analysis. Adv. Phys. 2003, 52, 119. [Google Scholar] [CrossRef]
- Anderson, W. The Resonating Valence Bond State in La2CuO4 and Superconductivity. Science 1987, 235, 1196. [Google Scholar] [CrossRef]
- Cancrini, N.; Caprara, S.; Castellani, C.; Di Castro, C.; Grilli, M.; Raimondi, R. Phase separation and superconductivity in the Kondo-like spin-hole coupled model. Europhys. Lett. 1991, 14, 597. [Google Scholar] [CrossRef]
- Müller, K.A.; Benedek, G. Phase Separation in Cuprate Superconductors; World Scientific: Singapore, 1993; p. 125. [Google Scholar]
- Bianconi, A. The instability close to the 2D generalized Wigner polaron crystal density: A possible pairing mechanism indicated by a key experiment. Phys. C 1994, 235–240, 269. [Google Scholar] [CrossRef]
- Caprara, S.; Grilli, M. Three Band t-J Model: A Systematic Large-N Analysis. Phys. Rev. B 1994, 49, 6971. [Google Scholar] [CrossRef] [PubMed]
- Caprara, S.; Di Castro, C.; Grilli, M. Magnetic and charge-transfer phase separation in the three band t-J model. Phys. Rev. B 1995, 51, 9286. [Google Scholar] [CrossRef]
- Caprara, S.; Castellani, C.; Di Castro, C.; Grilli, M. Phase separation and superconductivity in strongly interacting electron systems. Phys. C 1994, 235–240, 2155. [Google Scholar] [CrossRef]
- Jorgensen, J.D.; Dabrowski, B.; Pei, S.; Hinks, D.G.; Soderholm, L.; Morosin, B.; Schirber, J.E.; Venturini, E.L.; Ginley, D.S. Superconducting phase of La2CuO4+δ: A superconducting composition resulting from phase separation. Phys. Rev. B 1988, 38, 11337. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, A.; Saini, N.L.; Lanzara, A.; Missori, M.; Rossetti, T.; Oyanagi, H.; Yamaguchi, H.; Oka, K.; Ito, T. Determination of the Local Lattice Distortions in the CuO2 plane of La1.85Sr0.15CuO4. Phys. Rev. Lett. 1996, 76, 3412. [Google Scholar] [CrossRef]
- Bianconi, A.; Lusignoli, M.; Saini, N.L.; Bordet, P.; Kvik, Å.; Radaelli, P.G. Stripe structure of the CuO2 plane in Bi2Sr2CaCu2O8+y. by anomalous X-ray diffraction. Phys. Rev. B 1996, 54, 4310. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, A.; Saini, N.L.; Rossetti, T.; Lanzara, A.; Perali, A.; Missori, M.; Oyanagi, H.; Yamaguchi, H.; Nishihara, Y.; Ha, D.H. Stripe structure in the CuO2 plane of perovskite superconductors. Phys. Rev. B 1996, 54, 12018. [Google Scholar] [CrossRef] [PubMed]
- Caprara, S.; Castellani, C.; Di Castro, C.; Grilli, M.; Sadori, A. The Stripe-Quantum-Critical-Point as a key to the physics of the cuprates. Journale de Physique IV (Colloques) 1999, 9, 329–332. [Google Scholar] [CrossRef]
- Caprara, S.; Castellani, C.; Di Castro, C.; Grilli, M.; Perali, A. Charge and spin inhomogeneity as a key to the physics of the high-Tc cuprates. Phys. B 2000, 280, 196. [Google Scholar] [CrossRef]
- Di Castro, C.; Benfatto, L.; Caprara, S.; Castellani, C.; Grilli, M. The physics of the stripe quantum critical point. in the superconducting cuprates. Phys. C 2000, 341, 1715–1718. [Google Scholar] [CrossRef]
- Bianconi, A.; Bianconi, G.; Caprara, S.; Di Castro, D.; Oyanagi, H.; Saini, N.L. The stripe critical point for cuprates. J. Phys. Cond. Matt. 2000, 12, 10655. [Google Scholar] [CrossRef]
- Caprara, S.; Castellani, C.; Di Castro, C.; Grilli, M.; Perali, A.; Sulpizi, M. The stripe-phase Quantum-Critical-Point scenario for high-Tc superconductors. In Proceedings of the Conference Stripes 98, Rome, Italy, 4–7 June 1998; p. 45. [Google Scholar]
- Di Castro, C.; Grilli, M.; Caprara, S. Strong correlation, electron-phonon interaction and critical fluctuations: isotope effect, pseudogap formation, and phase diagram of the cuprates. J. Phys. Chem. Solids 2002, 63, 2219. [Google Scholar] [CrossRef]
- Caprara, S.; Di Castro, C.; Werner, P.; Zwerger, W. Vertex corrections near the stripe phase. Phys. Rev. Lett. 2002, 88, 066403. [Google Scholar] [CrossRef]
- Caprara, S. Reduction of the charge-density-wave amplitude in a strongly correlated system. J. Phys. Cond. Matt. 1998, 10, 5389. [Google Scholar] [CrossRef]
- Caprara, S.; Sulpizi, M.; Bianconi, A.; Di Castro, C.; Grilli, M. Single-particle properties of a model for coexisting charge and spin quasi-critical fluctuations coupled to electrons. Phys. Rev. B 1999, 59, 14980. [Google Scholar] [CrossRef]
- Saini, N.L.; Avila, J.; Bianconi, A.; Lanzara, A.; Asensio, M.C.; Tajima, S.; Gu, G.D.; Koshizuka, N. Topology of the pseudogap and shadow bands in Bi2Sr2CaCu2O8+δ at optimum doping. Phys. Rev. Lett. 1997, 79, 3467. [Google Scholar] [CrossRef]
- Bianconi, A.; Saini, N.L.; Valletta, A.; Lanzara, A.; Avila, J.; Asensio, M.C.; Tajima, S.; Gu, G.D.; Koshizuka, N. The Fermi surface of a high-Tc superconductor at optimum doping by angle-scanning photoemission spectroscopy. J. Phys. Chem. Solids. 1998, 59, 1884. [Google Scholar] [CrossRef]
- Saini, N.L.; Avila, J.; Asensio, M.C.; Tajima, S.; Gu, G.D.; Koshizuka, N.; Lanzara, A.; Bianconi, A. Evidence for a second one-dimensional set of states shedding light on the normal phase of high-Tc superconductors. Phys. Rev. B 1998, 57, R11101. [Google Scholar] [CrossRef]
- Saini, N.L.; Lanzara, A.; Bianconi, A.; Avila, J.; Asensio, M.C.; Tajima, S.; Gu, G.D.; Koshizuka, N. Antiferromagnetic and superconducting correlations in the pseudogap state of high-Tc cuprates. In Proceedings of the Second International Conference Stripes and High-Tc Superconductivity, Rome, Italy, 2–6 June 1998. [Google Scholar]
- Caprara, S.; Perali, A.; Sulpizi, M. Shadow bands, gap and pseudogaps in high-Tc superconductors. J. Superconduct. 1999, 12, 71. [Google Scholar] [CrossRef]
- Caprara, S.; Di Castro, C.; Grilli, M.; Perali, A.; Sulpizi, M. Fermi surface and gap parameter in high-Tc superconductors: The stripe quantum critical point scenario. Phys. C 1999, 317–318, 230–237. [Google Scholar] [CrossRef]
- Caprara, S.; Di Castro, C.; Grilli, M. Single-particle spectra near a stripe instability. Phys. B 2000, 284–288, 983. [Google Scholar] [CrossRef]
- Graf, J.; Gweon, G.-H.; McElroy, K.; Zhou, S.Y.; Jozwiak, C.; Rotenberg, E.; Bill, A.; Sasagawa, T.; Eisaki, H.; Uchida, S.; et al. Universal high energy anomaly in the angle-resolved photoemission spectra of high temperature superconductors: Possible evidence of spinon and holon branches. Phys. Rev. Lett. 2007, 98, 067004. [Google Scholar] [CrossRef]
- Chang, J.; Pailhés, S.; Shi, M.; Manson, M.; Claesson, T.; Tjernberg, O.; Voigt, J.; Perez, V.; Patthey, L.; Momono, N.; et al. When low- and high-energy electronic responses meet in cuprate superconductors. Phys. Rev. B 2007, 75, 224508. [Google Scholar] [CrossRef]
- Mazza, G.; Grilli, M.; Di Castro, C.; Caprara, S. Evidence for phonon-like charge and spin fluctuations from an analysis of angle-resolved photoemission spectra of La2−xSrxCuO4 superconductors. Phys. Rev. B 2013, 87, 014511. [Google Scholar] [CrossRef]
- Caprara, S.; Grilli, M. Single-particle spectra and Fermi surface near a stripe instability. Journale de Physique IV (Colloques) 1999, 9, Pr10–337. [Google Scholar] [CrossRef]
- Benfatto, L.; Caprara, S.; Perali, A. The pseudogap state in high-Tc superconductors. Phys. A 2000, 280, 185. [Google Scholar] [CrossRef]
- Benfatto, L.; Caprara, S.; Di Castro, C. Gap and pseudogap evolution within the charge-ordering scenario for superconducting cuprates. Eur. Phys. J. B 2000, 17, 95. [Google Scholar] [CrossRef]
- Benfatto, L.; Caprara, S. Gap and pseudogap evolution in underdoped cuprates. Int. J. Mod. Phys. B 2000, 14, 3006. [Google Scholar] [CrossRef]
- Caprara, S.; Grilli, M.; Di Castro, C.; Seibold, G. Pseudogap and (an)isotropic scattering in the fluctuating charge-density wave phase of cuprates. J. Superconduct. Novel Magn. 2017, 30, 25. [Google Scholar] [CrossRef]
- Caprara, S.; Di Castro, C.; Grilli, M.; Suppa, D. Charge-fluctuation contribution to the Raman response in superconducting cuprates. Phys. Rev. Lett. 2005, 95, 117004. [Google Scholar] [CrossRef] [PubMed]
- Tassini, L.; Venturini, F.; Zhang, Q.-M.; Hackl, R.; Kikugawa, N.; Fujita, T. Dynamical Properties of Charged Stripes in La2−xSrxCuO4. Phys. Rev. Lett. 2005, 95, 117002. [Google Scholar] [CrossRef] [PubMed]
- Di Castro, C.; Grilli, M.; Caprara, S.; Suppa, D. Charge critical fluctuations in cuprates: Isotope effect, pseudogap, conductivity and Raman spectroscopy. J. Phys. Chem. Solids. 2006, 67, 160. [Google Scholar] [CrossRef]
- Grilli, M.; Caprara, S.; Di Castro, C.; Suppa, D. Spectroscopic evidences of quantum critical charge fluctuations in cuprates. Phys. C Superconduct. 2007, 460–462, 1103. [Google Scholar] [CrossRef]
- Caprara, S.; Di Castro, C.; Enss, T.; Grilli, M. Low-energy signatures of charge and spin fluctuations in Raman and optical spectra of the cuprates. J. Phys. Chem. Solids. 2008, 69, 2155. [Google Scholar] [CrossRef]
- Caprara, S.; Di Castro, C.; Enss, T.; Grilli, M. On the contribution of nearly-critical spin and charge collective modes to the Raman spectra of high-Tc cuprates. J. Magn. Magn. Mater. 2009, 321, 686. [Google Scholar] [CrossRef]
- Grilli, M.; Caprara, S.; Di Castro, C.; Enss, T.; Hackl, R.; Muschler, B.; Prestel, W. Spectral signatures of critical charge and spin fluctuations in cuprates. Phys. B 2009, 404, 3070. [Google Scholar] [CrossRef]
- Caprara, S.; Di Castro, C.; Muschler, B.; Prestel, W.; Hackl, R.; Lambacher, M.; Erb, A.; Komiya, S.; Ando, Y.; Grilli, M. Extracting the dynamical effective interaction and competing order from an analysis of Raman spectra of the high-temperature La2−xSrxCuO4 superconductor. Phys. Rev. B 2011, 84, 054508. [Google Scholar] [CrossRef]
- Fanfarillo, L.; Mori, M.; Campetella, M.; Grilli, M.; Caprara, S. Glue function of optimally and overdoped cuprates from inversion of the Raman spectra. J. Phys. Cond. Matt. 2016, 28, 065701. [Google Scholar] [CrossRef][Green Version]
- Caprara, S.; Di Castro, C.; Fratini, S.; Grilli, M. Anomalous optical absorption in the normal state of overdoped cuprates near the charge-ordering instability. Phys. Rev. Lett. 2002, 88, 147001. [Google Scholar] [CrossRef]
- Caprara, S.; Di Castro, C.; Grilli, M. Collective transport and optical absorption near the stripe criticality. J. Magn. Magn Mater. 2004, 272–276, 134. [Google Scholar] [CrossRef]
- Caprara, S.; Grilli, M.; Di Castro, C.; Enss, T. Optical conductivity near finite-wavelength quantum criticality. Phys. Rev. B 2007, 75, 140505(R). [Google Scholar] [CrossRef]
- Capati, M.; Caprara, S.; Di Castro, C.; Grilli, M.; Seibold, G.; Lorenzana, J. Electronic polymers and soft-matter-like broken symmetries in underdoped cuprates. Nat. Commun. 2015, 6, 7691. [Google Scholar] [CrossRef] [PubMed]
- Kivelson, S.A.; Fradkin, E.; Emery, V.J. Electronic liquid-crystal phases of a doped Mott insulator. Nature 1998, 393, 550. [Google Scholar] [CrossRef]
- Hinkov, V.; Haug, D.; Fauqué, B.; Bourges, P.; Sidis, Y.; Ivanov, A.; Bernhard, C.; Lin, C.T.; Keimer, B. Electronic liquid crystal state in the high-temperature superconductor YBa2Cu3O6.45. Science 2008, 319, 597. [Google Scholar] [CrossRef]
- Daou, R.; Chang, J.; LeBoeuf, D.; Cyr-Choinière, O.; Laliberté, F.; Doiron-Leyraud, N.; Ramshaw, B.J.; Liang, R.; Bonn, D.A.; Hardy, W.N.; et al. Broken rotational symmetry in the pseudogap phase of a high-Tc superconductor. Nature 2010, 463, 519. [Google Scholar] [CrossRef]
- Mesaros, A.; Fujita, K.; Eisaki, H.; Uchida, S.; Davis, J.C.; Sachdev, S.; Zaanen, J.; Lawler, M.J.; Kim, E.-A. Topological Defects Coupling Smectic Modulations to Intra–Unit-Cell Nematicity in Cuprates. Science 2011, 333, 426. [Google Scholar] [CrossRef] [PubMed]
- Lawler, M.J.; Fujita, K.; Lee, J.; Schmidt, A.R.; Kohsaka, Y.; Kim, C.K.; Eisaki, H.; Uchida, S.; Davis, J.C.; Sethna, J.P.; et al. Intra-unit-cell electronic nematicity of the high-Tc copper-oxide pseudogap states. Nature 2010, 466, 347. [Google Scholar] [CrossRef] [PubMed]
- Caprara, S.; Colonna, M.; Di Castro, C.; Hackl, R.; Muschler, B.; Tassini, L.; Grilli, M. Signatures of nematic quantum critical fluctuations in the Raman spectra of lightly doped cuprates. Phys. Rev. B 2015, 91, 205115. [Google Scholar] [CrossRef]
- Perali, A.; Castellani, C.; Di Castro, C.; Grilli, M. d-wave superconductivity near charge instabilities. Phys. Rev. B 1996, 54, 16216. [Google Scholar] [CrossRef] [PubMed]
- Sangiovanni, G.; Capone, M.; Caprara, S.; Castellani, C.; Di Castro, C.; Grilli, M. Doping-driven transition to a time-reversal breaking state in the phase diagram of the cuprates. Phys. Rev. B 2003, 67, 174507. [Google Scholar] [CrossRef]
- Sangiovanni, G.; Capone, M.; Caprara, S. Time reversal breaking superconducting state in the phase diagram of the cuprates. Int. J. Mod. Phys. B 2003, 17, 614. [Google Scholar] [CrossRef]
- Caprara, S.; Grilli, M.; Leridon, B.; Lesueur, J. Extended paraconductivity regime in underdoped cuprates. Phys. Rev. B 2005, 72, 104509. [Google Scholar] [CrossRef]
- Leridon, B.; Caprara, S.; Vanacken, J.; Moshchalkov, V.V.; Attanasi, A.; Grilli, M.; Lorenzana, J. Protected superconductive pairing at the boundaries of charge-density-wave domains. arXiv 2019, arXiv:1905.05606. [Google Scholar]
- Wu, T.; Mayaffre, H.; Krämer, S.; Horvatić, M.; Berthier, C.; Hardy, W.N.; Liang, R.; Bonn, D.A.; Julien, M.-H. Magnetic-field-induced charge-stripe order in the high-temperature superconductor YBa2Cu3Oy. Nature 2011, 477, 191. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Mayaffre, H.; Krämer, S.; Horvatić, M.; Berthier, C.; Kuhns, P.L.; Reyes, A.P.; Liang, R.; Hardy, W.N.; Bonn, D.A.; et al. Emergence of charge order from the vortex state of a high-temperature superconductor. Nat. Commun. 2013, 4, 2113. [Google Scholar] [CrossRef] [PubMed]
- Caprara, S.; Grilli, M.; Lorenzana, J.; Leridon, B. Competing order and double-step superconducting transition in La2−xSrxCuO4. 2019; in preparation. [Google Scholar]
- Campi, G.; Di Castro, D.; Bianconi, G.; Agrestini, S.; Saini, N.L.; Oyanagi, H.; Bianconi, A. Photo-Induced phase transition to a striped polaron crystal in cuprates. Phase Trans. 2002, 75, 927–933. [Google Scholar] [CrossRef]
- Campi, G.; Ricci, A.; Poccia, N.; Fratini, M.; Bianconi, A. X-Rays Writing/Reading of charge density waves in the CuO2 plane of a simple cuprate superconductor. Condense. Matt. 2017, 2, 26. [Google Scholar] [CrossRef]
- Kusmartsev, F.V.; Di Castro, D.; Bianconi, G.; Bianconi, A. Transformation of strings into an inhomogeneous phase of stripes and itinerant carriers. Phys. Lett. A 2000, 275, 118–123. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A. A case of complex matter: coexistence of multiple phase separations in cuprates. In Symmetry and Heterogeneity in High Temperature Superconductors; Springer: Dordrecht, The Netherlands, 2006; pp. 147–156. [Google Scholar]
- Innocenti, D.; Ricci, A.; Poccia, N.; Campi, G.; Fratini, M.; Bianconi, A. A model for liquid-striped liquid phase separation in liquids of anisotropic polarons. J. Superconduct. Novel Magn. 2009, 22, 529–533. [Google Scholar] [CrossRef]
- Campi, G.; Innocenti, D.; Bianconi, A. CDW and similarity of the Mott insulator-to-metal transition in cuprates with the gas-to-liquid-liquid transition in supercooled water. J. Superconduct. Novel Magn. 2015, 28, 1355–1363. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A. High-Temperature superconductivity in a hyperbolic geometry of complex matter from nanoscale to mesoscopic scale. J. Superconduct. Novel Magn. 2016, 29, 627–631. [Google Scholar] [CrossRef]
- Ghiringhelli, G.; Le Tacon, M.; Minola, M.; Blanco-Canosa, S.; Mazzoli, C.; Brookes, N.B.; De Luca, G.M.; Frano, A.; Hawthorn, D.G.; He, F.; et al. Long-range incommensurate charge fluctuations in (Y,Nd)Ba2Cu3O6+x. Science 2012, 337, 821. [Google Scholar] [CrossRef] [PubMed]
- Chang, J.; Blackburn, E.; Holmes, A.T.; Christensen, N.B.; Larsen, J.; Mesot, J.; Liang, R.; Bonn, D.A.; Hardy, W.N.; Watenphul, A.; et al. Direct observation of competition between superconductivity and charge density wave order in YBa2Cu3O6.67. Nat. Phys. 2012, 8, 871. [Google Scholar] [CrossRef]
- Comin, R.; Frano, A.; Yee, M.M.; Yoshida, Y.; Eisaki, H.; Schierle, E.; Weschke, E.; Sutarto, R.; He, F.; Soumyanarayanan, A.; et al. Charge order driven by Fermi-arc instability in Bi2Sr2−xLaxCuO6+δ. Science 2014, 343, 390. [Google Scholar] [CrossRef]
- Blanco-Canosa, S.; Frano, A.; Schierle, E.; Porras, J.; Loew, T.; Minola, M.; Bluschke, M.; Weschke, E.; Keimer, B.; Le Tacon, M. Resonant X-ray scattering study of charge-density- wave correlations in YBa2Cu3O6+x. Phys. Rev. B 2014, 90, 054513. [Google Scholar] [CrossRef]
- Peng, Y.Y.; Fumagalli, R.; Ding, Y.; Minola, M.; Caprara, S.; Betto, D.; De Luca, G.M.; Kummer, K.; Lefranois, E.; Salluzzo, M.; et al. Reentrant charge order in overdoped (Bi,Pb)2.12Sr1.88CuO6+δ outside the pseudogap regime. Nat. Mater. 2018, 17, 697. [Google Scholar] [CrossRef] [PubMed]
- Arpaia, R.; Caprara, S.; Fumagalli, R.; De Vecchi, G.; Peng, Y.Y.; Andersson, E.; Betto, D.; De Luca, G.M.; Brookes, N.B.; Lombardi, F.; et al. Dynamical charge density fluctuations pervading the phase diagram of a Cu-based high-Tc superconductor. arXiv 2019, arXiv:1809.04949. [Google Scholar]
- Campi, G.; Bianconi, A.; Poccia, N.; Bianconi, G.; Barba, L.; Arrighetti, G.; Innocenti, D.; Karpinski, J.; Zhigadlo, N.D.; Kazakov, S.M.; et al. Inhomogeneity of charge-density-wave order and quenched disorder in a high-Tc superconductor. Nature 2015, 525, 359. [Google Scholar] [CrossRef]
- Seibold, G.; Arpaia, R.; Peng, Y.Y.; Fumagalli, R.; Braicovich, L.; Di Castro, C.; Grilli, M.; Ghiringhelli, G.; Caprara, S. Marginal Fermi Liquid behaviour from charge density fluctuations in cuprates. arXiv 2019, arXiv:1905.10232. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).