Evaluating Superconductors through Current Induced Depairing
Abstract
1. Introduction
1.1. Superfluid Density
1.2. Normal-State Resistivity
2. Relationship between the Depairing Current and Other Parameters
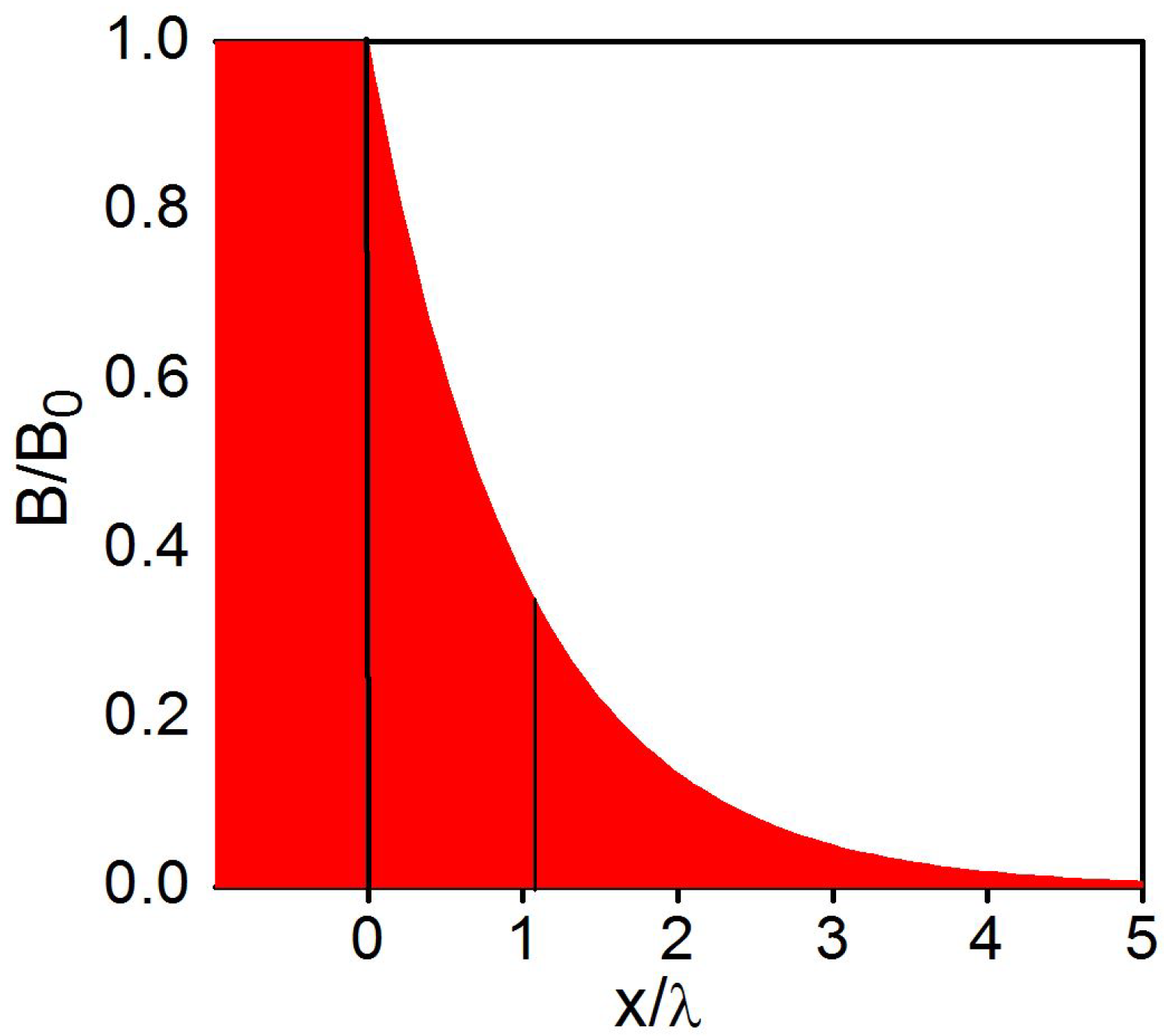
2.1. London Formulation
2.2. Ginzburg–Landau Formulation
2.3. Microscopic Formulations and Generalizations
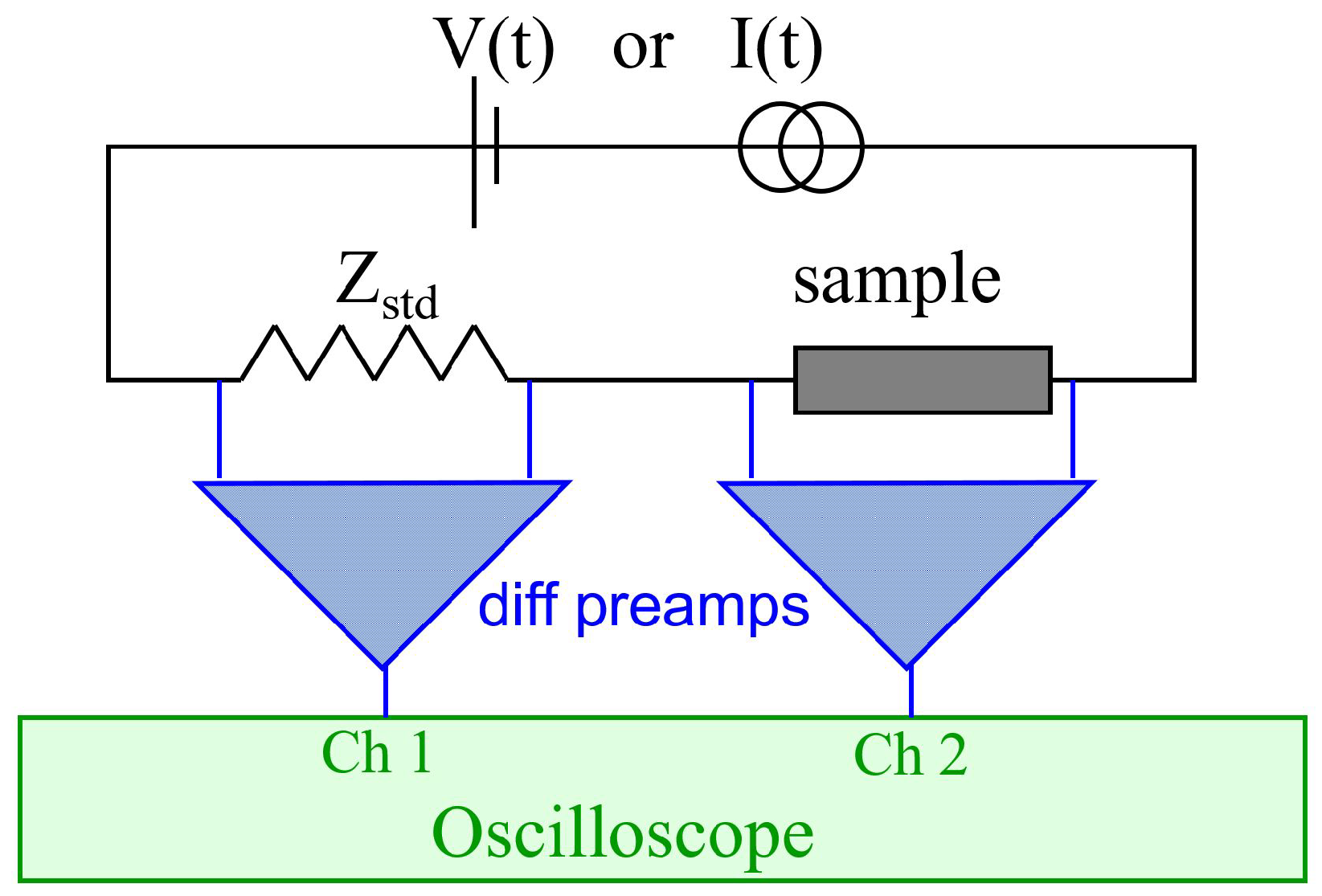
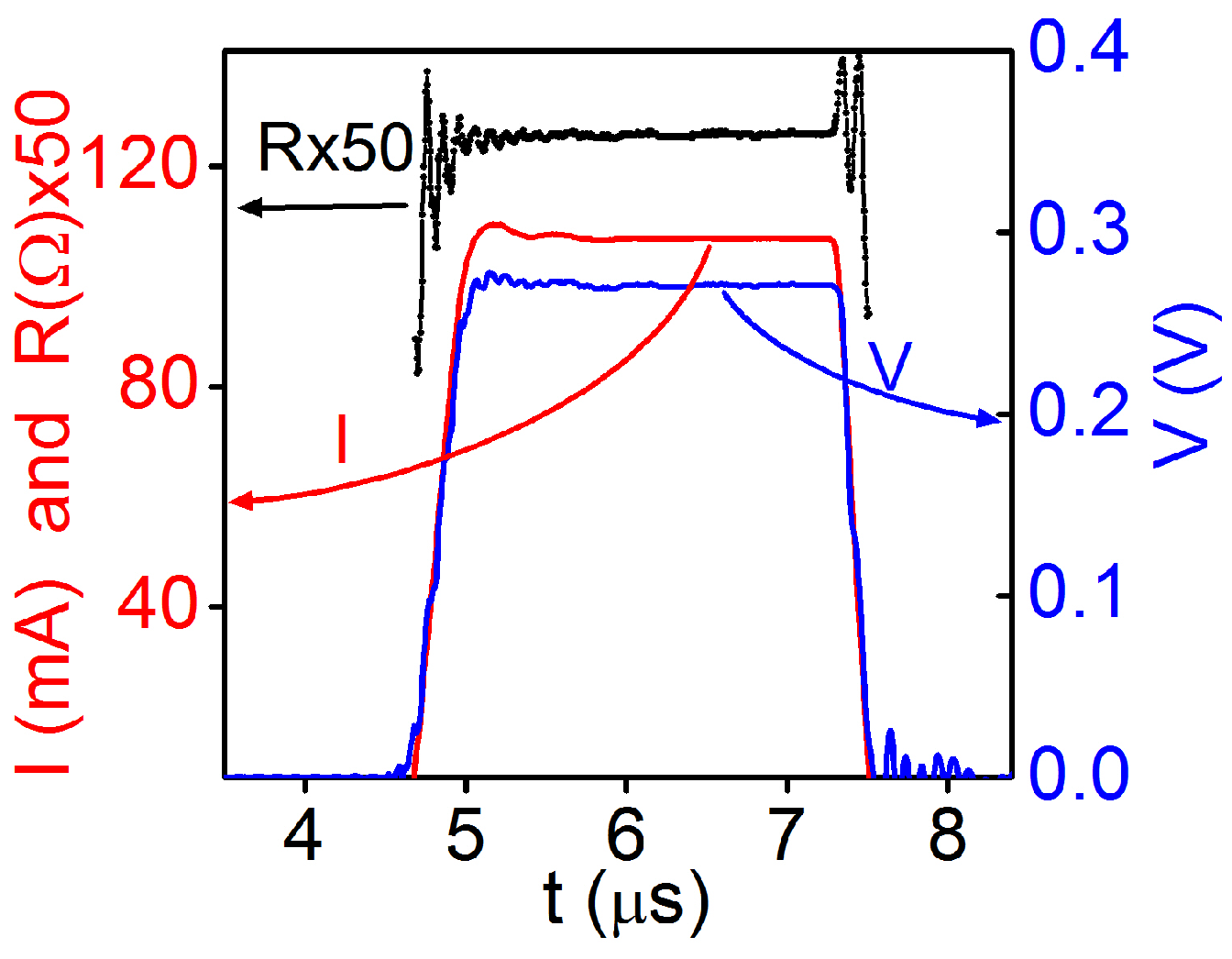
3. Pulsed Measurement Technique
4. Investigations in a Topological Insulator/Chalcogenide Interfacial Superconductor
4.1. Background
4.2. Samples and Experimental Information
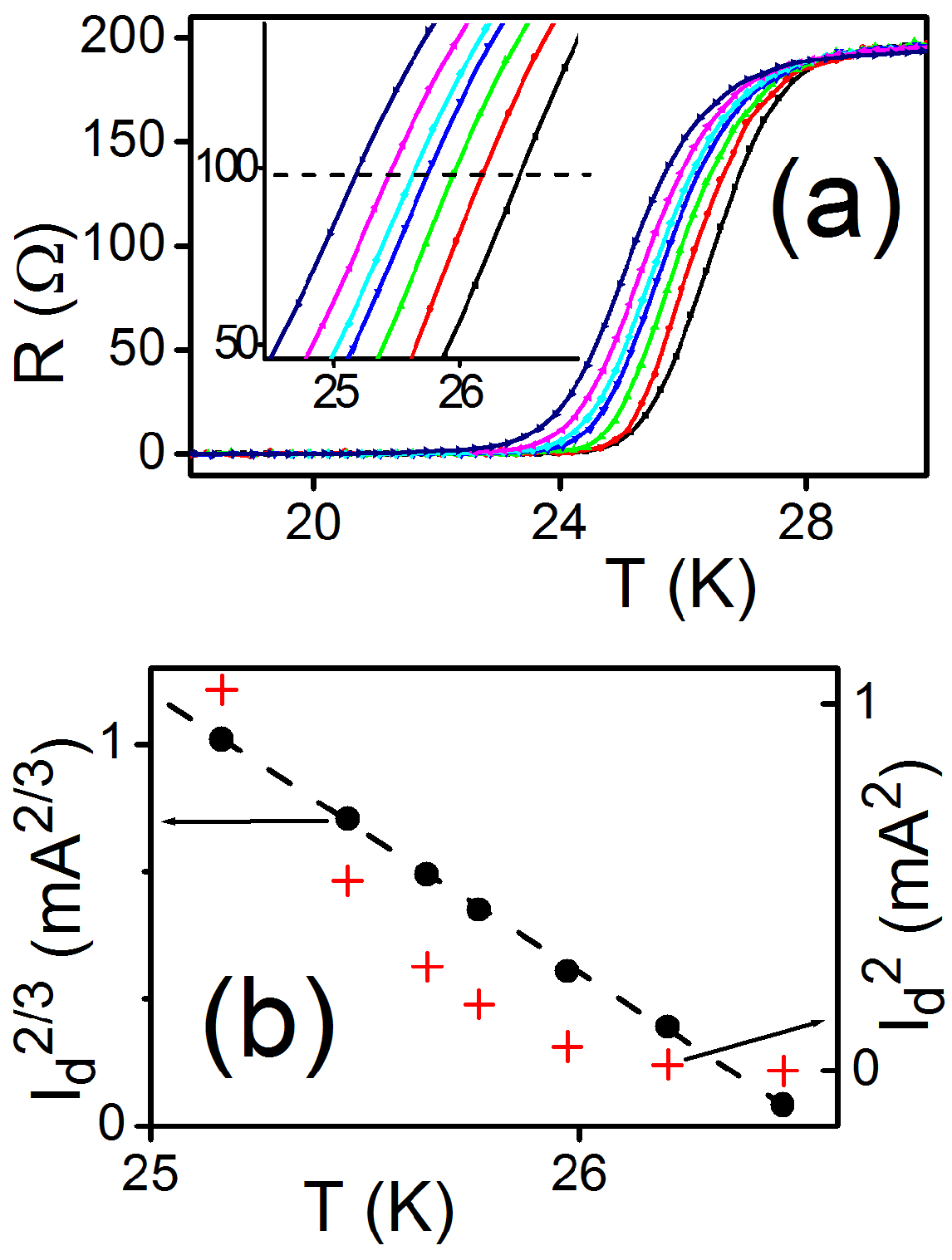
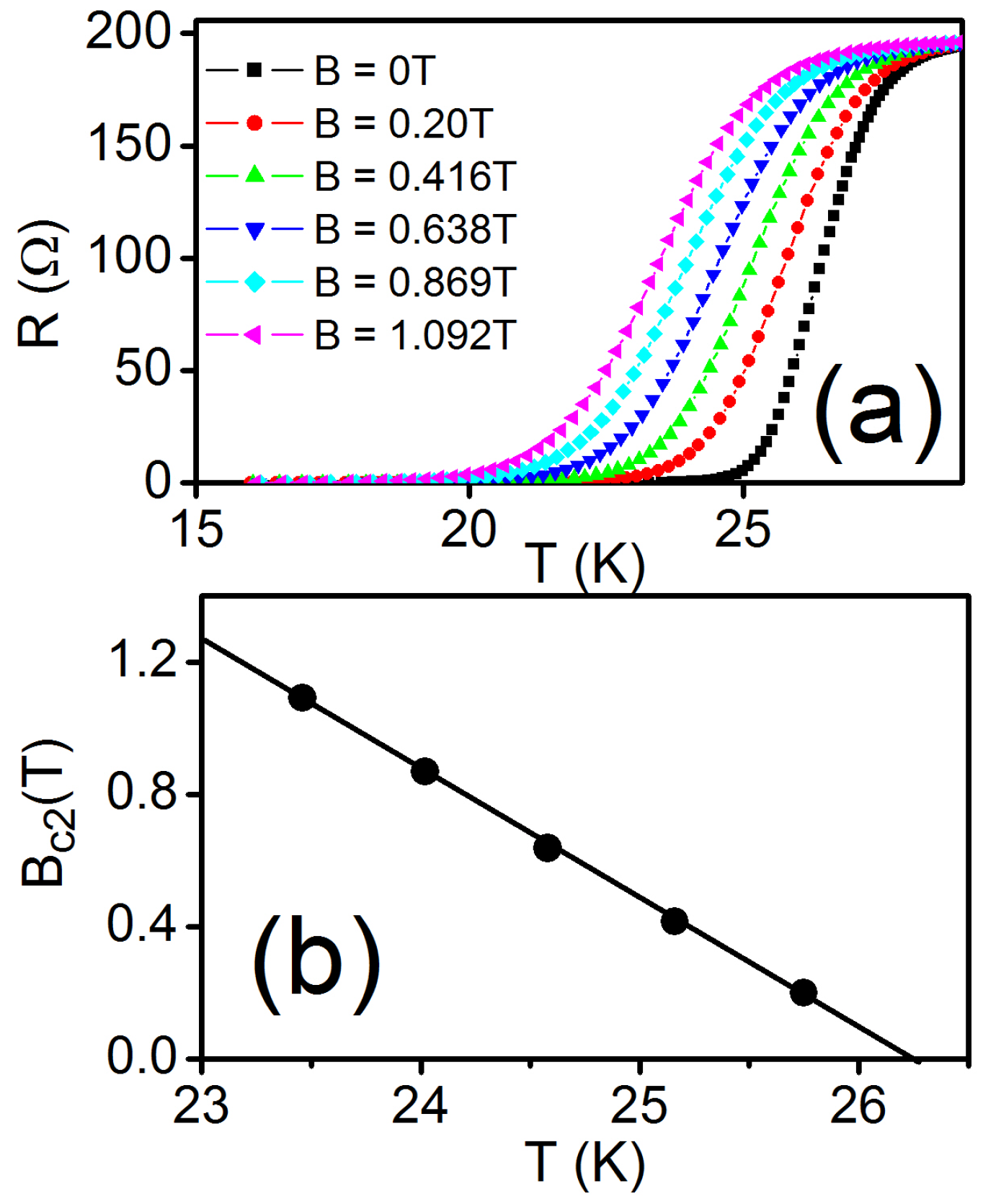
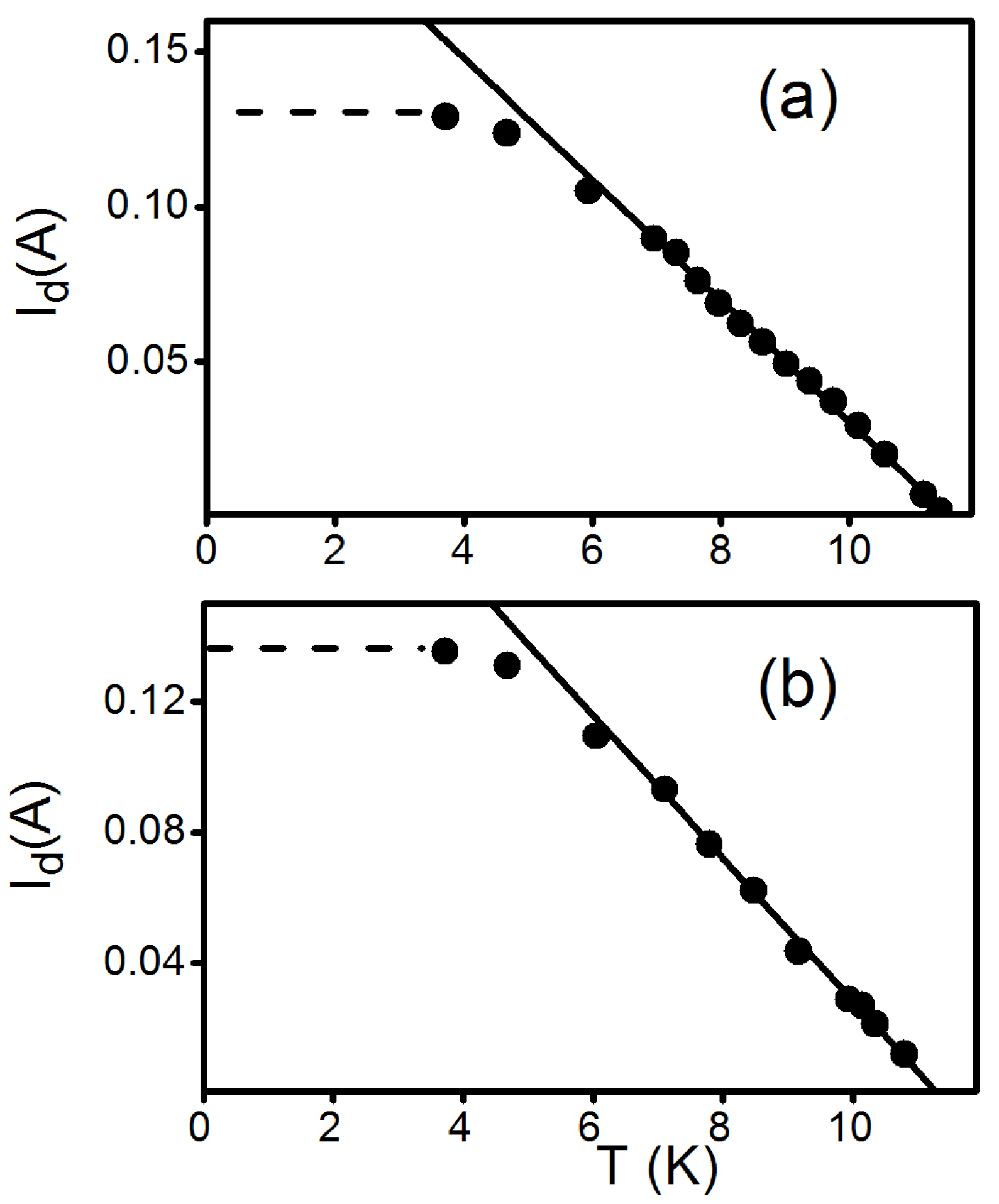
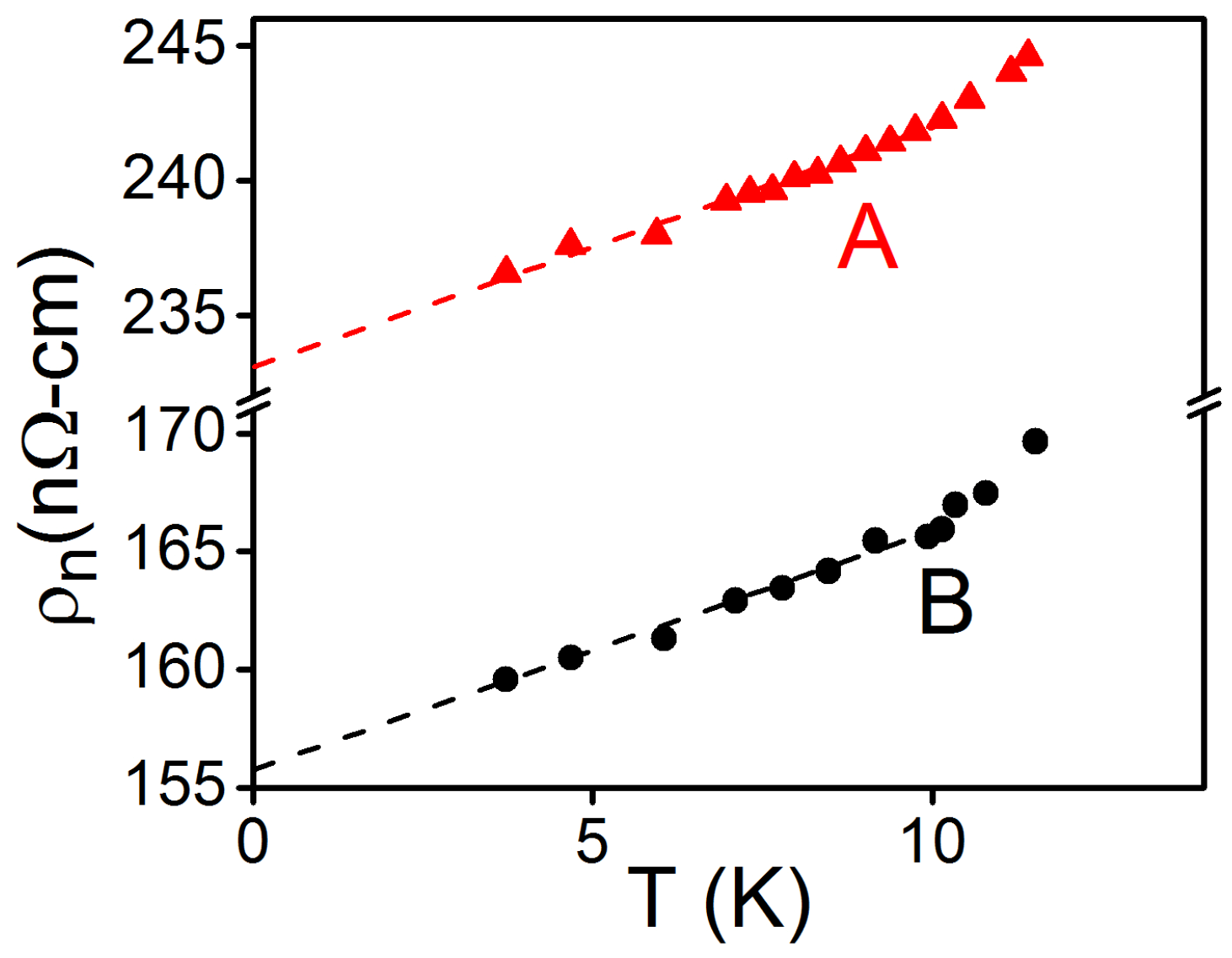
4.3. Results and Discussion
5. Concluding Remarks
Funding
Acknowledgments
Conflicts of Interest
References
- Onnes, K.H. Further experiments with liquid helium. C. On the change of electric resistance of pure metals at very low temperatures, etc. IV. The resistance of pure mercury at helium temperatures. In Through Measurement to Knowledge; Springer: Dordrecht, The Netherlands, 1911; pp. 261–263. [Google Scholar] [CrossRef]
- Somayazulu, M.; Ahart, M.; Mishra, A.K.; Geballe, Z.M.; Baldini, M.; Meng, Y.; Struzhkin, V.V.; Hemley, R.J. Evidence for Superconductivity above 260 K in Lanthanum Superhydride at Megabar Pressures. Phys. Rev. Lett. 2019, 122, 027001–027004. [Google Scholar] [CrossRef] [PubMed]
- Drozdov, A.P.; Kong, P.P.; Minkov, V.S.; Besedin, S.P.; Kuzovnikov, M.A.; Mozaffari, S.; Balicas, L.; Balakirev, F.; Graf, D.; Prakapenka, V.B.; et al. Superconductivity at 250 K in lanthanum hydride under high pressures. Nature 2019, 569, 528–531. [Google Scholar] [CrossRef] [PubMed]
- Tinkham, M. Introduction to Superconductivity, 2nd ed.; Dover Publications: Mineola, NY, USA, 2004; ISBN-10: 0486435032; ISBN-13: 978-0486435039. [Google Scholar]
- Emery, V.J.; Kivelson, S.A. Importance of phase fluctuations in superconductors with small superfluid density. Nature 1995, 374, 434–437. [Google Scholar] [CrossRef]
- Uemura, Y.J.; Luke, G.M.; Sternlieb, B.J.; Brewer, J.H.; Carolan, J.F.; Hardy, W.N.; Kadono, R.; Kempton, J.R.; Kiefl, R.F.; Kreitzman, S.R.; et al. Universal Correlations between Tc and ns/m* (Carrier Density over Effective Mass) in High-Tc Cuprate Superconductors. Phys. Rev. Lett. 1989, 62, 2317–2320. [Google Scholar] [CrossRef] [PubMed]
- Uemura, Y.J.; Le, L.P.; Luke, G.M.; Sternlieb, B.J.; Wu, W.D.; Brewer, J.H.; Riseman, T.M.; Seaman, C.L.; Maple, M.B.; Ishikawa, M.; et al. Basic similarities among cuprate, bismuthate, organic, Chevrel-phase, and heavy-fermion superconductors shown by penetration-depth measurements. Phys. Rev. Lett. 1991, 66, 2665–2668. [Google Scholar] [CrossRef] [PubMed]
- Hardy, W.N.; Bonn, D.A.; Morgan, D.C.; Liang, R.; Zhang, K. Precision measurements of the temperature dependence of λ in Y1Ba2Cu3O7: Strong evidence for nodes in the gap function. Phys. Rev. Lett. 1993, 70, 3999–4002. [Google Scholar] [CrossRef] [PubMed]
- Felcher, G.P.; Kampwirth, R.T.; Gray, K.E.; Felici, R. Polarized-Neutron Reflections: A New Technique Used to Measure the Magnetic Field Penetration Depth in Superconducting Niobium. Phys. Rev. Lett. 1984, 52, 1539–1542. [Google Scholar] [CrossRef]
- Claassen, J.H.; Evetts, J.E.; Somekh, R.E.; Barber, Z.H. Observation of the superconducting proximity effect from kinetic-inductance measurements. Phys. Rev. B 1991, 44, 9605–9608. [Google Scholar] [CrossRef]
- Yong, J.; Lee, S.; Jiang, J.; Bark, C.W.; Weiss, J.D.; Hellstrom, E.E.; Larbalestier, D.C.; Eom, C.B.; Lemberger, T.R. Superfluid density measurements of Ba(CoxFe1−x)2As2 films near optimal doping. Phys. Rev. B 2011, 83, 104510–104514. [Google Scholar] [CrossRef]
- Boghosian, C.; Meyer, H.; Rives, J.E. Density, Coefficient of Thermal Expansion, and Entropy of Compression of Liquid Helium-3 under Pressure below 1.2 K. Phys. Rev. 1966, 146, 110–119. [Google Scholar] [CrossRef]
- Van Degrift, C.T. Tunnel diode oscillator for 0.001 ppm measurements at low temperatures. Rev. Sci. Instr. 1975, 46, 599. [Google Scholar] [CrossRef]
- Sonier, J.E. Muon spin rotation studies of electronic excitations and magnetism in the vortex cores of superconductors. Rep. Prog. Phys. 2007, 70, 1717–1756. [Google Scholar] [CrossRef]
- Luan, L.; Auslaender, O.M.; Lippman, T.M.; Hicks, C.W.; Kalisky, B.; Chu, J.-H.; Analytis, J.G.; Fisher, I.R.; Kirtley, J.R.; Moler, K.A. Local measurement of the penetration depth in the pnictide superconductor Ba(Fe0.95Co0.05)2As2. Phys. Rev. B 2010, 81, 100501–100504. [Google Scholar] [CrossRef]
- Shibauchi, T.; Kitano, H.; Uchinokura, K.; Maeda, A.; Kimura, T.; Kishio, K. Anisotropic penetration depth in La2-xSrxCuO4. Phys. Rev. Lett. 1994, 72, 2263–2266. [Google Scholar] [CrossRef]
- Lee, J.Y.Y.; Lemberger, T.R. Penetration depth λ(T) of Y1Ba2Cu3O7 films determined from the kinetic inductance. Appl. Phys. Lett. 1993, 62, 2419–2421. [Google Scholar] [CrossRef]
- Saracila, G.F.; Kunchur, M.N. Ballistic acceleration of a supercurrent in a superconductor. Phys. Rev. Lett. 2009, 102, 077001–077004. [Google Scholar] [CrossRef] [PubMed]
- Diener, P.; Leduc, H.G.; Yates, S.J. Design and Testing of Kinetic Inductance Detectors Made of Titanium Nitride. J. Low Temp. Phys. 2012, 167, 305–310. [Google Scholar] [CrossRef][Green Version]
- Jochem, B. Kinetic Inductance Detectors. J. Low Temp. Phys. 2012, 167, 292–304. [Google Scholar]
- Kunchur, M.N.; Dean, C.; Liang, M.; Moghaddam, N.S.; Guarino, A.; Nigro, A.; Grimaldi, G.; Leo, A. Depairing current density of Nd2−xCexCuO4 superconducting films. Physica C 2013, 495, 66–68. [Google Scholar] [CrossRef]
- Kunchur, M.N.; Ivlev, B.I.; Christen, D.K.; Phillips, J.M. Metallic Normal State of Y1Ba2Cu3O7. Phys. Rev. Lett. 2000, 84, 5204–5207. [Google Scholar] [CrossRef] [PubMed]
- Larkin, A.I.; Ovchinnikov, Y.U.N. Nonlinear conductivity of superconductors in the mixed state. Sov. Phys.—JETP 1976, 41, 960–965. [Google Scholar]
- Blatter, G.; Feigel’man, M.V.; Mikhail, V.B.; Larkin, A.I.; Valerii, V.M. Vortices in high-temperature superconductors. Rev. Mod. Phys. 1994, 66, 1125–1388. [Google Scholar] [CrossRef]
- Kunchur, M.N. Unstable flux flow due to heated electrons in superconducting films. Phys. Rev. Lett. 2002, 89, 137005–137008. [Google Scholar] [CrossRef] [PubMed]
- Kunchur, M.N. Current-induced pair breaking in Magnesium Diboride. J. Phys. Condens. Matter. 2004, 16, R1183–R1204. [Google Scholar] [CrossRef]
- London, F.; London, H. The electromagnetic equations of the supraconductor. Proc. Roy. Soc. 1935, A149, 71–88. [Google Scholar] [CrossRef]
- Ginzburg, V.L.; Landau, L.D. On the Theory of superconductivity. Zh. Eksperim. Teor. Fiz. 1950, 20, 1064–1082. [Google Scholar]
- Bardeen, J. Critical Fields and Currents in Superconductors. Rev. Mod. Phys. 1962, 34, 667–681. [Google Scholar] [CrossRef]
- Romijn, J.; Klapwijk, T.M.; Renne, M.J.; Mooij, J.E. Critical pair-breaking current in superconducting aluminum strips far below Tc. Phys. Rev. B 1982, 26, 3648–3655. [Google Scholar] [CrossRef]
- Maki, K. On Persistent Currents in a Superconducting Alloy. II. Progr. Theor. Phys. 1963, 29, 333–340. [Google Scholar] [CrossRef]
- Ovchinnikov, Y.U.N. Critical current of thin films for diffuse reflection from the walls. Sov. Phys.—JETP 1969, 29, 853–860. [Google Scholar]
- Kupriyanov, M.Y.; Lukichev, V.F. Temperature dependence of pair-breaking current in superconductors. Sov. J. Low Temp. Phys. 1980, 6, 210. [Google Scholar]
- Bauer, E.; Paul, C.; Berger, S.; Majumdar, S.; Michor, H.; Giovannini, M.; Saccone, A.; Bianconi, A. Thermal conductivity of superconducting MgB2. J. Phys. Condens. Matter 2001, 13, L487–L493. [Google Scholar] [CrossRef][Green Version]
- Agrestini, S.; Metallo, C.; Filippi, M.; Simonelli, L.; Campi, G.; Sanipoli, C.; Liarokapis, E.; De Negri, S.; Giovannini, M.; Saccone, A.; et al. Substitution of Sc for Mg in MgB2: Effects on transition temperature and Kohn anomaly. Phys. Rev. B 2004, 70, 134514–134518. [Google Scholar] [CrossRef]
- Kagan, M.Y.; Bianconi, A. Fermi-Bose Mixtures and BCS-BEC Crossover in High-Tc Superconductors. Condens. Matter 2019, 4, 51. [Google Scholar] [CrossRef]
- Kunchur, M.N.; Christen, D.K.; Klabunde, C.E.; Phillips, J.M. Pair-breaking effect of high current densities on the superconducting transition in Y1Ba2Cu3O7. Phys. Rev. Lett. 1994, 72, 752–775. [Google Scholar] [CrossRef]
- Liang, M.; Kunchur, M.N.; Fruchter, L.; Li, Z.Z. Depairing current density of infinite-layer Sr1−xLaxCuO2 superconducting films. Physica C 2013, 492, 178–180. [Google Scholar] [CrossRef]
- Werthamer, N.R.; Helfand, E.; Hohenberg, P.C. Temperature and Purity Dependence of the Superconducting Critical Field, Hc2. III. Electron Spin and Spin-Orbit Effects. Phys. Rev. 1966, 147, 295–302. [Google Scholar] [CrossRef]
- Gurevich, A. Enhancement of the upper critical field by nonmagnetic impurities in dirty two-gap superconductors. Phys. Rev. B 2003, 67, 184515–184527. [Google Scholar] [CrossRef]
- He, Q.L.; Liu, H.; He, M.; Lai, Y.H.; He, H.; Wang, G.; Law, K.T.; Lortz, R.; Wang, J.; Sou, I.K. Two-dimensional superconductivity at the interface of a Bi2Te3/FeTe heterostructure. Nat. Commun. 2014, 5, 4247–4254. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A.; Poccia, N.; Bianconi, G.; Barba, L.; Arrighetti, G.; Innocenti, D.; Karpinski, J.; Zhigadlo, N.D.; Kazakov, S.M.; et al. Inhomogeneity of charge-density-wave order and quenched disorder in a high-Tc superconductor. Nature 2015, 525, 359–362. [Google Scholar] [CrossRef] [PubMed]
- Jarlborg, T.; Bianconi, A. Multiple Electronic Components and Lifshitz Transitions by Oxygen Wires Formation in Layered Cuprates and Nickelates. Condens. Matter 2019, 4, 15. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A. High Temperature superconductivity in a hyperbolic geometry of complex matter from nanoscale to mesoscopic scale. J. Supercond. Nov. Magn. 2016, 29, 627–631. [Google Scholar] [CrossRef]
- Dean, C.L.; Kunchur, M.N.; He, Q.L.; Liu, H.; Wang, J.; Lortz, R.; Sou, I.K. Current driven vortex-antivortex pair breaking and vortex explosion in the Bi2Te3/FeTe interfacial superconductor. Physica C 2016, 527, 46–49. [Google Scholar] [CrossRef]
- Dean, C.L.; Kunchur, M.N.; He, Q.L.; Liu, H.; Wang, J.; Lortz, R.; Sou, I.K. Current-induced depairing in the Bi2Te3/FeTe interfacial superconductor. Phys. Rev. B 2015, 92, 094502–094506. [Google Scholar] [CrossRef]
- Pan, Z.-H.; Fedorov, A.V.; Gerdner, D.; Lee, Y.S.; Chu, S.; Valla, T. Measurement of an Exceptionally Weak Electron-Phonon Coupling on the Surface of the Topological Insulator Bi2Se3 Using Angle-Resolved Photoemission Spectroscopy. Phys. Rev. Lett. 2012, 108, 187001–187005. [Google Scholar] [CrossRef]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kunchur, M.N. Evaluating Superconductors through Current Induced Depairing. Condens. Matter 2019, 4, 54. https://doi.org/10.3390/condmat4020054
Kunchur MN. Evaluating Superconductors through Current Induced Depairing. Condensed Matter. 2019; 4(2):54. https://doi.org/10.3390/condmat4020054
Chicago/Turabian StyleKunchur, Milind N. 2019. "Evaluating Superconductors through Current Induced Depairing" Condensed Matter 4, no. 2: 54. https://doi.org/10.3390/condmat4020054
APA StyleKunchur, M. N. (2019). Evaluating Superconductors through Current Induced Depairing. Condensed Matter, 4(2), 54. https://doi.org/10.3390/condmat4020054



