Scaling between Superfluid Density and Tc in Overdoped La2−xSrxCuO4 Films
Abstract
1. Introduction
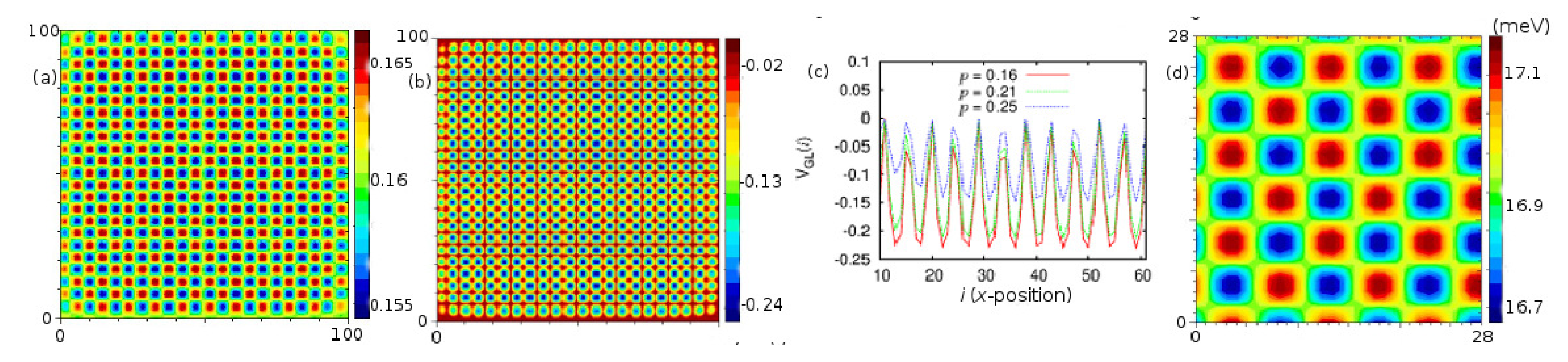
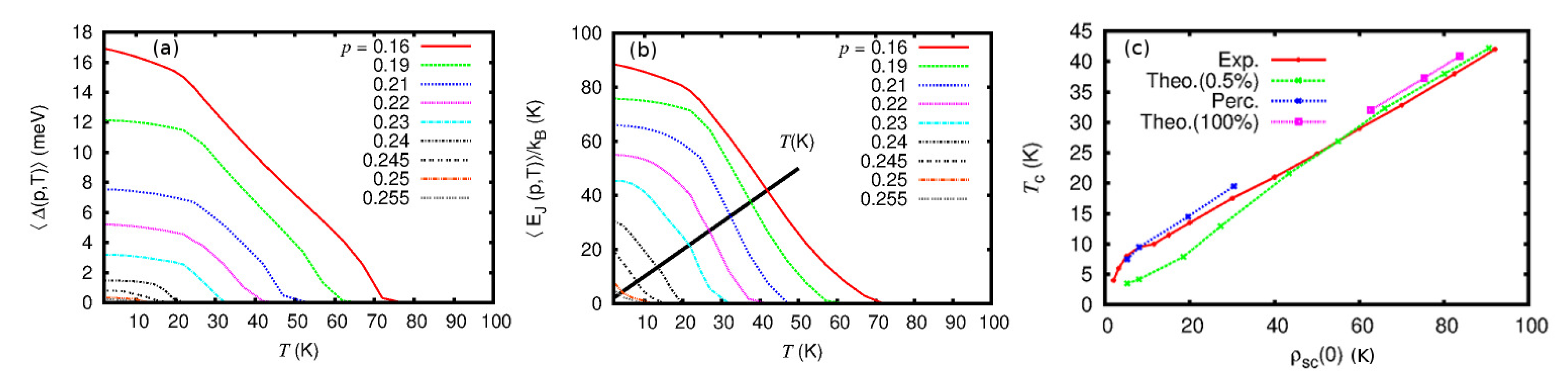
2. Results
3. Discussion
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Božović, I.; He, X.; Wu, J.; Bollinger, A.T. Dependence of the critical temperature in overdoped copper oxides on superfluid density. Nature 2016, 536, 309–311. [Google Scholar] [CrossRef]
- Torchinsky, D.H.; Mahmood, F.; Bollinger, A.T.; Božović, I.; Gedik, N. Fluctuating charge-density waves in a cuprate superconductor. Nat. Mater. 2013, 12, 387–391. [Google Scholar] [CrossRef]
- Wu, J.; Bollinger, A.T.; He, X.; Božović, I. Spontaneous breaking of rotational symmetry in copper oxide superconductors. Nature 2017, 547, 432–435. [Google Scholar] [CrossRef]
- Comin, R.; Damascelli, A. Resonant X-Ray Scattering Studies of Charge Order in Cuprates. Ann. Rev. Condens. Mat. Phys. 2016, 7, 369. [Google Scholar] [CrossRef]
- Dean, M.P.M.; Dellea, G.; Springell, R.S.; Yakhou-Harris, F.; Kummer, K.; Brookes, N.B.; Liu, X.; Sun, Y.-J.; Strle, J.; Schmitt, T.; et al. Persistence of magnetic excitations in La2−xSrxCO4 from the undoped insulator to the heavily overdoped non-superconducting metal. Nat. Mater. 2013, 12, 1019–1023. [Google Scholar] [CrossRef]
- Yamada, K.; Lee, C.H.; Kurahashi, K.; Wada, J.; Wakimoto, S.; Ueki, S.; Kimura, H.; Endoh, Y.; Hosoya, S.; Shirane, G.; et al. Doping dependence of the spatially modulated dynamical spin correlations and the superconducting-transition temperature in La2−xSrxCuO4. Phys. Rev. B 1998, 57, 6165–6172. [Google Scholar] [CrossRef]
- Tranquada, J.M.; Axe, J.D.; Ichikawa, N.; Moodenbaugh, A.R.; Nakamura, Y.; Uchida, S. Coexistence of, and Competition between, Superconductivity and Charge-Stripe Order in La1.6−xNd0.4SrxCuO4. Phys. Rev. Lett. 1997, 78, 338–341. [Google Scholar] [CrossRef]
- Mahmood, F.; He, X.; Božović, I.; Armitage, N.P. Locating the Missing Superconducting Electrons in the Overdoped Cuprates La2−xSrxCuO4. Phys. Rev. Lett. 2019, 122, 027003. [Google Scholar] [CrossRef]
- Lee-Hone, N.R.; Dodge, J.S.; Broun, D.M. Disorder and superfluid density in overdoped cuprate superconductors. Phys. Rev. B 2017, 96, 024501. [Google Scholar] [CrossRef]
- Vojta, M. Superconducting charge-ordered states in cuprates. Phys. Rev. B 2002, 66, 104505. [Google Scholar] [CrossRef]
- Ortix, C.; Lorenzana, J.; Di Castro, C. Coulomb-Frustrated Phase Separation Phase Diagram in Systems with Short-Range Negative Compressibility. Phys. Rev. Lett. 2008, 100, 246402. [Google Scholar] [CrossRef]
- Nie, L.; Maharaj, A.V.; Fradkin, E.; Kivelson, S.A. Vestigial nematicity from spin and/or charge order in the cuprates. Phys. Rev. B 2017, 96, 085142. [Google Scholar] [CrossRef]
- Okamoto, S.; Sénéchal, D.; Civelli, M.; Tremblay, A.M.S. Dynamical electronic nematicity from Mott physics. Phys. Rev. B 2010, 82, 180511. [Google Scholar] [CrossRef]
- Ghiringhelli, G.; Le Tacon, M.; Minola, M.; Blanco-Canosa, S.; Mazzoli, C.; Brookes, N.B.; De Luca, G.M.; Frano, A.; Hawthorn, D.G.; He, F.; et al. Long-range incommensurate charge fluctuations in (Y,Nd)Ba2Cu3O(6+x). Science 2012, 337, 821–825. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A.; Poccia, N.; Bianconi, G.; Barba, L.; Arrighetti, G.; Innocenti, D.; Karpinski, J.; Zhigadlo, N.D.; Kazakov, S.M.; et al. Inhomogeneity of charge-density-wave order and quenched disorder in a high-Tc superconductor. Nature 2015, 525, 359–362. [Google Scholar] [CrossRef]
- de Mello, E.; da Silveira Filho, O.T. Numerical study of the Cahn–Hilliard equation in one, two and three dimensions. Physica A 2005, 347, 429–443. [Google Scholar] [CrossRef]
- de Mello, E.V.L.; Kasal, R.B.; Passos, C.A.C. Electronic phase separation transition as the origin of the superconductivity and pseudogap phase of cuprates. J. Phys. Condens. Matt. 2009, 21, 235701. [Google Scholar] [CrossRef][Green Version]
- de Mello, E.V.L. Disordered-based theory of pseudogap, superconducting gap, and Fermi arc of cuprates. Eur. Phys. Lett. 2012, 99, 37003. [Google Scholar] [CrossRef]
- de Mello, E.V.L.; Sonier, J.E. Charge segregation model for superconducting correlations in cuprates above T c. J. Phys. Condens. Matt. 2014, 26, 492201. [Google Scholar] [CrossRef][Green Version]
- de Mello, E.V.L.; Sonier, J.E. Superconducting correlations induced by charge ordering in cuprate superconductors and Fermi-arc formation. Phys. Rev. B 2017, 95, 184520. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free Energy of a Nonuniform System. I. Interfacial Free Energy. J. Chem. Phys. 1958, 28, 258. [Google Scholar] [CrossRef]
- Corson, J.; Mallozzi, R.; Orenstein, J. Vanishing of phase coherence in underdoped Bi2Sr2CaCu2O8+x. Nature 1999, 406, 221–223. [Google Scholar] [CrossRef]
- Xu, Z.A.; Ong, N.P.; Wang, Y.; Kakeshita, T.; Uchida, S. Vortex-like excitations and the onset of superconducting phase fluctuation in underdoped La2−xSrxCuO4. Nature 2000, 406, 486–488. [Google Scholar] [CrossRef]
- Spivak, B.I.; Kivelson, S.A. Negative local superfluid densities: The difference between dirty superconductors and dirty Bose liquids. Phys. Rev. B 1991, 43, 3740–3743. [Google Scholar] [CrossRef]
- Lang, K.M.; Madhavan, V.; Hoffman, J.E.; Hudson, E.W.; Eisaki, H.; Uchida, S.; Davis, J.C. Imaging the granular structure of high-Tc superconductivity in underdoped Bi2Sr2CaCu2O8+d. Nature 2002, 415, 412–416. [Google Scholar] [CrossRef]
- Imry, Y.; Strongin, M.; Homes, C.C. ns − Tc Correlations in Granular Superconductors. Phys. Rev. Lett. 2012, 109, 067003. [Google Scholar] [CrossRef]
- Wang, Y.; Li, L.; Ong, N.P. Nernst effect in high-Tc superconductors. Phys. Rev. B 2006, 73, 024510. [Google Scholar] [CrossRef]
- Gomes, K.K.; Pasupathy, A.N.; Pushp, A.; Ono, S.; Ando, Y.; Yazdani, A. Visualizing pair formation on the atomic scale in the high-Tc superconductor Bi2Sr2CaCu2O8+δ. Nature 2007, 447, 569–572. [Google Scholar] [CrossRef]
- Bray, A. Theory of phase-ordering kinetics. Adv. Phys. 1994, 43, 357–459. [Google Scholar] [CrossRef]
- Kharkov, Y.A.; Sushkov, O.P. The amplitudes and the structure of the charge density wave in YBCO. Sci. Rep. 2016, 6, 34551. [Google Scholar] [CrossRef]
- Hücker, M.; Christensen, N.B.; Holmes, A.T.; Blackburn, E.; Forgan, E.M.; Liang, R.; Bonn, D.A.; Hardy, W.N.; Gutowski, O.; Zimmermann, M.V.; et al. Competing charge, spin, and superconducting orders in underdoped YBa2Cu3Oy. Phys. Rev. B 2014, 90, 1–11. [Google Scholar] [CrossRef]
- Chang, J.; Blackburn, E.; Holmes, T.; Christensen, N.B.; Larsen, J.; Mesot, J.; Liang, R.; Bonn, D.A.; Hardy, W.N.; Watenphul, A.; et al. Direct observation of competition between superconductivity and charge density wave order in YBa2Cu3O6.67. Nat. Phys. 2012, 8, 871–876. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Müller, K.A. Superconductivity in Complex Systems; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Saini, N.L.; Oyanagi, H.; Wu, Z.; Bianconi, A. Lattice fluctuations and inhomogeneous charge states of high-Tc superconductors Supercondors. Sci. Technol. 2002, 15, 439–449. [Google Scholar] [CrossRef]
- Saini, N.L.; Oyanagi, H.; Ito, T.; Scagnoli, V.; Filippi, M.; Agrestini, S.; Bianconi, A. Lattice fluctuations and inhomogeneous charge states of high-Tc superconductors Supercondors. Eur. Phys. J. B Condens. Matt. Complex Syst. 2003, 36, 75–80. [Google Scholar] [CrossRef]
- Saini, N.L.; Oyanagi, H.; Scagnoli, V.; Ito, T.; Oka, K.; Bianconi, A. Different temperature-dependent local displacements in the underdoped and overdoped La2−xSrxCuO4 system. EPL 2003, 63, 125–131. [Google Scholar] [CrossRef]
- Saini, N.L.; Oyanagi, H.; Scagnoli, V.; Ito, T.; Oka, K.; Bianconi, A. Study of Temperature Dependent Local Structure by Polarized Cu K-edge EXAFS Measurements on La2−xSrxCuO4 (x=0.105, 0.13, 0.20). J. Phys. Soc. Jpn 2003, 72, 829–834. [Google Scholar] [CrossRef]
- Lanzara, A.; meng Zhao, G.; Saini, N.L.; Bianconi, A.; Conder, K.; Keller, H.; Müller, K.A. Oxygen-isotope shift of the charge-stripe ordering temperature in La2−xSrxCuO4 from x-ray absorption spectroscopy. J. Phys. Condens. Matt. 1999, 11, L541–L546. [Google Scholar] [CrossRef]
- Bendele, M.; von Rohr, F.; Guguchia, Z.; Pomjakushina, E.; Conder, K.; Bianconi, A.; Simon, A.; Bussmann-Holder, A.; Keller, H. Evidence for strong lattice effects as revealed from huge unconventional oxygen isotope effects on the pseudogap temperature in La2−xSrxCuO4. Phys. Rev. B 2017, 95, 014514. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Keller, H.; Khasanov, R.; Simon, A.; Bianconi, A.; Bishop, A.R. Isotope and interband effects in a multi-band model of superconductivity. New J. Phys. 2011, 13, 093009. [Google Scholar] [CrossRef]
- Kusmartsev, F.V.; Castro, D.D.; Bianconi, G.; Bianconi, A. Transformation of strings into an inhomogeneous phase of stripes and itinerant carriers. Phys. Lett. A 2000, 275, 118–123. [Google Scholar] [CrossRef]
- Poccia, N.; Fratini, M.; Ricci, A.; Campi, G.; Barba, L.; Vittorini-Orgeas, A.; Bianconi, G.; Aeppli, G.; Bianconi, A. Evolution and control of oxygen order in a cuprate superconductor. Nat. Mater. 2011, 10, 12. [Google Scholar] [CrossRef]
- Yoshida, T.; Hashimoto, M.; Vishik, I.M.; Shen, Z.X.; Fujimori, A. Pseudogap, Superconducting Gap, and Fermi Arc in High-Tc Cuprates Revealed by Angle-Resolved Photoemission Spectroscopy. J. Phys. Soc. Jpn 2012, 81, 011006. [Google Scholar] [CrossRef]
- Dubroka, A.; Rössle, M.; Kim, K.W.; Malik, V.K.; Munzar, D.; Basov, D.N.; Schafgans, A.A.; Moon, S.J.; Lin, C.T.; Haug, D.; et al. Evidence of a precursor superconducting phase at temperatures as high as 180 K in RBa2Cu3O(7−δ) (R=Y,Gd,Eu) superconducting crystals from infrared spectroscopy. Phys. Rev. Lett. 2011, 106, 1–4. [Google Scholar] [CrossRef]
- Deutcher, G. From Granular Superconductivity to High Tc in High-Tc Copper Oxide Superconductors and Related Novel Materials; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Shamoto, S.i. Local Structure of Functional Solids. J. Phys. Soc. Jpn 2019, 88, 081008. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A. Evolution of Complexity in Out-of-Equilibrium Systems by Time-Resolved or Space-Resolved Synchrotron Radiation Techniques. Condense. Matt. 2019, 4, 32. [Google Scholar] [CrossRef]
- Jarlborg, T.; Bianconi, A. Multiple Electronic Components and Lifshitz Transitions by Oxygen Wires Formation in Layered Cuprates and Nickelates. Condense. Matt. 2019, 4, 15. [Google Scholar] [CrossRef]
- Oleś, A.M.; Wohlfeld, K.; Khaliullin, G. Orbital Symmetry and Orbital Excitations in High-Tc Superconductors. Condense. Matt. 2019, 4, 46. [Google Scholar] [CrossRef]
- Mou, Y.; Liu, Y.; Tan, S.; Feng, S. Doping and momentum dependence of coupling strength in cuprate superconductors. arXiv 2019, arXiv:1903.00803. [Google Scholar]
- Gavrichkov, V.A.; Shan’ko, Y.; Zamkova, N.G.; Bianconi, A. Is There Any Hidden Symmetry in the Stripe Structure of Perovskite High-Temperature Superconductors? J. Phys. Chem. Lett. 2019, 10, 1840–1844. [Google Scholar] [CrossRef]
- Bianconi, A.; Jarlborg, T. Superconductivity above the lowest Earth temperature in pressurized sulfur hydride. EPL 2015, 112, 37001. [Google Scholar] [CrossRef]
- Mozaffari, S.; Sun, D.; Minkov, V.S.; Knyazev, D.; Betts, J.B.; Einaga, M.; Balakirev, F.F. Superconducting Phase-Diagram of H3S under High Magnetic Fields. arXiv 2019, arXiv:1901.11208. [Google Scholar]
- Jarlborg, T.; Bianconi, A. Breakdown of the Migdal approximation at Lifshitz transitions with giant zero-point motion in the H3S superconductor. Sci. Rep. 2016, 6, 24816. [Google Scholar] [CrossRef]
- Villa-Cortés, S.; Baquero, R. The thermodynamics and the inverse isotope effect of superconducting palladium hydride compounds under pressure. J. Phys. Chem. Solids 2018, 123, 371–377. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Mello, E.V.L. Scaling between Superfluid Density and Tc in Overdoped La2−xSrxCuO4 Films. Condens. Matter 2019, 4, 52. https://doi.org/10.3390/condmat4020052
de Mello EVL. Scaling between Superfluid Density and Tc in Overdoped La2−xSrxCuO4 Films. Condensed Matter. 2019; 4(2):52. https://doi.org/10.3390/condmat4020052
Chicago/Turabian Stylede Mello, Evandro V. L. 2019. "Scaling between Superfluid Density and Tc in Overdoped La2−xSrxCuO4 Films" Condensed Matter 4, no. 2: 52. https://doi.org/10.3390/condmat4020052
APA Stylede Mello, E. V. L. (2019). Scaling between Superfluid Density and Tc in Overdoped La2−xSrxCuO4 Films. Condensed Matter, 4(2), 52. https://doi.org/10.3390/condmat4020052




