Fermi-Bose Mixtures and BCS-BEC Crossover in High-Tc Superconductors
Abstract
1. Introduction
- 1)
- A single electronic component;
- 2)
- High electron density and high Fermi energy EF;
- 3)
- Low values of the ratio ω0/EF between the energy cut off of the attractive interaction ω0 and the Fermi energy;
- 4)
- Large Fermi surface and high Fermi momentum kF;
- 5)
- Superconducting energy gap much smaller than the Fermi energy Δ << EF;
- 6)
- Large ratio between the coherence length ξ0 and the average distance between electrons.
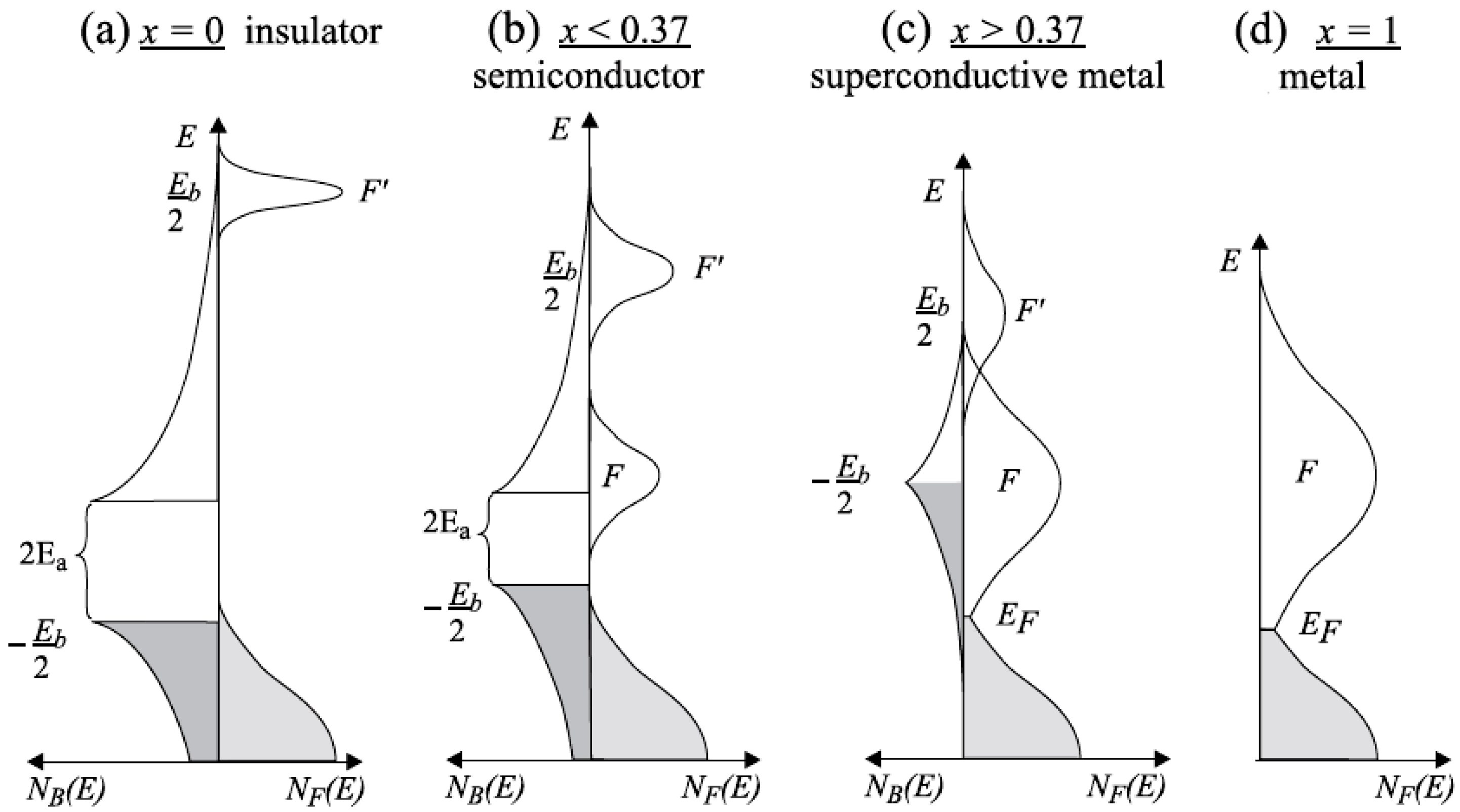
2. Superconductivity in the Fermi-Bose Mixture Model—Theoretical Considerations
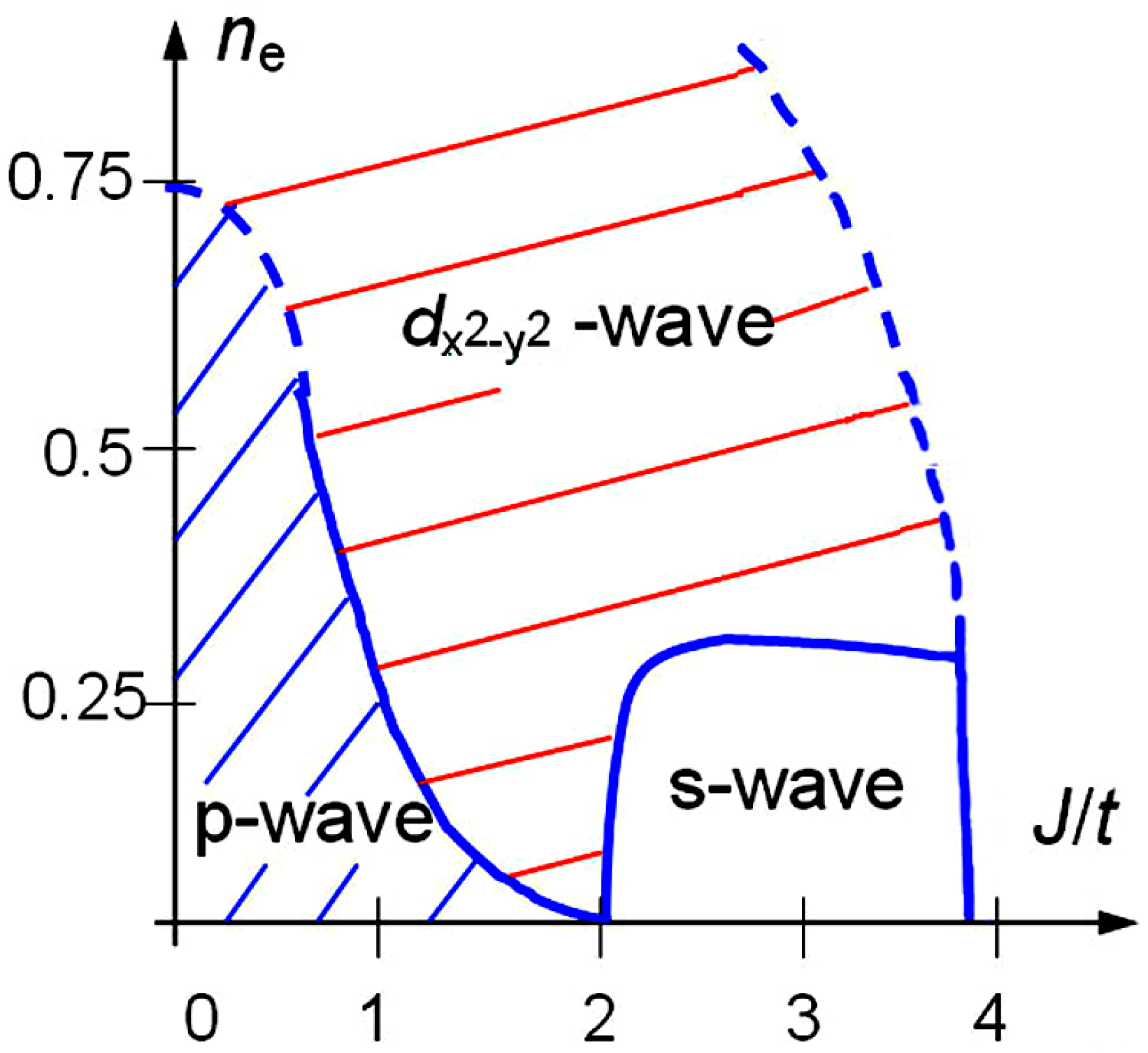
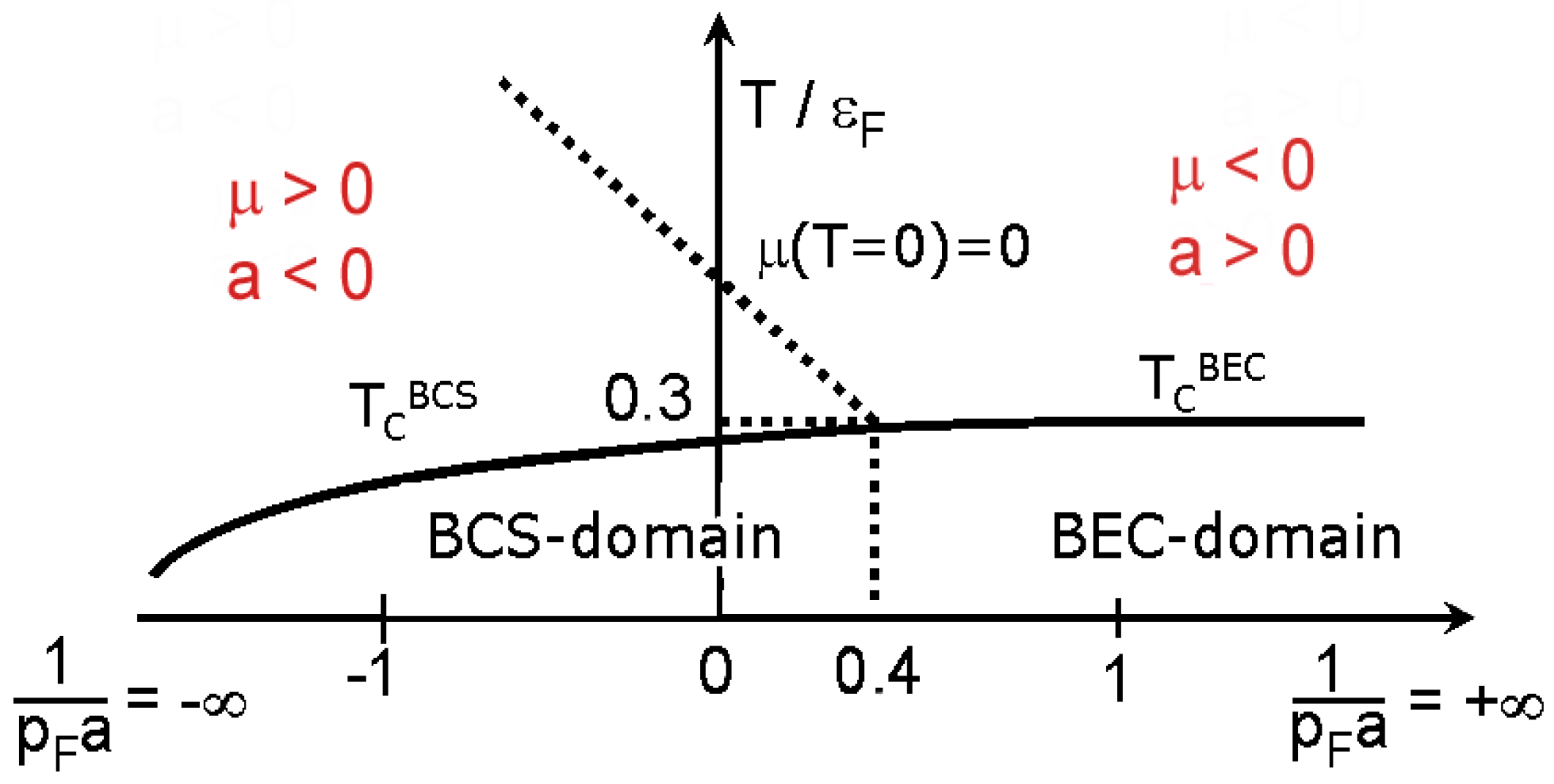
3. The 3D and 2D Models of BCS-BEC Crossover
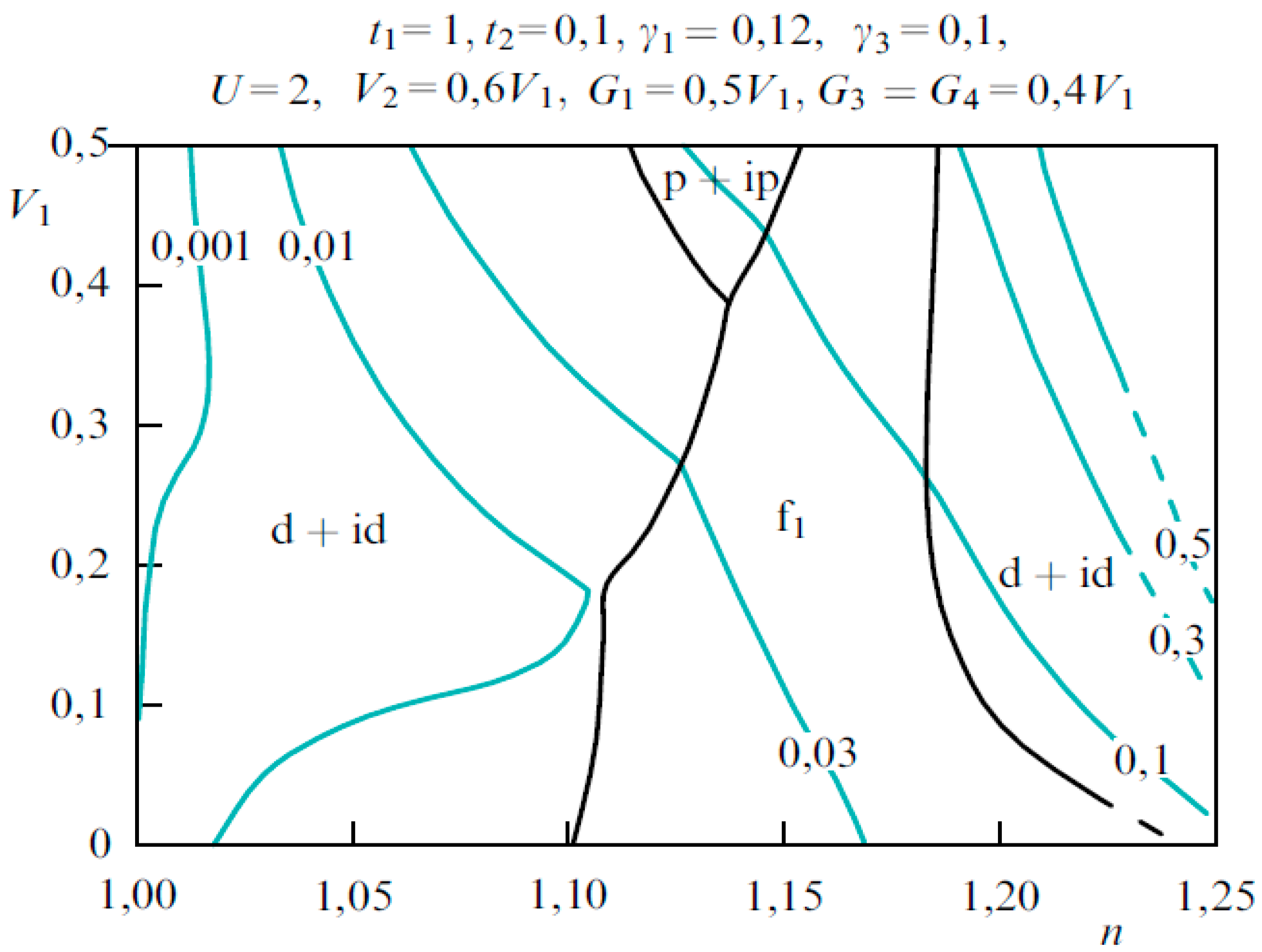
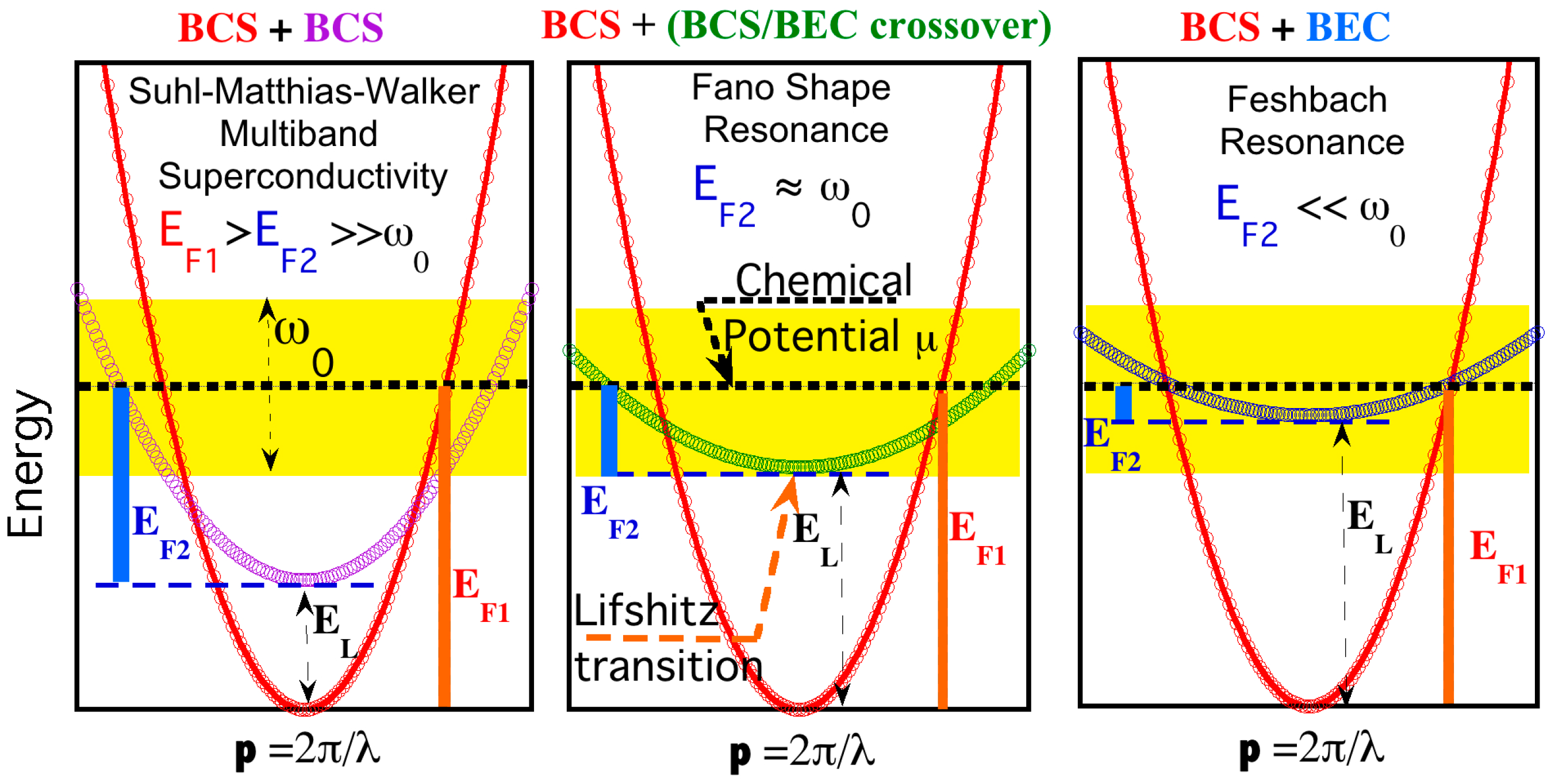
4. Fano Resonances in Multigap BCS-BEC Superconductivity in the Regime of the BCS-BEC Crossover at Lifshitz Transitions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bednorz, J.G.; Müller, K.A. Possible high Tc superconductivity in the Ba− La− Cu− O system. Zeitschrift für Physik B Condens. Matt. 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Bednorz, J.G.; Müller, K.A. Perovskite-type oxides—the new approach to high-Tc superconductivity. Rev. Modern Phys. 1988, 60, 585. [Google Scholar] [CrossRef]
- Anderson, P.W. The resonating valence bond state in La2CuO4 and superconductivity. Science 1987, 235, 1196–1198. [Google Scholar] [CrossRef] [PubMed]
- Schrieffer, J.R.; Wen, X.G.; Zhang, S.C. Dynamic spin fluctuations and the bag mechanism of high-Tc superconductivity. Phys. Rev. B 1989, 39, 11663. [Google Scholar] [CrossRef]
- Kampf, A.; Schrieffer, J.R. Pseudogaps and the spin-bag approach to high-Tc superconductivity. Phys. Rev. B 1990, 41, 6399–6408. [Google Scholar] [CrossRef]
- Anderson, P.W.; Schrieffer, R. A dialogue on the theory of high Tc. Phys. Today 1991, 44, 54–61. [Google Scholar] [CrossRef]
- Scalapino, D.J.; Loh Jr, E.; Hirsch, J.E. D-wave pairing near a spin-density-wave instability. Phys. Rev. B 1986, 34, 8190. [Google Scholar] [CrossRef]
- Miyake, K.; Schmitt-Rink, S.; Varma, C.M. Spin-fluctuation-mediated even-parity pairing in heavy-fermion superconductors. Phys. Rev. B 1986, 34, 6554. [Google Scholar] [CrossRef]
- Fukuyama, H.; Hasegawa, Y.; Narikiyo, O. Two-Dimensional Hubbard Model at Low Electron Density. J. Phys. Soc. Jpn 1991, 60, 2013–2030. [Google Scholar] [CrossRef]
- Zhang, F.C.; Rice, T.M. Effective Hamiltonian for the superconducting Cu oxides. Phys. Rev. B 1988, 37, 3759. [Google Scholar] [CrossRef]
- Laughlin, R.B. Superconducting ground state of noninteracting particles obeying fractional statistics. Phys. Rev. Lett. 1988, 60, 2677–2680. [Google Scholar] [CrossRef] [PubMed]
- Lee, P.A.; Nagaosa, N. Gauge theory of the normal state of high-T c superconductors. Phys. Rev. B 1992, 46, 5621. [Google Scholar] [CrossRef]
- Varma, C.M.; Littlewood, P.B.; Schmitt-Rink, S.; Abrahams, E.; Ruckenstein, A.E. Phenomenology of the normal state of Cu-O high-temperature superconductors. Phys. Rev. Lett. 1989, 63, 1996. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, A.; Saini, N.L. Stripes and Related Phenomena; Springer Science Business Media: Berlin, Germany, 2001. [Google Scholar]
- Leggett, T. Superconducting thoughts meet sceptical resistance. Phys. World 1997, 10, 51. [Google Scholar] [CrossRef]
- Wollman, D.A.; Van Harlingen, D.J.; Lee, W.C.; Ginsberg, D.M.; Leggett, A.J. Experimental determination of the superconducting pairing state in YBCO from the phase coherence of YBCO-Pb dc SQUIDs. Phys. Rev. Lett. 1993, 71, 2134. [Google Scholar] [CrossRef]
- Kagan, M.Y.; Chubukov, A.V. Possibility of a superfluid transition in a slightly nonideal Fermi gas with repulsion. JETP Lett. 1988, 47, 614–617. [Google Scholar]
- Baranov, M.A.; Kagan, M.Y. D-wave pairing in the two-dimensional Hubbard model with low filling. Zeitschrift für Physik B Condens. Matt. 1992, 86, 237–239. [Google Scholar] [CrossRef]
- Baranov, M.A.; Chubukov, A.V.; Kagan, Y.M. Superconductivity and superfluidity in fermi systems with repulsive interactions. Int. J. Modern Phys. B 1992, 6, 2471–2497. [Google Scholar] [CrossRef]
- Kagan, M.Y.; Mitskan, V.A.; Korovushkin, M.M. Anomalous superconductivity and superfluidity in repulsive fermion systems. Physics-Uspekhi 2015, 58, 733. [Google Scholar] [CrossRef]
- Kagan, M.Y. Unconventional superconductivity in low density electron systems and conventional superconductivity in hydrogen metallic alloys. JETP Lett. 2016, 103, 728–738. [Google Scholar] [CrossRef]
- Kagan, M.Y.; Mitskan, V.A.; Korovushkin, M.M. Phase diagram of the Kohn-Luttinger superconducting state for bilayer graphene. Eur. Phys. J. B 2015, 88, 157. [Google Scholar] [CrossRef][Green Version]
- Kagan, M.Y.; Val’kov, V.V.; Mitskan, V.A.; Korovushkin, M.M. The Kohn–Luttinger superconductivity in idealized doped graphene. Solid State Commun. 2014, 188, 61–66. [Google Scholar] [CrossRef][Green Version]
- Kagan, M.Y.; Val’kov, V.V.; Mitskan, V.A.; Korovushkin, M.M. The Kohn-Luttinger effect and anomalous pairing in new superconducting systems and graphene. JETP 2014, 118, 995–1011. [Google Scholar] [CrossRef]
- Kohn, W.; Luttinger, J.M. New mechanism for superconductivity. Phys. Rev. Lett. 1965, 15, 524. [Google Scholar] [CrossRef]
- Fay, D.; Layzer, A. Superfluidity of low-density fermion systems. Phys. Rev. Lett. 1968, 20, 187. [Google Scholar] [CrossRef]
- Galitskii, V.M. The energy spectrum of a non-ideal Fermi gas. Soviet Phys. JETP-USSR 1958, 7, 104–112. [Google Scholar]
- Hubbard, J. Electron correlations in narrow energy bands. Proceedings of the Royal Society of London. Series A. Math. Phys. Sci. 1963, 276, 238–257. [Google Scholar]
- Shubin, S.; Wonsovsky, S. Zur Elektronentheorie der Metalle. Z. Sow. Phys 1935, 7, 10. [Google Scholar]
- Shubin, S.P.; Vonsovskii, S.V. On the Electron Theory of Metals, II. Sow. Phys. 1936, 10, 348. [Google Scholar]
- Kagan, M.Y.; Chubukov, A.V. Increase in superfluid transition temperature in polarized Fermi gas with repulsion. JETP Lett. 1989, 50, 517–520. [Google Scholar]
- Kagan, M.Y. Strong Tc enhancement in the two-dimensional two-band Hubbard model with low filling. Phys. Lett. A 1991, 152, 303–305. [Google Scholar] [CrossRef]
- Baranov, M.A.; Kagan, M.Y. Superconductivity in a low-density two-band model with a repulsive interaction: Extended analysis. J. Exp. Theor. Phys. 1992, 75, 165–171. [Google Scholar]
- Kagan, M.Y. Fermi-gas approach to the problem of superfluidity in three-and two-dimensional solutions of 3He in 4He. Physics-Uspekhi 1994, 37, 69. [Google Scholar] [CrossRef]
- Baranov, M.A.; Kagan, Y.; Kagan, M.Y. On the possibility of a superfluid transition in a Fermi gas of neutral particles at ultralow temperatures. JETP Lett. 1996, 64, 301–304. [Google Scholar] [CrossRef]
- Kagan, M.Y.; Val’kov, V.V. Anomalous resistivity and the origin of the heavy mass in the two-band model with one narrow band. JETP 2011, 113, 156. [Google Scholar] [CrossRef]
- Kagan, M.Y.; Val’kov, V.V. Anomalous resistivity and superconductivity in the two-band Hubbard model with one narrow band. Low Temper. Phys. 2011, 37, 69–82. [Google Scholar] [CrossRef]
- Kagan, M.Y.; Rice, T.M. Superconductivity in the two-dimensional tJ model at low electron density. J. Phys. Condens. Matt. 1994, 6, 3771. [Google Scholar] [CrossRef]
- Yu Kagan, M. Modern Trends in Superconductivity and Superfluidity, Lecture Notes in Physics; Springer: Berlin, Germany, 2013. [Google Scholar]
- Plakida, N.M. Antiferromagnetic exchange mechanism of superconductivity in cuprates. J. Exp. Theor. Phys. Lett. 2001, 74, 36–40. [Google Scholar] [CrossRef]
- Plakida, N.M.; Anton, L.; Adam, S.; Adam, G. Exchange and spin-fluctuation mechanisms of superconductivity in cuprates. JETP 2003, 97, 331. [Google Scholar] [CrossRef][Green Version]
- Ginzburg, V.L. On superconductivity and superfluidity (what I have and have not managed to do), as well as on the ‘physical minimum’ at the beginning of the XXI century (December 8, 2003). Physics-Uspekhi 2004, 47, 1155. [Google Scholar] [CrossRef]
- Plakida, N.M.; Aksenov, V.L.; Drechsler, S.L. Anharmonic Model for High-Tc Superconductors. Europhys. Lett. 1987, 4, 1309. [Google Scholar] [CrossRef]
- Dzyaloshinskii, I.E. Maximal increase of the superconducting transition temperature due to the presence of van’t Hoff singularities. JETP Lett. 1988, 46, 118. [Google Scholar]
- Izyumov, Y.A. The t-J model for strongly correlated electrons. Uspekhi Fizicheskikh Nauk 1997, 167, 465–498. [Google Scholar] [CrossRef]
- Kozlov, A.I. D-wave pairing in the two-dimensional Fermi-liquid with repulsion. Superconduct. Phys. Chem. Eng. 1989, 2, 64. (in Russian). [Google Scholar]
- Wiegmann, P. Topological superconductivity. Prog. Theor. Phys. Suppl. 1992, 107, 243–279. [Google Scholar] [CrossRef]
- Ioffe, L.B.; Larkin, A.I. Two-dimensional Hubbard model with strong electron repulsion. Phys. Rev. B 1988, 37, 5730. [Google Scholar] [CrossRef]
- Ovchinnikov, S.G. Quasiparticles in strongly correlated electron systems in copper oxides. Physics-Uspekhi 1997, 40, 993. [Google Scholar] [CrossRef]
- Babichenko, V.S.; Kagan, Y. s pairing as a result of antiferromagnetic fluctuations in a high-Tc superconductor. Jetp Letters c/c of Pis’ma V Zhurnal Eksperimental’noi Teoreticheskoi Fiziki 1992, 56, 303. [Google Scholar]
- Balatsky, A.; Abrahams, E. New class of singlet superconductors which break the time reversal and parity. Phys. Rev. B 1992, 45, 13125. [Google Scholar] [CrossRef]
- Nagaev, E.L. Phase separation in high-temperature superconductors and related magnetic materials. Uspekhi Fizicheskikh Nauk 1995, 165, 529–554. [Google Scholar] [CrossRef]
- Khodel, V.A.; Shaginyan, V.R. Superfluidity in system with fermion condensate. JETP Lett. 1990, 51, 553. [Google Scholar]
- Belyavsky, V.I.; Kopaev, Y.V. Biordered superconductivity and strong pseudogap state. Phys. Rev. B 2007, 76, 214506. [Google Scholar] [CrossRef]
- Heikkilä, T.T.; Kopnin, N.B.; Volovik, G.E. Flat bands in topological media. JETP Lett. 2011, 94, 233. [Google Scholar] [CrossRef]
- Pudalov, V.M.; Omel’yanovskii, O.E.; Khlybov, E.P.; Sadakov, A.V.; El’tsev, Y.F.; Mitsen, K.V.; Dormidontov, A.S. VL Ginzburg and the development of experimental work on high-temperature superconductivity at LPI:‘iron superconductors’. Physics-Uspekhi 2011, 54, 648. [Google Scholar] [CrossRef]
- Gor’kov, L.P. Developing BCS Ideas in the Former Soviet Union. In BCS: 50 Years, Cooper, L.N and Feldman, D edit; World Scientific: Singapore, 2011; pp. 107–126. [Google Scholar]
- Sadovsky, M.V. Electron-phonon coupling in Eliashberg-McMillan theory beyond adiabatic approximation. JETP 2019, 128, 455–463. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of superconductivity. Phys. Rev. 1957, 108, 1175. [Google Scholar] [CrossRef]
- Leggett, A.J. Cooper pairing in spin-polarized Fermi systems. Le Journal de Physique Colloques 1980, 41, C7–C19. [Google Scholar] [CrossRef]
- Nozieres, P.; Schmitt-Rink, S. Bose condensation in an attractive fermion gas: From weak to strong coupling superconductivity. J. Low Temper. Phys. 1985, 59, 195–211. [Google Scholar] [CrossRef]
- Landau, L.D. The Theory of a Fermi Liquid. JETP 1956, 3, 920. [Google Scholar]
- Landau, L.D. Oscillations in a Fermi Liquid. JETP 1957, 5, 101. [Google Scholar]
- Anderson, P.W. Luttinger-liquid behavior of the normal metallic state of the 2D Hubbard model. Phys. Rev. Lett. 1990, 64, 1839. [Google Scholar] [CrossRef] [PubMed]
- Fetter, A.L.; Hanna, C.B.; Laughlin, R.B. Random-phase approximation in the fractional-statistics gas. Phys. Rev. B 1989, 39, 9679. [Google Scholar] [CrossRef]
- Wen, X.G.; Lee, P.A. Theory of underdoped cuprates. Phys. Rev. Lett. 1996, 76, 503. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.C. A unified theory based on SO (5) symmetry of superconductivity and antiferromagnetism. Science 1997, 275, 1089–1096. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, Y. Perspective: Crystal structure prediction at high pressures. J. Chem. Phys. 2014, 140, 040901. [Google Scholar] [CrossRef] [PubMed]
- Duan, D.; Liu, Y.; Tian, F.; Li, D.; Huang, X.; Zhao, Z.; Cui, T. Pressure-induced metallization of dense (H2S)2H2 with high-T c superconductivity. Sci. Rep. 2014, 4, 6968. [Google Scholar] [CrossRef] [PubMed]
- Drozdov, A.P.; Eremets, M.I.; Troyan, I.A.; Ksenofontov, V.; Shylin, S.I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 2015, 525, 73. [Google Scholar] [CrossRef]
- Schrieffer, J.R. Theory of Superconductivity; W.A. Benjamin: Reading, MA, USA, 1964. [Google Scholar]
- Migdal, A.B. Interaction between Electrons and Lattice Vibrations in a Normal Metal. JETP 1958, 7, 996. [Google Scholar]
- Eliashberg, G.M. Interactions between Electrons and Lattice Vibrations in a Superconductor. JETP 1960, 11, 696. [Google Scholar]
- Bianconi, A.; Jarlborg, T. Lifshitz transitions and zero point lattice fluctuations in sulfur hydride showing near room temperature superconductivity. Novel Superconduct. Mater. 2015, 1, 37–49. [Google Scholar] [CrossRef]
- Bianconi, A.; Jarlborg, T. Superconductivity above the lowest Earth temperature in pressurized sulfur hydride. EPL 2015, 112, 37001. [Google Scholar] [CrossRef]
- Jarlborg, T.; Bianconi, A. Breakdown of the Migdal approximation at Lifshitz transitions with giant zero-point motion in the H3S superconductor. Sci. Rep. 2016, 6, 24816. [Google Scholar] [CrossRef]
- Mazziotti, M.V.; Valletta, A.; Campi, G.; Innocenti, D.; Perali, A.; Bianconi, A. Possible Fano resonance for high-Tc multi-gap superconductivity in p-Terphenyl doped by K at the Lifshitz transition. EPL 2017, 118, 37003. [Google Scholar] [CrossRef]
- Bianconi, A.; Poccia, N.; Sboychakov, A.O.; Rakhmanov, A.L.; Kugel, K.I. Intrinsic arrested nanoscale phase separation near a topological Lifshitz transition in strongly correlated two-band metals. Superconduc. Sci. Technol. 2015, 28, 024005. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Köhler, J.; Simon, A.; Whangbo, M.H.; Bianconi, A.; Perali, A. The road map toward Room-Temperature superconductivity: Manipulating different pairing channels in systems composed of multiple electronic components. Condens. Matt. 2017, 2, 24. [Google Scholar] [CrossRef]
- Bianconi, A.; Innocenti, D.; Valletta, A.; Perali, A. Shape Resonances in superconducting gaps in a 2DEG at oxide-oxide interface. J. Phys. Conf. Series 2014, 529, 012007. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A.; Poccia, N.; Bianconi, G.; Barba, L.; Arrighetti, G.; Burghammer, M. Inhomogeneity of charge-density-wave order and quenched disorder in a high-T c superconductor. Nature 2015, 525, 359. [Google Scholar] [CrossRef]
- Duan, D.; Yu, H.; Xie, H.; Cui, T. Ab Initio Approach and Its Impact on Superconductivity. J. Superconduct. Novel Magnet. 2019, 32, 53–60. [Google Scholar] [CrossRef]
- Mozaffari, S.; Sun, D.; Minkov, V.S.; Knyazev, D.; Betts, J.B.; Einaga, M.; Balakirev, F.F. Superconducting Phase-Diagram of H3S under High Magnetic Fields. arXiv 2019, arXiv:1901.11208. [Google Scholar]
- Somayazulu, M.; Ahart, M.; Mishra, A.K.; Geballe, Z.M.; Baldini, M.; Meng, Y.; Hemley, R.J. Evidence for superconductivity above 260 K in lanthanum superhydride at megabar pressures. Phys. Rev. Lett. 2019, 122, 027001. [Google Scholar] [CrossRef]
- Drozdov, A.P.; Kong, P.P.; Minkov, V.S.; Besedin, S.P.; Kuzovnikov, M.A.; Mozaffari, S.; Greenberg, E. Superconductivity at 250 K in lanthanum hydride under high pressures. Nature 2019, 569, 528. [Google Scholar] [CrossRef] [PubMed]
- Zurek, E.; Bi, T. High-temperature superconductivity in alkaline and rare earth polyhydrides at high pressure: A theoretical perspective. J. Chem. Phys. 2019, 150, 050901. [Google Scholar] [CrossRef] [PubMed]
- Ashcroft, N.W. Metallic hydrogen: A high-temperature superconductor? Phys. Rev. Lett. 1968, 21, 1748. [Google Scholar] [CrossRef]
- Ashcroft, N.W. Hydrogen dominant metallic alloys: high temperature superconductors? Phys. Rev. Lett. 2004, 92, 187002. [Google Scholar] [CrossRef] [PubMed]
- Brovman, E.G.; Kagan, Y.; Kholas, A. Structure of metallic hydrogen at zero pressure. JETP 1972, 34, 1300–1315. [Google Scholar]
- Brovman, E.G.; Kagan, Y.; Kholas, A.; Pushkarev, V.V. Role of electron-electron interaction in the formation of a metastable state of metallic hydrogen. JETP Lett. 1973, 18, 160. [Google Scholar]
- Andreev, A.F.; Kagan, M. Hydrodynamics of a rotating superfluid liquid. JETP 1984, 59, 318. [Google Scholar]
- Abrikosov, A.A. On the magnetic properties of superconductors of the second group. JETP 1957, 5, 1174–1182. [Google Scholar]
- Andreev, A.F.; Lifshits, I.M. Quantum theory of defects in crystals. JETP 1969, 29, 1107. [Google Scholar]
- Kim, E.; Chan, M.H.W. Observation of superflow in solid helium. Science 2004, 305, 1941–1944. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Kutukov, A.A.; Mazur, E.A. Critical temperature of metallic hydrogen sulfide at 225 GPa pressure. J. Exp. Theor. Phys. 2017, 124, 143–150. [Google Scholar] [CrossRef]
- Turlapov, A.V.; Kagan, M.Y. Fermi-to-Bose crossover in a trapped quasi-2D gas of fermionic atoms. J. Phys. Condens. Matt. 2017, 29, 383004. [Google Scholar] [CrossRef] [PubMed]
- Kagan, M.Y.; Efremov, D.V. Two-particle pairing and phase separation in a two-dimensional Bose gas with one or two sorts of bosons. Phys. Rev. B 2002, 65, 195103. [Google Scholar] [CrossRef]
- Bardeen, J.; Baym, G.; Pines, D. Effective Interaction of He3 Atoms in Dilute Solutions of He3 in He4 at Low Temperatures. Phys. Rev. 1967, 156, 207. [Google Scholar] [CrossRef]
- Bashkin, E.P.; Meyerovich, A.E. 3He-4He quantum solutions. Adv. Phys. 1981, 30, 1–92. [Google Scholar] [CrossRef]
- Van de Haar, P.G.; Frossati, G.; Bedell, K.S. (Enhancedp-wave pairing in polarized 3 He-4 He mixtures. J. Low Temper. Phys. 1989, 77, 35–59. [Google Scholar] [CrossRef]
- Modugno, G.; Roati, G.; Riboli, F.; Ferlaino, F.; Brecha, R.J.; Inguscio, M. Collapse of a degenerate Fermi gas. Science 2002, 297, 2240–2243. [Google Scholar] [CrossRef]
- Efremov, D.V.; Viverit, L. p-wave Cooper pairing of fermions in mixtures of dilute Fermi and Bose gases. Phys. Rev. B 2002, 65, 134519. [Google Scholar] [CrossRef]
- Kagan, M.Y.; Brodsky, I.V.; Efremov, D.V.; Klaptsov, A.V. Composite fermions, trios, and quartets in a Fermi-Bose mixture. Phys. Rev. A 2004, 70, 023607. [Google Scholar] [CrossRef]
- Feshbach, H. A unified theory of nuclear reactions. II. An. Phys. 1962, 19, 287–313. [Google Scholar] [CrossRef]
- Gurarie, V.; Radzihovsky, L. Resonantly paired fermionic superfluids. An. Phys. 2007, 322, 2–119. [Google Scholar] [CrossRef]
- Friedberg, R.; Lee, T.D. Gap energy and long-range order in the boson-fermion model of superconductivity. Phys. Rev. B 1989, 40, 6745. [Google Scholar] [CrossRef]
- Micnas, R.; Ranninger, J.; Robaszkiewicz, S. Superconductivity in narrow-band systems with local nonretarded attractive interactions. Rev. Modern Phys. 1990, 62, 113. [Google Scholar] [CrossRef]
- Geshkenbein, V.B.; Ioffe, L.B.; Larkin, A.I. Superconductivity in a system with preformed pairs. Phys. Rev. B 1997, 55, 3173. [Google Scholar] [CrossRef]
- Landau, L.D.; Ginzburg, V.L. On the theory of superconductivity. Zh. Eksp. Teor. Fiz. 1950, 20, 1064. [Google Scholar]
- Dagotto, E.; Rice, T.M. Surprises on the way from one-to two-dimensional quantum magnets: the ladder materials. Science 1996, 271, 618–623. [Google Scholar] [CrossRef]
- Menushenkov, A.P.; Klementev, K.V.; Kuznetsov, A.V.; Kagan, M.Y. Superconductivity in Ba1−xKxBiO3: Possible scenario of spatially separated Fermi-Bose mixture. J. Exp. Theor. Phys. 2001, 93, 615–624. [Google Scholar] [CrossRef]
- Menushenkov, A.P.; Kuznetsov, A.V.; Klementiev, K.V.; Kagan, M.Y. Fermi-Bose mixture in Ba(K)BiO3 superconducting oxide. J. Superconduct. Novel Magnet. 2016, 29, 701–705. [Google Scholar] [CrossRef]
- Bulaevski, L.N.; Nagaev, E.L.; Khomskii, D.I. A new type of auto-localized state of a conduction electron in an antiferromagnetic semiconductor. Sov. J. Exp. Theor. Phys. 1968, 27, 836. [Google Scholar]
- Brinkman, W.F.; Rice, T.M. Single-particle excitations in magnetic insulators. Phys. Rev. B 1970, 2, 1324. [Google Scholar] [CrossRef]
- Kagan, M.Y.; Klaptsov, A.V.E.; Brodsky, I.Y.V.; Combescot, R.; Leyronas, X. Composite fermions and bosons in ultracold gases and in high-temperature superconductors. Physics-Uspekhi 2006, 49, 1079–1084. [Google Scholar]
- Combescot, R.; Leyronas, X.; Kagan, M.Y. Self-consistent theory for molecular instabilities in a normal degenerate Fermi gas in the BEC-BCS crossover. Phys. Rev. A 2006, 73, 023618. [Google Scholar] [CrossRef]
- Alexandrov, A.; Ranninger, J. Theory of bipolarons and bipolaronic bands. Phys. Rev. B 1981, 23, 1796. [Google Scholar] [CrossRef]
- Alexandrov, A.; Ranninger, J. Bipolaronic superconductivity. Phys. Rev. B 1981, 24, 1164. [Google Scholar] [CrossRef]
- Bogoliubov, N.N. On the theory of superfluidity. J. Phys. 1947, 11, 23. [Google Scholar]
- Einstein, A. Quantentheorie des einatomigen idealen Gases. SB Preuss. Akad. Wiss. phys.-math. Klasse 1925, 1, 3. [Google Scholar]
- Kashurnikov, V.A.; Prokof’ev, N.V.; Svistunov, B.V. Critical temperature shift in weakly interacting Bose gas. Phys. Rev. Lett. 2001, 87, 120402. [Google Scholar] [CrossRef]
- Petrov, D.S.; Salomon, C.; Shlyapnikov, G.V. Scattering properties of weakly bound dimers of fermionic atoms. Phys. Rev. A 2005, 71, 012708. [Google Scholar] [CrossRef]
- Brodsky, I.Y.V.; Klaptsov, A.V.E.; Kagan, M.Y.; Combescot, R.; Leyronas, X. Bound states of three and four resonantly interacting particles. J. Exp. Theor. Phys. Lett. 2005, 82, 273–278. [Google Scholar] [CrossRef][Green Version]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, Part 1: Volume 5; Butterworth-Heinemann: Oxford, UK, 1980. [Google Scholar]
- Kagan, M.Y.; Frésard, R.; Capezzali, M.; Beck, H. One-electron spectral functions of the attractive Hubbard model for intermediate coupling. Phys. Rev. B 1998, 57, 5995. [Google Scholar] [CrossRef]
- Kagan, M.Y.; Frésard, R.; Capezzali, M.; Beck, H. One-electron spectral functions of the attractive Hubbard model at intermediate coupling. Phys. B Condens. Matt. 2000, 284, 447–448. [Google Scholar] [CrossRef]
- Fisher, D.S.; Hohenberg, P.C. Dilute Bose gas in two dimensions. Physical Review B 1988, 37, 4936. [Google Scholar] [CrossRef]
- Petrov, D.S.; Baranov, M.A.; Shlyapnikov, G.V. Superfluid transition in quasi-two-dimensional Fermi gases. Phys. Rev. A 2003, 67, 031601. [Google Scholar] [CrossRef]
- Majorana, E. Über die Kerntheorie. Zeits.Phys. A Hadrons and Nuclei 1933, 82, 137. [Google Scholar]
- Brink, D. The story of Majorana’s exchange force. Proc. Sci. 2006. [Google Scholar] [CrossRef]
- Heisenberg, W. On the structure of atomic nuclei. I. Zeit. Phys. 1932, 77, 1. [Google Scholar] [CrossRef]
- Heisenberg, W. On the structure of atomic nuclei. III. Zeit. Phys. 1933, 80, 587. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. The Interacting Boson Model; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Iachello, F.; Van Isacker, P. The Interacting Boson-Fermion Model; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Iachello, F. Algebraic models of many-body systems and their dynamic symmetries and supersymmetries. J. Phys. Conf. Series 2019, 1194, 012048. [Google Scholar] [CrossRef]
- Iachello, F. Symmetry of High-Tc Superconductors. In Symmetry and Heterogeneity in High Temperature Superconductors; Springer: Berlin, Germany, 2006; pp. 165–180. [Google Scholar]
- Fano, U. Sullo spettro di assorbimento dei gas nobili presso il limite dello spettro d’arco. Nuovo Cimento 1935, 12, 154. [Google Scholar] [CrossRef]
- Fano, U. Effects of configuration interaction on intensities and phase shifts. Phys. Rev. 1961, 124, 1866. [Google Scholar] [CrossRef]
- Palumbo, F.; Marcelli, A.; Bianconi, A. From the pion cloud of Tomonaga to the electron pairs of Schrieffer: many body wave functions from nuclear physics to condensed matter physics. J. Superconduct. Novel Magnet. 2016, 29, 3107–3111. [Google Scholar] [CrossRef]
- Bardsley, J.N.; Mandl, F. Resonant scattering of electrons by molecules. Rep. Prog. Phys. 1968, 31, 471. [Google Scholar] [CrossRef]
- Bianconi, A.; Vittorini-Orgeas, A. From the Majorana Theory of “Incomplete P’ Triplets” to Feshbach Resonances. PoS 2007, 037. [Google Scholar] [CrossRef][Green Version]
- Bianconi, A. Ugo Fano and shape resonances. AIP Conf. Proc. 2003, 652, 13. [Google Scholar]
- Vittorini-Orgeas, A.; Bianconi, A. From Majorana theory of atomic autoionization to Feshbach resonances in high temperature superconductors. J. Superconduct. Novel Magnet. 2009, 22, 21. [Google Scholar] [CrossRef]
- Bianconi, A.; Missori, M. The Coupling of a Wigner Polaronic Charge Density Wave with a Fermi Liquid Arising from the Instability of a Wigner Polaron Crystal: A Possible Pairing Mechanism in High Tc Superconductors. In Phase Separation in Cuprate Superconductors; Springer: Berlin/Heidelberg, Germany, 1994; pp. 272–289. [Google Scholar]
- Bianconi, A.; Missori, M. The instability of a 2D electron gas near the critical density for a Wigner polaron crystal giving the quantum state of cuprate superconductors. Solid State Commun. 1994, 91, 287–293. [Google Scholar] [CrossRef]
- Bianconi, A. The instability close to the 2D generalized Wigner polaron crystal density: A possible pairing mechanism indicated by a key experiment. Physica C Superconduct. 1994, 235, 269–272. [Google Scholar] [CrossRef]
- Valletta, A.; Bianconi, A.; Perali, A.; Saini, N.L. Electronic and superconducting properties of a superlattice of quantum stripes at the atomic limit. Zeitschrift für Physik B Condens. Matt. 1997, 104, 707–713. [Google Scholar] [CrossRef]
- Bianconi, A.; Valletta, A.; Perali, A.; Saini, N.L. Superconductivity of a striped phase at the atomic limit. Physica C Superconduct. 1998, 296, 269–280. [Google Scholar] [CrossRef]
- Perali, A.; Innocenti, D.; Valletta, A.; Bianconi, A. Anomalous isotope effect near a 2.5 Lifshitz transition in a multi-band multi-condensate superconductor made of a superlattice of stripes. Superconduct. Sci. Technol. 2012, 25, 124002. [Google Scholar] [CrossRef]
- Bianconi, A.; Di Castro, D.; Bianconi, G.; Pifferi, A.; Saini, N.L.; Chou, F.C.; Colapietro, M. Coexistence of stripes and superconductivity: Tc amplification in a superlattice of superconducting stripes. Physica C Superconduct. 2000, 341, 1719–1722. [Google Scholar] [CrossRef]
- Kusmartsev, F.V.; Di Castro, D.; Bianconi, G.; Bianconi, A. Transformation of strings into an inhomogeneous phase of stripes and itinerant carriers. Phys. Lett. A 2000, 275, 118–123. [Google Scholar] [CrossRef]
- Bianconi, A.; Saini, N.L.; Agrestini, S.; Castro, D.D.; Bianconi, G. The strain quantum critical point for superstripes in the phase diagram of all cuprate perovskites. Int. J. Modern Phys. B 2000, 14, 3342–3355. [Google Scholar] [CrossRef]
- Kagan, M.Y.; Kugel, K.I. Inhomogeneous charge distributions and phase separation in manganites. Physics-Uspekhi 2001, 44, 553. [Google Scholar] [CrossRef]
- Bianconi, A. Superstripes. Int. J. Modern Phys. B 2000, 14, 3289–3297. [Google Scholar] [CrossRef]
- Bianconi, A.; Di Castro, D.; Agrestini, S.; Campi, G.; Saini, N.L.; Saccone, A.; Giovannini, M. A superconductor made by a metal heterostructure at the atomic limit tuned at the shape resonance’: MgB2. J. Phys. Condens. Matt. 2001, 13, 7383. [Google Scholar] [CrossRef]
- Bianconi, A.; Filippi, M. Feshbach shape resonances in multiband high Tc superconductors. In Symmetry and Heterogeneity in High Temperature Superconductors; Springer: Berlin, Germany, 2006; pp. 21–53. [Google Scholar]
- Agrestini, S.; Metallo, C.; Filippi, M.; Simonelli, L.; Campi, G.; Sanipoli, C.; Latini, A. Substitution of Sc for Mg in MgB2: effects on transition temperature and Kohn anomaly. Phys. Rev. B 2004, 70, 134514. [Google Scholar] [CrossRef]
- Ricci, A.; Poccia, N.; Ciasca, G.; Fratini, M.; Bianconi, A. The microstrain-doping phase diagram of the iron pnictides: heterostructures at atomic limit. J. Superconduct. Novel Magnet. 2009, 22, 589–593. [Google Scholar] [CrossRef]
- Caivano, R.; Fratini, M.; Poccia, N.; Ricci, A.; Puri, A.; Ren, Z.A.; Barba, L. Feshbach resonance and mesoscopic phase separation near a quantum critical point in multiband FeAs-based superconductors. Superconduct. Sci. Technol. 2008, 22, 014004. [Google Scholar] [CrossRef]
- Innocenti, D.; Poccia, N.; Ricci, A.; Valletta, A.; Caprara, S.; Perali, A.; Bianconi, A. Resonant and crossover phenomena in a multiband superconductor: Tuning the chemical potential near a band edge. Phys. Rev. B 2010, 82, 184528. [Google Scholar] [CrossRef]
- Bianconi, A. Quantum materials: Shape resonances in superstripes. Nat. Phys. 2013, 9, 536–537. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A. Evolution of Complexity in Out-of-Equilibrium Systems by Time-Resolved or Space-Resolved Synchrotron Radiation Techniques. Condens. Matt. 2019, 4, 32. [Google Scholar] [CrossRef]
- Ricci, A.; Poccia, N.; Campi, G.; Coneri, F.; Barba, L.; Arrighetti, G.; Bianconi, A. Networks of superconducting nano-puddles in 1/8 doped YBa2Cu3O6.5+y controlled by thermal manipulation. New J. Phys. 2014, 16, 053030. [Google Scholar] [CrossRef]
- Poccia, N.; Chorro, M.; Ricci, A.; Xu, W.; Marcelli, A.; Campi, G.; Bianconi, A. Percolative superconductivity in La2CuO4.06 by lattice granularity patterns with scanning micro x-ray absorption near edge structure. Appl. Phys. Lett. 2014, 104, 221903. [Google Scholar] [CrossRef]
- Bendele, M.; Barinov, A.; Joseph, B.; Innocenti, D.; Iadecola, A.; Bianconi, A.; Hatakeda, T. Spectromicroscopy of electronic phase separation in KxFe2−ySe2 superconductor. Sci. Rep. 2014, 4, 5592. [Google Scholar] [CrossRef]
- Ricci, A.; Poccia, N.; Campi, G.; Joseph, B.; Arrighetti, G.; Barba, L.; Takano, Y. Nanoscale phase separation in the iron chalcogenide superconductor K0.8Fe1.6Se2 as seen via scanning nanofocused x-ray diffraction. Phys. Rev. B 2011, 84, 060511. [Google Scholar] [CrossRef]
- Ricci, A.; Poccia, N.; Joseph, B.; Innocenti, D.; Campi, G.; Zozulya, A.; Takeya, H. Direct observation of nanoscale interface phase in the superconducting chalcogenide KxFe2−ySe2 with intrinsic phase separation. Phys. Rev. B 2015, 91, 020503. [Google Scholar] [CrossRef]
- Duan, C.; Yang, J.; Ren, Y.; Thomas, S.M.; Louca, D. Appearance of superconductivity at the vacancy order-disorder boundary in KxFe2−ySe2. Phys. Rev. B 2018, 97, 184502. [Google Scholar] [CrossRef]
- Fratini, M.; Poccia, N.; Bianconi, A. The Feshbach resonance and nanoscale phase separation in a polaron liquid near the quantum critical point for a polaron Wigner crystal. J. Phys. Conf. Series 2008, 108, 012036. [Google Scholar] [CrossRef]
- Gavrichkov, V.A.; Shanko, Y.; Zamkova, N.G.; Bianconi, A. Is there any hidden symmetry in the stripe structure of perovskite high temperature superconductors? J. Phys. Chem. Lett. 2019, 10, 1840. [Google Scholar] [CrossRef]
- Bianconi, A. Shape resonances in multi-condensate granular superconductors formed by networks of nanoscale-striped puddles. J. Phys. Conf. Series 2013, 449, 012002. [Google Scholar] [CrossRef]
- Bianconi, G. Quantum statistics in complex networks. Phys. Rev. E 2002, 66, 056123. [Google Scholar] [CrossRef] [PubMed]
- Innocenti, D.; Ricci, A.; Poccia, N.; Campi, G.; Fratini, M.; Bianconi, A. A model for liquid-striped liquid phase separation in liquids of anisotropic polarons. J. Superconduct. Novel Magnet. 2009, 22, 529–533. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A. High-Temperature superconductivity in a hyperbolic geometry of complex matter from nanoscale to mesoscopic scale. J. Superconduct. Novel Magnet. 2016, 29, 627–631. [Google Scholar] [CrossRef]
- Bianconi, G.; Rahmede, C. Emergent hyperbolic network geometry. Sci. Rep. 2017, 7, 41974. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Zhang, Q.; Ghaemi, P.; Sarachik, M.P. Evidence for mixed phases and percolation at the metal-insulator transition in two dimensions. Phys. Rev. B 2019, 99, 155302. [Google Scholar] [CrossRef]
- Kuntsevich, A.Y.; Bryzgalov, M.A.; Prudkoglyad, V.A.; Martovitskii, V.P.; Selivanov, Y.G.; Chizhevskii, E.G. Structural distortion behind the nematic superconductivity in Sr x Bi2Se3. New J. Phys. 2018, 20, 103022. [Google Scholar] [CrossRef]
- Volosheniuk, S.O.; Selivanov, Y.G.; Bryzgalov, M.A.; Martovitskii, V.P.; Kuntsevich, A. Y of Sr doping on structure, morphology, and transport properties of Bi 2 Se 3 epitaxial thin films. J. Appl. Phys. 2019, 125, 095103. [Google Scholar] [CrossRef]
- Whittaker, L.; Patridge, C.J.; Banerjee, S. Microscopic and nanoscale perspective of the metal− insulator phase transitions of VO2: some new twists to an old tale. J. Phys. Chem. Lett. 2011, 2, 745–758. [Google Scholar] [CrossRef]
- Bianconi, A. Multiplet splitting of final-state configurations in x-ray-absorption spectrum of metal VO2: Effect of core-hole-screening, electron correlation, and metal-insulator transition. Phys. Rev. B 1982, 26, 2741. [Google Scholar] [CrossRef]
- Singer, A.; Ramirez, J.G.; Valmianski, I.; Cela, D.; Hua, N.; Kukreja, R.; Chollet, M. Non equilibrium phase precursors during a photoexcited insulator-to-metal transition in V2O3. Phys. Rev. Lett. 2018, 120, 207601. [Google Scholar] [CrossRef] [PubMed]
- Marcelli, A.; Coreno, M.; Stredansky, M.; Xu, W.; Zou, C.; Fan, L.; Bianconi, A. Nanoscale phase separation and lattice complexity in VO2: The metal–insulator transition investigated by XANES via Auger electron yield at the vanadium L23-edge and resonant photoemission. Condens. Matt. 2017, 2, 38. [Google Scholar] [CrossRef]
- Kaplan, D.; Imry, Y. High-temperature superconductivity using a model of hydrogen bonds. PNAS 2018, 115, 5709. [Google Scholar] [CrossRef] [PubMed]
- Fleck, M.; Lichtenstein, A.I.; Oleś, A.M. Spectral properties and pseudogap in the stripe phases of cuprate superconductors. Phys. Rev. B 2001, 64, 134528. [Google Scholar] [CrossRef]
- Corboz, P.; Rice, T.M.; Troyer, M. Competing states in the t-J model: Uniform d-wave state versus stripe state. Phys. Rev. Lett. 2014, 113, 046402. [Google Scholar] [CrossRef]
- Bianconi, G.; Rahmede, C. Network geometry with flavor: from complexity to quantum geometry. Phys. Rev. E 2016, 93, 032315. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, A.; Agrestini, S.; Bianconi, G.; Di Castro, D.; Saini, N.L. A quantum phase transition driven by the electron lattice interaction gives high Tc superconductivity. J. Alloys Compound. 2001, 317, 537–541. [Google Scholar] [CrossRef]
- Jarlborg, T.; Bianconi, A. Multiple electronic components and Lifshitz transitions by oxygen wires formation in layered cuprates and nickelates. Condens. Matt. 2019, 4, 15. [Google Scholar] [CrossRef]
- Bauer, E.; Paul, C.; Berger, S.; Majumdar, S.; Michor, H.; Giovannini, M.; Bianconi, A. Thermal conductivity of superconducting MgB2. J. Phys. Condens. Matt. 2001, 13, L487. [Google Scholar] [CrossRef][Green Version]
- Schreck, F.; Khaykovich, L.; Corwin, K.L.; Ferrari, G.; Bourdel, T.; Cubizolles, J.; Salomon, C. Quasipure Bose-Einstein condensate immersed in a Fermi sea. Phys. Rev. Lett. 2001, 87, 080403. [Google Scholar] [CrossRef] [PubMed]
- Di Castro, D.; Agrestini, S.; Campi, G.; Cassetta, A.; Colapietro, M.; Congeduti, A.; Nardone, M. The amplification of the superconducting Tc by combined effect of tuning of the Fermi level and the tensile micro-strain in Al1−xMgxB2. EPL 2002, 58, 278. [Google Scholar] [CrossRef]
- Perali, A.; Pieri, P.; Strinati, G.C.; Castellani, C. Pseudogap and spectral function from superconducting fluctuations to the bosonic limit. Phys. Rev. B 2002, 66, 024510. [Google Scholar] [CrossRef]
- Regal, C.A.; Jin, D.S. Measurement of positive and negative scattering lengths in a Fermi gas of atoms. Phys. Rev. Lett. 2003, 90, 230404. [Google Scholar] [CrossRef] [PubMed]
- Palestini, F.; Perali, A.; Pieri, P.; Strinati, G.C. Dispersions, weights, and widths of the single-particle spectral function in the normal phase of a Fermi gas. Phys. Rev. B 2012, 85, 024517. [Google Scholar] [CrossRef]
- Tajima, H.; Yerin, Y.; Perali, A.; Pieri, P. Enhanced critical temperature, pairing fluctuation effects, and BCS-BEC crossover in a two-band Fermi gas. Phys. Rev. B 2019, 99, 180503(R). [Google Scholar] [CrossRef]
- Guidini, A.; Perali, A. Band-edge BCS–BEC crossover in a two-band superconductor: physical properties and detection parameters. Superconduct. Sci. Technol. 2014, 2, 124002. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kagan, M.Y.; Bianconi, A. Fermi-Bose Mixtures and BCS-BEC Crossover in High-Tc Superconductors. Condens. Matter 2019, 4, 51. https://doi.org/10.3390/condmat4020051
Kagan MY, Bianconi A. Fermi-Bose Mixtures and BCS-BEC Crossover in High-Tc Superconductors. Condensed Matter. 2019; 4(2):51. https://doi.org/10.3390/condmat4020051
Chicago/Turabian StyleKagan, Maxim Yu., and Antonio Bianconi. 2019. "Fermi-Bose Mixtures and BCS-BEC Crossover in High-Tc Superconductors" Condensed Matter 4, no. 2: 51. https://doi.org/10.3390/condmat4020051
APA StyleKagan, M. Y., & Bianconi, A. (2019). Fermi-Bose Mixtures and BCS-BEC Crossover in High-Tc Superconductors. Condensed Matter, 4(2), 51. https://doi.org/10.3390/condmat4020051