Majorana Fermions in One-Dimensional Structures at LaAlO3/SrTiO3 Oxide Interfaces
Abstract
1. Introduction
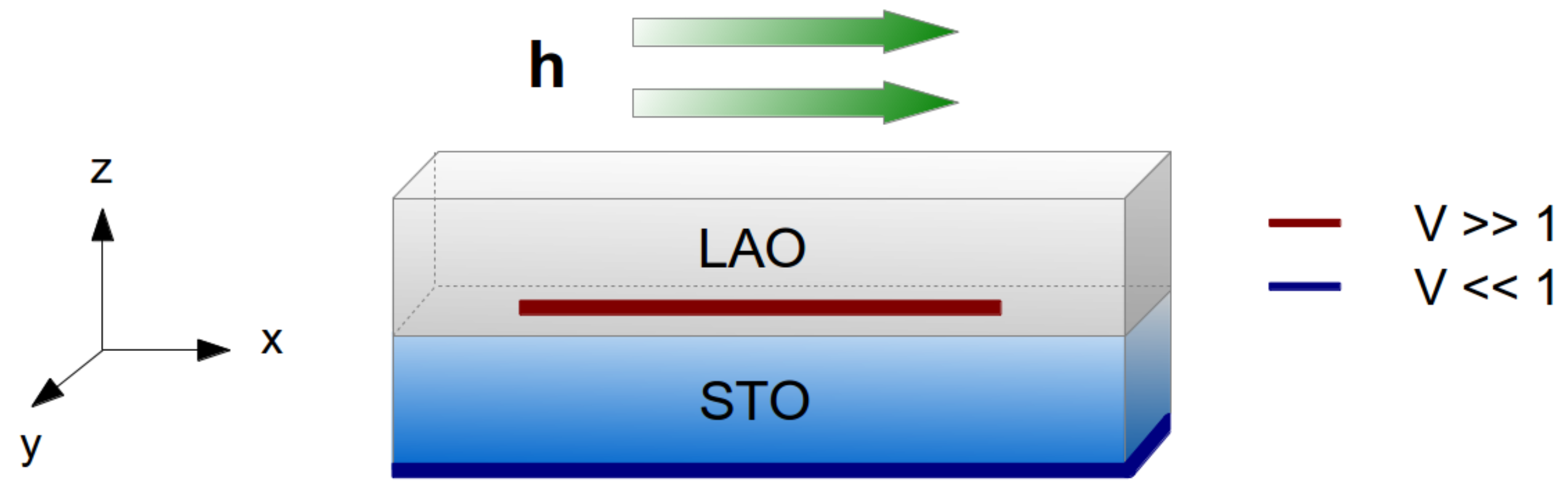
2. The Model
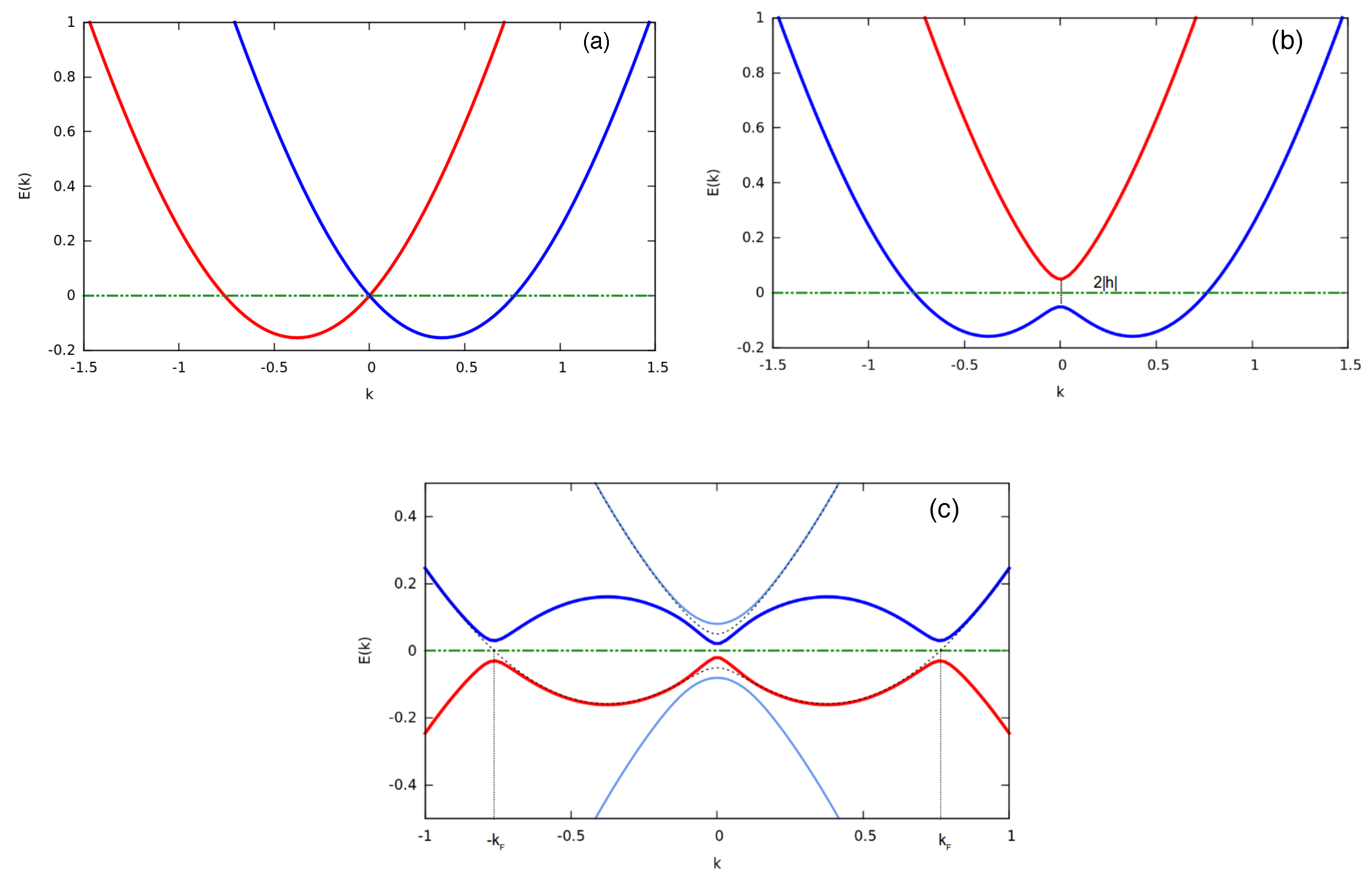
3. Description of the Topological Phase in Reciprocal Space
Topological Criterion
- , for or ,
- , for .
4. Description of the Topological Phase in Real Space
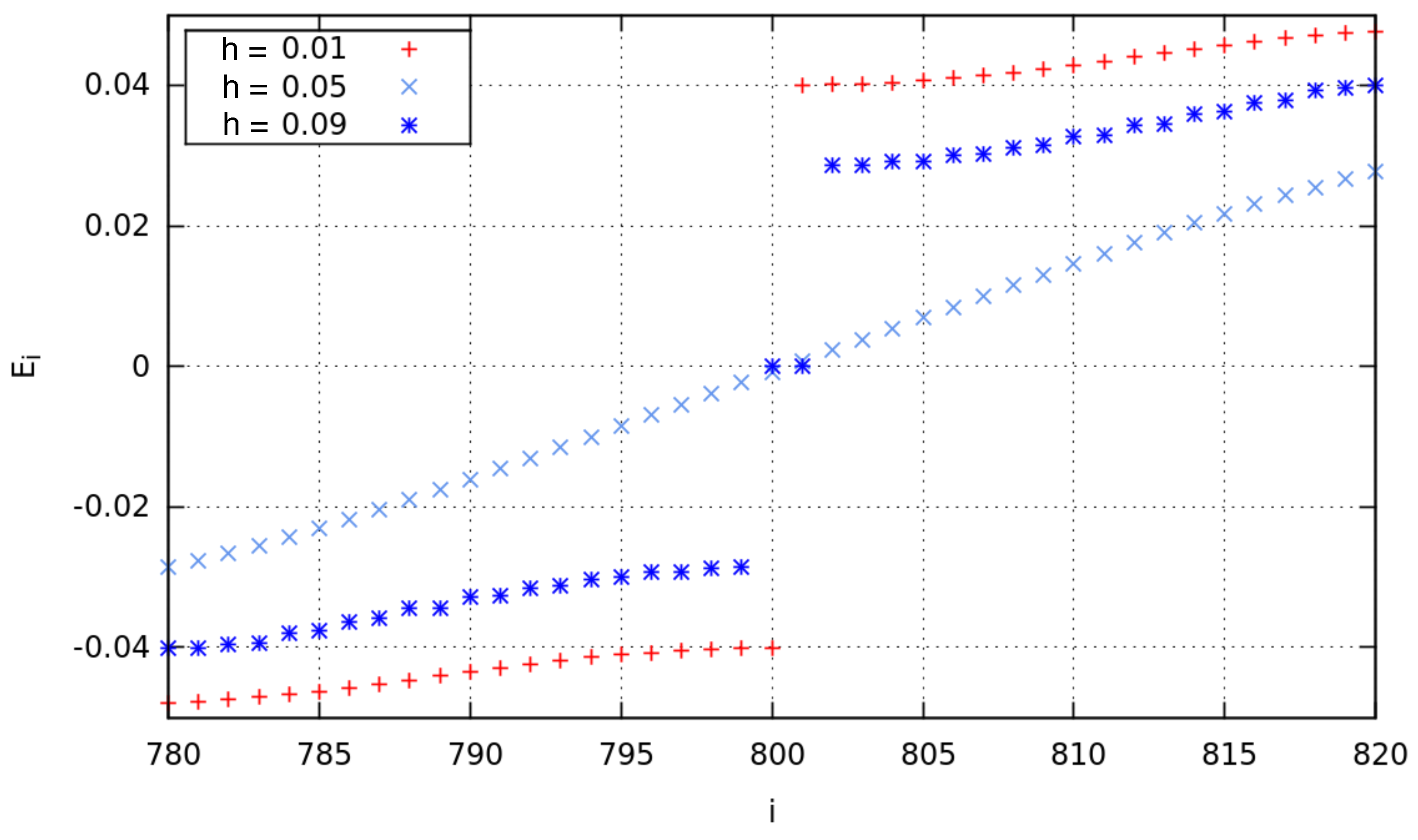
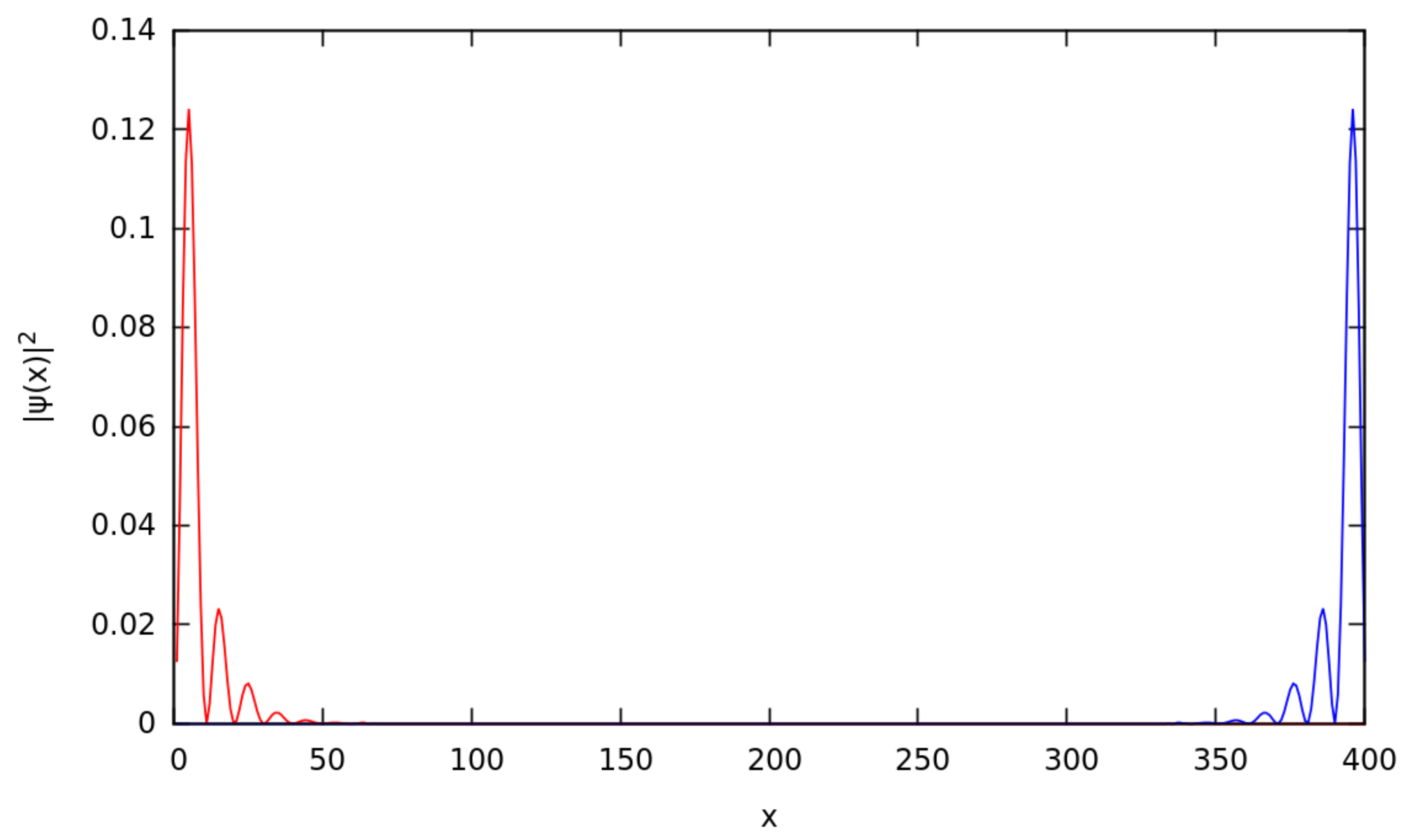
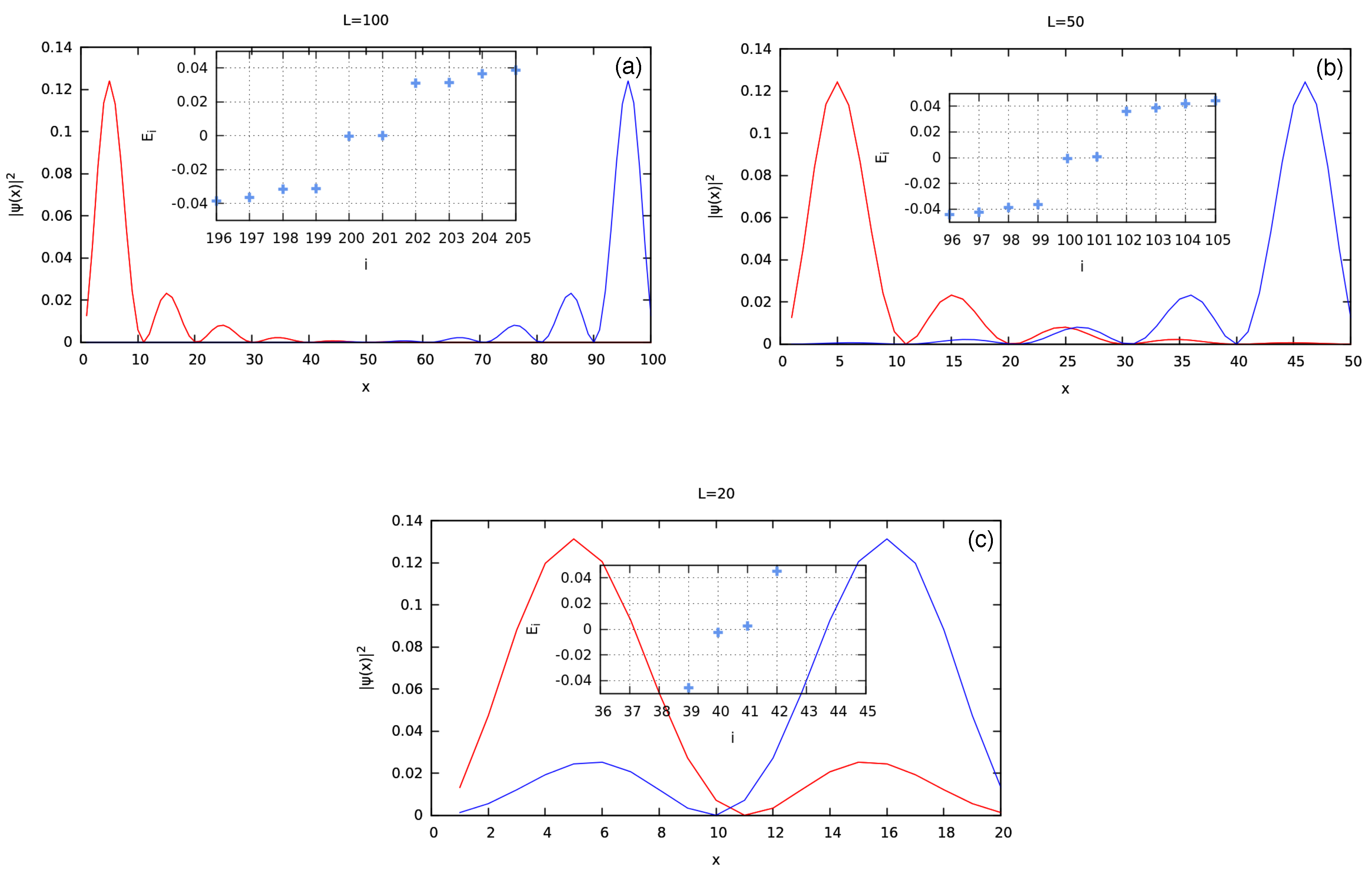
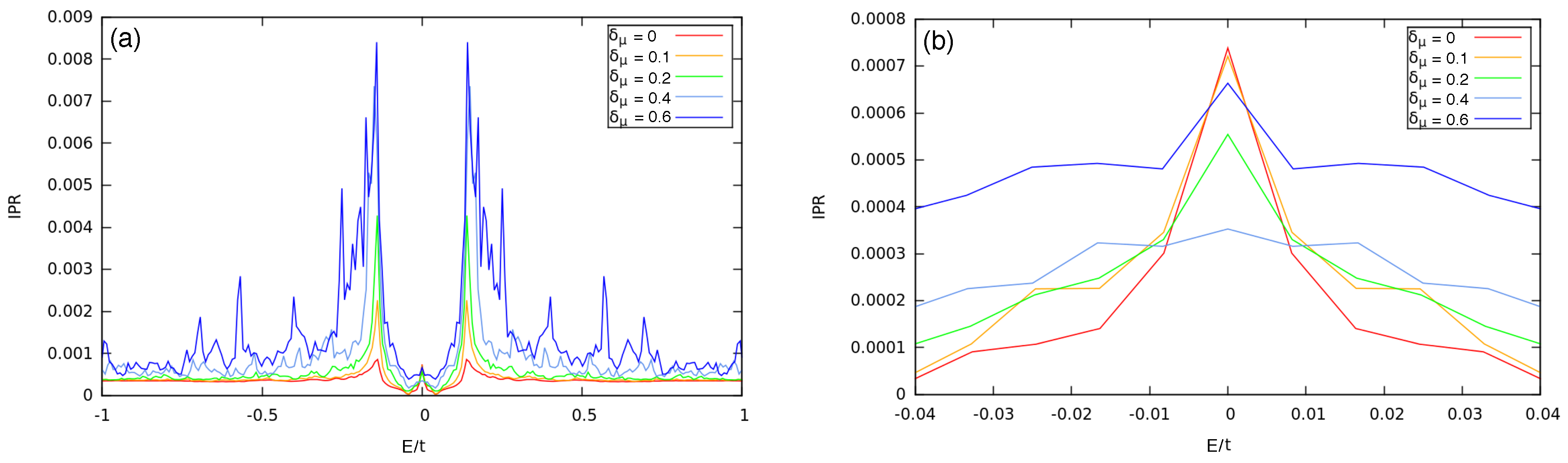
4.1. MFs at the Different Chain Lengths
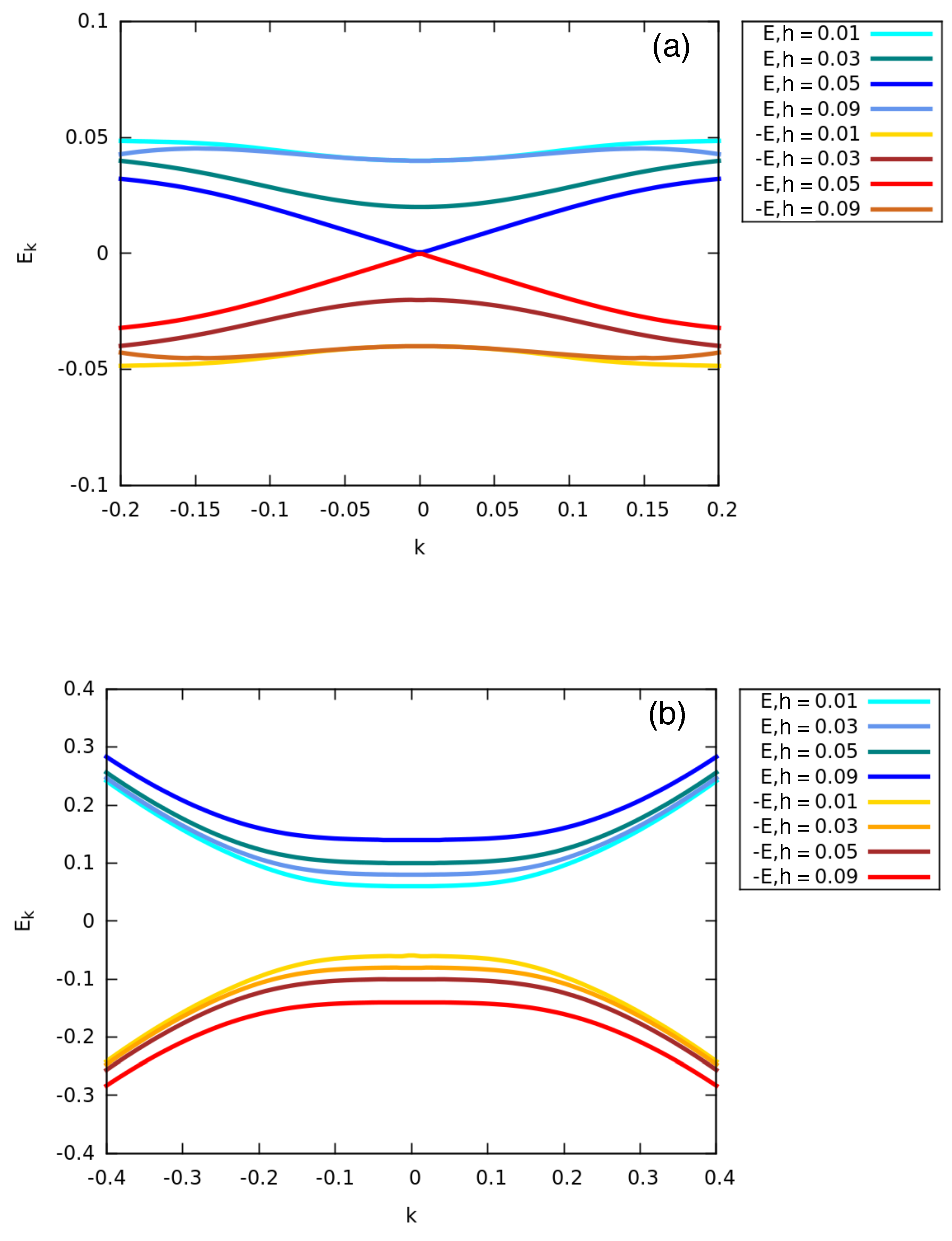
4.2. MFs at Different Magnetic Fields
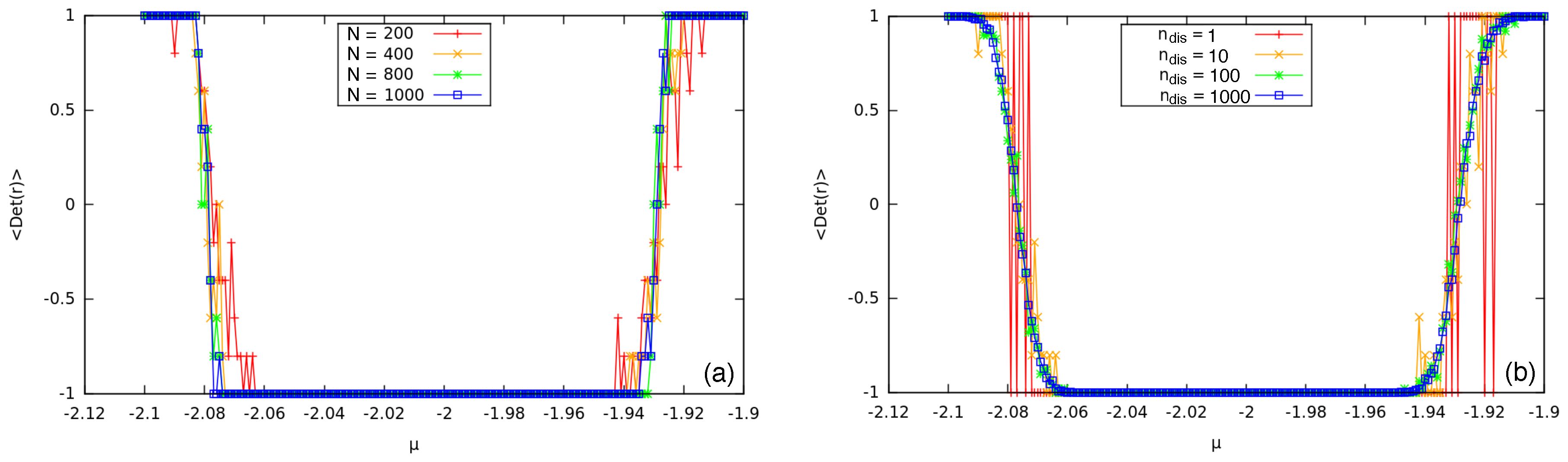
5. The Disordered 1D Chain
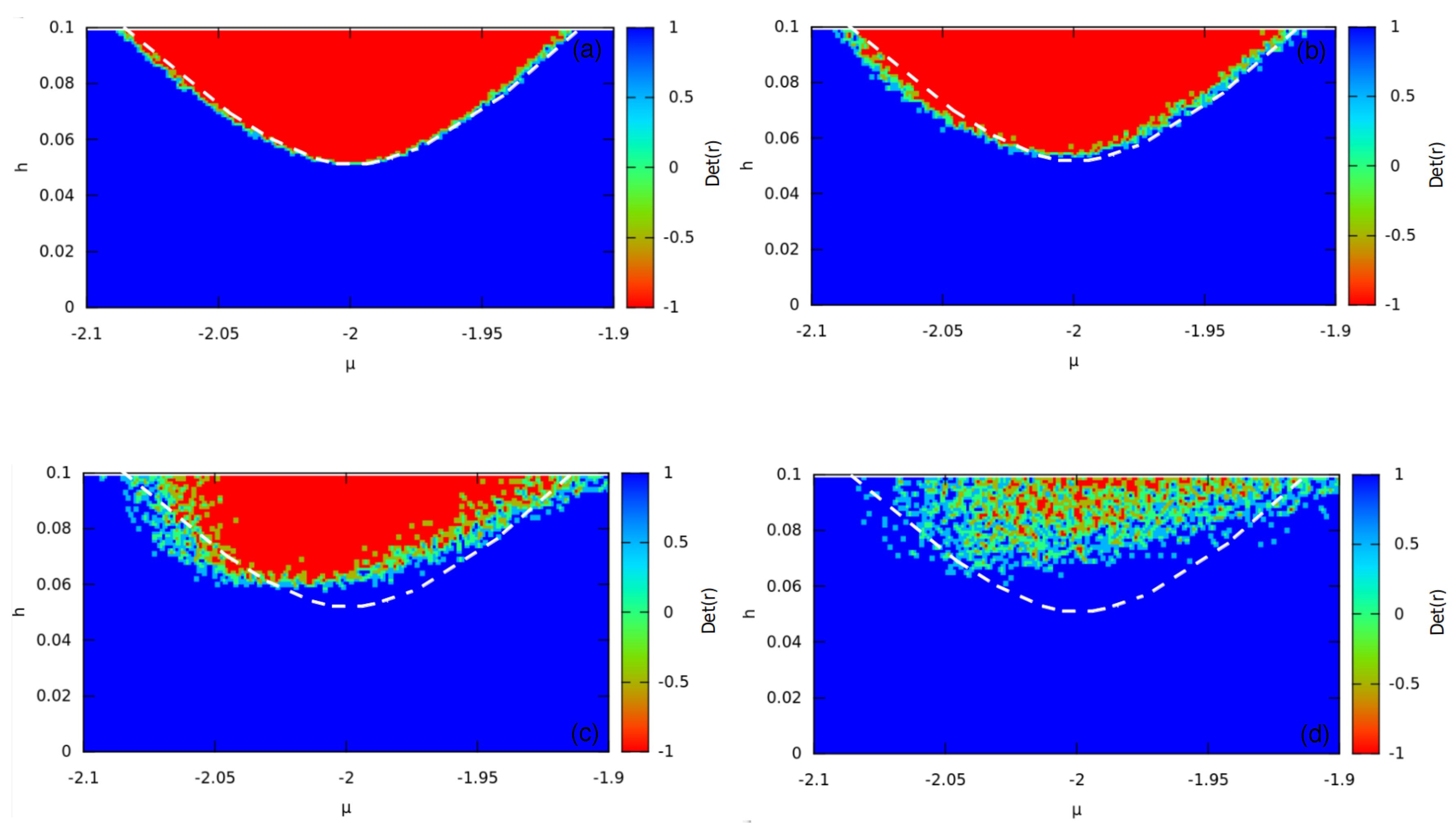
5.1. Disordered Tight-Binding Model
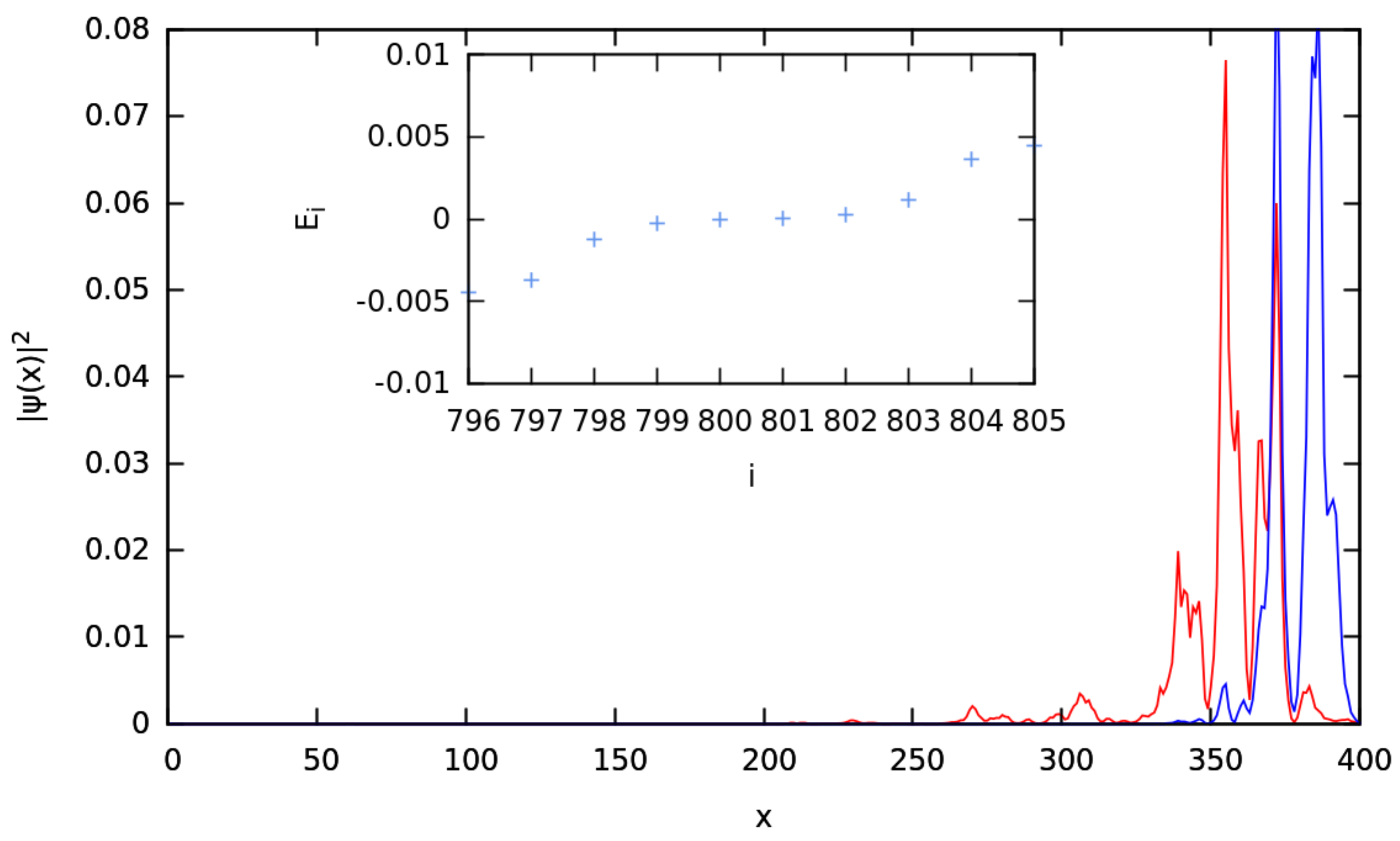
5.2. Results
6. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MFs | Majorana fermions |
| 1D | one-dimensional |
| 2D | two-dimensional |
| LAO/STO | LaAlO/SrTiO |
| RSOC | Rashba spin-orbit coupling |
| IPR | inverse participation ratio |
Appendix A. Scattering Matrix Method

References
- Alicea, J. New directions in the pursuit of Majorana fermions in solid state systems. Rep. Prog. Phys. 2012, 75, 076501. [Google Scholar] [CrossRef] [PubMed]
- Leijnse, M.; Flensberg, K. Introduction to topological superconductivity and Majorana fermions. Semicond. Sci. Technol. 2012, 27, 124003. [Google Scholar] [CrossRef]
- Elliott, S.; Franz, M. Colloquium: Majorana fermions in nuclear, particle and solid-state physics. Rev. Mod. Phys. 2015, 87, 137. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Unpaired Majorana fermions in quantum wires. Phys. Uspekhi 2001, 44, 131. [Google Scholar] [CrossRef]
- Alicea, J.; Oreg, Y.; Rafael, G.; von Oppen, F.; Fisher, M.P.A. Non-Abelian statistics and topological quantum information processing in 1D wire networks. Nat. Phys. 2011, 7, 412. [Google Scholar] [CrossRef]
- Moore, G.; Read, N. Nonabelions in the fractional quantum Hall effect. Nucl. Phys. B 1991, 360, 362. [Google Scholar] [CrossRef]
- Bernevig, B.A. Topological Insulators and Topological Superconductors; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Resta, R. The insulating state of matter: A geometrical theory. Eur. Phys. J. B 2011, 79, 121–137. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Fault-tolerant quantum computation by anyons. Ann. Phys. 2003, 303, 2–30. [Google Scholar] [CrossRef]
- Read, N.; Green, D. Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries and the fractional quantum Hall effect. Phys. Rev. B 2000, 61, 10267. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L. Superconducting proximity effect and Majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 2008, 100, 096407. [Google Scholar] [CrossRef] [PubMed]
- Lutchyn, R.M.; Sau, J.D.; Sarma, S.D. Majorana fermions and topological phase transition in semiconductor-superconductor heterostructures. Phys. Rev. Lett. 2010, 105, 077001. [Google Scholar] [CrossRef] [PubMed]
- Perge, S.N.; Drozdov, I.K.; Li, J.; Chen, H.; Jeon, S.; Seo, J.; MacDonald, A.H.; Bernevig, B.A.; Yazdani, A. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor. Science 2014, 346, 1259327. [Google Scholar]
- Mourik, V.; Zuo, V.K.; Frolov, S.M.; Plissard, S.R.; Bakkers, E.P.A.M.; Kouwenhoven, L.P. Signatures of Majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science 2012, 336, 1003. [Google Scholar] [CrossRef] [PubMed]
- Albrecht, S.M.; Higginbotham, A.P.; Madsen, M.; Kuemmeth, F.; Jespersen, T.S.; Nygard, J.; Krogstrup, P.; Marcus, C.M. Exponential protection of zero modes in Majorana islands. Nature 2016, 531, 206. [Google Scholar] [CrossRef] [PubMed]
- Gariglio, S.; Reyren, N.; Caviglia, A.D.; Triscone, J.M. Superconductivity at the LAO/STO interface. J. Phys. Condens. Matter 2009, 21, 164213. [Google Scholar] [CrossRef] [PubMed]
- Fidowski, L.; Jiang, H.C.; Lutchyn, R.M.; Nayak, C. Magnetic and superconducting ordering in one-dimensional nanostructures at the LAO/STO interface. Phys. Rev. B 2013, 87, 014436. [Google Scholar] [CrossRef]
- Gariglio, S.; Triscone, J.M. Oxide interface superconductivity. C. R. Phys. 2011, 12, 591–599. [Google Scholar] [CrossRef]
- Reyren, N.; Thiel, S.; Caviglia, A.D.; Kourkoutis, L.F.; Hammerel, G.; Richter, C.; Schneider, C.W.; Kopp, T.; Ruetschi, A.S.; Jaccard, D.; et al. Superconducting interfaces between insulating oxides. Science 2007, 317, 1196. [Google Scholar] [CrossRef] [PubMed]
- Eerkes, P.D.; van der Wiel, W.G.; Hilgenkamp, H. Modulation of conductance and superconductivity by top-gating in LAO/STO 2-dimensional electron systems. Appl. Phys. Lett. 2013, 103, 201603. [Google Scholar] [CrossRef]
- Prawiroatmodjo, G.E.D.K.; Trier, F.; Christensen, D.V.; Chen, Y.; Pryds, N.; Jespersen, T.S. Gate-tunable superconductivity at the amorphous LAO/STO interface. arXiv, 2015; arXiv:1510.01199v1. [Google Scholar]
- Wang, X.A.; Baskaran, G.; Liu, Z.Q.; Huijben, J.; Yi, J.B.; Annadi, A.; Roy Barman, A.; Rusydi, A.; Dhar, S.; Feng, Y.P.; et al. Electronic phase separation at the LAO/STO interface. Nat. Commun. 2011, 2, 188. [Google Scholar]
- Biscaras, J.; Bergeal, N.; Hurand, S.; Feuillet-Palma, C.; Rastogi, A.; Budhani, R.C.; Grilli, M.; Caprara, S.; Lesueur, J. Multiple quantum criticality in a two-dimensional superconductor. Nat. Mater. 2013, 12, 542–548. [Google Scholar] [CrossRef] [PubMed]
- Biscaras, J.; Bergeal, N.; Hurand, S.; Grossetête, C.; Rastogi, A.; Budhani, R.C.; LeBoeuf, D.; Proust, C.; Lesueur, J. Two-dimensional superconducting phase in LAO/STO heterostructures induced by hight-mobility carrier doping. Phys. Rev. Lett. 2012, 108, 247004. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Richter, C.; Mannhart, J.; Ashoori, R.C. Coexistence of magnetic order and two-dimensional superconductivity at LAO/STO interfaces. Nat. Phys. 2011, 7, 762–766. [Google Scholar] [CrossRef]
- Gariglio, S.; Reyren, N.; Jaccard, D.; Schneider, T. Anisotropy of the superconducting transport properties of the LAO/STO interface. App. Phys. Lett. 2009, 94, 112506. [Google Scholar]
- Caviglia, A.D.; Gabay, M.; Gariglio, S.; Reyren, N.; Cancellieri, C.; Triscone, J.-M. Tunable Rashba Spin-Orbit Interaction at Oxide Interfaces. Phys. Rev. Lett. 2010, 104, 126803. [Google Scholar] [CrossRef] [PubMed]
- Ben Shalom, M.; Ron, A.; Palevski, A.; Dagan, Y. Shubnikov-De Haas Oscillations in SrTiO3/LaAlO3 Interface. Phys. Rev. Lett. 2010, 105, 206401. [Google Scholar] [CrossRef] [PubMed]
- Caprara, S.; Peronaci, F.; Grilli, M. Intrinsic instability of electronic interfaces with strong Rashba coupling. Phys. Rev. Lett. 2012, 109, 196401. [Google Scholar] [CrossRef] [PubMed]
- Bucheli, D.; Grilli, M.; Peronaci, F.; Seibold, G.; Caprara, S. Phase diagrams of voltage-gated oxide interfaces with strong Rashba coupling. Phys. Rev. B 2014, 89, 195448. [Google Scholar] [CrossRef]
- Hurand, S.; Jouan, A.; Feuillet-Palma, C.; Singh, G.; Biscaras, J.; Lesne, E.; Reyen, N.; Barthélémy, A.; Bibes, M.; Villegas, J.; et al. Field-effect control of superconductivity and Rashba spin-orbit coupling in top-gated LaAlO3/SrTiO3 devices. Sci. Rep. 2015, 5, 12751. [Google Scholar] [CrossRef] [PubMed]
- Schreuer, M.S.; Schmalian, J. Topological superconductivity and unconventional pairing in oxide interfaces. Nat. Commun. 2015, 6, 6005. [Google Scholar] [CrossRef] [PubMed]
- Loder, F.; Kampf, A.P.; Kopp, T. Route to Topological Superconductivity via Magnetic Field Rotation. Sci. Rep. 2015, 5, 15302. [Google Scholar] [CrossRef] [PubMed]
- Salluzzo, M.; Cezar, J.C.; Brookes, N.B.; Bisogni, V.; De Luca, G.M.; Richter, C.; Thiel, S.; Mannhart, J.; Huijben, M.; Brinkman, A.; et al. Orbital Reconstruction and the Two-Dimensional Electron Gas at the LaAlO3/SrTiO3 Interface. Phys. Rev. Lett. 2009, 102, 166804. [Google Scholar] [CrossRef] [PubMed]
- Popovic, Z.S.; Satpathy, S.; Martin, R.M. Origin of the two-dimensional electron gas carrier density at the LAO/STO interface. Phys. Rev. Lett. 2008, 101, 256801. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Z.; Töth, A.; Held, K. Theory of spin-orbit coupling at LaAlO3/SrTiO3 interfaces and SrTiO3 surfaces. Phys. Rev. B 2013, 87, 161102(R). [Google Scholar] [CrossRef]
- Gariglio, S.; Gabay, M.; Triscone, J.-M. Research Update: Conductivity and beyond at the LaAlO3/SrTiO3 interface. Appl. Phys. Lett. Mater. 2016, 4, 060701. [Google Scholar] [CrossRef]
- Li, L.; Richter, C.; Paetel, S.; Kopp, T.; Mannhart, J.; Ashoori, R.C. Very Large Capacitance Enhancement in a Two-Dimensional Electron System. Science 2011, 332, 825–828. [Google Scholar] [CrossRef] [PubMed]
- Bi, F.; Huang, M.; Bark, C.W.; Ryu, S.; Lee, S.; Eom, C.-B.; Irvin, P.; Levy, J. Electro-Mechanical Response of Top-Gated LAO/STO Heterostructures. J. Appl. Phys. 2016, 119, 025309. [Google Scholar] [CrossRef]
- Caprara, S.; Bucheli, D.; Grilli, M.; Biscaras, J.; Bergeal, N.; Hurand, S.; Feuillet-Palma, C.; Rastogi, A.; Budhani, R.C.; Lesueur, J. Inhomogeneous electron gas at oxide interfaces with strong Rashba spin-orbit coupling. SPIN 2014, 4, 1440004. [Google Scholar] [CrossRef]
- Scopigno, N.; Bucheli, D.; Caprara, S.; Biscaras, J.; Bergeal, N.; Lesueur, J.; Grilli, M. Phase separation from electron confinement at oxide interfaces. Phys. Rev. Lett. 2016, 116, 026804. [Google Scholar] [CrossRef] [PubMed]
- Singh, G.; Jouan, A.; Benfatto, L.; Couëdo, F.; Kumar, P.; Dogra, A.; Budhani, R.C.; Caprara, S.; Grilli, M.; Lesne, E.; et al. Competition between electron pairing and phase coherence in superconducting interfaces. Nat. Commun. 2018, 9, 407. [Google Scholar] [CrossRef] [PubMed]
- Caviglia, A.D.; Gariglio, S.; Reyren, N.; Jaccard, D.; Schneider, T.; Gabay, M.; Thiel, S.; Hemmerl, G.; Mannhart, J.; Triscone, J.-M. Electric field control of the LAO/STO interface ground state. Nature 2008, 456, 624. [Google Scholar] [CrossRef] [PubMed]
- Santander-Syro, A.F.; Copie, O.; Kondo, T.; Fortuna, F.; Pailhès, S.; Weht, R.; Qiu, X.G.; Bertran, F.; Nicolaou, A.; Taleb-Ibrahimi, A.; et al. Two-dimensional electron gas with universal sub bands at the surface of SrTiO3. Nature 2011, 469, 189–193. [Google Scholar] [CrossRef] [PubMed]
- Fete, A.; Gariglio, S.; Caviglia, A.D.; Triscone, J.M.; Gabay, M. Rashba induced magnetoconductance oscillations in the LaAlO3-SrTiO3 heterostructure. Phys. Rev. B 2012, 86, 201105(R). [Google Scholar] [CrossRef]
- Herranz, G.; Singh, G.; Bergeal, N.; Jouan, A.; Lesueur, J.; Gazquez, J.; Varela, M.; Scigaj, M.; Dix, N.; Sanchez, F.; Fontcuberta, J. Engineering two-dimensional superconductivity and Rashba spin-orbit coupling in LAO/STO quantum wells by selective orbital occupancy. Nat. Commun. 2015, 6, 6028. [Google Scholar] [CrossRef] [PubMed]
- Mohanta, N.; Taraphder, A. Topological superconductivity and Majorana bound states at the LaAlO3/SrTiO3 interface. EPL 2014, 108, 60001. [Google Scholar] [CrossRef]
- Chen, W.; Legner, M.; Rüegg, A.; Sigrist, M. Correlation length, universality classes, and scaling laws associated with topological phase transitions. Phys. Rev. B 2017, 95, 075116. [Google Scholar] [CrossRef]
- Zhang, P.; Nori, F. Majorana bound states in a disordered quantum dot-superconductor chain. New J. Phys. 2016, 18, 043033. [Google Scholar] [CrossRef]
- Brouwer, P.W.; Duckheim, M.; Romito, A.; von Oppen, F. Probability Distribution of Majorana End-State Energies in Disordered Wires. Phys. Rev. Lett. 2011, 107, 196804. [Google Scholar] [CrossRef] [PubMed]
- Brouwer, P.W.; Duckheim, M.; Romito, A.; von Oppen, F. Topological superconducting phases in disordered quantum wires with strong spin-orbit coupling. Phys. Rev. B 2011, 84, 144526. [Google Scholar] [CrossRef]
- Pekerten, B.; Teker, A.; Bozat, O.; Wimmer, M.; Adagideli, I. Disorder-induced topological transitions in multichannel Majorana wires. Phys. Rev. B 2017, 95, 064507. [Google Scholar] [CrossRef]
- Klinovaja, J.; Loss, D. Fermionic and Majorana bound states in hybrid nanowires with non-uniform spin-orbit interaction. Eur. Phys. J. B 2015, 88, 62. [Google Scholar] [CrossRef]
- Cai, X.; Lang, L.-J.; Chen, S.; Wang, Y. Topological superconductor to Anderson localization transition in one-dimensional incommensurate lattice. Phys. Rev. Lett. 2013, 110, 176403. [Google Scholar] [CrossRef] [PubMed]
- DeGottardi, W.; Sen, D.; Vishveshwara, S. Fermions in Superconducting 1D Systems Having Periodic, Quasiperiodic, and Disordered Potentials. Phys. Rev. Lett. 2013, 110, 146404. [Google Scholar] [CrossRef] [PubMed]
- Choy, T.P.; Edge, J.M.; Akhmerov, A.R.; Beenakker, C.W.J. Majorana fermions emerging from magnetic nanoparticles on a superconductor without spin-orbit coupling. Phys. Rev. Lett. 2011, 84, 195442. [Google Scholar] [CrossRef]
- Altland, A.; Zirnbauer, M.R. Nonstandard symmetry classes in mesoscopic normal-superconducting hybrid structures. Phys. Rev. B 1997, 55, 1142. [Google Scholar] [CrossRef]
- Fulga, I.C.; Akhmerov, A.R.; Beenakker, C.W.J. Scattering formula for the topological quantum number of a disordered multimode wire. Phys. Rev. B 2011, 83, 155429. [Google Scholar] [CrossRef]
- Fulga, I.C.; Hassler, F.; Akhmerov, A.R. Scattering theory of topological insulators and superconductors. Phys. Rev. B 2012, 85, 165409. [Google Scholar] [CrossRef]
- Beenakker, C.W.J. Random-matrix theory of Majorana fermions and topological superconductors. Rev. Mod. Phys. 2015, 87, 1037. [Google Scholar] [CrossRef]
- Mello, P.A.; Pereyra, P.; Kumar, N. Macroscopic approach to multichannel disordered conductors. Ann. Phys. 1988, 181, 290–317. [Google Scholar] [CrossRef]
- Akhmerov, A.R.; Dahlhaus, J.P.; Hassler, F.; Wimmer, M.; Beenakker, C.W.J. Quantized conductance at the Majorana phase transition in a disordered superconducting wire. Phys. Rev. Lett. 2011, 106, 057001. [Google Scholar] [CrossRef] [PubMed]
- Wegner, F. Inverse participation ratio in 2 + ε dimensions. Z. Phys. B 1980, 36, 209–214. [Google Scholar] [CrossRef]
- Beenakker, C.W.J. Random-matrix theory of quantum transprt. Rev. Mod. Phys. 1997, 69, 731. [Google Scholar] [CrossRef]
- Guhr, T.; Groeling, A.M.; Weidenumuller, H.A. Random-matrix theories in quantum physics: Common concepts. Phys. Rep. 1998, 299, 189–425. [Google Scholar] [CrossRef]
- Snyman, I.; Tworzydlo, J.; Beenakker, C.W.J. Calculation of the conductance of a graphene sheet using the Chalker-Coddington network model. Phys. Rev. B 2008, 78, 045118. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazziotti, M.V.; Scopigno, N.; Grilli, M.; Caprara, S. Majorana Fermions in One-Dimensional Structures at LaAlO3/SrTiO3 Oxide Interfaces. Condens. Matter 2018, 3, 37. https://doi.org/10.3390/condmat3040037
Mazziotti MV, Scopigno N, Grilli M, Caprara S. Majorana Fermions in One-Dimensional Structures at LaAlO3/SrTiO3 Oxide Interfaces. Condensed Matter. 2018; 3(4):37. https://doi.org/10.3390/condmat3040037
Chicago/Turabian StyleMazziotti, Maria Vittoria, Niccolò Scopigno, Marco Grilli, and Sergio Caprara. 2018. "Majorana Fermions in One-Dimensional Structures at LaAlO3/SrTiO3 Oxide Interfaces" Condensed Matter 3, no. 4: 37. https://doi.org/10.3390/condmat3040037
APA StyleMazziotti, M. V., Scopigno, N., Grilli, M., & Caprara, S. (2018). Majorana Fermions in One-Dimensional Structures at LaAlO3/SrTiO3 Oxide Interfaces. Condensed Matter, 3(4), 37. https://doi.org/10.3390/condmat3040037






