Localization Parameters for Two Interacting Particles in Disordered Two-Dimensional Finite Lattices
Abstract
:1. Introduction
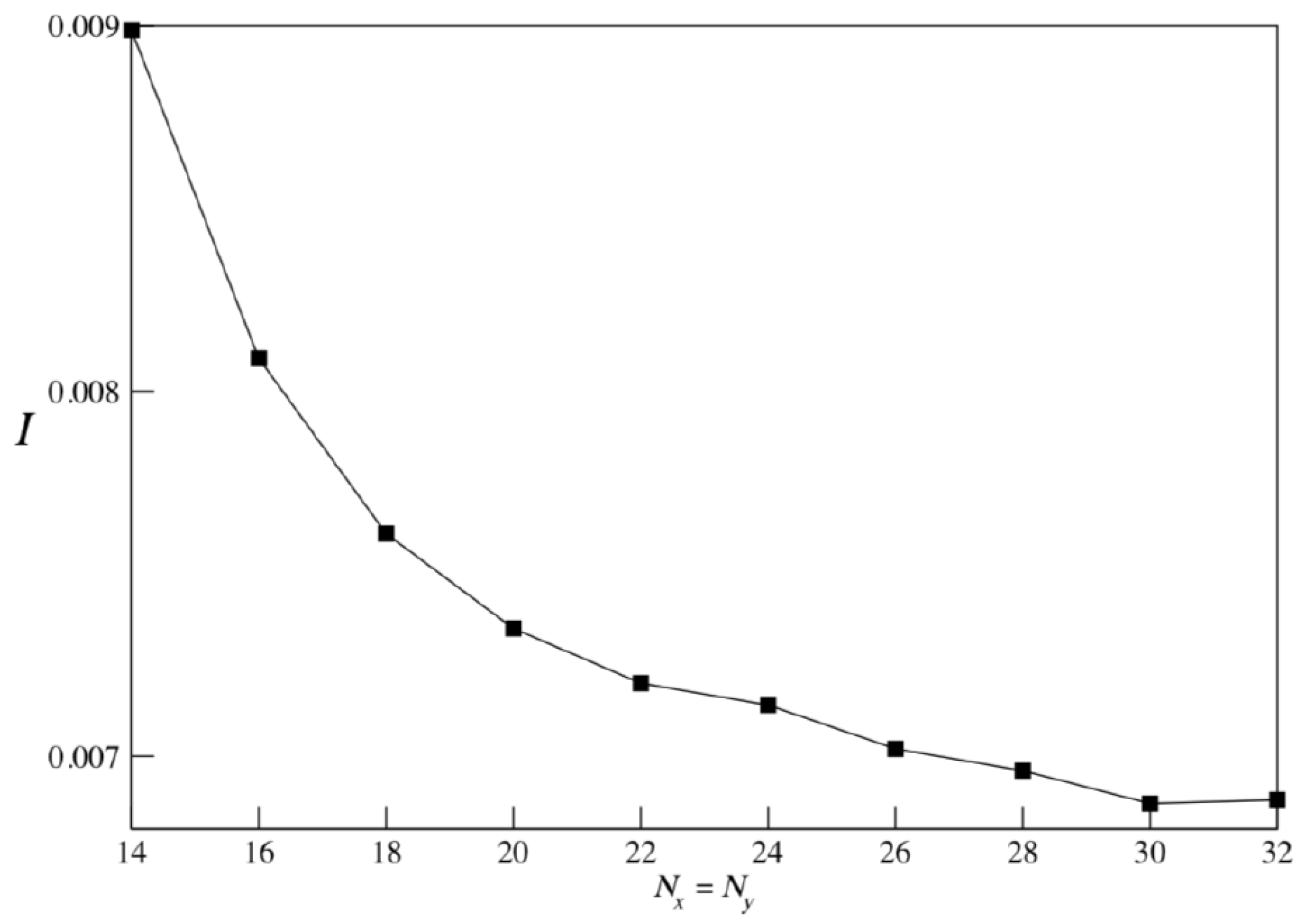
2. Method
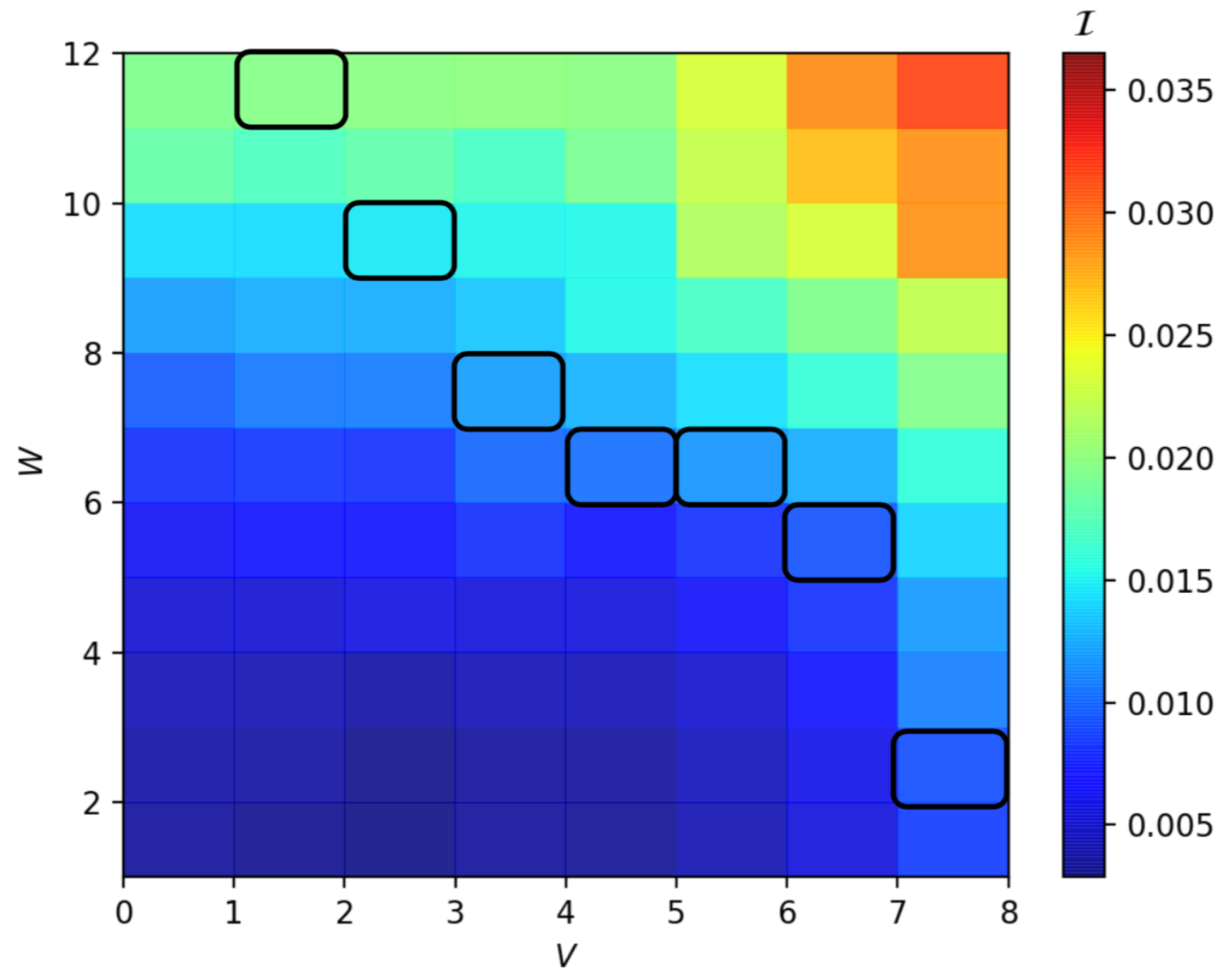
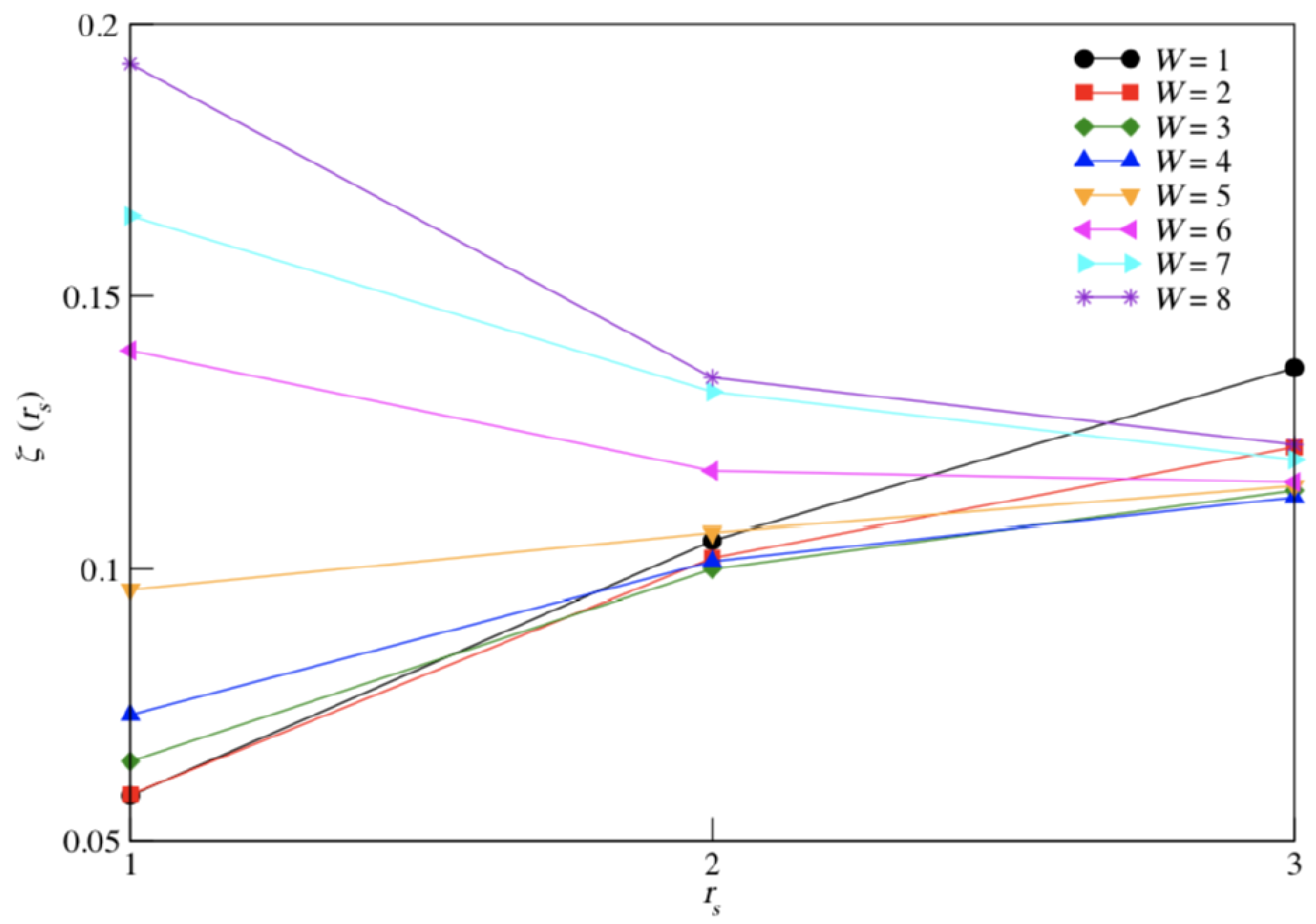
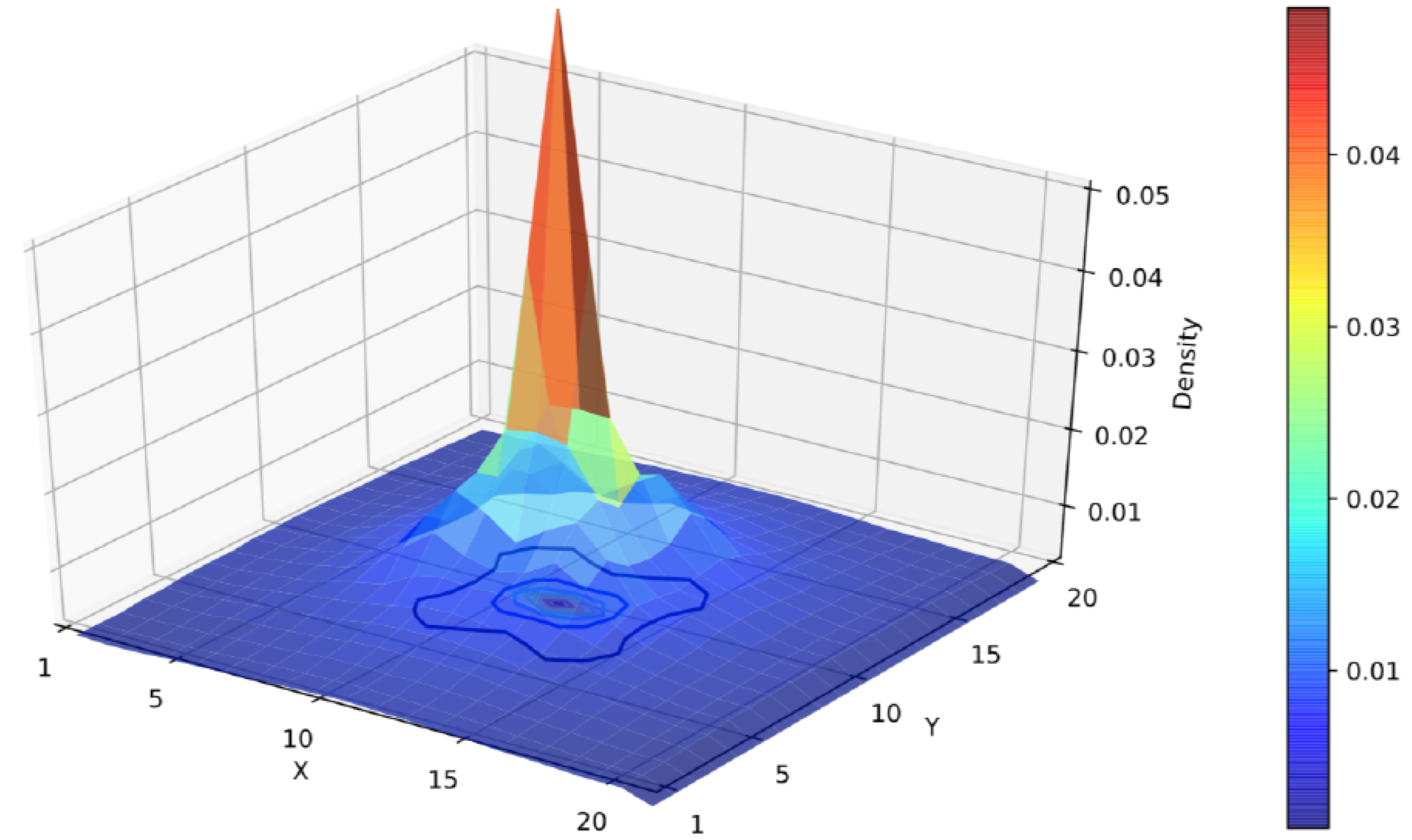
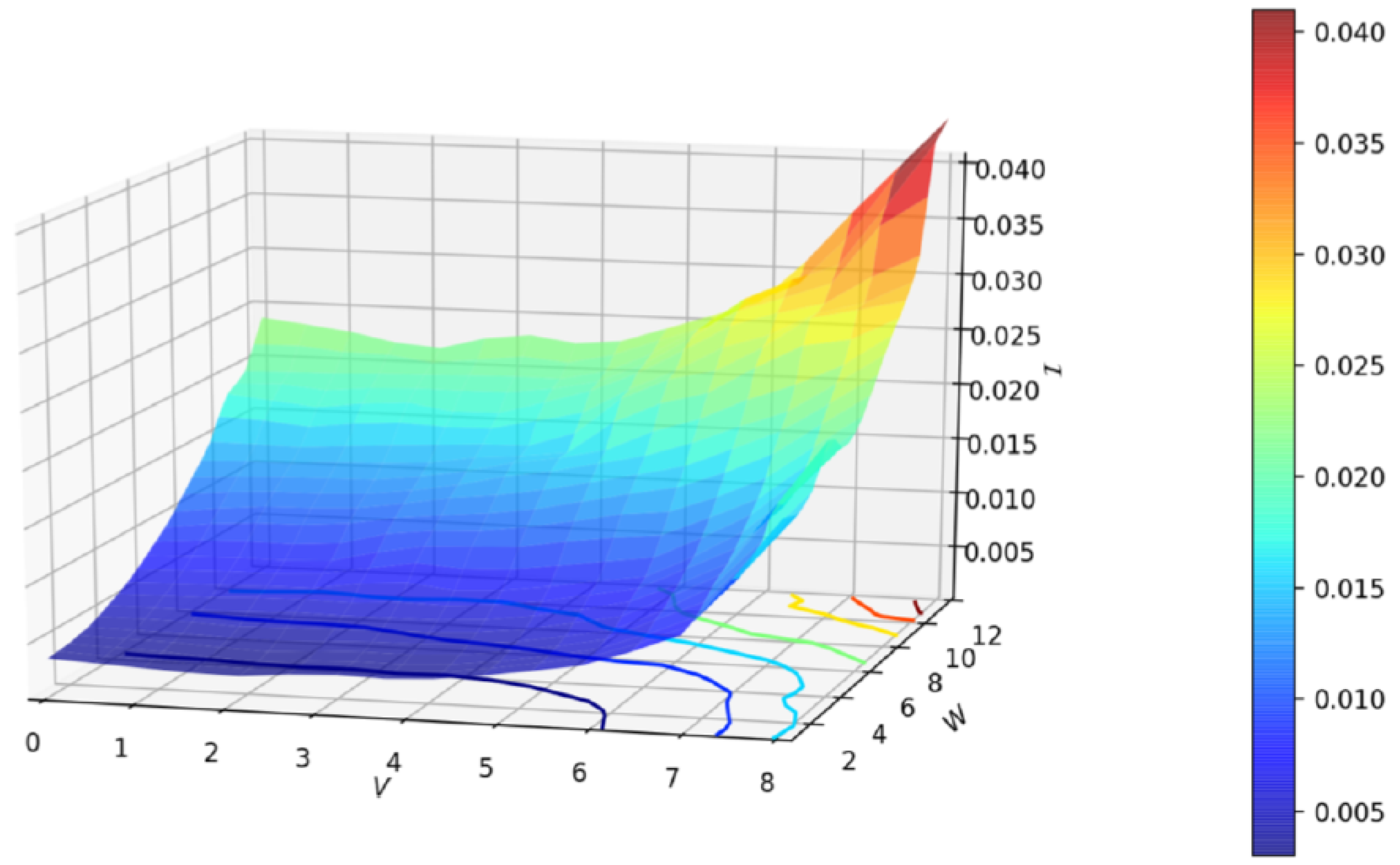
3. Results
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Anderson, P.W. Absence of Diffusion in Certain Random Lattices. Phys. Rev. 1957, 109, 1492. [Google Scholar] [CrossRef]
- Abrahams, E.; Anderson, P.W.; Licciardello, D.C.; Ramakrishnan, T.V. Scaling theory of localization: Absence of quantum diffusion in two dimensions. Phys. Rev. Lett. 1979, 42, 673. [Google Scholar] [CrossRef]
- Fleishman, L.; Anderson, P.W. Interactions and the Anderson transition. Phys. Rev. B 1980, 21, 2366. [Google Scholar] [CrossRef]
- Finkelshtein, A.M. Influence of f Coulomb interaction on the properties of disordered metals. Zh. Eksp. Teor. Fiz. 1983, 84, 168. [Google Scholar]
- Giamarchi, T.; Schulz, H.J. Anderson localization and interactions in one-dimensional metals. Phys. Rev. B 1988, 37, 325. [Google Scholar] [CrossRef]
- Basko, D.M.; Aleiner, I.L.; Altshuler, B.L. Metal-insulator transition in a weakly interacting many-electron system with localized single-particle states. Ann. Phys. 2006, 321, 1126. [Google Scholar] [CrossRef]
- Gornyi, I.V.; Mirlin, A.D.; Polyakov, D.G. Interacting Electrons in Disordered Wires: Anderson Localization and Low-T Transport. Phys. Rev. Lett. 2005, 95, 206603. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, M.; Hodgman, S.S.; Bordia, P.; Luschen, H.P.; Fischer, M.H.; Vosk, R.; Altman, E.; Schneider, U.; Bloch, I. Observation of many-body localization of interacting fermions in a quasirandom optical lattice. Science 2015, 349, 842. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.-Y.; Hild, S.; Zeiher, J.; Schauß, P.; Rubio-Abadal, A.; Yefsah, T.; Khemani, V.; Huse, D.A.; Bloch, I.; Gross, C. Exploring the many-body localization transition in two dimensions. Science 2016, 352, 1547. [Google Scholar] [CrossRef] [PubMed]
- Lukin, A.; Rispoli, M.; Schittko, R.; EricTai, M.; Kaufman, A.M.; Choi, S.; Khemani, V.; Leonard, J.; Greiner, M. Probing entanglement in a many-body-localized system. arXiv, 2018; arXiv:1805.09819. [Google Scholar]
- Krimer, D.O.; Khomeriki, R.; Flach, S. Two interacting particles in a random potential. JETP Lett. 2011, 94, 406. [Google Scholar] [CrossRef]
- Romer, R.A.; Schreiber, M.; Vojta, T. Disorder and two-particle interaction in low-dimensional quantum systems. Physica E 2001, 9, 397. [Google Scholar] [CrossRef]
- Frahm, K.M. Eigenfunction structure and scaling of two interacting particles in the one-dimensional Anderson model. Eur. Phys. J. B 2016, 89, 115. [Google Scholar] [CrossRef]
- Von Oppen, F.; Wettig, T.; Muller, J. Interaction-induced delocalization of two particles in a random potential: Scaling properties. Phys. Rev. Lett. 1996, 76, 491. [Google Scholar] [CrossRef] [PubMed]
- Waintal, X.; Pichard, J.L. Two interacting particles in a disordered chain I: Multifractality of the interaction matrix elements. Eur. Phys. J. B 1998, 6, 117. [Google Scholar] [CrossRef]
- Arias, S.T.; Waintal, X.; Pichard, J.L. Two interacting particles in a disorder chain III: Dynamical aspects of the interplay disorder-interaction. Eur. Phys. J. B 1999, 10, 149. [Google Scholar] [CrossRef]
- Chattaraj, T.; Krems, R.V. Effects of long-range hopping and interactions on quantum walks in ordered and disordered lattices. Phys. Rev. A 2016, 94, 023601. [Google Scholar] [CrossRef]
- Ambegaokar, V.; Eckern, U. Coherence and persistent currents in mesoscopic rings. Phys. Rev. Lett. 1990, 65, 381. [Google Scholar] [CrossRef] [PubMed]
- Levy, L.P.; Dolan, G.; Dunsmuir, J.; Bouchiat, H. Magnetization of mesoscopic copper rings: Evidence for persistent currents. Phys. Rev. Lett. 1990, 64, 2074. [Google Scholar] [CrossRef] [PubMed]
- Chandrasekhar, V.; Webb, R.A.; Brady, M.J.; Ketchen, M.B.; Gallagher, W.J.; Kleinsasser, A. Magnetic response of a single, isolated gold loop. Phys. Rev. Lett. 1991, 67, 3578. [Google Scholar] [CrossRef] [PubMed]
- Kravchenko, S.V.; Simonian, D.; Sarachik, M.P.; Mason, W.; Furneaux, J.E. Possible metal/insulator transition at B=0 in two dimensions. Phys. Rev. B 1994, 50, 8039. [Google Scholar] [CrossRef]
- Kravchenko, S.V.; Simonian, D.; Sarachik, M.P.; Mason, W.; Furneaux, J.E. Electric field scaling at a B=0 metal-insulator transition in two dimensions. Phys. Rev. Lett. 1996, 77, 4983. [Google Scholar] [CrossRef] [PubMed]
- Ortuno, M.; Cuevas, E. Localized to extended states transition for two interacting particles in a two-dimensional random potential. Europhys. Lett. 1999, 46, 224. [Google Scholar] [CrossRef]
- Frahm, K.M.; Shepelyansky, D.L. Delocalization of two interacting particles in the 2D Harper model. Eur. Phys. J. B 2016, 89, 8. [Google Scholar] [CrossRef]
- Vasseur, G.; Weinmann, D. Delocalization due to correlations in two-dimensional disordered systems. Eur. Phys. J. B 2004, 42, 279. [Google Scholar] [CrossRef]
- Martinez, M.; Pichard, J.L. From independent particle towards collective motion for two polarized electrons on a square lattice. Eur. Phys. J. B 2002, 30, 93. [Google Scholar] [CrossRef]
- Berciu, M.; Cook, A.M. Efficient computation of lattice green’s functions for models with nearest-neighbour hopping. Europhys. Lett. 2010, 92, 40003. [Google Scholar] [CrossRef]
- Chattaraj, T. Recursive computation of Green’s functions for interacting particles in disordered lattices and binary trees. arXiv, 2018; arXiv:1808.04898. [Google Scholar]
- Song, P.H.; von Oppen, F. General localization lengths for two interacting particles in a disordered chain General localization lengths for two interacting particles in a disordered chain. Phys. Rev. B 1999, 59, 46. [Google Scholar] [CrossRef]
- MacKinnon, A.; Kramer, B. The scaling theory of electrons in disordered solids: Additional numerical results. Z. Phys. 1983, 53, 1. [Google Scholar] [CrossRef]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chattaraj, T. Localization Parameters for Two Interacting Particles in Disordered Two-Dimensional Finite Lattices. Condens. Matter 2018, 3, 38. https://doi.org/10.3390/condmat3040038
Chattaraj T. Localization Parameters for Two Interacting Particles in Disordered Two-Dimensional Finite Lattices. Condensed Matter. 2018; 3(4):38. https://doi.org/10.3390/condmat3040038
Chicago/Turabian StyleChattaraj, Tirthaprasad. 2018. "Localization Parameters for Two Interacting Particles in Disordered Two-Dimensional Finite Lattices" Condensed Matter 3, no. 4: 38. https://doi.org/10.3390/condmat3040038
APA StyleChattaraj, T. (2018). Localization Parameters for Two Interacting Particles in Disordered Two-Dimensional Finite Lattices. Condensed Matter, 3(4), 38. https://doi.org/10.3390/condmat3040038




