Titanium Pnictide Oxide Superconductors
Abstract
:1. Introduction
2. Road to the Discovery of Superconductivity in Titanium Pnictide Oxides
2.1. Crystal Structure of ATi2Pn2O (A = Ba, Na2, (SrF)2; Pn = As, Sb)
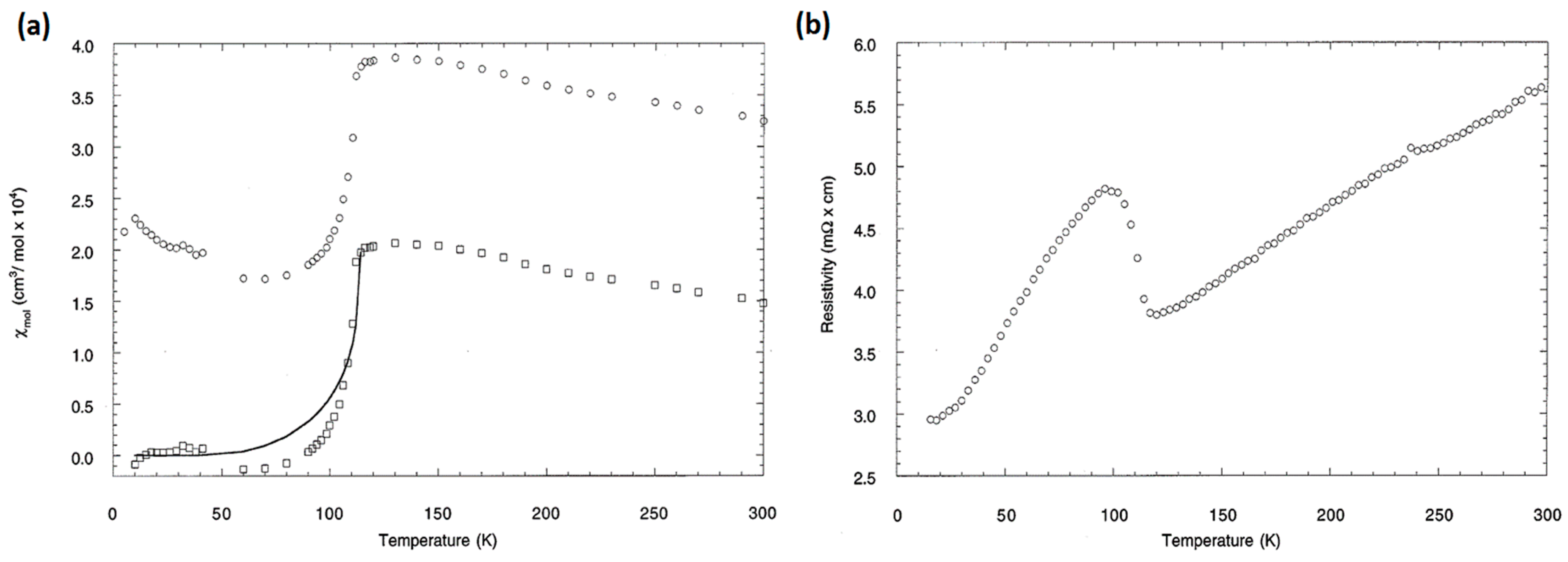
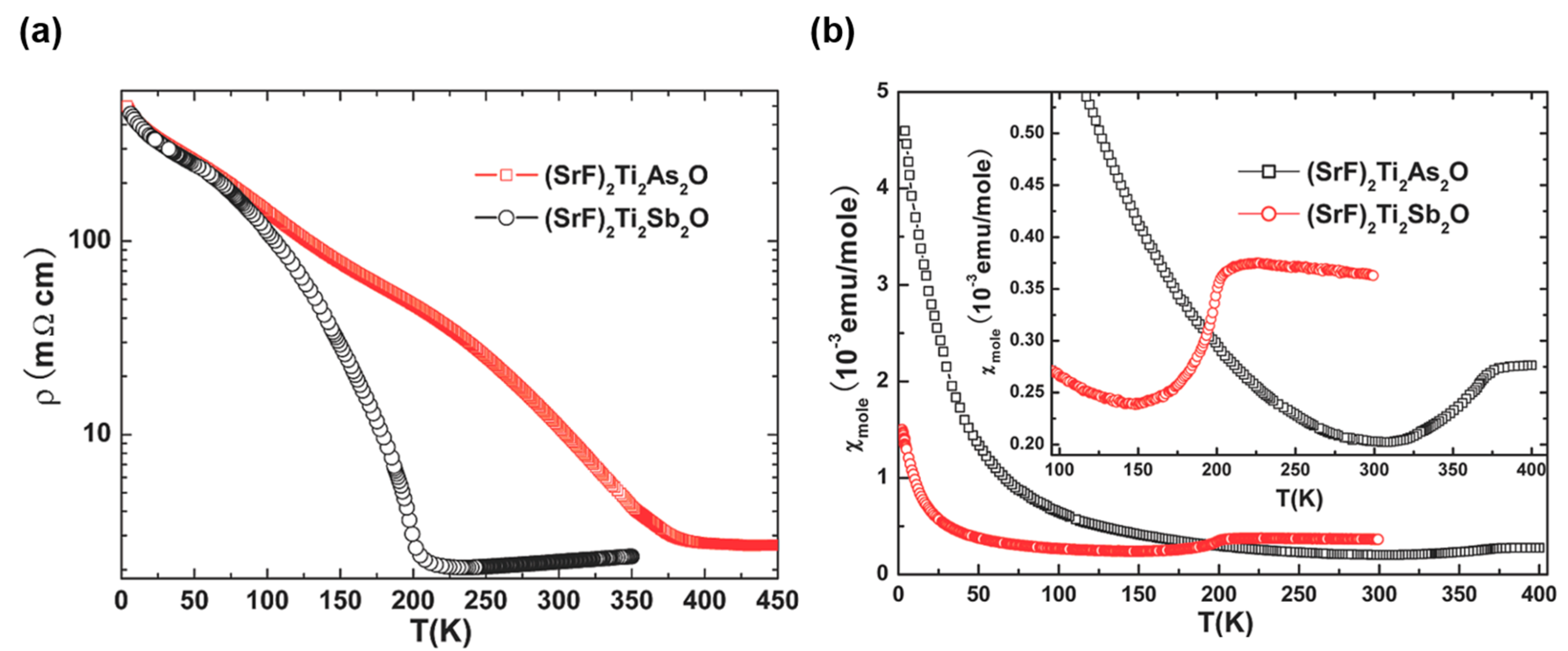
2.2. Physical Properties of ATi2Pn2O (A = Ba, Na2, (SrF)2; Pn = As, Sb)
3. Superconductivity in BaTi2Pn2O (Pn = Sb, Bi)
3.1. Synthesis and Crystal Structure
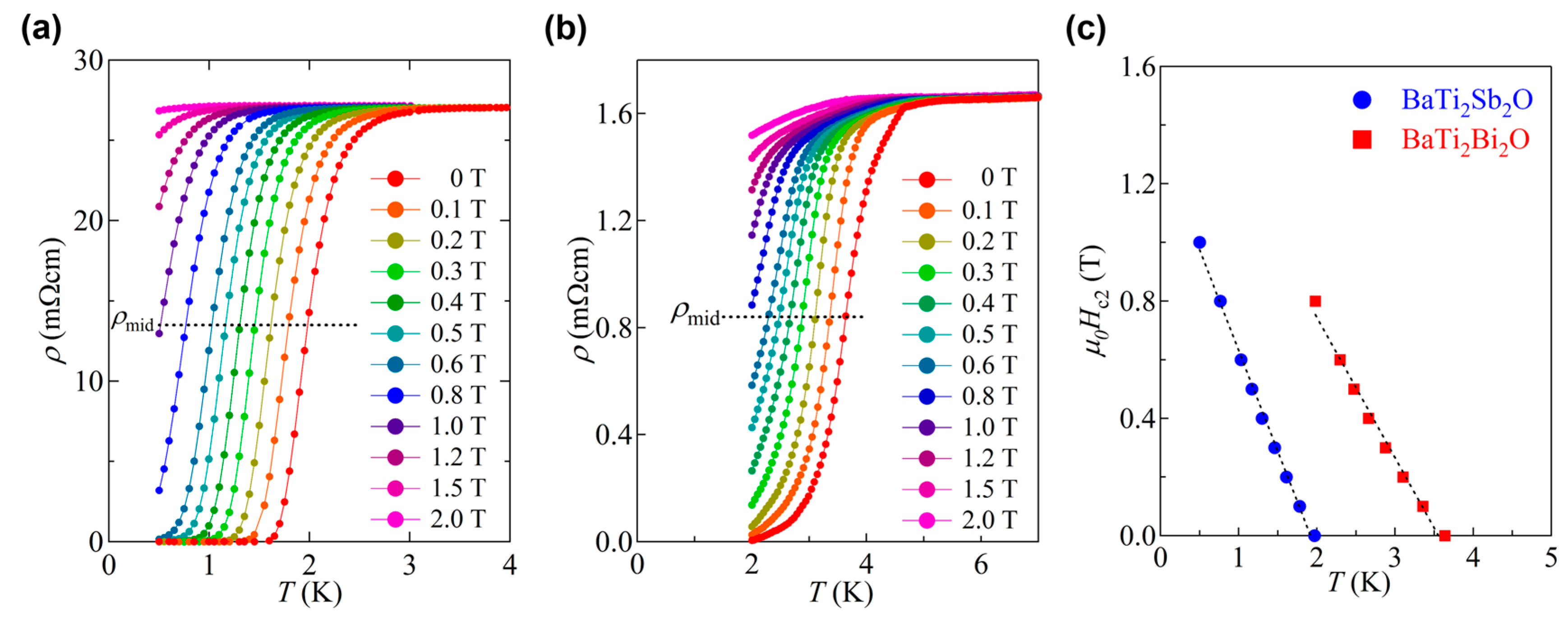
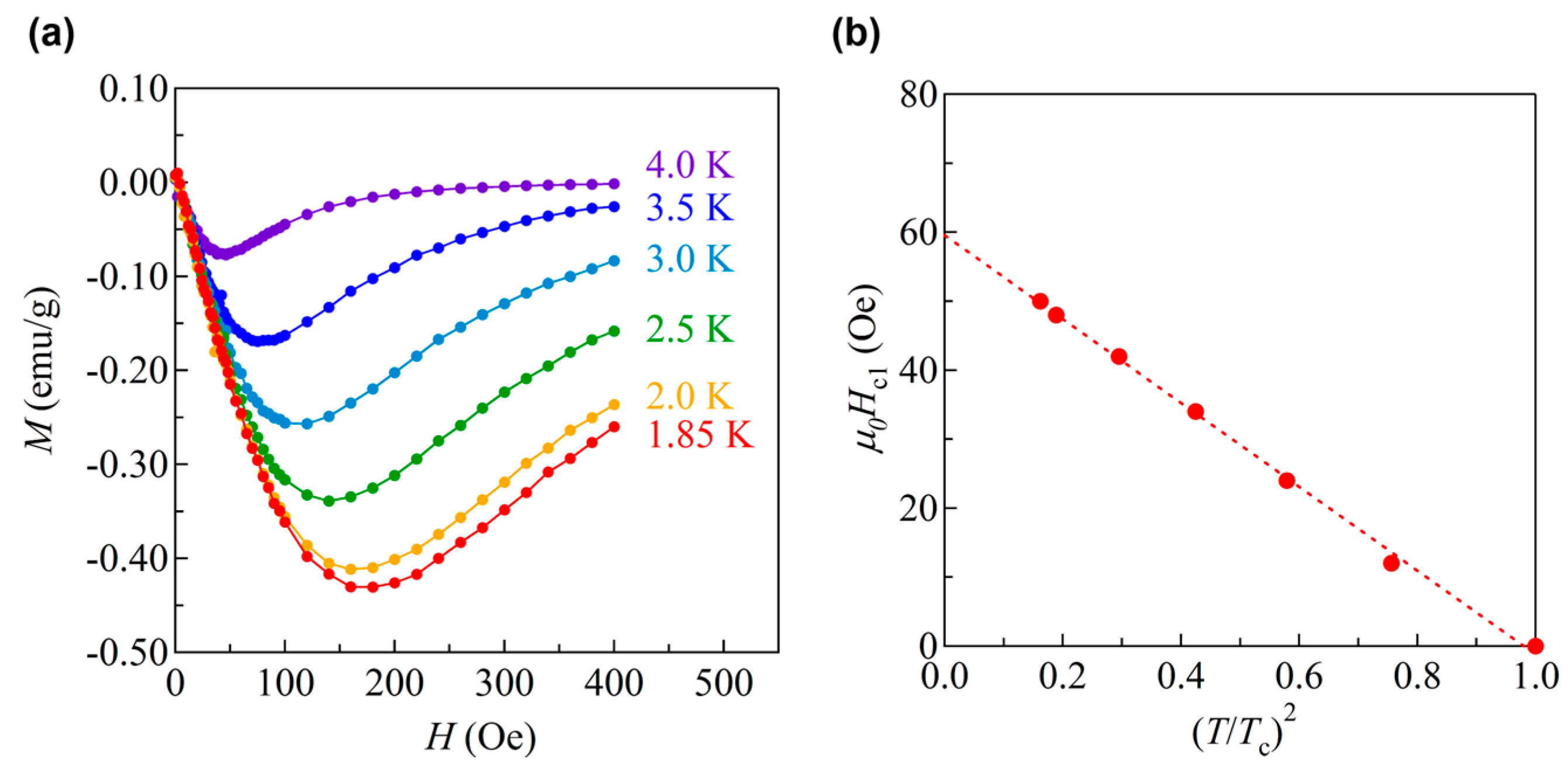
3.2. Superconductivity in BaTi2Pn2O and Its Superconducting Properties
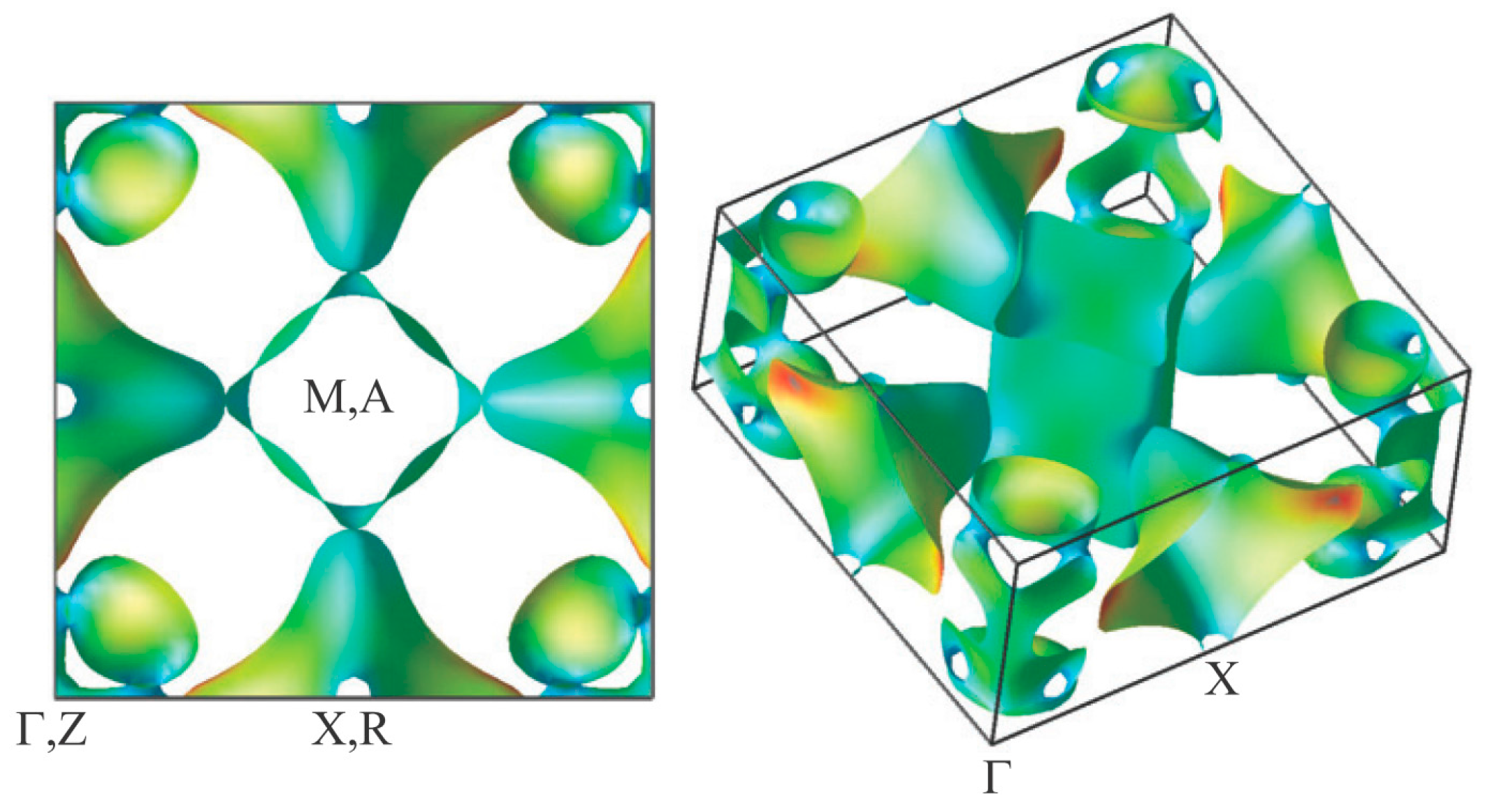
3.3. Electronic Structure of BaTi2Pn2O
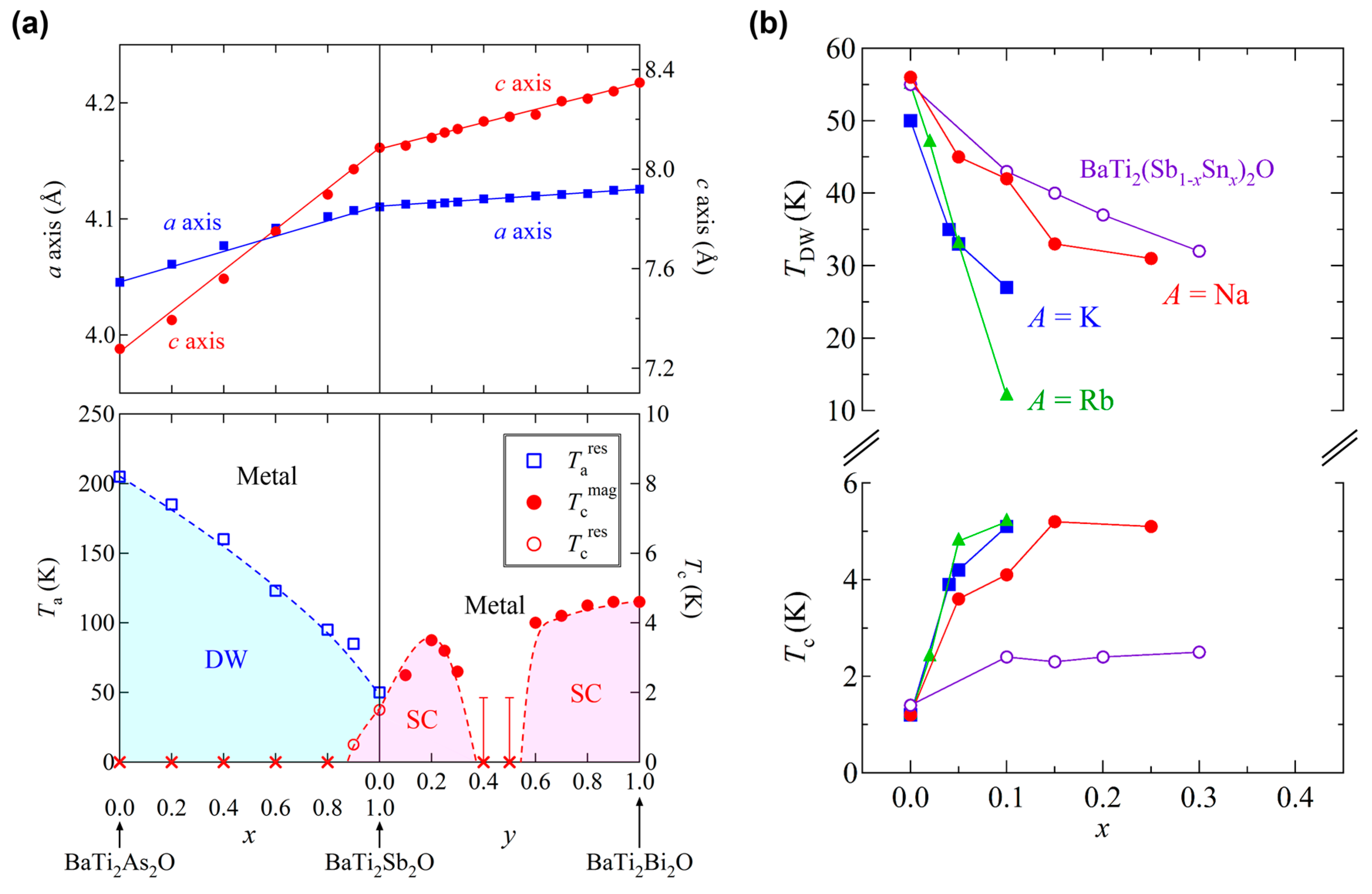
3.4. Isovalent Substitution Effect on BaTi2Pn2O
3.5. Aliovalent Substitution Effect on BaTi2Pn2O
3.6. Substitution Effect on Other Titanium Pnictide Oxides
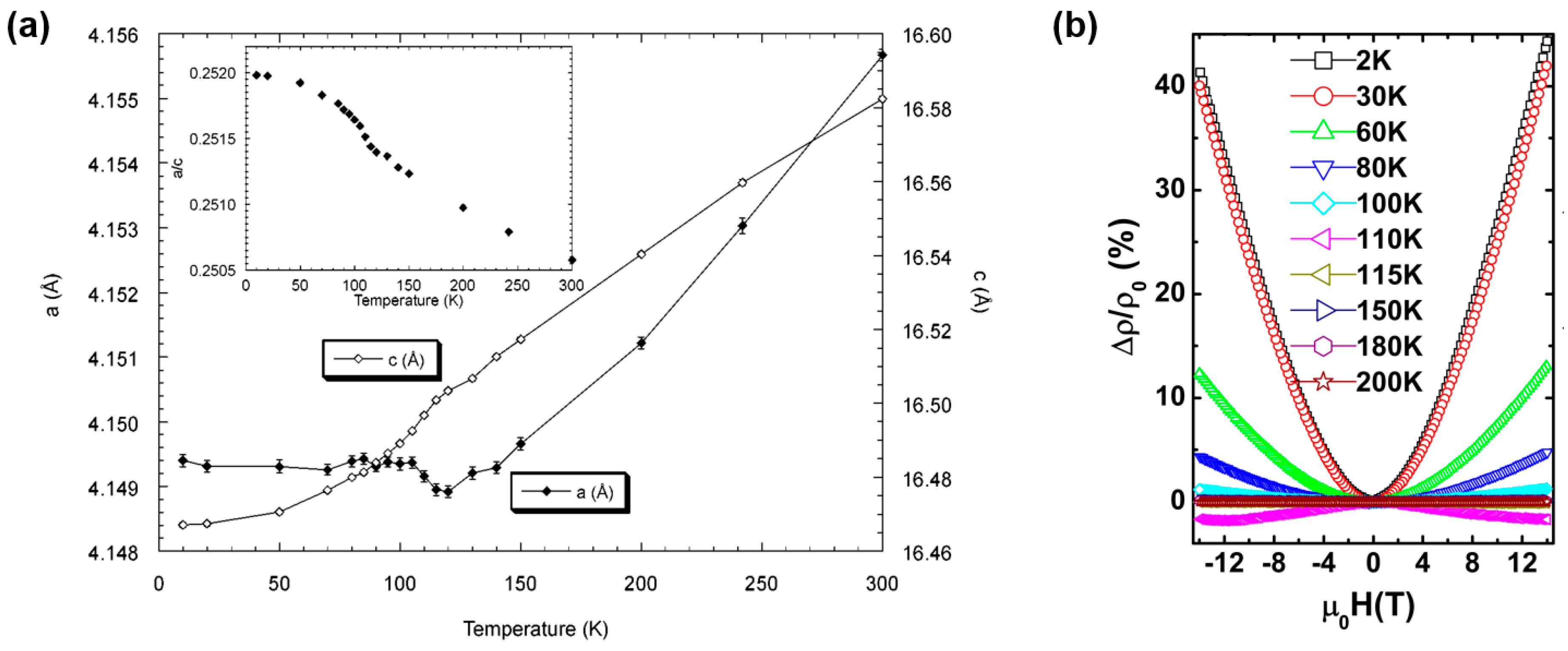
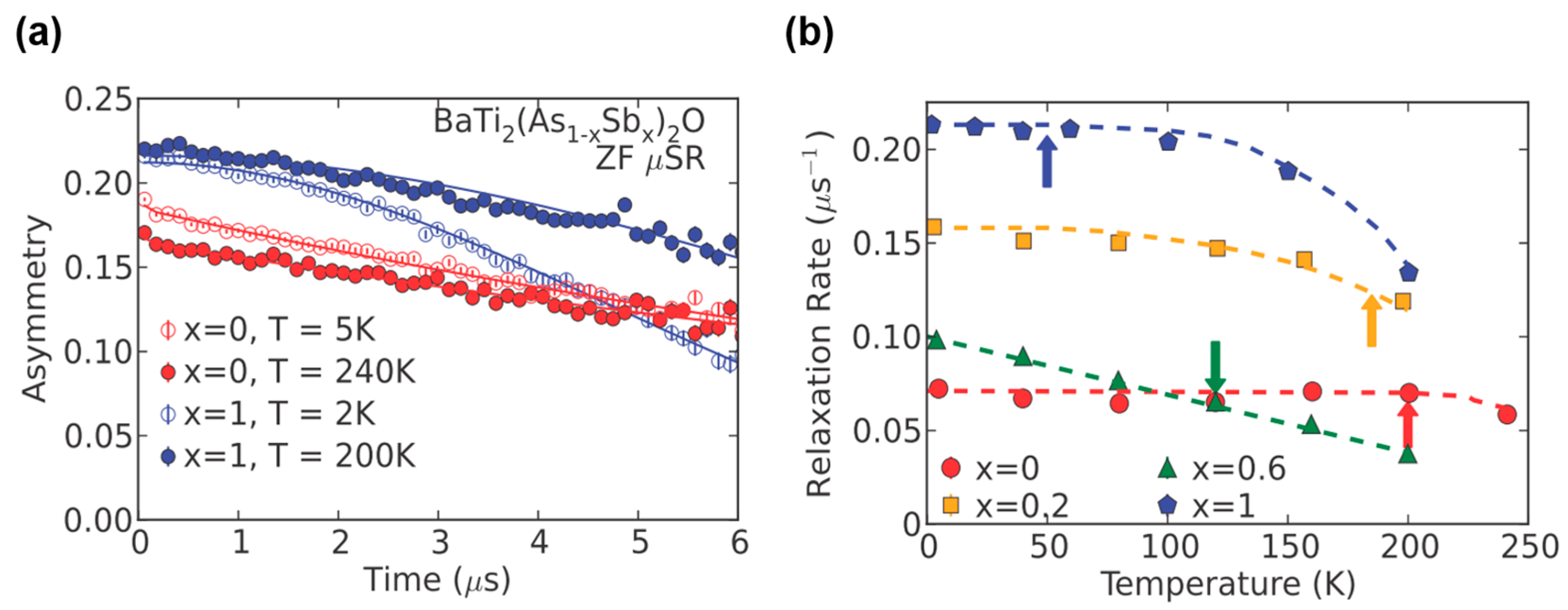
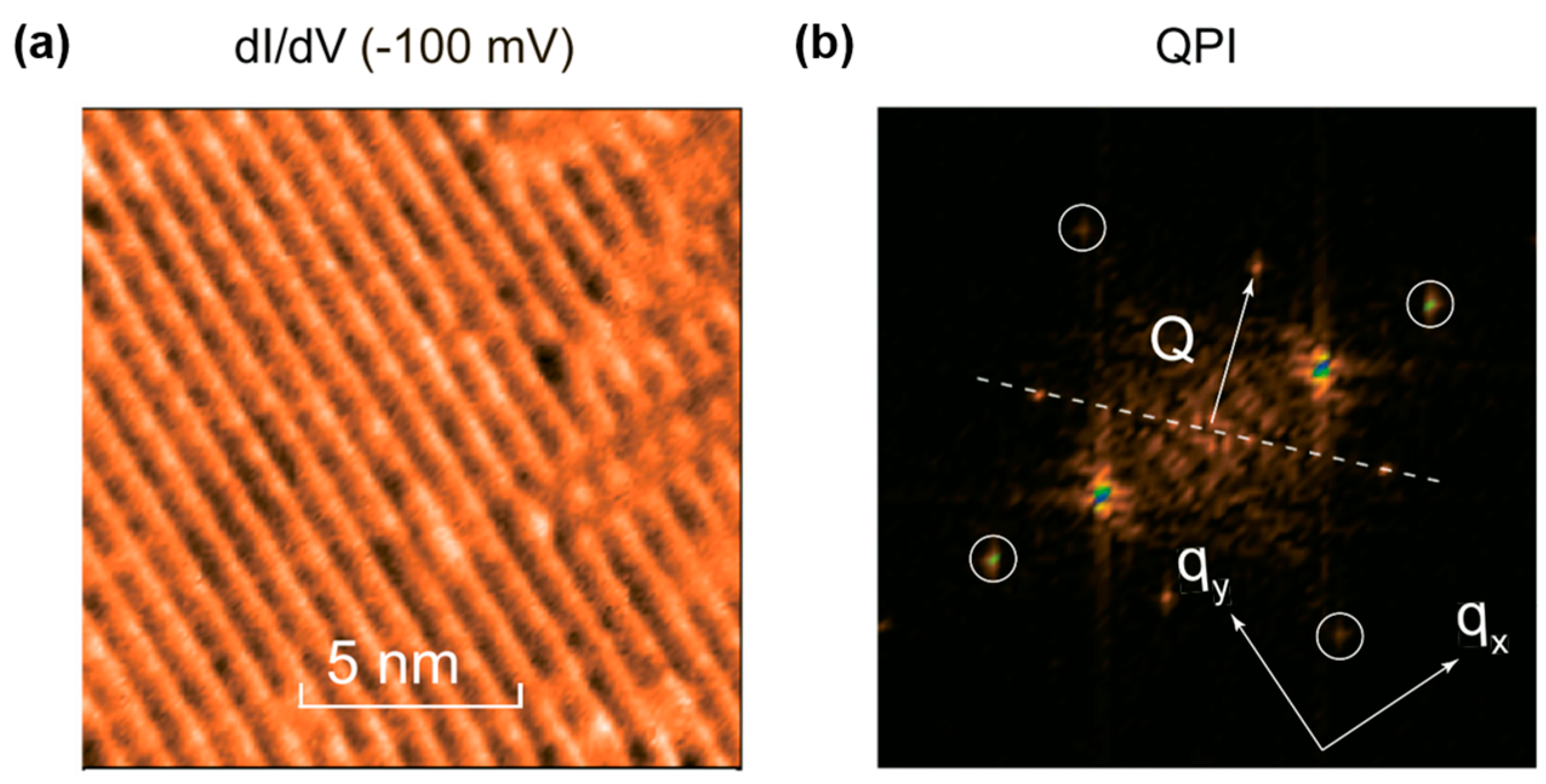
4. The DW Instability in BaTi2Pn2O
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Bednorz, J.G.; Müller, K.A. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z. Phys. B 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Nagamatsu, J.; Nakagawa, N.; Muranaka, T.; Zenitani, Y.; Akimitsu, J. Superconductivity at 39 K in magnesium diboride. Nature 2001, 410, 63–64. [Google Scholar] [CrossRef] [PubMed]
- Yamanaka, S.; Hotehama, K.I.; Kawaji, H. Superconductivity at 25.5 K in electron-doped layered hafnium nitride. Nature 1998, 392, 580–582. [Google Scholar] [CrossRef]
- Maeno, Y.; Hashimoto, H.; Yoshida, K.; Nishizaki, S.; Fujita, T.; Bednorz, J.G.; Lichtenberg, F. Superconductivity in a layered perovskite without copper. Nature 1994, 372, 532–534. [Google Scholar] [CrossRef]
- Takada, K.; Sakurai, H.; Takayama-Muromachi, E.; Izumi, F.; Dilanian, R.A.; Sasaki, T. Superconductivity in two-dimensional CoO2 layers. Nature 2003, 422, 53–55. [Google Scholar] [CrossRef] [PubMed]
- Kamihara, Y.; Watanabe, T.; Hirano, M.; Hosono, H. Iron-Based Layered Superconductor La(O1‒xFx)FeAs (x = 0.05–0.12) with Tc = 26 K. J. Am. Chem. Soc. 2008, 130, 3296–3297. [Google Scholar] [CrossRef] [PubMed]
- Mizuguchi, Y.; Demura, S.; Deguchi, K.; Takano, Y.; Fujihisa, H.; Gotoh, Y.; Izawa, H.; Miura, O. Superconductivity in Novel BiS2-Based Layered Superconductor LaO1‒xFxBiS2. J. Phys. Soc. Jpn. 2012, 81, 114725. [Google Scholar] [CrossRef]
- Hor, Y.S.; Williams, A.J.; Checkelsky, J.G.; Roushan, P.; Seo, J.; Xu, Q.; Zandbergen, H.W.; Yazdani, A.; Ong, N.P.; Cava, R.J. Superconductivity in CuxBi2Se3 and its implications for pairing in the undoped topological insulator. Phys. Rev. Lett. 2010, 104, 057001. [Google Scholar] [CrossRef] [PubMed]
- Pyon, S.; Kudo, K.; Nohara, M. Superconductivity induced by bond breaking in the triangular lattice of IrTe2. J. Phys. Soc. Jpn. 2012, 81, 053701. [Google Scholar] [CrossRef]
- Kudo, K.; Ishii, H.; Takasuga, M.; Iba, K.; Nakano, S.; Kim, J.; Fujiwara, A.; Nohara, M. Superconductivity Induced by Breaking Te2 Dimers of AuTe2. J. Phys. Soc. Jpn. 2013, 82, 063704. [Google Scholar] [CrossRef]
- Adam, A.; Schuster, H.-U. Darstellung und Kristallstruktur der Pnictidoxide Na2Ti2As2O und Na2Ti2Sb2O. ZAAC 1990, 584, 150–158. (In German) [Google Scholar] [CrossRef]
- Morosan, E.; Zandbergen, H.W.; Dennis, B.S.; Bos, J.W.G.; Onose, Y.; Klimczuk, T.; Ramirez, A.P.; Ong, N.P.; Cava, R.J. Superconductivity in CuxTiSe2. Nat. Phys. 2006, 2, 544–550. [Google Scholar] [CrossRef]
- Wu, W.; Cheng, J.; Matsubayashi, K.; Kong, P.; Lin, F.; Jin, C.; Wang, N.; Uwatoko, Y.; Luo, J. Superconductivity in the vicinity of antiferromagnetic order in CrAs. Nat. Commun. 2014, 5, 5508. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.F.; Yan, Y.J.; Ying, J.J.; Li, Q.J.; Zhang, M.; Xu, N.; Chen, X.H. Structure and physical properties for a new layered pnictide-oxide: BaTi2As2O. J. Phys. Condens. Matter 2010, 22, 075702. [Google Scholar] [CrossRef]
- Yajima, T.; Nakano, K.; Takeiri, F.; Ono, T.; Hosokoshi, Y.; Matsushita, Y.; Hester, J.; Kageyama, H. Superconductivity in BaTi2Sb2O with a d1 square lattice. J. Phys. Soc. Jpn. 2012, 81, 103706. [Google Scholar] [CrossRef]
- Yajima, T.; Nakano, K.; Takeiri, F.; Hester, J.; Yamamoto, T.; Kobayashi, Y.; Tsuji, N.; Kim, J.; Fujiwara, A.; Kageyama, H. Synthesis and physical properties of the new oxybismuthides BaTi2Bi2O and (SrF)2Ti2Bi2O with a d1 square net. J. Phys. Soc. Jpn. 2012, 82, 013703. [Google Scholar] [CrossRef]
- Liu, R.H.; Song, Y.A.; Li, Q.J.; Ying, J.J.; Yan, Y.J.; He, Y.; Chen, X.H. Structure and Physical Properties of the Layered Pnictide-Oxides: (SrF)2Ti2Pn2O (Pn= As, Sb) and (SmO)2Ti2Sb2O. Chem. Mater. 2010, 22, 1503–1508. [Google Scholar] [CrossRef]
- Yajima, T.; Nakano, K.; Takeiri, F.; Nozaki, Y.; Kobayashi, Y.; Kageyama, H. Two Superconducting Phases in the Isovalent Solid Solutions BaTi2Pn2O (Pn = As, Sb, and Bi). J. Phys. Soc. Jpn. 2013, 82, 033705. [Google Scholar] [CrossRef]
- Frandsen, B.A.; Bozin, E.S.; Hu, H.; Zhu, Y.; Nozaki, Y.; Kageyama, H.; Uemura, Y.J.; Yinm, W.G.; Billinge, S.J. Intra-unit-cell nematic charge order in the titanium-oxypnictide family of superconductors. Nat. Commun. 2014, 5, 5761. [Google Scholar] [CrossRef] [PubMed]
- Deslandes, F.; Nazzal, A.I.; Torrance, J.B. Search for superconductivity in analogues of La2−xSrxCuO4: Sr2−xLnxVO4 (Ln = La, Ce, Pr, Nd, Eu). Physica C 1991, 179, 85–90. [Google Scholar] [CrossRef]
- Arita, R.; Yamasaki, A.; Held, K.; Matsuno, J.; Kuroki, K. Sr2VO4 and Ba2VO4 under pressure: An orbital switch and potential d1 superconductor. Phys. Rev. B 2007, 75, 174521. [Google Scholar] [CrossRef]
- Axtell, E.A.; Ozawa, T.; Kauzlarich, S.M.; Singh, R.R. Phase transition and spin-gap behavior in a layered tetragonal pnictide oxide. J. Solid State Chem. 1997, 134, 423–426. [Google Scholar] [CrossRef]
- Shi, Y.G.; Wang, H.P.; Zhang, X.; Wang, W.D.; Huang, Y.; Wang, N.L. Strong anisotropy in the electromagnetic properties of Na2Ti2X2O (X = As, Sb) crystals. Phys. Rev. B 2013, 88, 144513. [Google Scholar] [CrossRef]
- Pickett, W.E. Electronic instability in inverse-K2NiF4-structure Na2Sb2Ti2O. Phys. Rev. B 1998, 58, 4335–4340. [Google Scholar] [CrossRef]
- Fabrizi de Biani, F.; Alemany, P.; Canadell, E. Concerning the Resistivity Anomaly in the Layered Pnictide Oxide Na2Ti2Sb2O. Inorg. Chem. 1998, 37, 5807–5810. [Google Scholar] [CrossRef]
- Ozawa, T.C.; Pantoja, R.; Axtell, E.A.; Kauzlarich, S.M.; Greedan, J.E.; Bieringer, M.; Richardson, J.W. Powder Neutron Diffraction Studies of Na2Ti2Sb2O and Its Structure–Property Relationships. J. Solid State Chem. 2000, 153, 275–281. [Google Scholar] [CrossRef]
- Liu, R.H.; Tan, D.; Song, Y.A.; Li, Q.J.; Yan, Y.J.; Ying, J.J.; Xie, Y.L.; Wang, X.F.; Chen, X.H. Physical properties of the layered pnictide oxides Na2Ti2P2O (P = As, Sb). Phys. Rev. B 2009, 80, 144516. [Google Scholar] [CrossRef]
- Ozawa, T.C.; Kauzlarich, S.M. Single crystal growth and characterization of a layered transition metal pnictide oxide: Na2Ti2Sb2O. J. Cryst. Growth 2004, 265, 571–576. [Google Scholar] [CrossRef]
- Song, Y.J.; Ghim, J.S.; Min, B.H.; Kwon, Y.S.; Jung, M.H.; Rhyee, J.S. Synthesis, anisotropy, and superconducting properties of LiFeAs single crystal. Appl. Phys. Lett. 2010, 96, 212508. [Google Scholar] [CrossRef]
- Tanatar, M.A.; Ni, N.; Samolyuk, G.D.; Bud’ko, S.L.; Canfield, P.C.; Prozorov, R. Resistivity anisotropy of AFe2As2 (A = Ca, Sr, Ba): Direct versus Montgomery technique measurements. Phys. Rev. B 2009, 79, 134528. [Google Scholar] [CrossRef]
- Jesche, A.; Nitsche, F.; Probst, S.; Doert, Th.; Müller, P.; Ruck, M. Anisotropic electrical resistivity of LaFeAsO: Evidence for electronic nematicity. Phys. Rev. B 2012, 86, 134511. [Google Scholar] [CrossRef]
- Suetin, D.V.; Ivanovskii, A.L. Structural, electronic properties, and chemical bonding in quaternary layered titanium pnictide-oxides Na2Ti2Pn2O and BaTi2Pn2O (Pn = As, Sb) from FLAPW–GGA calculations. J. Alloy Compd. 2013, 564, 117–124. [Google Scholar] [CrossRef]
- Doan, P.; Gooch, M.; Tang, Z.; Lorenz, B.; Möller, A.; Tapp, J.; Chu, P.C.W.; Guloy, A.M. Ba1–xNaxTi2Sb2O (0.0 ≤ x ≤ 0.33): A Layered Titanium-Based Pnictide Oxide Superconductor. J. Am. Chem. Soc. 2012, 134, 16520–16523. [Google Scholar] [CrossRef] [PubMed]
- Kasahara, S.; Shibauchi, T.; Hashimoto, K.; Ikada, K.; Tonegawa, S.; Okazaki, R.; Shishido, H.; Ikeda, H.; Takeya, H.; Hirata, K.; et al. Evolution from non-Fermi-to Fermi-liquid transport via isovalent doping in BaFe2(As1−xPx)2 superconductors. Phys. Rev. B 2010, 81, 184519. [Google Scholar] [CrossRef]
- Hoffmann, R.; Zheng, C. Making and Breaking Bonds in the Solid State: The ThCr2Si2 Structure. J. Phys. Chem. 1985, 89, 4175–4181. [Google Scholar] [CrossRef]
- Gooch, M.; Doan, P.; Tang, Z.; Lorenz, B.; Guloy, A.M.; Chu, P.C. Weak coupling BCS-like superconductivity in the pnictide oxide Ba1−xNaxTi2Sb2O (x = 0 and 0.15). Phys. Rev. B 2013, 88, 064510. [Google Scholar] [CrossRef]
- Kitagawa, S.; Ishida, K.; Nakano, K.; Yajima, T.; Kageyama, H. s-wave superconductivity in superconducting BaTi2Sb2O revealed by 121/123Sb-NMR/nuclear quadrupole resonance measurements. Phys. Rev. B 2013, 87, 060510. [Google Scholar] [CrossRef]
- Nozaki, Y.; Nakano, K.; Yajima, T.; Kageyama, H.; Frandsen, B.; Liu, L.; Cheung, S.; Goko, T.; Uemura, Y.J.; Munsie, T.S.J.; et al. Muon spin relaxation and electron/neutron diffraction studies of BaTi2(As1−xSbx)2O: Absence of static magnetism and superlattice reflections. Phys. Rev. B 2013, 88, 214506. [Google Scholar] [CrossRef]
- Yajima, T.; Nakano, K.; Nozaki, Y.; Kageyama, H. Superconducting properties of BaTi2Pn2O (Pn = Sb, Bi). Physica C 2014, 504, 36–38. [Google Scholar] [CrossRef]
- Singh, D.J. Electronic structure, disconnected Fermi surfaces and antiferromagnetism in the layered pnictide superconductor NaxBa1−xTi2Sb2O. New J. Phys. 2012, 14, 123003. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, H.; Zhang, L.; Liu, C. The electronic structure and magnetism of BaTi2Sb2O. J. Appl. Phys. 2013, 113, 243904. [Google Scholar] [CrossRef]
- Nakaoka, H.; Yamakawa, Y.; Kontani, H. Theoretical prediction of nematic orbital-ordered state in the Ti oxypnictide superconductor BaTi2(As,Sb)2O. Phys. Rev. B 2016, 93, 245122. [Google Scholar] [CrossRef]
- Nakano, K.; Hongo, K.; Maezono, R. Phonon dispersions and Fermi surfaces nesting explaining the variety of charge ordering in titanium-oxypnictides superconductors. Sci. Rep. 2016, 6, 29661. [Google Scholar] [CrossRef] [PubMed]
- Suetin, D.V.; Ivanovskii, A.L. Electronic properties and fermi surface for new Fe-free layered pnictide-oxide superconductor BaTi2Bi2O from first principles. JETP Lett. 2013, 97, 220–225. [Google Scholar] [CrossRef]
- Yan, X.W.; Lu, Z.Y. Layered pnictide-oxide Na2Ti2Pn2O (Pn= As, Sb): A candidate for spin density waves. J. Phys. Condens. Matter 2013, 25, 365501. [Google Scholar] [CrossRef] [PubMed]
- Song, Q.; Yan, Y.J.; Ye, Z.R.; Ren, M.Q.; Xu, D.F.; Tan, S.Y.; Niu, X.H.; Xie, B.P.; Zhang, T.; Peng, R.; et al. Electronic structure of the titanium-based oxypnictide superconductor Ba0.95Na0.05Ti2Sb2O and direct observation of its charge density wave order. Phys. Rev. B 2016, 93, 024508. [Google Scholar] [CrossRef]
- Subedi, A. Electron-phonon superconductivity and charge density wave instability in the layered titanium-based pnictide BaTi2Sb2O. Phys. Rev. B 2013, 87, 054506. [Google Scholar] [CrossRef]
- Zhai, H.F.; Jiao, W.H.; Sun, Y.L.; Bao, J.K.; Jiang, H.; Yang, X.J.; Tang, Z.T.; Tao, Q.; Xu, X.F.; Li, Y.K.; et al. Superconductivity, charge-or spin-density wave, and metal-nonmetal transition in BaTi2(Sb1−xBix)2O. Phys. Rev. B 2013, 87, 100502. [Google Scholar] [CrossRef]
- Hiraishi, M.; Iimura, S.; Kojima, K.M.; Yamaura, J.; Hiraka, H.; Ikeda, K.; Miao, P.; Ishikawa, Y.; Torii, S.; Miyazaki, M.; et al. Bipartite magnetic parent phases in the iron oxypnictide superconductor. Nat. Phys. 2014, 10, 300–303. [Google Scholar] [CrossRef]
- Mukuda, H.; Engetsu, F.; Yamamoto, K.; Lai, K.T.; Yashima, M.; Kitaoka, Y.; Takemori, A.; Miyasaka, S.; Tajima, S. Enhancement of superconducting transition temperature due to antiferromagnetic spin fluctuations in iron pnictides LaFe(As1−xPx)(O1−yFy): 31P-NMR studies. Phys. Rev. B 2014, 89, 064511. [Google Scholar] [CrossRef]
- Matsuishi, S.; Maruyama, T.; Iimura, S.; Hosono, H. Controlling factors of Tc dome structure in 1111-type iron arsenide superconductors. Phys. Rev. B 2014, 89, 094510. [Google Scholar] [CrossRef]
- Pachmayr, U.; Johrendt, D. Superconductivity in Ba1−xKxTi2Sb2O (0 ≤ x ≤ 1) controlled by the layer charge. Solid State Sci. 2014, 28, 31–34. [Google Scholar] [CrossRef]
- Von Rohr, F.; Nesper, R.; Schilling, A. Superconductivity in rubidium-substituted Ba1−xRbxTi2Sb2O. Phys. Rev. B 2014, 89, 094505. [Google Scholar] [CrossRef]
- Nakano, K.; Yajima, T.; Takeiri, F.; Green, M.A.; Hester, J.; Kobayashi, Y.; Kageyama, H. Tc Enhancement by Aliovalent Anionic Substitution in Superconducting BaTi2(Sb1−xSnx)2O. J. Phys. Soc. Jpn. 2013, 82, 074707. [Google Scholar] [CrossRef]
- Gooch, M.; Doan, P.; Lorenz, B.; Tang, Z.J.; Guloy, A.M.; Chu, C.W. High pressure study of the normal and superconducting states of the layered pnictide oxide Ba1−xNaxTi2Sb2O with x = 0, 0.10, and 0.15. Supercond. Sci. Technol. 2013, 26, 125011. [Google Scholar] [CrossRef]
- Ji, Q.; Ma, Y.; Hu, K.; Gao, B.; Mu, G.; Li, W.; Hu, T.; Zhang, G.; Zhao, Q.; Zhang, H.; et al. Synthesis, Structural, and Transport Properties of Cr-Doped BaTi2As2O. Inorg. Chem. 2014, 53, 13089–13092. [Google Scholar] [CrossRef] [PubMed]
- Ozawa, T.C.; Naka, T.; Matsushita, A.; Kauzlarich, S.M.; Sasaki, T. Chemical composition and magnetic property modifications of Na2Ti2Sb2O using PTFE as an alkali–metal ion extraction reagent. J. Fluor. Chem. 2014, 168, 189–192. [Google Scholar] [CrossRef]
- Fujita, K.; Hamidian, M.H.; Edkins, S.D.; Kim, C.K.; Kohsaka, Y.; Azuma, M.; Takano, M.; Takagi, H.; Eisaki, H.; Uchida, S.; et al. Direct phase-sensitive identification of a d-form factor density wave in underdoped cuprates. Proc. Natl. Acad. Sci. USA 2014, 111, E3026–E3032. [Google Scholar] [CrossRef] [PubMed]
- Yamakawa, Y.; Kontani, H. Spin-Fluctuation-Driven Nematic Charge-Density Wave in Cuprate Superconductors: Impact of Aslamazov-Larkin Vertex Corrections. Phys. Rev. Lett. 2015, 114, 257001. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.L.; Jiang, H.; Zhai, H.F.; Bao, J.K.; Jiao, W.H.; Tao, Q.; Shen, C.Y.; Zeng, Y.W.; Xu, Z.A.; Cao, G.H. Ba2Ti2Fe2As4O: A new superconductor containing Fe2As2 layers and Ti2O sheets. J. Am. Chem. Soc. 2012, 134, 12893–12896. [Google Scholar] [CrossRef] [PubMed]
- Valldor, M.; Merz, P.; Prots, Y.; Schnelle, W. Bad-Metal-Layered Sulfide Oxide CsV2S2O. Eur. J. Inorg. Chem. 2016, 2016, 23–27. [Google Scholar] [CrossRef]
- Valldor, M.; Merz, P.; Prots, Y.; Watier, Y.; Schnelle, W. Synthesis and Characterization of Cs1–xTi2Te2O (x ≈ 0.2): Electron Doping by Te Resulting in a Layered Metal. Inorg. Chem. 2016, 55, 11337–11341. [Google Scholar] [CrossRef] [PubMed]
- Mizoguchi, H.; Park, S.; Hiraka, H.; Ikeda, K.; Otomo, T.; Hosono, H. An Anti CuO2-type Metal Hydride Square Net Structure in Ln2M2As2Hx (Ln = La or Sm, M = Ti, V, Cr, or Mn). Angew. Chem. Int. Ed. 2015, 54, 2932–2935. [Google Scholar] [CrossRef] [PubMed]
- Takeiri, F.; Matsumoto, Y.; Yamamoto, T.; Hayashi, N.; Li, Z.; Tohyama, T.; Tassel, C.; Ritter, C.; Narumi, Y.; Hagiwara, M.; et al. High-pressure synthesis of the layered iron oxyselenide BaFe2Se2O with strong magnetic anisotropy. Phys. Rev. B 2016, 94, 184426. [Google Scholar] [CrossRef]
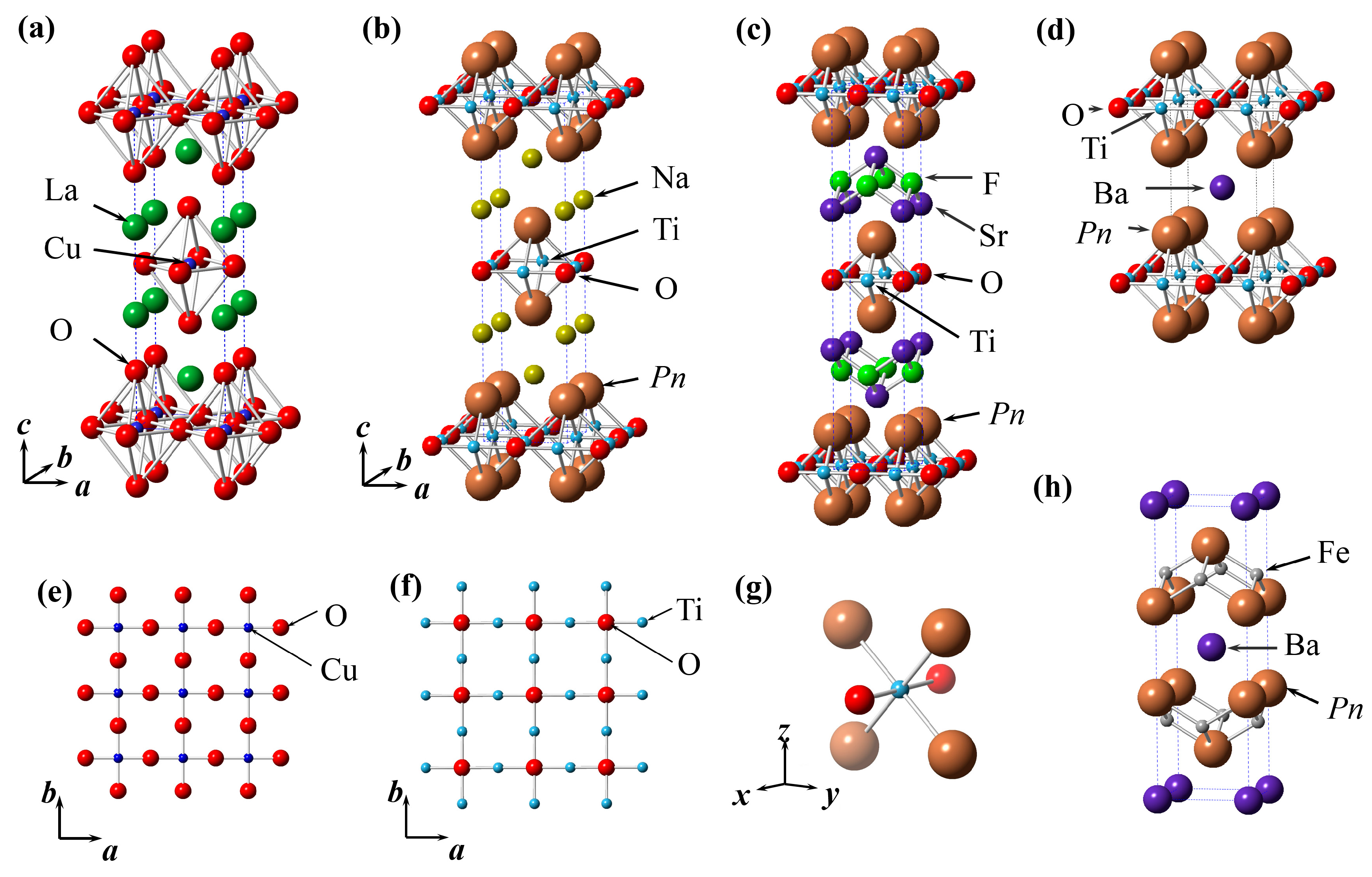
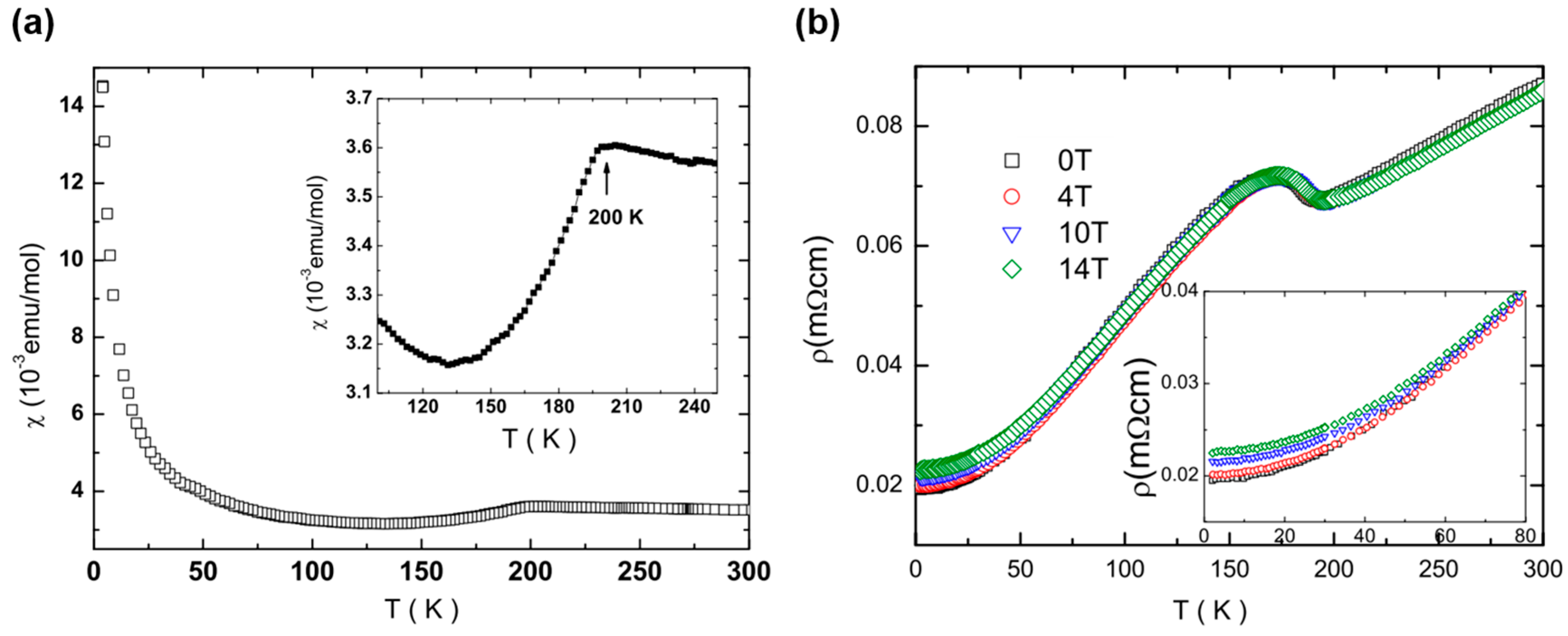
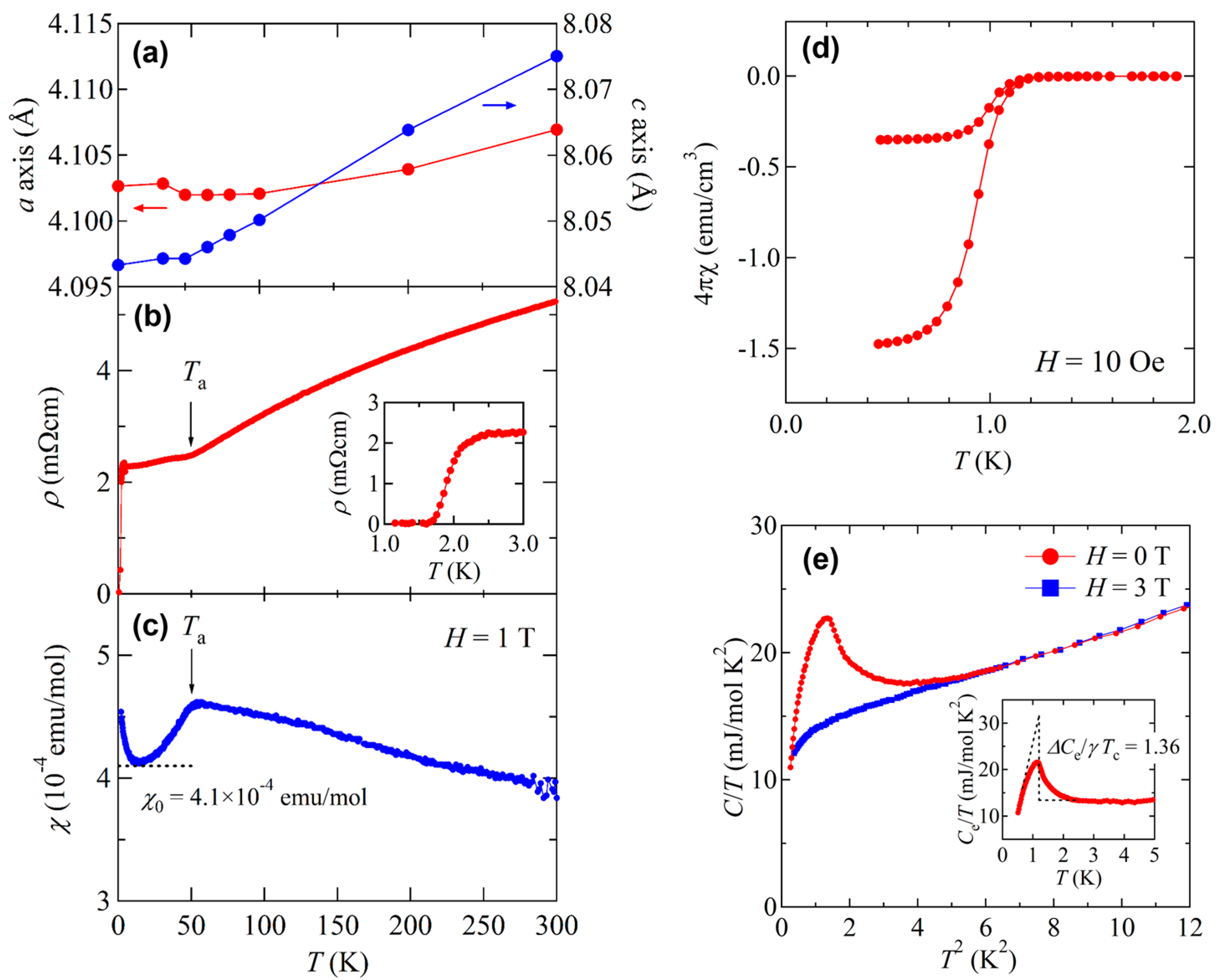
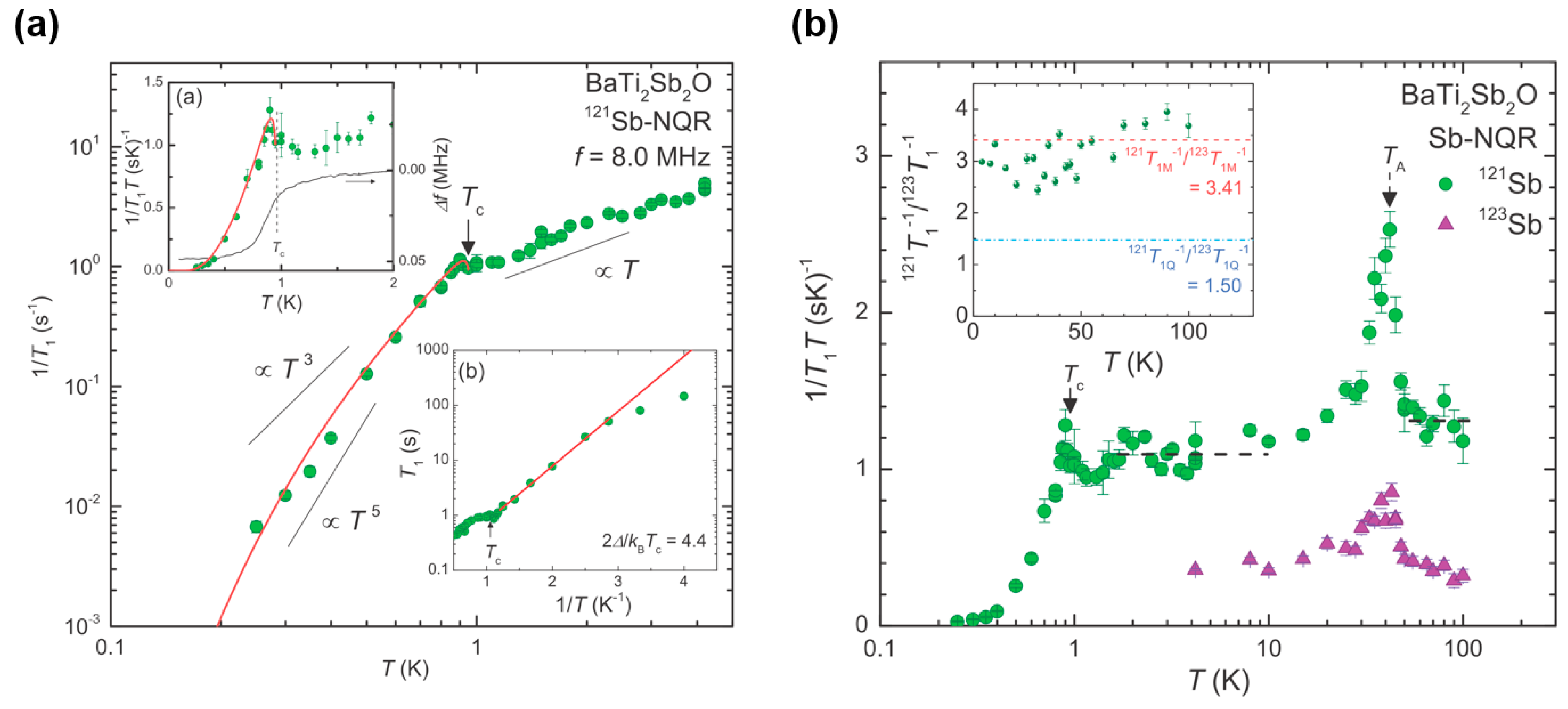
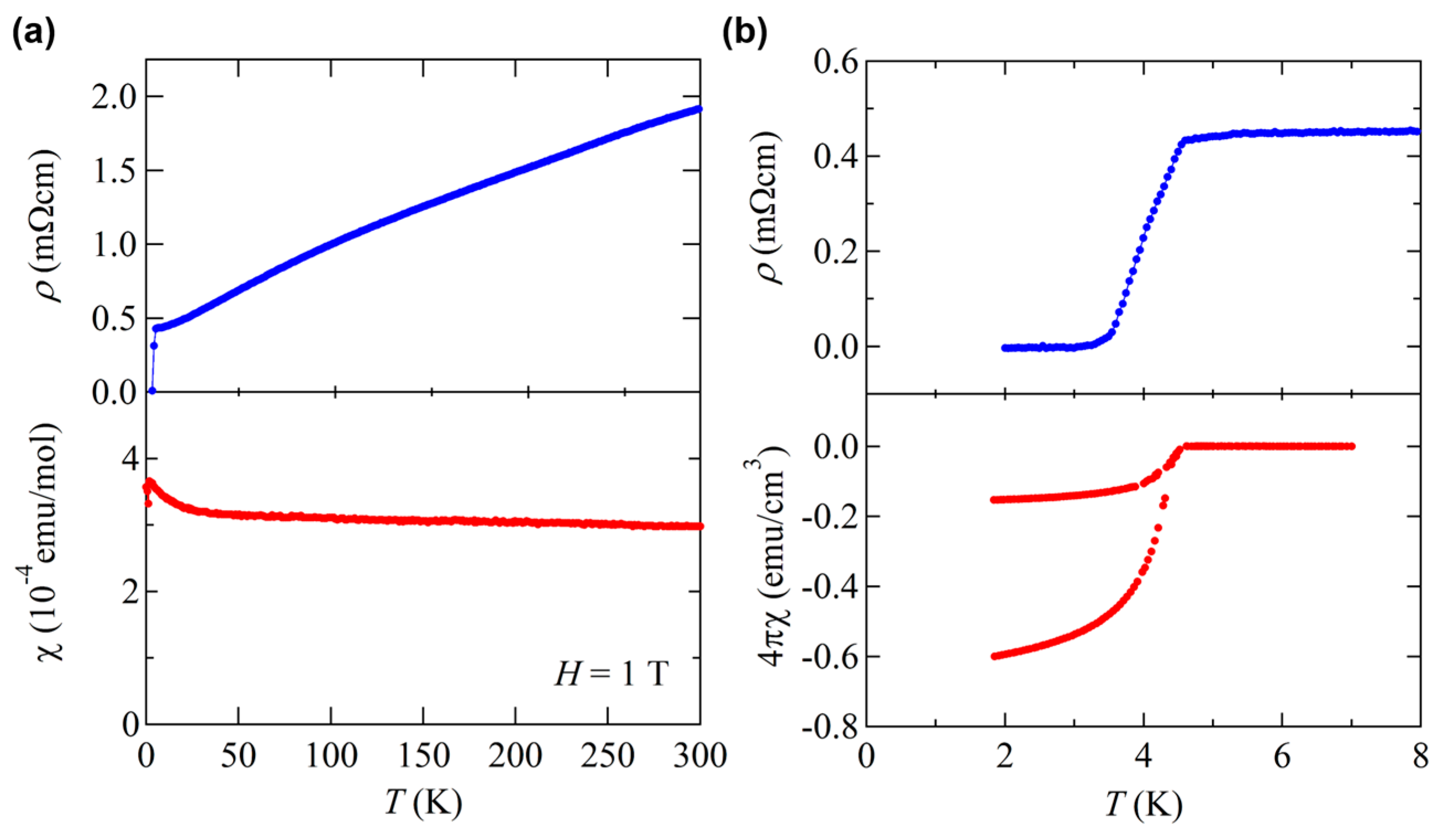

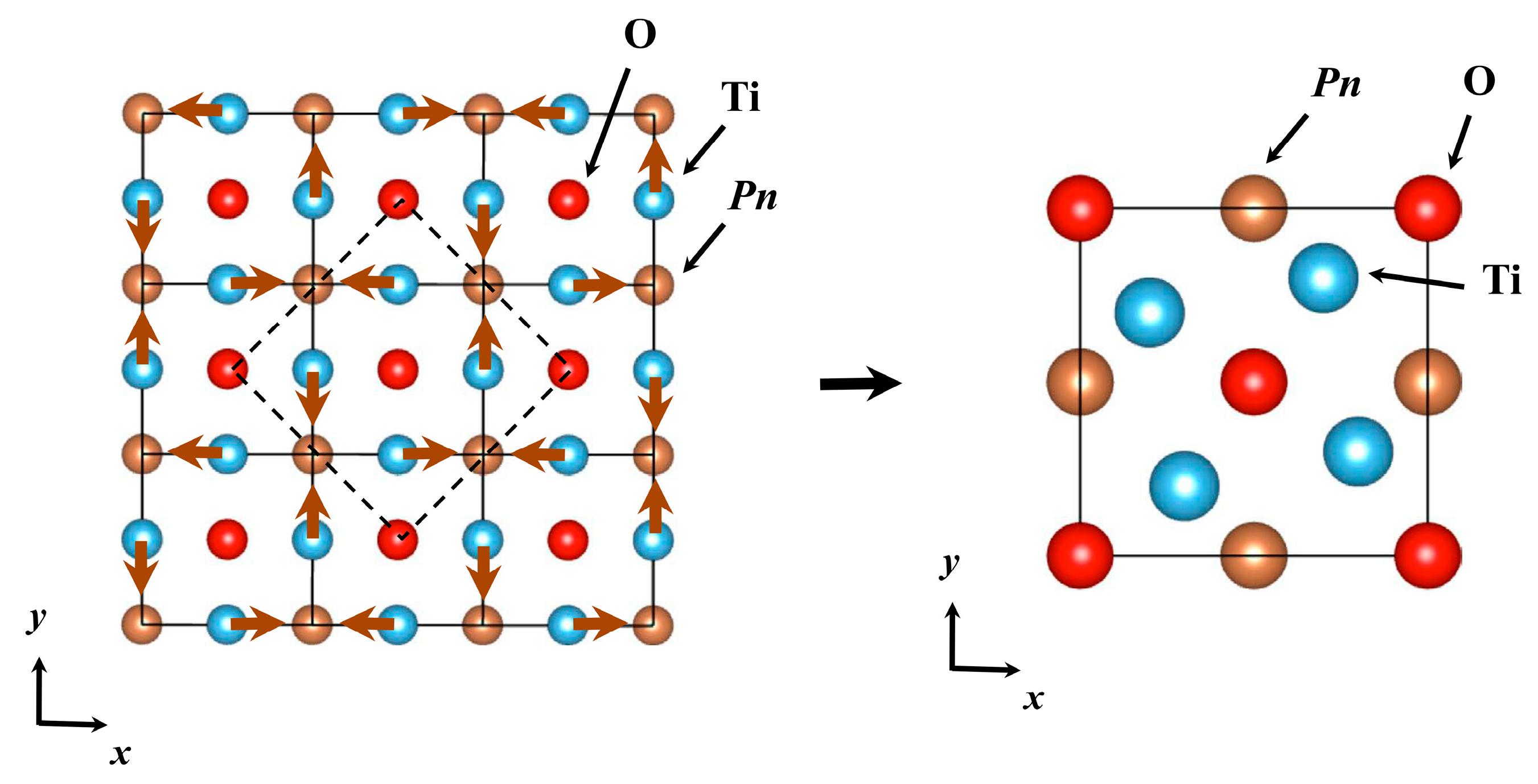
| Compound | Space Group | a (Å) | c (Å) | Interlayer Distance d (Å) | TDW (K) | Tc (K) | Ref. |
|---|---|---|---|---|---|---|---|
| Na2Ti2As2O | I4/mmm | 4.070(2) | 15.288(4) | 7.644 | 320 | N/A | [11] |
| Na2Ti2Sb2O | I4/mmm | 4.144(1) | 16.561(1) | 8.281 | 120 | N/A | [11] |
| (SrF)2Ti2As2O | I4/mmm | 4.04865(5) | 19.4204(2) | 9.7102 | 380 | N/A | [17] |
| (SrF)2Ti2Sb2O | I4/mmm | 4.1095(1) | 20.8858(5) | 10.4429 | 200 | N/A | [17] |
| (SrF)2Ti2Bi2O | I4/mmm | 4.11782(2) | 21.3703(2) | 10.68515 | N/A | N/A | [16] |
| BaTi2As2O | P4/nmm | 4.047(3) | 7.275(4) | 7.275 | 200 | N/A | [14] |
| BaTi2Sb2O | P4/nmm | 4.11039(2) | 8.08640(4) | 8.0864 | 50 | 1.2 | [15] |
| BaTi2Bi2O | P4/nmm | 4.12316(4) | 8.3447(1) | 8.3447 | N/A | 4.6 | [16] |
| Compound | Tc (K) | γ (mJ·mol−1·K−2) | θD (K) | ΔC/γTc | μ0Hc1(0) (Oe) | μ0Hc2(0) (T) | Ref. |
|---|---|---|---|---|---|---|---|
| BaTi2Sb2O | 1.2 | 13.5 | 239 | 1.36 | N/A | 1.32 | [15,39] |
| BaTi2Sb2O | 1.1 | 10.9 | 230 | 0.9 | N/A | 0.08 | [36] |
| (Ba0.85Na0.15)Ti2Sb2O | 4.2 | 13.0 | 210 | 1.43 | N/A | 1.7 | [36] |
| (Ba0.8Rb0.2)Ti2Sb2O | 5.4 | 14 | 193 | 1.60 | 38 | 2.3 | [54] |
| BaTi2(Sb0.9Sn0.1)2O | 2.3 | 17.1 | 257 | 1.39 | N/A | N/A | [55] |
© 2017 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yajima, T. Titanium Pnictide Oxide Superconductors. Condens. Matter 2017, 2, 4. https://doi.org/10.3390/condmat2010004
Yajima T. Titanium Pnictide Oxide Superconductors. Condensed Matter. 2017; 2(1):4. https://doi.org/10.3390/condmat2010004
Chicago/Turabian StyleYajima, Takeshi. 2017. "Titanium Pnictide Oxide Superconductors" Condensed Matter 2, no. 1: 4. https://doi.org/10.3390/condmat2010004
APA StyleYajima, T. (2017). Titanium Pnictide Oxide Superconductors. Condensed Matter, 2(1), 4. https://doi.org/10.3390/condmat2010004





