The Response of a Linear, Homogeneous and Isotropic Dielectric and Magnetic Sphere Subjected to an External Field, DC or Low-Frequency AC, of Any Form

Abstract

Maxwell’s equations epitomize our knowledge of standard electromagnetic theory in vacuums and matter. Here, we report the clearcut results of an extensive, ongoing investigation aiming to mathematically digest Maxwell’s equations in virtually all problems based on the three standard building units, dielectric and magnetic, found in practice (i.e., spheres, cylinders and plates). 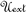Specifically, we address the static/quasi-static case of a linear, homogeneous and isotropic dielectric and magnetic sphere subjected to a DC/low-frequency AC external scalar potential, (vector field, 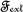), of any form, produced by a primary/free source residing outside the sphere. To this end, we introduce an expansion-based mathematical strategy that enables us to obtain immediate access to the response of the dielectric and magnetic sphere, i.e., to the internal scalar potential, (vector field, ), produced by the induced secondary/bound source. 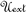Accordingly, the total scalar potential, = + (vector field, 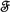= 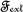+ ), is immediately accessible as well. Our approach provides ready-to-use expressions for and ( and 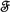) in all space, i.e., both inside and outside the dielectric and magnetic sphere, applicable for any form of 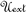(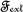). Using these universal expressions, we can obtain and ( and 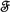) in essentially one step, without the need to solve each particular problem of different 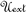(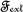) every time from scratch. 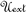The obtained universal relation between and ( and 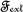) provides a means to tailor the responses of dielectric and magnetic spheres at all instances, thus facilitating applications. Our approach surpasses conventional mathematical procedures that are employed to solve analytically addressable problems of electromagnetism.

1. Introduction

Spherical structures of dielectric and magnetic materials, e.g., compact spheres and hollow spherical shells of non-zero or practically zero thickness, have been employed widely in applications during the last few decades. Regarding dielectric spherical structures, they are utilized in applications that relate to scattering [1,2], the modeling of biological cells [3,4], the manipulation of biological cells and colloidal particles [5,6,7], polymer science [8] and drug delivery [9,10]. Referring to magnetic spherical structures, they are used in invisibility cloaks [11,12], catalysis [13,14], the environment [15,16], biomedicine [17,18], the sorting and manipulation of biological cells [19,20,21,22,23,24], diagnosis [25,26,27] and therapy [28,29,30,31,32].

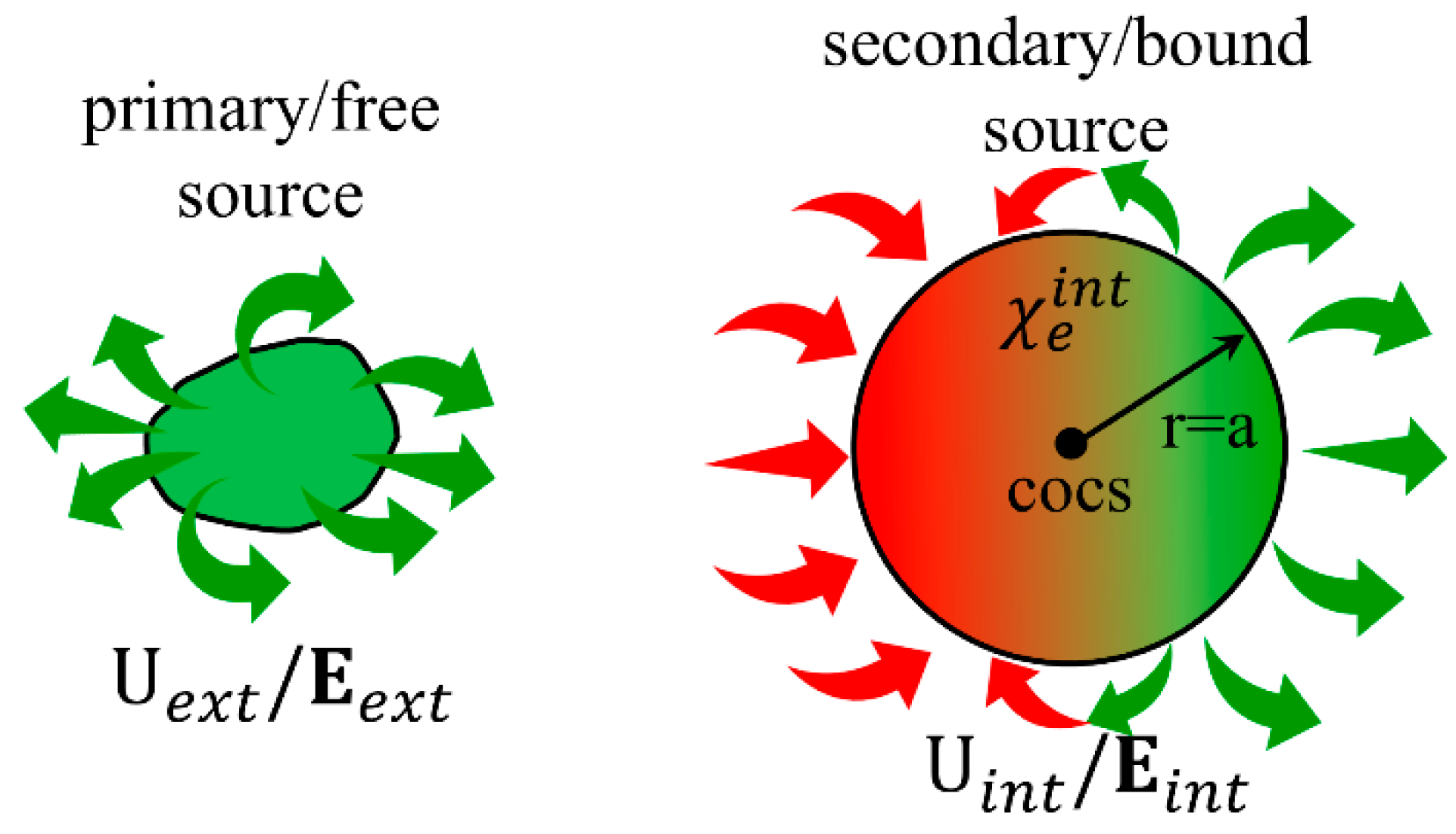
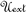In practically all these cases, the dielectric and magnetic sphere is subjected to an external scalar potential, (r) (electric, U_ext(r), and magnetic, U_m,ext(r), respectively), else to an external vector field, 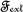(r) (electric, E_ext(r), and magnetic, H_ext(r), respectively), originating from a primary/free source placed outside the sphere. The response of the dielectric and magnetic sphere is represented by the internal scalar potential, (r) (electric, U_int(r), and magnetic, U_m,int(r), respectively), else the internal vector field, (r) (electric, E_int(r), and magnetic, H_int(r), respectively), originating from a secondary/bound source residing at the sphere [33,34,35,36]. 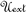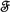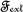The total scalar potential, (r) = (r) + (r) (electric, U(r) = U_ext(r) + U_int(r), and magnetic, U_m(r) = U_m,ext(r) + U_m,int(r), respectively), else the total vector field, (r) = (r) + (r) (electric, E(r) = E_ext(r) + E_int(r), and magnetic, H(r) = H_ext(r) + H_int(r), respectively), is simply provided by the superposition principle [33,34,35,36]. 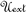For any applied external (r)/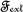(r), the internal (r)/(r) and total (r)/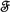(r) are the physical entities of interest needed throughout the whole space, i.e., both inside and outside the sphere, to describe all subsequent physical processes. Here, we focus on this case for a linear, homogeneous and isotropic dielectric and magnetic sphere of known intrinsic susceptibility, x^int ($0\le {\mathrm{\chi }}_{\mathrm{e}}^{\mathrm{i}\mathrm{n}\mathrm{t}}$ for a dielectric material and $-1\le {\mathrm{\chi }}_{\mathrm{m}}^{\mathrm{i}\mathrm{n}\mathrm{t}}$ for a magnetic material), subjected to an external scalar potential/vector field, 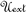(r)/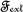(r) (DC or AC of low frequency; static and quasi-static case, respectively). We stress that, here, we handle the most general case where the external entities, 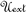(r)/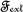(r), are of any form and are produced by a primary/free source that resides outside the sphere. Our aim is to find the internal, (r)/(r), and total, (r)/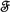(r), throughout the whole space of interest, i.e., both inside and outside the sphere. To this end, we employ a mathematical strategy that relies on the expansion of all—external, internal and total—potentials/fields on the basis of spherical harmonics (SH). Our approach condenses all lengthy calculations, enabling us to obtain standalone expressions for all (r), (r), (r) and 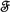(r), both inside and outside the dielectric and magnetic sphere. Importantly, these universal expressions are applicable for any form of 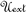(r)/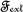(r), so that we can obtain all (r), (r), (r) and 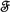(r) immediately, without the need to apply lengthy calculations for each particular problem when a different 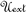(r)/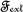(r) is applied. Our mathematical strategy is characterized by profound convenience and documented reliability.

2. Dielectric Sphere—Linear, Homogeneous and Isotropic—Subjected to an External Electric Scalar Potential/Vector Field of Any Form

In most applications, a dielectric spherical structure is subjected to an external electric scalar potential/vector field, ${\mathrm{U}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$/${\mathbf{E}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$, applied by a user. Here, we investigate a compact dielectric sphere of radius a, consisting of a linear, homogeneous and isotropic material of intrinsic susceptibility, ${\mathrm{\chi }}_{\mathrm{e}}^{\mathrm{i}\mathrm{n}\mathrm{t}}$ (all results obtained below can be easily translated to the case of a magnetic sphere). The external ${\mathrm{U}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$/${\mathbf{E}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$ are produced by a primary/free source placed outside the sphere. The secondary/bound source that resides at the sphere, due to nonhomogeneous/discontinuous polarization, $\mathbf{P}\left(\mathbf{r}\right)$, will produce the internal ${\mathrm{U}}_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(\mathbf{r}\right)$/${\mathbf{E}}_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(\mathbf{r}\right)$. The case under discussion is schematically presented in Figure 1.

In the problem discussed here, we seek the response of the dielectric sphere, i.e., the internal electric scalar potential/vector field, ${\mathrm{U}}_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(\mathbf{r}\right)$/${\mathbf{E}}_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(\mathbf{r}\right)$, under the application of the external ones, ${\mathrm{U}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$/${\mathbf{E}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$. To this end, we may focus on the scalar potential provided by the Poisson/Laplace differential equation in spaces where sources (whether primary/free or secondary/bound) do/do not exist [33,34,35,36]. Then, from the scalar potential, the electric field can easily be derived. In our case, the area of interest is the inside space of the primary/free source (so that infinity is excluded, while the origin of the coordinate system is included). In addition, due to the linear, homogeneous and isotropic nature of the dielectric sphere, secondary/bound sources exist only at its surface, while any volume density sources that, in general, could possibly exist, in this case, are zero (see below). Under these conditions, our problem is based on the differential equation of Laplace for the scalar potential. The general solution is well known in spherical coordinates, $U\left(\mathit{r}\right)={\sum }_{l=0}^{\infty }{\sum }_{m=-l}^l\left(A_l^m{r}^l+B_l^m{r}^{-\left(l+1\right)}\right)Y_l^m(\theta ,\phi )$ [33,34,35,36]. Here, the boundary condition on the zeroing of the potential at the origin of the coordinate system dictates the rejection of the terms, $r^{-\left(l+1\right)}$, so that $B_l^m=0$ should hold for all $(l,m)$. Notably, the above holds for all external, internal and total potentials, ${\mathrm{U}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$, ${\mathrm{U}}_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(\mathbf{r}\right)$ and $\mathrm{U}\left(\mathbf{r}\right)$, respectively. In addition, the potential should be continuous at the surface of the dielectric sphere [33,34,35,36]. Finally, we recall that the total potential and field are given by the external and internal ones through the superposition principle. Accordingly, the total $\mathrm{U}\left(\mathbf{r}\right)$/$\mathbf{E}\left(\mathbf{r}\right)$ are provided by the relations

$$U\left(\mathit{r}\right)=U_{ext}\left(\mathit{r}\right)+U_{int}\left(\mathit{r}\right)$$

(1)

and

$$\mathit{E}\left(\mathit{r}\right)={\mathit{E}}_{ext}\left(\mathit{r}\right)+{\mathit{E}}_{int}\left(\mathit{r}\right)$$

(2)

Importantly, here, we investigate the generic case where the external ${\mathrm{U}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$/${\mathbf{E}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$ can be of any form. Under the conditions discussed above, ${\mathrm{U}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$ can be expanded in the following form [37]:

$$U_{ext}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }\sum _{m=-l}^l{U}_{l,ext}^m\left(\mathit{r}\right)=\sum _{l=0}^{\infty }\sum _{m=-l}^l{A}_l^m{r}^l{Y}_l^m(\theta ,\phi )=\sum _{l=0}^{\infty }{r}^l\sum _{m=-l}^l{A}_l^m{Y}_l^m(\theta ,\phi )$$

(3)

where the general term of the expansion is defined as

$$U_{l,ext}^m\left(\mathit{r}\right)=A_l^m{r}^l{Y}_l^m(\theta ,\phi )$$

(4)

Similarly, ${\mathbf{E}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$, due to the constitutive relation ${\mathbf{E}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)=-\nabla {\mathrm{U}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$, should follow the respective expansion

$${\mathit{E}}_{ext}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }\sum _{m=-l}^l{\mathit{E}}_{l,ext}^m\left(\mathit{r}\right)=-\sum _{l=0}^{\infty }\sum _{m=-l}^l{A}_l^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$$

(5)

where the general term of the expansion is defined as

$${\mathit{E}}_{l,ext}^m\left(\mathit{r}\right)=-A_l^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$$

(6)

It should be noted that the above expressions for the external ${\mathrm{U}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$/${\mathbf{E}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$ hold for both the inside and outside spaces of the sphere (while we are still at the inside space of the primary/free source). In these expressions, the SH, $Y_l^m\left(\theta ,\phi \right)$, are given by

$$Y_l^m\left(\theta ,\phi \right)=\sqrt{{\displaystyle \frac{2l+1}{4\pi }}{\displaystyle \frac{\left(l-m\right)!}{\left(l+m\right)!}}}{P}_l^m\left(cos\theta \right)e^{im\phi }$$

(7)

so that the expansion coefficients $A_l^m$ are obtained through the relation

$$A_l^m={\displaystyle \frac{1}{r^l}}\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{\pi }{\int }}{U}_{ext}\left(\mathit{r}\right)Y_l^{m\ast }\left(\theta ,\phi \right)sin\theta d\theta d\phi$$

(8)

where $Y_l^{m\ast }\left(\theta ,\phi \right)$ is the complex conjugate of $Y_l^m\left(\theta ,\phi \right)$ [33,34,38]. The mode $\left(l,m\right)=\left(\mathrm{0,0}\right)$ is not considered since it refers to a null output (constant potential/zero field). Given that ${\mathrm{U}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$ obeys the separation of variables, ${\mathrm{U}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)~{\mathrm{U}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathrm{r}\right){\mathrm{U}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathrm{\theta }\right){\mathrm{U}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathrm{\phi }\right)$, its radial component, ${\mathrm{U}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathrm{r}\right)$, can be brought out of the integral so that the term $1/r^l$ is cancelled, ultimately providing constant expansion coefficients, $A_l^m$.

Now, we turn our interest to the internal ${\mathrm{U}}_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(\mathbf{r}\right)$/${\mathbf{E}}_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(\mathbf{r}\right)$ produced by the secondary/bound source, which, in general, can reside equally well at the volume, ${\mathrm{\rho }}_{\mathrm{b}}\left(\mathbf{r}\right)=-\nabla ·\mathbf{P}\left(\mathbf{r}\right)$, and the surface, ${\mathrm{\sigma }}_{\mathrm{b}}\left(\mathbf{r}\right)=\left(\mathbf{P}\right(\mathbf{r})·\widehat{\mathbf{n}}){|}_{\mathrm{S}}$, of the sphere, due to nonhomogeneous and discontinuous polarization, $\mathbf{P}\left(\mathbf{r}\right)={\mathrm{\epsilon }}_0{\mathrm{\chi }}_{\mathrm{e}}^{\mathrm{i}\mathrm{n}\mathrm{t}}\mathbf{E}\left(\mathbf{r}\right)$, respectively. Accordingly, the internal scalar potential, ${\mathrm{U}}_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(\mathbf{r}\right)$, can be easily obtained through the secondary/bound sources by means of the generalized law of Coulomb [34,35]. In our case, $\nabla ·\mathbf{P}\left(\mathbf{r}\right)=0$, so that ${\mathrm{U}}_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(\mathbf{r}\right)$ is given by the relation

$$U_{int}\left(\mathit{r}\right)={\displaystyle \frac{1}{4\pi {\epsilon }_0}}\underset{S^{\prime }}{\int }{\displaystyle \frac{{\sigma }_b\left({\mathit{r}}^{\prime }\right)}{|\mathit{r}-{\mathit{r}}^{\prime }|}}d{S}^{\prime }={\displaystyle \frac{1}{4\pi {\epsilon }_0}}\underset{S^{\prime }}{\int }{\displaystyle \frac{\left(\mathit{P}\right({\mathit{r}}^{\prime })·{\widehat{\mathit{n}}}^{\prime }){|}_{S^{\prime }}}{|\mathit{r}-{\mathit{r}}^{\prime }|}}d{S}^{\prime }$$

(9)

The surface integral can be modified based on the multipole expansion on the basis of SH. Since we are interested in finding the total electric field everywhere in space, we employ the proper expansion of ${|\mathbf{r}-{\mathbf{r}}^{\prime }|}^{-1}$ for the inside space ($\mathrm{r}<{\mathrm{r}}^{\prime }$) and outside space (${\mathrm{r}}^{\prime }<\mathrm{r}$) given by [33,34,35,38]

$${\displaystyle \frac{1}{|\mathit{r}-{\mathit{r}}^{\prime }|}}=4\pi \sum _{l=0}^{\infty }\sum _{m=-l}^l{\displaystyle \frac{1}{2l+1}}{\displaystyle \frac{r^l}{{r^{\prime }}^{l+1}}}{Y}_l^m(\theta ,\phi )Y_l^{m\ast }\left({\theta }^{\prime },{\phi }^{\prime }\right), r<r^{\prime }$$

(10)

and

$${\displaystyle \frac{1}{|\mathit{r}-{\mathit{r}}^{\prime }|}}=4\pi \sum _{l=0}^{\infty }\sum _{m=-l}^l{\displaystyle \frac{1}{2l+1}}{\displaystyle \frac{{r^{\prime }}^l}{r^{l+1}}}{Y}_l^m(\theta ,\phi )Y_l^{m\ast }\left({\theta }^{\prime },{\phi }^{\prime }\right), r^{\prime }<r$$

(11)

where $\mathbf{r}$ and ${\mathbf{r}}^{\prime }$ run over the volume of observation and secondary/bound source, ${\mathrm{\sigma }}_{\mathrm{b}}\left({\mathbf{r}}^{\prime }\right)$, respectively. By using the above relations (10) and (11) in relation (9), we get, for the internal scalar potential,

$$U_{int}^{in}\left(\mathit{r}\right)={\displaystyle \frac{1}{{\epsilon }_0}}\sum _{l=0}^{\infty }\sum _{m=-l}^l{\displaystyle \frac{1}{2l+1}}{r}^l{Y}_l^m(\theta ,\phi )\underset{S^{\prime }}{\int }(\mathit{P}({\mathit{r}}^{\prime })·{\widehat{\mathit{n}}}^{\prime }){|}_{S^{\prime }}{\displaystyle \frac{Y_l^{m\ast }\left({\theta }^{\prime },{\phi }^{\prime }\right)}{{r^{\prime }}^{l+1}}}d{S}^{\prime }$$

(12)

at the inside space of the sphere and

$$U_{int}^{out}\left(\mathit{r}\right)={\displaystyle \frac{1}{{\epsilon }_0}}\sum _{l=0}^{\infty }\sum _{m=-l}^l{\displaystyle \frac{1}{2l+1}}{\displaystyle \frac{Y_l^m(\theta ,\phi )}{r^{l+1}}}\underset{S^{\prime }}{\int }\left(\mathit{P}\right({\mathit{r}}^{\prime })·{\widehat{\mathit{n}}}^{\prime }){|}_{S^{\prime }}{r^{\prime }}^l{Y}_l^{m\ast }\left({\theta }^{\prime },{\phi }^{\prime }\right)d{S}^{\prime }$$

(13)

at the outside space of the sphere.

We define the respective surface integrals through the following relations:

$$I_{l,sur}^{m,in}=\underset{S^{\prime }}{\int }(\mathit{P}({\mathit{r}}^{\prime })·{\widehat{\mathit{n}}}^{\prime }){|}_{S^{\prime }}{\displaystyle \frac{Y_l^{m\ast }\left({\theta }^{\prime },{\phi }^{\prime }\right)}{{r^{\prime }}^{l+1}}}d{S}^{\prime }, r^{\prime }=\mathrm{a}$$

(14)

and

$$I_{l,sur}^{m,out}=\underset{S^{\prime }}{\int }\left(\mathit{P}\right({\mathit{r}}^{\prime })·{\widehat{\mathit{n}}}^{\prime }){|}_{S^{\prime }}{r^{\prime }}^l{Y}_l^{m\ast }\left({\theta }^{\prime },{\phi }^{\prime }\right)d{S}^{\prime }, r^{\prime }=\mathrm{a}$$

(15)

Accordingly, the above relations (12) and (13) become

$$U_{int}^{in}\left(\mathit{r}\right)={\displaystyle \frac{1}{{\epsilon }_0}}\sum _{l=0}^{\infty }\sum _{m=-l}^l{\displaystyle \frac{1}{2l+1}}{I}_{l,sur}^{m,in}{r}^l{Y}_l^m(\theta ,\phi )$$

(16)

and

$$U_{int}^{out}\left(\mathit{r}\right)={\displaystyle \frac{1}{{\epsilon }_0}}\sum _{l=0}^{\infty }\sum _{m=-l}^l{\displaystyle \frac{1}{2l+1}}{I}_{l,sur}^{m,out}{\displaystyle \frac{Y_l^m(\theta ,\phi )}{r^{l+1}}}$$

(17)

Realizing that the two surface integrals, $I_{l,sur}^{m,in}$ and $I_{l,sur}^{m,out}$, are scalar constants, the internal component of the electric field has the form

$${\mathit{E}}_{int}^{in}\left(\mathit{r}\right)=-{\displaystyle \frac{1}{{\epsilon }_0}}\sum _{l=0}^{\infty }\sum _{m=-l}^l{\displaystyle \frac{1}{2l+1}}{I}_{l,sur}^{m,in}\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$$

(18)

for the inside space of the sphere and

$${\mathit{E}}_{int}^{out}\left(\mathit{r}\right)=-{\displaystyle \frac{1}{{\epsilon }_0}}\sum _{l=0}^{\infty }\sum _{m=-l}^l{\displaystyle \frac{1}{2l+1}}{I}_{l,sur}^{m,out}\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$$

(19)

for the outside space of the sphere.

Thus far, we have established expressions for the external and internal potentials and fields for both inside and outside the sphere. We still require the expressions for the two surface integrals, $I_{l,sur}^{m,in}$ and $I_{l,sur}^{m,out}$. Below, we provide all necessary details in this respect.

2.1. Inside Space of the Dielectric Sphere

Here, we give all necessary details for the case of the inside space of the sphere. The results for the outside space of the sphere are provided in brief at the end of this detailed derivation. We argue that, inside the sphere, the total field is given by the relation

$${\mathit{E}}^{in}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }\sum _{m=-l}^l{\mathit{E}}_l^{m,in}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }\sum _{m=-l}^l{C}_l^m{\mathit{E}}_{l,ext}^{m,in}\left(\mathit{r}\right)$$

(20)

This means that the general term of the expansion of the total field of the inside space is analogous to that of the external field. Using relation (6), the general term ${\mathit{E}}_l^{m,in}\left(\mathit{r}\right)$ obtains the form

$${\mathit{E}}_l^{m,in}\left(\mathit{r}\right)=-C_l^m{A}_l^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$$

(21)

so that the total field becomes

$${\mathit{E}}^{in}\left(\mathit{r}\right)=-\sum _{l=0}^{\infty }\sum _{m=-l}^l{C}_l^m{A}_l^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$$

(22)

Recalling the constitutive relation ${\mathbf{E}}^{\mathrm{i}\mathrm{n}}\left(\mathbf{r}\right)=-\nabla {\mathrm{U}}^{\mathrm{i}\mathrm{n}}\left(\mathit{r}\right)$, we see that the respective expression of the total potential inside the sphere is given by the relation

$$U^{in}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }\sum _{m=-l}^l{C}_l^m{A}_l^m\left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$$

(23)

Now, we are ready to recruit relations (1) and (2). Starting from relation (2), and by using relations (5), (18) and (22), we easily get

$$\sum _{l=0}^{\infty }\sum _{m=-l}^l{C}_l^m{A}_l^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)=\sum _{l=0}^{\infty }\sum _{m=-l}^l{A}_l^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)+{\displaystyle \frac{1}{{\epsilon }_0}}\sum _{l=0}^{\infty }\sum _{m=-l}^l{\displaystyle \frac{1}{2l+1}}{I}_{l,sur}^{m,in}\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$$

(24)

else

$$\sum _{l=0}^{\infty }\sum _{m=-l}^l{C}_l^m{A}_l^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)=\sum _{l=0}^{\infty }\sum _{m=-l}^l\left(A_l^m+{\displaystyle \frac{1}{{\epsilon }_0}}{\displaystyle \frac{1}{2l+1}}{I}_{l,sur}^{m,in}\right)\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$$

(25)

Accordingly, due to the fact that the vectors $\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$ are linearly independent, the following relation should hold for the respective coefficients:

$$C_l^m{A}_l^m=A_l^m+{\displaystyle \frac{1}{{\epsilon }_0}}{\displaystyle \frac{1}{2l+1}}{I}_{l,sur}^{m,in}$$

(26)

We still require the integral coefficients $I_{l,sur}^{m,in}$. These can be calculated from relation (14) by introducing the polarization $\mathit{P}\left({\mathit{r}}^{\prime }\right)={\epsilon }_0{\mathrm{\chi }}_{\mathrm{e}}^{\mathrm{i}\mathrm{n}\mathrm{t}}{\mathit{E}}^{in}\left({\mathit{r}}^{\prime }\right)$, using relation (22), recalling that ${\widehat{\mathit{n}}}^{\prime }={\widehat{\mathit{r}}}^{\prime }$ and $S^{\prime }: r^{\prime }=\mathrm{a}$ and that $\left({\nabla }^{\prime }\left({r^{\prime }}^{l^{\prime }}{Y}_{l^{\prime }}^{m^{\prime }}\left({\theta }^{\prime },{\phi }^{\prime }\right)\right)\right)·{\widehat{\mathit{r}}}^{\prime }{|}_{S^{\prime }}={\displaystyle \frac{d{r^{\prime }}^{l^{\prime }}}{d{r}^{\prime }}}{|}_{r^{\prime }=\mathrm{a}}{Y}_{l^{\prime }}^{m^{\prime }}\left({\theta }^{\prime },{\phi }^{\prime }\right)=l^{\prime }{\mathrm{a}}^{l^{\prime }-1}{Y}_{l^{\prime }}^{m^{\prime }}\left({\theta }^{\prime },{\phi }^{\prime }\right)$. By means of simple algebra, we obtain the following relation:

$$I_{l,sur}^{m,in}=-{\epsilon }_0{\chi }_e^{int}{\displaystyle \frac{1}{a^{l+1}}}\sum _{l^{\prime }=0}^{\infty }\sum _{m^{\prime }=-l^{\prime }}^{l^{\prime }}{C}_{l^{\prime }}^{m^{\prime }}{A}_{l^{\prime }}^{m^{\prime }}{l}^{\prime }{a}^{l^{\prime }+1}\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{ \pi }{\int }}{Y}_{l^{\prime }}^{m^{\prime }}\left({\theta }^{\prime },{\phi }^{\prime }\right)Y_l^{m\ast }\left({\theta }^{\prime },{\phi }^{\prime }\right)sin{\theta }^{\prime }d{\theta }^{\prime }d{\phi }^{\prime }$$

(27)

We recall the orthogonality relation of the SH [33,34,38]

$$\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{ \pi }{\int }}{Y}_{l^{\prime }}^{m^{\prime }}\left({\theta }^{\prime },{\phi }^{\prime }\right)Y_l^{m\ast }\left({\theta }^{\prime },{\phi }^{\prime }\right)\mathrm{s}\mathrm{i}\mathrm{n}{\theta }^{\prime }d{\theta }^{\prime }d{\phi }^{\prime }={\delta }_{l{l}^{\prime }}{\delta }_{{mm}^{\prime }}$$

(28)

so that the above relation becomes

$$I_{l,sur}^{m,in}=-{\epsilon }_0{\chi }_e^{int}{\displaystyle \frac{1}{a^{l+1}}}\sum _{l^{\prime }=0}^{\infty }\sum _{m^{\prime }=-l^{\prime }}^{l^{\prime }}{C}_{l^{\prime }}^{m^{\prime }}{A}_{l^{\prime }}^{m^{\prime }}{l}^{\prime }{a}^{l^{\prime }+1}{\delta }_{l{l}^{\prime }}{\delta }_{{mm}^{\prime }}$$

(29)

else

$$I_{l,sur}^{m,in}=-{\epsilon }_0{\chi }_e^{int}{C}_l^m{A}_l^{m}l$$

(30)

Substituting the above relation of $I_{l,sur}^{m,in}$ into relation (26), we finally obtain

$$C_l={\displaystyle \frac{1}{1+\frac{l}{2l+1}{\chi }_e^{int}}}$$

(31)

where we have rejected the upper index since the expansion coefficients do not depend on the order $m$ of the mode $(l,m)$. By defining the depolarization factor

$$N_l={\displaystyle \frac{l}{2l+1}}$$

(32)

we finally obtain

$$C_l={\displaystyle \frac{1}{1+N_l{\chi }_e^{int}}}$$

(33)

These definitions agree with the ones introduced in [37]. Relation (32), which defines the depolarization factor, $N_l$, of each specific mode, $(l,m)$, is important since it relates the internal/response potential/field produced by the secondary bound sources to the external/user-applied potential/field (see below, relations (43) and (48)). Notably, $N_l$ is degenerate on the order $m$, since it depends only on the degree, $l$, of the external/user-applied mode $(l,m)$. Moreover, see Section 4.1 below.

Once the expansion coefficients, $C_l$, have been determined, and given that the expansion coefficients, $A_l^m$, are defined by relation (8), the total field inside the sphere, i.e., relation (22), is given through

$${\mathit{E}}^{in}\left(\mathit{r}\right)=-\sum _{l=0}^{\infty }{C}_l\sum _{m=-l}^l{A}_l^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$$

(34)

Moreover, using relation (18), we can easily show that the internal field inside the sphere is given through

$${\mathit{E}}_{int}^{in}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }\sum _{m=-l}^l{\mathit{E}}_{l,int}^{m,in}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }{N}_l{\chi }_{e,l}^{ext}\sum _{m=-l}^l{A}_l^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$$

(35)

where we define the general term of the expansion and the extrinsic electric susceptibility through

$${\mathit{E}}_{l,int}^{m,in}\left(\mathit{r}\right)=N_l{\chi }_{e,l}^{ext}{A}_l^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$$

(36)

and

$${\chi }_{e,l}^{ext}={\displaystyle \frac{{\chi }_e^{int}}{1+N_l{\chi }_e^{int}}}$$

(37)

This relation that defines the extrinsic susceptibility, ${\chi }_{e,l}^{ext}$, of each specific mode, $(l,m)$, with respect to the depolarization factor, $N_l$, and the intrinsic susceptibility, ${\chi }_e^{int}$, is important since it relates the exogenous properties of each specimen studied during an experiment with the endogenous properties of the parent material. Notably, ${\chi }_{e,l}^{ext}$ is degenerate on the order, $m$, since it depends only on the degree, $l$, of the external/user-applied mode $(l,m)$. Moreover, see Section 4.1 below.

By means of the above definitions of $C_l$ (relation (33)) and ${\mathrm{\chi }}_{\mathrm{e},l}^{\mathrm{e}x\mathrm{t}}$ (relation (37)), the total electric field inside the sphere can be rewritten as

$${\mathit{E}}^{in}\left(\mathit{r}\right)=-{\displaystyle \frac{1}{{\chi }_e^{int}}}\sum _{l=0}^{\infty }{\chi }_{e,l}^{ext}\sum _{m=-l}^l{A}_l^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$$

(38)

Once we know ${\mathbf{E}}^{\mathrm{i}\mathrm{n}}\left(\mathbf{r}\right)$, the polarization $\mathbf{P}\left(\mathbf{r}\right)={\mathrm{\epsilon }}_0{\mathrm{\chi }}_{\mathrm{e}}^{\mathrm{i}\mathrm{n}\mathrm{t}}{\mathbf{E}}^{\mathrm{i}\mathrm{n}}\left(\mathbf{r}\right)$ can be obtained immediately, resulting in

$$\mathit{P}\left(\mathit{r}\right)=-{\epsilon }_0\sum _{l=0}^{\infty }{\chi }_{e,l}^{ext}\sum _{m=-l}^l{A}_l^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$$

(39)

a relation that is in good agreement with the result obtained in [37].

From relations (6) and (36), we can directly obtain the relationship between the general terms of the internal and external fields. It follows that

$${\mathit{E}}_{l,int}^{m,in}\left(\mathit{r}\right)=-N_l{\chi }_{e,l}^{ext}{\mathit{E}}_{l,ext}^{m,in}\left(\mathit{r}\right)$$

(40)

This relation is useful in applications since it provides immediately the response of the dielectric sphere to the triggering cause. Moreover, by means of relation (37), we easily see that the prefactor can be written as follows:

$$N_l{\chi }_{e,l}^{ext}={\displaystyle \frac{N_l{\chi }_e^{int}}{1+N_l{\chi }_e^{int}}}$$

(41)

By defining the effective intrinsic electric susceptibility through

$${\chi }_{e,l}^{N_l}=N_l{\chi }_e^{int}$$

(42)

the above relation (40) can be rewritten as follows:

$${\mathit{E}}_{l,int}^{m,in}\left(\mathit{r}\right)=-{\displaystyle \frac{{\chi }_{e,l}^{N_l}}{1+{\chi }_{e,l}^{N_l}}}{\mathit{E}}_{l,ext}^{m,in}\left(\mathit{r}\right)$$

(43)

Finally, we summarize the relations of the respective internal and total potentials for the inside space of the sphere. In connection to relation (3) of the external potential, the respective relations of the internal and total ones can be easily obtained as follows:

$$\begin{gathered} U_{int}^{in}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }\sum _{m=-l}^l{U}_{l,int}^{m,in}\left(\mathit{r}\right)=-\sum _{l=0}^{\infty }{N}_l{\chi }_{e,l}^{ext}\sum _{m=-l}^l{A}_l^m{r}^l{Y}_l^m\left(\theta ,\phi \right) \\ =-\sum _{l=0}^{\infty }{N}_l{\chi }_{e,l}^{ext}{r}^l\sum _{m=-l}^l{A}_l^m{Y}_l^m(\theta ,\phi ) \end{gathered}$$

(44)

and

$$U^{in}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }\sum _{m=-l}^l{U}_l^{m,in}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }{C}_l\sum _{m=-l}^l{A}_l^m{r}^l{Y}_l^m(\theta ,\phi )=\sum _{l=0}^{\infty }{C}_l{r}^l\sum _{m=-l}^l{A}_l^m{Y}_l^m(\theta ,\phi )$$

(45)

where we define the relevant general term of each expansion through

$$U_{l,int}^{m,in}\left(\mathit{r}\right)=-N_l{\chi }_{e,l}^{ext}{A}_l^m{r}^l{Y}_l^m(\theta ,\phi )$$

(46)

and

$$U_l^{m,in}\left(\mathit{r}\right)=C_l{A}_l^m{r}^l{Y}_l^m(\theta ,\phi )$$

(47)

Accordingly, we easily see that the general terms of the internal and external potentials follow the relation

$$U_{l,int}^{m,in}\left(\mathit{r}\right)=-N_l{\chi }_{e,l}^{ext}{U}_{l,ext}^{m,in}\left(\mathit{r}\right)$$

(48)

2.2. Outside Space of the Dielectric Sphere

Here, we summarize the results for the outside space of the sphere without the algebraic details. First of all, we note that the external potential/field, ${\mathrm{U}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$/${\mathbf{E}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$, are given by the same relations (3) and (5) as for the inside space of the sphere. Regarding the internal and total electric potential and field, we use the same algebraic approach described above. We obtain the following results:

$$\begin{gathered} {\mathit{E}}_{int}^{out}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }\sum _{m=-l}^l{\mathit{E}}_{l,int}^{m,out}\left(\mathit{r}\right)={\chi }_e^{int}\sum _{l=0}^{\infty }{N}_l{C}_l{\mathrm{a}}^{2l+1}\sum _{m=-l}^l{A}_l^m\nabla \left({\displaystyle \frac{Y_l^m\left(\theta ,\phi \right)}{r^{l+1}}}\right) \\ =\sum _{l=0}^{\infty }{N}_l{\chi }_{e,l}^{ext}{\mathrm{a}}^{2l+1}\sum _{m=-l}^l{A}_l^m\nabla \left({\displaystyle \frac{Y_l^m\left(\theta ,\phi \right)}{r^{l+1}}}\right) \end{gathered}$$

(49)

for the internal electric field and

$$\begin{gathered} {\mathit{E}}^{out}\left(\mathit{r}\right)=-\sum _{l=0}^{\infty }\sum _{m=-l}^l{A}_l^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)+{\chi }_e^{int}\sum _{l=0}^{\infty }{N}_l{C}_l{\mathrm{a}}^{2l+1}\sum _{m=-l}^l{A}_l^m\nabla \left({\displaystyle \frac{Y_l^m\left(\theta ,\phi \right)}{r^{l+1}}}\right) \\ =-\sum _{l=0}^{\infty }\sum _{m=-l}^l{A}_l^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)+\sum _{l=0}^{\infty }{N}_l{\chi }_{e,l}^{ext}{\mathrm{a}}^{2l+1}\sum _{m=-l}^l{A}_l^m\nabla \left({\displaystyle \frac{Y_l^m\left(\theta ,\phi \right)}{r^{l+1}}}\right) \end{gathered}$$

(50)

for the total electric field.

The respective relations for the internal and total electric potentials are the following:

$$U_{int}^{out}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }\sum _{m=-l}^l{U}_{l,int}^{m,out}\left(\mathit{r}\right)=-{\chi }_e^{int}\sum _{l=0}^{\infty }{N}_l{C}_l{\displaystyle \frac{{\mathrm{a}}^{2l+1}}{r^{l+1}}}\sum _{m=-l}^l{A}_l^m{Y}_l^m\left(\theta ,\phi \right)=-\sum _{l=0}^{\infty }{N}_l{\chi }_{e,l}^{ext}{\displaystyle \frac{{\mathrm{a}}^{2l+1}}{r^{l+1}}}\sum _{m=-l}^l{A}_l^m{Y}_l^m\left(\theta ,\phi \right)$$

(51)

and

$$\begin{gathered} U^{out}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }{r}^l\sum _{m=-l}^l{A}_l^m{Y}_l^m\left(\theta ,\phi \right)-{\chi }_e^{int}\sum _{l=0}^{\infty }{N}_l{C}_l{\displaystyle \frac{{\mathrm{a}}^{2l+1}}{r^{l+1}}}\sum _{m=-l}^l{A}_l^m{Y}_l^m\left(\theta ,\phi \right) \\ =\sum _{l=0}^{\infty }{r}^l\sum _{m=-l}^l{A}_l^m{Y}_l^m\left(\theta ,\phi \right)-\sum _{l=0}^{\infty }{N}_l{\chi }_{e,l}^{ext}{\displaystyle \frac{{\mathrm{a}}^{2l+1}}{r^{l+1}}}\sum _{m=-l}^l{A}_l^m{Y}_l^m\left(\theta ,\phi \right) \end{gathered}$$

(52)

Obviously, the obtained results hold for the case where the external electric field, ${\mathbf{E}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$, is either DC (static case) or AC, time-harmonic but of low frequency (quasi-static case), e.g., ${\mathbf{E}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r},\mathrm{t}\right)={\mathbf{E}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t\right)$. Thus, these results can be utilized in many applications of dielectric spheres.

3. Magnetic Sphere—Linear, Homogeneous and Isotropic—Subjected to an External Magnetic Scalar Pseudopotential/Vector Field of Any Form

Here, we summarize the relations obtained for the relevant case of the respective magnetic sphere of radius a, consisting of a linear, homogeneous and isotropic material of intrinsic susceptibility ${\mathrm{\chi }}_{\mathrm{m}}^{\mathrm{i}\mathrm{n}\mathrm{t}}$, subjected to an external magnetic scalar pseudopotential/vector field, ${\mathrm{U}}_{\mathrm{m},\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$/${\mathbf{H}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$. The latter are produced by a primary/free source (e.g., magnetic pseudocharges) that resides outside the sphere. The secondary/bound source that resides at the sphere, due to nonhomogeneous/discontinuous polarization, $\mathbf{M}\left(\mathbf{r}\right)$, will produce the internal ${\mathrm{U}}_{\mathrm{m},\mathrm{i}\mathrm{n}\mathrm{t}}\left(\mathbf{r}\right)$/${\mathbf{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(\mathbf{r}\right)$. Following the same strategy discussed above for the dielectric sphere, for the magnetic sphere discussed in this section, ${\mathrm{U}}_{\mathrm{m},\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$ can be expanded in a series analogous to relation (3), while the respective coefficients, $A_{l,m}^m$, can be obtained by an integral analogous to relation (8). The external magnetic field, ${\mathbf{H}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$, can be obtained from ${\mathrm{U}}_{\mathrm{m},\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$ by using the constitutive relation ${\mathbf{H}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)=-\nabla {\mathrm{U}}_{\mathrm{m},\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$. Finally, the total pseudopotential and field are given by the external (${\mathrm{U}}_{\mathrm{m},\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$ and ${\mathbf{H}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$) and internal (${\mathrm{U}}_{\mathrm{m},\mathrm{i}\mathrm{n}\mathrm{t}}\left(\mathbf{r}\right)$ and ${\mathbf{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(\mathbf{r}\right)$) ones through the superposition principle. Below, we provide the relations for the respective internal and total components for both the inside and outside spaces of the magnetic sphere.

3.1. Inside Space of the Magnetic Sphere

Here, we summarize the results for the inside space of the sphere without providing the algebraic details. For the internal magnetic field, we obtain

$${\mathit{H}}_{int}^{in}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }\sum _{m=-l}^l{\mathit{H}}_{l,int}^{m,in}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }{N}_l{\chi }_{m,l}^{ext}\sum _{m=-l}^l{A}_{l,m}^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$$

(53)

where the general term of the expansion is given by the relation

$${\mathit{H}}_{l,int}^{m,in}\left(\mathit{r}\right)=N_l{\chi }_{m,l}^{ext}{A}_{l,m}^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$$

(54)

while the extrinsic magnetic susceptibility is provided through the relation

$${\chi }_{m,l}^{ext}={\displaystyle \frac{{\chi }_m^{int}}{1+N_l{\chi }_m^{int}}}$$

(55)

where the depolarization factor is still given through relation (32).

The total magnetic field inside the sphere is given through

$${\mathit{H}}^{in}\left(\mathit{r}\right)=-\sum _{l=0}^{\infty }{C}_{l,m}\sum _{m=-l}^l{A}_{l,m}^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$$

(56)

where the coefficients, $C_{l,m}$, are given by the relation

$$C_{l,m}={\displaystyle \frac{1}{1+\frac{l}{2l+1}{\chi }_m^{int}}}={\displaystyle \frac{1}{1+N_l{\chi }_m^{int}}}$$

(57)

so that the total magnetic field can be rewritten as follows:

$${\mathit{H}}^{in}\left(\mathit{r}\right)=-{\displaystyle \frac{1}{{\chi }_m^{int}}}\sum _{l=0}^{\infty }{\chi }_{m,l}^{ext}\sum _{m=-l}^l{A}_{l,m}^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$$

(58)

The relationship between the general terms of the internal and external magnetic fields is found to be

$${\mathit{H}}_{l,int}^{m,in}\left(\mathit{r}\right)=-N_l{\chi }_{m,l}^{ext}{\mathit{H}}_{l,ext}^{m,in}\left(\mathit{r}\right)$$

(59)

Once again, by defining

$$N_l{\chi }_{m,l}^{ext}={\displaystyle \frac{N_l{\chi }_m^{int}}{1+N_l{\chi }_m^{int}}}$$

(60)

and the effective intrinsic magnetic susceptibility through

$${\chi }_{m,l}^{N_l}=N_l{\chi }_m^{int}$$

(61)

we get the equivalent relation

$${\mathit{H}}_{l,int}^{m,in}\left(\mathit{r}\right)=-{\displaystyle \frac{{\chi }_{m,l}^{N_l}}{1+{\chi }_{m,l}^{N_l}}}{\mathit{H}}_{l,ext}^{m,in}\left(\mathit{r}\right)$$

(62)

The respective magnetic polarization $\mathbf{M}\left(\mathbf{r}\right)={\mathrm{\chi }}_{\mathrm{m}}^{\mathrm{i}\mathrm{n}\mathrm{t}}{\mathbf{H}}^{\mathrm{i}\mathrm{n}}\left(\mathbf{r}\right)$ is obtained immediately as

$$\mathit{M}\left(\mathit{r}\right)=-\sum _{l=0}^{\infty }{\chi }_{m,l}^{ext}\sum _{m=-l}^l{A}_{l,m}^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$$

(63)

in agreement with the result obtained in [37].

The relations of the respective internal and total magnetic pseudopotentials for the inside space of the magnetic sphere are as follows:

$$\begin{gathered} U_{m,int}^{in}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }\sum _{m=-l}^l{U}_{l,m,int}^{m,in}\left(\mathit{r}\right)=-\sum _{l=0}^{\infty }{N}_l{\chi }_{m,l}^{ext}\sum _{m=-l}^l{A}_{l,m}^m{r}^l{Y}_l^m\left(\theta ,\phi \right) \\ =-\sum _{l=0}^{\infty }{N}_l{\chi }_{m,l}^{ext}{r}^l\sum _{m=-l}^l{A}_{l,m}^m{Y}_l^m(\theta ,\phi ) \end{gathered}$$

(64)

and

$$U_m^{in}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }\sum _{m=-l}^l{U}_{l,m}^{m,in}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }{C}_{l,m}\sum _{m=-l}^l{A}_{l,m}^m{r}^l{Y}_l^m(\theta ,\phi )=\sum _{l=0}^{\infty }{C}_{l,m}{r}^l\sum _{m=-l}^l{A}_{l,m}^m{Y}_l^m(\theta ,\phi )$$

(65)

where we define the relevant general term of each expansion as follows:

$$U_{l,m,int}^{m,in}\left(\mathit{r}\right)=-N_l{\chi }_{m,l}^{ext}{A}_{l,m}^m{r}^l{Y}_l^m(\theta ,\phi )$$

(66)

and

$$U_{l,m}^{m,in}\left(\mathit{r}\right)=C_{l,m}{A}_{l,m}^m{r}^l{Y}_l^m(\theta ,\phi )$$

(67)

We easily see that the general terms of the internal and external pseudopotentials follow the relation

$$U_{l,m,int}^{m,in}\left(\mathit{r}\right)=-N_l{\chi }_{m,l}^{ext}{U}_{l,m,ext}^{m,in}\left(\mathit{r}\right)$$

(68)

3.2. Outside Space of the Magnetic Sphere

For the outside space of the magnetic sphere, we obtain the following results:

$$\begin{gathered} {\mathit{H}}_{int}^{out}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }\sum _{m=-l}^l{\mathit{H}}_{l,int}^{m,out}\left(\mathit{r}\right)={\chi }_m^{int}\sum _{l=0}^{\infty }{N}_l{C}_{l,m}{\mathrm{a}}^{2l+1}\sum _{m=-l}^l{A}_{l,m}^m\nabla \left({\displaystyle \frac{Y_l^m\left(\theta ,\phi \right)}{r^{l+1}}}\right) \\ =\sum _{l=0}^{\infty }{N}_l{\chi }_{m,l}^{ext}{\mathrm{a}}^{2l+1}\sum _{m=-l}^l{A}_{l,m}^m\nabla \left({\displaystyle \frac{Y_l^m\left(\theta ,\phi \right)}{r^{l+1}}}\right) \end{gathered}$$

(69)

for the internal magnetic field and

$$\begin{gathered} {\mathit{H}}^{out}\left(\mathit{r}\right)=-\sum _{l=0}^{\infty }\sum _{m=-l}^l{A}_{l,m}^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)+{\chi }_m^{int}\sum _{l=0}^{\infty }{N}_l{C}_{l,m}{\mathrm{a}}^{2l+1}\sum _{m=-l}^l{A}_{l,m}^m\nabla \left({\displaystyle \frac{Y_l^m\left(\theta ,\phi \right)}{r^{l+1}}}\right) \\ =-\sum _{l=0}^{\infty }\sum _{m=-l}^l{A}_{l,m}^m\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)+\sum _{l=0}^{\infty }{N}_l{\chi }_{m,l}^{ext}{\mathrm{a}}^{2l+1}\sum _{m=-l}^l{A}_{l,m}^m\nabla \left({\displaystyle \frac{Y_l^m\left(\theta ,\phi \right)}{r^{l+1}}}\right) \end{gathered}$$

(70)

for the total magnetic field.

The respective relations for the internal and total magnetic pseudopotentials for the outside space of the sphere are the following:

$$\begin{gathered} U_{m,int}^{out}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }\sum _{m=-l}^l{U}_{l,m,int}^{m,out}\left(\mathit{r}\right)=-{\chi }_m^{int}\sum _{l=0}^{\infty }{N}_l{C}_{l,m}{\displaystyle \frac{{\mathrm{a}}^{2l+1}}{r^{l+1}}}\sum _{m=-l}^l{A}_{l,m}^m{Y}_l^m\left(\theta ,\phi \right) \\ =-\sum _{l=0}^{\infty }{N}_l{\chi }_{m,l}^{ext}{\displaystyle \frac{{\mathrm{a}}^{2l+1}}{r^{l+1}}}\sum _{m=-l}^l{A}_{l,m}^m{Y}_l^m\left(\theta ,\phi \right) \end{gathered}$$

(71)

and

$$\begin{gathered} U_m^{out}\left(\mathit{r}\right)=\sum _{l=0}^{\infty }{r}^l\sum _{m=-l}^l{A}_{l,m}^m{Y}_l^m\left(\theta ,\phi \right)-{\chi }_m^{int}\sum _{l=0}^{\infty }{N}_l{C}_{l,m}{\displaystyle \frac{{\mathrm{a}}^{2l+1}}{r^{l+1}}}\sum _{m=-l}^l{A}_{l,m}^m{Y}_l^m\left(\theta ,\phi \right) \\ =\sum _{l=0}^{\infty }{r}^l\sum _{m=-l}^l{A}_{l,m}^m{Y}_l^m\left(\theta ,\phi \right)-\sum _{l=0}^{\infty }{N}_l{\chi }_{m,l}^{ext}{\displaystyle \frac{{\mathrm{a}}^{2l+1}}{r^{l+1}}}\sum _{m=-l}^l{A}_{l,m}^m{Y}_l^m\left(\theta ,\phi \right) \end{gathered}$$

(72)

Finally, we stress that the obtained results hold for the case where ${\mathbf{H}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)$ is either a DC field (static case) or a time-harmonic AC field, but of low frequency (quasi-static case), e.g., ${\mathbf{H}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r},\mathrm{t}\right)={\mathbf{H}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathbf{r}\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t\right)$. Thus, these results can be useful in many applications of magnetic spheres.

4. Summary of Our Findings, Connection with the Literature and Utilization in Applications

Here, we summarize our findings and highlight a connection with the literature. In addition, we discuss how we can utilize the above relations in practice. To this end, we survey two representative applications: one for a dielectric and one for a magnetic sphere subjected to a field of rather unusual form (at least in mathematical terms). Finally, we present simulations of the performance of a dielectric sphere in shielding its interior from an external electric potential of general term $U_{l,ext}^{m,in}\left(\mathit{r}\right)$, with respect to its intrinsic susceptibility, ${\chi }_e^{int}$, and to the degree $l$ of the specific mode.

4.1. Summary of Our Findings and Connection with the Literature

Here, we summarize the findings of our study, which refers to an LHI dielectric or magnetic sphere subjected to an external/user-applied static (DC) or quasi-static (low-frequency AC) potential/field. In addition, we provide a brief discussion of important contributions regarding the propagation theory of arbitrary-shaped electromagnetic beams at high frequencies (e.g., laser beams) and the respective scattering processes by particles and aggregates (e.g., homogeneous spheres, multilayered spheres, ellipsoids, etc.). This field has been under extensive investigation for many decades and is still an active research area. Concepts such as the generalized Lorenz–Mie theory (GLMT) and the T-matrix method are successfully employed to describe these high-frequency processes in both dielectric and magnetic media [39,40,41,42,43,44,45,46,47,48,49,50,51,52]. Indeed, the interaction between arbitrary-shaped electromagnetic beams and particles with a shape that is sufficiently symmetrical to allow us to use the method of separation of variables to tackle Maxwell’s equations has been investigated for more than three decades [39,40,41,42,43,44,45,46,47]. When the scatterers have high symmetry, the GLMT results in entirely analytical solutions, while scatterers of low symmetry can be addressed computationally. The efficacy of a software-based computational approach employing the GLMT has been discussed in [53], in comparison to other candidate methods such as the one that decomposes the incident beam into a basis of plane waves [54,55]. The specific highly symmetric case of a homogeneous dielectric and magnetic sphere, addressed here regarding the static (DC) or quasi-static (low-frequency AC) limits, has been successfully investigated in the past in the opposite limit of high frequencies using the GLMT when the diameter and the complex refractive index of the particular homogeneous scatterer are known. Most importantly, the GLMT has also been employed in the case of multilayered spheres, circular and elliptical cylinders, spheres with an off-center spherical inclusion, assemblies of distinct spheres and aggregates, etc. (see [47] and references therein). Referring to the T-matrix formulation [48,49,50,51,52], it is also employed to describe the illumination of a scattering particle (e.g., a homogeneous sphere, multilayered sphere, etc.) by an electromagnetic field. Its main characteristic is that it relates the expansion coefficients of both the incident and scattered fields over a set of functions that forms an appropriate basis (e.g., see [47] and [56,57] and references therein). Specifically, the expansion coefficients of the scattered electromagnetic field are expressed through the expansion coefficients of the incident one by using the so-called transition matrix (T-matrix formulation). This is also a very effective method for the analytical description of relevant scattering processes when possible; otherwise, a computational approach should be employed [57].

Returning to our study, for the linear, homogeneous and isotropic dielectric sphere, the starting point is the expansion of the external/user-applied potential, $U_{ext}\left(\mathit{r}\right)$, and field, ${\mathit{E}}_{ext}\left(\mathit{r}\right)$, given by relations (3) and (5), respectively. The necessary expansion coefficients, $A_l^m$, are obtained through relation (8). These relations hold for both inside and outside the dielectric sphere. For the relevant magnetic sphere, the external/user-applied pseudopotential, $U_{m,ext}\left(\mathit{r}\right)$, and field, ${\mathit{H}}_{ext}\left(\mathit{r}\right)$, together with the expansion coefficients, $A_{l,m}^m$, can be obtained by analogous relations. We recall that the potentials/pseudopotentials $U_{ext}\left(\mathit{r}\right)$/$U_{m,ext}\left(\mathit{r}\right)$ and fields ${\mathit{E}}_{ext}\left(\mathit{r}\right)$/${\mathit{H}}_{ext}\left(\mathit{r}\right)$ studied here are of a static (DC) or quasi-static (low-frequency AC) nature and can be of any form with respect to their spatial variation. Obviously, only specific forms of the external/user-applied potential and field can be addressed analytically in the sense that the desired expansion coefficients can be calculated straightforwardly by hand. In most cases, a software-aided process should be employed to obtain the expansion coefficients computationally.

Our study adds to the important works existing in the literature [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57] in a complementary way and can be useful for static (DC) or quasi-static (low-frequency AC) applications [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32] for the following reasons.

(a)

It eliminates all algebra, since we have the solutions beforehand, for any form of the external/user-applied potential/pseudopotential and field, by means of simple substitutions. However, prior to using these universal expressions to calculate the internal and total potential/pseudopotential, the external/user-applied ones should be obtained on the basis of the SH. To this end, the non-zero expansion coefficients—$A_l^m$ for the dielectric and $A_{l,m}^m$ for the magnetic case—and non-null modes $(l,m)$ should be obtained through relation (8). Moreover, the expansion coefficients—$C_l$ for the dielectric and $C_{l,m}$ for the magnetic case—can be calculated immediately from relations (31) and (57), respectively. Then, both the internal and total potentials can be calculated everywhere in space through the respective relations. For the dielectric case, relations (44) and (45) should be used to obtain $U_{int}^{in}\left(\mathit{r}\right)$ and $U^{in}\left(\mathit{r}\right)$, respectively, inside the sphere, while relations (51) and (52) should be employed to obtain $U_{int}^{out}\left(\mathit{r}\right)$ and $U^{out}\left(\mathit{r}\right)$, respectively, outside the sphere. For the magnetic case, relations (64) and (65) should be used to obtain the internal and total pseudopotentials, respectively, inside the sphere, while relations (71) and (72) should be employed to obtain the respective entities outside the sphere. Moreover, the respective electric/magnetic fields can be calculated by the already known potentials/pseudopotentials (dielectric sphere: relations (35), (38), (49) and (50); magnetic sphere: relations (53), (58), (69) and (70)). To this end, the vector functions $\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$ and $\nabla (Y_l^m\left(\theta ,\phi \right)/r^{l+1})$ are needed for the non-null modes $(l,m)$. These should not be calculated from scratch. Tables of $\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$ and $\nabla (Y_l^m\left(\theta ,\phi \right)/r^{l+1})$ may be easily constructed for general use, without the need to recalculate each one of these functions whenever necessary. For instance, the functions $\nabla \left(r^l{Y}_l^m\left(\theta ,\phi \right)\right)$ for degrees up to $l=2$ can be found in [37], where only the polarization was considered at the inside space of the sphere.

(b)

It introduces an explicit closed-form relation for the depolarization factor, $N_l$, i.e., relation (32). This physical parameter (see [58] and references therein) is important since it reveals how bound sources influence the internal/response field of the dielectric/magnetic sphere and how the latter relates to the external/user-applied one. We reveal that $N_l$ is degenerate on the order, $m$, since it depends only on the degree, $l$, of the external/user-applied mode $(l,m)$. More importantly, we reveal the exact ways in which the expansion coefficients of both the internal/response and total potentials and fields depend on the depolarization factor, $N_l$.

(c)

It also introduces an explicit closed-form relation for the extrinsic susceptibility, ${\chi }^{ext}$, of the studied dielectric and magnetic sphere, together with its direct connection with the intrinsic susceptibility, ${\chi }^{int}$, of the parent material. Notice that ${\chi }^{int}$ depends solely on the endogenous properties of the parent material, so that it is an important parameter to be determined from experiments. However, in experiments, we have direct access only to the extrinsic susceptibility, ${\chi }^{ext}$, an exogenous property that relates to the shape and limited size of the studied specimen (see [58] and references therein). Thus, a reliable relation to translate the experimentally measured extrinsic susceptibility, ${\chi }^{ext}$, to the desired intrinsic one, ${\chi }^{int}$, is urgently needed. Relations (37) and (55) for the dielectric and magnetic sphere, respectively, together with (32), serve this need in a direct way. Finally, we reveal that the extrinsic susceptibility is degenerate on the order, $m$, since it depends only on the degree, $l$, of the external/user-applied mode $(l,m)$.

(d)

It minimizes the required effort and time, since we do not have to solve each particular problem from the beginning by applying the same, time-consuming algebraic manipulations whenever the external/user-applied field is different. The solutions are provided by the relations discussed above through immediate substitution. Thus, these relations are ready-to-use and hold for any form of the external/user-applied field, as discussed above.

(e)

It is absolutely reliable, since the solutions provided by the relations discussed above are obtained through the incorporation of all necessary boundary conditions from the very beginning. The reliability of our solutions is documented, analytically, through two representative cases (one for a dielectric and one for a magnetic sphere) discussed below. The solutions found by our relations, in practically a single step, are identical to those found through extensive algebraic calculations by standard mathematical approaches.

(f)

It can be used by non-experts in the field, since the user does not have to apply the extensive algebraic calculations required by standard mathematical approaches. Reliable solutions are provided by our ready-to-use relations by means of simple substitutions, as discussed above.

(g)

It can be employed in computational studies to minimize the requirements for resources. When entirely analytical solutions cannot be obtained by hand, our universal expressions can still be employed in a software-aided computational approach to find the desired solutions.

4.2. Utilization in Applications

To clarify the advantages of our approach, here, we address two representative cases found in applications: the first one refers to a dielectric sphere, while the second one considers a magnetic sphere. Finally, we present simulations of the shielding efficiency of a dielectric sphere subjected to a generic electric field.

4.2.1. Dielectric Case

The first case refers to a linear, homogeneous and isotropic dielectric sphere of radius $\mathrm{a}$ and intrinsic susceptibility, ${\chi }_e^{int}$, subjected to an external potential $U_{ext}\left(\mathit{r}\right)$, produced from a point free charge, $Q_f$, that resides on the positive z axis at point $z=b$ ($b>\mathrm{a}$). This system has azimuthal symmetry so that the order of the SH is $m=0$. The external potential, $U_{ext}\left(\mathit{r}\right)$, at the inside space of the point charge ($r<\mathrm{b}$) is given by the relation

$$U_{ext}\left(\mathit{r}\right)={\displaystyle \frac{Q_f}{4\pi {\epsilon }_0}}\sum _{l=0}^{\infty }{\displaystyle \frac{1}{b^{l+1}}}{r}^l{P}_l(cos\theta )$$

(73)

By using relation (8), we obtain the expansion coefficients ($A_l^m=A_l^0=A_l$):

$$A_l={\displaystyle \frac{Q_f}{{\epsilon }_0}}{\displaystyle \frac{1}{\sqrt{4\pi }}}{\displaystyle \frac{1}{\sqrt{2l+1}}}{\displaystyle \frac{1}{b^{l+1}}}$$

(74)

We have immediate access to the depolarization factor, $N_l$, from relation (32); the expansion coefficients, $C_l$, from relation (31); and the extrinsic susceptibility, ${\chi }_{e,l}^{ext}$, from relation (37). Substituting this information into the appropriate relations, we can obtain the internal and total potentials and fields for both the inside and outside spaces of the dielectric sphere.

Inside space: We simply substitute $N_l$ and ${\chi }_{e,l}^{ext}$ into relation (44) and obtain the internal potential,

$$\begin{gathered} U_{int}^{in}\left(\mathit{r}\right)=-{\displaystyle \frac{Q_f}{4\pi {\epsilon }_0}}\sum _{l=0}^{\infty }{\displaystyle \frac{l}{2l+1}}{\displaystyle \frac{{\chi }_e^{int}}{1+\frac{l}{2l+1}{\chi }_e^{int}}}{\displaystyle \frac{1}{b^{l+1}}}{r}^l{P}_l(cos\theta ) \\ =-{\displaystyle \frac{Q_f}{4\pi {\epsilon }_0}}\sum _{l=0}^{\infty }{\displaystyle \frac{l({\epsilon }_r-1)}{l({\epsilon }_r+1)+1}}{\displaystyle \frac{1}{b^{l+1}}}{r}^l{P}_l(cos\theta ) \end{gathered}$$

(75)

where ${\epsilon }_r={\chi }_e^{int}+1$ is the relative permittivity. Moreover, by simply substituting $C_l$ into relation (45), we obtain the total potential,

$$\begin{gathered} U^{in}\left(\mathit{r}\right)={\displaystyle \frac{Q_f}{4\pi {\epsilon }_0}}\sum _{l=0}^{\infty }{\displaystyle \frac{1}{1+\frac{l}{2l+1}{\chi }_e^{int}}}{\displaystyle \frac{1}{b^{l+1}}}{r}^l{P}_l(cos\theta ) \\ ={\displaystyle \frac{Q_f}{4\pi {\epsilon }_0}}\sum _{l=0}^{\infty }{\displaystyle \frac{2l+1}{l\left({\epsilon }_r+1\right)+1}}{\displaystyle \frac{1}{b^{l+1}}}{r}^l{P}_l(cos\theta ) \end{gathered}$$

(76)

This result is in agreement with that presented in [59] (see §9(h), page 84) and in [60,61].

Outside space: Again, by substituting $N_l$ and ${\chi }_{e,l}^{ext}$ into relation (51), we obtain the internal potential,

$$\begin{gathered} U_{int}^{out}\left(\mathit{r}\right)=-{\displaystyle \frac{Q_f}{4\pi {\epsilon }_0}}\sum _{l=0}^{\infty }{\displaystyle \frac{l}{2l+1}}{\displaystyle \frac{{\chi }_e^{int}}{1+\frac{l}{2l+1}{\chi }_e^{int}}}{\displaystyle \frac{1}{b^{l+1}}}{\displaystyle \frac{{\mathrm{a}}^{2l+1}}{r^{l+1}}}{P}_l(cos\theta ) \\ =-{\displaystyle \frac{Q_f}{4\pi {\epsilon }_0}}\sum _{l=0}^{\infty }{\displaystyle \frac{l({\epsilon }_r-1)}{l({\epsilon }_r+1)+1}}{\displaystyle \frac{1}{b^{l+1}}}{\displaystyle \frac{{\mathrm{a}}^{2l+1}}{r^{l+1}}}{P}_l(cos\theta ) \end{gathered}$$

(77)

While, by using relation (52), we obtain the total potential,

$$\begin{gathered} U^{out}\left(\mathit{r}\right)={\displaystyle \frac{Q_f}{4\pi {\epsilon }_0}}\sum _{l=0}^{\infty }\left(r^l-{\displaystyle \frac{l}{2l+1}}{\displaystyle \frac{{\chi }_e^{int}}{1+\frac{l}{2l+1}{\chi }_e^{int}}}{\displaystyle \frac{{\mathrm{a}}^{2l+1}}{r^{l+1}}}\right){\displaystyle \frac{1}{b^{l+1}}}{P}_l(cos\theta ) \\ ={\displaystyle \frac{Q_f}{4\pi {\epsilon }_0}}\sum _{l=0}^{\infty }\left(r^l-{\displaystyle \frac{l({\epsilon }_r-1)}{l({\epsilon }_r+1)+1}}{\displaystyle \frac{{\mathrm{a}}^{2l+1}}{r^{l+1}}}\right){\displaystyle \frac{1}{b^{l+1}}}{P}_l(cos\theta ) \end{gathered}$$

(78)

This result is in agreement with that presented in [59] (see §9(h), page 84) and in [60,61]. By using the respective relations for the internal and total electric fields, we can find these entities both inside, ${\mathit{E}}_{int}^{in}\left(\mathit{r}\right)$ and ${\mathit{E}}^{in}\left(\mathit{r}\right)$, and outside, ${\mathit{E}}_{int}^{out}\left(\mathit{r}\right)$ and ${\mathit{E}}^{out}\left(\mathit{r}\right)$, the dielectric sphere.

4.2.2. Magnetic Case

The second case refers to a linear, homogeneous and isotropic magnetic sphere of radius $\mathrm{a}$ and intrinsic susceptibility, ${\chi }_m^{int}$, subjected to an external magnetic pseudopotential, $U_{m,ext}\left(\mathit{r}\right)$, produced from a surface density of magnetic pseudocharge, ${\sigma }_m\left(R,\theta ,\phi \right)=-{3H}_{0}sin\theta sin\phi$, that resides on a spherical shell of radius $R$ ($R>\mathrm{a}$). Now, the system does not have azimuthal symmetry, so that SH with $m\ne 0$ exist. The external magnetic pseudopotential, $U_{m,ext}\left(\mathit{r}\right)$, is given by the relation

$$U_{m,ext}\left(\mathit{r}\right)=-H_{0}rsin\theta sin\phi$$

(79)

By using relation (8), we obtain the non-zero expansion coefficients of the modes $\left(l,m\right)=\left(1,-1\right)$ and $\left(\mathrm{1,1}\right)$:

$$A_1^1=A_1^{-1}=-i{H}_0\sqrt{{\displaystyle \frac{2\pi }{3}}}$$

(80)

Once again, substituting the depolarization factor, $N_l$, from relation (32), the expansion coefficients, $C_{l,m}$, from relation (57), and the extrinsic susceptibility, ${\chi }_{m,l}^{ext}$, from relation (55), into the appropriate relations, we can obtain the internal and total pseudopotentials and fields for both the inside and outside spaces of the magnetic sphere.

Inside space: We simply substitute $N_1$ and ${\chi }_{m,1}^{ext}$ into relation (64) and obtain the internal pseudopotential,

$$U_{m,int}^{in}\left(\mathit{r}\right)={\displaystyle \frac{{\chi }_m^{int}}{3+{\chi }_m^{int}}}{H}_{0}rsin\theta sin\phi ={\displaystyle \frac{{\mu }_r-1}{{\mu }_r+2}}{H}_{0}rsin\theta sin\phi$$

(81)

where ${\mu }_r={\chi }_m^{int}+1$ is the relative permeability. Moreover, by simply substituting $C_{l,m}$ into relation (65), we obtain the total pseudopotential,

$$U_{m }^{in}\left(\mathit{r}\right)=-{\displaystyle \frac{3}{3+{\chi }_m^{int}}}{H}_{0}rsin\theta sin\phi =-{\displaystyle \frac{3}{{\mu }_r+2}}{H}_{0}rsin\theta sin\phi$$

(82)

Outside space: Again, by substituting $N_1$ and ${\chi }_{m,1}^{ext}$ into relation (71), we obtain the internal pseudopotential,

$$U_{m,int}^{out}\left(\mathit{r}\right)={\displaystyle \frac{{\chi }_m^{int}}{3+{\chi }_m^{int}}}{H}_0{\displaystyle \frac{{\mathrm{a}}^3}{r^2}}sin\theta sin\phi ={\displaystyle \frac{{\mu }_r-1}{{\mu }_r+2}}{H}_0{\displaystyle \frac{{\mathrm{a}}^3}{r^2}}sin\theta sin\phi$$

(83)

while, by using relation (72), we obtain the total pseudopotential,

$$\begin{gathered} U_{m }^{out}\left(\mathit{r}\right)=-H_{0}rsin\theta sin\phi +{\displaystyle \frac{{\chi }_m^{int}}{3+{\chi }_m^{int}}}{H}_0{\displaystyle \frac{{\mathrm{a}}^3}{r^2}}sin\theta sin\phi \\ =-H_{0}rsin\theta sin\phi +{\displaystyle \frac{{\mu }_r-1}{{\mu }_r+2}}{H}_0{\displaystyle \frac{{\mathrm{a}}^3}{r^2}}sin\theta sin\phi \end{gathered}$$

(84)

The above results are in agreement with those obtained by using the standard techniques (Laplace, multipole expansion, etc.) that are based on lengthy calculations. By using the respective relations for the internal and total magnetic fields, we can find these entities both inside, ${\mathit{H}}_{int}^{in}\left(\mathit{r}\right)$ and ${\mathit{H}}^{in}\left(\mathit{r}\right)$, and outside, ${\mathit{H}}_{int}^{out}\left(\mathit{r}\right)$ and ${\mathit{H}}^{out}\left(\mathit{r}\right)$, the magnetic sphere.

4.2.3. Simulations for the Dielectric Case

Finally, we consider the shielding ability of a linear, homogeneous and isotropic dielectric sphere of radius a and intrinsic susceptibility, ${\chi }_e^{int}$, subjected to an external electric potential of general term, $U_{l,ext}^{m,in}\left(\mathit{r}\right)$. To this end, we employ the expression of the inside space, relation (48), aided by the general relations (32) and (37). The investigated range is $0\le {\chi }_e^{int}\le 50$ for the intrinsic susceptibility and $0 \mathrm{V}\le U_{l,ext}^{m,in}\left(\mathit{r}\right)\le 100 \mathrm{V}$ for the external potential. In Figure 2a–f below, we provide detailed simulations for the response of the sphere, i.e., for the internal potential $U_{l,int}^{m,in}\left(\mathit{r}\right)$, with respect to both ${\chi }_e^{int}$ and $U_{l,ext}^{m,in}\left(\mathit{r}\right)$, for different values of the degree $l=1, 2$ and $10$.

From these data, we see how $U_{l,int}^{m,in}\left(\mathit{r}\right)$ depends on $U_{l,ext}^{m,in}\left(\mathit{r}\right)$, with modes of higher degree, $l$, to be suppressed more effectively inside the dielectric sphere (notice that the two groups of panels (a), (c) and (e) and panels (b), (d) and (f) retain the same range in ${\chi }_e^{int}$ and $U_{l,ext}^{m,in}\left(\mathit{r}\right)$). For the maximum value, ${\chi }_e^{int}=50$, considered here, $U_{l,int}^{m,in}\left(\mathit{r}\right)$ reaches −94.5%, −95.5% and −96% of $U_{l,ext}^{m,in}\left(\mathit{r}\right)$ for $l=1,2$ and $10$, respectively, limiting the total electric potential inside the sphere, $U_l^{m,in}\left(\mathit{r}\right)$, at 5.5%, 4.5% and 4%. Eventually, for $l\gg 1$, the depolarization factor of degree $l$, $N_l$, saturates to ½ (relation (32)), while, for relatively high values of ${\chi }_e^{int}$, the prefactor of relation (48), $N_l{\chi }_{e,l}^{ext}$, practically reaches unity. Under these circumstances, the almost complete elimination of $U_{l,ext}^{m,in}\left(\mathit{r}\right)$ from the inside space of the dielectric sphere is achieved. Of course, for more typical, lower values of ${\chi }_e^{int}$, the shielding of the inside space of the dielectric sphere is not so efficient. In any case, the universal relations provided here for the internal and total electric potentials/fields for any form of the external ones provide a means to predict the response of this particular building unit with respect to a generic external cause.

5. Conclusions

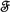Here, we introduce a mathematical strategy that enables us to calculate, both easily and reliably, in essentially one step, the total scalar potential/vector field, /, for the case of a linear, homogeneous and isotropic dielectric and magnetic sphere subjected to an external scalar potential/vector field, 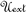/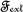, of any form. Our approach surpasses all time-consuming, conventional methods that rely on extensive, step-by-step algebraic calculations. The universal, ready-to-use relations of the total scalar potential/vector field, /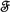, introduced here for the first time, have already digested all lengthy algebraic calculations. Our approach is characterized by unparalleled convenience and clear reliability; thus, it can be used as a means of tailoring the responses of dielectric and magnetic spheres, i.e., of the internal scalar potential/vector field, /, for every external scalar potential/vector field, 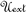/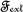. Except for understanding the underlying physics, our approach can promote relevant applications.