Feature Selection for Explaining Yellowfin Tuna Catch per Unit Effort Using Least Absolute Shrinkage and Selection Operator Regression
Abstract
1. Introduction
2. Data and Methods
2.1. Data Processing
2.1.1. Data Sources
2.1.2. CPUE Calculation
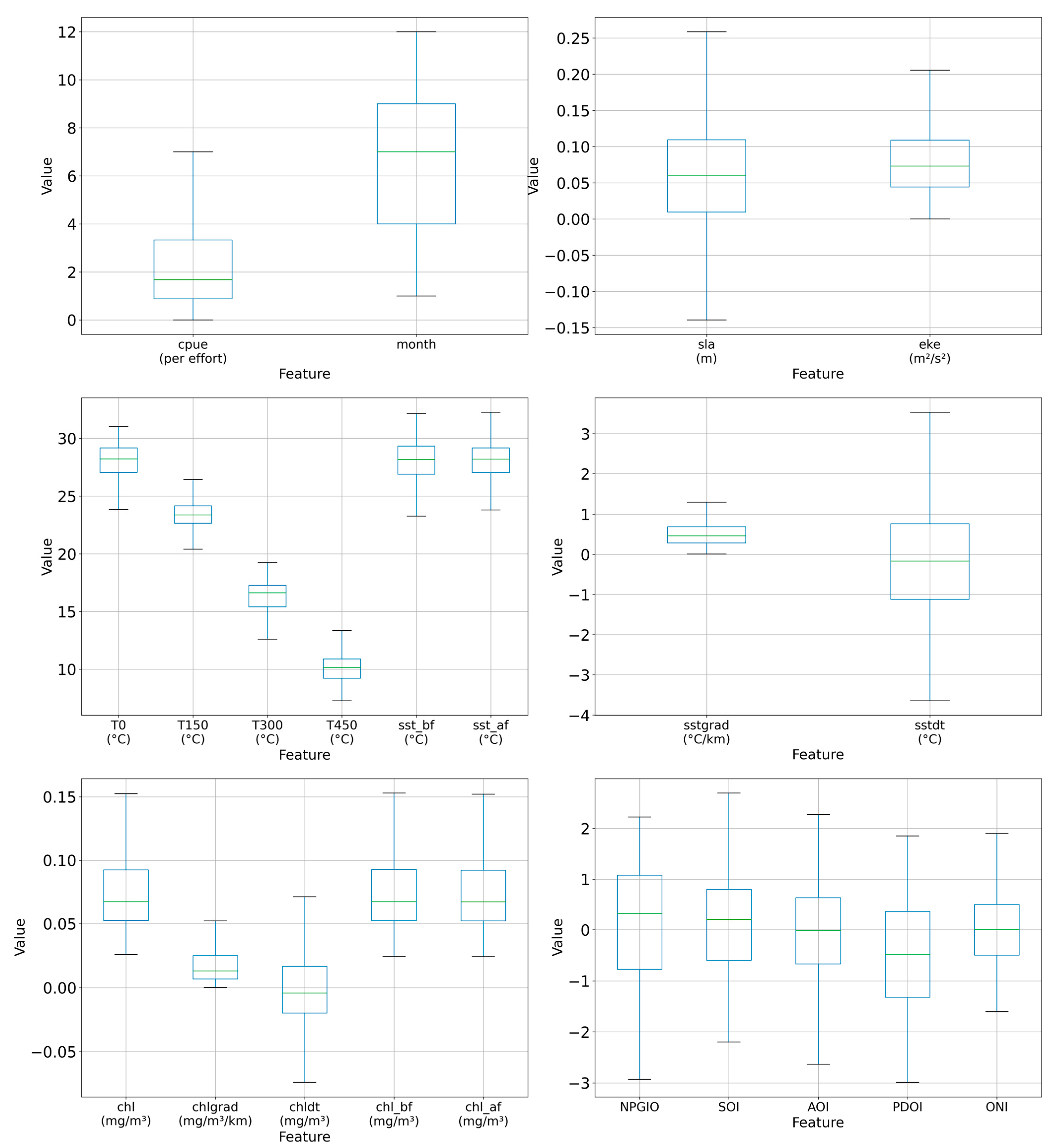
2.1.3. Data Preprocessing
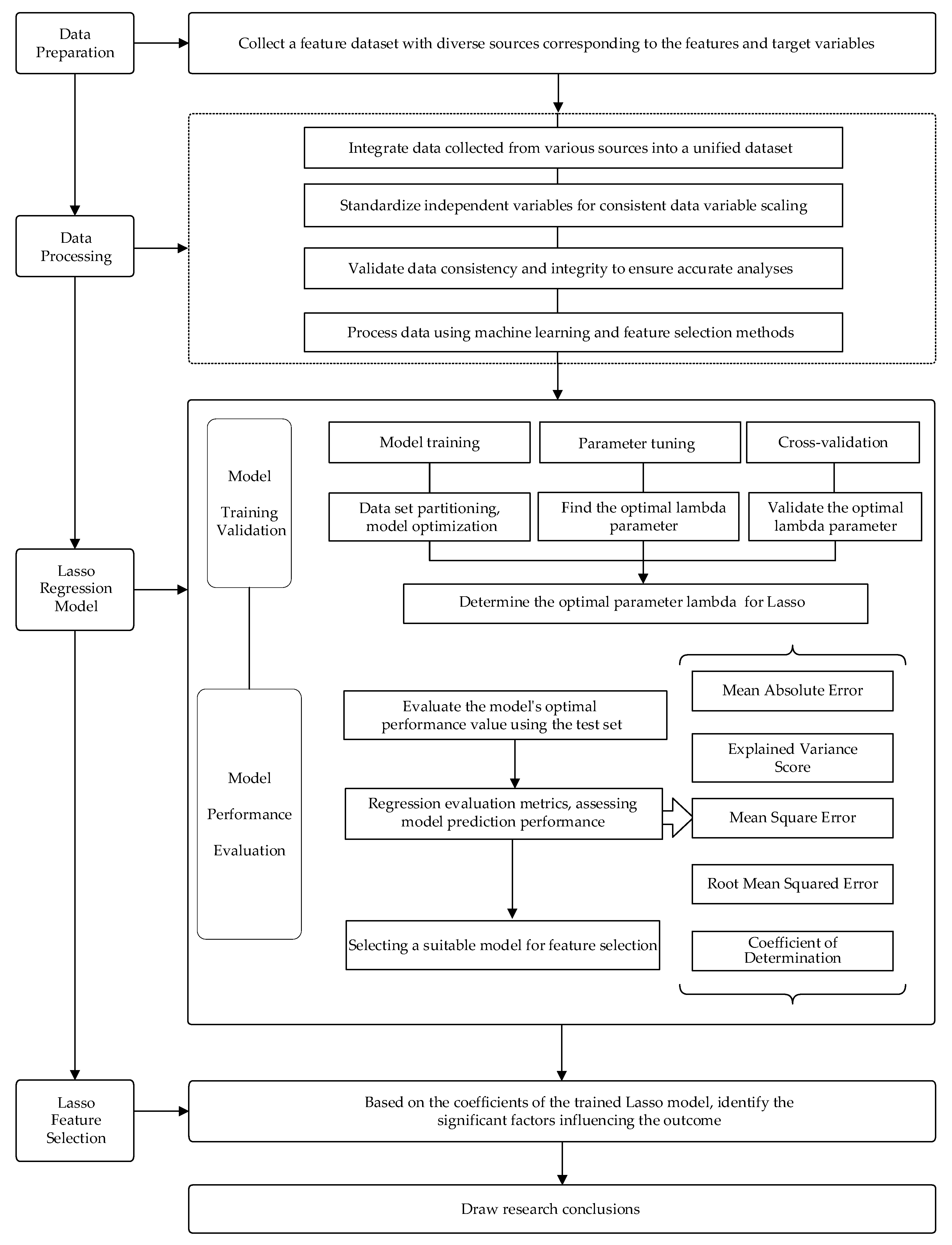
2.2. Research Method
2.2.1. Lasso Regression Introduction
2.2.2. Screening Variables and Feature Selection
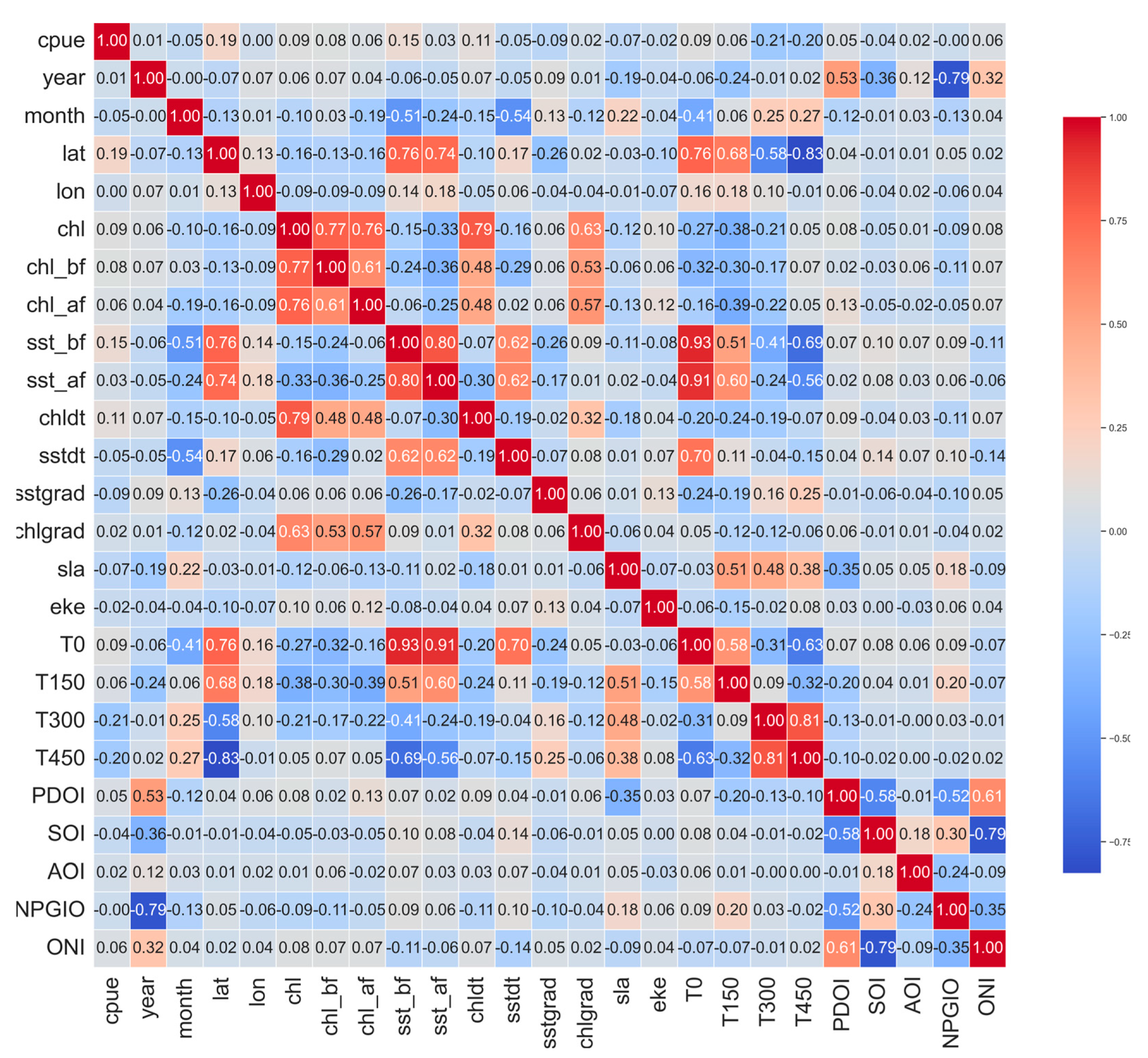
2.2.3. Pearson Coefficient Correlation Analysis
2.2.4. Model Evaluation Methods
- 1.
- The mean absolute error (MAE) calculates the residual for each data point, taking the absolute value of each residual to ensure that negative and positive residuals do not cancel each other out. MAE is used to assess the degree of proximity between the predicted results and the actual dataset, where a smaller value indicates a better fit. The formula for MAE is as follows, where n represents the number of samples, represents the predicted value, represents the actual value, and the sum is the sum of the absolute differences between the predicted and actual values:
- 2.
- The explained variance score (EVS) is a metric used to measure the performance of a regression model. Its value ranges from 0 to 1, where a value closer to 1 indicates that the independent variables explain the variance in the dependent variable well, while a smaller value suggests poorer performance. The formula for EVS is as follows, where y represents the true values, f represents the corresponding predicted values, and Var is the variance of the actual values:
- 3.
- The mean squared error (MSE) is a measure of the disparity between the estimator and the estimated value. A smaller MSE indicates less difference between the predicted and actual values, reflecting better model fit. The formula for MSE is as follows, where represents the total number of samples, represents the predicted value for the i-th sample, and is the corresponding true value; the sum is the squared sum of the differences between the predicted values and the true values :
- 4.
- The root-mean-square error (RMSE), also known as standard error, is used to measure the deviation between observed values and true values. If there is a significant difference between predicted values and true values, the RMSE value will be large. Therefore, the standard error can effectively reflect the precision of measurements. RMSE is the square root of the sum of MSE; the calculation formula is as follows:
- 5.
- : the coefficient of determination (R-squared) assesses the goodness of fit of the predictive model to the real data. Its value ranges from 0 to 1, where a higher value indicates less error and a better ability of the model to explain the variability of the dependent variable, implying a better fit of the model. The formula for calculating R-squared is as follows: where n represents the total number of samples, represents the predicted value for the i-th sample, represents the i-th actual observed value, and is the mean of the actual observed values. R-squared is the ratio of the sum of squared differences between predicted values and the mean of observed values to the total sum of squares.
2.2.5. Regression Model Methods
2.2.6. Comprehensive Score
3. CPUE Feature Selection Analysis Results
3.1. Correlation Analysis between CPUE and Features
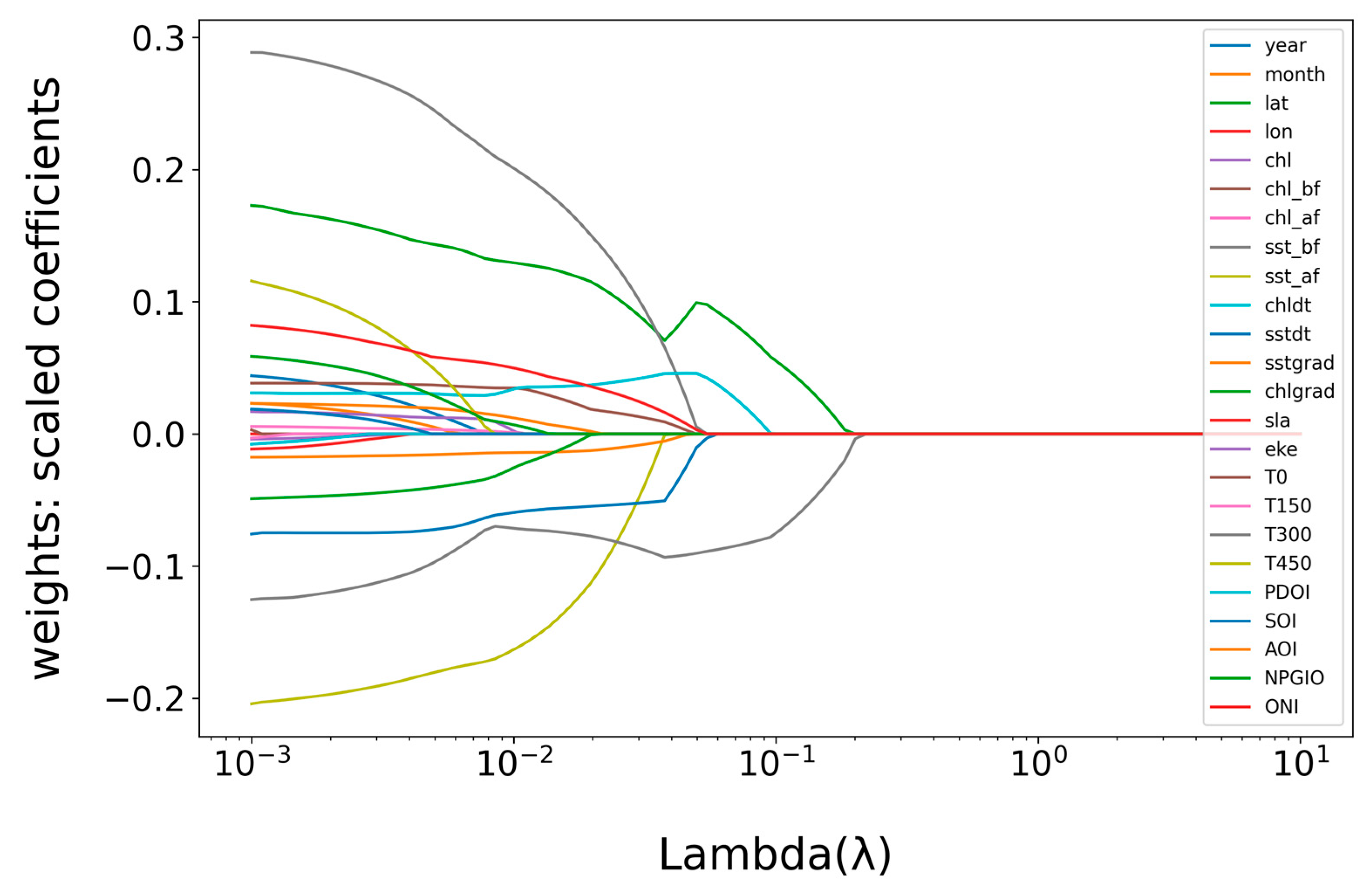
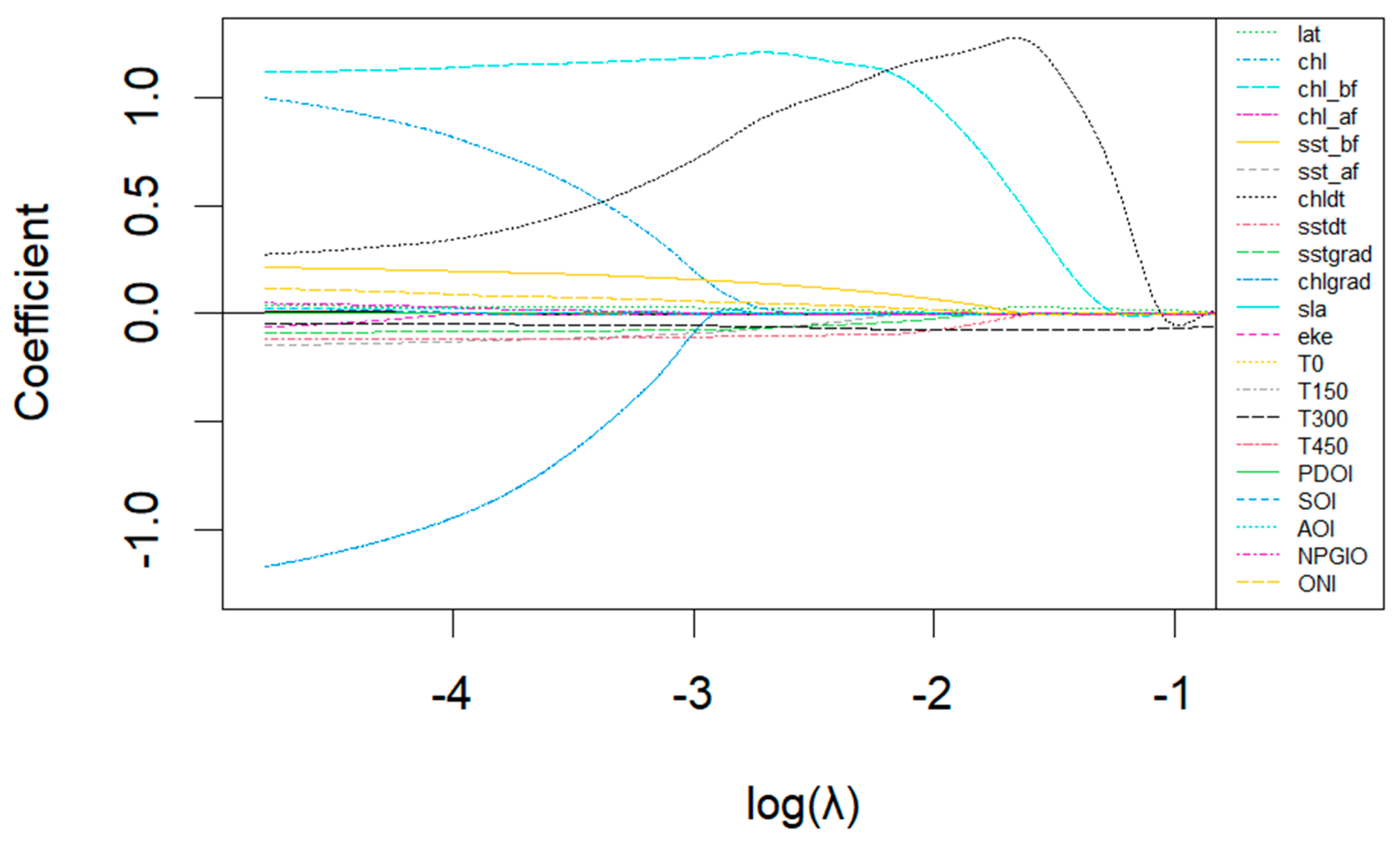
3.2. Cross-Validation Features
3.3. Performance Evaluation of Lasso Regression Model
3.3.1. Lasso Regression Model Parameter Prediction Results
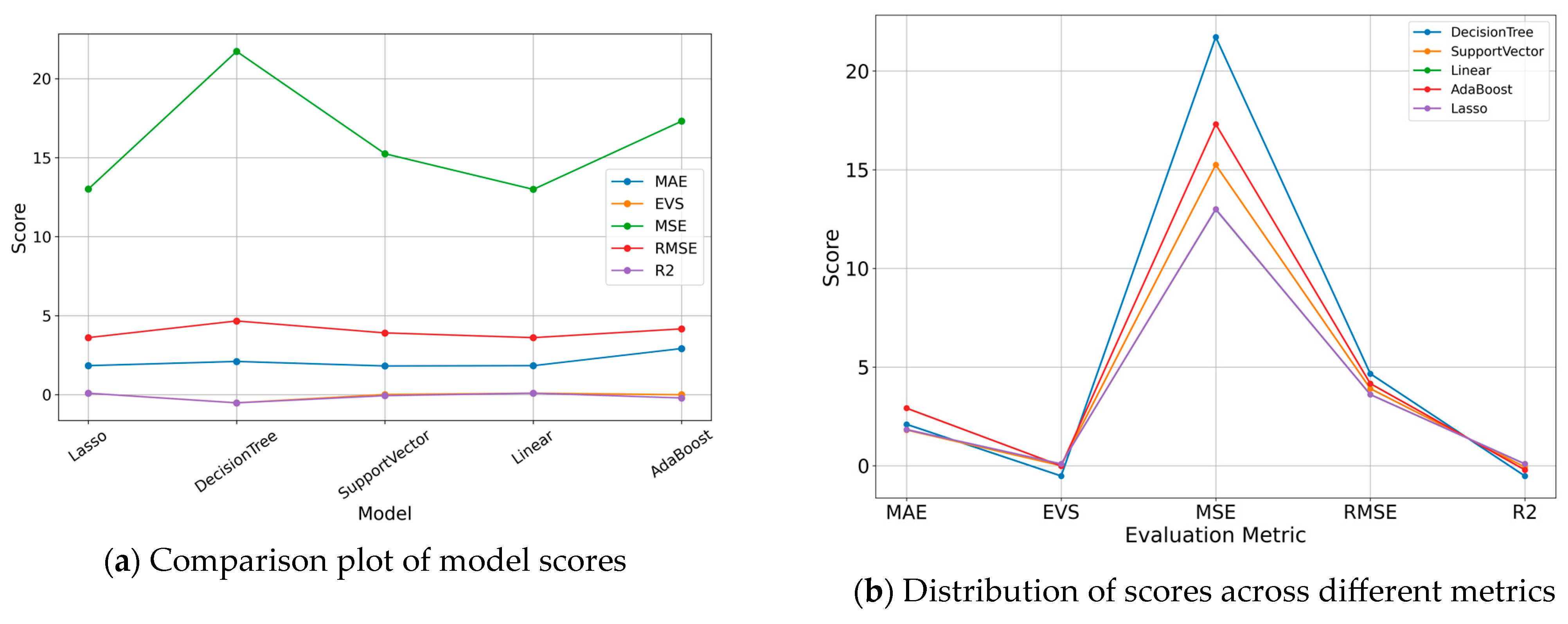
3.3.2. Lasso Regression Model Comparison Score
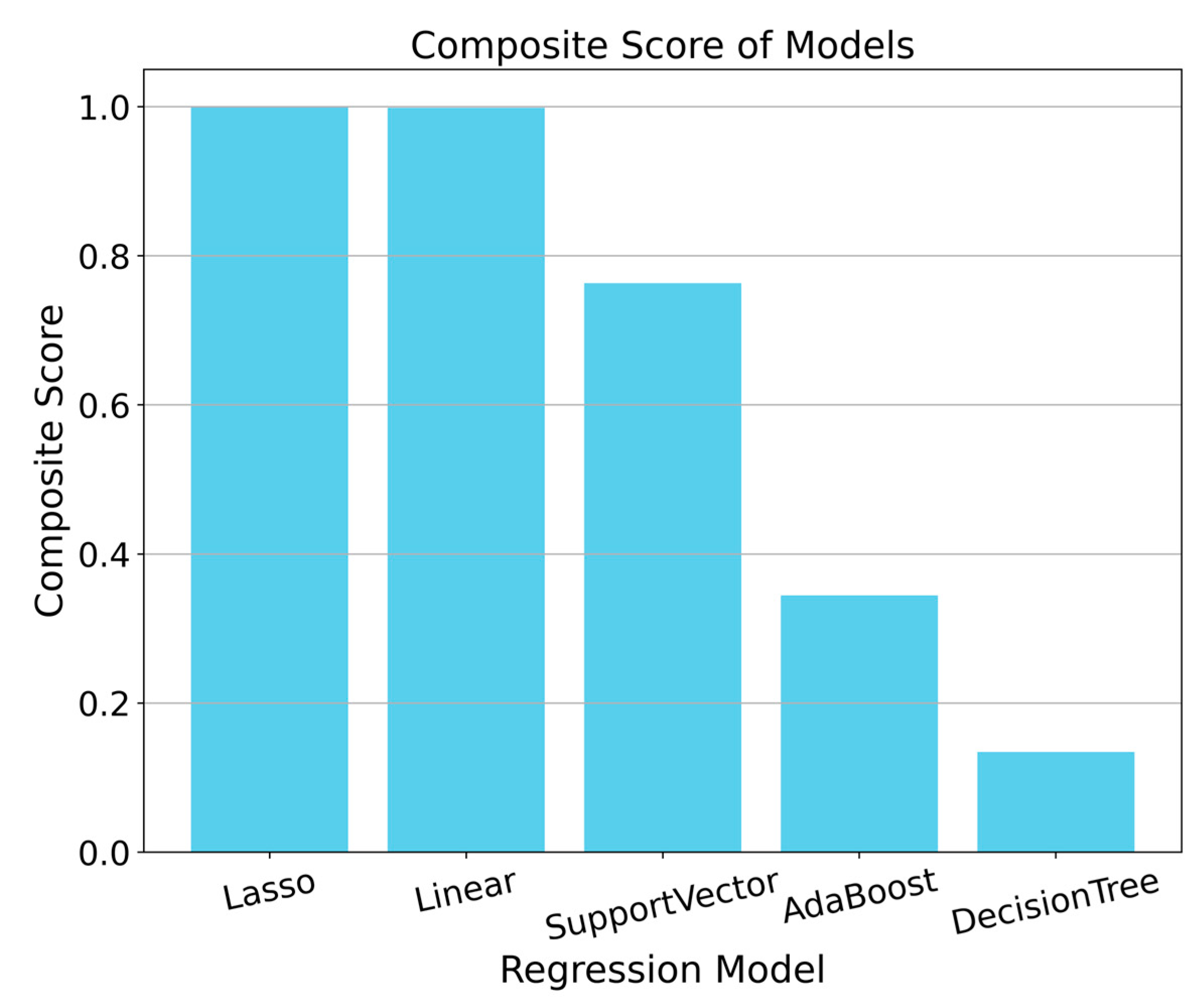
3.3.3. Comprehensive Score
3.4. Important Feature Analysis Results
4. Discussion
4.1. Lasso Feature Selection and Analysis Results
4.2. Model Comparison Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meng, X.; Ye, Z.; Wang, Y. Current Status and Advances in Biological Research of Yellowfin Tuna Fisheries Worldwide. South. Fish. 2007, 4, 74–80. [Google Scholar]
- Carson, S.; Shackell, N.; Mills Flemming, J. Local overfishing may be avoided by examining parameters of a spatio-temporal model. PLoS ONE 2017, 12, e0184427. [Google Scholar] [CrossRef] [PubMed]
- Skirtun, M.; Pilling, G.M.; Reid, C.; Hampton, J. Trade-offs for the southern longline fishery in achieving a candidate South Pacific albacore target reference point. Mar. Policy 2019, 100, 66–75. [Google Scholar]
- Maunder, M.N.; Sibert, J.R.; Fonteneau, A.; Hampton, J.; Kleiber, P.; Harley, S.J. Interpreting catch per unit effort data to assess the status of individual stocks and communities. Ices J. Mar. Sci. 2006, 63, 1373–1385. [Google Scholar] [CrossRef]
- Wu, Y.-L.; Lan, K.-W.; Tian, Y. Determining the effect of multiscale climate indices on the global yellowfin tuna (Thunnus albacares) population using a time series analysis. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2020, 175, 104808. [Google Scholar] [CrossRef]
- Vandana, C.; Chikkamannur, A.A. Feature selection: An empirical study. Int. J. Eng. Trends Technol. 2021, 69, 165–170. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zou, H. The adaptive lasso and its oracle properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
- Lu, W.; Jubo, S. Application of Lasso Regression Method in Feature Variable Selection. J. Jilin Eng. Technol. Norm. Coll. 2021, 37, 109–112. [Google Scholar]
- Ogutu, J.O.; Schulz-Streeck, T.; Piepho, H.-P. Genomic selection using regularized linear regression models: Ridge regression, lasso, elastic net and their extensions. In BMC Proceedings; BioMed Central: London, UK, 2012; pp. 1–6. [Google Scholar]
- Chintalapudi, N.; Angeloni, U.; Battineni, G.; Di Canio, M.; Marotta, C.; Rezza, G.; Sagaro, G.G.; Silenzi, A.; Amenta, F. LASSO regression modeling on prediction of medical terms among seafarers’ health documents using tidy text mining. Bioengineering 2022, 9, 124. [Google Scholar] [CrossRef]
- Lee, J.H.; Shi, Z.; Gao, Z. On LASSO for predictive regression. J. Econom. 2022, 229, 322–349. [Google Scholar] [CrossRef]
- Rasmussen, M.A.; Bro, R. A tutorial on the Lasso approach to sparse modeling. Chemom. Intell. Lab. Syst. 2012, 119, 21–31. [Google Scholar] [CrossRef]
- Czaja, R., Jr.; Hennen, D.; Cerrato, R.; Lwiza, K.; Pales-Espinosa, E.; O’Dwyer, J.; Allam, B. Using LASSO regularization to project recruitment under CMIP6 climate scenarios in a coastal fishery with spatial oceanographic gradients. Can. J. Fish. Aquat. Sci. 2023, 80, 1032–1046. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, X.; Lu, J.; Pan, J. Lasso regression: From explanation to prediction. Adv. Psychol. Sci. 2020, 28, 1777. [Google Scholar] [CrossRef]
- Feng, G.; Polson, N.; Wang, Y.; Xu, J. Sparse Regularization in Marketing and Economics. 2018. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3022856 (accessed on 23 April 2024). [CrossRef]
- Zhang, C.; Zhou, W.; Tang, F.; Shi, Y.; Fan, W. Prediction Model of Yellowfin Tuna Fishing Ground in the Central and Western Pacific Based on Machine Learning. Trans. Chin. Soc. Agric. Eng. 2022, 38, 330–338. [Google Scholar]
- Feng, Y.; Chen, X.; Gao, F.; Liu, Y. Impacts of changing scale on Getis-Ord Gi* hotspots of CPUE: A case study of the neon flying squid (Ommastrephes bartramii) in the northwest Pacific Ocean. Acta Oceanol. Sin. 2018, 37, 67–76. [Google Scholar] [CrossRef]
- Liu, P.; Ma, Y.; Guo, Y. Exploration of Factors Influencing Food Consumption Expenditure of Rural Residents in Sichuan Province Based on LASSO Method. China Agric. Resour. Reg. Plan. 2020, 41, 213–219. [Google Scholar]
- Sheng, Z.; Xie, S.; Pan, C. Probability Theory and Mathematical Statistics; Higher Education Press: Beijing, China, 2008; pp. 106–112. [Google Scholar]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y. Research on Ship Daily Fuel Consumption Prediction Based on LASSO. Navig. China 2022, 45, 129–132. [Google Scholar]
- Song, L.; Shen, Z.; Zhou, J.; Li, D. Influence of Marine Environmental Factors on Yellowfin Tuna Catch Rate in the Waters of the Cook Islands. J. Shanghai Ocean. Univ. 2016, 25, 454–464. [Google Scholar]
- Cui, X.; Fan, W.; Zhang, J. Distribution of Pacific Yellowfin Tuna Longline Fishing Catches and Analysis of Fishing Ground Water Temperature. Mar. Sci. Bull. 2005, 5, 54–59. [Google Scholar]
- Ji, S.; Zhou, W.; Wang, L.; Tang, F.; Wu, Z.; Chen, G. Relationship between temporal-spatial distribution of yellowfin tuna Thunnus albacares fishing grounds and sea surface temperature in the South China Sea and adjacent waters. Mar. Fish. 2016, 38, 9–16. [Google Scholar]
- Zhang, H.; Dai, Y.; Yang, S.; Wang, X.; Liu, G.; Chen, X. Vertical movement characteristics of tuna (Thunnus albacares) in Pacific Ocean determined using pop-up satellite archival tags. Trans. Chin. Soc. Agric. Eng. 2014, 30, 196–203. [Google Scholar]
- Burrows, M.T.; Bates, A.E.; Costello, M.J.; Edwards, M.; Edgar, G.J.; Fox, C.J.; Halpern, B.S.; Hiddink, J.G.; Pinsky, M.L.; Batt, R.D. Ocean community warming responses explained by thermal affinities and temperature gradients. Nat. Clim. Chang. 2019, 9, 959–963. [Google Scholar] [CrossRef]
- Song, T.; Fan, W.; Wu, Y. Application Overview of Satellite Remote Sensing Sea Surface Height Data in Fishery Analysis. Mar. Bull. 2013, 32, 474–480. [Google Scholar]
- Adnan, N.A.; Izdihar, R.M.A.; Qistina, F.; Fadilah, S.; Kadir, S.T.S.A.; Mat, A.; Sulaiman, S.A.M.P.; Seah, Y.G.; Muslim, A.M. Chlorophyll-a estimation and relationship analysis with sea surface temperature and fish diversity. J. Sustain. Sci. Manag. 2022, 17, 133–150. [Google Scholar] [CrossRef]
- Sagarminaga, Y.; Arrizabalaga, H. Relationship of Northeast Atlantic albacore juveniles with surface thermal and chlorophyll-a fronts. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2014, 107, 54–63. [Google Scholar] [CrossRef]
- Wyrtki, K.; Magaard, L.; Hager, J. Eddy energy in the oceans. J. Geophys. Res. 1976, 81, 2641–2646. [Google Scholar] [CrossRef]
- Wang, J. Response of Abundance of Main Small Pelagic Fish Resources in the Northwestern Pacific to Large-Scale Climate-Ocean Environmental Changes. Doctoral Dissertation, Shanghai Ocean University, Shanghai, China, 2021. [Google Scholar]
- Mantua, N.J.; Hare, S.R. The Pacific decadal oscillation. J. Oceanogr. 2002, 58, 35–44. [Google Scholar] [CrossRef]
- Vimont, D.J. The contribution of the interannual ENSO cycle to the spatial pattern of decadal ENSO-like variability. J. Clim. 2005, 18, 2080–2092. [Google Scholar] [CrossRef]
- Vaihola, S.; Yemane, D.; Kininmonth, S. Spatiotemporal Patterns in the Distribution of Albacore, Bigeye, Skipjack, and Yellowfin Tuna Species within the Exclusive Economic Zones of Tonga for the Years 2002 to 2018. Diversity 2023, 15, 1091. [Google Scholar] [CrossRef]
- Wiryawan, B.; Loneragan, N.; Mardhiah, U.; Kleinertz, S.; Wahyuningrum, P.I.; Pingkan, J.; Wildan; Timur, P.S.; Duggan, D.; Yulianto, I. Catch per unit effort dynamic of yellowfin tuna related to sea surface temperature and chlorophyll in Southern Indonesia. Fishes 2020, 5, 28. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, W.; Fan, W. Research on Prediction Model of Yellowfin Tuna Fishing Ground in the South Pacific Based on ADASYN and Stacking Ensemble. Mar. Fish. 2023, 45, 544–558. [Google Scholar]
- Yang, S.; Zhang, B.; Zhang, H.; Zhang, S.; Wu, Y.; Zhou, W.; Feng, C. Research Progress on Vertical Movement and Water Column Distribution of Yellowfin Tuna. Fish. Sci. 2019, 38, 119–126. [Google Scholar]
- Schaefer, K.M.; Fuller, D.W.; Block, B.A. Movements, behavior, and habitat utilization of yellowfin tuna (Thunnus albacares) in the northeastern Pacific Ocean, ascertained through archival tag data. Mar. Biol. 2007, 152, 503–525. [Google Scholar] [CrossRef]
- Mao, Z.; Zhu, Q.; Gong, F. Satellite Remote Sensing of Chlorophyll-a Concentration in the North Pacific Fishing Grounds. J. Fish. Sci. 2005, 2, 270–274. [Google Scholar]
- Brandini, F.P.; Boltovskoy, D.; Piola, A.; Kocmur, S.; Röttgers, R.; Abreu, P.C.; Lopes, R.M. Multiannual trends in fronts and distribution of nutrients and chlorophyll in the southwestern Atlantic (30–62 S). Deep. Sea Res. Part I Oceanogr. Res. Pap. 2000, 47, 1015–1033. [Google Scholar] [CrossRef]
- Charlock, T.P. Mid-latitude model analysis of solar radiation, the upper layers of the sea, and seasonal climate. J. Geophys. Res. Ocean. 1982, 87, 8923–8930. [Google Scholar] [CrossRef]
- Wu, Y.-L.; Lan, K.-W.; Evans, K.; Chang, Y.-J.; Chan, J.-W. Effects of decadal climate variability on spatiotemporal distribution of Indo-Pacific yellowfin tuna population. Sci. Rep. 2022, 12, 13715. [Google Scholar] [CrossRef]
- Zhou, W.; Hu, H.; Fan, W.; Jin, S. Impact of abnormal climatic events on the CPUE of yellowfin tuna fishing in the central and western Pacific. Sustainability 2022, 14, 1217. [Google Scholar] [CrossRef]
- Lian, P.; Gao, L. Impacts of central-Pacific El Niño and physical drivers on eastern Pacific bigeye tuna. J. Oceanol. Limnol. 2024, 1–16. Available online: https://link.springer.com/article/10.1007/s00343-023-3051-3 (accessed on 23 April 2024).
- Di Lorenzo, E.; Schneider, N.; Cobb, K.M.; Franks, P.; Chhak, K.; Miller, A.J.; McWilliams, J.C.; Bograd, S.J.; Arango, H.; Curchitser, E. North Pacific Gyre Oscillation links ocean climate and ecosystem change. Geophys. Res. Lett. 2008, 35. Available online: https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2007GL032838 (accessed on 23 April 2024). [CrossRef]
- Fan, L.; Chen, S.; Li, Q.; Zhu, Z. Variable selection and model prediction based on lasso, adaptive lasso and elastic net. In Proceedings of the 2015 4th International Conference on Computer Science and Network Technology (ICCSNT), Harbin, China, 19–20 December 2015; pp. 579–583. [Google Scholar]
- Abbas, F.; Cai, Z.; Shoaib, M.; Iqbal, J.; Ismail, M.; Ullah, A.; Alrefaei, A.F.; Albeshr, M.F. Uncertainty Analysis of Predictive Models for Water Quality Index: Comparative Analysis of XGBoost, Random Forest, SVM, KNN, Gradient Boosting, and Decision Tree Algorithms. 2024. Available online: https://www.preprints.org/manuscript/202402.0828/v1 (accessed on 23 April 2024).

| Optimal Parameter Names | Values | Parameter Description |
|---|---|---|
| Optimal metric value | 0.088 | Optimal performance value of the model |
| λ | 0.001 | Regularization parameter controlling model complexity |
| Max_iter | 6522 | Maximum number of iterations |
| Random_state | 74 | Seed number for the random number generator |
| Model\Score | MAE | EVS | MSE | RMSE | R2 |
|---|---|---|---|---|---|
| Lasso | 1.911046 | 0.071288 | 13.894650 | 3.727553 | 0.069545 |
| DecisionTree | 2.131442 | −0.390487 | 20.764380 | 4.556795 | −0.390487 |
| SupportVector | 1.918458 | 0.003234 | 16.189937 | 4.023672 | −0.084159 |
| Linear | 1.911564 | 0.070548 | 13.906065 | 3.729084 | 0.068780 |
| AdaBoost | 3.057544 | −0.064498 | 18.747417 | 4.329829 | −0.255421 |
| Feature | Coefficients | Absolute Coefficients | Feature | Coefficients | Absolute Coefficients |
|---|---|---|---|---|---|
| sst_bf | 1.07429 | 1.07429 | year | 0.13599 | 0.13599 |
| sst_af | 0.73373 | 0.73373 | month | 0.11473 | 0.11473 |
| lat | 0.48905 | 0.48905 | sstgrad | −0.08588 | 0.08588 |
| T300 | −0.42464 | 0.42464 | AOI | 0.07261 | 0.07261 |
| T450 | 0.37660 | 0.37660 | SOI | 0.06958 | 0.06958 |
| sstdt | −0.36844 | 0.36844 | T150 | −0.06753 | 0.06753 |
| ONI | 0.27822 | 0.27822 | chldt | 0.04875 | 0.04875 |
| NPGIO | 0.20137 | 0.20137 | chl_af | −0.03257 | 0.03257 |
| chlgrad | −0.17869 | 0.17869 | eke | −0.00739 | 0.00739 |
| chl | 0.16932 | 0.16932 | PDOI | −0.00466 | 0.00466 |
| chl_bf | 0.15967 | 0.15967 | lon | 0.00410 | 0.00410 |
| T0 | 0.15039 | 0.15039 | sla | −0.00366 | 0.00366 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Zhou, W. Feature Selection for Explaining Yellowfin Tuna Catch per Unit Effort Using Least Absolute Shrinkage and Selection Operator Regression. Fishes 2024, 9, 204. https://doi.org/10.3390/fishes9060204
Yang L, Zhou W. Feature Selection for Explaining Yellowfin Tuna Catch per Unit Effort Using Least Absolute Shrinkage and Selection Operator Regression. Fishes. 2024; 9(6):204. https://doi.org/10.3390/fishes9060204
Chicago/Turabian StyleYang, Ling, and Weifeng Zhou. 2024. "Feature Selection for Explaining Yellowfin Tuna Catch per Unit Effort Using Least Absolute Shrinkage and Selection Operator Regression" Fishes 9, no. 6: 204. https://doi.org/10.3390/fishes9060204
APA StyleYang, L., & Zhou, W. (2024). Feature Selection for Explaining Yellowfin Tuna Catch per Unit Effort Using Least Absolute Shrinkage and Selection Operator Regression. Fishes, 9(6), 204. https://doi.org/10.3390/fishes9060204





