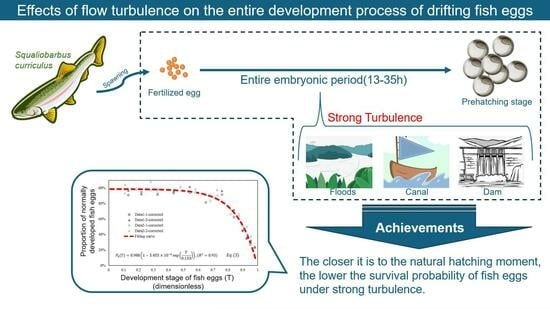
Effects of Flow Turbulence on the Entire Development Process of Drifting Fish Eggs
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Equipments
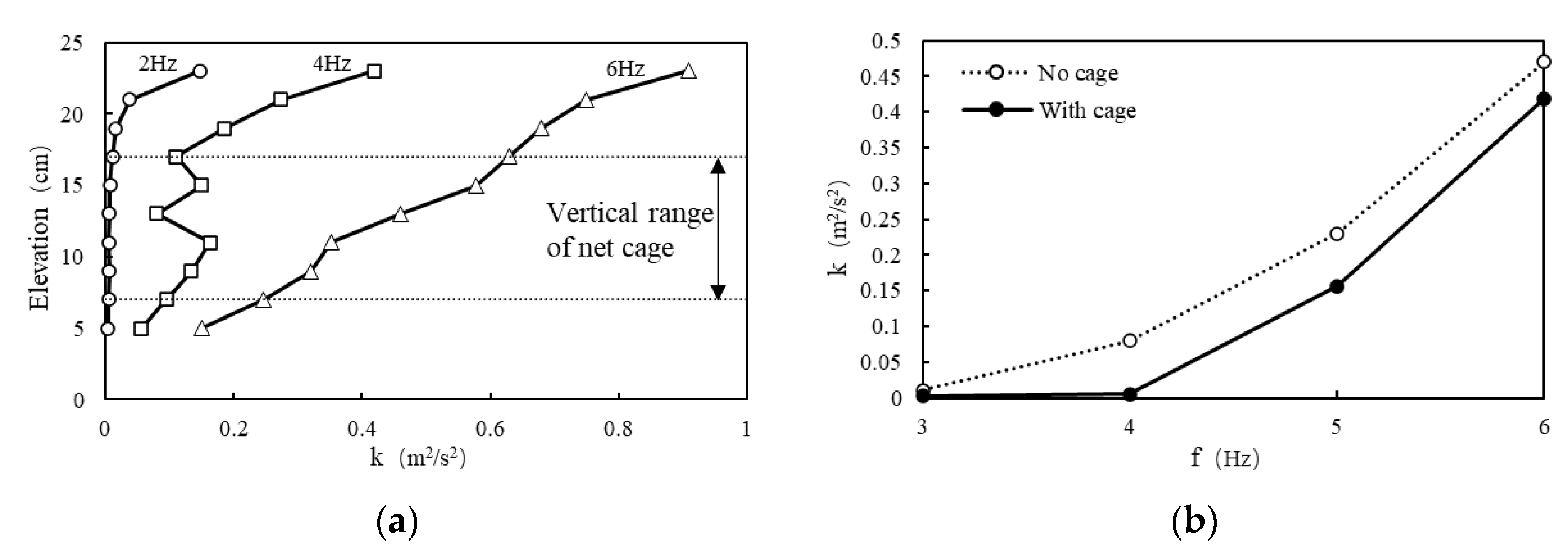
2.2. Calibration of the Tank Flow Turbulence
2.3. Experimental Protocol
3. Results
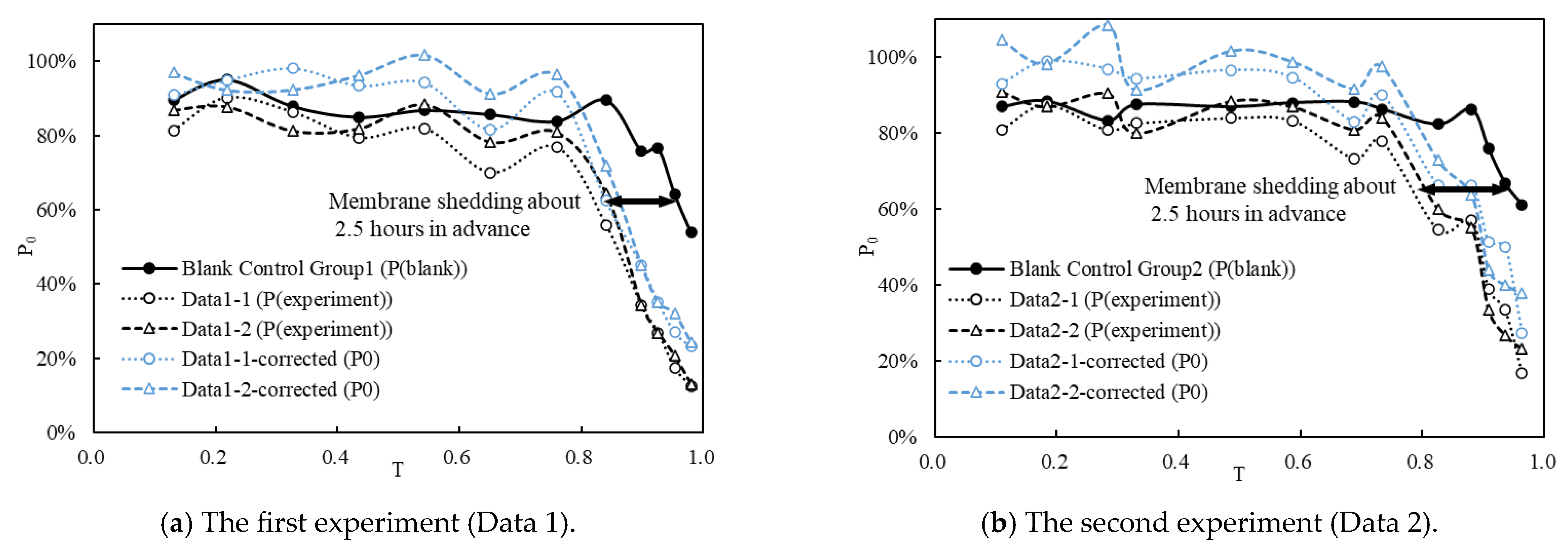
3.1. Effects of Typical FTC on Fish Eggs at Various Developmental Stages
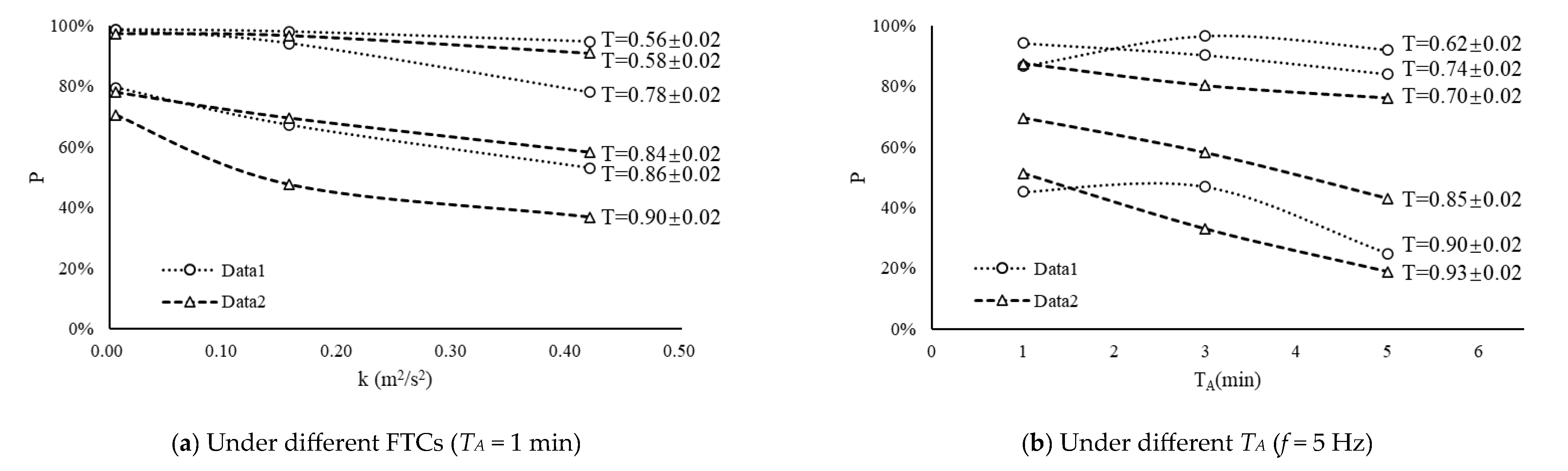
3.2. Effects of FTCs and TA on Fish Eggs
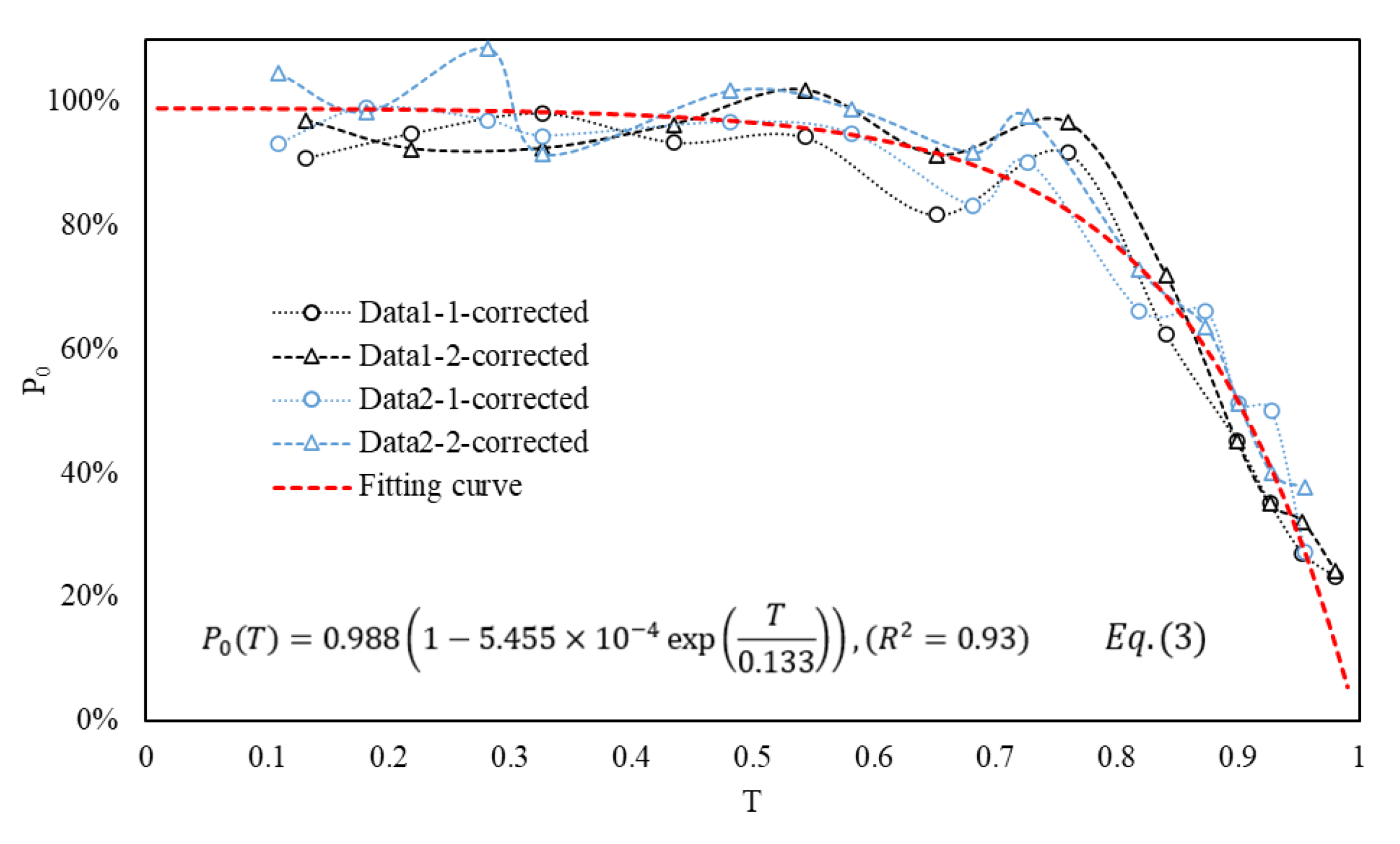
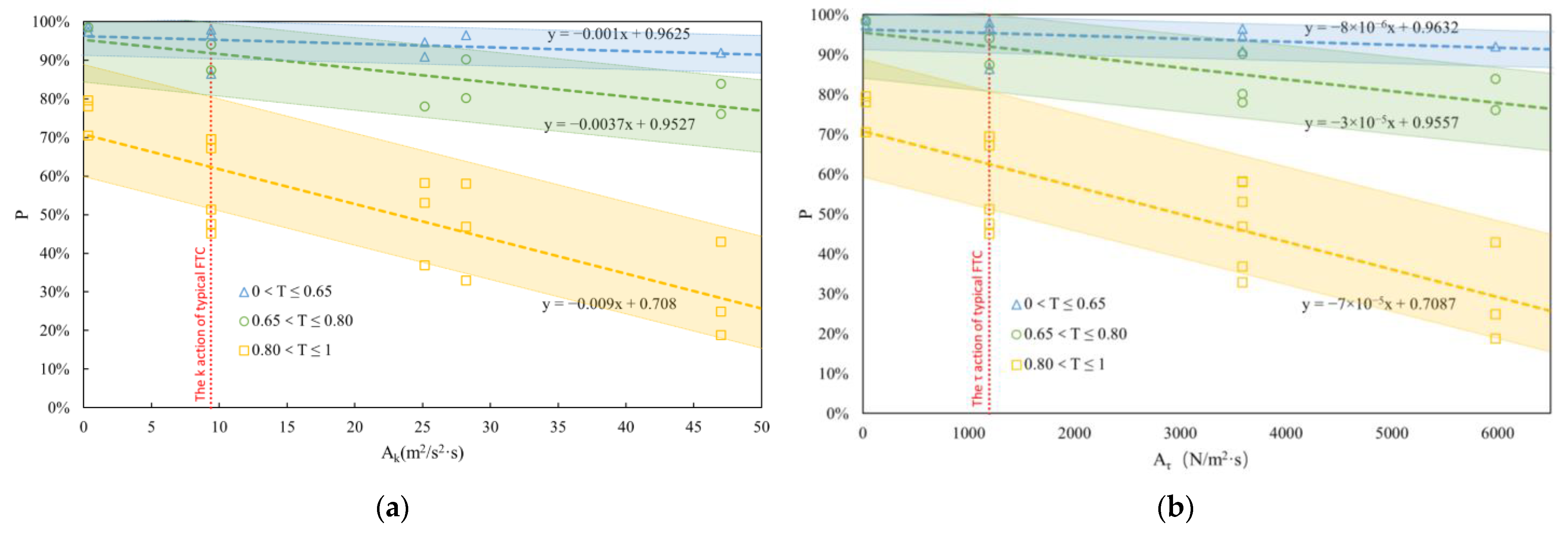
3.3. Establishment of Empirical Formulas
4. Discussion
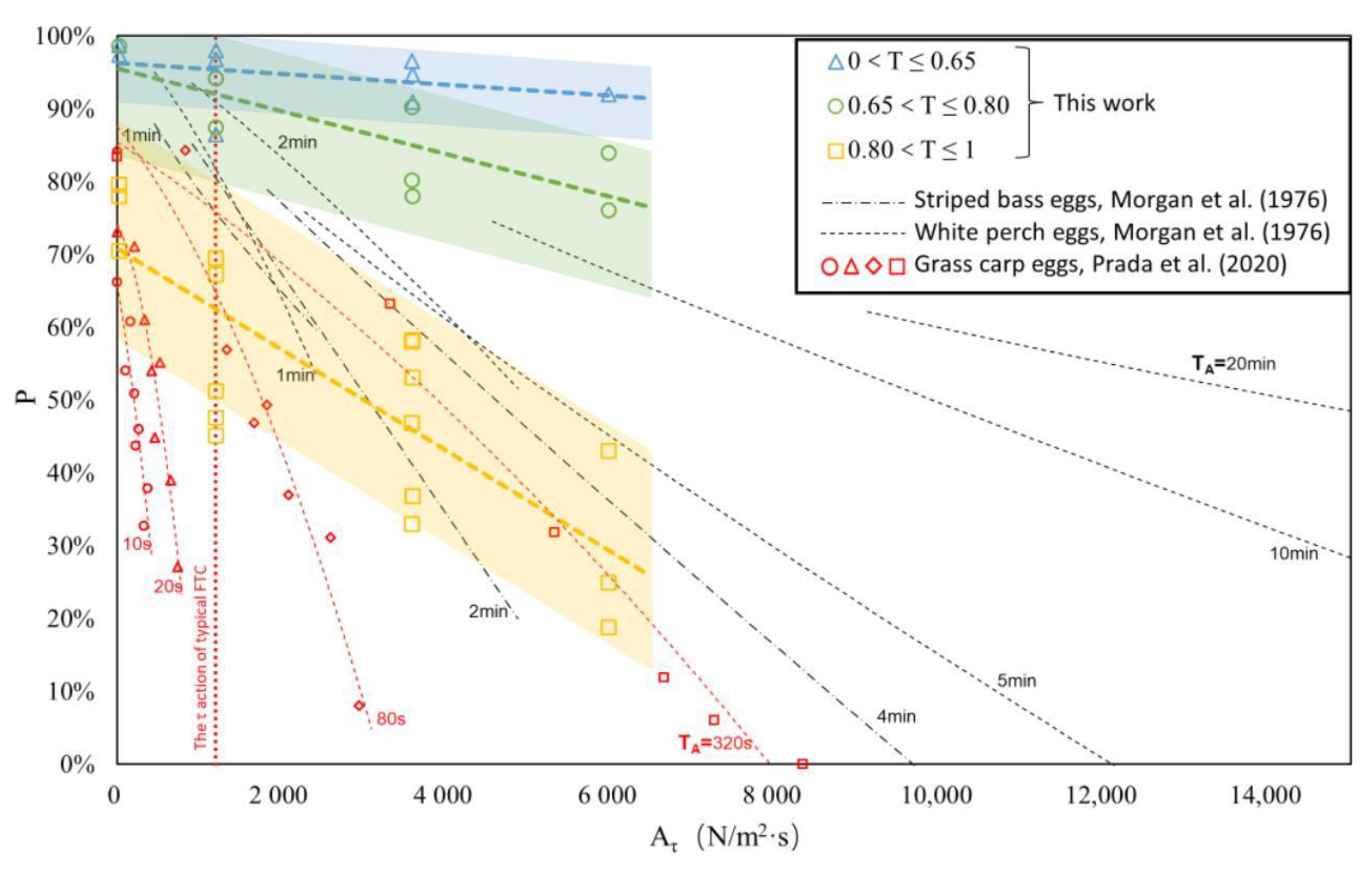
4.1. Comparison with Existing Achievements
4.2. Internal Mechanism of Fish Egg Hatching
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Coutant, C.C.; Whitney, R.R. Fish Behavior in Relation to Passage through Hydropower Turbines: A Review. Trans. Am. Fish. Soc. 2000, 129, 351–380. [Google Scholar] [CrossRef]
- Odeh, M.; Noreika, J.F.; Haro, A. Evaluation of the Effects of Turbulence on the Behavior of Migratory Fish, Final Report 2002; Bonneville Power Administration (BPA): Portland, OR, USA, 2002. [Google Scholar]
- Duan, J.G. Mean Flow and Turbulence around a Laboratory Spur Dike. J. Hydraul. Eng. 2009, 135, 803–811. [Google Scholar] [CrossRef]
- Quaranta, E.; Katopodis, C.; Revelli, R.; Comoglio, C. Turbulent flow field comparison and related suitability for fish passage of a standard and a simplified low-gradient vertical slot fishway. River Res. Appl. 2017, 33, 1295–1305. [Google Scholar] [CrossRef]
- Deng, Y.; Cao, M.; Ma, A.; Hu, Y.; Chang, L. Mechanism study on the impacts of hydraulic alteration on fish habitat induced by spur dikes in a tidal reach. Ecol. Eng. 2019, 134, 78–92. [Google Scholar] [CrossRef]
- Ye, F.; Zhang, J. Fish Ecology; Guangdong Higher Education Press: Guangzhou, China, 2002. [Google Scholar]
- Killgore, K.J.; Maynord, S.T.; Chan, M.D.; Morgan, R.P. Evaluation of Propeller-Induced Mortality on Early Life Stages of Selected Fish Species. N. Am. J. Fish. Manag. 2001, 21, 947–955. [Google Scholar] [CrossRef]
- Čada, G.F. The Development of Advanced Hydroelectric Turbines to Improve Fish Passage Survival. Fisheries 2001, 26, 14–23. [Google Scholar] [CrossRef]
- Morgan, R.P.; Ulanowicz, R.E.; Rasin, V.J.; Noe, L.A.; Gray, G.B. Effects of Shear on Eggs and Larvae of Striped Bass, Morone saxatilis, and White Perch, M. americana. Trans. Am. Fish. Soc. 1976, 105, 149–154. [Google Scholar] [CrossRef]
- Zeng, Z.; Guo, B.; Li, X.; Fu, X.; Chen, Y.; Wu, H.; Zhang, L.; Chen, J.; Ding, S. A simple and smart AND-gate DNA nanoprobe for correlated enzymes tracking and cell-selective imaging. Biosens. Bioelectron. 2022, 217, 114724. [Google Scholar] [CrossRef]
- Fedorenko, A.; Fraiser, F. Review of Grass Carp Biology. Fisheries and Marine Service Technical Rep No.786; Fisheries and Marine Serice: Vancouver, BC, Canada, 1978. [Google Scholar]
- Garcia, T.; Murphy, E.A.; Jackson, P.R.; Garcia, M.H. Application of the FluEgg model to predict transport of Asian carp eggs in the Saint Joseph River (Great Lakes tributary). J. Great Lakes Res. 2015, 41, 374–386. [Google Scholar] [CrossRef]
- Embke, H.S.; Kocovsky, P.M.; Garcia, T.; Mayer, C.M.; Qian, S.S. Modeling framework to estimate spawning and hatching locations of pelagically spawned eggs. Can. J. Fish. Aquat. Sci. 2019, 76, 597–607. [Google Scholar] [CrossRef]
- Jennings, D.P. Bighead Carp (Hypophthalmichthys nobilis): Biological Synopsis; Fish and Wildlife Service, US Department of the Interior: Washington, DC, USA, 1988; Volume 88, No. 29. [Google Scholar]
- Chapman, D.C. Early Development of Four Cyprinids Native to the Yangtze River, China. USGS Prof. Pap. 2006, 239, 1–51. [Google Scholar] [CrossRef]
- Yi, Y.; Wang, Z.; Yang, Z. Impact of the Gezhouba and Three Gorges Dams on habitat suitability of carps in the Yangtze River. J. Hydrol. 2010, 387, 283–291. [Google Scholar] [CrossRef]
- Deng, Y. Mechanism Study on the Impacts of Flow on Fish Living Environment around Spur Dikes in a Tidal Reach. Ph.D. Thesis, Hohai University, Nanjing, China, 2020. [Google Scholar]
- Albrecht, A.B. Some observations on factors associated with survival of striped bass eggs and larvae. Calif. Fish Game 1964, 50, 100–113. [Google Scholar]
- Conover, G.; Simmonds, R.; Whalen, M. Management and Control Plan for Bighead, Black, Grass, and Silver Carps in the United States; Asian Carp Working Group, Aquatic Nuisance Species Task Force: Washington, DC, USA, 2007; p. 223. [Google Scholar]
- Murphy, E.A.; Jackson, P.R. Hydraulic and water-quality data collection for the investigation of Great Lakes tributaries for Asian carp spawning and egg-transport suitability. In U.S. Geological Survey Scientific Investigations Report 2013–5106; U.S. Geological Survey: Sunrise Valley Drive Reston, VA, USA, 2013; p. 30. [Google Scholar] [CrossRef]
- George, A.E.; Chapman, D.C. Embryonic and larval development and early behavior in grass carp, Ctenopharyngodon idella: Implications for recruitment in rivers. PLoS ONE 2015, 10, e0119023. [Google Scholar] [CrossRef]
- Liu, M.; Lin, J.; Peng, Q.; Yu, L.; Chen, D.; Liu, S.; Duan, X. Relationship between the Distribution of Broodstock and Vorticity of Spawning Grounds of Four Major Chinese Carps in the Middle Reaches of the Yangtze River during Ecological Operation of the Three Gorges Dam. Water 2018, 10, 1487. [Google Scholar] [CrossRef]
- Prada, A.F.; George, A.E.; Stahlschmidt, B.H.; Chapman, D.C.; Tinoco, R.O. Survival and drifting patterns of grass carp eggs and larvae in response to interactions with flow and sediment in a laboratory flume. PLoS ONE 2018, 13, e0208326. [Google Scholar] [CrossRef]
- Ruggles, C.P. A Review of the Downstream Migration of Atlantic Salmon; Govemment of Canada Fisheries and Oceans: Halifax, NS, Canada, 1980. [Google Scholar]
- Ruggles, C.P.; Murray, D.G. A Review of Fish Response to Spillways; Govemment of Canada Fisheries and Oceans: Halifax, NS, Canada, 1983. [Google Scholar]
- Čada, G.F.; Coutant, C.C.; Whitney, R.R. Development of Biological Criteria for the Design of Advanced Hydropower Turbines; EERE Publication and Product Library: Washington, DC, USA, 1997. [Google Scholar]
- Čada, G.; Carlson, T.; Ferguson, J.; Richmond, M.; Sale, M. Exploring the Role of Shear Stress and Severe Turbulence in Downstream Fish Passage. In Proceedings of the Waterpower Conference, Las Vegas, NV, USA, 6–9 July 1999; pp. 1–9. [Google Scholar] [CrossRef]
- Pracheil, B.M.; DeRolph, C.R.; Schramm, M.P.; Bevelhimer, M.S. A fish-eye view of riverine hydropower systems: The current understanding of the biological response to turbine passage. Rev. Fish Biol. Fish. 2016, 26, 153–167. [Google Scholar] [CrossRef]
- Maynord, S.T. Concentric Cylinder Experiments of Shear Mortality of Eggs and Larval Fish.Upper Mississippi River-Illinois Waterway, Environmental Report; U.S. Army Engineer Research and Development Center: Vicksburg, MS, USA, 2000. [Google Scholar]
- Prada, A.F.; George, A.E.; Stahlschmidt, B.H.; Jackson, P.R.; Chapman, D.C.; Tinoco, R.O. Influence of turbulence and in-stream structures on the transport and survival of grass carp eggs and larvae at various developmental stages. Aquat. Sci. 2019, 82, 16. [Google Scholar] [CrossRef]
- Hockley, F.A.; Wilson, C.A.; Brew, A.; Cable, J. Fish responses to flow velocity and turbulence in relation to size, sex and parasite load. J. R. Soc. Interface 2014, 11, 20130814. [Google Scholar] [CrossRef]
- Goettel, M.T.; Atkinson, J.F.; Bennett, S.J. Behavior of western blacknose dace in a turbulence modified flow field. Ecol. Eng. 2015, 74, 230–240. [Google Scholar] [CrossRef]
- Suga, N. Change of the Toughness of the Chorion of Fish Eggs. Embryologia 1963, 8, 63–74. [Google Scholar] [CrossRef]
- Prada Sepulveda, A.F. The Effect of Turbulence on Survival, Dispersal, and Swimming Behavior of Grass Carp Eggs and Larvae. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Urbana, IL, USA, 2020. [Google Scholar]
- Song, X.; Xu, G. Research progress on reproductive biology of Squaliobarbus curriculus. Hebei Fish. 2007, 06, 6–8+49+53. [Google Scholar]
- Silva, A.T.; Katopodis, C.; Santos, J.M.; Ferreira, M.T.; Pinheiro, A.N. Cyprinid swimming behaviour in response to turbulent flow. Ecol. Eng. 2012, 44, 314–328. [Google Scholar] [CrossRef]
- Srdic, A.; Fernando, H.J.S.; Montenegro, L. Generation of nearly isotropic turbulence using two oscillating grids. Exp. Fluids 1996, 20, 395–397. [Google Scholar] [CrossRef]
- Hu, J. Hydraulic Characteristics of a New Permeable Spur Dike and Its Effect on Fish Behavior. Ph.D. Thesis, Chongqing Jiaotong University, Chongqing, China, 2021. [Google Scholar]
- Yang, S. River Dynamic Characteristics and Pattern Discriminant Method Influenced by Riparian Vegetation. Ph.D. Thesis, Tianjin University, Tianjin, China, 2019. [Google Scholar]
- Marriner, B.A.; Baki, A.B.M.; Zhu, D.Z.; Thiem, J.D.; Cooke, S.J.; Katopodis, C. Field and numerical assessment of turning pool hydraulics in a vertical slot fishway. Ecol. Eng. 2014, 63, 88–101. [Google Scholar] [CrossRef]
- Maeda, S.; Yoshida, K.; Kuroda, H. Turbulence and energetics of fish nest and pool structures in agricultural canal. Paddy Water Environ. 2018, 16, 493–505. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, J. Numerical Modeling of 3D Flow Field among a Compound Stilling Basin. Math. Probl. Eng. 2019, 2019, 1–17. [Google Scholar] [CrossRef]
- Lancaster, J.; Hildrew, A.G. Characterizing In-stream Flow Refugia. Can. J. Fish. Aquat. Sci. 1993, 50, 1663–1675. [Google Scholar] [CrossRef]
- Costa, J.E. Hydraulics and basin morphometry of the largest flash floods in the conterminous United States. J. Hydrol. 1987, 93, 313–338. [Google Scholar] [CrossRef]
- George, A.E.; Garcia, T.; Chapman, D.C. Comparison of Size, Terminal Fall Velocity, and Density of Bighead Carp, Silver Carp, and Grass Carp Eggs for Use in Drift Modeling. Trans. Am. Fish. Soc. 2017, 146, 834–843. [Google Scholar] [CrossRef]
- Yamagami, K. Mechanisms of Hatching in Fish: Secretion of Hatching Enzyme and Enzymatic Choriolysis. Am. Zool. 1981, 21, 459–471. [Google Scholar] [CrossRef]
- Torby, B.J.; Saunders, H. Advanced Dynamics For Engineers. J. Vib. Acoust. 1988, 110, 124–125. [Google Scholar] [CrossRef]
- Wen, X.; Feng, H.; Li, W.; Zhang, Y.; Zhang, R. Observation on early embryonic development of grass carp. Chin. J. Vet. Sci. 1991, 1, 90–171. [Google Scholar] [CrossRef]
- Hurley, N.M., Jr. Transport Simulation of Striped Bass Eggs in the Congaree, Wateree, and Santee Rivers, South Carolina. Water-Resources Investigations Report 91-4088; U.S. Geological Survey: Sunrise Valley Drive Reston, VA, USA, 1991. [Google Scholar]
- Mansueti, R.J. Eggs, Larvae, and Young of the White Perch, Roccus americanus, with Comments on Its Ecology in the Estuary. Chesap. Sci. 1964, 5, 3–45. [Google Scholar] [CrossRef]
- Fraysse, B.; Mons, R.; Garric, J. Development of a zebrafish 4-day embryo-larval bioassay to assess toxicity of chemicals. Ecotoxicol. Environ. Saf. 2006, 63, 253–267. [Google Scholar] [CrossRef]
- Helvik, J.V.; Oppen-Berntsen, D.O.; Flood, P.R.; Walther, B.T. Morphogenesis of the hatching gland of Atlantic halibut (Hippoglossus hippoglossus). Rouxs. Arch. Dev. Biol. 1991, 200, 180–187. [Google Scholar] [CrossRef]
- Melby, A.E.; Warga, R.M.; Kimmel, C.B. Specification of cell fates at the dorsal margin of the zebrafish gastrula. Development 1996, 122, 2225–2237. [Google Scholar] [CrossRef]
- Inohaya, K.; Yasumasu, S.; Yasumasu, I.; Iuchi, I.; Yamagami, K. Analysis of the origin and development of hatching gland cells by transplantation of the embryonic shield in the fish, Oryzias latipes. Dev. Growth Differ. 1999, 41, 557–566. [Google Scholar] [CrossRef]
- Hiroi, J.; Yasumasu, S.; Kawazu, K.; Kaneko, T. Hatching enzymes in the Japanese eel. Eel. Biol. 2003, 31, 445–456. [Google Scholar] [CrossRef]
- Rosenthal, H.; Iwai, T. Hatching glands in herring embryos. Mar. Ecol. Prog. Ser. 1979, 1, 123–127. [Google Scholar] [CrossRef]
- Rechulicz, J. Incubation temperature effects on the development of hatching gland cells in ide, Leuciscus idus [L.]. Electron. J. Pol. Agric. Univ. Ser. Fish. 2001, 4, 3. [Google Scholar]
- Ostaszewska, T. Hatching gland clls in embryos of pikeperch (Stizostedion lucioperca). Ann. Wars. Agric. Univ. Anim. Sci. 1989, 24, 3–5. [Google Scholar]
- Garcia, T.; Jackson, P.R.; Murphy, E.A.; Valocchi, A.J.; Garcia, M.H. Development of a Fluvial Egg Drift Simulator to evaluate the transport and dispersion of Asian carp eggs in rivers. Ecol. Model. 2013, 263, 211–222. [Google Scholar] [CrossRef]
- Li, G.; Wang, B.; Elliott, C.M.; Call, B.C.; Chapman, D.C.; Jacobson, R.B. A three-dimensional Lagrangian particle tracking model for predicting transport of eggs of rheophilic-spawning carps in turbulent rivers. Ecol. Model. 2022, 470, 110035. [Google Scholar] [CrossRef]
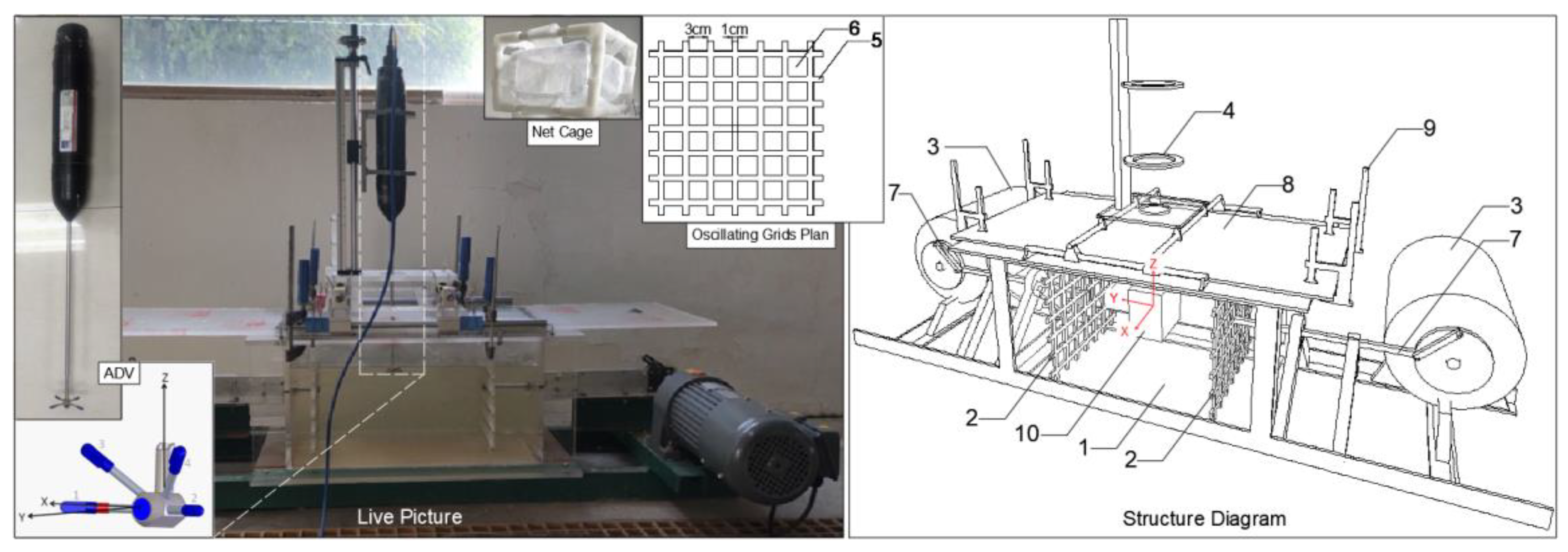
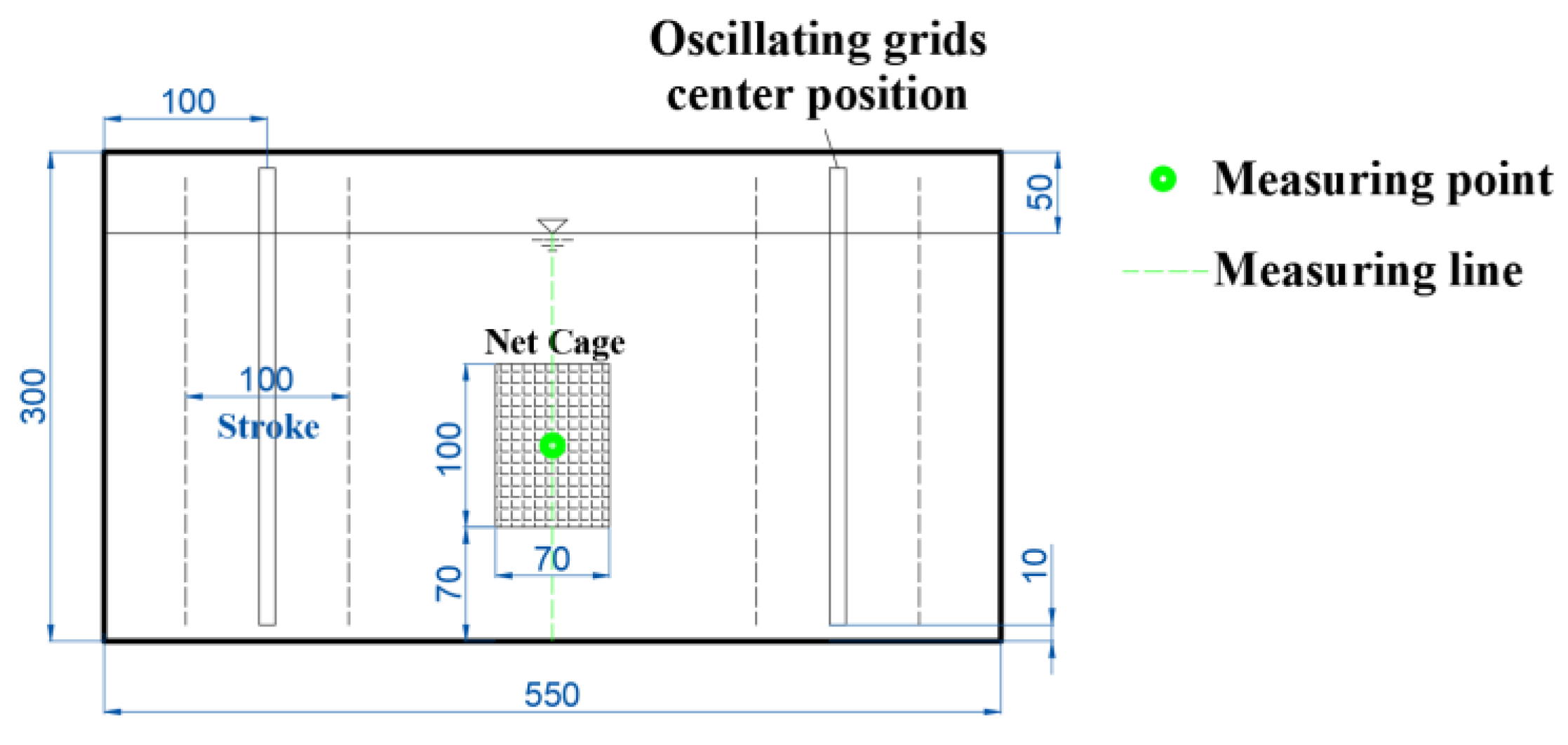

| Experimental Equipment | Size (cm) (l × w × h) | Main Usage |
|---|---|---|
| Transverse-oscillating-grids turbulence tank | 55 × 30 × 30 | Used to quantitatively generate the FTCs (abbreviation of flow turbulence conditions) required for the experiment. |
| ADV system | / | Used to calibrate the FTCs in the tank. |
| Net cage | 10 × 7× 10 | Used to limit the drift range of the eggs, prevent the mechanical collision caused by the oscillating grids to the eggs, and facilitate the collection of statistics. |
| Experiment | The First Experiment | The Second Experiment | ||||
|---|---|---|---|---|---|---|
| Insemination time | 31 August 2022 22:27 | 2 September 2022 21:00 | ||||
| Water temperature | 26 (±0.5) °C | 26.5 (±0.5) °C | ||||
| Parental attributes | Length cm | Width cm | Weight kg | Length cm | Width cm | Weight kg |
| Male fish 1 | 31 | 10 | 0.38 | 27 | 7 | 0.32 |
| Male fish 2 | 28 | 9 | 0.35 | 32 | 10 | 0.37 |
| Female fish 1 | 27 | 6 | 0.32 | 28 | 7 | 0.33 |
| Female fish 2 | 33 | 7 | 0.39 | 30 | 8 | 0.37 |
| Fertilization rate | >95% | >95% | ||||
| Hatching duration | 18.5 (±0.5) h | 18.2 (±0.5) h | ||||
| Experimental Conditions | f (Hz) | TA (min) | Remark |
|---|---|---|---|
| 0 | 0 | 0 | The blank group: Stillwater environment. Used to eliminate the influence generated by the experimental procedure. |
| 1 | 5 | 1 | Typical group intervals: 0.5–2 h, increasing frequency nearing hatching, covering entire fish egg development. |
| 2 | 4 | 1 | 1. Standard group initiation at P0 ≈ 75%. 2. Standard group intervals: 1–2 h, repeated three times. |
| 3 | 5 | 1 | |
| 4 | 6 | 1 | |
| 5 | 5 | 3 | |
| 6 | 5 | 5 |
| Reference | Experimental Equipment | Fish Egg Traits | Water Temp. (°C) | Experimental Conditions | |||||
|---|---|---|---|---|---|---|---|---|---|
| τ (N/m2) | TA | ||||||||
| Species | Property | Egg Diameter (mm) | Specific Gravity | Developmental Stage | |||||
| Morgan et al. (1976) [9] | Three-layer rotatable barrel | Striped bass 1 | Drifting eggs | 3.5 ± 0.5 | 1.00115 | Not mentioned | Not mentioned | 7.6–40.4 | 1–20 min |
| White perch | Sticky eggs | 0.9 ± 0.2 | High specific gravity | ||||||
| Prada et al. (2020) [34] | Oscillating-grid stirred turbulence tank | Grass carp | Drifting eggs | 4.5 ± 0.6 | 1.00210 | Water-hardened eggs | 23–24 | 0–40 | 10–320 s |
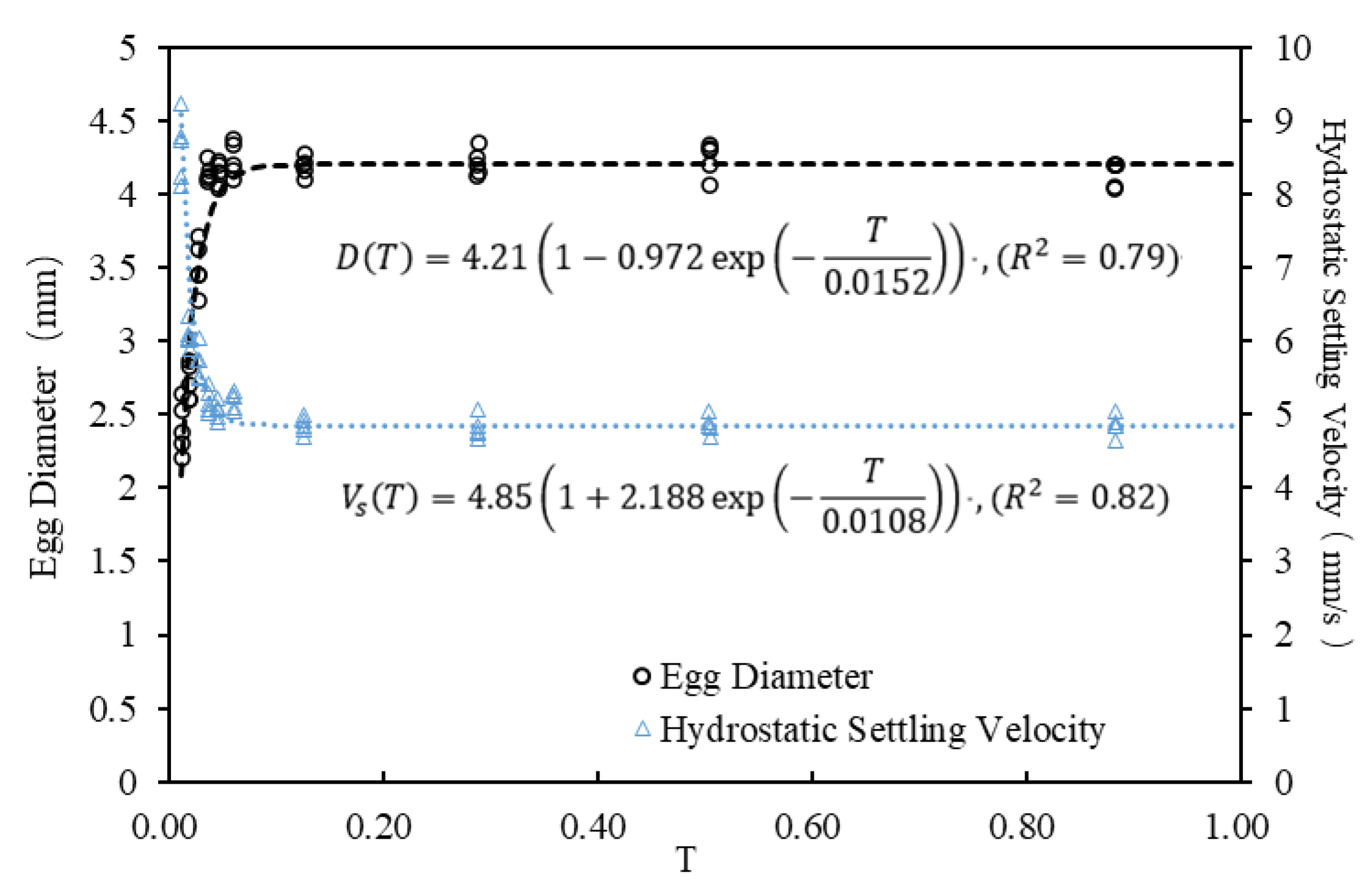
| This work | Transverse-oscillating-grid turbulence tank | S. curriculus | Drifting eggs | 4.2 ± 0.4 | 1.00101 | Entire embryonic period | 26–27 | 0.4–59.8 | 1–5 min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Ma, A.; Deng, Y.; Cao, M.; Hu, Y.; Cheng, Z.; Zhu, L. Effects of Flow Turbulence on the Entire Development Process of Drifting Fish Eggs. Fishes 2024, 9, 88. https://doi.org/10.3390/fishes9030088
Wei Y, Ma A, Deng Y, Cao M, Hu Y, Cheng Z, Zhu L. Effects of Flow Turbulence on the Entire Development Process of Drifting Fish Eggs. Fishes. 2024; 9(3):88. https://doi.org/10.3390/fishes9030088
Chicago/Turabian StyleWei, Yuchong, Aixing Ma, Ya Deng, Minxiong Cao, Ying Hu, Zhaoyi Cheng, and Lijun Zhu. 2024. "Effects of Flow Turbulence on the Entire Development Process of Drifting Fish Eggs" Fishes 9, no. 3: 88. https://doi.org/10.3390/fishes9030088
APA StyleWei, Y., Ma, A., Deng, Y., Cao, M., Hu, Y., Cheng, Z., & Zhu, L. (2024). Effects of Flow Turbulence on the Entire Development Process of Drifting Fish Eggs. Fishes, 9(3), 88. https://doi.org/10.3390/fishes9030088