Multilinear Regression Analysis between Local Bioimpedance Spectroscopy and Fish Morphological Parameters
Abstract
1. Introduction
1.1. Context
1.2. Conventional Bioimpedance Analysis
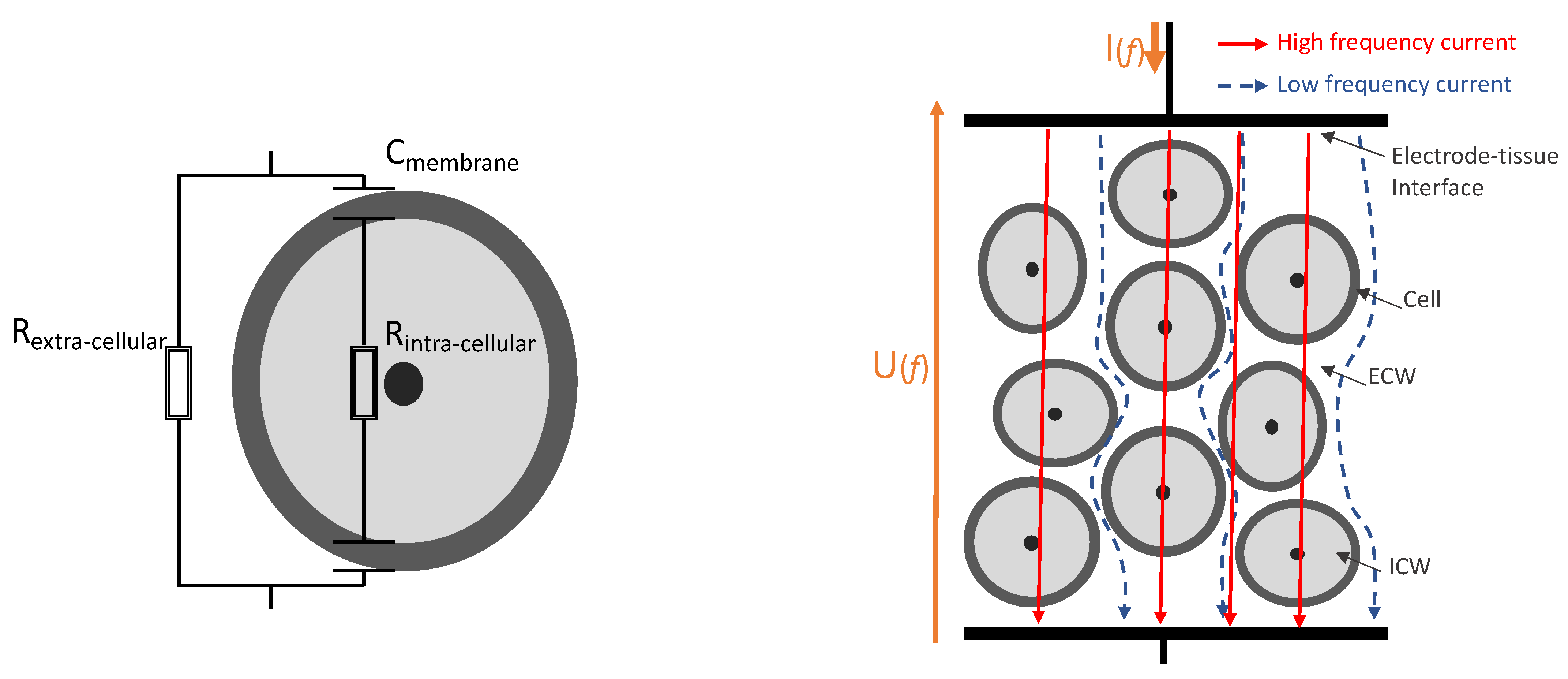
1.2.1. Bioimpedance Analysis Principle
1.2.2. Bioimpedance Analysis in Medicine
1.2.3. Bioimpedance for Fish
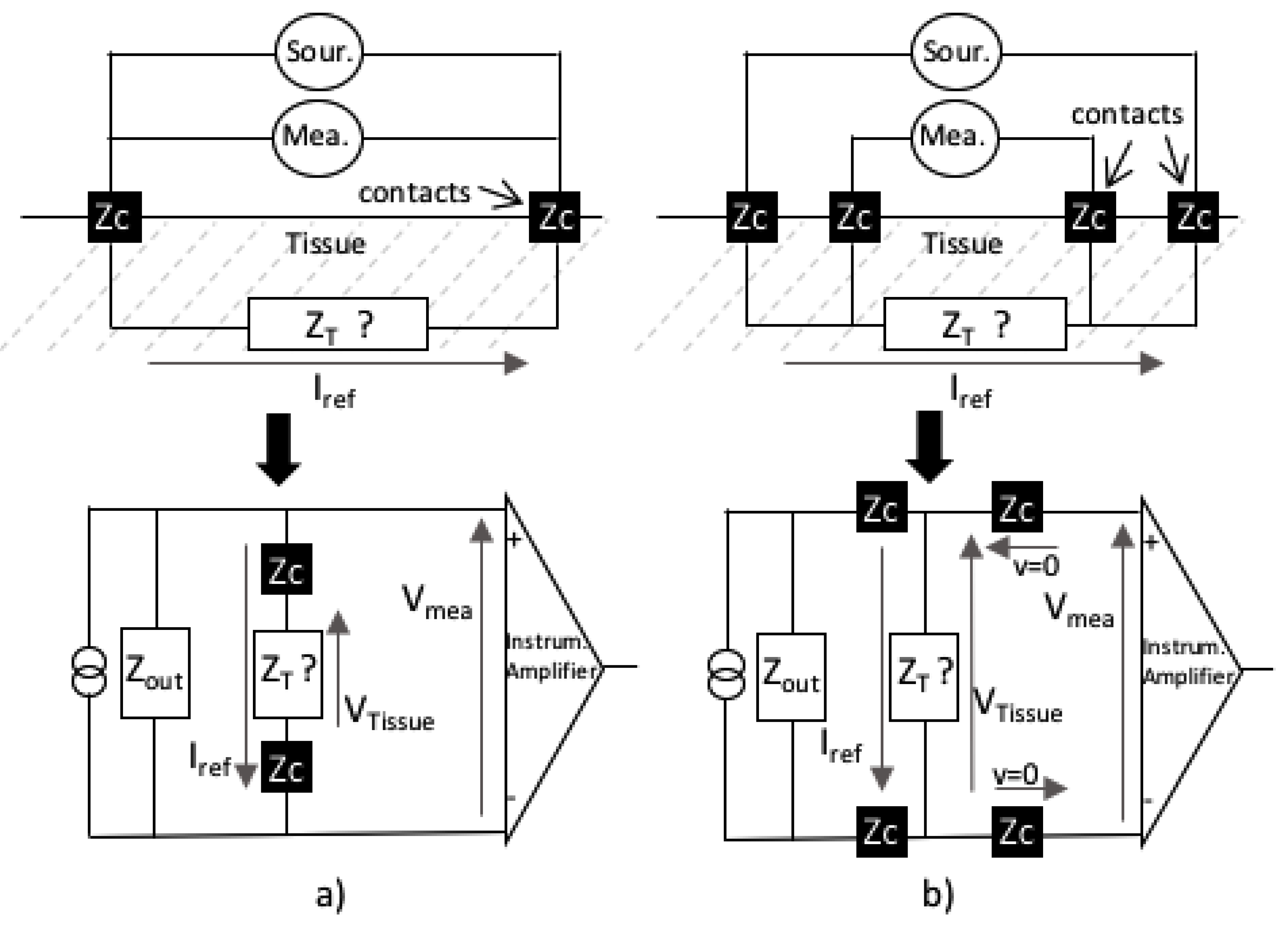
1.2.4. Instrumentation for Bioimpedance Analysis on Fish
2. Materials and Methods
2.1. Ethical Statement
2.2. Preliminary Remark
2.3. Method
- First, the fish was anesthetized and both total length and weight (called here experimental weight Wexp and length Lexp) were measured.
- Second, a monolithic electrode of 4 cm long and 0.5 cm wide with two sets of needle electrodes, each consisting of a signal and detecting electrode, were inserted to a depth of cm. The monolithic electrode was placed towards the back of the fish under the dorsal fin, which corresponds to the pterygiophores region.
- Third, a first PIS (PIS1) was connected to the electrode wire: A current of 100 A was generated for 512 different frequencies, ranging from 0.3 Hz to 100 kHz, and the corresponding voltages were measured. Then, a second current of 400 A was generated with the same 512 frequencies, and the corresponding voltages were measured. For each measurement, the PIS1 instrument provided the real part and the imaginary part of the corresponding impedance .
- Fourth, the PIS1 was disconnected from the electrode wire, and a second spectroscope, the PIS2, was connected: again 512 measurements were performed with a current of 100 A and 512 measurements with 400 A. It is important to note that spectroscopes 1 and 2 were interchanged by disconnecting the spectroscope from the wire, but without moving the electrode. This part of the procedure helps evaluate the possible inaccuracy that could come from the instruments.
- First, with six electrical parameters and 11 frequencies, the number of different terms is 6 × 11 = 66.
- Second, considering a regression with variable, the linear equations are made of terms. So, the number of different equations corresponds to the number of combinations with no repetition, i.e., 66 choose :
3. Results
3.1. Individual Parameter Analysis
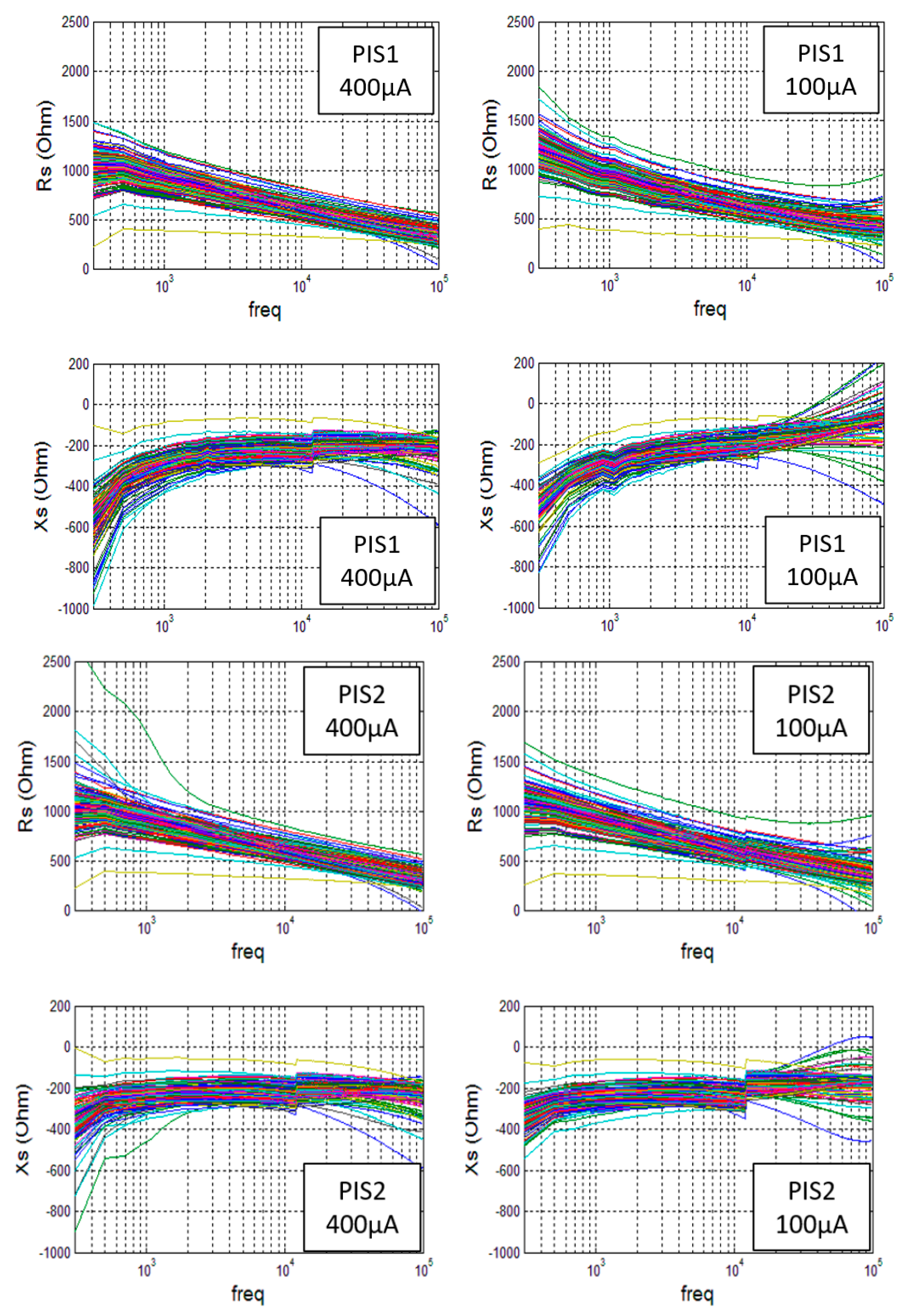
- Firstly, a good consistency may be noted for Rs(f) in a range from 1 kHz and 50 kHz. In the low frequency domain, the two spectroscopes provide very similar results when using the 400 A current, but the PIS1 gives higher values than the PIS2 when a low current of 100 A is used. A similar inconsistency can be observed for frequencies higher than 50 kHz.
- Secondly, a good consistency may be noted for Xs(f) in a very limited range of 2 kHz to 6 kHz. In the low frequency domain, a single PIS gives consistent results for different currents, while two different PIS give very different values. In the high frequency domain, the two different PIS give consistent results but only for a current of 400 A.
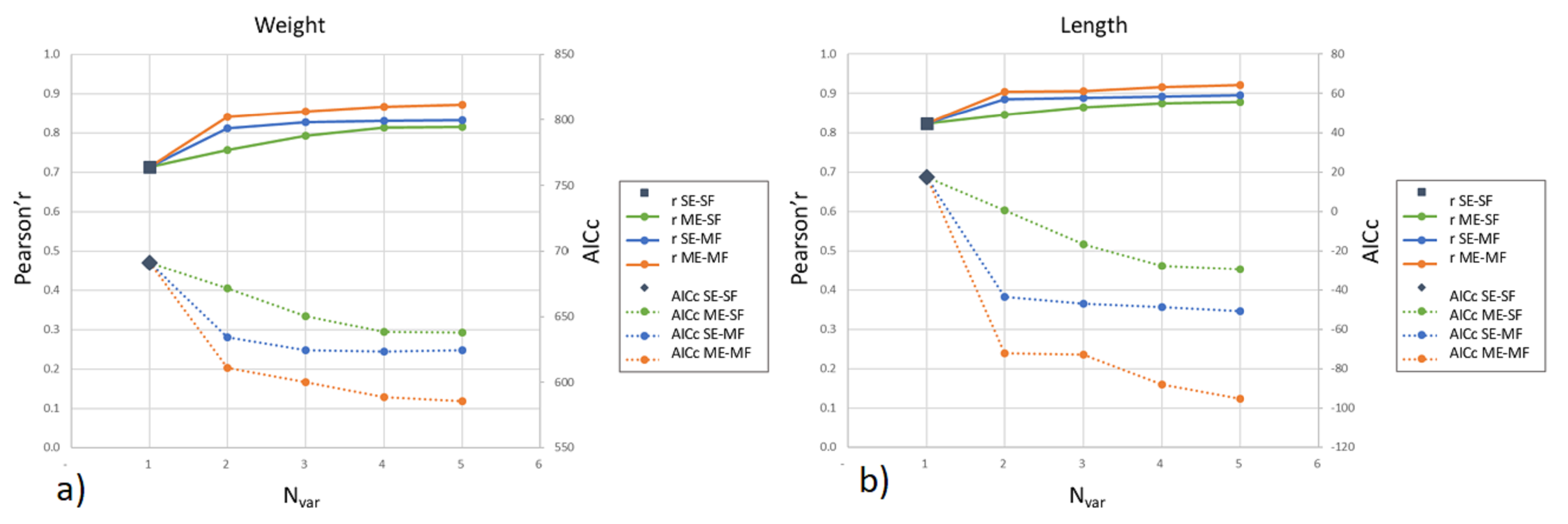
3.2. One to Five-Parameter Multilinear Regression Models
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AIC | Akaike Information Criterion |
| BIVA | Bioelectrical Impedance Vector Analysis |
| ECL | Extracellular Liquid |
| ECW | Extracellular Water |
| EIS | Electrical Impedance Spectroscopy |
| EMFF | European Maritime and Fisheries Fund |
| DXA | Dual-Energy X-ray absorptiometry |
| FFM | Fat Free Mass |
| FM | Fat Mass |
| ICW | Intracellular Water |
| ME-SF | Multiple Epar Single Frequency |
| ME-MF | Multiple Epar Multiple Frequencies |
| MF-BIA | Multiple Frequencies BioImpedance Analysis |
| PIS | Portable Impedance Spectroscope |
| SE-MF | Single Epar Multiple Frequencies |
| TBW | Total Body Water |
References
- Van Weerd, J.; Komen, J. The influence of environmental stressors on fish growth. Comp. Physiol. Biochem. 1998, 120, 107–112. [Google Scholar] [CrossRef]
- McCormick, S.D.; Hansen, L.P.; Quinn, T.P.; Saunders, R.L. Movement, migration, and smolting of Atlantic salmon (Salmo salar). Can. J. Fish. Aquat. Sci. 1998, 55, 77–92. [Google Scholar] [CrossRef]
- Kyle, U.G.; Bosaeus, I.; De Lorenzo, A.D.; Deurenberg, P.; Elia, M.; Gómez, J.M.; Heitmann, B.L.; Kent-Smith, L.; Melchior, J.C.; Pirlich, M.; et al. Bioelectrical impedance analysis—Part I: Review of principles and methods. Clin. Nutr. 2004, 23, 1226–1243. [Google Scholar] [CrossRef]
- Jaffrin, M.Y.; Morel, H. Body fluid volumes measurements by impedance: A review of bioimpedance spectroscopy (BIS) and bioimpedance analysis (BIA) methods. Med. Eng. Phys. 2008, 30, 1257–1269. [Google Scholar] [CrossRef] [PubMed]
- Mcconnell, G.C.; Butera, R.J.; Bellamkonda, R.V.; Dodde, R.E.; Bull, J.L.; Shih, A.J. Bioimpedance of soft tissue under compression Bioimpedance modeling of chronic electrodes Bioimpedance of soft tissue under compression. Physiol. Meas. 2012, 33, 1095–1099. [Google Scholar] [CrossRef]
- Kyle, U.G.; Bosaeus, I.; De Lorenzo, A.D.; Deurenberg, P.; Elia, M.; Manuel Gómez, J.; Lilienthal Heitmann, B.; Kent-Smith, L.; Melchior, J.C.; Pirlich, M.; et al. Bioelectrical impedance analysis-part II: Utilization in clinical practice. Clin. Nutr. 2004, 23, 1430–1453. [Google Scholar] [CrossRef]
- Aroom, K.R.; Harting, M.T.; Cox, C.S.; Radharkrishnan, R.S.; Smith, C.; Gill, B.S. Bioimpedance Analysis: A Guide to Simple Design and Implementation. J. Surg. Res. 2009, 153, 23–30. [Google Scholar] [CrossRef]
- Chouinard, L.E.; Schoeller, D.A.; Watras, A.C.; Clark, R.R.; Close, R.N.; Buchholz, A.C. Bioelectrical impedance vs. four-compartment model to assess body fat change in overweight adults. Obesity 2007, 15, 85–92. [Google Scholar] [CrossRef] [PubMed]
- Genton, L.; Herrmann, F.R.; Spörri, A.; Graf, C.E. Association of mortality and phase angle measured by different bioelectrical impedance analysis (BIA) devices. Clin. Nutr. 2018, 37, 1066–1069. [Google Scholar] [CrossRef]
- Khalil, S.F.; Mohktar, M.S.; Ibrahim, F. The theory and fundamentals of bioimpedance analysis in clinical status monitoring and diagnosis of diseases. Sensors 2014, 14, 10895–10928. [Google Scholar] [CrossRef]
- Åberg, P.; Nicander, I.; Hansson, J.; Geladi, P.; Holmgren, U.; Ollmar, S. Skin cancer identification using multifrequency electrical impedance—A potential screening tool. IEEE Trans. Biomed. Eng. 2004. [Google Scholar] [CrossRef]
- Dai, T.; Adler, A. In vivo blood characterization from bioimpedance spectroscopy of blood pooling. IEEE Trans. Instrum. Meas. 2009. [Google Scholar] [CrossRef]
- Schwenk, A.; Beisenherz, A.; Romer, K.; Kremer, G.; Salzberger, B.; Elia, M. Phase angle from bioelectrical impedance analysis remains an independent predictive marker in HIV-infected patients in the era of highly active antiretroviral treatment. Am. J. Clin. Nutr. 2000, 72, 496–501. [Google Scholar] [CrossRef] [PubMed]
- Wasyluk, W.; Wasyluk, M.; Zwolak, A.; Łuczyk, R.J. Limits of body composition assessment by bioelectrical impedance analysis (BIA). J. Educ. Health Sport 2019, 29, 35–44. [Google Scholar]
- Nwosu, A.C.; Mayland, C.R.; Mason, S.; Cox, T.F.; Varro, A.; Stanley, S.; Ellershaw, J. Bioelectrical impedance vector analysis (BIVA) as a method to compare body composition differences according to cancer stage and type. Clin. Nutr. ESPEN 2019, 30, 59–66. [Google Scholar] [CrossRef] [PubMed]
- Piccoli, A.; Piazza, P.; Noventa, D.; Pillon, L.; Zaccaria, M. A new method for monitoring hydration at high altitude by bioimpedance analysis. Med. Sci. Sport. Exerc. 1996, 12, 1517–1522. [Google Scholar] [CrossRef] [PubMed]
- Atilano, X.; Luis.Miguel, J.; Martínez, J.; Sánchez, R.; Selgas, R. Bioimpedance Vector Analysis as a Tool for determination and Adjustment of Dry Weight in Hemodialysis Patients. Kidney Res. Clin. Pract. 2012. [Google Scholar] [CrossRef]
- Grossi, M.; Riccò, B. Electrical impedance spectroscopy (EIS) for biological analysis and food characterization: A review. J. Sens. Syst. 2017, 6, 303–325. [Google Scholar] [CrossRef]
- Pichler, G.P.; Amouzadeh-Ghadikolai, O.; Leis, A.; Skrabal, F. A critical analysis of whole body bioimpedance spectroscopy (BIS) for the estimation of body compartments in health and disease. Med. Eng. Phys. 2013, 35, 616–625. [Google Scholar] [CrossRef] [PubMed]
- Seoane, F.; Buendía, R.; Gil-Pita, R. Cole parameter estimation from electrical bioconductance spectroscopy measurements. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBC’10, Buenos Aires, Argentina, 31 August–4 September 2010; Volume 4, pp. 3495–3498. [Google Scholar] [CrossRef]
- Buendía Lopez, R. Improvements in Bioimpedance Spectroscopy Data Analysis: Artefact Correction, Cole Parameters, and Body Fluid Estimation. Ph.D. Thesis, Univerity of Boras, Borås, Sweden, 2013. [Google Scholar]
- Buendia, R.; Gil-Pita, R.; Seoane, F. Cole parameter estimation from total right side electrical bioimpedance spectroscopy measurements Influence of the number of frequencies and the upper limit. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Boston, MA, USA, 30 August–3 September 2011; pp. 1843–1846. [Google Scholar] [CrossRef]
- Lukaski, H.C.; Johnson, P.E.; Bolonchuk, W.W.; Lykken, G.I. Assessment of fat-free mass using bioelectrical impedance measurements of the human body. Am. J. Clin. Nutr. 1985, 41, 810–817. [Google Scholar] [CrossRef]
- Ward, L.C. Bioelectrical impedance analysis for body composition assessment: Reflections on accuracy, clinical utility, and standardisation. Eur. J. Clin. Nutr. 2019, 73, 194–199. [Google Scholar] [CrossRef] [PubMed]
- Cox, M.K.; Hartman, K.J. Nonlethal estimation of proximate composition in fish. Can. J. Fish. Aquat. Sci. 2005, 62, 269–275. [Google Scholar] [CrossRef]
- Dibble, K.L.; Yard, M.D.; Ward, D.L.; Yackulic, C.B. Does bioelectrical impedance analysis accurately estimate the physiological condition of threatened and endangered desert fish species? Trans. Am. Fish. Soc. 2017, 146, 888–902. [Google Scholar] [CrossRef]
- Hartman, K.J.; Margraf, F.J.; Hafs, A.W.; Cox, M.K. Bioelectrical Impedance Analysis: A New Tool for Assessing Fish Condition. Fisheries 2015, 40, 590–600. [Google Scholar] [CrossRef]
- Caldarone, E.M.; MacLean, S.A.; Sharack, B. Evaluation of bioelectrical impedance analysis and Fulton’s condition factor as nonlethal techniques for estimating short-term responses in postsmolt Atlantic salmon (Salmo salar) to food availability. Fish. Bull. 2012, 110, 257–270. [Google Scholar]
- Hartman, K.J.; Phelan, B.A.; Rosendale, J.E. Temperature Effects on Bioelectrical Impedance Analysis (BIA) Used to Estimate Dry Weight as a Condition Proxy in Coastal Bluefish. Mar. Coast. Fish. 2011, 3, 307–316. [Google Scholar] [CrossRef]
- Fitzhugh, G.R.; Wuenschel, M.J.; McBride, R.S. Evaluation of bioelectrical impedance analysis (BIA) to measure condition and energy allocated to reproduction in marine fishes. J. Physics: Conf. Ser. 2010, 224, 012137. [Google Scholar] [CrossRef]
- Bugeon, J.; Lefevre, F.; Cardinal, M.; Uyanik, A.; Davenel, A.; Haffray, P. Flesh quality in large rainbow trout with high or low fillet yield. J. Muscle Foods 2010, 21, 702–721. [Google Scholar] [CrossRef]
- Cox, M.K. Bioelectrical impedance analysis measures of body composition and condition, and its sensitivity to the freezing process. J. Aquat. Food Prod. Technol. 2015, 24, 368–377. [Google Scholar] [CrossRef]
- Willis, J.; Hobday, A.J. Application of bioelectrical impedance analysis as a method for estimating composition and metabolic condition of southern bluefin tuna (Thunnus maccoyii) during conventional tagging. Fish. Res. 2008, 93, 64–71. [Google Scholar] [CrossRef]
- Haus, W.O.; Hartman, K.J.; Jacobs, J.M.; Harrell, R.M. Development of striped bass relative condition models with bioelectrical impedance analysis and associated temperature corrections. Trans. Am. Fish. Soc. 2017, 146, 917–926. [Google Scholar] [CrossRef]
- Vue, S.; Samways, K.M.; Cunjak, R.A. Bioelectrical Impedance Analysis to Estimate Lipid Content in Atlantic Salmon Parr as Influenced by Temperature, PIT Tags, and Instrument Precision and Application in Field Studies. Trans. Am. Fish. Soc. 2015, 144, 235–245. [Google Scholar] [CrossRef]
- Queiros, Q.; Fromentin, J.m.; Gasset, E.; Dutto, G.; Huiban, C.; Metral, L.; Leclerc, L.; Schull, Q.; McKenzie, D.; Saraux, C. Food in the Sea: Size Also Matters for Pelagic Fish. Front. Mar. Sci. 2019, 6. [Google Scholar] [CrossRef]
- Zimmerman, A.M.; Lowery, M.S. Hyperplastic development and hypertrophic growth of muscle fibers in the white seabass (Atractoscion nobilis). J. Exp. Zool. 1999, 3, 299–308. [Google Scholar] [CrossRef]
- Rutz, C.; Hays, G.C. New frontiers in biologging science. Biol. Lett. 2009, 5, 289–292. [Google Scholar] [CrossRef]
- Rouyer, T.; Bonhommeau, S.; Giordano, N.; Ellul, S.; Ellul, G.; Deguara, S.; Wendling, B.; Belhaj, M.M.; Kerzerho, V.; Bernard, S. Tagging Atlantic bluefin tuna from a farming cage: An attempt to reduce handling times for large scale deployments. Fish. Res. 2019, 211, 27–31. [Google Scholar] [CrossRef]

| Weight | Length | |
|---|---|---|
| Mean Value | 21.4 | 13.4 |
| Standard Deviation | 12.4 | 1.8 |
| Coefficient of Variation | 57.9% | 13.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kerzérho, V.; Azaïs, F.; Bernard, S.; Bonhommeau, S.; Brisset, B.; De Knyff, L.; Julien, M.; Renovell, M.; Rouyer, T.; Saraux, C.; et al. Multilinear Regression Analysis between Local Bioimpedance Spectroscopy and Fish Morphological Parameters. Fishes 2023, 8, 88. https://doi.org/10.3390/fishes8020088
Kerzérho V, Azaïs F, Bernard S, Bonhommeau S, Brisset B, De Knyff L, Julien M, Renovell M, Rouyer T, Saraux C, et al. Multilinear Regression Analysis between Local Bioimpedance Spectroscopy and Fish Morphological Parameters. Fishes. 2023; 8(2):88. https://doi.org/10.3390/fishes8020088
Chicago/Turabian StyleKerzérho, Vincent, Florence Azaïs, Serge Bernard, Sylvain Bonhommeau, Blandine Brisset, Laurent De Knyff, Mohan Julien, Michel Renovell, Tristan Rouyer, Claire Saraux, and et al. 2023. "Multilinear Regression Analysis between Local Bioimpedance Spectroscopy and Fish Morphological Parameters" Fishes 8, no. 2: 88. https://doi.org/10.3390/fishes8020088
APA StyleKerzérho, V., Azaïs, F., Bernard, S., Bonhommeau, S., Brisset, B., De Knyff, L., Julien, M., Renovell, M., Rouyer, T., Saraux, C., & Soulier, F. (2023). Multilinear Regression Analysis between Local Bioimpedance Spectroscopy and Fish Morphological Parameters. Fishes, 8(2), 88. https://doi.org/10.3390/fishes8020088







