Evaluation Performance of Three Standardization Models to Estimate Catch-per-Unit-Effort: A Case Study on Pacific Sardine (Sardinops sagax) in the Northwest Pacific Ocean
Abstract
1. Introduction
2. Materials and Methods
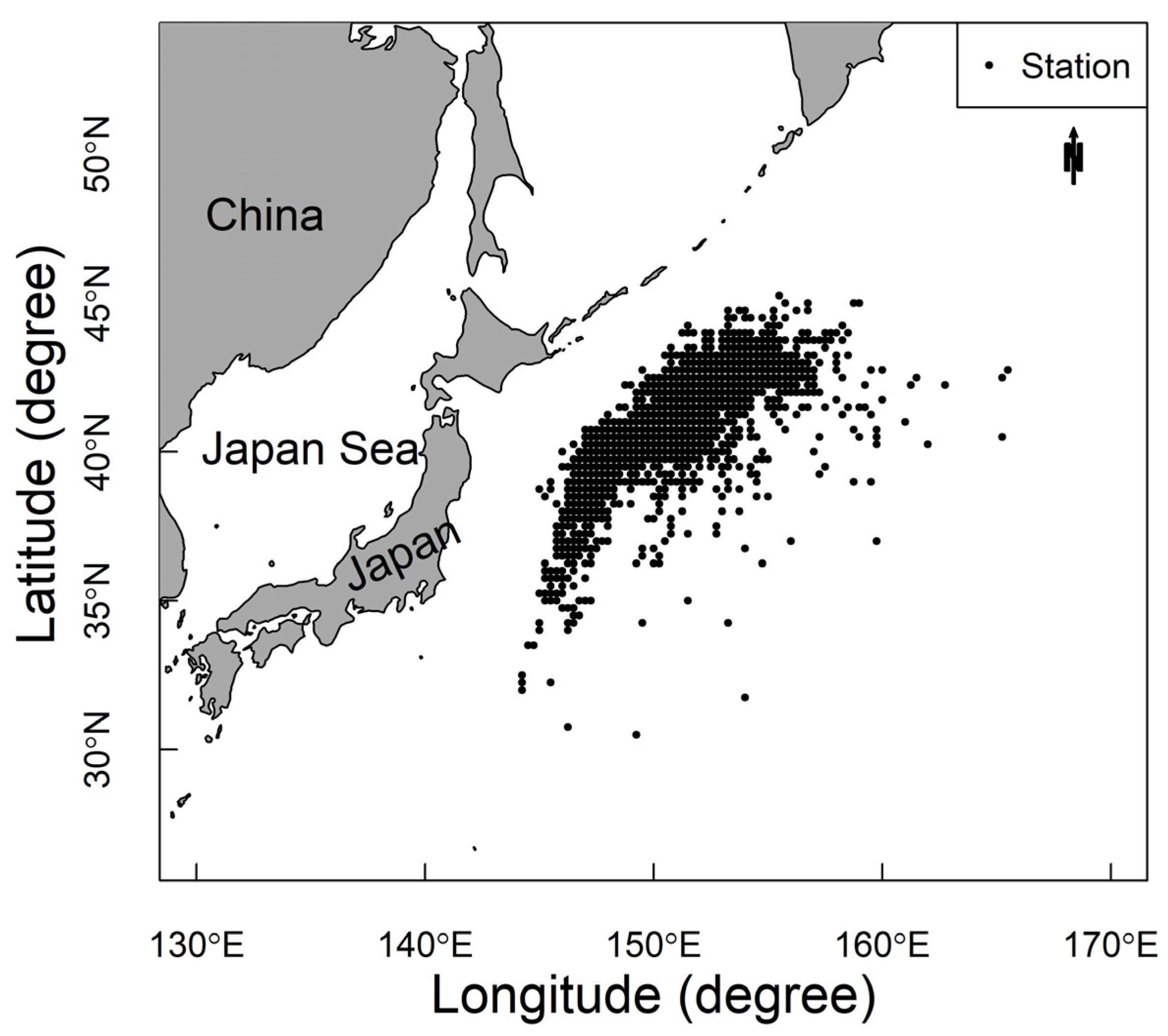
2.1. Data Sources
2.2. Methods
2.2.1. General Linear Models
2.2.2. Generalized Linear Mixed Models
2.2.3. Spatio-Temporal GLMM (VAST)
2.2.4. Model Evaluation
2.2.5. Standardized CPUE Value
2.2.6. The Impact of Predictor Variables on Standardized CPUE
2.2.7. Simulation Testing for Three Models
3. Results
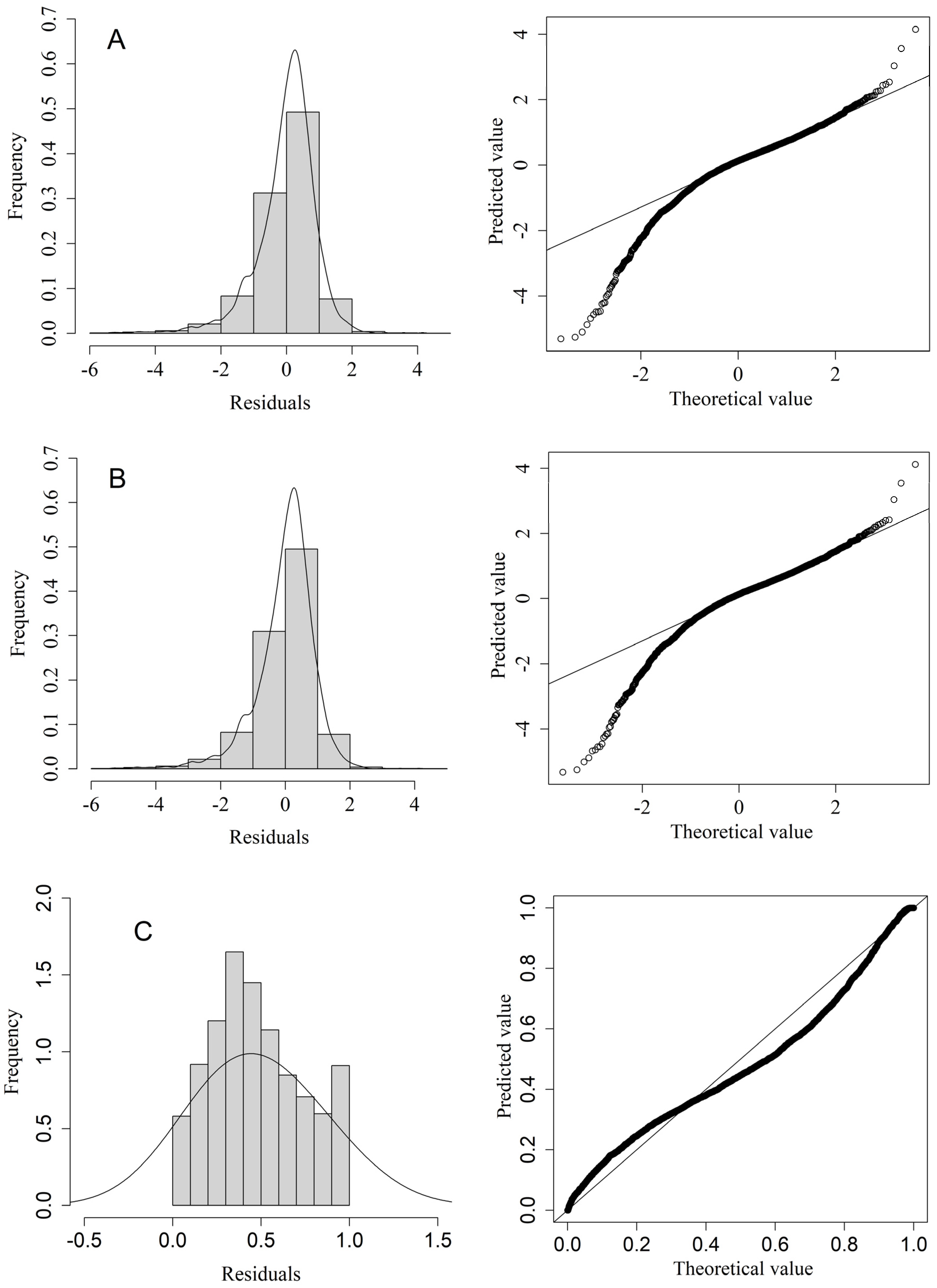
3.1. Diagnostic and Selection of Three Model
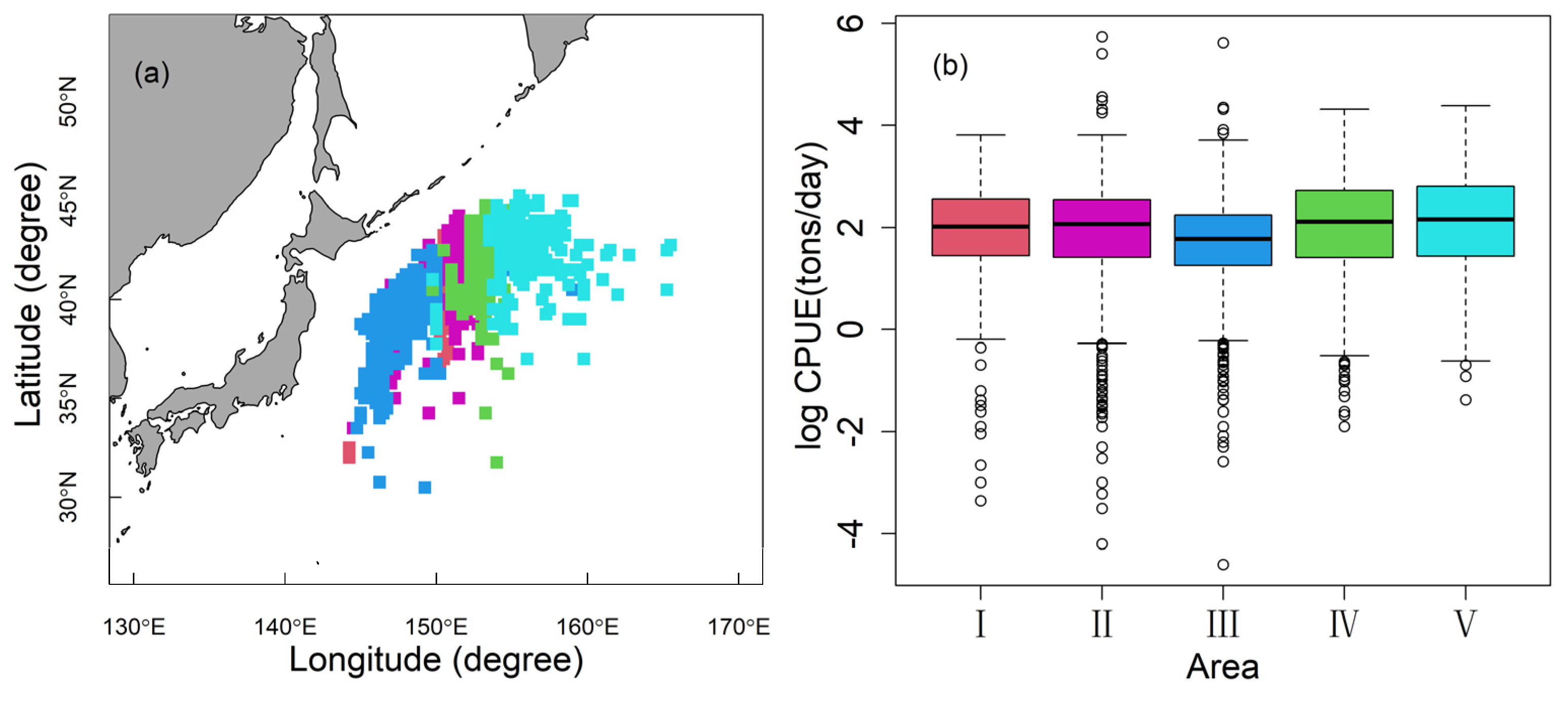
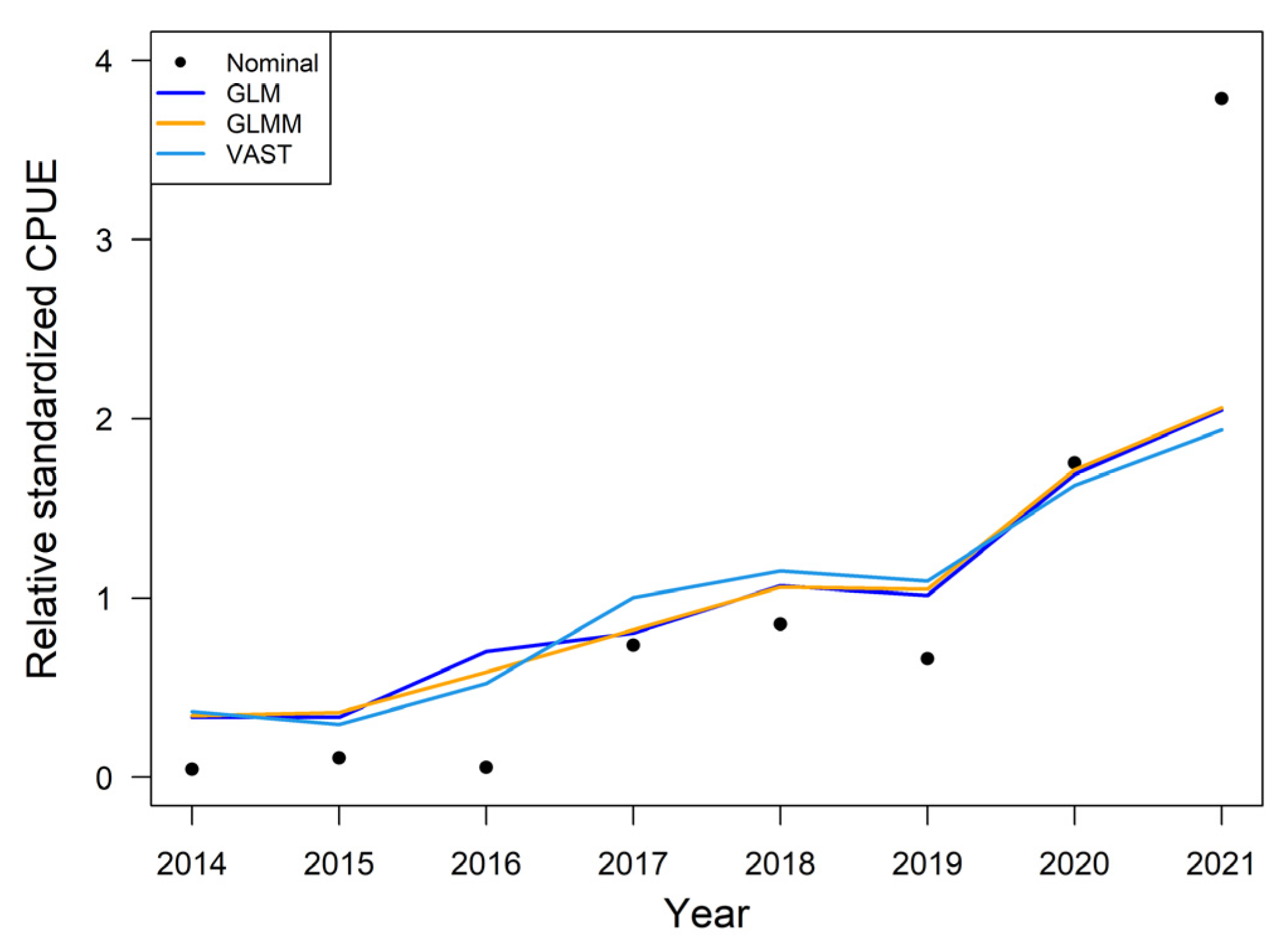
3.2. The Nominal and Standardized CPUE
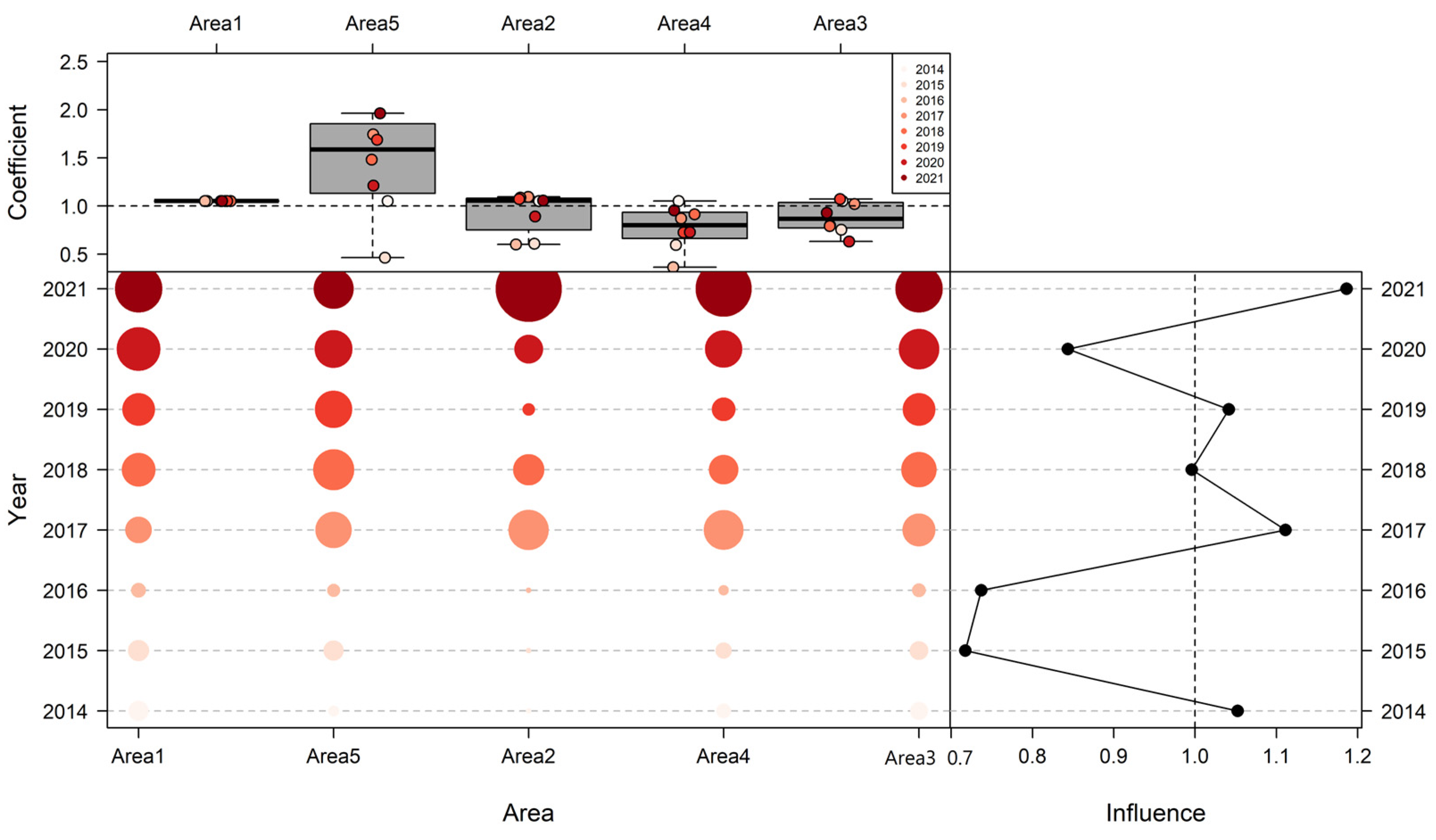
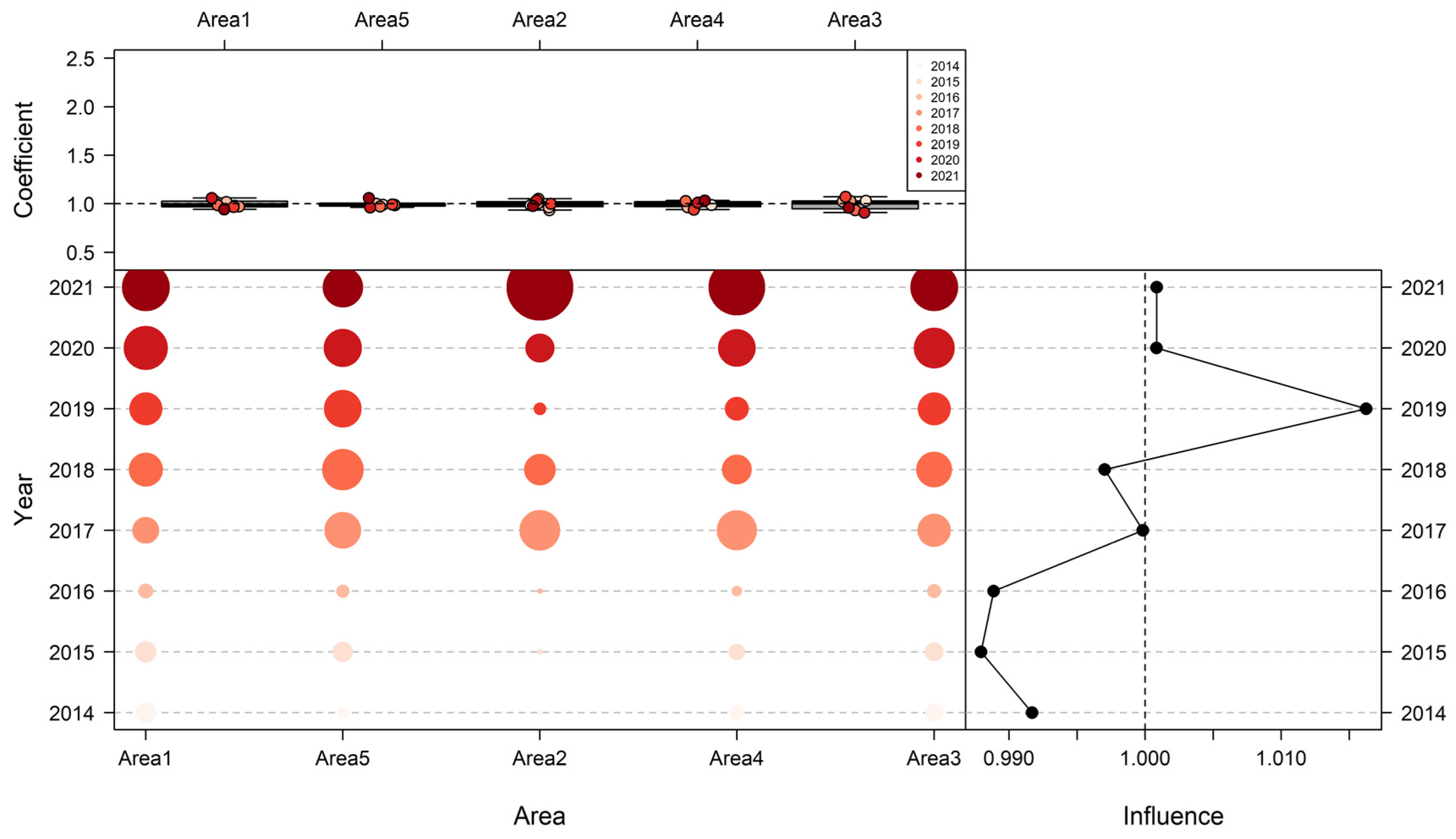
3.3. Influence of Explanatory Variables
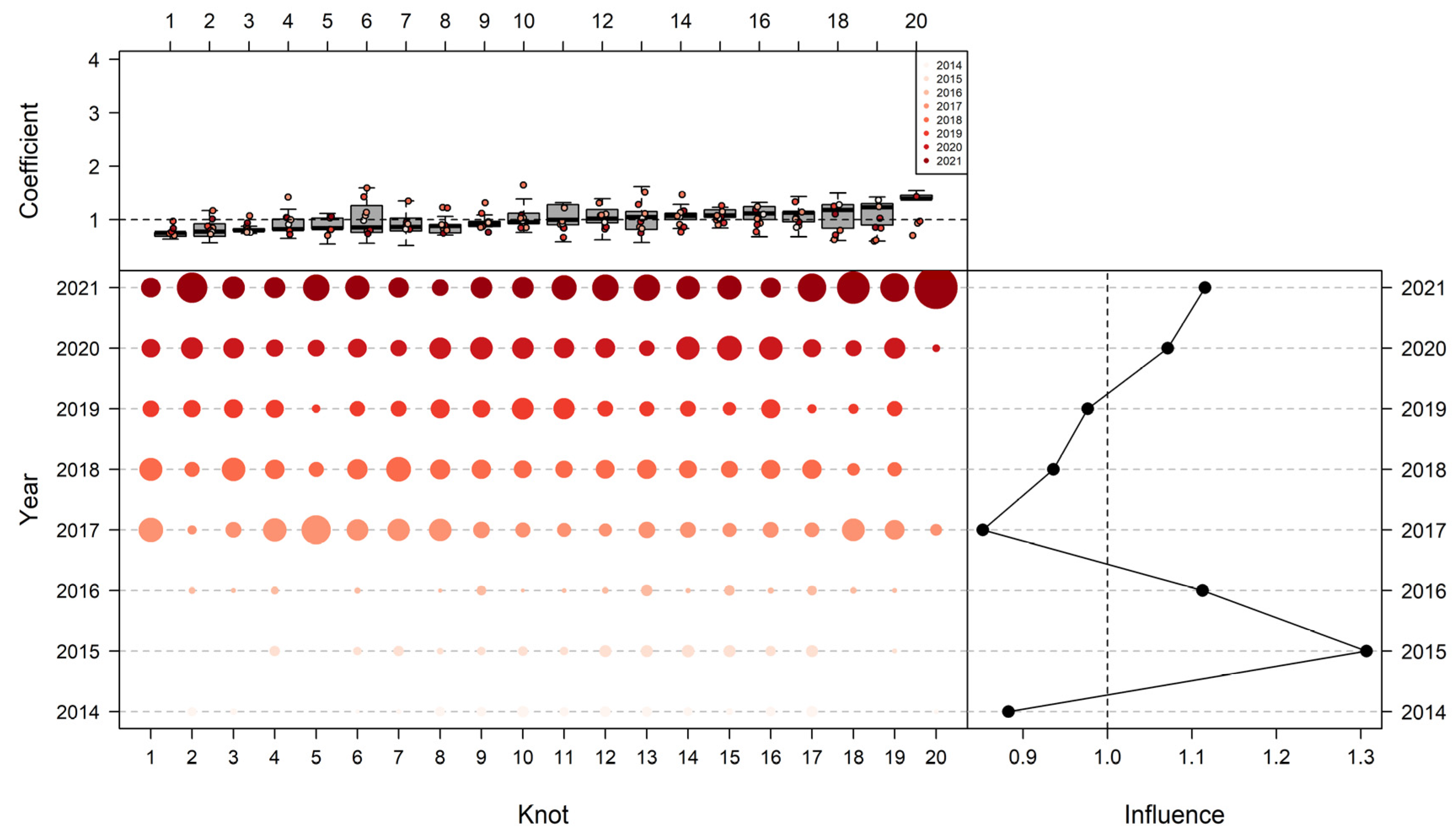
3.4. The Influence of Various Models on Yearly Standardized CPUE
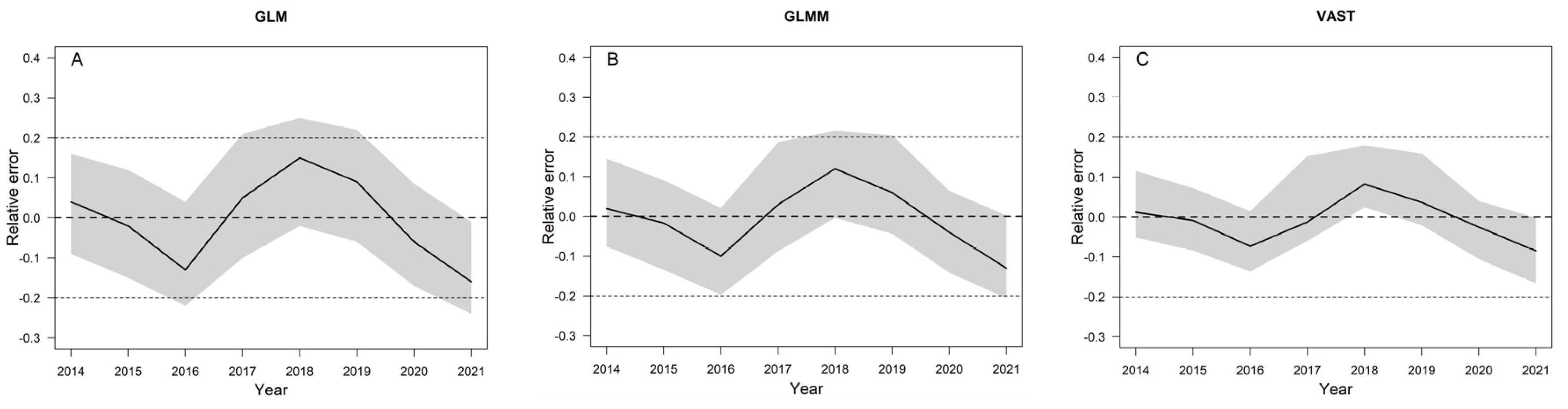
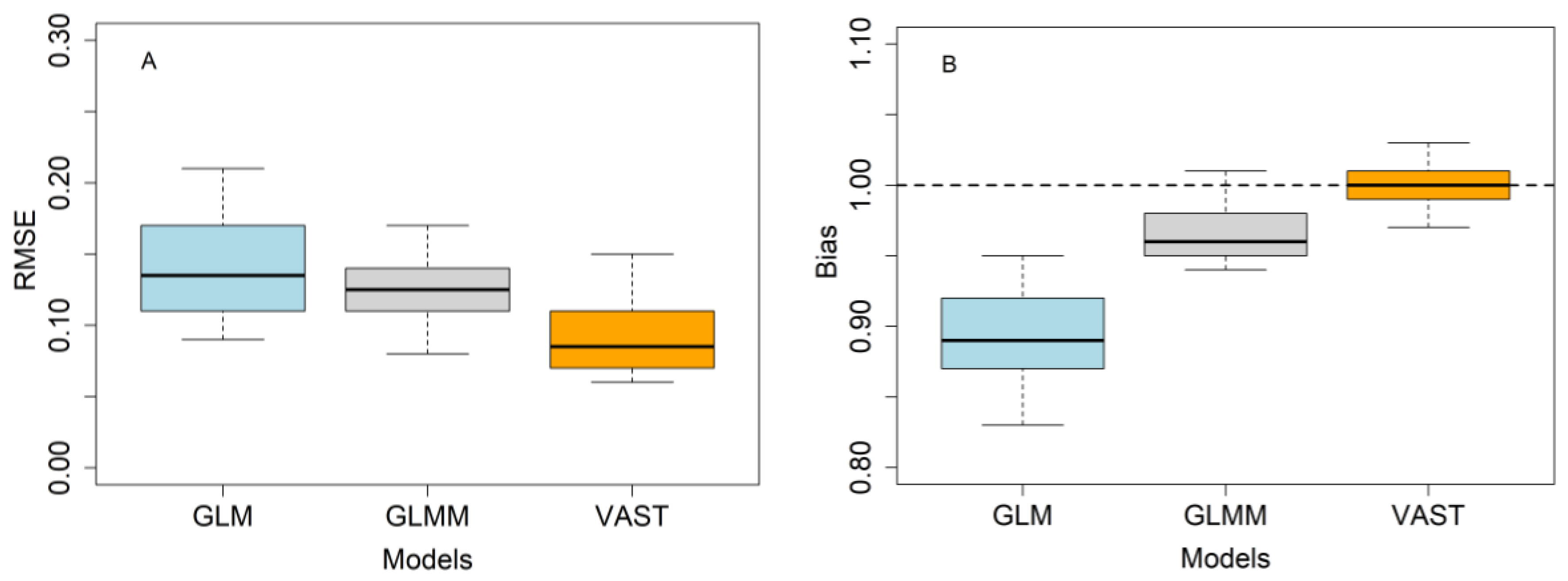
3.5. Model Evaluation Using a Simulation Test
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Campbell, R.A. CPUE standardisation and the construction of indices of stock abundance in a spatially varying fishery using general linear models. Fish. Res. 2004, 70, 209–227. [Google Scholar] [CrossRef]
- Hilborn, R.; Walters, C.J. Quantitative Fisheries Stock Assessment and Management: Choice, Dynamics and Uncertainty; Chapman & Hall: New York, NY, USA, 1992; p. 570. [Google Scholar]
- Callwood, K.A. Examining the development of a parrotfish fishery in The Bahamas: Social considerations & management implications. Glob. Ecol. Conserv. 2021, 28, e01677. [Google Scholar]
- Harley, S.J.; Myers, R.A.; Dunn, A. Is catch-per-unit-effort proportional to abundance? Can. J. Fish. Aquat. Sci. 2001, 58, 1760–1772. [Google Scholar] [CrossRef]
- Cao, J.; Thorson, J.T.; Richards, R.A.; Chen, Y. Spatiotemporal index standardization improves the stock assessment of northern shrimp in the Gulf of Maine. Can. J. Fsih. Aquat. Sci. 2017, 74, 1781–1793. [Google Scholar] [CrossRef]
- Walters, C. Folly and fantasy in the analysis of spatial catch rate data. Can. J. Fish. Aquat. Sci. 2003, 60, 1433–1436. [Google Scholar] [CrossRef]
- Li, G.; Lu, Z.W.; Cao, Y.M.; Zou, L.J.; Chen, X.J. CPUE Estimation and Standardization Based on VMS: A Case Study for Squid-Jigging Fishery in the Equatorial of Eastern Pacific Ocean. Fish 2023, 8, 2. [Google Scholar] [CrossRef]
- Hashimoto, M.; Nishijima, S.; Yukami, R.; Watanabe, C.; Kamimura, Y.; Furuichi, S.; Ichinokawa, M.; Okamura, H. Spatiotemporal dynamics of the Pacific chub mackerel revealed by standardized abundance indices. Fish. Res. 2019, 219, 105315. [Google Scholar] [CrossRef]
- Hazin, H.G.; Hazin, F.; Mourato, B.; Carvalho, F.; Frédou, T. Standardized catch rates of swordfish (Xiphias gladius) caught by the Brazilian fleet (1978–2012) using generalized linear mixed models (GLMM) using delta log approach. Collect. Vol. Sci. Pap. ICCAT. 2014, 70, 1875–1884. [Google Scholar]
- Thorson, J.T.; Shelton, A.O.; Ward, E.J.; Skaug, H.J. Geostatistical delta-generalized linear mixed models improve precision for estimated abundance indices for West Coast groundfishes. ICES J. Mar. Sci. 2015, 72, 1297–1310. [Google Scholar] [CrossRef]
- Maunder, M.N.; Punt, A.E. Standardizing catch and effort data: A review of recent approaches. Fish. Res. 2004, 70, 141–159. [Google Scholar] [CrossRef]
- Rodriguez, M.E.; Arrizabalaga, H.; Ortiz, M.; Rodriguez, C.C.; Moreno, G.; Kell, L.T. Standardization of bluefin tuna (Thurmus thynnus) catch per unit effort in the bait boat fishery of the Bay of Biscay (Eastern Atlantic). ICES J. Mar. Sci. 2003, 60, 1216–1231. [Google Scholar] [CrossRef]
- Cortes, G.G.; Montanez, J.A.D.A.; Sánchez, F.A.; Salas, S.; Balart, E.F. How do environmental factors affect the stock–recruitment relationship? The case of the Pacific sardine (Sardinops sagax) of the northeastern Pacific Ocean. Fish. Res. 2010, 102, 173–183. [Google Scholar] [CrossRef]
- Yang, C.; Han, H.B.; Zhang, H.; Shi, Y.C.; Su, B.; Jiang, P.W.; Xiang, D.L.; Sun, Y.Y.; Li, Y. Assessment and management recommendations for the status of Japanese sardine Sardinops melanostictus population in the Northwest Pacific. Ecol. Indic. 2023, 148, 110111. [Google Scholar] [CrossRef]
- Tameishi, H.; Shinomiya, H.; Aoki, I.; Sugimoto, T. Understanding Japanese sardine migrations using acoustic and other aids. ICES J. Mar. Sci. 1996, 53, 167–171. [Google Scholar] [CrossRef]
- Sarr, O.; Kindong, R.; Tian, S.Q. Knowledge on the Biological and Fisheries Aspects of the Japanese Sardine, Sardinops melanostictus (Schlegel, 1846). J. Mar. Sci. Eng. 2021, 9, 1403. [Google Scholar] [CrossRef]
- Furuichi, S.; Niino, Y.; Kamimura, Y.; Yukami, R. Time-varying relationships between early growth rate and recruitment in Japanese sardine. Fish. Res. 2020, 232, 105723. [Google Scholar] [CrossRef]
- FAO. FAO Yearbook; Fishery and Aquaculture Statistics: Rome, Italy, 2021; p. 13. [Google Scholar]
- Shi, Y.C.; Zhang, X.M.; He, Y.R.; Fan, W.; Tang, F.H. Stock Assessment Using Length-Based Bayesian Evaluation Method for Three Small Pelagic Species in the Northwest Pacific Ocean. Front. Mar. Sci. 2022, 9, 775180. [Google Scholar] [CrossRef]
- Zhao, G.Q.; Shi, Y.C.; Fan, W.; Cui, X.S.; Tang, F.H. Study on main catch composition and fishing ground change of light purse seine in Northwest Pacific. S. China Fish. Sci. 2022, 18, 33–42, (In Chinese with English Abstract). [Google Scholar]
- North Pacific Fisheries Commission. NPFC Yearbook 2017; North Pacific Fisheries Commission: Tokyo, Japan, 2017; p. 385. Available online: www.npfc.int (accessed on 21 November 2017).
- Shi, Y.C.; Kang, B.; Fan, W.; Xu, L.L.; Zhang, S.M.; Cui, X.S.; Dai, Y. Spatio-Temporal Variations in the Potential Habitat Distribution of Pacific Sardine (Sardinops sagax) in the Northwest Pacific Ocean. Fish 2023, 8, 86. [Google Scholar] [CrossRef]
- Takasuka, A.; Oozeki, Y.; Aoki, I. Optimal growth temperature hypothesis: Why do anchovy flourish and sardine collapse or vice versa under the same ocean regime? Can. J. Fish. Aquat. Sci. 2007, 64, 768–776. [Google Scholar] [CrossRef]
- Ito, S. Fishery biology of the sardine, Sardinops melanosticta (T. & S.), in the waters around Japan. Bull. Jpn. Sea Reg. Fish. Res. Lab. 1961, 9, 1–227, (In Japanese with English abstract). [Google Scholar]
- Wada, T.; Jacobson, L.D. Regimes and stock-recruitment relationships in Japanese sardine (Sardinops melanostictus), 1951–1995. Can. J. Fish. Aquat. Sci. 1998, 55, 2455–2463. [Google Scholar] [CrossRef]
- Matsuyama, M.; Adachi, S.; Nagahama, Y.; Kitajima, C.; Matsuura, M.S. Annual reproductive cycle of the captive female Japanese sardine (Sardinops melanostictus): Relationship to ovarian development and serum levels of gonadal steroid hormones. J. Mar. Biol. 1991, 108, 21–29. [Google Scholar] [CrossRef]
- Nyuji, M.; Hongo, Y.; Yoneda, M.; Nakamura, M. Transcriptome characterization of BPG axis and expression profiles of ovarian steroidogenesis-related genes in the Japanese sardine. BMC Genom. 2020, 21, 668. [Google Scholar] [CrossRef] [PubMed]
- Muko, S.; Ohshimo, S.; Kurota, H.; Yasuda, T.; Fukuwaka, M.A. Long-term distribution changes in distribution of Japanese sardine in the Sea of Japan during the stock fluctuations. Mar. Ecol. Prog. Ser. 2018, 593, 141–154. [Google Scholar] [CrossRef]
- Sakamoto, T.; Komatsu, K.; Shirai, K.; Higuchi, T.; Ishimura, T.; Setou, T.; Kamimura, Y.; Watanabe, C.; Kawabata, A. Combining microvolume isotope analysis and numerical simulation to reproduce fish migration history. Methods Ecol. Evol. 2019, 10, 59–69. [Google Scholar] [CrossRef]
- Bentley, N.; Kendrick, T.H.; Starr, P.J.; Breen, P.A. Influence plots and metrics: Tools for better understanding fisheries catch-per-unit-effort standardizations. ICES J. Mar. Sci. 2012, 69, 84–88. [Google Scholar] [CrossRef][Green Version]
- Howell, E.A.; Kobayashi, D.R. El Niño effects in the Palmyra Atoll region: Oceanographic changes and bigeye tuna (Thunnusobesus) catch rate variability. Fish. Oceanogr. 2006, 15, 477–489. [Google Scholar] [CrossRef]
- Graham, M.H. Confronting multicollinearity in ecological multiple regression. Ecology 2003, 84, 2809–2815. [Google Scholar] [CrossRef]
- Tien, B.D.; Lofman, O.; Revhaug, I.; Dick, O. Landslide susceptibility analysis in the Hoa Binh province of Vietnam using statistical index and logistic regression. Nat. Hazards 2011, 59, 1413–1444. [Google Scholar]
- Hsu, J.; Chang, Y.J.; Ducharme-Barth, N.D. Evaluation of the influence of spatial treatments on catch-per-unit-effort standardization: A fishery application and simulation study of Pacific saury in the Northwestern Pacific Ocean. Fish. Res. 2022, 255, 106440. [Google Scholar] [CrossRef]
- Ono, K.; Punt, A.E.; Hilborn, R. Think outside the grids: An objective approach to define spatial strata for catch and effort analysis. Fish. Res. 2015, 170, 89–101. [Google Scholar] [CrossRef]
- Tian, S.Q.; Chen, X.J. Impacts of different calculating methods for nominal CPUE on CPUE standardization. J. Shanghai Ocean Univ. 2010, 19, 240–245. [Google Scholar]
- Pinheiro, J.C.; Bates, D.M. Linear mixed-effects models: Basic concepts and examples. In Mixed-Effects Models in S and S-Plus; Springer: Berlin/Heidelberg, Germany, 2000; pp. 3–56. [Google Scholar]
- Mikkonen, S.; Rahikainen, M.; Virtanen, J.; Lehtonen, R.; Kuikka, S.; Ahvonen, A. A linear mixed model with temporal covariance structures in modelling catch per unit effort of Baltic herring. ICES J. Mar. Sci. 2008, 65, 1645–1654. [Google Scholar] [CrossRef]
- Forrestal, F.C.; Schirripa, M.; Goodyear, C.P.; Arrizabalaga, H.; Babcock, E.A.; Coelho, R.; Ingram, W.; Lauretta, M.; Ortiz, M.; Sharma, R. Testing robustness of CPUE standardization and inclusion of environmental variables with simulated longline catch datasets. Fish. Res. 2019, 210, 1–13. [Google Scholar] [CrossRef]
- Sculley, M.L.; Brodziak, J. Quantifying the distribution of swordfish (Xiphias gladius) density in the Hawaii-based longline fishery. Fish. Res. 2020, 230, 105638. [Google Scholar] [CrossRef]
- Grüss, A.; Walter III, J.F.; Babcock, E.A.; Forrestal, F.C.; Thorson, J.T.; Lauretta, M.V.; Schirripa, M.J. Evaluation of the impacts of different treatments of spatio-temporal variation in catch-per-unit-effort standardization models. Fish. Res. 2019, 213, 75–93. [Google Scholar] [CrossRef]
- Kristensen, K.; Nielsen, A.; Berg, C.W.; Skaug, H.; Bell, B. TMB: Automatic Differentiation and Laplace Approximation. J. Stat. Softw. 2016, 70, 1–21. [Google Scholar] [CrossRef]
- Greven, S.; Kneib, T. On the behaviour of marginal and conditional AIC in linear mixed models. Biometrika 2010, 97, 773–789. [Google Scholar] [CrossRef]
- Nakagawa, S.; Schielzeth, H. A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods Ecol. Evol. 2013, 4, 133–142. [Google Scholar] [CrossRef]
- Carruthers, T.R.; Li, C.J.; McAllister, M.K. Assessing methods for detecting marine ecosystem regime shifts: A simulation test. Fish. Res. 2004, 67, 173–187. [Google Scholar]
- Methratta, E.T.; Link, J.S.; Dow, D.M. Simulation testing of stock assessment models. Fish. Res. 2003, 65, 253–264. [Google Scholar]
- Ducharme-Barth, N.D.; Grüss, A.; Vincent, M.T.; Kiyofuji, H.; Aoki, Y.; Pilling, G.; Hampton, J.; Thorson, J.T. Impacts of fisheries-dependent spatial sampling patterns on catch-per-unit-effort standardization: A simulation study and fishery application. Fish. Res. 2022, 246, 106169. [Google Scholar] [CrossRef]
- Wilberg, M.J.; Thorson, J.T.; Linton, B.C.; Berkson, J. Incorporating time-varying catchability into population dynamic stock assessment models. Rev. Fish. Sci. 2010, 18, 7–24. [Google Scholar] [CrossRef]
- Nakai, Z. Studies relevant to mechanisms underlying the fluctuation in the catch of the Japanese sardine, Sardinops melanosticta. Jpn. J. Ichthyol. 1962, 9, 1–115. [Google Scholar]
- Saito, R.; Oozeki, Y.; Takasaki, K.; Saito, T.; Uehara, S.; Miyahara, M. Transshipment activities in the North Pacific Fisheries Commission Convention Area. Mar. Policy 2022, 146, 105299. [Google Scholar] [CrossRef]
- Watanabe, Y.; Zenitani, H.; Kimura, R. Population decline of the Japanese sardine Sardinops melanostictus owing to recruitment failures. Can. J. Fish. Aquat. Sci. 1995, 52, 1609–1616. [Google Scholar] [CrossRef]
- Thorson, J.T.; Barnett, L.A. Comparing estimates of abundance trends and distribution shifts using single-and multispecies models of fishes and biogenic habitat. ICES J. Mar. Sci. 2017, 74, 1311–1321. [Google Scholar] [CrossRef]
- Song, H.; Miller, A.J.; McClatchie, S.; Weber, E.D.; Nieto, K.M.; Checkley, D.M.J. Application of a data-assimilation model to variability of Pacific sardine spawning and survivor habitats with ENSO in the California Current System. J. Geophys. Res. 2012, 117, C03009. [Google Scholar] [CrossRef]
- Vander, L.C.D.; Castro, L.; Drapeau, L.; Checkley, D., Jr. (Eds.) Report of a GLOBEC-SPACC Workshop on Characterizing and Comparing the Spawning Habitats of Small Pelagic Fish; GLOBEC Report 21; GLOBEC: Swindon, UK, 2005; Volume 7, p. 33. [Google Scholar]
- Kai, M. Spatio-temporal changes in catch rates of pelagic sharks caught by Japanese research and training vessels in the western and central North Pacific. Fish. Res. 2019, 216, 177–195. [Google Scholar] [CrossRef]
- Thorson, J.T. Guidance for decisions using the Vector Autoregressive Spatio-Temporal (VAST) package in stock, ecosystem, habitat and climate assessments. Fish. Res. 2019, 210, 143–161. [Google Scholar] [CrossRef]
- Han, Q.P.; Shan, X.J.; Jin, X.S.; Gorfine, H. Overcoming gaps in a seasonal time series of Japanese anchovy abundance to analyse interannual trends. Ecol. Indic. 2023, 149, 110189. [Google Scholar] [CrossRef]
- Thorson, J.T.; Adams, C.F.; Brooks, E.N.; Eisner, L.B.; Kimmel, D.G.; Legault, C.M.; Rogers, L.A.; Yasumiishi, E.M. Seasonal and interannual variation in spatio-temporal models for index standardization and phenology studies. ICES J. Mar. Sci. 2020, 77, 1879–1892. [Google Scholar] [CrossRef]
- Quirijns, F.; Poos, J.; Rijnsdorp, A. Standardizing commercial CPUE data in monitoring stock dynamics: Accounting for targeting behaviour in mixed fisheries. Fish. Res. 2008, 89, 1–8. [Google Scholar] [CrossRef]
- Campbell, R.A. A new spatial framework incorporating uncertain stock and fleet dynamics for estimating fish abundance. Fish Fish. Oxf. 2016, 17, 56–77. [Google Scholar] [CrossRef]
- Nakano, H. Stock status of Pacific swordfish, Xiphias gladius, inferred from CPUE of the Japanese longline fleet standardized using general linear models. US Nat. Mar. Fish. Serv. NOAA Tech. Rep. NMFS 1998, 142, 195–209. [Google Scholar]
- Ichinokawa, M.; Brodziak, J. Using adaptive area stratification to standardize catch rates with application to North Pacific swordfish (Xiphias gladius). Fish. Res. 2010, 106, 249–260. [Google Scholar] [CrossRef]

| Explanatory Variables | Year | Area | Vessel | SST | SSTG | SSH |
|---|---|---|---|---|---|---|
| VIF | 1.02 | 1.01 | 1.02 | 1.18 | 1.06 | 1.16 |
| No. | GLM Model | AIC |
|---|---|---|
| 1 | Ln(CPUE)~Year + Area + Year: Area | 9755.40 |
| 2 | Ln(CPUE)~Year + Area + Year:Area + Vessel | 9720.78 |
| 3 | Ln(CPUE)~Year + Area + Year:Area + Vessel + SST | 9722.72 |
| 4 | Ln(CPUE)~Year + Area + Year:Area + Vessel + SST + SSTG | 9708.86 |
| 5 | Ln(CPUE)~Year + Area + Year:Area + Vessel + SST + SSTG + SSH | 9710.58 |
| No. | GLMM Model | AIC |
|---|---|---|
| 1 | Ln(CPUE)~Year + Area + Year: Area | 9795.28 |
| 2 | Ln(CPUE)~Year + Area + Year:Area + Vessel | 9765.51 |
| 3 | Ln(CPUE)~Year + Area + Year:Area + Vessel + SST | 9776.61 |
| 4 | Ln(CPUE)~Year + Area + Year:Area + Vessel + SST + SSTG | 9761.08 |
| 5 | Ln(CPUE)~Year + Area + Year:Area + Vessel + SST + SSTG + SSH | 9765.23 |
| No. | Covariates | AIC |
|---|---|---|
| 1 | None | 8789.27 |
| 2 | SST | 8782.16 |
| 3 | SST + SSTG | 8785.38 |
| 4 | SST + SSTG + SSH | 8787.45 |
| Model | Conditional R2 | CAIC |
|---|---|---|
| GLM | 0.27 | 9709.18 |
| GLMM | 0.32 | 9690.90 |
| VAST | 0.36 | 8776.27 |
| Model | Variable | Overall Influence |
|---|---|---|
| GLM | Year | 0.258 |
| Area | 0.173 | |
| Year × Area | 0.287 | |
| SST | 0.015 | |
| GLMM | Year | 0.196 |
| Area | 0.204 | |
| Year × Area | 0.303 | |
| SST | 0.015 | |
| VAST | Year | 0.217 |
| Area | 0.209 | |
| spatio-temporal | 0.312 | |
| SST | 0.015 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Han, H.; Tang, F.; Zhang, S.; Fan, W.; Zhang, H.; Wu, Z. Evaluation Performance of Three Standardization Models to Estimate Catch-per-Unit-Effort: A Case Study on Pacific Sardine (Sardinops sagax) in the Northwest Pacific Ocean. Fishes 2023, 8, 606. https://doi.org/10.3390/fishes8120606
Shi Y, Han H, Tang F, Zhang S, Fan W, Zhang H, Wu Z. Evaluation Performance of Three Standardization Models to Estimate Catch-per-Unit-Effort: A Case Study on Pacific Sardine (Sardinops sagax) in the Northwest Pacific Ocean. Fishes. 2023; 8(12):606. https://doi.org/10.3390/fishes8120606
Chicago/Turabian StyleShi, Yongchuang, Haibin Han, Fenghua Tang, Shengmao Zhang, Wei Fan, Heng Zhang, and Zuli Wu. 2023. "Evaluation Performance of Three Standardization Models to Estimate Catch-per-Unit-Effort: A Case Study on Pacific Sardine (Sardinops sagax) in the Northwest Pacific Ocean" Fishes 8, no. 12: 606. https://doi.org/10.3390/fishes8120606
APA StyleShi, Y., Han, H., Tang, F., Zhang, S., Fan, W., Zhang, H., & Wu, Z. (2023). Evaluation Performance of Three Standardization Models to Estimate Catch-per-Unit-Effort: A Case Study on Pacific Sardine (Sardinops sagax) in the Northwest Pacific Ocean. Fishes, 8(12), 606. https://doi.org/10.3390/fishes8120606







