Nonlinearity and Spatial Autocorrelation in Species Distribution Modeling: An Example Based on Weakfish (Cynoscion regalis) in the Mid-Atlantic Bight
Abstract
1. Introduction
2. Materials and Method
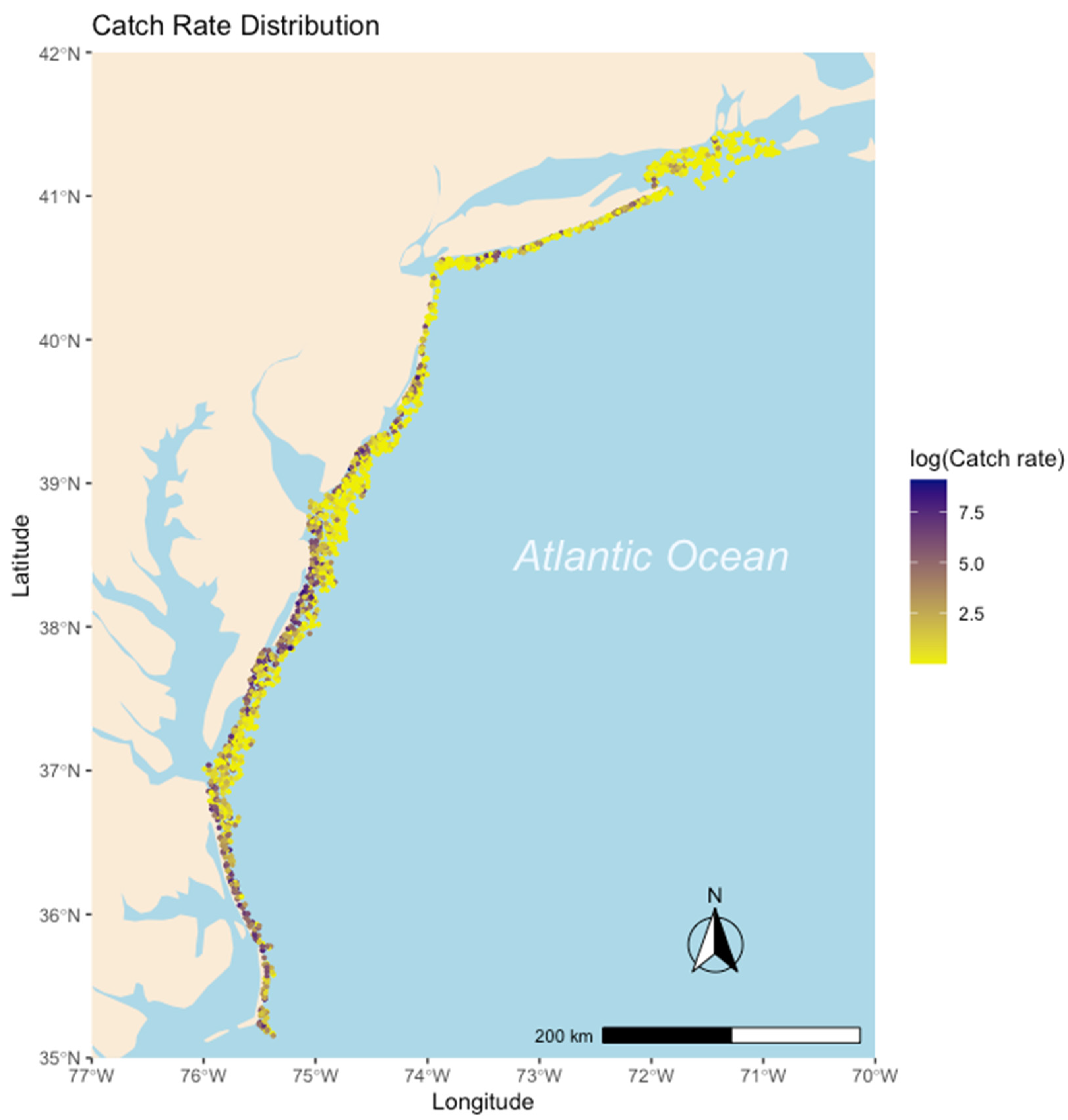
2.1. Weakfish Case Study
2.2. Models Considered
2.2.1. Generalized Linear Model (GLM)
2.2.2. Generalized Additive Model (GAM)
2.2.3. Spatial GAM
2.2.4. Autoregressive Models
2.2.5. Auto-Covariate Regression
2.2.6. Software
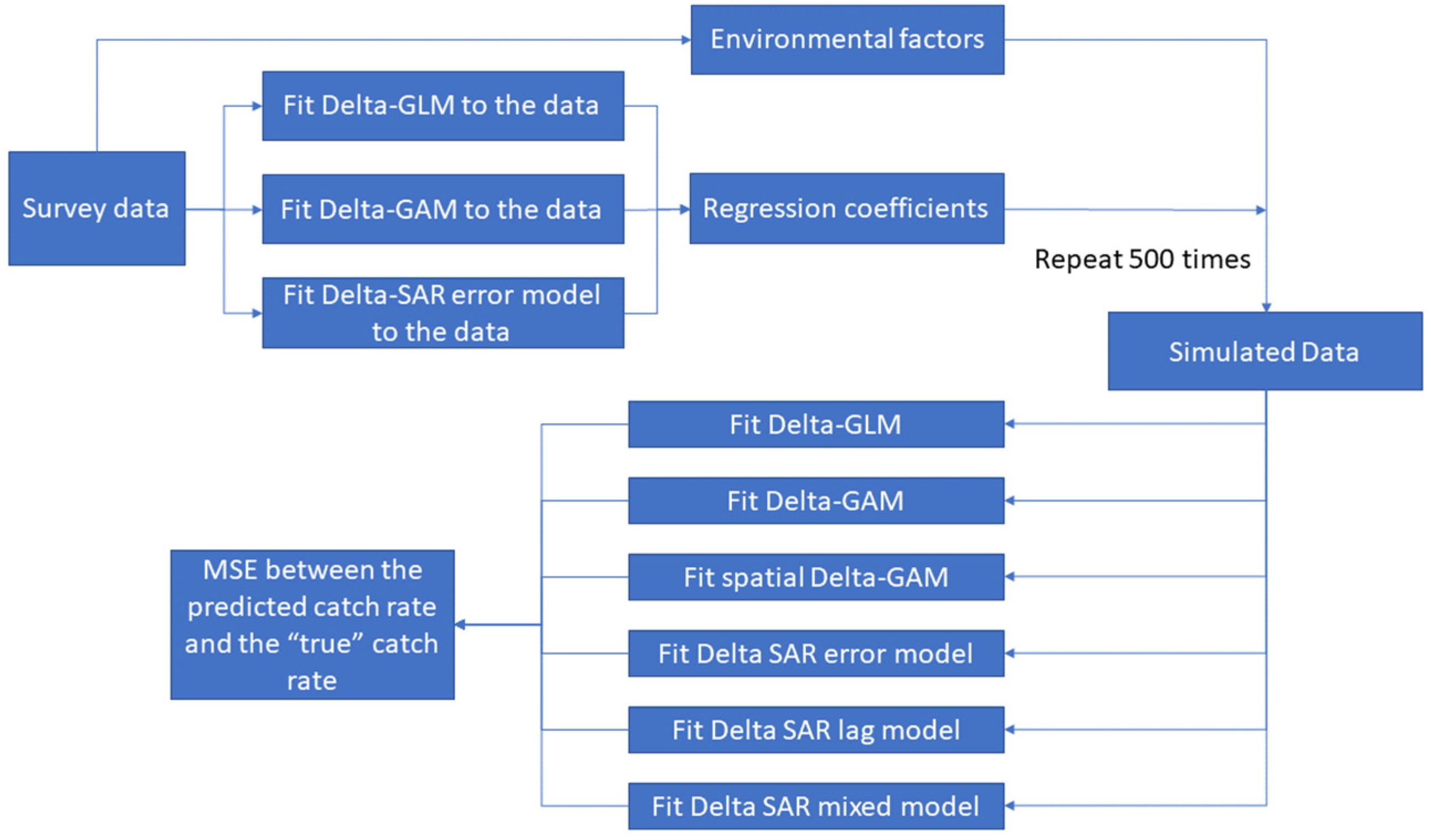
2.3. Simulation
2.4. Model Evaluation
2.4.1. Akaike’s Information Criterion (AIC)
2.4.2. Cross-Validation
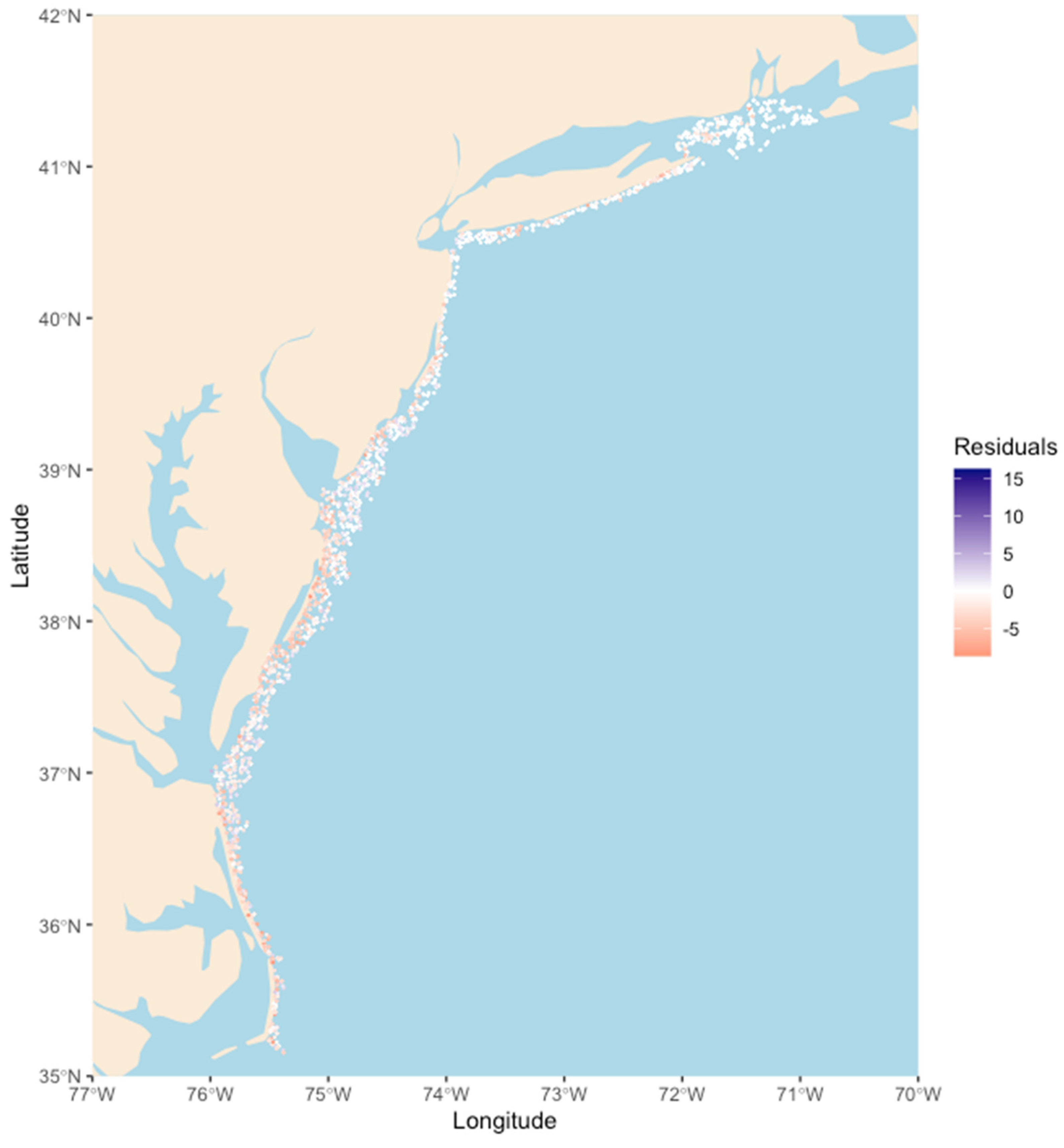
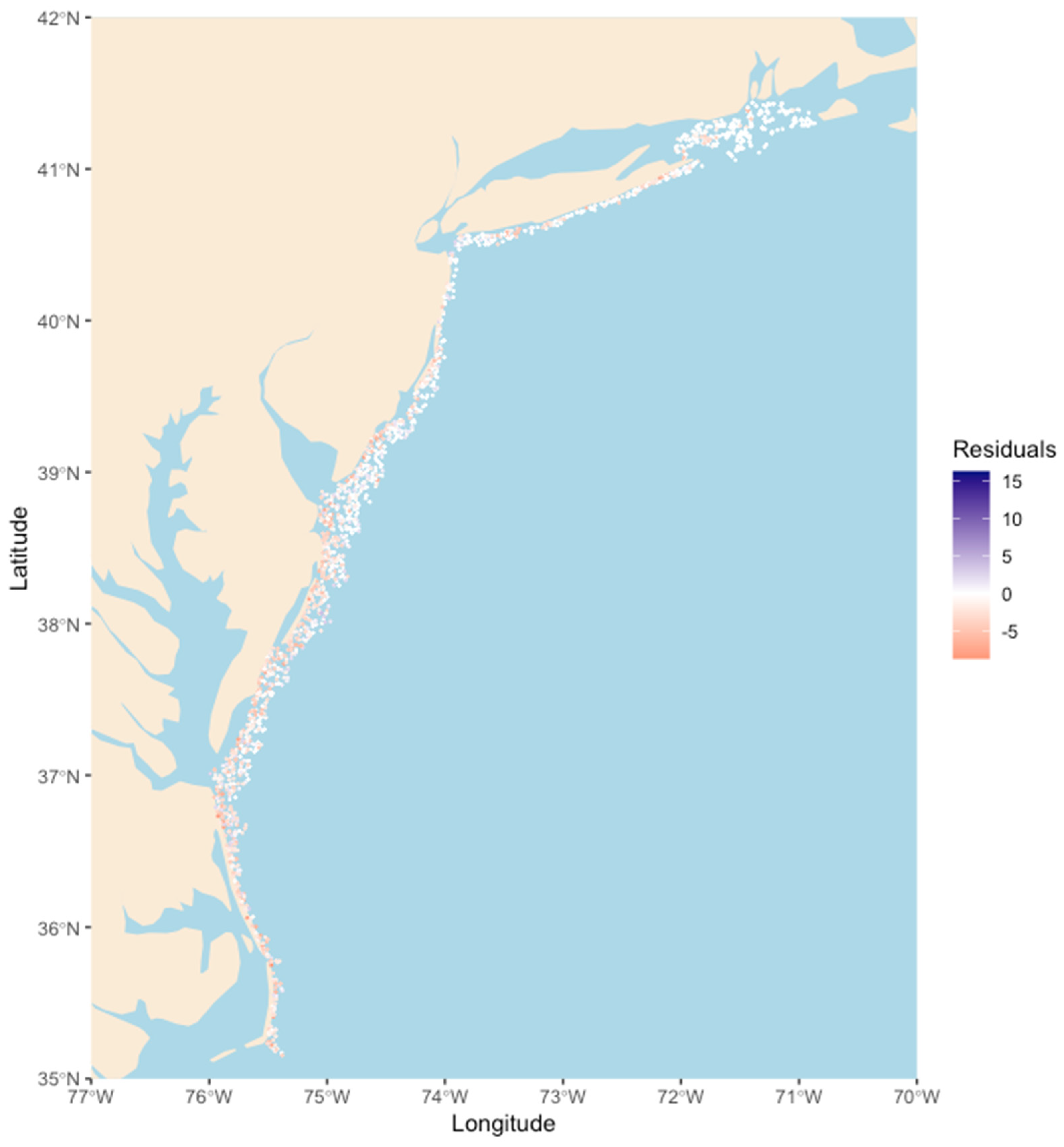
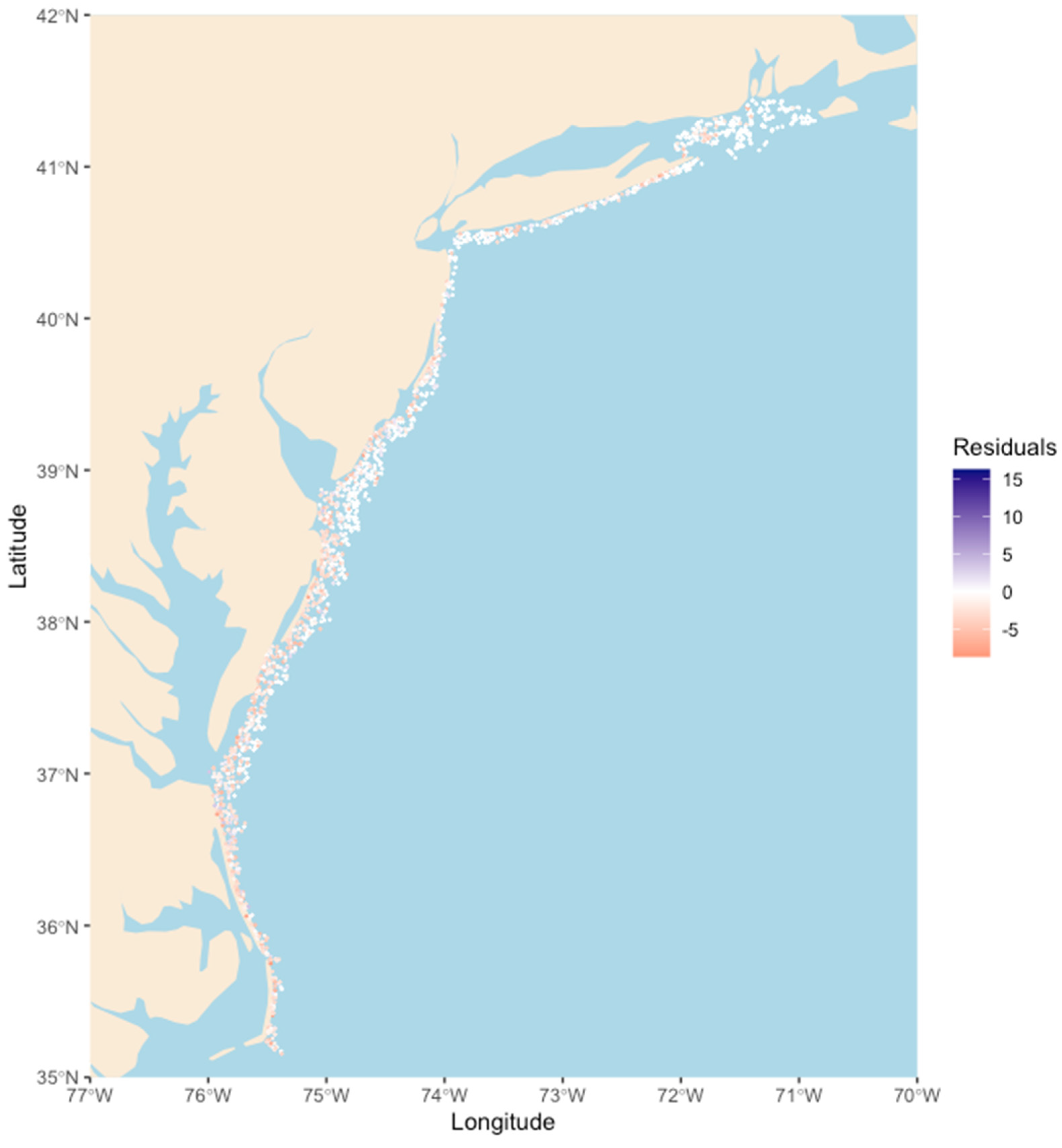
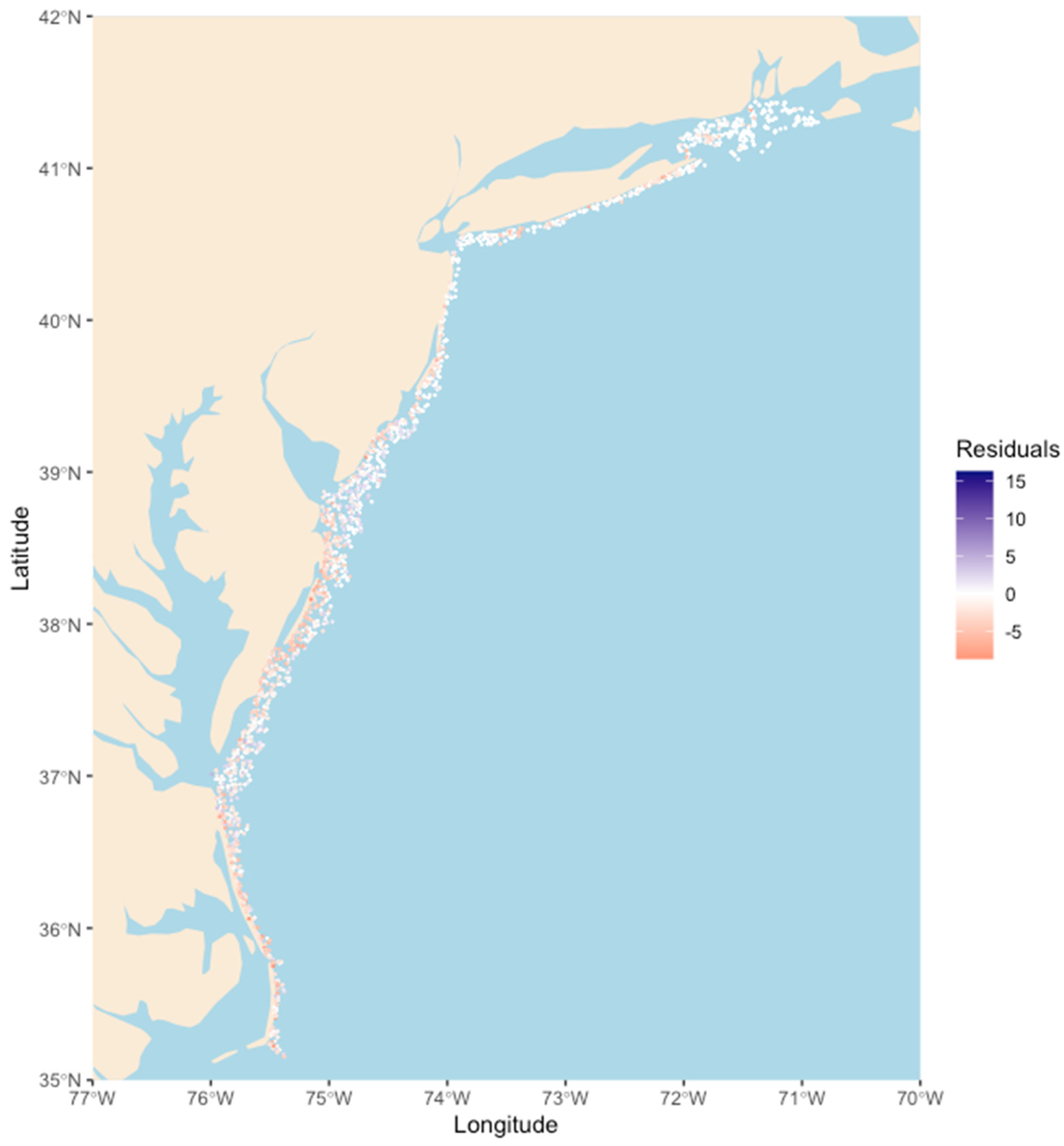
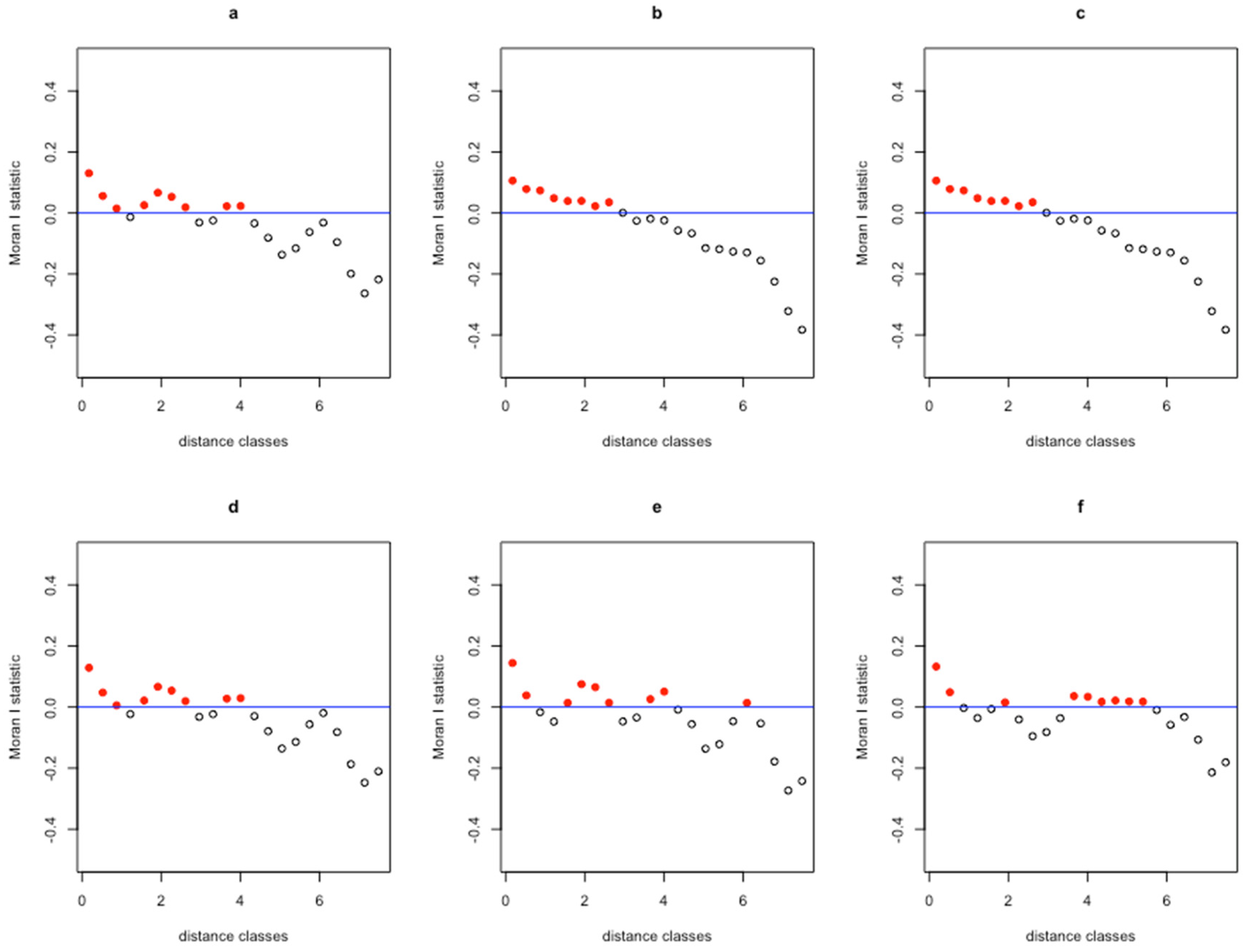
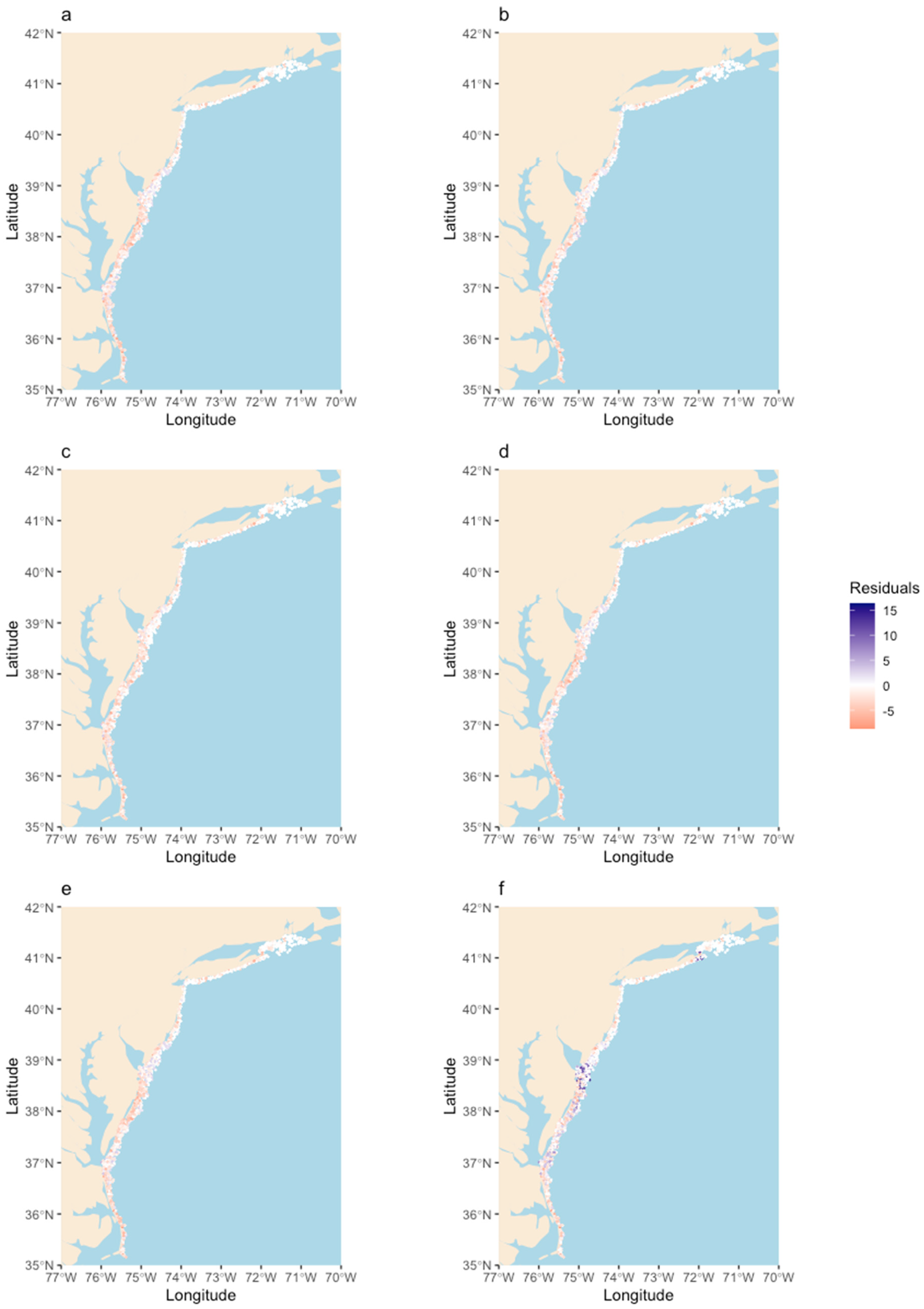
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Conan, G. Assessment of shellfish stocks by geostatistical techniques. ICES CM 1985, 1985, 372. [Google Scholar]
- Freire, J.; González-Gurriarán, E.; Fernández, L. Geostatistical analysis of spatial distribution of Liocarcinus depurator, Macropipus tuberculatus and Polybius henslowii (Crustacea: Brachyura) over the Galician continental shelf (NW Spain). Mar. Biol. 1993, 115, 453–461. [Google Scholar]
- Vignaux, M. Analysis of spatial structure in fish distribution using commercial catch and effort data from the New Zealand hoki fishery. Can. J. Fish. Aquat. Sci. 1996, 53, 963–973. [Google Scholar] [CrossRef]
- Walter, J.F., III; Christman, M.C.; Hoenig, J.M.; Mann, R. Combining data from multiple years or areas to improve variogram estimation. Environ. Off. J. Int. Environ. Soc. 2007, 18, 583–598. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Yu, H.; Jiao, Y.; Winter, A. Catch-Rate Standardization for Yellow Perch in Lake Erie: A Comparison of the Spatial Generalized Linear Model and the Generalized Additive Model. Trans. Am. Fish. Soc. 2011, 140, 905–918. [Google Scholar] [CrossRef]
- Drexler, M.; Ainsworth, C.H. Generalized Additive Models Used to Predict Species Abundance in the Gulf of Mexico: An Ecosystem Modeling Tool. PLoS ONE 2013, 8, e64458. [Google Scholar] [CrossRef]
- Legendre, P. Spatial autocorrelation: Trouble or new paradigm? Ecology 1993, 74, 1659–1673. [Google Scholar] [CrossRef]
- Legendre, P.; Fortin, M.J. Spatial pattern and ecological analysis. Vegetatio 1989, 80, 107–138. [Google Scholar] [CrossRef]
- Legendre, P.; Legendre, L. Numerical Ecology; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Besag, J. Spatial interaction and the statistical analysis of lattice systems. J. R. Stat. Soc. Ser. B Methodol. 1974, 36, 192–225. [Google Scholar] [CrossRef]
- Legendre, P.; Dale, M.R.; Fortin, M.J.; Gurevitch, J.; Hohn, M.; Myers, D. The consequences of spatial structure for the design and analysis of ecological field surveys. Ecography 2002, 25, 601–615. [Google Scholar] [CrossRef]
- McCullagh, P.; Nelder, J. Binary Data. In Generalized Linear Models; Springer: Berlin/Heidelberg, Germany, 1989; pp. 98–148. [Google Scholar]
- Maunder, M.N.; Punt, A.E. Standardizing catch and effort data: A review of recent approaches. Fish. Res. 2004, 70, 141–159. [Google Scholar] [CrossRef]
- Nelder, J.A.; Wedderburn, R.W. Generalized linear models. J. R. Stat. Soc. Ser. A Gen. 1972, 135, 370–384. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2. [Google Scholar]
- Zimmermann, N.E.; Edwards, T.C., Jr.; Graham, C.H.; Pearman, P.B.; Svenning, J.C. New trends in species distribution modelling. Ecography 2010, 33, 985–989. [Google Scholar] [CrossRef]
- Dormann, C.F.; McPherson, J.M.; Araújo, M.B.; Bivand, R.; Bolliger, J.; Carl, G.; Davies, R.G.; Hirzel, A.; Jetz, W.; Kissling, W.D.; et al. Methods to account for spatial autocorrelation in the analysis of species distributional data: A review. Ecography 2007, 30, 609–628. [Google Scholar] [CrossRef]
- Pinheiro, J.; Bates, D. Mixed-Effects Models in S and S-PLUS; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Cliff, A.D.; Ord, J.K. Spatial Processes: Models & Applications; Taylor & Francis: Abingdon-on-Thames, UK, 1981. [Google Scholar]
- Anselin, L. Spatial Econometrics: Methods and Models; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1988; Volume 4. [Google Scholar]
- Anselin, L.; Bera, A.K. Spatial dependence in linear regression models with an introduction to spatial econometrics. Stat. Textb. Monogr. 1998, 155, 237–290. [Google Scholar]
- Cressie, N. Statistics for Spatial Data; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- NEFSC. 48th Northeast Regional Stock Assessment Workshop (48th SAW) Assessment Summary Report, Part C: Weakfish Assessment Summary for 2009; National Marine Fisheries Service: Silver Spring, MD, USA, 2009. [Google Scholar]
- Bonzek, C.; Gartland, J.; Johnson, R.; Lange Jr, J. NEAMAP Near Shore Trawl Survey: Peer Review Documentation; A report to the Atlantic States Marine Fisheries Commission by the Virginia Institute of Marine Science; Virginia Institute of Marine Science: Gloucester Point, VA, USA, 2008. [Google Scholar]
- Damalas, D.; Megalofonou, P.; Apostolopoulou, M. Environmental, spatial, temporal and operational effects on swordfish (Xiphias gladius) catch rates of eastern Mediterranean Sea longline fisheries. Fish. Res. 2007, 84, 233–246. [Google Scholar] [CrossRef]
- Wu, H.; Huffer, F. Modelling the distribution of plant species using the autologistic regression model. Environ. Ecol. Stat. 1997, 4, 31–48. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Ortiz, M.; Legault, C.M.; Ehrhardt, N.M. An alternative method for estimating bycatch from the US shrimp trawl fishery in the Gulf of Mexico, 1972–1995. Fish. Bull. 2000, 98, 583. [Google Scholar]
- Lo, N.C.-H.; Jacobson, L.D.; Squire, J.L. Indices of Relative Abundance from Fish Spotter Data based on Delta-Lognornial Models. Can. J. Fish. Aquat. Sci. 1992, 49, 2515–2526. [Google Scholar] [CrossRef]
- Pennington, M. Estimating the mean and variance from highly skewed marine data. Fish. Bull. 1996, 94, 498–505. [Google Scholar]
- Stefansson, G. Analysis of groundfish survey abundance data: Combining the GLM and delta approaches. ICES J. Mar. Sci. 1996, 53, 577–588. [Google Scholar] [CrossRef]
- Ye, Y.; Al-Husaini, M.; Al-Baz, A. Use of generalized linear models to analyze catch rates having zero values: The Kuwait driftnet fishery. Fish. Res. 2001, 53, 151–168. [Google Scholar] [CrossRef]
- Murray, K.T. Magnitude and distribution of sea turtle bycatch in the sea scallop (Placopecten magellanicus) dredge fishery in two areas of the northwestern Atlantic Ocean, 2001–2002. Fish. Bull. 2004, 102, 671–681. [Google Scholar]
- Lichstein, J.W.; Simons, T.R.; Shriner, S.A.; Franzreb, K.E. Spatial autocorrelation and autoregressive models in ecology. Ecological monographs 2002, 72, 445–463. [Google Scholar] [CrossRef]
- Haining, R.P.; Haining, R. Spatial Data Analysis: Theory and Practice; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Dormann, C.F. Effects of incorporating spatial autocorrelation into the analysis of species distribution data. Glob. Ecol. Biogeogr. 2007, 16, 129–138. [Google Scholar] [CrossRef]
- Knapp, R.A.; Matthews, K.R.; Preisler, H.K.; Jellison, R. Developing probabilistic models to predict amphibian site occupancy in a patchy landscape. Ecol. Appl. 2003, 13, 1069–1082. [Google Scholar] [CrossRef]
- Gumpertz, M.L.; Graham, J.M.; Ristaino, J.B. Autologistic Model of Spatial Pattern of Phytophthora Epidemic in Bell Pepper: Effects of Soil Variables on Disease Presence. J. Agric. Biol. Environ. Stat. 1997, 2, 131. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Wood, S.N. Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. J. R. Stat. Soc. Ser. B 2010, 73, 3–36. [Google Scholar] [CrossRef]
- Bivand, R.; Millo, G.; Piras, G. A Review of Software for Spatial Econometrics in R. Mathematics 2021, 9, 1276. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Selected Papers of Hirotugu Akaike; Parzen, E., Tanabe, K., Kitagawa, G., Eds.; Springer: New York, NY, USA, 1998; pp. 199–213. [Google Scholar]
- Li, Y.; Jiao, Y.; He, Q. Decreasing uncertainty in catch rate analyses using Delta-AdaBoost: An alternative approach in catch and bycatch analyses with high percentage of zeros. Fish. Res. 2011, 107, 261–271. [Google Scholar] [CrossRef]
- Wood, S.N. Generalized Additive Models: An Introduction with R; Chapman and Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar]

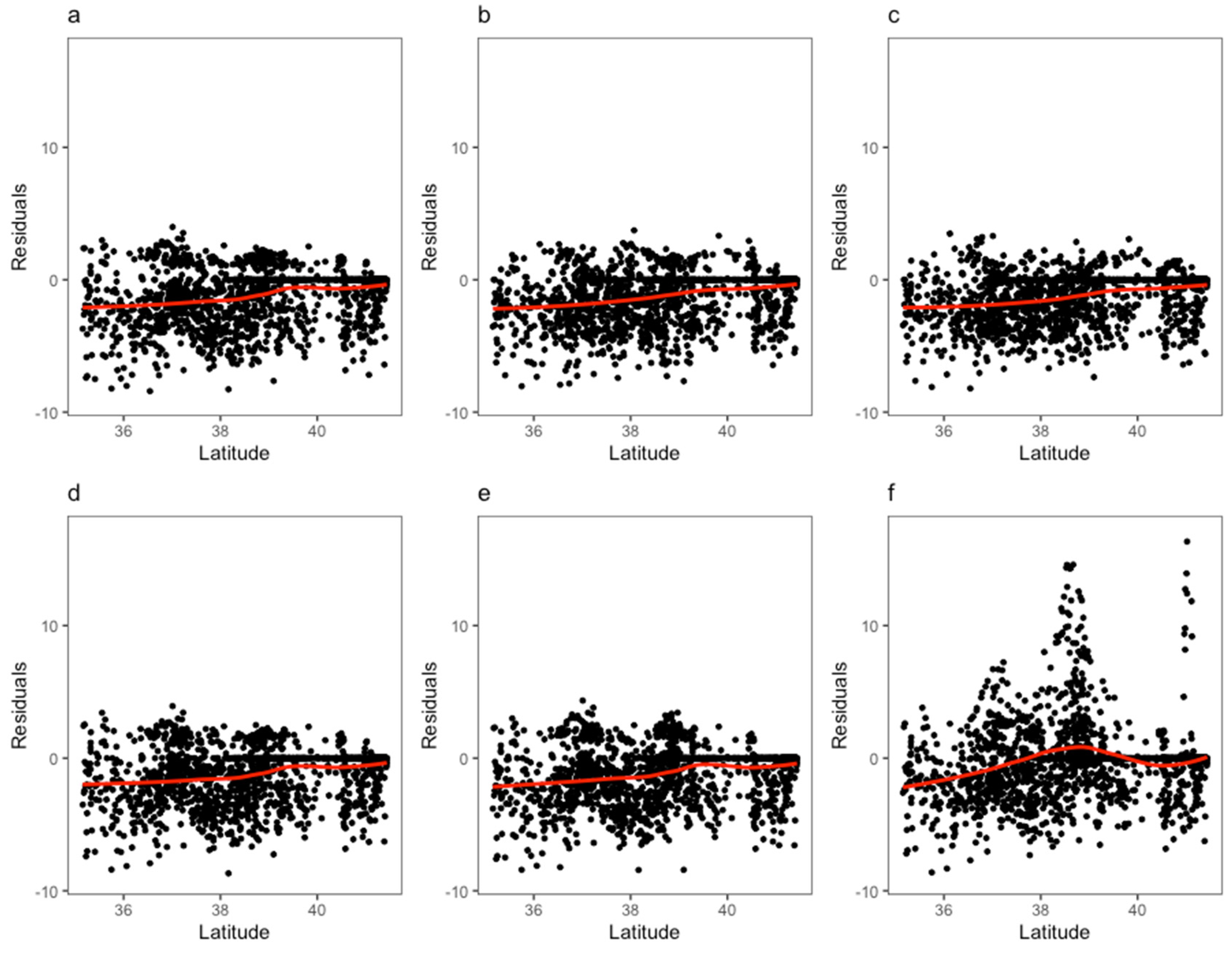
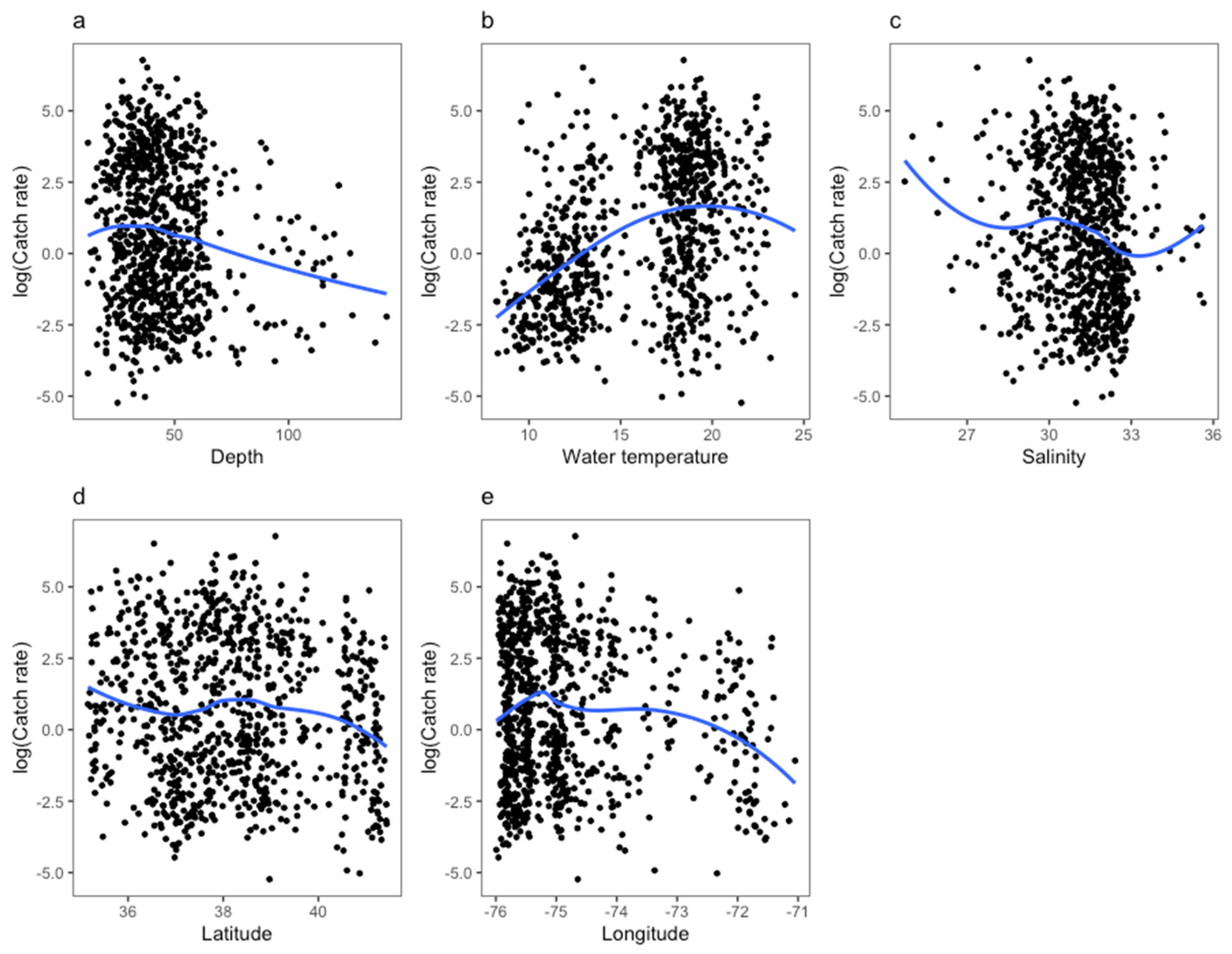
| Scenario | |||
|---|---|---|---|
| 1 | 2 | 3 | |
| Positive catch model a | |||
| GLM | 3985 | 4002 | 3983 |
| GAM | 3925 | 3886 | 3883 |
| Spatial GAM | 3886 | 3845 | 3843 |
| SAR error model | 3965 | 3976 | 3961 |
| SAR lag model | 3975 | 3989 | 3972 |
| SAR mixed model | 3962 | 3977 | 3957 |
| Presence-absence model b | |||
| GLM | 1741 | 1785 | 1717 |
| GAM | 1651 | 1602 | 1554 |
| Spatial GAM | 1487 | 1445 | 1408 |
| Auto covariate model | 1723 | 1750 | 1687 |
| Model | Delta GLM | Delta GAM | Delta Spatial GAM | Delta SAR Error Model | Delta SAR Lag Model | Delta SAR Mixed Model |
|---|---|---|---|---|---|---|
| Moran’s I | 0.21 | 0.18 | 0.20 | 0.21 | 0.22 | 0.55 |
| p-value | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| Model | Delta GLM | Delta GAM | Delta Spatial GAM | Delta SAR Error Model | Delta SAR Lag Model | Delta SAR Mixed Model |
|---|---|---|---|---|---|---|
| Training error | 5.46 | 5.03 | 4.78 | 5.40 | 6.74 | 8.03 |
| Testing error | 5.55 | 5.21 | 5.01 | 5.50 | 6.26 | 6.36 |
| “True” Model | Delta GLM | Delta GAM | Delta Spatial GAM | Delta SAR Error Model | Delta SAR Lag Model | Delta SAR Mixed Model |
|---|---|---|---|---|---|---|
| GLM | 85.75 | 85.58 | 85.51 | 85.88 | 85.93 | 86.00 |
| GAM | 191.14 | 190.97 | 190.94 | 191.31 | 191.43 | 191.91 |
| SAR error model | 99.18 | 99.07 | 99.03 | 99.34 | 99.41 | 99.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Jiao, Y.; Latour, R.J. Nonlinearity and Spatial Autocorrelation in Species Distribution Modeling: An Example Based on Weakfish (Cynoscion regalis) in the Mid-Atlantic Bight. Fishes 2023, 8, 27. https://doi.org/10.3390/fishes8010027
Zhang Y, Jiao Y, Latour RJ. Nonlinearity and Spatial Autocorrelation in Species Distribution Modeling: An Example Based on Weakfish (Cynoscion regalis) in the Mid-Atlantic Bight. Fishes. 2023; 8(1):27. https://doi.org/10.3390/fishes8010027
Chicago/Turabian StyleZhang, Yafei, Yan Jiao, and Robert J. Latour. 2023. "Nonlinearity and Spatial Autocorrelation in Species Distribution Modeling: An Example Based on Weakfish (Cynoscion regalis) in the Mid-Atlantic Bight" Fishes 8, no. 1: 27. https://doi.org/10.3390/fishes8010027
APA StyleZhang, Y., Jiao, Y., & Latour, R. J. (2023). Nonlinearity and Spatial Autocorrelation in Species Distribution Modeling: An Example Based on Weakfish (Cynoscion regalis) in the Mid-Atlantic Bight. Fishes, 8(1), 27. https://doi.org/10.3390/fishes8010027








