Next Article in Journal
Environmental DNA Metabarcoding Reflects Fish DNA Dynamics in Lentic Ecosystems: A Case Study of Freshwater Ponds
Previous Article in Journal
Properties of Protein Hydrolysates and Bioinformatics Prediction of Peptides Derived from Thermal and Enzymatic Process of Skipjack Tuna (Katsuwonus pelamis) Roe
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Fishes
Volume 7
Issue 5
10.3390/fishes7050256
fishes-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Analysis of At-Haulback Mortality and Influencing Factors of Indian Ocean Swordfish (Xiphias gladius)

by
Yingcong Guo
1,
Xuefang Wang
1,2,3,*,
Xiuzhen Li
1,
Feng Wu
1,2,3,* and
Jiangfeng Zhu
1,2,3
1
College of Marine Sciences, Shanghai Ocean University, Shanghai 201306, China
2
Key Laboratory of Sustainable Exploitation of Oceanic Fisheries Resources, Ministry of Education, Shanghai Ocean University, Shanghai 201306, China
3
National Engineering Research Center for Oceanic Fisheries, Shanghai 201306, China
*
Authors to whom correspondence should be addressed.
Fishes 2022, 7(5), 256; https://doi.org/10.3390/fishes7050256
Submission received: 10 August 2022 / Revised: 13 September 2022 / Accepted: 21 September 2022 / Published: 25 September 2022
(This article belongs to the Section Biology and Ecology)
Browse Figures
Versions Notes

Abstract

:
The at-haulback mortality of swordfish (Xiphias gladius), a highly migratory fish, in the Indian Ocean during tuna longline fishery is a concern of the Indian Ocean Tuna Commission Fisheries Management. We obtained the data of 1144 swordfish recorded in 1925 operations in the Indian Ocean by Chinese tuna longline observers from 2012–2018. A generalized linear model was used to analyze the at-haulback mortality of swordfish and the potential influencing factors. The overall mortality rate of swordfish was 64.0%, and the average female size was 166.3 cm (SD = 32.5 cm), with an observed at-haulback mortality rate of 64.3%. The average male size was 155.1 cm (SD = 25.6 cm), which was smaller than females. The observed at-haulback mortality rate was 63.6%. No significant difference was observed between the sexes. Quarter, longitude, hook type, and Lower Jaw-Fork Length (LJFL) had a significant effect on the at-haulback condition when fish were retrieved onboard. Longitude and LJFL had a significant effect on the at-haulback mortality of swordfish. When the capture position was closer to the east, the at-haulback mortality decreased and LJFL increased. The interaction term of hook type and LJFL had a significant effect on at-haulback mortality. When using the circle hook and other hook types, the greater the LFJL, the greater the mortality rate; the opposite was true for Japanese tuna hooks. We provide information for understanding the at-haulback mortality of swordfish bycatch by Chinese tuna longline fishing fleets in the Indian Ocean and its influencing factors, which will help the future conservation and management of swordfish.

1. Introduction

Swordfish (Xiphias gladius) is the top predator in the food web [1] observed in pelagic fisheries [2]. In addition, it is also a very important bycatch in tuna longline fishery. This species is highly migratory in tropical and temperate waters [3], and the depth of migration varies with the water temperature environment [4]. Swordfish show sexual dimorphism in terms of the maximum size, growth rate, and age at maturity. Females grow faster and mature later than males, [5,6] and have a larger size at first maturity.
In the waters under the jurisdiction of the Indian Ocean Tuna Commission (IOTC), the catch of swordfish from 2016 to 2019 was 30,743–33,588 tons, of which the average annual catch of longline fishing was 19,304.5 tons, accounting for about 60.2% [7]. IOTC’s 19th Working Party on Billfish (WPB) used stock synthesis to assess swordfish stock in 2020. This assessment showed that although the population is not currently overfished and overfishing [8], the risk of overfished and overfishing in the future is high [9], so studying at-haulback mortality (hooking mortality) is very important for assessing the effect of longline fishing on the populations of these species [10]. It can also provide a basis for reducing the negative effect of fishing bycatch on marine ecosystems [11]. It also contributes to reducing the persistent negative effects of tuna longline fleet bycatch on pelagic ecosystems [11].
At-haulback condition refers to the state (alive or dead) of fish when they are retrieved onboard [12]. At-haulback mortality represents the percentage of deaths to the total number of catches when the fishing tackle is retrieved onboard [13]. Extensive research on at-haulback mortality has been conducted in longline fisheries worldwide. In the Indian Ocean, research on at-haulback mortality for swordfish, sea turtles, sharks is also gradually being carried out [14,15,16]. In addition to focusing on the level of at-haulback mortality of target fish species, many studies have also assessed the potential factors affecting at-haulback mortality. These include sex and lower jaw-fork length (LJFL), among other biological characteristics [17,18], as well as hook type [19,20] and marine environmental characteristics [18,21].
At present, reports of swordfish at-haulback mortality are mostly focused in the Atlantic Ocean [16,20]. However, information on this topic in the Indian Ocean tuna longline fisheries is less, which prevents the IOTC from further improving and developing more effective conservation and management measures [16]. Therefore, this study used a generalized linear model (GLM) to examine the at-haulback mortality of Indian Ocean swordfish based on data from the Chinese Pelagic Fisheries Observer Program. The aim of this study is as follows: (1) to analyze if differences are present in the level of at-haulback mortality of swordfish of different genders and LJFL; (2) to assess the effect of a variety of potential factors, such as biological, environmental, as well as fishing gear characteristics, on at-haulback mortality; and (3) to use GLM to predict at-haulback mortality under specific conditions.

2. Materials and Methods

2.1. Data Collection

The data used in this study was obtained from the Indian Ocean tuna longline fishery dataset provided by the Chinese Pelagic Fisheries Observer Program. During the period 2012–2018, scientific observers collected operational information on Chinese tuna longline fishing vessels on 18 voyages, including 16 fishing vessels, and observed 1925 fishing sets in total. Figure 1 shows the location distribution of the survey sites in this study. The main area was the western Indian Ocean 40° N–11° S, 23° E–90° E. The target species were bigeye tuna (Thunnus obesus) and albacore tuna (Thunnus alalunga). In general, the starting time of deploying gear was between 03:00 and 08:00 local time, and lasted for about 5 h. The time of retrieving gear was between 11:00 and 16:00. Total operation would last for 10~15 h. The main line of the fishing tackle is composed of nylon braided rope or glass filament monofilament, and the length of the mainline is approximately 70,000–249,570 m. The length of the mainline between the two floats of the fishing tackle was 726–1102m (the number of branch lines was 16~29, branch line set interval was 30~56.6 m), the length of the float line was 20~40m, and the length of the branch line was 18~52 m. The fishing hooks used were mainly Japanese tuna hooks (88.8%), followed by some circle hooks (2.7%), and other hook types (8.3%).
The observers measured and recorded the biological information of fish by species, including the lower jaw-fork length, sex, and at-haulback condition. The at-haulback condition was divided into alive (recorded as “A1/A2/A3” according to the condition of the swordfish retrieved onboard, which are combined as “A” in this study) and death (recorded as “D”) and used as the response variable in this study. A total of 1942 swordfish were caught in all the voyages. Because of the incomplete records of some fish, this study used the data of 1144 swordfish for analysis.
Reevesa and Bruesewitz (2007) reported that water temperature has a significant effect on the at-haulback mortality of Walleyes (Sander vitreus) [22], and Muoneke (1994) found that for most fish such as salmonids, centrarchids, etc., the lower the dissolved oxygen (DO) lead to the greater the at-haulback mortality [13]. We selected sea surface temperature (SST) and DO as potential explanatory variables. SST and DO were downloaded from the Copernicus Marine Environment Monitoring Service (https://marine.copernicus.eu/, 5 August 2021). The time resolution of SST and DO was the month, and the spatial resolution was 0.25° × 0.25°. The latitude and longitude information was matched with the downloaded SST and DO and with the information of each fish. The names, types, and ranges of all explanatory variables selected in this study are listed in Table 1.

2.2. Data Analysis

The chi-square test was performed to test the difference in the at-haulback mortality of different gender groups, quarters, hook types, and target fish species. To eliminate linear correlation problems between continuous variables, the variance inflation factor (VIF) of all continuous explanatory variables was calculated, and variables with VIF values greater than five were deleted [23]. The response variable belongs to the binomial distribution of the 0–1 response, so the relationship between the at-haulback condition and the influencing factors was expressed by a generalized linear model in which the connection function was the logarithmic connection function in the binomial distribution family. The formula for the model was as follows:
l o g i t ( P ) = log ( P 1 − P ) = β 0 + β 1 S e x + β 2 L J F L + β 3 S S T + β 4 D O + β 5 Q u a r t e r + β 6 L o n + β 7 L a t + β 8 H T + β 9 T F P + ε i
where P is the probability of a swordfish dying after being retrieved onboard, β 0 is the intercept of the model, β i (i = 1, 2, 3, …, 9) is the coefficient estimated by the maximum likelihood method, “Sex” represents the sex of the swordfish, “LJFL” represents the lower jaw-fork length of the swordfish, “SST” represents the sea surface temperature when the swordfish was caught, “DO” refers the dissolved oxygen when the swordfish was caught, “Quarter” means the quarter when the swordfish was caught, “Lon” and “Lat” refers to the longitude and latitude where the swordfish was caught, “HT” refers to the hook type when the swordfish is caught, and “TFP” refers to the target fish species when the hook is setting, and ε i is the error term of the model.
All the above variables were used to establish a model. Subsequently, the best model for the analysis of individual mortality was selected based on the Akaike information criterion (AIC) backward stepwise regression method [24]. The best model was the model with the smallest AIC value. If some explanatory variables in the model were not significant (p > 0.05), according to the magnitude of the deviance explanation of each covariate in the model, the covariates with smaller deviance explanation were eliminated in turn until all covariates were fitted as important variables [25]. In this step, according to the recommendations of Hosmer and Lemeshow (2000) [26], the variables deleted during AIC screening were added to the model for further testing to prevent the deletion of important covariates. Based on the above model, possible interaction terms were added, and the same steps as above were used to filter the interaction terms.

2.3. Model Diagnosis and Goodness of Fit Test

The Hosmer-Lemeshow Goodness of Fit (GOF) test was performed on the model before and after an interaction item was added [26]. The K-fold cross-validation procedure was used to evaluate the model’s ability to predict individual mortality. The verification process divides the data into K sub-samples, one sample was designated as the test set, and the remaining K-1 samples were the training set. After performing the analysis on the training set, a model was obtained. The prediction results were compared and tested using the test set. The evaluation indicators of the model were saved, and this step was repeated K times until each sub-sample participated in the verification. We calculated the average of K groups of evaluation indicators as an estimate of model accuracy and subsequently calculated the area under the curve (AUC) below the receiver operating characteristic curve (ROC), and the 95% confidence interval of the model after K-fold cross-validation [27]. The K value in this study was 10. The two models were compared before and after adding the interaction term, and the model with better performance was selected. We performed an outlier test and Cooks distance test to observe whether data affect the accuracy of the model.
All statistical analyses were performed using the statistical software R (version 4.0.3). Firstly, we used the “usdm” package for continuous variable VIF screening [28] and the “cvAUC” package for cross-validation [29]. Next, we used the “visreg” package to analyze the explanatory variables and response variables in the GLM model, mapping the relationship between variables [30]. We used the “car” and “ResourceSelection” packages to diagnose the residuals of the model [31]. Lastly, we used the “mapdata” and “maptools” packages to complete the survey site map [32,33].

3. Results

3.1. Analysis of Observed At-Haulback Mortality

Among the 1144 swordfish captured in this study, we found a total of 732 dead samples, and the overall at-haulback mortality of swordfish was 64.0%. The female samples accounted for 54.4%, of which the average LJFL was 166.3 cm (SD = 32.5 cm) and the at-haulback mortality was 64.3%. The male samples accounted for 45.6% of the total, and the average size was 155.1 cm (SD = 25.6 cm). The observed at-haulback mortality rate was 63.6% (Figure 2). The chi-square test was used to test the mortality of male and female samples, and no significant difference was found in the mortality between males and females (chi-square = 0.062, df = 1, p = 0.804). However, considering that the sex of swordfish has significant differences in biological characteristics, sex is still used to establish a parsimonious model of GLM. In addition, the chi-square test results showed significant differences in the at-haulback mortality of different hook types and different target fish species (chi-square = 24.588, df = 2, p-value < 0.001; chi-square = 15.760, df = 1, p < 0.001).

3.2. The Establishment of the GLM Model

The VIF value of the continuous variable was calculated, and the VIF values of the SST and DO were both greater than 5 in the first test. After deleting DO with the largest VIF value (16.573), the remaining four variables all cleared the test, and the VIF values were 1.024, 1.676, 3.903, and 3.418.
The model was screened according to the AIC and the important variables were fitted. The LJFL, quarter, longitude, and hook type were all variables that had a significant effect on the probability of dying. The pairwise interaction terms of the above four explanatory variables were added to the model for testing, and it was found that quarter, hook type, LJFL, and longitude were still significant in the model (p < 0.05). The interaction term between hook type and LJFL, LJFL, and longitude were also significant in the model (p < 0.05) (Table 2 and Table 3).
Regression diagnosis and comparison were performed on the model before and after the interaction term, and the model after the interaction term was added. No over-fitting or over-spreading of the two models was observed. In terms of goodness of fit, both models fulfilled the Hosmer–Lemeshaw test. The X-squared value of the parsimonious model was 14.501 (p = 0.070). After the interaction term was added, the model fitted better, with an X-squared value of 12.007 (p = 0.151). By adding the interaction term, the predictive ability of the model improved. The average AUC of a hundred cross-validation of the parsimonious model was 0.618, with a 95% confidence level between 52.0% and 72.0%. After adding the interaction term, the average AUC of the model was 0.655, and the confidence level was between 55.5% and 75.3%.
Residual analysis was performed on the model after adding the interaction term. The final verification of the residual analysis did not reveal any significant outliers. The Cook distance determined several data points, whose values were relatively higher than the rest, but these points do not affect the estimated model parameters, so they were not removed from the final model.

3.3. Predictions of the Probabilities of At-Haulback Mortality

In the model with the interaction term added, the hook type was still the factor that has the greatest influence on the probability of swordfish dying at haulback. The predictions of the probabilities of swordfish dying at-haulback if caught by circle hooks and others were 28.0% and 33.1%, respectively, and swordfish caught by Japanese tuna hooks had a significantly higher probability (59.7%) of dying (Figure 3a). The quarter was the factor with the least effect on the probability of death of swordfish. The highest mortality was found in the third quarter, and the differences in mortality rates in the first, second, and fourth quarters were less (Figure 3b).
The LJFL of swordfish and the longitude also had a certain effect on the predictions of the probabilities of at-haulback mortality. The smaller the LJFL of swordfish, the greater the probabilities of mortality, and the range of change was between 43.0% and 72.7%, which was slightly smaller than the range of probabilities of mortality for different longitudes (39–75%). Predictions showed that the mortality of the captured swordfish was lower when the capture location was closer to the east (Figure 4).
The interaction between hook type and LJFL showed that the effect of LJFL on swordfish at-haulback mortality varies depending on the hook type. As the LJFL increases, the probability of the swordfish dying at-haulback decreases when using Japanese tuna hooks. Swordfish caught by circle hooks and other hook types showed the opposite trend. As the length of the LJFL increased, the probability of dying at-haulback increased. For swordfish with a smaller LJFL, the probability of death if caught by circle hooks was significantly lower (Figure 5).
The interaction term of LJFL and longitude also had a significant effect on the probabilities of at-haulback mortality (Figure 6). Generally, the larger the LJFL of swordfish, the smaller the probability of dying. When the capture longitude was about 60° E, the difference in the at-haulback mortality between different LJFLs was the smallest. However, the predicted mortality of swordfish caught around 69° E increased gradually with LJFL.

4. Discussion

The mortality rate of swordfish caught in longline fisheries has attracted the attention of many scholars around the world. These mortality rates include natural mortality [34,35], post-release mortality [36,37], and at-haulback mortality [16,20,38,39].

4.1. Observed At-Haulback Mortality

In this study, the number of dead swordfish samples accounted for 64.0% of the total number of samples, which was close to the Epperly et al. (2012) average at-haulback mortality rate of 67.5% for North Atlantic longline swordfish. However, it was significantly lower than other studies in the Atlantic, which was about 85.0% [16,40] and higher than the average level of 43.2% of swordfish caught by longline fishing in Hawaiian waters [38]. The difference in the level of at-haulback mortality may be related to many factors, such as the hook type used by the specific fleet, location, operating habits, and marine environment.
It should be pointed out that the swordfish at-haulback mortality analyzed in this study was short-term at-haulback mortality, and the released individuals will still die due to fishing injuries. Research on the post-release mortality of swordfish based on pop-up satellite archival tags has shown that 22.0% and 38.0% of swordfish died after being released in the North Atlantic and East Pacific waters, respectively [36]. West et al. (2012) found that the post-release mortality of Indian Ocean swordfish was 64.0% [37]. Therefore, considering the post-release mortality levels estimated by multiple studies, the overall mortality rate of swordfish caused by longline fishing may reach 71.9–87.0% (Overall mortality rate = survival rate × post-release mortality + at-haulback mortality).

4.2. Factors Affecting the At-Haulback Mortality of Swordfish

In this study, hook type was the single largest factor affecting swordfish at-haulback mortality. Previous studies in the Atlantic ocean, Pacific ocean, Mediterranean sea, and the Gulf of Mexico in the United States have found that hook type has a significant effect on the at-haulback mortality of swordfish, tuna, sharks, and sea turtles [12,20,41]. These studies generally indicate that circle hooks can effectively reduce their at-haulback mortality compared with other types of hooks. However, some studies believe that hook types have no significant effect on the at-haulback mortality of target species [22,40]. In this study of Indian Ocean swordfish, the swordfish caught by the circle hook had the lowest at-haulback mortality, whereas the mortality of swordfish caught by Japanese tuna hooks was significantly higher. This was believed to be due to the difference in the shape of the various hooks and the position where the hook enters the fish’s body [19]. After the fish was hooked, the circle hook usually hooks the fish’s mouth or jaw and rotates in the mouth, so the fish caught by the circle hook had no obvious injuries [19]. The Japanese tuna hook usually enters deeper positions, such as the throat or intestine of the fish [42], causing greater damage to the fish or even death, resulting in higher mortality when retrieved onboard. Based on the analysis results of this study, we suggest that tuna longline fishing vessels can preferentially use circle hooks to reduce the at-haulback mortality of swordfish.
The interaction between hook type and LJFL has a significant effect on the at-haulback mortality of swordfish. However, with other hook types, the LJFL had a different effect on the probability of death of the swordfish (Figure 5). Many studies have found that LJFL is an important factor that affects at-haulback mortality. A study on the at-haulback mortality of swordfish and blue sharks (Prionace glauca) caught by J-style hooks (“J-style hooks” and “tuna hooks”) in the Atlantic longline fishery found that as LJFL increases, the mortality rate gradually decreases [10,16]. Japanese tuna hooks in this study support this pattern. For circle hooks and other hook types, Morgan and Carlson (2010) studied sharks in the Atlantic Ocean and found that the at-haulback mortality increased with an increase in LJFL [43]. This may be due to the larger mouth of the larger shark. Due to the special shape of the circle hook, the hook was more likely to slide deeper into the fish (viscera, etc.), causing damage to the fish. On the other hand, the Japanese tuna hook was easier to hook the snout of the fish rather than slipping down to the internal organs. However, whether this phenomenon is universal in the fish species caught in longline fishing needs further investigation because Neilson et al. (1989) analyzed the Atlantic halibut (Hippoglossus hippoglossus) caught by the circle hook in the longline fishery and found that the at-haulback mortality rate decreased with an increase in body length [44].
Longitude was the second largest single factor affecting swordfish at-haulback mortality. Longitude also has a greater effect on the at-haulback mortality of swordfish, showing a trend of lower mortality rates closer to the East Indian Ocean (Figure 4). Coelho et al. (2019) studied a variety of elasmobranchs in the Atlantic Ocean and found that this change was affected by the location and species of capture [16]. Blue sharks and crocodile sharks (Pseudocarcharias kamoharai) have higher at-haulback mortality in the equatorial and South Atlantic regions, whereas shortfin Mako (Isurus oxyrinchus) has a lower mortality rate in the northeastern Atlantic Ocean. The interaction between longitude and LJFL showed that the greater the LJFL, the greater the at-haulback mortality when the capture position was closer to the west. When the capture position was closer to the east, the mortality decreased gradually with the increase in LJFL. Coelho et al. (2013) found that the interaction term between LJFL and longitude had a significant effect on the at-haulback mortality of the blue shark in the Atlantic Ocean. The greater the LJFL of the blue shark caught in the longer longitude area, the lower the mortality rate, which is consistent with the results of this study [21].
The quarter was the factor that had the least effect on swordfish at-haulback mortality. The differences in mortality between quarters can be due to the different LJFL of swordfish in different quarters [45] and can also be affected by different temperatures in different quarters [46]. Poisson and Fauvel (2009) found that Indian Ocean swordfish were larger during the spawning period (October to April) [45]. In this study, swordfish caught in the third quarter (July to September) had the highest mortality rate, matching the pattern of relatively higher at-haulback mortality for swordfish with smaller LJFL. The influence of quarters on the at-haulback mortality rate of swordfish can be caused by temperature differences in different quarters [46]. Muoneke (1992) found that quarter and temperature affect at-haulback mortality at the same time. Quarters with high temperatures have a higher risk of at-haulback mortality [46]. The studies of Epperly et al. (2012) and Coelho et al. (2019) on the at-haulback mortality of swordfish in the case of Portuguese longline fishing fleets in the Atlantic also support this view. The ocean temperature has a significant effect on the mortality of swordfish, and the at-haulback mortality increases when the ocean temperature increases [16,39]. However, in this study, SST was not a significant variable of the model. Whether this is caused by differences in the marine environments requires further research.
Sex had no significant effect on at-haulback mortality of swordfish in this study. Braccini et al. (2019) found that sex did not significantly affect at-haulback mortality in Atlantic Sandbar shark (Carcharhinus plumbeus), Milk shark (Rhizoprionodon acutus), and Spot-tail shark (Carcharhinus sorrah) [47]. However, Coelho et al. (2013) [21] found that sex was an important variable affecting at-haulback mortality in a study of Atlantic blue sharks, and a study of crocodile sharks also reached the same conclusion [10]. This was due to the different distribution of LJFL in different sexes [10]. In this study, both the chi-square test and the GLM model showed no significant difference between males and females. Further research is needed on whether sex affects swordfish at-haulback mortality.
Sea surface temperature was also an insignificant variable in this study. However, Reeves and Bruesewitz (2007) found that the at-haulback mortality was lower when the water temperature was low, and the higher water temperature resulted in higher at-haulback mortality [22]. Dotson (1982) and Nuhfer et al. (1992) also observed the same phenomenon [48,49]. The insignificance of SST in this study can be because swordfish are generally distributed in a water layer of about 350 m [37] and SST cannot completely represent the real water temperature where swordfish are located.
In addition to existing influencing factors, bait type, hook size, hook location, soak time, and hook depth can also potentially affect at-haulback mortality [22,38,39,50]. Epperly et al. (2012) found that the bait type was an important factor affecting the at-haulback mortality of the Atlantic swordfish [39]. Curran and Bigelow (2011) also included the hook size to study the at-haulback mortality of the target species [38]. Reeves and Bruesewitz (2007) found that different hook sizes and hook positions have different effects on the at-haulback mortality of swordfish, which are mainly affected by the different LJFL of the fish and the different positions where hooks the fish [22]. Morgan et al. (2007, 2010) studied Atlantic sharks and found that soak time had an effect on at-haulback mortality, and measures that limit soak time in longline fishing can reduce bycatch mortality [43,51]. Orbesen et al. (2019) also concluded that hook depth had no significant effect on at-haulback mortality in the bluefin tuna from the Gulf of Mexico [52]. These results need to be obtained using a targeted experimental design or specialized instruments, and further analysis is recommended in future studies.

Author Contributions

Conceptualization, Y.G. and X.W.; methodology, Y.G. and X.W.; software, Y.G., X.L.; validation, Y.G.; formal analysis, Y.G., X.L.; investigation, F.W.; resources, F.W. and J.Z.; data curation, Y.G., F.W.; writing—original draft preparation, Y.G.; writing—review and editing, X.W., F.W., J.Z.; visualization, Y.G. and X.L.; supervision, X.W. and J.Z.; project administration, F.W., J.Z.; funding acquisition, F.W., J.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This project was supported financially by the National Key R&D Programs of China (Grant No. 2019YFD0901404), the National Programme on Global Change and Air-Sea Interaction (GASI-01-EIND-YD01aut/spr/02 aut), National Observer Programme of Pelagic Fisheries, and the Ministry of Agriculture and Rural Affairs of the People’s Republic of China (Grant No. 17220255).

Institutional Review Board Statement

The study was conducted according to the guidelines of the Code of Ethics of the University Department of Marine Studies.

Data Availability Statement

The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.

Acknowledgments

We thank the Tuna Technical Group of the China Ocean Fisheries Association for providing the fishery scientific observer data of the Chinese fleet for this study. We are also deeply grateful for the collaboration of 17 observers and 16 tuna longline fishing vessels.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kitchell, J.F.; Martell, S.J.D.; Walters, C.J.; Jensen, O.P.; Kaplan, I.C.; Watters, J.; Essington, T.E.; Boggs, C.H. Billfishes in an ecosystem context. Bull. Mar. Sci. 2006, 79, 669–682. [Google Scholar]
  2. Nakamura, I. Billfishes of the world. An annotated and illustrated catalogue of marlins, sailfishes, spearfishes and swordfishes known to Date. FAO Fish. Synop. 1985, 5, 125. [Google Scholar]
  3. Neilson, J.D.; Smith, S.; Royer, F.; Paul, S.D.; Porter, J.M.; Lutcavage, M. Investigations of horizontal movements of Atlantic swordfish using pop-up satellite archival tags. In Tagging and Tracking of Marine Animals with Electronic Devices; Springer: Dordrecht, The Netherlands, 2009; Volume 9, pp. 145–159. [Google Scholar]
  4. Takahashi, M.; Okamura, H.; Yokawa, K.; Okazaki, M. Swimming behaviour and migration of a swordfish recorded by an archival tag. Mar. Freshwater. Res. 2003, 54, 527–534. [Google Scholar] [CrossRef]
  5. Poisson, F.; Fauvel, C. Reproductive dynamics of swordfish (Xiphias gladius) in the southwestern Indian Ocean (Reunion Island). Part 1: Oocyte development, sexual maturity and spawning. Aquat. Living. Resour. 2009, 22, 45–58. [Google Scholar] [CrossRef]
  6. Wang, S.P.; Lin, C.H.; Chiang, W.C. Age and growth analysis of swordfish (Xiphias gladius) in the Indian Ocean based on the specimens collected by Taiwanese observer program. In Proceedings of the 8th Session of the IOTC Working Party on Billfish, Victoria, Seychelles, 12 July 2010. IOTC-2010-WPB-08-rev1. [Google Scholar]
  7. IOTC Secretariat. Nominal Catches by Fleet, Year, Gear, IOTC Area and Species. In Proceedings of the 19th Session of the IOTC Working Party on Billfish, Online/Virtual, 13–16 September 2021; IOTC-2021-WPB19-DATA03. Available online: https://iotc.org/WPB/19/Data/03-NC (accessed on 13 September 2022).
  8. IOTC Secretariat. Outcomes of the 23rd Scientific Committee meeting. In Proceedings of the 19th Session of the IOTC Working Party on Billfish, Online/Virtual, 13–16 September 2021; IOTC–2021–WPB19–03. Available online: https://iotc.org/documents/WPB/19/03 (accessed on 13 September 2022).
  9. Wang, S.P. Stock Assessment of Swordfish (Xiphias gladius) in the Indian Ocean Using A Stock Production Model Incorporating Covariates (ASPIC). In Proceedings of the 15th Session of the IOTC Working Party on Billfish, San Sebastián, Spain, 10–14 September 2017. IOTC–2017–WPB15–21. [Google Scholar]
  10. Coelho, R.; Fernandez-Carvalho, J.; Lino, P.G.; Santos, M.S. An overview of the hooking mortality of elasmobranchs caught in a swordfish pelagic longline fishery in the Atlantic Ocean. Aquat. Living. Resour. 2012, 25, 311–319. [Google Scholar] [CrossRef]
  11. Carruthers, E.H.; Neilson, J.D.; Smith, S.C. Overlooked bycatch mitigation opportunities in pelagic longline fisheries: Soak time and temperature effects on swordfish (Xiphias gladius) and blue shark (Prionace glauca) catch. Fish. Res. 2011, 108, 112–120. [Google Scholar] [CrossRef]
  12. Gilman, E.; Huang, H.W. Review of effects of pelagic longline hook and bait type on sea turtle catch rate, anatomical hooking position and at-vessel mortality rate. Rev. Fish. Biol. Fish. 2017, 27, 43–52. [Google Scholar] [CrossRef]
  13. Muoneke, M.I.; Childress, W.M. Hooking mortality: A review for recreational fisheries. Rev. Fish. Sci. 1994, 2, 123–156. [Google Scholar] [CrossRef]
  14. Coelho, R.; Lino, P.G.; Santos, M.N. At-Haulback Mortality of Elasmobranchs Caught on the Portuguese Longline Swordfish Fishery in the Indian Ocean. In Proceedings of the 9th Session of the IOTC Working Party on Billfish, Victoria, Seychelles, 4–7 July 2011. IOTC–2011–WPEB07–31 2011. [Google Scholar]
  15. Poisson, F.; Filmalter, J.D.; Vernet, A.L.; Laurent, D. Mortality rate of silky sharks (Carcharhinus falciformis) caught in the tropical tuna purse seine fishery in the Indian Ocean. Can. J. Fish. Aquat. Sci. 2014, 71, 795–798. [Google Scholar] [CrossRef]
  16. Coelho, R.; Muñoz-Lechuga, R. Hooking mortality of swordfish in pelagic longlines: Comments on the efficiency of minimum retention sizes. Rev. Fish. Biol. Fish. 2019, 29, 453–463. [Google Scholar] [CrossRef]
  17. Eddy, C.; Brill, R.; Bernal, D. Rates of at-vessel mortality and post-release survival of pelagic sharks captured with tuna purse seines around drifting fish aggregating devices (FADs) in the equatorial eastern Pacific Ocean. Fish. Res. 2016, 174, 109–117. [Google Scholar] [CrossRef]
  18. Butcher, P.A.; Peddemors, V.M.; Mandelman, J.W.; McGrath, S.P.; Cullis, B.R. At-vessel mortality and blood biochemical status of elasmobranchs caught in an Australian commercial longline fishery. Glob. Ecol. Conserv. 2015, 3, 878–889. [Google Scholar] [CrossRef]
  19. Cooke, S.J.; Suski, C.D. Are circle hooks effective tools for conserving freshwater and marine recreational catch-and-release fisheries? Aquat. Conserv. Mar. Freshwat. Ecosyst. 2004, 14, 299–326. [Google Scholar] [CrossRef]
  20. Reinhardt, J.F.; Weaver, J.; Latham, P.J.; Dell’Apa, A.; Serafy, J.E.; Browder, J.A.; Christman, M.; Foster, D.G.; Blankinship, D.R. Catch rate and at-vessel mortality of circle hooks versus J-hooks in pelagic longline fisheries: A global meta-analysis. Fish Fish. 2018, 19, 413–430. [Google Scholar] [CrossRef]
  21. Coelho, R.; Infante, P.; Santos, M.N. Application of generalized linear models and generalized estimation equations to model at-haulback mortality of blue sharks captured in a pelagic longline fishery in the Atlantic Ocean. Fish. Res. 2013, 145, 66–75. [Google Scholar] [CrossRef]
  22. Reeves, K.A.; Bruesewitz, R.E. Factors influencing the hooking mortality of walleyes caught by recreational anglers on Mille Lacs, Minnesota. N. Am. J. Fish. Manag. 2007, 27, 443–452. [Google Scholar] [CrossRef]
  23. Ghani, I.M.M.; Ahmad, S. Stepwise multiple regression method to forecast fish landing. Procedia-Soc. Behav. Sci. 2010, 8, 549–554. [Google Scholar] [CrossRef]
  24. Akaike, H. Information theory and an extension of the maximum likelihood principle. Bull. Int. Stat. Inst. 1973, 50, 267–281. [Google Scholar]
  25. Xue, Y.; Chen, L.P. Statistical Modeling and R Software, 1st ed.; Tsinghua University Press: Beijing, China, 2007. [Google Scholar]
  26. Hosmer, D.W.; Lemeshow, S. Applied Logistic Regression, 2nd ed.; Wiley: New York, NY, USA, 2000. [Google Scholar]
  27. Fushiki, T. Estimation of prediction error by using K-fold cross-validation. Stat. Comput. 2011, 21, 137–146. [Google Scholar] [CrossRef]
  28. Naimi, B. Usdm: Uncertainty Analysis for Species Distribution Models, R Package Version 1.1-18; Springer: New York, NY, USA, 25 June 2017. Available online: https://cran.r-project.org/web/packages/usdm/index.html (accessed on 13 September 2022).
  29. LeDell, E.; Petersen, M.; Laan, M.V.D. cvAUC: Cross-Validated Area Under the ROC Curve Confidence Intervals, R Package Version 1.1.4; Springer: New York, NY, USA, 2022. Available online: https://cran.r-project.org/web/packages/cvAUC/index.html (accessed on 13 September 2022).
  30. Breheny, P.; Burchett, W. Visualization of regression models using visreg. R. J. 2017, 9, 56–71. [Google Scholar] [CrossRef]
  31. Fox, J.; Weisberg, S. Car: Companion to Applied Regression, R Package Version 3.1-0; Springer: New York, NY, USA, 2022. Available online: https://cran.r-project.org/web/packages/car/index.html (accessed on 13 September 2022).
  32. Brownrigg, M.R. Mapdata: Extra Map Databases, R Package Version 2.3.0; Springer: New York, NY, USA, 2018. Available online: https://cran.r-project.org/web/packages/mapdata/index.html (accessed on 13 September 2022).
  33. Bivand, R.; Lewin-Koh, N.J.; Pebesma, J.; Archer, E.; Bivand, R. maptools: Tools for Handling Spatial Objects, R Package Version 1.1-4; Springer: New York, NY, USA, 2022. Available online: https://cran.r-project.org/web/packages/maptools/index.html (accessed on 13 September 2022).
  34. Sun, C.L.; Wang, S.P.; Porch, C.E.; Yeh, S.Z. Sex-specific yield per recruit and spawning stock biomass per recruit for the swordfish, Xiphias gladius, in the waters around Taiwan. Fish. Res. 2005, 71, 61–69. [Google Scholar] [CrossRef]
  35. Punt, A.E.; Campbell, R.A.; Smith, A.D.M. Evaluating empirical indicators and reference points for fisheries management: Application to the broadbill swordfish fishery off eastern Australia. Mar. Freshw. Res. 2001, 52, 819–832. [Google Scholar] [CrossRef]
  36. Dewar, H.; Prince, E.D.; Musyl, M.K.; Brill, R.W.; Sepulveda, C.; Luo, J.G.; Foley, D.; Orbesen, E.S.; Domeier, M.L.; Nasby-lucas, N.; et al. Movements and behaviors of swordfish in the atlantic and pacific oceans examined using pop-up satellite archival tags. Fish. Oceanogr. 2011, 20, 219–241. [Google Scholar] [CrossRef]
  37. West, W.M.; Kerwath, S.E.; Silva, D.C.; Wilke, C.G.; Marsac, F. Horizontal and Vertical Movements of Swordfish Tagged with Pop Up-Satellite Transmitters in the South-West Indian Ocean, off South Africa. In Proceedings of the 10th Session of the IOTC Working Party on Billfish, Cape Town, South Africa, 11–15 September 2012. IOTC-2012-WPB10-16. [Google Scholar]
  38. Curran, D.; Bigelow, K. Effects of circle hooks on pelagic catches in the Hawaii-based tuna longline fishery. Fish. Res. 2011, 109, 265–275. [Google Scholar] [CrossRef]
  39. Epperly, S.P.; Watson, J.W.; Foster, D.G.; Shah, A.K. Anatomical hooking location and condition of animals captured with pelagic longlines: The grand banks experiments 2002–2003. Bull. Mar. Sci. 2012, 88, 513–527. [Google Scholar] [CrossRef]
  40. Huang, H.W.; Swimmer, Y.; Bigelow, K.; Bigelow, K.; Gutierrez, A.; Foster, D.G. Influence of hook type on catch of commercial and bycatch species in an Atlantic tuna fishery. Mar. Policy 2016, 65, 68–75. [Google Scholar] [CrossRef]
  41. Godin, A.C.; Carlson, J.K.; Burgener, V. The effect of circle hooks on shark catchability and at-vessel mortality rates in longlines fisheries. Bull. Mar. Sci. 2012, 88, 469–483. [Google Scholar] [CrossRef]
  42. Aneesh Kumar, K.V.; Paresh, S.K.; Pravin, P.; Madhu, V.R.; Meenakumari, B. Effect of hook design on longline catches in Lakshadweep Sea, India. Indian J. Fish. 2013, 60, 21–27. [Google Scholar]
  43. Morgan, A.; Carlson, J.K. Capture time, size and hooking mortality of bottom longline-caught sharks. Fish. Res. 2010, 101, 32–37. [Google Scholar] [CrossRef]
  44. Neilson, D.J.; Waiwood, G.; Smith, S.J. Survival of Atlantic Halibut (Hippoglossus hippoglossus) caught by longline and otter trawl gear. Can. J. Fish. Aquat. Sci. 1989, 46, 887–897. [Google Scholar] [CrossRef]
  45. Poisson, F.; Fauvel, C. Reproductive dynamics of swordfish (Xiphias gladius) in the southwestern Indian Ocean (Reunion Island). Part 2: Fecundity and spawning pattern. Aquat. Living Resour. 2009, 22, 59–68. [Google Scholar] [CrossRef]
  46. Muoneke, M.I. Seasonal hooking mortality of bluegills caught on natural baits. N. Am. J. Fish. Manag. 1992, 12, 645–649. [Google Scholar] [CrossRef]
  47. Braccini, J.M.; Waltrick, D. Species-specific at-vessel mortality of sharks and rays captured by demersal longlines. Mar. Policy 2019, 99, 94–98. [Google Scholar] [CrossRef]
  48. Dotson, T. Mortalities in trout caused by gear type and angler-induced stress. N. Am. J. Fish. Manag. 1982, 2, 60–65. [Google Scholar] [CrossRef]
  49. Nuhfer, A.J.; Alexander, G.R. Hooking mortality of trophy-sized wild brook trout caught on artificial lures. N. Am. J. Fish. Manag. 1992, 12, 634–644. [Google Scholar] [CrossRef]
  50. Veiga, P.; Gonçalves, J.M.S.; Erzin, K. Short-term hooking mortality of three marine fish species (Sparidae) caught by recreational angling in the south Portugal. Fish. Res. 2011, 108, 58–64. [Google Scholar] [CrossRef]
  51. Morgan, A.; Burgess, G.H. At-vessel fishing mortality for six species of sharks caught in the northwest Atlantic and Gulf of Mexico. Gulf. Caribb. Res. 2007, 19, 123–129. [Google Scholar] [CrossRef]
  52. Orbesen, E.S.; Brown, C.A.; Snodgrass, D.; Serafy, J.E.; Walter, J.F., III. At-vessel and postrelease mortality rates of bluefin tuna (Thunnus thynnus) associated with pelagic longline gear in the northern Gulf of Mexico. Fish. Bull. 2019, 117, 15–32. [Google Scholar]
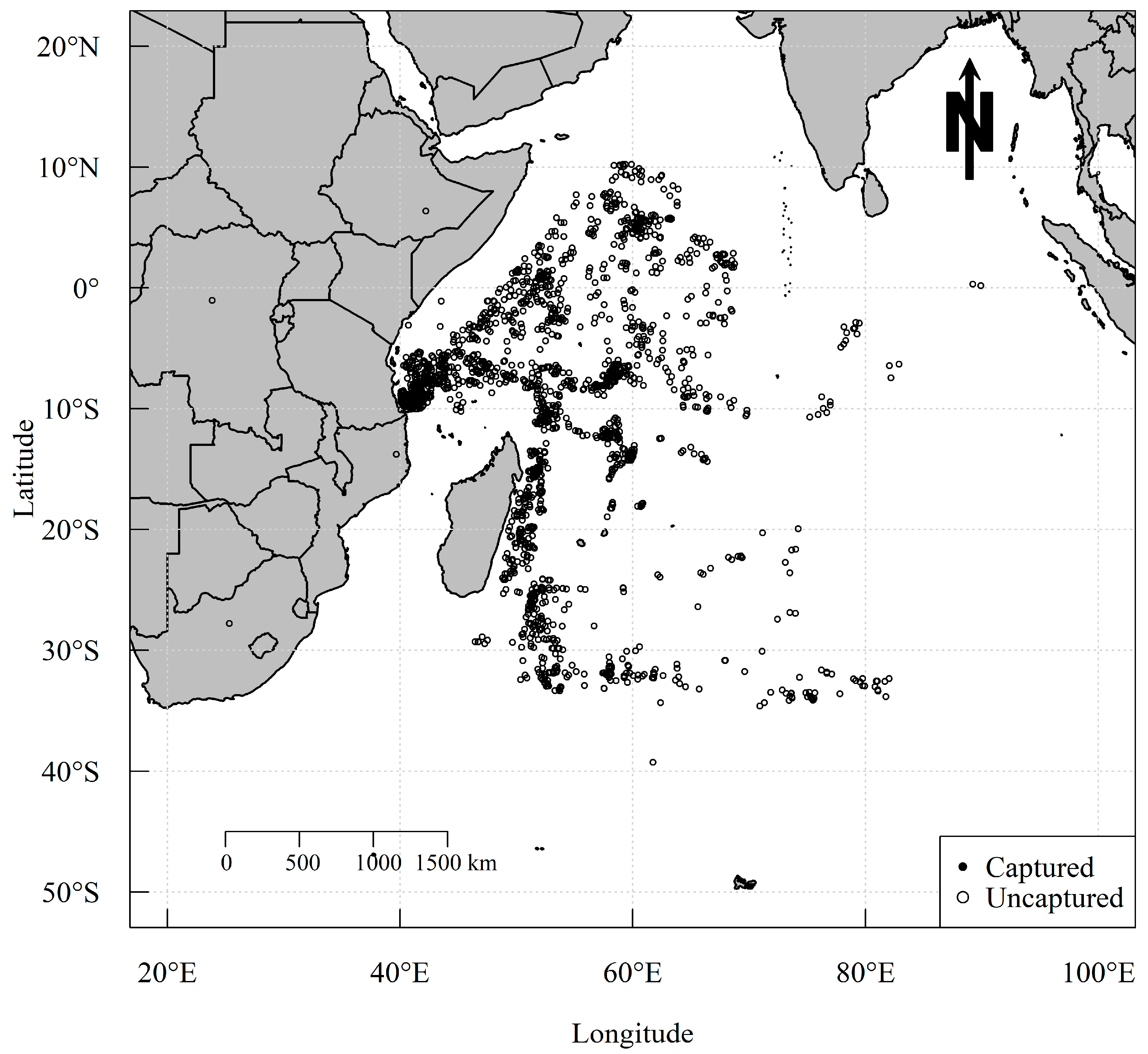
Fishes 07 00256 g001 550
Figure 1. The location distribution of longline fishing survey sites in the China Ocean Fisheries Observer Program from 2012 to 2018.
Figure 1. The location distribution of longline fishing survey sites in the China Ocean Fisheries Observer Program from 2012 to 2018.
Fishes 07 00256 g001
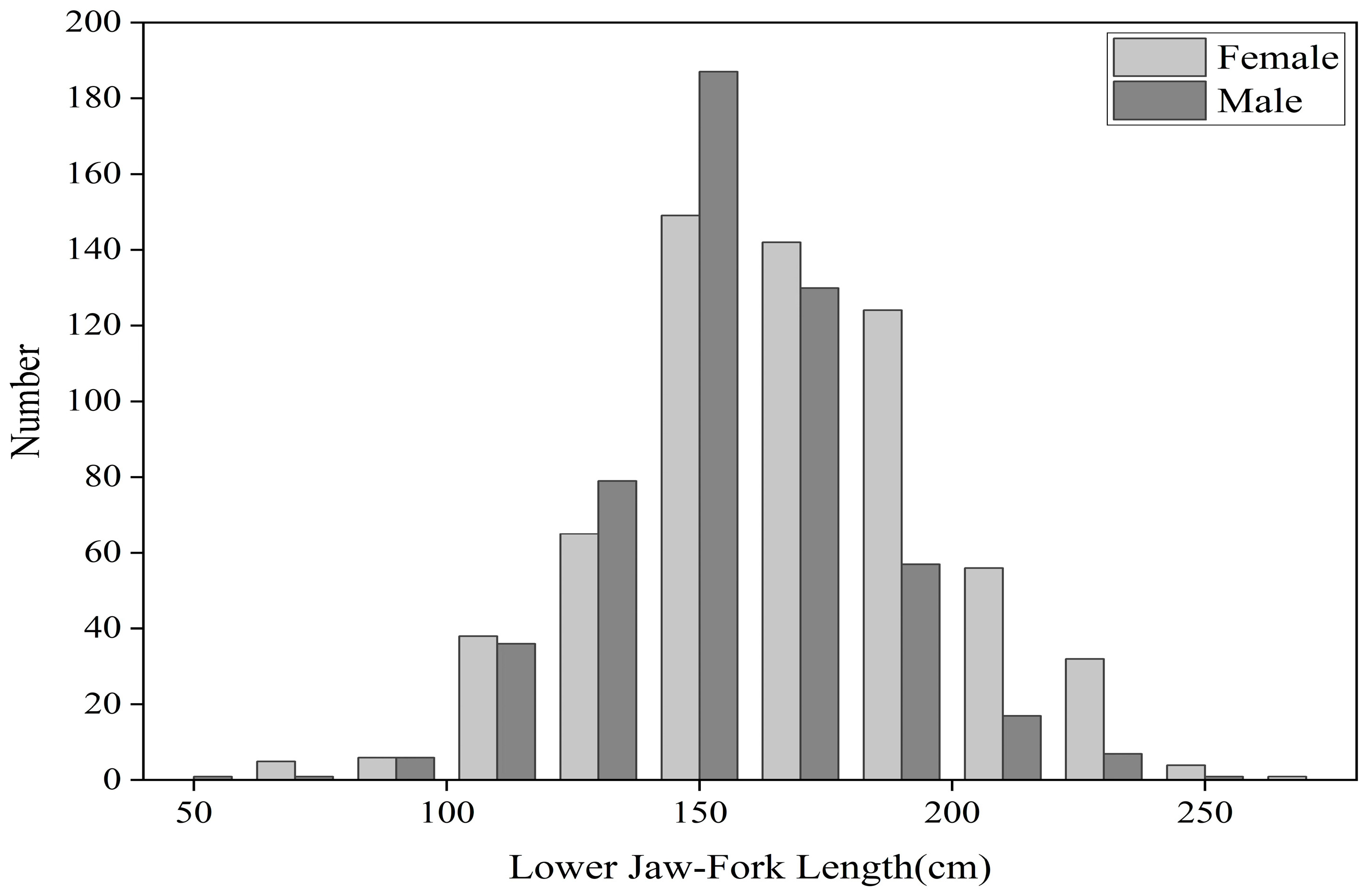
Fishes 07 00256 g002 550
Figure 2. The distribution of lower jaw-fork length of female and male swordfish in the Indian Ocean from 2012 to 2018 in this study.
Figure 2. The distribution of lower jaw-fork length of female and male swordfish in the Indian Ocean from 2012 to 2018 in this study.
Fishes 07 00256 g002
Fishes 07 00256 g003 550
Figure 3. The impact of different hook types (a) and different catch quarters (b) on the at-haulback mortality of Indian Ocean swordfish. The black solid line represents the predicted probability of death of the hook type, and the gray shaded represents the 95% confidence interval of the categorical variable. The short line segments at the top and bottom indicate the number of fish species under different classifications of the variable. The top indicates the number of deaths, and the bottom indicates the number of survivors.
Figure 3. The impact of different hook types (a) and different catch quarters (b) on the at-haulback mortality of Indian Ocean swordfish. The black solid line represents the predicted probability of death of the hook type, and the gray shaded represents the 95% confidence interval of the categorical variable. The short line segments at the top and bottom indicate the number of fish species under different classifications of the variable. The top indicates the number of deaths, and the bottom indicates the number of survivors.
Fishes 07 00256 g003
Fishes 07 00256 g004 550
Figure 4. Effects of Lower Jaw-Fork Length (LJFL) variation (a) and longitude variation (b) on at-haulback mortality in Indian Ocean swordfish. The solid line represents the change in the predicted mortality with LJFL and longitude, and the gray shaded part represents the 95% confidence interval of the explanatory variable. The short lines at the top and bottom of the picture indicate the number of samples that died and survived at a certain longitude.
Figure 4. Effects of Lower Jaw-Fork Length (LJFL) variation (a) and longitude variation (b) on at-haulback mortality in Indian Ocean swordfish. The solid line represents the change in the predicted mortality with LJFL and longitude, and the gray shaded part represents the 95% confidence interval of the explanatory variable. The short lines at the top and bottom of the picture indicate the number of samples that died and survived at a certain longitude.
Fishes 07 00256 g004
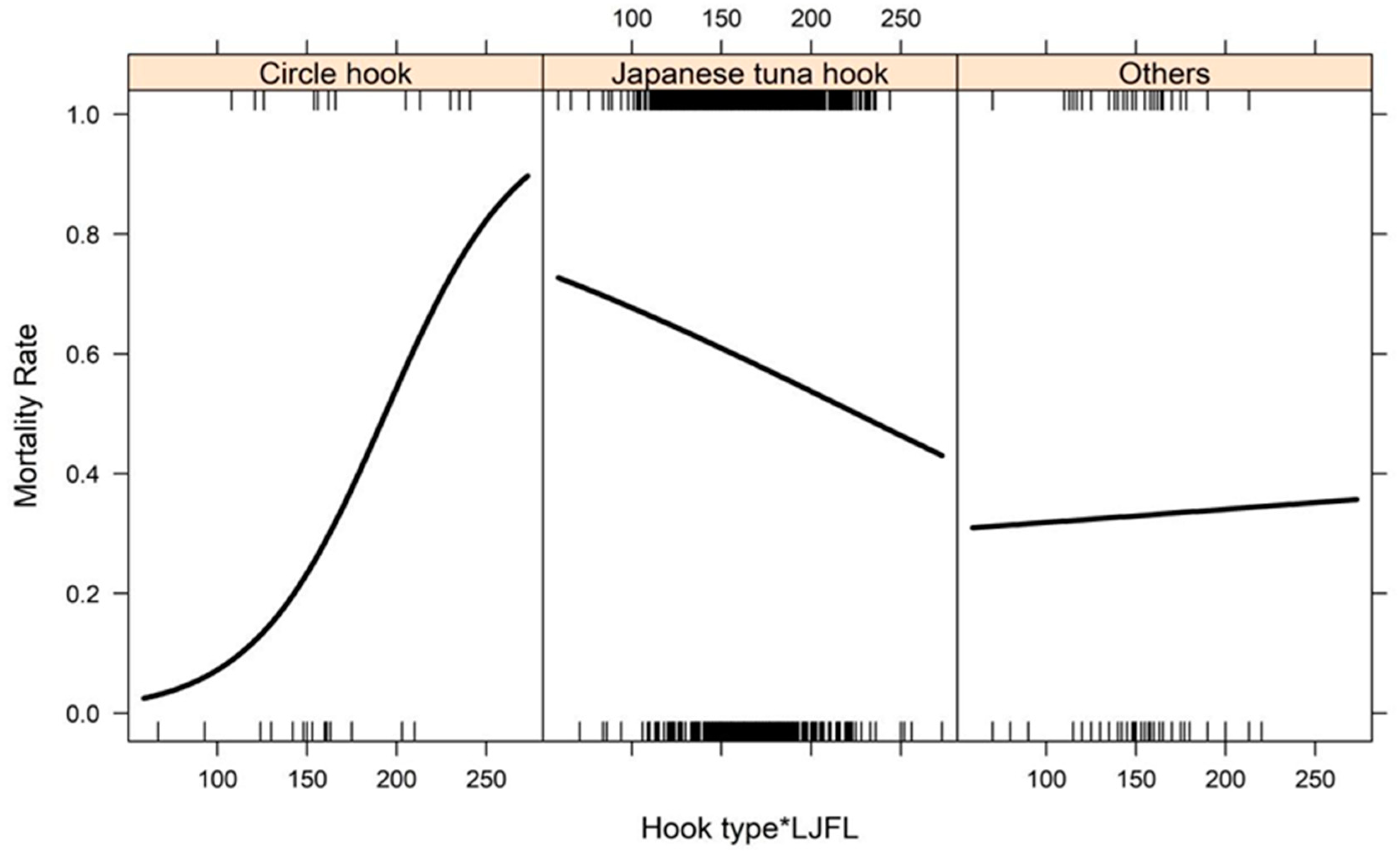
Fishes 07 00256 g005 550
Figure 5. The effect of the interaction term between hook type and lower jaw fork length (LJFL) on the at-haulback mortality of Indian Ocean swordfish. The different boxes indicate the variation of the at-haulback mortality of the Indian Ocean swordfish with the LJFL when the hook type (circle hook, Japanese tuna hook, others) is used. The short lines at the top and bottom of the picture respectively indicate the number of samples that died and survived under the LJFL.
Figure 5. The effect of the interaction term between hook type and lower jaw fork length (LJFL) on the at-haulback mortality of Indian Ocean swordfish. The different boxes indicate the variation of the at-haulback mortality of the Indian Ocean swordfish with the LJFL when the hook type (circle hook, Japanese tuna hook, others) is used. The short lines at the top and bottom of the picture respectively indicate the number of samples that died and survived under the LJFL.
Fishes 07 00256 g005
Fishes 07 00256 g006 550
Figure 6. The effect of the interaction term between longitude and lower jaw fork length (LJFL) on the at-haulback mortality of Indian Ocean swordfish. The different boxes indicate the variation of the at-haulback mortality with LJFL for swordfish caught at different longitudes. The short lines at the top and bottom of the picture respectively indicate the number of samples that died and survived under the LJFL.
Figure 6. The effect of the interaction term between longitude and lower jaw fork length (LJFL) on the at-haulback mortality of Indian Ocean swordfish. The different boxes indicate the variation of the at-haulback mortality with LJFL for swordfish caught at different longitudes. The short lines at the top and bottom of the picture respectively indicate the number of samples that died and survived under the LJFL.
Fishes 07 00256 g006
Table
Table 1. The scope of each continuous explanatory variable and the classification of each categorical explanatory variable were evaluated for importance in the at-haulback mortality of Xiphias gladius.
Table 1. The scope of each continuous explanatory variable and the classification of each categorical explanatory variable were evaluated for importance in the at-haulback mortality of Xiphias gladius.
Explanatory VariableNameTypeScope/Classification
Biological CharacteristicsSexCategoricalFemale/Male
Lower Jaw-fork LengthContinuous59–273 (cm)
Environmental FactorsSea Surface TemperatureContinuous13.88–30.37 (°C)
Dissolved OxygenContinuous196.87–247.93
Space-time ElementsQuarterCategoricalFirst (Jan, Feb, Mar)/Second (Apr, May, Jun)/Third (Jul, Aug, Sept)/Forth (Oct, Nov, Dec) (Quarter)
LongitudeContinuous40° E–81° E
LatitudeContinuous40° N–11° S
Hook TypeCategoricalJapanese Tuna Hook/Circle Hook/Others
Target Fish SpeciesCategoricalBigeye Tuna/Albacore Tuna
Table
Table 2. The deviation explanation after adding the interaction terms to the generalized linear model of the at-haulback mortality of swordfish (Xiphias gladius) in the Indian Ocean.
Table 2. The deviation explanation after adding the interaction terms to the generalized linear model of the at-haulback mortality of swordfish (Xiphias gladius) in the Indian Ocean.
dfDevianceResid.DfResid.Dev
NULL 11431495.2
Quarter36.417811401488.8
Hook.type222.126911381466.7
LJFL112.685611371454.0
Lon114.361411361439.6
Hook.type:LJFL27.193511341432.4
LJFL:Lon124.535411331407.9
Note: “Df” is the degree of freedom, and “Deviance” is a measure of error. “Resid.Df” is the residual degrees of freedom and “Resid.Dev” is the residual deviation. The term is not affected by the order of addition.
Table
Table 3. The parameter estimation and significance of the model after adding the interaction term for studying the at-haulback mortality of swordfish (Xiphias gladius) in the Indian Ocean.
Table 3. The parameter estimation and significance of the model after adding the interaction term for studying the at-haulback mortality of swordfish (Xiphias gladius) in the Indian Ocean.
EstimateStd. Errorz ValuePr(>|z|)
(Intercept)9.1412.9423.107<0.01
Quarter20.0500.2940.1710.864
Quarter 30.5880.2842.068<0.05
Quarter 40.0200.2600.0750.940
Hook type Japanese tuna hook6.6071.8433.585<0.01
Hook type Others4.4172.2201.989<0.05
LJFL−0.0500.018−2.779<0.01
Lon−0.2470.045−5.439<0.01
Hook type Japanese tuna hook: LJFL−0.0330.011−3.008<0.01
Hook type Others: LJFL−0.0260.014−1.9000.057
LJFL: Lon0.0010.0014.770<0.01
Note: “Estimate” is the estimated parameter, “Std. error” is the standard error. The significance of the explanatory variable was provided by the p-value corresponding to the z test (p < 0.05).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Guo, Y.; Wang, X.; Li, X.; Wu, F.; Zhu, J. Analysis of At-Haulback Mortality and Influencing Factors of Indian Ocean Swordfish (Xiphias gladius). Fishes 2022, 7, 256. https://doi.org/10.3390/fishes7050256

AMA Style

Guo Y, Wang X, Li X, Wu F, Zhu J. Analysis of At-Haulback Mortality and Influencing Factors of Indian Ocean Swordfish (Xiphias gladius). Fishes. 2022; 7(5):256. https://doi.org/10.3390/fishes7050256

Chicago/Turabian Style

Guo, Yingcong, Xuefang Wang, Xiuzhen Li, Feng Wu, and Jiangfeng Zhu. 2022. "Analysis of At-Haulback Mortality and Influencing Factors of Indian Ocean Swordfish (Xiphias gladius)" Fishes 7, no. 5: 256. https://doi.org/10.3390/fishes7050256

APA Style

Guo, Y., Wang, X., Li, X., Wu, F., & Zhu, J. (2022). Analysis of At-Haulback Mortality and Influencing Factors of Indian Ocean Swordfish (Xiphias gladius). Fishes, 7(5), 256. https://doi.org/10.3390/fishes7050256

Article Metrics

Back to TopTop