Fish Biomass Estimation Under Occluded Features: A Framework Combining Imputation and Regression
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Acquisition
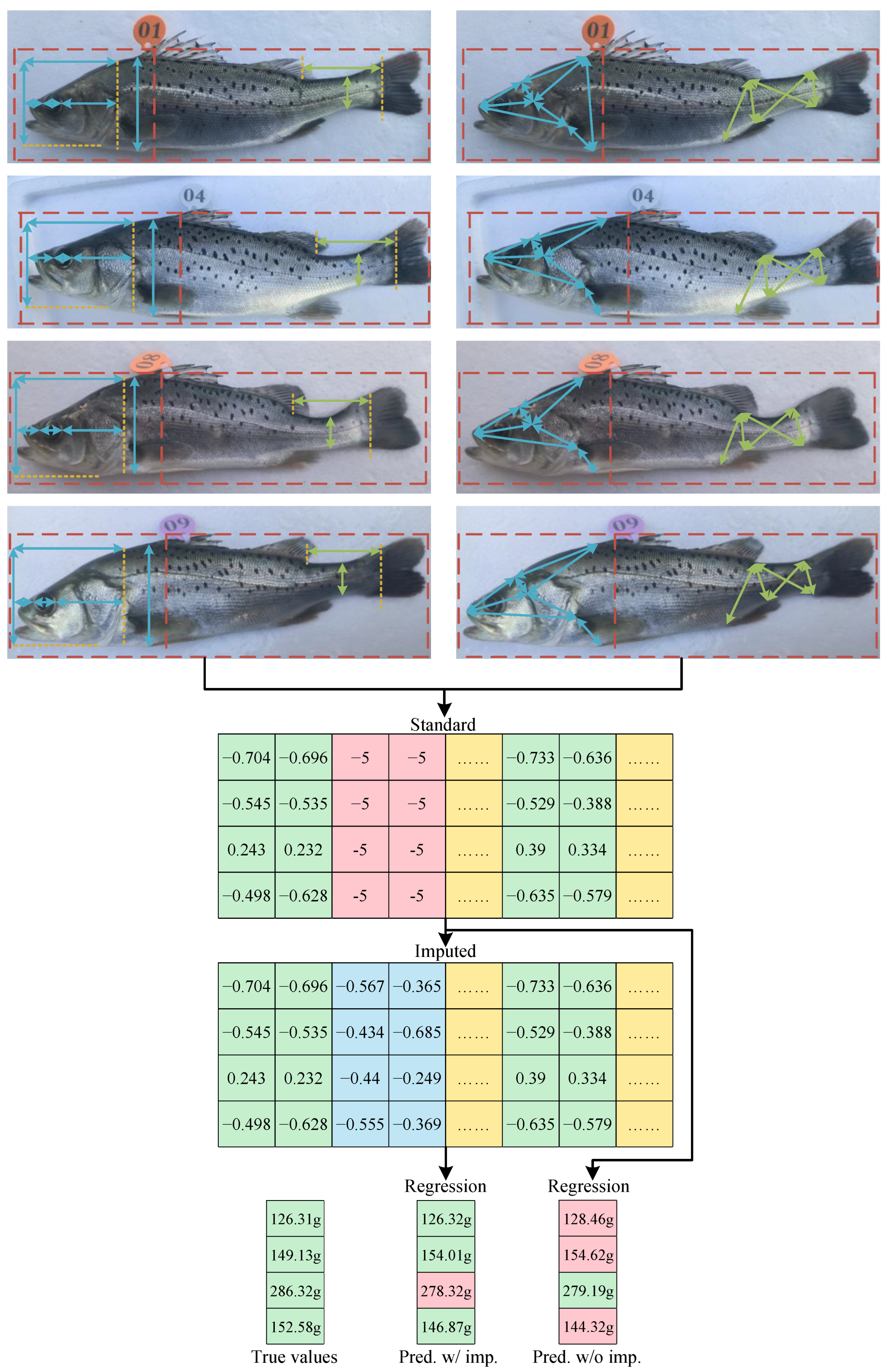
2.2. Overview of the Imputation-Regression Framework
2.3. Masking and Imputation
2.4. Regression Models
2.5. Hyperparameter Grid Search
2.6. Evaluation Metrics
3. Results and Discussion
3.1. Model Performance Without Feature Missingness
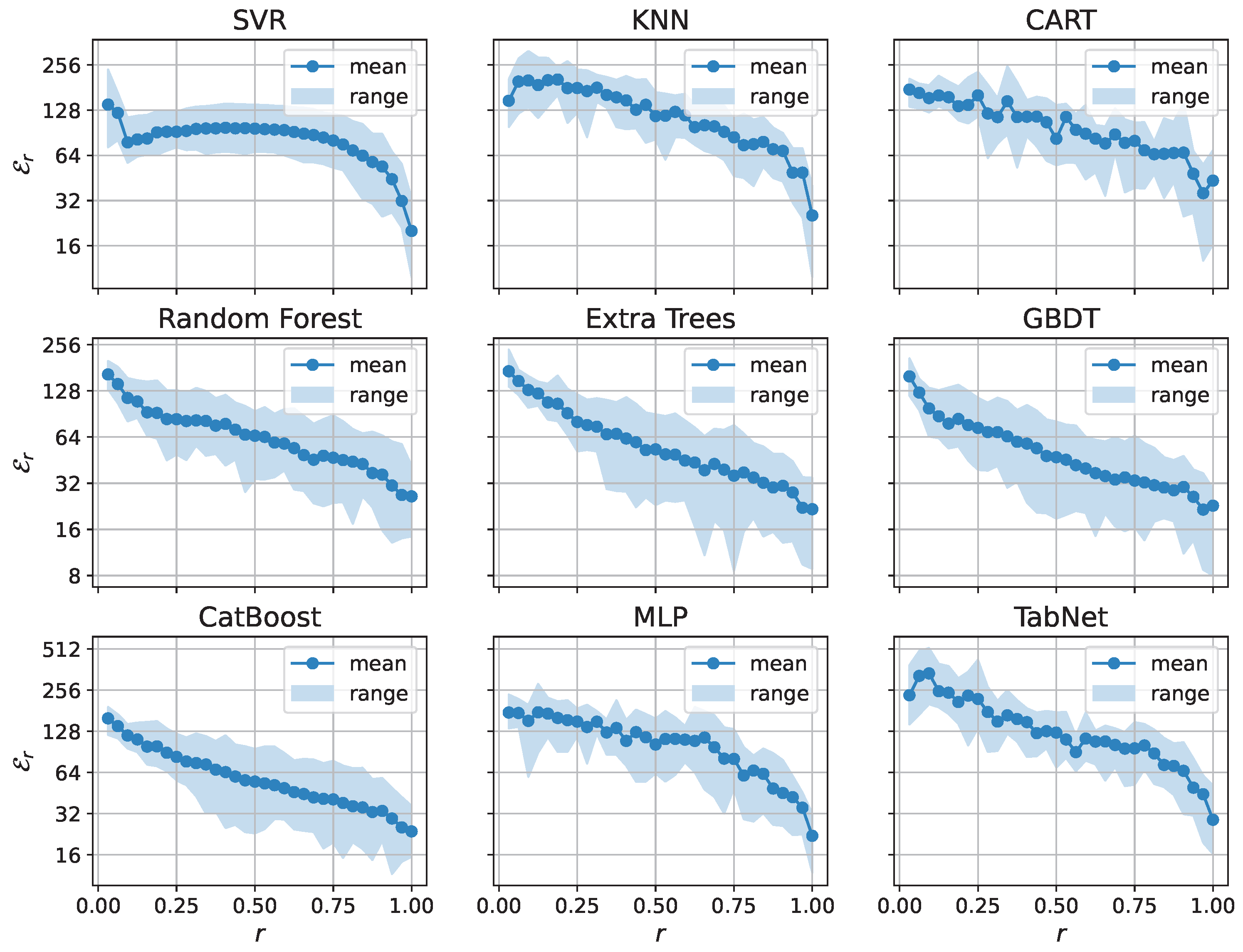
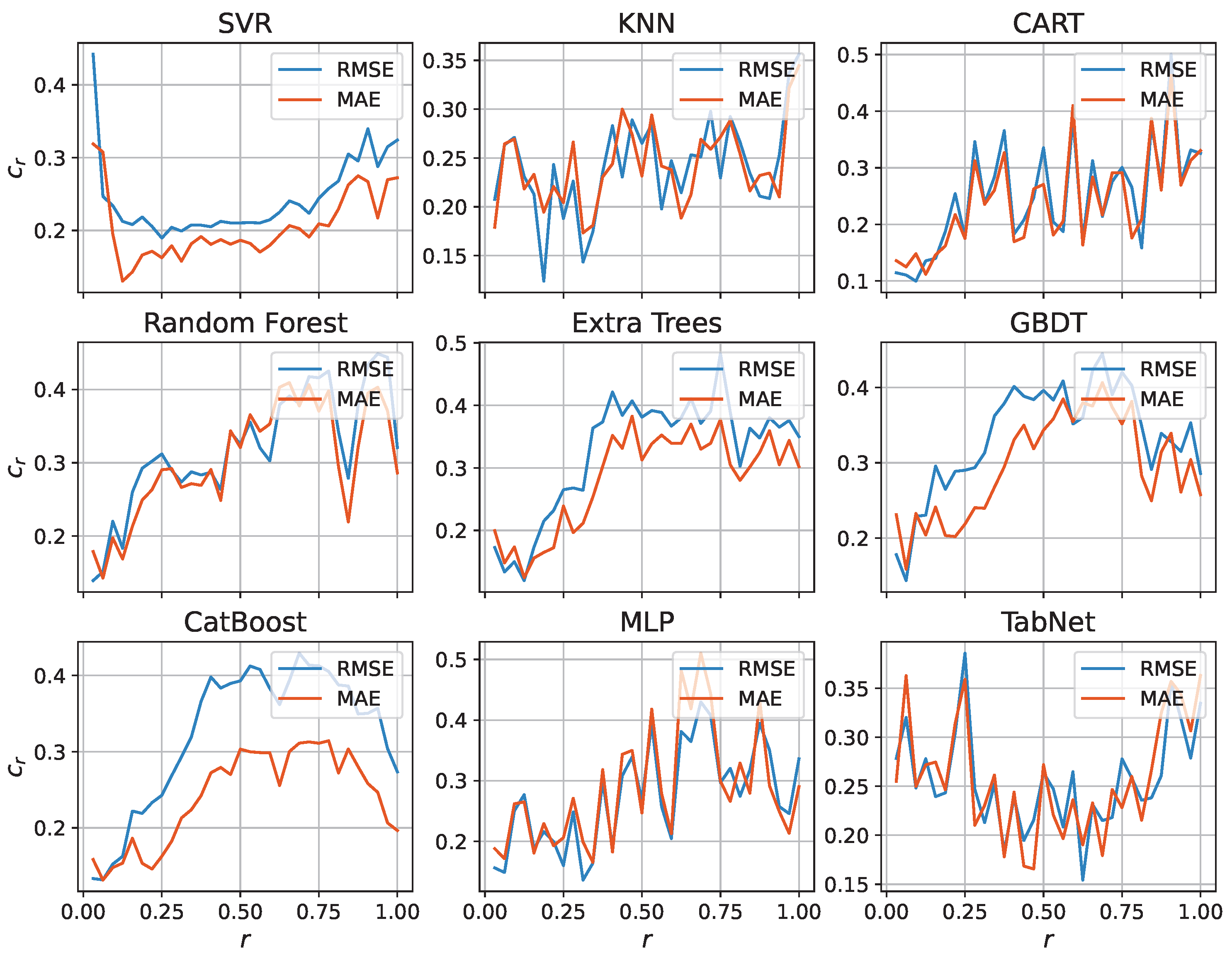
3.2. Model Robustness Under Feature Missingness
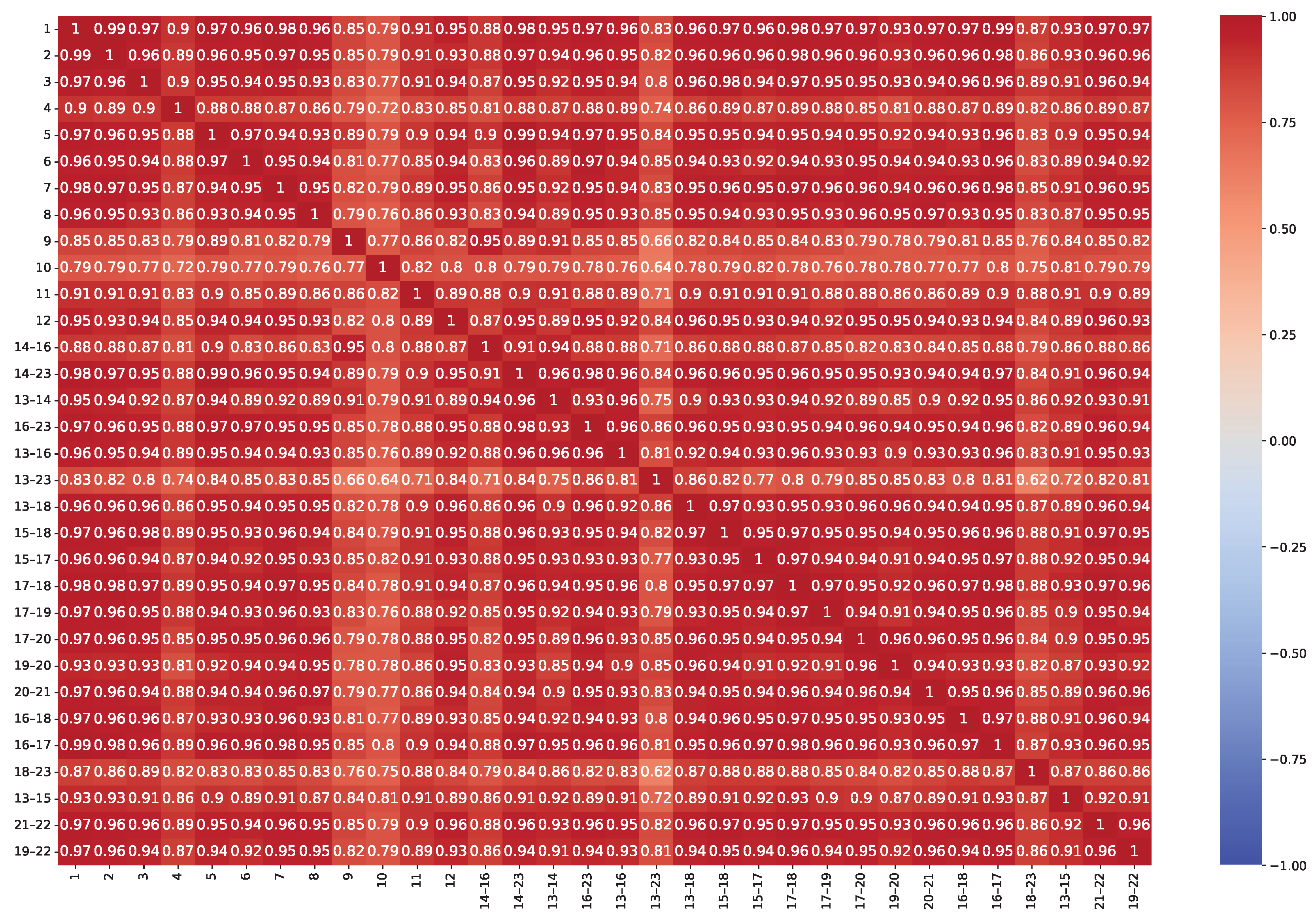
3.3. Imputation Evaluation
3.4. Mass Estimation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Antonucci, F.; Costa, C. Precision aquaculture: A short review on engineering innovations. Aquac. Int. 2020, 28, 41–57. [Google Scholar] [CrossRef]
- Føre, M.; Frank, K.; Norton, T.; Svendsen, E.; Alfredsen, J.A.; Dempster, T.; Eguiraun, H.; Watson, W.; Stahl, A.; Sunde, L.M.; et al. Precision fish farming: A new framework to improve production in aquaculture. Biosyst. Eng. 2018, 173, 176–193. [Google Scholar] [CrossRef]
- Wu, Y.; Duan, Y.; Wei, Y.; An, D.; Liu, J. Application of intelligent and unmanned equipment in aquaculture: A review. Comput. Electron. Agric. 2022, 199, 107201. [Google Scholar] [CrossRef]
- Davison, P.C.; Koslow, J.A.; Kloser, R.J. Acoustic biomass estimation of mesopelagic fish: Backscattering from individuals, populations, and communities. ICES J. Mar. Sci. 2015, 72, 1413–1424. [Google Scholar] [CrossRef]
- Wanzenböck, J.; Mehner, T.; Schulz, M.; Gassner, H.; Winfield, I.J. Quality assurance of hydroacoustic surveys: The repeatability of fish-abundance and biomass estimates in lakes within and between hydroacoustic systems. ICES J. Mar. Sci. 2003, 60, 486–492. [Google Scholar] [CrossRef]
- Takahara, T.; Minamoto, T.; Yamanaka, H.; Doi, H.; Kawabata, Z. Estimation of fish biomass using environmental DNA. PLoS ONE 2012, 7, e35868. [Google Scholar] [CrossRef]
- Kamoroff, C.; Goldberg, C.S. Environmental DNA quantification in a spatial and temporal context: A case study examining the removal of brook trout from a high alpine basin. Limnology 2018, 19, 335–342. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Zhou, Q.; Diao, C.; Jia, H.; Xian, W.; Zhang, H. Species identification and biomass assessment of Gnathanodon speciosus based on environmental DNA technology. Ecol. Indic. 2024, 160, 111821. [Google Scholar] [CrossRef]
- Abinaya, N.; Susan, D.; Sidharthan, R.K. Deep learning-based segmental analysis of fish for biomass estimation in an occulted environment. Comput. Electron. Agric. 2022, 197, 106985. [Google Scholar] [CrossRef]
- Swethaa, S.; Sneha, E.; Sivasakthi, T. Fish biomass estimation based on object detection using YOLOv7. In Proceedings of the 2023 4th International Conference for Emerging Technology (INCET), Belgaum, India, 26–28 May 2023; pp. 1–6. [Google Scholar]
- Tang, N.T.; Lim, K.G.; Yoong, H.P.; Ching, F.F.; Wang, T.; Teo, K.T.K. Non-intrusive biomass estimation in aquaculture using structure from motion within decision support systems. In Proceedings of the 2024 IEEE International Conference on Artificial Intelligence in Engineering and Technology (IICAIET), Kota Kinabalu, Malaysia, 26–28 August 2024; pp. 682–686. [Google Scholar]
- Demer, D.A.; Hewitt, R.P. Bias in acoustic biomass estimates of Euphausia superba due to diel vertical migration. Deep. Sea Res. Part I Oceanogr. Res. Pap. 1995, 42, 455–475. [Google Scholar] [CrossRef]
- Dejean, T.; Valentini, A.; Duparc, A.; Pellier-Cuit, S.; Pompanon, F.; Taberlet, P.; Miaud, C. Persistence of environmental DNA in freshwater ecosystems. PLoS ONE 2011, 6, e23398. [Google Scholar] [CrossRef] [PubMed]
- Tsuji, S.; Ushio, M.; Sakurai, S.; Minamoto, T.; Yamanaka, H. Water temperature-dependent degradation of environmental DNA and its relation to bacterial abundance. PLoS ONE 2017, 12, e0176608. [Google Scholar] [CrossRef] [PubMed]
- Saberioon, M.; Gholizadeh, A.; Cisar, P.; Pautsina, A.; Urban, J. Application of machine vision systems in aquaculture with emphasis on fish: State-of-the-art and key issues. Rev. Aquac. 2017, 9, 369–387. [Google Scholar] [CrossRef]
- Li, D.; Hao, Y.; Duan, Y. Nonintrusive methods for biomass estimation in aquaculture with emphasis on fish: A review. Rev. Aquac. 2020, 12, 1390–1411. [Google Scholar] [CrossRef]
- Fernandes, A.F.A.; de Almeida Silva, M.; de Alvarenga, E.R.; de Alencar Teixeira, E.; da Silva Junior, A.F.; de Oliveira Alves, G.F.; de Salles, S.C.M.; Manduca, L.G.; Turra, E.M. Morphometric traits as selection criteria for carcass yield and body weight in Nile tilapia (Oreochromis niloticus L.) at five ages. Aquaculture 2015, 446, 303–309. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, Y.; Liu, Y.; Liu, C.; Zhao, R.; Li, D.; Shi, C. Fully automatic system for fish biomass estimation based on deep neural network. Ecol. Inform. 2024, 79, 102399. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J.; Duan, Q. Estimation for fish mass using image analysis and neural network. Comput. Electron. Agric. 2020, 173, 105439. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4. [Google Scholar]
- Deng, L.; Yu, D. Deep learning: Methods and applications. Found. Trends Signal Process. 2014, 7, 197–387. [Google Scholar] [CrossRef]
- Marcelino, C.G.; Leite, G.M.; Celes, P.; Pedreira, C.E. Missing data analysis in regression. Appl. Artif. Intell. 2022, 36, 2032925. [Google Scholar] [CrossRef]
- Tang, F.; Ishwaran, H. Random forest missing data algorithms. Stat. Anal. Data Min. Asa Data Sci. J. 2017, 10, 363–377. [Google Scholar] [CrossRef] [PubMed]
- Ayilara, O.F.; Zhang, L.; Sajobi, T.T.; Sawatzky, R.; Bohm, E.; Lix, L.M. Impact of missing data on bias and precision when estimating change in patient-reported outcomes from a clinical registry. Health Qual. Life Outcomes 2019, 17, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1997, 28, 779–784. [Google Scholar]
- Muja, M.; Lowe, D.G. Fast approximate nearest neighbors with automatic algorithm configuration. VISAPP 2009, 2, 2. [Google Scholar]
- Breiman, L.; Friedman, J.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Routledge: London, UK, 2017. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Dorogush, A.V.; Ershov, V.; Gulin, A. CatBoost: Gradient boosting with categorical features support. arXiv 2018, arXiv:1810.11363. [Google Scholar]
- Arik, S.Ö.; Pfister, T. Tabnet: Attentive interpretable tabular learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual Event, 19–21 May 2021; Volume 35, pp. 6679–6687. [Google Scholar]
- Gretton, A.; Borgwardt, K.M.; Rasch, M.J.; Schölkopf, B.; Smola, A. A kernel two-sample test. J. Mach. Learn. Res. 2012, 13, 723–773. [Google Scholar]
- Thomas, T.; Rajabi, E. A systematic review of machine learning-based missing value imputation techniques. Data Technol. Appl. 2021, 55, 558–585. [Google Scholar] [CrossRef]
- Batista, G.E.; Monard, M.C. A study of K-nearest neighbour as an imputation method. His 2002, 87, 48. [Google Scholar]
- Jadhav, A.; Pramod, D.; Ramanathan, K. Comparison of performance of data imputation methods for numeric dataset. Appl. Artif. Intell. 2019, 33, 913–933. [Google Scholar] [CrossRef]
- Duan, Y.; Lv, Y.; Kang, W.; Zhao, Y. A deep learning based approach for traffic data imputation. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 912–917. [Google Scholar]
- Wong, L.Z.; Chen, H.; Lin, S.; Chen, D.C. Imputing missing values in sensor networks using sparse data representations. In Proceedings of the 17th ACM International Conference on Modeling, Analysis and Simulation of Wireless and Mobile Systems, Montreal, QC, Canada, 21–26 September 2014; pp. 227–230. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. Experiments with a new boosting algorithm. In Proceedings of the ICML: Citeseer, Bari, Italy, 3–6 July 1996; Volume 96, pp. 148–156. [Google Scholar]
- Sutton, C.D. Classification and regression trees, bagging, and boosting. Handb. Stat. 2005, 24, 303–329. [Google Scholar]
- Mendes-Moreira, J.; Soares, C.; Jorge, A.M.; Sousa, J.F.D. Ensemble approaches for regression: A survey. ACM Comput. Surv. 2012, 45, 1–40. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]



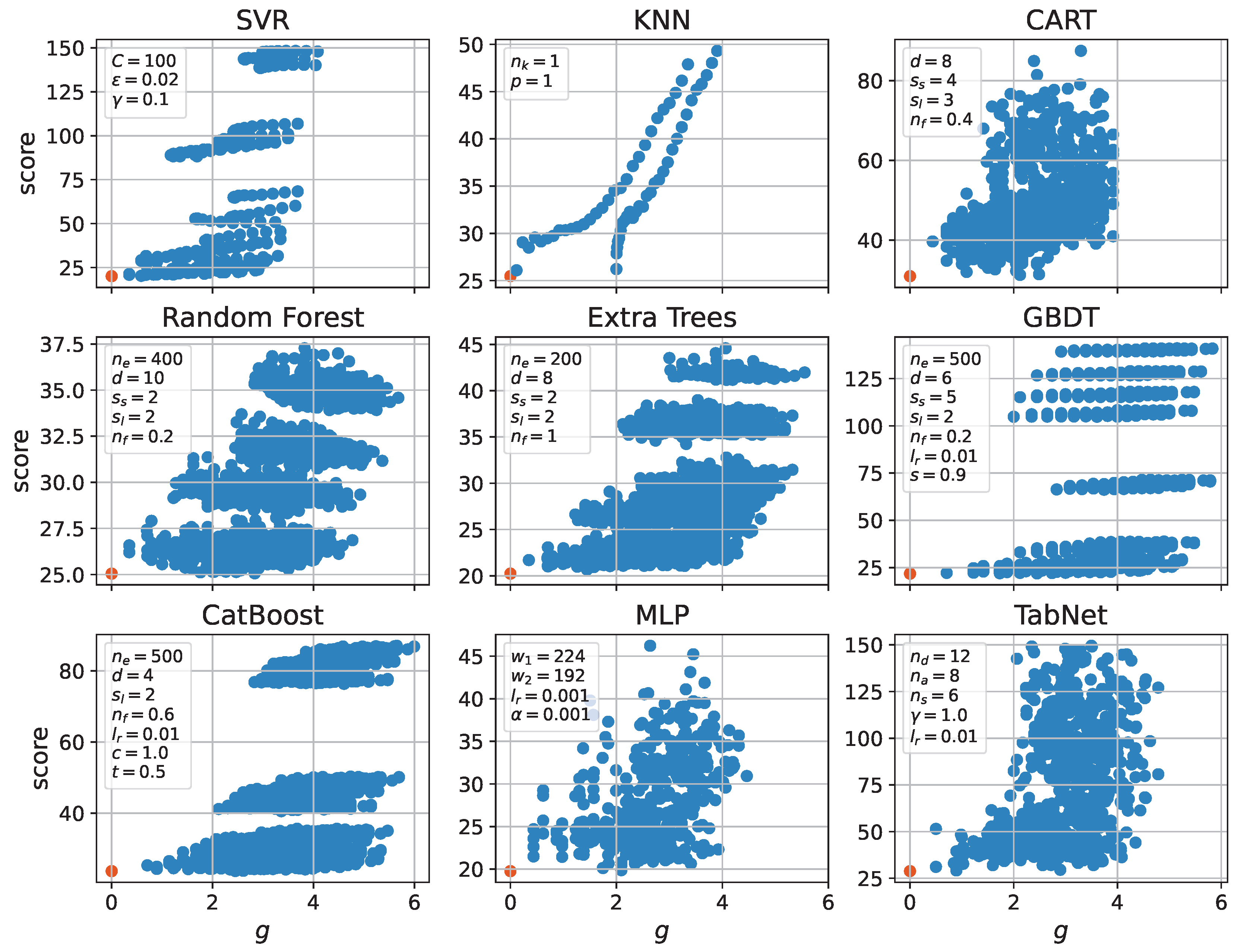
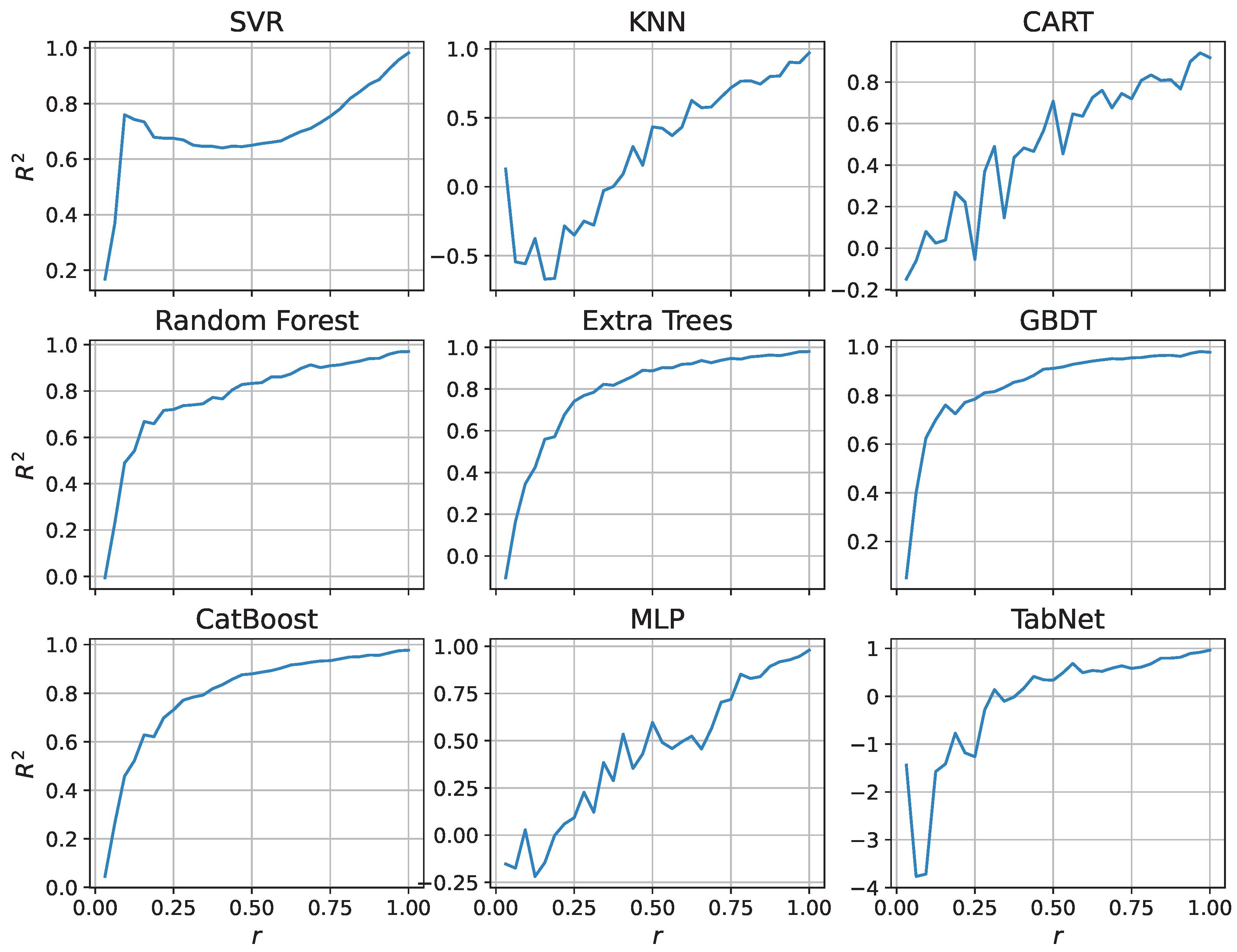
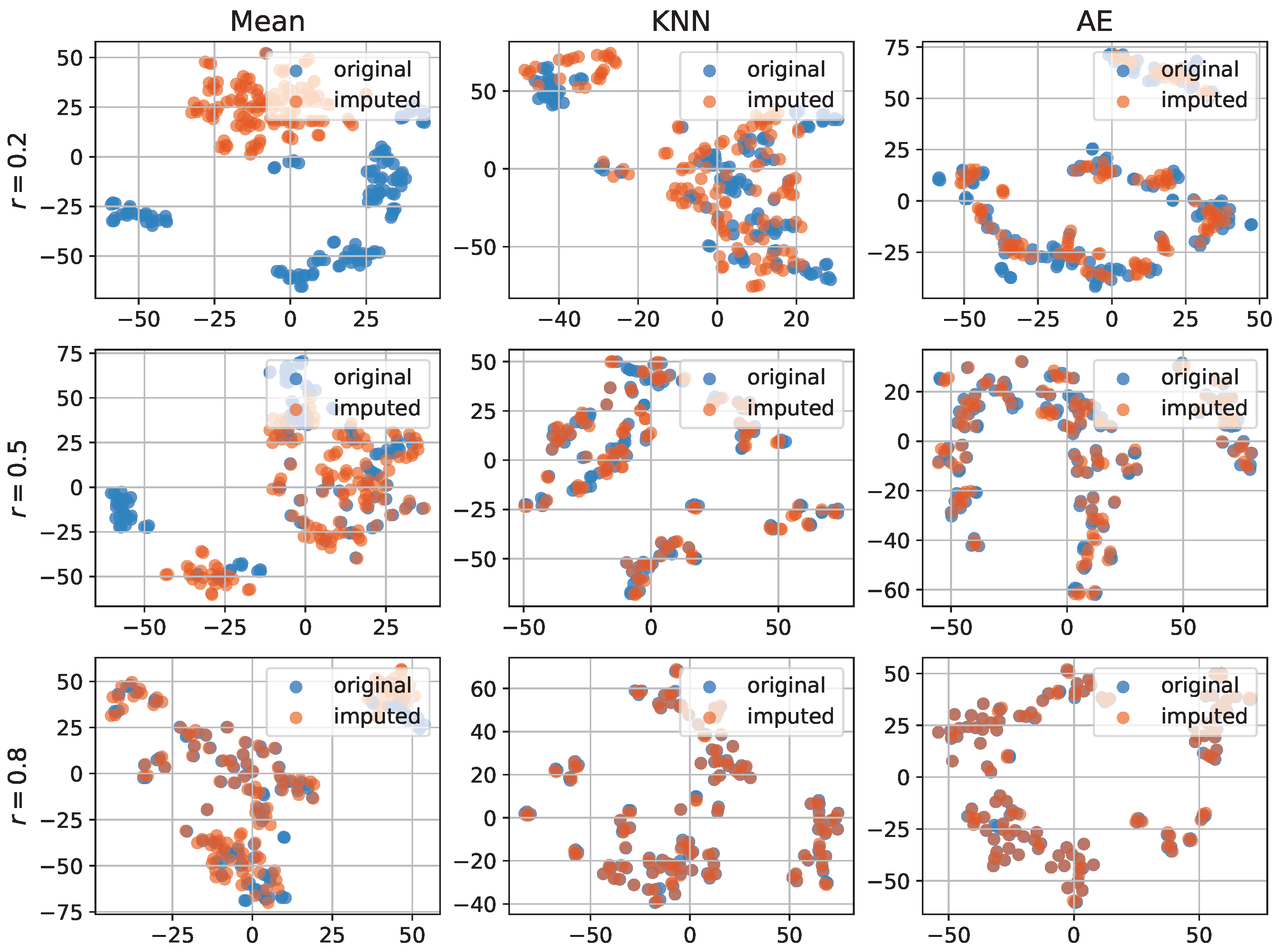
| Model | Dim. | Params | Grid | Score | Time (s) | Train (h) |
|---|---|---|---|---|---|---|
| SVR [26] | 3 | 360 | 20.10 | 0.15 | 0.01 | |
| KNN [27] | 2 | 60 | 25.47 | 0.15 | nan | |
| CART [28] | 4 | 1000 | 38.41 ± 4.53 | 0.14 | 0.04 | |
| Random Forest [29] | 5 | 2250 | 26.19 ± 0.45 | 4.55 | 2.79 | |
| Extra Trees [30] | 5 | 2250 | 21.92 ± 0.25 | 2.63 | 1.56 | |
| GBDT [31] | 7 | 2430 | 22.17 ± 0.31 | 4.01 | 2.62 | |
| CatBoost [32] | 6 | 2160 | 23.71 | 9.41 | 5.65 | |
| MLP [20] | 4 | 384 | 23.71 ± 2.08 | 2.06 | 0.22 | |
| TabNet [33] | 5 | 840 | 28.84 | 102.64 | 23.95 |
| Model | 5-Fold | 10-Fold | ||||
|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | |||
| SVR [26] | 23.22 | 14.98 | 0.98 | 20.10 | 13.75 | 0.98 |
| KNN [27] | 30.88 | 18.53 | 0.96 | 25.47 | 16.04 | 0.97 |
| CART [28] | 39.54 ± 4.21 | 26.30 ± 2.62 | 0.94 ± 0.02 | 38.41 ± 4.53 | 25.59 ± 2.68 | 0.93 ± 0.02 |
| Random Forest [29] | 28.51 ± 0.44 | 17.66 ± 0.26 | 0.97 | 26.19 ± 0.45 | 16.91 ± 0.26 | 0.97 |
| Extra Trees [30] | 23.98 ± 0.62 | 14.97 ± 0.35 | 0.98 | 21.92 ± 0.25 | 14.34 ± 0.23 | 0.98 |
| GBDT [31] | 24.50 ± 0.53 | 15.32 ± 0.36 | 0.98 | 22.17 ± 0.31 | 14.47 ± 0.22 | 0.98 |
| CatBoost [32] | 25.76 | 16.55 | 0.98 | 23.71 | 15.85 | 0.98 |
| MLP [20] | 26.99 ± 1.97 | 17.26 ± 0.86 | 0.97 ± 0.01 | 23.71 ± 2.08 | 17.05 ± 1.38 | 0.97 ± 0.01 |
| TabNet [33] | 40.73 | 31.21 | 0.92 | 28.84 | 23.76 | 0.96 |
| Model | Feature Reservation Ratio r | ||
|---|---|---|---|
| 0.2 | 0.5 | 0.8 | |
| Mean imputation | 0.23 | 0.17 | 0.11 |
| KNN imputation | 0.13 | 0.05 | 0.03 |
| Autoencoder imputation | 0.07 | 0.04 | 0.03 |
| Model | Head | Body | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE (g) | MAE (g) | Time (s) | RMSE (g) | MAE (g) | Time (s) | |||
| SVR [26] | 21.10 ± 1.17 | 14.17 ± 0.50 | 0.98 | 1.68 ± 0.11 | 31.39 ± 1.75 | 21.66 ± 0.91 | 0.97 | 1.42 ± 0.07 |
| Extra Trees [30] | 2.49 ± 0.23 | 1.48 ± 0.11 | 1.00 | 0.08 | 4.47 ± 0.38 | 2.83 ± 0.24 | 1.00 | 0.09 |
| MLP [20] | 18.40 ± 1.24 | 13.10 ± 0.95 | 0.99 | 2.37 ± 0.65 | 25.21 ± 1.85 | 18.48 ± 1.47 | 0.98 | 3.07 ± 0.27 |
| AE + SVR | 6.53 ± 0.23 | 5.68 ± 0.07 | 1.00 | 1.66 ± 0.02 | 6.52 ± 0.32 | 5.67 ± 0.09 | 1.00 | 3.27 ± 0.03 |
| AE + Extra Trees | 1.95 ± 0.41 | 0.93 ± 0.16 | 1.00 | 1.49 ± 0.02 | 2.09 ± 0.45 | 1.01 ± 0.16 | 1.00 | 3.27 ± 0.09 |
| AE + MLP | 5.09 ± 1.90 | 3.27 ± 1.37 | 1.00 | 2.24 ± 0.11 | 3.99 ± 0.66 | 2.60 ± 0.41 | 1.00 | 4.39 ± 0.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Zhang, L.; Liu, Z.; Luo, T.; Bao, B.; Zhou, L.; Xu, J. Fish Biomass Estimation Under Occluded Features: A Framework Combining Imputation and Regression. Fishes 2025, 10, 306. https://doi.org/10.3390/fishes10070306
Yang Y, Zhang L, Liu Z, Luo T, Bao B, Zhou L, Xu J. Fish Biomass Estimation Under Occluded Features: A Framework Combining Imputation and Regression. Fishes. 2025; 10(7):306. https://doi.org/10.3390/fishes10070306
Chicago/Turabian StyleYang, Yaohui, Lijun Zhang, Zhixiang Liu, Tuyan Luo, Baolong Bao, Liping Zhou, and Jingxiang Xu. 2025. "Fish Biomass Estimation Under Occluded Features: A Framework Combining Imputation and Regression" Fishes 10, no. 7: 306. https://doi.org/10.3390/fishes10070306
APA StyleYang, Y., Zhang, L., Liu, Z., Luo, T., Bao, B., Zhou, L., & Xu, J. (2025). Fish Biomass Estimation Under Occluded Features: A Framework Combining Imputation and Regression. Fishes, 10(7), 306. https://doi.org/10.3390/fishes10070306







