Model Selection Applied to Growth of the Stingray Urotrygon chilensis (Günther, 1872) in the Southeastern Mexican Pacific
Abstract
1. Introduction
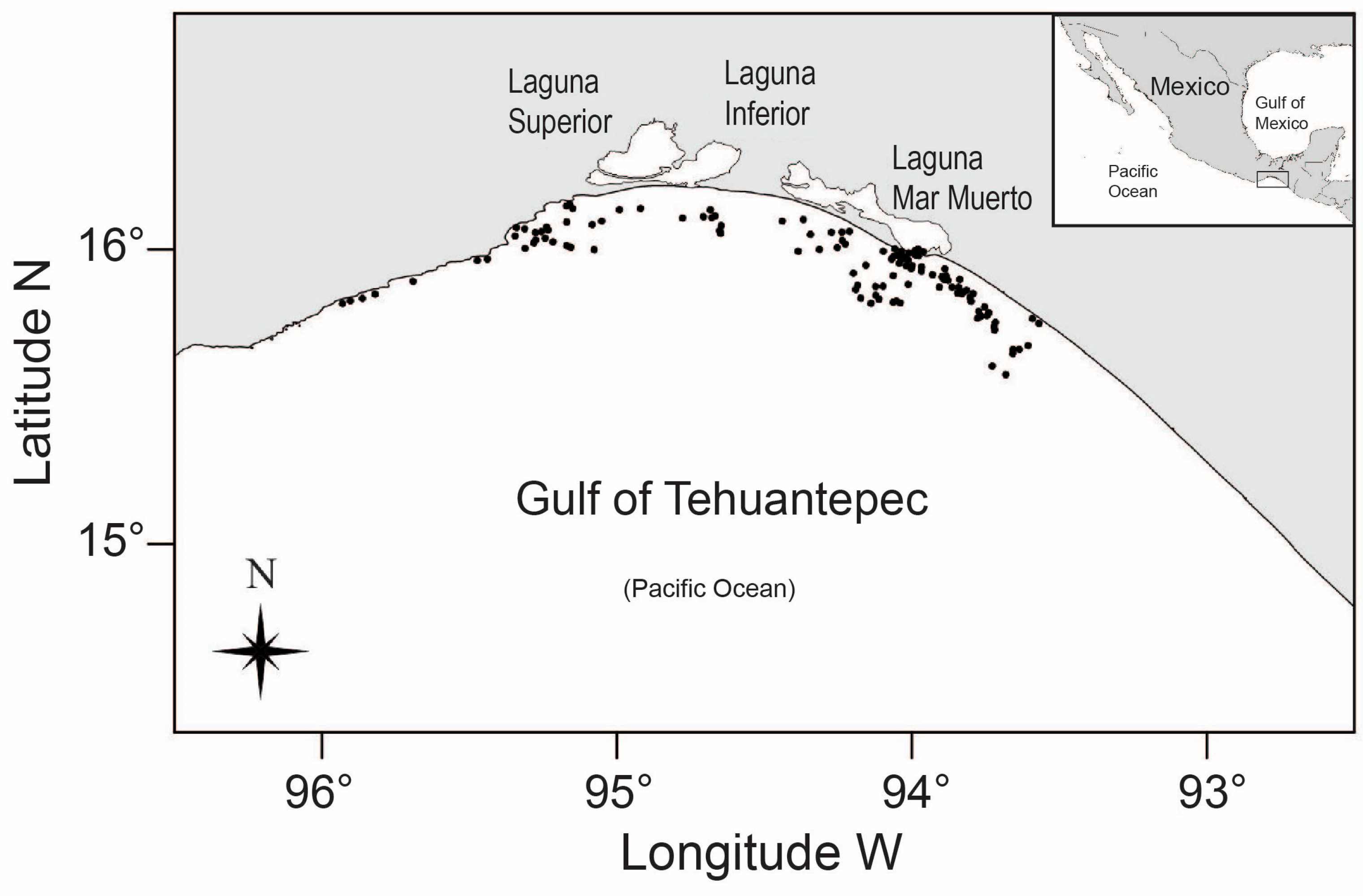
2. Materials and Methods
2.1. Vertebrae Preparation
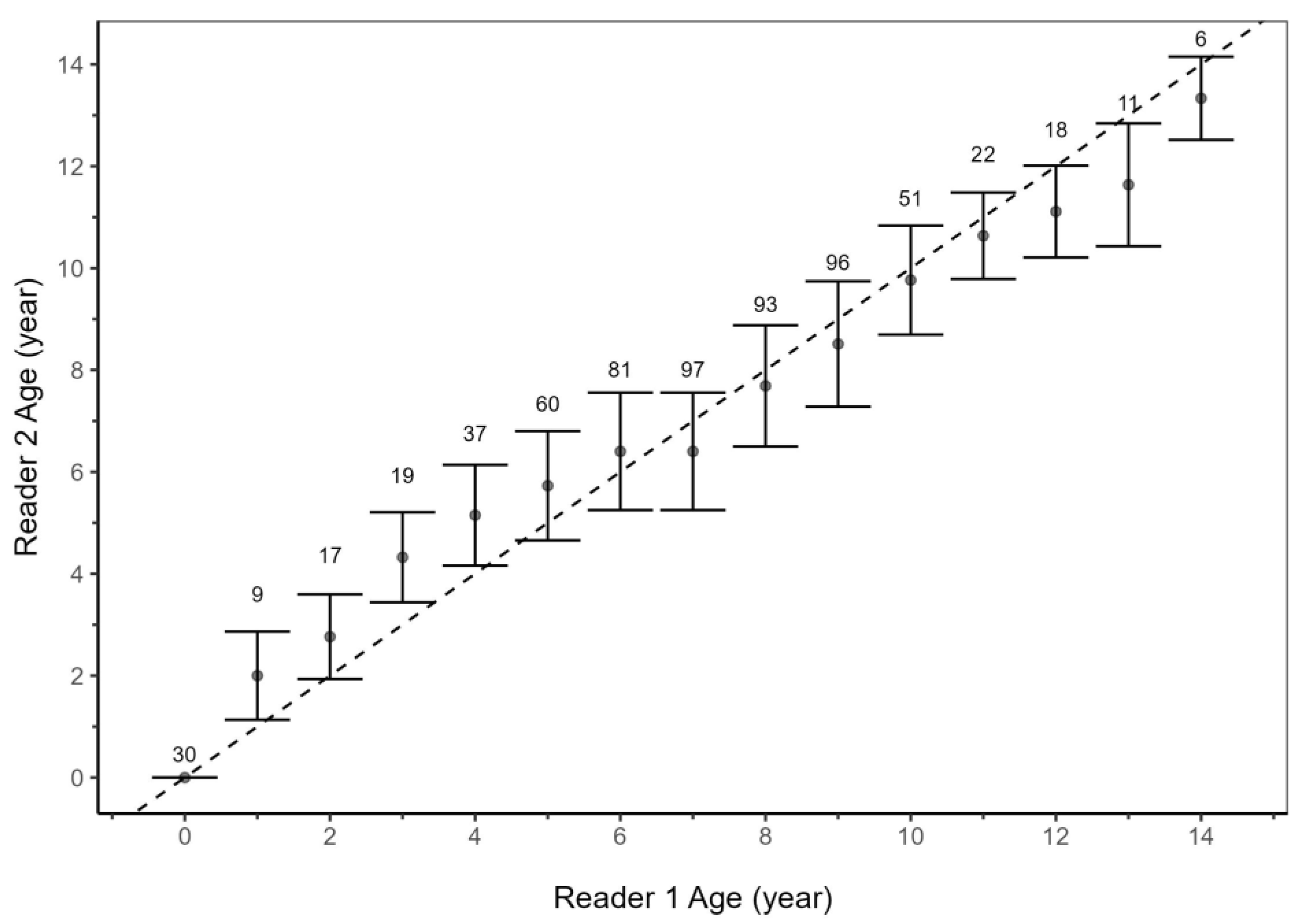
2.2. Precision and Bias
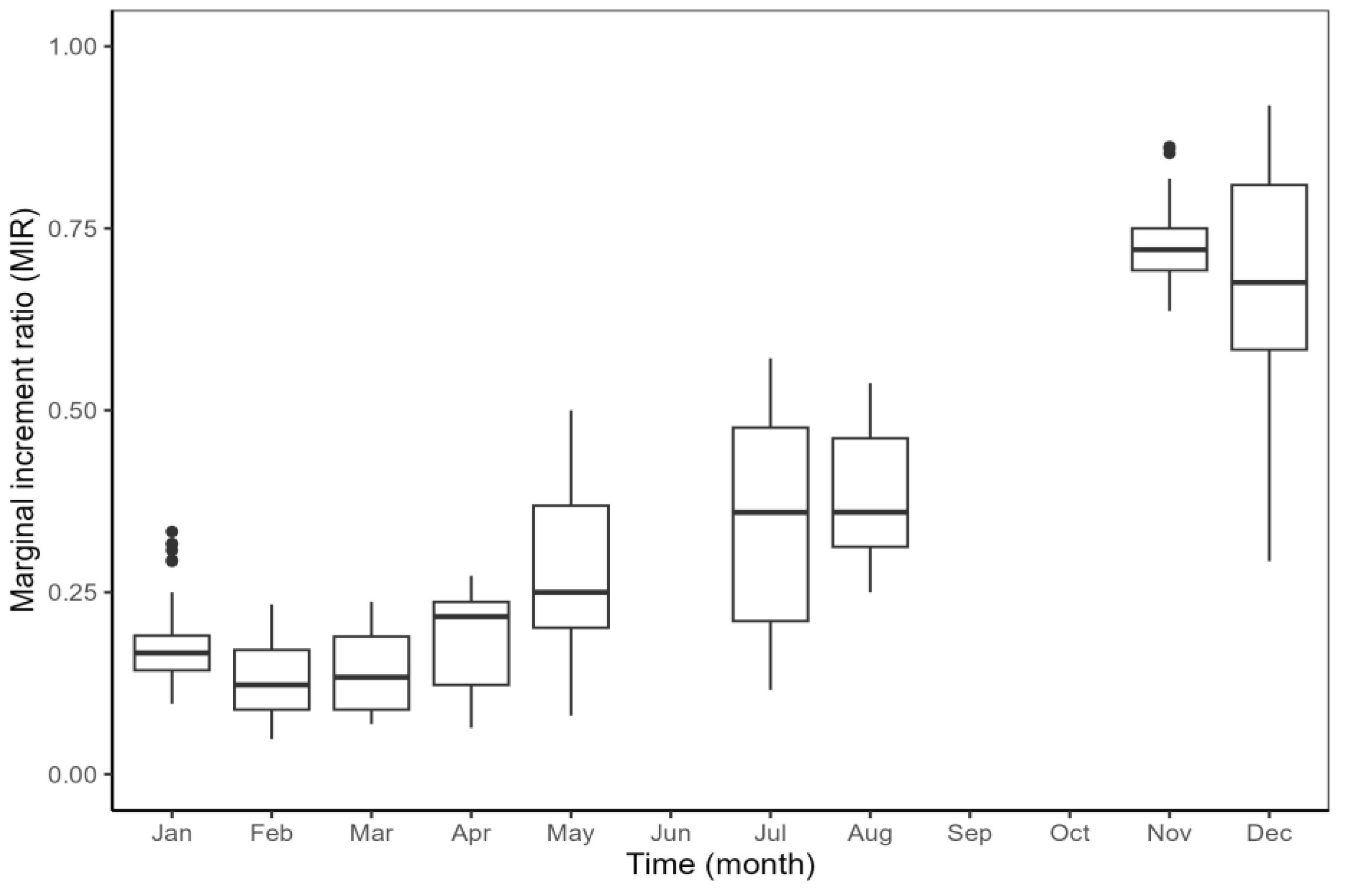
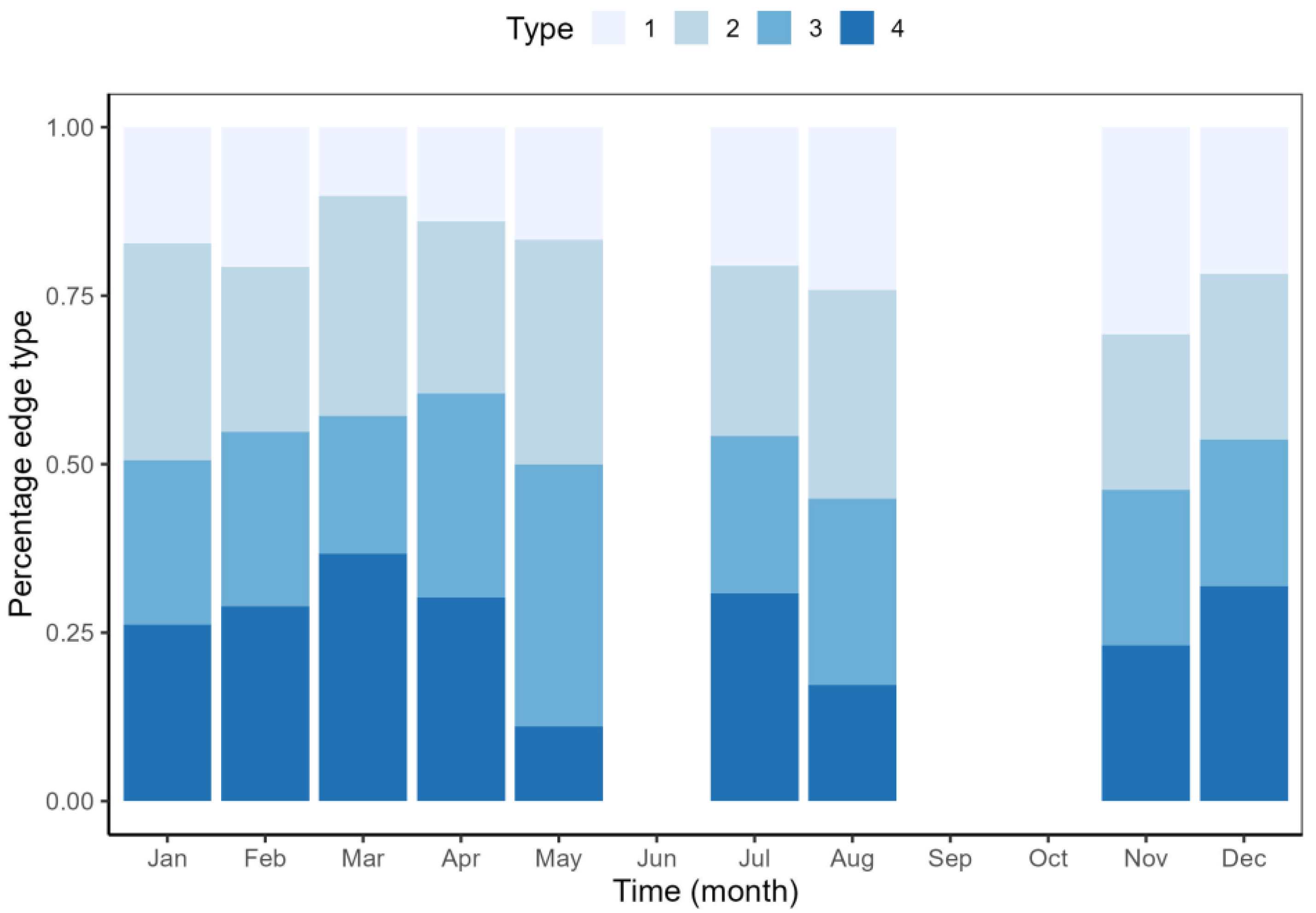
2.3. Age Verification
2.4. Growth Models and Parameter Estimation
2.5. Confidence Intervals
2.6. Model Selection
3. Results
3.1. Age Estimates and Verification
3.2. Growth Coefficients and Model Selection
4. Discussion
4.1. Age Verification
4.2. Fitted Growth Models
4.3. Growth Model Selection
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beebe, W.; Beebe, W.; Tee-Van, J. Eastern Pacific Expeditions of the New York Zoological Society. XXVIII. Fishes from the Tropical Eastern Pacific. From Cedros Island, Lower California, South to the Galapagos Islands and Northern Peru. Part 3. Rays, Mantas and Chimaeras. Zool. Sci. Contrib. N. Y Zool. Soc. 1941, 26, 245–280. [Google Scholar] [CrossRef]
- Villavicencio Garayzar, C.J. Distribución Temporal y Condición Reproductiva de Las Rayas (Pisces: Batoidei), Capturadas Comercialmente En Bahía Almejas, Baja California Sur, México. Rev. Investig. Cient. Rev. Investig. Cient 1995, 6, 1–12. [Google Scholar]
- Márquez-Farías, J.F. The Artisanal Ray Fishery in the Gulf of California: Development, Fisheries Research, and Management Issues. Shark News 2002, 14, 12–13. [Google Scholar]
- Cisneros-Montemayor, A.M.; Cisneros-Mata, M.A.; Harper, S.; Pauly, D. Extent and Implications of IUU Catch in Mexico’s Marine Fisheries. Mar. Pol. 2013, 39, 283–288. [Google Scholar] [CrossRef]
- IUCN The IUCN Red List of Threatened Species. Version 2024-2. Available online: https://www.iucnredlist.org (accessed on 25 February 2025).
- Brander, K. Disappearance of Common Skate Raia Batis from Irish Sea. Nature 1981, 290, 48–49. [Google Scholar] [CrossRef]
- Casey, J.M.; Myers, R.A. Near Extinction of a Large, Widely Distributed Fish. Science 1998, 281, 690–692. [Google Scholar] [CrossRef]
- Bizzarro, J.J.; Smith, W.D.; Márquez-Farías, J.F.; Hueter, R.E. Artisanal Fisheries and Reproductive Biology of the Golden Cownose Ray, Rhinoptera Steindachneri Evermann and Jenkins, 1891, in the Northern Mexican Pacific. Fish. Res. 2007, 84, 137–146. [Google Scholar] [CrossRef]
- Dellapa, A.; Kimmel, D.G.; Cl, S. Trends of Fish and Elasmobranch Landings in Italy: Associated Management Implications. ICES J. Mar. Sci. 2012, 69, 1045–1052. [Google Scholar] [CrossRef]
- Ruocco, N.L.; Lucifora, L.O.; Díaz De Astarloa, J.M.; Wöhler, O. Reproductive Biology and Abundance of the White-Dotted Skate, Bathyraja albomaculata, in the Southwest Atlantic. ICES J. Mar. Sci. 2006, 63, 105–116. [Google Scholar] [CrossRef]
- Baum, J.K.; Myers, R.A. Shifting Baselines and the Decline of Pelagic Sharks in the Gulf of Mexico. Ecol. Lett. 2004, 7, 135–145. [Google Scholar] [CrossRef]
- Le Port, A.; Lavery, S.; Montgomery, J.C. Conservation of Coastal Stingrays: Seasonal Abundance and Population Structure of the Short-Tailed Stingray Dasyatis brevicaudata at a Marine Protected Area. ICES J. Mar. Sci. 2012, 69, 1427–1435. [Google Scholar] [CrossRef]
- Ainsley, S.M.; Ebert, D.A.; Natanson, L.J.; Cailliet, G.M. A Comparison of Age and Growth of the Bering Skate, Bathyraja interrupta (Gill and Townsend, 1897), from Two Alaskan Large Marine Ecosystems. Fish. Res. 2014, 154, 17–25. [Google Scholar] [CrossRef]
- Kadri, H.; Marouani, S.; Saïdi, B.; Bradai, M.N.; Bouaïn, A.; Morize, E. Age, Growth, Sexual Maturity and Reproduction of the Thornback Ray, Raja clavata (L.), of the Gulf of Gabès (South-Central Mediterranean Sea). Mar. Biol. Res. 2014, 10, 416–425. [Google Scholar] [CrossRef]
- Alvarez-Fuentes, C.J.; Tovar-Ávila, J.; Payan-Alejo, J.; Chávez-Arrenquín, D.A.; Salgado-Ugarte, I.H.; Amezcua, F. Reproductive Ecology of the Chilean Round Ray (Urotrygon chilensis, Günther, 1872) in the Southern Gulf of California. Fishes 2023, 8, 193. [Google Scholar] [CrossRef]
- Ordoñez-López, J. Aspectos Reproductivos y Alimenticios de la Raya Pinta Urotrygon chilensis (Gunther, 1871) (Pisces: Usolophidae) en el Pacifico Central mexicano. Bachelor’s Thesis, Universidad Nacional Autónoma de México, Mexico City, Mexico, 2004. [Google Scholar]
- Torres-Huerta, A.M.; López-Pérez, R.A.; Tapia-García, M.; Gracía, A. Distribution of Batoid Demersal Assemblages on the Continental Shelf of the Gulf of Tehuantepec. Mar. Freshw. Res. 2019, 70, 1445–1458. [Google Scholar] [CrossRef]
- Guzman-Castellanos, A.B. Historia de Vida de la Raya Chilena Urotrygon chilensis (Günther, 1872) en el Sureste del Pacífico Mexicano. Ph.D. Thesis, Centro de Investigaciones Biológicas del Noroeste S.C., La Paz, Bolivia, 2015. [Google Scholar]
- Cailliet, G.M.; Goldman, K.J. Age Determination and Validation in Chondrichthyan Fishes. In Biology of Sharks and Their Relatives; CRC Press: Boca Raton, FL, USA, 2004; pp. 399–448. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach, 2nd ed.; Springer: NewYork, NY, USA, 2002. [Google Scholar]
- Katsanevakis, S. Modelling Fish Growth: Model Selection, Multi-Model Inference and Model Selection Uncertainty. Fish. Res. 2006, 81, 229–235. [Google Scholar] [CrossRef]
- Flinn, S.A.; Midway, S.R. Trends in Growth Modeling in Fisheries Science. Fishes 2021, 6, 1. [Google Scholar] [CrossRef]
- Kume, G.; Furumitsu, K.; Yamaguchi, A. Age, Growth and Age at Sexual Maturity of Fan Ray Platyrhina sinensis (Batoidea: Platyrhinidae) in Ariake Bay, Japan. Fish. Sci. 2008, 74, 736–742. [Google Scholar] [CrossRef]
- Aversa, M.I.; Dans, S.L.; García, N.A.; Crespo, E.A. Growth Models Fitted to Dipturus chilensis Length-at-Age Data Support a Two-Phase Growth. Rev. Chil. Hist. Nat. 2011, 84, 33–49. [Google Scholar] [CrossRef]
- Cailliet, G.M.; Martin, L.K.; Kushner, D.; Wolf, P.; Welden, B.A. Techniques for Enhancing Vertebral Bands in Age Estimation of California Elasmobranchs. In Proceedings of the International Workshop on Age Determination of Oceanic Pelagic Fishes: Tunas, Billfishes, Sharks, Miami, FL, USA, 15–18 February 1983. NOAA Tech. Rep. NMFS 8. [Google Scholar]
- Brown, C.A.; Gruber, S.H. Age Assessment of the Lemon Shark, Negaprion Brevirostris, Using Tetracycline Validated Vertebral Centra. Copeia 1988, 1988, 747–753. [Google Scholar] [CrossRef]
- Goldman, K.J. 6. Age and Growth. In Elasmobranch Fisheries Management Techniques; Musick, J.A., Bonfil, R., Eds.; FAO Fisheries Technical Paper No. 474; FAO: Rome, Italy, 2005; pp. 76–102. [Google Scholar]
- Graphical and Statistical Methods for Determining the Consistency of Age Determinations—Campana—1995—Transactions of the American Fisheries Society—Wiley Online Library. Available online: https://afspubs.onlinelibrary.wiley.com/doi/abs/10.1577/1548-8659%281995%29124%3C0131%3AGASMFD%3E2.3.CO%3B2 (accessed on 6 September 2024).
- Beamish, R.J.; Fournier, D.D.A. A Method for Comparing the Precision of a Set of Age Determinations. Can. J. Fish. Aquat. Sci. 1981, 38, 982–983. [Google Scholar] [CrossRef]
- Chang, W.Y.B. A Statistical Method for Evaluating the Reproducibility of Age Determination. Can. J. Fish. Aquat. Sci. 2011, 39, 1208–1210. [Google Scholar] [CrossRef]
- Cailliet, G.M.; Smith, W.D.; Mollet, H.F.; Goldman, K.J. Age and Growth Studies of Chondrichthyan Fishes: The Need for Consistency in Terminology, Verification, Validation, and Growth Function Fitting. Environ. Biol. Fishes 2006, 77, 211–228. [Google Scholar] [CrossRef]
- Smith, W.D.; Cailliet, G.M.; Melendez, E.M. Maturity and Growth Characteristics of a Commercially Exploited Stingray. Mar. Freshw. Res. 2007, 58, 54–66. [Google Scholar] [CrossRef]
- Campana, S.E. Accuracy, Precision and Quality Control in Age Determination, Including a Review of the Use and Abuse of Age Validation Methods. J. Fish. Biol. 2001, 59, 197–242. [Google Scholar] [CrossRef]
- Lessa, R.; Santana, F.M.; Duarte-Neto, P. A Critical Appraisal of Marginal Increment Analysis for Assessing Temporal Periodicity in Band Formation among Tropical Sharks. Environ. Biol. Fishes 2006, 77, 309–315. [Google Scholar] [CrossRef]
- James, K.C.; Ebert, D.A.; Natanson, L.J.; Cailliet, G.M. Age and Growth Characteristics of the Starry Skate, Raja stellulata, with a Description of Life History and Habitat Trends of the Central California, U.S.A., Skate Assemblage. Environ. Biol. Fishes 2014, 97, 435–448. [Google Scholar] [CrossRef]
- Zar, J. Biostatistical Analysis, 4th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1999; 266p. [Google Scholar]
- Gallagher, M.; Nolan, C.P. A Novel Method for the Estimation of Age and Growth in Rajids Using Caudal Thorns. Can. J. Fish. Aquat. Sci. 1999, 56, 1590–1599. [Google Scholar] [CrossRef]
- Yudin, K.G.; Cailliet, G.M. Age and Growth of the Gray Smoothhound, Mustelus californicus, and the Brown Smoothhound, M. Henlei, Sharks from Central California. Copeia 1990, 1990, 191–204. [Google Scholar] [CrossRef]
- Yokota, L.; Lessa, R.P. A Nursery Area for Sharks and Rays in Northeastern Brazil. Environ. Biol. Fishes 2006, 75, 349–360. [Google Scholar] [CrossRef]
- Hilborn, R.; Mangel, M. The Ecological Detective. Confronting Models with Data; Princeton University Press: Princeton, NJ, USA, 1997; p. 315. [Google Scholar]
- Luquin-Covarrubias, M.A.; Morales-Bojórquez, E.; Scarry-González, S.; Lluch-Cota, D.B. Joint Likelihood Function Based on Multinomial and Normal Distributions for Analyzing the Phenotypic Growth Variability of Geoduck Clam Panopea globosa. CalCOFI Rep. 2016, 57, 151–162. [Google Scholar]
- Hilborn, R.; Walters, C.J. Quantitative Fisheries Stock Assessment: Choice, Dynamics and Uncertainty; Springer: New York, NY, USA, 1992. [Google Scholar]
- Fournier, D.; Archibald, C.P. A General Theory for Analyzing Catch at Age Data Fisheries. Can. J. Fish. Aquat. Sci. 1982, 39, 1195–1207. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; CRC Press Taylor & Francis Group 6000 Broken: Boca Raton, FL, USA, 2013; 642p. [Google Scholar]
- Magnusson, A.; Punt, A.E.; Hilborn, R. Measuring Uncertainty in Fisheries Stock Assessment: The Delta Method, Bootstrap, and MCMC. Fish Fish. 2013, 14, 325–342. [Google Scholar] [CrossRef]
- Haddon, M. Modelling and Quantitative Methods in Fisheries, 2nd ed.; Chapman and Hall/CRC: New York, NY, USA, 2011; ISBN 9780429109492. [Google Scholar]
- Hobbs, N.T.; Hilborn, R. Alternatives to Statistical Hypothesis Testing in Ecology: A Guide to Self Teaching. Ecol. Appl. 2006, 16, 5–19. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.B.; Omland, K.S. Model Selection in Ecology and Evolution. Trends Ecol. Evol. 2004, 19, 101–108. [Google Scholar] [CrossRef]
- Kimura, D.K. Likelihood Methods for the von Bertalanffy Growth Curve. Fish. Bull. 1980, 77, 765–776. [Google Scholar]
- Stobutzki, I.; Miller, M.; Brewer, D. Sustainability of Fishery Bycatch: A Process for Assessing Highly Diverse and Numerous Bycatch. Environ. Conserv. 2001, 28, 167–181. [Google Scholar] [CrossRef]
- Braccini, J.M.; Gillanders, B.M.; Walker, T.I.; Tovar-Avila, J. Comparison of Deterministic Growth Models Fitted to Length-at-Age Data of the Piked Spurdog (Squalus megalops) in South-Eastern Australia. Mar. Freshw. Res. 2007, 58, 24–33. [Google Scholar] [CrossRef]
- Simpfendorfer, C.A.; Heupel, M.R.; White, W.T.; Dulvy, N.K. The Importance of Research and Public Opinion to Conservation Management of Sharks and Rays: A Synthesis. Mar. Freshw. Res. 2011, 62, 518–527. [Google Scholar] [CrossRef]
- Natanson, L.J.; Cailliet, G.M. Vertebral Growth Zone Deposition in Pacific Angel Sharks. Copeia 1990, 1133–1145. [Google Scholar] [CrossRef]
- Mejía-Falla, P.A.; Cortés, E.; Navia, A.F.; Zapata, F.A. Age and Growth of the Round Stingray Urotrygon rogersi, a Particularly Fast-Growing and Short-Lived Elasmobranch. PLoS ONE 2014, 9, e96077. [Google Scholar] [CrossRef] [PubMed]
- Torres-Palacios, K.; Mejía-Falla, P.A.; Navia, A.F.; Cruz-Escalona, V.H.; Félix-Uraga, R.; Quiñonez-Velázquez, C. Age and Growth Parameters of the Panamic Stingray (Urotrygon aspidura). Fish. Bull. 2019, 117, 169–179. [Google Scholar] [CrossRef]
- Sulikowski, J.A.; Morin, M.D.; Suk, S.H.; Howell, W.H. Age and Growth Estimates of the Winter Skate (Leucoraja ocellata) in the Western Gulf of Maine. Fish. Bull. 2003, 101, 405–413. [Google Scholar]
- Okamura, H.; Punt, A.E.; Semba, Y.; Ichinokawa, M. Marginal Increment Analysis: A New Statistical Approach of Testing for Temporal Periodicity in Fish Age Verification. J. Fish. Biol. 2013, 82, 1239–1249. [Google Scholar] [CrossRef]
- Neer, J.A.; Thompson, B.A. Life History of the Cownose Ray, Rhinoptera bonasus, in the Northern Gulf of Mexico, with Comments on Geographic Variability in Life History Traits. Environ. Biol. Fishes 2005, 73, 321–331. [Google Scholar] [CrossRef]
- Natanson, L.J.; Sulikowski, J.a.; Kneebone, J.R.; Tsang, P.C. Age and Growth Estimates for the Smooth Skate, Malacoraja senta, in the Gulf of Maine. Environ. Biol. Fishes 2007, 80, 293–308. [Google Scholar] [CrossRef]
- Davis, C.D.; Cailliet, G.M.; Ebert, D.A. Age and Growth of the Roughtail Skate Bathyraja trachura (Gilbert 1892) from the Eastern North Pacific. Environ. Biol. Fishes 2007, 80, 219–230. [Google Scholar] [CrossRef]
- Joung, S.J.; Lee, P.H.; Liu, K.M.; Liao, Y.Y. Estimates of Life History Parameters of the Sharpspine Skate, Okamejei acutispina, in the Northeastern Waters of Taiwan. Fish. Res. 2011, 108, 258–267. [Google Scholar] [CrossRef]
- Natanson, L.J. Effect of Temperature on Band Deposition in the Little Skate, Raja erinacea. Copeia 1993, 199–206. [Google Scholar] [CrossRef]
- Sagarese, S.R.; Frisk, M.G. An Investigation on the Effect of Photoperiod and Temperature on Vertebral Band Deposition in Little Skate Leucoraja erinacea. J. Fish. Biol. 2010, 77, 935–946. [Google Scholar] [CrossRef]
- White, W.T.; Potter, I.C. Reproductive Biology, Size and Age Compositions and Growth of the Batoid (Urolophus paucimaculatus), Including Comparisons with Other Species of the Urolophidae. Mar. Freshw. Res. 2005, 56, 101–110. [Google Scholar] [CrossRef]
- Hale, L.F.; Lowe, C.G. Age and Growth of the Round Stingray Urobatis halleri at Seal Beach, California. J. Fish. Biol. 2008, 73, 510–523. [Google Scholar] [CrossRef]
- Jacobsen, I.P.; Bennett, M.B. Life History of the Blackspotted Whipray Himantura astra. J. Fish. Biol. 2011, 78, 1249–1268. [Google Scholar] [CrossRef]
- Araya, M.; Cubillos, L.A. Evidence of Two-Phase Growth in Elasmobranchs. Environ. Biol. Fishes 2006, 77, 293–300. [Google Scholar] [CrossRef]
- Pardo, S.A.; Cooper, A.B.; Dulvy, N.K. Avoiding Fishy Growth Curves. Methods Ecol. Evol. 2013, 4, 353–360. [Google Scholar] [CrossRef]
- Ainsley, S.M.; Ebert, D.A.; Cailliet, G.M. Age, Growth, and Maturity of the Whitebrow Skate, Bathyraja minispinosa, from the Eastern Bering Sea. ICES J. Mar. Sci. 2011, 68, 1426–1434. [Google Scholar] [CrossRef]
- Henningsen, A.D.; Leaf, R.T. Observations on the Captive Biology of the Southern Stingray. Trans. Am. Fish. Soc. 2010, 139, 783–791. [Google Scholar] [CrossRef]
- Matta, M.E.; Gunderson, D.R. Age, Growth, Maturity, and Mortality of the Alaska Skate, Bathyraja parmifera, in the Eastern Bering Sea. Environ. Biol. Fishes 2007, 80, 203–217. [Google Scholar] [CrossRef]
- Guzmán-Castellanos, A.B.; Morales-Bojórquez, E.; Balart, E.F. Individual Growth Estimation in Elasmobranchs: The Multi-Model Inference Approach. Hidrobiológica 2014, 24, 137–150. [Google Scholar]
- Pierce, S.J.; Bennett, M.B. Destined to Decline? Intrinsic Susceptibility of the Threatened Estuary Stingray to Anthropogenic Impacts. Mar. Freshw. Res. 2010, 61, 1468–1481. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Q. Comparison of Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) in Selection of Stock–Recruitment Relationships. Fish. Res. 2006, 77, 220–225. [Google Scholar] [CrossRef]
- Licandeo, R.R.; Lamilla, J.G.; Rubilar, P.G.; Vega, R.M. Age, Growth, and Sexual Maturity of the Yellownose Skate Dipturus chilensis in the South-Eastern Pacific. J. Fish. Biol. 2006, 68, 488–506. [Google Scholar] [CrossRef]
- White, W.T.; Platell, M.E.; Potter, I.C. Relationship between Reproductive Biology and Age Composition and Growth in Urolophus lobatus (Batoidea: Urolophidae). Mar. Biol. 2001, 138, 135–147. [Google Scholar] [CrossRef]
- White, W.T.; Hall, N.G.; Potter, I.C. Reproductive Biology and Growth during Pre- and Postnatal Life of Trygonoptera personata and T. mucosa (Batoidea: Urolophidae). Mar. Biol. 2002, 140, 699–712. [Google Scholar] [CrossRef]
- Ismen, A. Age, Growth, Reproduction and Food of Common Stingray (Dasyatis pastinaca L., 1758) in İskenderun Bay, the Eastern Mediterranean. Fish. Res. 2003, 60, 169–176. [Google Scholar] [CrossRef]
- Mollet, H.F.; Ezcurra, J.M.; O’Sullivan, J.B. Captive Biology of the Pelagic Stingray, Dasyatis violacea (Bonaparte, 1832). Mar. Freshw. Res. 2002, 53, 531–541. [Google Scholar] [CrossRef]
- Francise, M.P.; Maolagáin, C.Ó. Age and Growth of the Antarctic Skate (Amblyraja georgiana) in the Ross Sea. CCAMLR Sci. 2005, 12. [Google Scholar]
- Gburski, C.M.; Gaichas, S.K.; Kimura, D.K. Age and Growth of Big Skate (Raja binoculata) and Longnose Skate (R. rhina) in the Gulf of Alaska. Environ. Biol. Fishes. 2007, 80, 337–349. [Google Scholar] [CrossRef]
- Ismen, A.; Yigin, C.; Ismen, P. Age, Growth, Reproductive Biology and Feed of the Common Guitarfish (Rhinobatos rhinobatos Linnaeus, 1758) in İskenderun Bay, the Eastern Mediterranean Sea. Fish. Res. 2007, 84, 263–269. [Google Scholar] [CrossRef]
- Başusta, N.; Demirhan, S.A.; Çiçek, E.; Başusta, A.; Kuleli, T. Age and Growth of the Common Guitarfish, Rhinobatos rhinobatos, in Iskenderun Bay (North-Eastern Mediterranean, Turkey). J. Mar. Biol. Assoc. UK 2008, 88, 837–842. [Google Scholar] [CrossRef]
- Izzo, C.; Gillanders, B.M. Initial Assessment of Age, Growth and Reproductive Parameters of the Southern Fiddler Ray Trygonorrhina fasciata (Müller & Henle, 1841) from South Australia. Panam. J. Aquat. Sci. 2008, 3, 321–327. [Google Scholar]
- Cuevas-Zimbrón, E.; Sosa-Nishizaki, O.; Pérez-Jiménez, J.C.; O’Sullivan, J.B. An Analysis of the Feasibility of Using Caudal Vertebrae for Ageing the Spinetail Devilray, Mobula japanica (Müller and Henle, 1841). Environ. Biol. Fishes. 2013, 96, 907–914. [Google Scholar] [CrossRef]
- Yigin, C.C.; Ismen, A. Age, Growth and Reproduction of the Common Stingray, Dasyatis pastinaca from the North Aegean Sea. Mar. Biol. Res. 2012, 8, 644–653. [Google Scholar] [CrossRef]
- Mora-Zamacona, P.; Melo-Barrera, F.N.; Cruz-Escalona, V.H.; Navia, A.F.; Morales-Bojórquez, E.; Pérez-Palafox, X.A.; Mejía-Falla, P.A. Growth Modeling of the Giant Electric Ray Narcine entemedor in the Southern Gulf of California: Analyzing the Uncertainty of Three Data Sets. Animals 2022, 12, 19. [Google Scholar] [CrossRef]
- Santander-Nieto, J.; Santana, F.M.; Vasconcelos-Filho, J.E.; Lessa, R. Age and Growth of the Threatened Smalleye Round Ray, Urotrygon microphthalmum, Delsman, 1941, from Northeastern Brazil. Fishes 2023, 8, 160. [Google Scholar] [CrossRef]


| Name | Acronym | Model |
|---|---|---|
| Gompertz three parameters | GGM | |
| Gompertz two parameters | GGM-2 | |
| Gompertz two phases | GGM-2P | |
| Logistic three parameters | LGM | |
| Schnute (a ≠ 0, b ≠ 0) | SCHGM-1 | |
| Schnute (a ≠ 0, b = 0) | SCHGM-2 |
| Parameters | Description |
|---|---|
| Asymptotic length at which growth is zero | |
| Growth coefficient | |
| Age or time when length theoretically equals zero | |
| Mean size-at-birth | |
| Instantaneous rate of growth at time t | |
| Firts specified age | |
| Second specified age | |
| Constant relative rate of relative growth rate | |
| Incremental relative rate of relative growth rate |
| Model | Parameter | Value | Mean | Sd | CV | Bias | % Bias | Lower C.I. | Upper C.I. |
|---|---|---|---|---|---|---|---|---|---|
| GGM-2 | k | 1.42 | 1.65 | 0.05 | 0.02 | 0.24 | 14.52 | 1.33 | 1.51 |
| A | 0.15 | 0.16 | 0.00 | 0.04 | 0.04 | 8.31 | 0.15 | 0.15 | |
| GGM-2P | G | 1.41 | 1.41 | 0.01 | 0.00 | 0.00 | −0.37 | 1.39 | 1.43 |
| k | 0.15 | −0.20 | 0.00 | −0.02 | −0.05 | 26.79 | −0.15 | −0.19 | |
| GGM | L∞ | 40.35 | 38.83 | 0.39 | 0.01 | −1.51 | −3.90 | 39.59 | 41.11 |
| k | 0.19 | 0.20 | 0.00 | 0.01 | 0.01 | 5.09 | 0.19 | 0.19 | |
| t0 | 1.96 | 1.70 | 0.05 | 0.03 | −0.25 | −14.79 | 1.86 | 2.05 | |
| SCHGM-1 | A | 0.82 | 0.77 | 0.04 | 0.06 | −0.05 | −6.88 | 0.74 | −4.048 |
| B | −4.59 | −4.25 | 0.27 | −0.06 | 0.34 | −7.93 | −5.12 | 10.21 | |
| y1 | 10.10 | 10.20 | 0.06 | 0.01 | 0.12 | 1.13 | 9.99 | 33.28 | |
| y2 | 32.98 | 31.91 | 0.16 | 0.00 | −0.09 | −0.29 | 32.68 | ||
| y∞ | 31.91 | 31.89 | 0.15 | 0.00 | −0.09 | −0.29 | 31.62 | 32.20 | |
| τ | 4.16 | 4.16 | 0.45 | 0.23 | −0.29 | −0.28 | 3.51 | 5.27 | |
| y | 21.60 | 11.19 | 0.08 | 0.01 | 0.33 | 0.14 | 21.44 | 21.75 | |
| LGM | L∞ | 35.82 | 35.16 | 0.23 | 0.01 | −0.05 | −0.14 | 35.36 | 36.27 |
| k | 0.33 | 0.33 | 0.00 | 0.01 | 0.00 | 0.56 | 0.32 | 0.33 | |
| t0 | 3.12 | 2.95 | 0.06 | 0.02 | −0.02 | −0.83 | 3.01 | 3.23 | |
| SCHGM-2 | α | 0.19 | 0.20 | 0.00 | 0.02 | 0.01 | 4.91 | 0.18 | 0.20 |
| y1 | 10.26 | 9.46 | 0.05 | 0.01 | 0.06 | 0.60 | 10.16 | 10.35 | |
| y2 | 39.87 | 36.43 | 0.48 | 0.01 | −0.11 | −0.29 | 38.92 | 40.81 |
| Model | Parameter | Value | Mean | Sd | CV | Bias | % Bias | Lower C.I. | Upper C.I. |
|---|---|---|---|---|---|---|---|---|---|
| GGM-2 | α | 1.57 | 44.47 | 1.37 | 0.03 | −3.76 | −8.45 | 41.78 | 46.83 |
| k | 0.13 | 0.15 | 0.01 | 0.04 | 0.01 | 7.75 | 0.14 | 0.16 | |
| GGM-2P | G | 1.59 | 1.48 | 0.03 | 0.02 | −0.14 | −9.21 | 1.53 | 1.65 |
| k | 0.13 | −0.15 | 0.01 | −0.04 | −0.03 | 18.32 | −0.11 | −0.15 | |
| GGM | L∞ | 48.23 | 44.47 | 1.37 | 0.03 | −3.76 | −8.45 | 45.55 | 50.90 |
| k | 0.14 | 0.15 | 0.01 | 0.04 | 0.01 | 7.75 | 0.13 | 0.15 | |
| t0 | 3.13 | 2.52 | 0.22 | 0.09 | −0.61 | −24.26 | 2.70 | 3.56 | |
| SCHGM-2 | α | 0.14 | 0.91 | 0.08 | 0.09 | −0.05 | −5.34 | 0.13 | 0.15 |
| y1 | 11.04 | 10.75 | 0.07 | 0.01 | 0.07 | 0.66 | 10.91 | 11.17 | |
| y2 | 40.75 | 31.08 | 0.25 | 0.01 | −0.19 | −0.62 | 39.10 | 42.40 | |
| y∞ | 46.13 | 30.88 | 0.10 | 0.00 | −0.02 | −0.19 | 45.60 | 46.65 | |
| τ | 2.67 | 00 | 0.00 | 1.48 | 0.00 | 87.13 | 2.31 | 3.03 | |
| y | 16.97 | 22.00 | 0.08 | 0.01 | −0.33 | −0.14 | 13.17 | 20.76 | |
| LGM | L∞ | 38.59 | 37.10 | 0.58 | 0.02 | −0.54 | −1.46 | 35.90 | 38.19 |
| k | 0.27 | 0.28 | 0.01 | 0.02 | 0.01 | 2.79 | 0.27 | 0.29 | |
| t0 | 3.77 | 3.43 | 0.14 | 0.04 | −0.13 | −3.90 | 3.16 | 3.70 | |
| SCHGM-1 | α | 0.95 | 0.91 | 0.08 | 0.09 | −0.05 | −5.34 | 0.79 | 1.11 |
| b | −6.18 | −5.85 | 0.59 | −0.10 | 0.33 | −5.62 | −7.34 | −5.02 | |
| y1 | 10.68 | 10.75 | 0.07 | 0.01 | 0.07 | 0.66 | 10.55 | 10.80 | |
| y2 | 31.27 | 31.08 | 0.25 | 0.01 | −0.19 | −0.62 | 30.79 | 31.75 | |
| y∞ | 31.13 | 30.88 | 0.10 | 0.00 | −0.02 | −0.19 | 30.93 | 31.32 | |
| τ | 4.90 | 00 | 0.00 | 1.48 | 0.00 | 87.13 | 4.89 | 4.99 | |
| y | 22.40 | 22.00 | 0.08 | 0.01 | −0.33 | −0.14 | 22.24 | 22.55 |
| Acronym | -Ln Likelihood | RT | df | |||
|---|---|---|---|---|---|---|
| Females | Males | |||||
| GGM | 659.53 | 294.16 | 699.06 | 5.99 | 2 | <0.05 |
| GGM-2 | 643.39 | 293.86 | 704.68 | 7.81 | 3 | <0.05 |
| GGM-2P | 645.34 | 293.00 | 730.74 | 7.81 | 3 | <0.05 |
| LGM | 678.56 | 301.07 | 730.78 | 9.49 | 3 | <0.05 |
| SCHGM-1 | 699.56 | 312.46 | 754.98 | 7.81 | 4 | <0.05 |
| SCHGM-2 | 659.56 | 294.17 | 774.2 | 9.49 | 4 | <0.05 |
| Sex | Model | θi | -Ln Likelihood | AIC | Δi | ωi |
|---|---|---|---|---|---|---|
| Females | GGM-2 | 2 | 643.39 | 1290.77 | 0.00 | 87.5 |
| GGM-2P | 3 | 645.34 | 1294.67 | 3.90 | 12.5 | |
| GGM | 3 | 659.53 | 1325.07 | 34.29 | 0.00 | |
| SCHGM-2 | 4 | 659.56 | 1327.13 | 36.35 | 0.00 | |
| LGM | 3 | 678.56 | 1363.13 | 72.35 | 0.00 | |
| SCHGM-1 | 4 | 699.56 | 1407.94 | 117.17 | 0.00 | |
| Males | GGM-2P | 3 | 293.00 | 590.00 | 0.00 | 63.3 |
| GGM-2 | 2 | 293.86 | 591.73 | 1.72 | 26.7 | |
| GGM | 3 | 294.16 | 594.33 | 4.32 | 7.3 | |
| SCHGM-2 | 4 | 294.17 | 596.34 | 6.34 | 2.7 | |
| LGM | 3 | 301.07 | 608.13 | 18.13 | 0.00 | |
| SCHGM-1 | 4 | 312.46 | 632.91 | 42.91 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guzmán-Castellanos, A.B.; Morales-Bojórquez, E.; Aguirre-Villaseñor, H.; Tovar-Ávila, J. Model Selection Applied to Growth of the Stingray Urotrygon chilensis (Günther, 1872) in the Southeastern Mexican Pacific. Fishes 2025, 10, 232. https://doi.org/10.3390/fishes10050232
Guzmán-Castellanos AB, Morales-Bojórquez E, Aguirre-Villaseñor H, Tovar-Ávila J. Model Selection Applied to Growth of the Stingray Urotrygon chilensis (Günther, 1872) in the Southeastern Mexican Pacific. Fishes. 2025; 10(5):232. https://doi.org/10.3390/fishes10050232
Chicago/Turabian StyleGuzmán-Castellanos, Ana Bricia, Enrique Morales-Bojórquez, Hugo Aguirre-Villaseñor, and Javier Tovar-Ávila. 2025. "Model Selection Applied to Growth of the Stingray Urotrygon chilensis (Günther, 1872) in the Southeastern Mexican Pacific" Fishes 10, no. 5: 232. https://doi.org/10.3390/fishes10050232
APA StyleGuzmán-Castellanos, A. B., Morales-Bojórquez, E., Aguirre-Villaseñor, H., & Tovar-Ávila, J. (2025). Model Selection Applied to Growth of the Stingray Urotrygon chilensis (Günther, 1872) in the Southeastern Mexican Pacific. Fishes, 10(5), 232. https://doi.org/10.3390/fishes10050232







