Modeling Dress-Out Traits Based on Morphological Traits in the Siberian Prawn, Exopalaemon modestus (Heller, 1862)
Abstract
1. Introduction
2. Materials and Methods
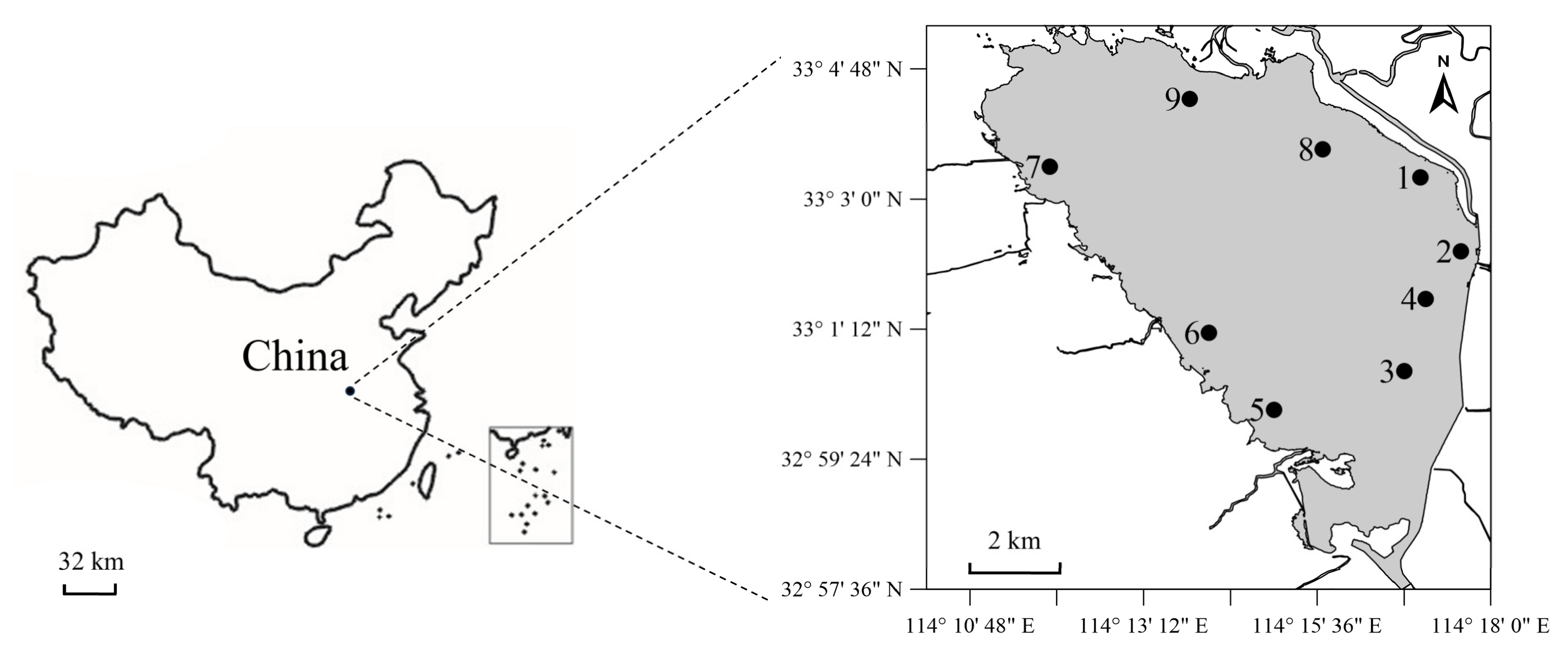
2.1. Sample Collection
2.2. Trait Measurement
2.3. Grey Relational Analysis
2.4. Path Analysis
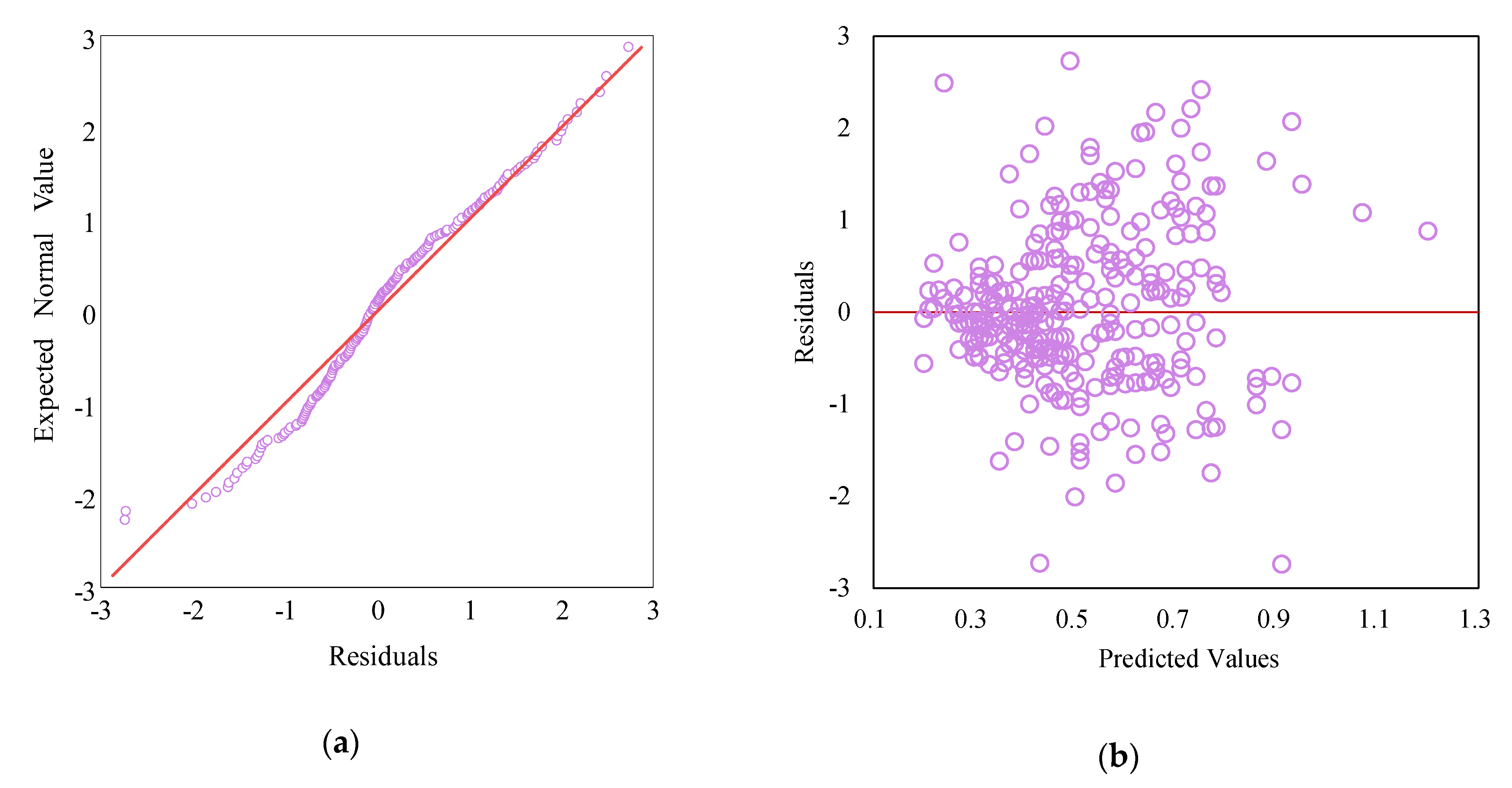
2.5. Model Adequacy Checking and Cross-Validation
3. Results
3.1. Statistical Analysis of Morphological and Dress-Out Traits in E. modestus
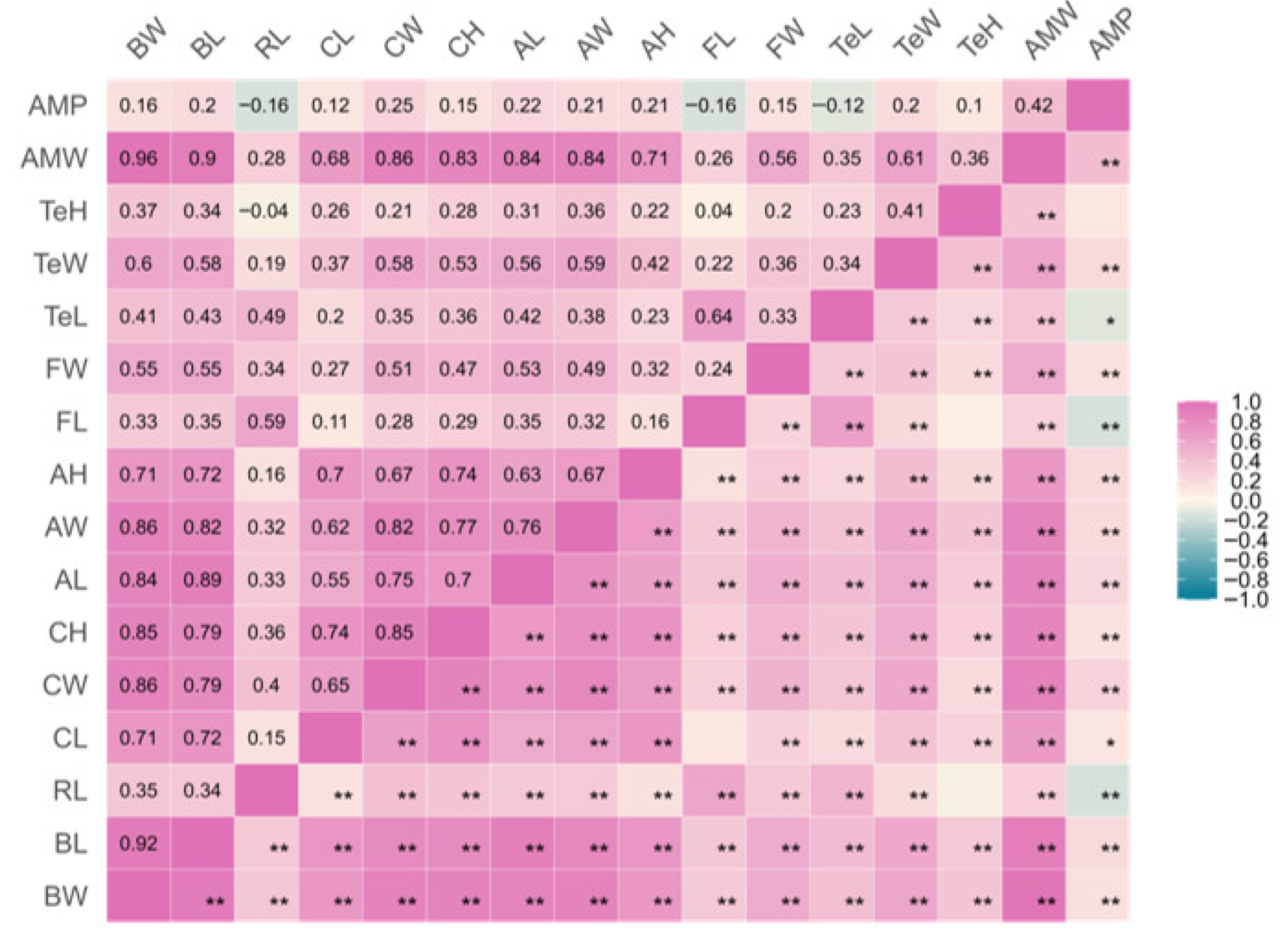
3.2. Correlation Coefficients Between Morphological and Dress-Out Traits in E. modestus
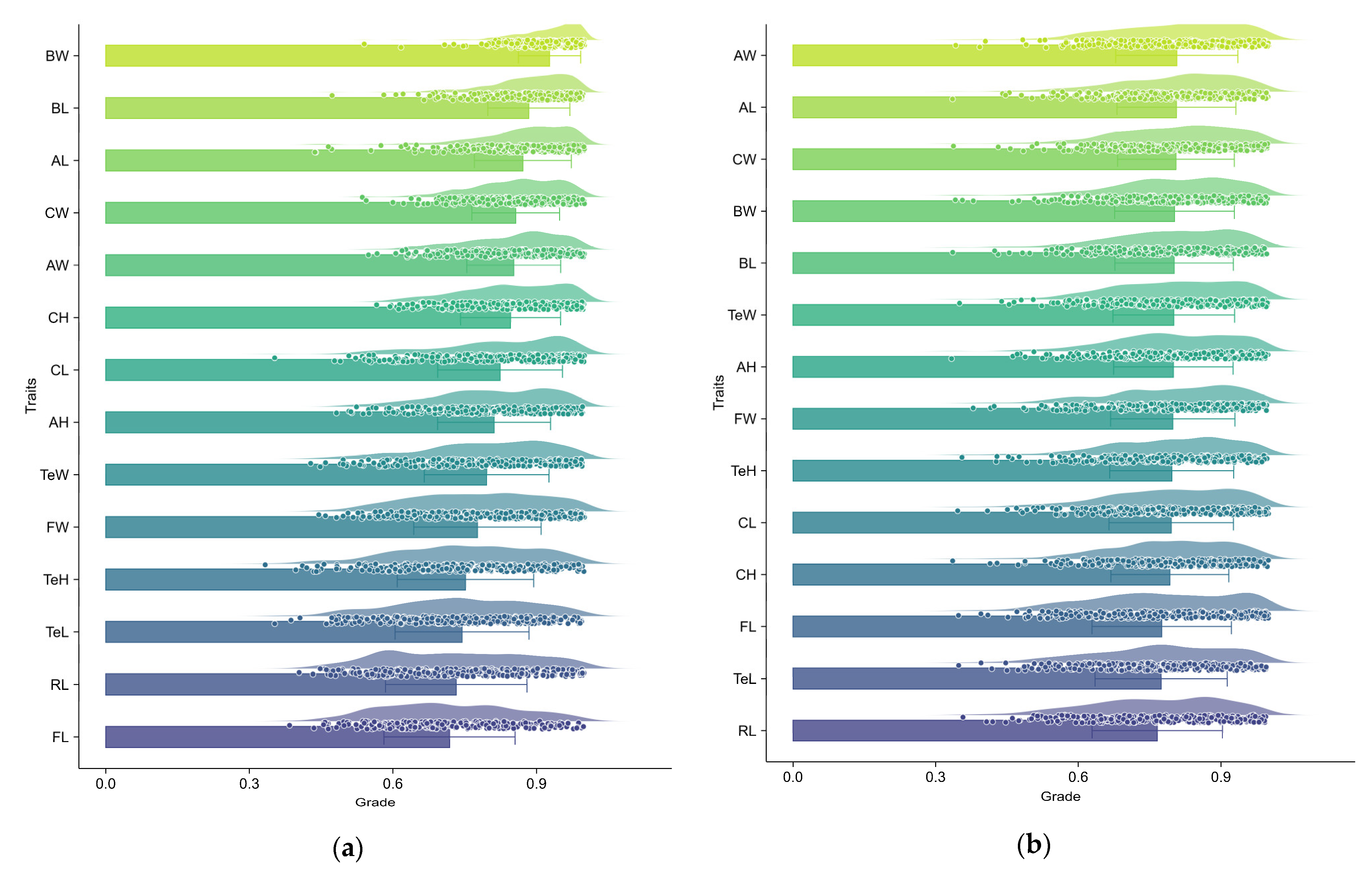
3.3. Grey Relational Analysis of Morphological Traits on Dress-Out Traits in E. modestus
3.4. Path Analysis of Morphological Traits on Dress-Out Traits in E. modestus
3.5. Regression Analysis of Morphological Traits on Dress-Out Traits in E. modestus
3.6. Model Validation and Cross-Validation for the AMW Trait in E. modestus
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chavanne, H.; Janssen, K.; Hofherr, J.; Contini, F.; Haffray, P.; Komen, H.; Nielsen, E.E.; Bargelloni, L. A comprehensive survey on selective breeding programs and seed market in the European aquaculture fish industry. Aquac. Int. 2016, 24, 1287–1307. [Google Scholar] [CrossRef]
- Wang, H.; Wang, L.; Shi, W.J.; Zhu, C.K.; Pan, Z.J.; Wu, N.; Qiang, J.; Xu, P. Estimates of heritability based on additive-dominance genetic analysis model in red swamp crayfish, Procambarus clarkii. Aquaculture 2019, 504, 1–6. [Google Scholar] [CrossRef]
- Campos-Montes, G.R.; Montaldo, H.H.; Armenta-Córdova, M.; Martínez-Ortega, A.; Caballero-Zamora, A.; Castillo-Juárez, H. Incorporation of tail weight and tail percentage at harvest size in selection programs for the Pacific white shrimp Penaeus (Litopenaeus) vannamei. Aquaculture 2017, 468, 293–296. [Google Scholar] [CrossRef]
- Neira, R.; Lhorente, J.P.; Araneda, C.; Díaz, N.; Bustos, E.; Alert, A. Studies on carcass quality traits in two populations of Coho salmon (Oncorhynchus kisutch): Phenotypic and genetic parameters. Aquaculture 2004, 241, 117–131. [Google Scholar] [CrossRef]
- Garcia, A.L.S.; de Oliveira, C.A.L.; Karim, H.M.; Sary, C.; Todesco, H.; Ribeiro, R.P. Genetic parameters for growth performance, fillet traits, and fat percentage of male Nile tilapia (Oreochromis niloticus). J. Appl. Genet. 2017, 58, 527–533. [Google Scholar] [CrossRef] [PubMed]
- Vandeputte, M.; Puledda, A.; Tyran, A.S.; Bestin, A.; Coulombet, C.; Bajek, A.; Baldit, G.; Vergnet, A.; Allal, F.; Bugeon, J.; et al. Investigation of morphological predictors of fillet and carcass yield in European sea bass (Dicentrarchus labrax) for application in selective breeding. Aquaculture 2017, 470, 40–49. [Google Scholar] [CrossRef]
- Yenmak, S.; Joerakate, W.; Poompuang, S. Prediction of fillet yield in hatchery populations of Asian sea bass, Lates calcarifer (Bloch, 1790) using body weight and measurements. Int. Aquat. Res. 2018, 10, 253–261. [Google Scholar] [CrossRef]
- Rutten, M.J.M.; Bovenhuis, H.; Komen, H. Modeling fillet traits based on body measurements in three Nile tilapia strains (Oreochromis niloticus L.). Aquaculture 2004, 231, 113–122. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Wang, L.; Guan, T.Y.; Chang, G.L.; Zhao, H.T.; Wu, N. Modeling the relationships of growth and morphometrics to dress-out traits in the oriental river prawn, Macrobrachium nipponense. Aquac. Rep. 2022, 26, 101295. [Google Scholar] [CrossRef]
- Sang, N.V.; Thomassen, M.; Klemetsdal, G.; Gjøen, H.M. Prediction of fillet weight, fillet yield, and fillet fat for live river catfish (Pangasianodon hypophthalmus). Aquaculture 2009, 288, 166–171. [Google Scholar] [CrossRef]
- Hung, D.; Nguyen, N.H. Modeling meat yield based on measurements of body traits in genetically improved giant freshwater prawn (GFP) Macrobrachium rosenbergii. Aquac. Int. 2014, 22, 619–631. [Google Scholar] [CrossRef]
- Oh, C.W.; Suh, H.L.; Park, K.Y.; Ma, C.W.; Lim, H.S. Growth and reproductive biology of the freshwater shrimp Exopalaemon modestus (Decapoda: Palaemonidae) in a lake of Korea. J. Crustac. Biol. 2002, 22, 357–366. [Google Scholar] [CrossRef]
- Guo, Z.L.; Wang, X.Q.; Zhang, J.P. On the genus Exopalaemon (Decapoda, Caridea, Palaemonidae) in Guangdong Province, southern China. Crustaceana 2005, 78, 839–850. Available online: https://www.jstor.org/stable/20107552 (accessed on 1 September 2025). [CrossRef]
- FAO. Fishery and Aquaculture Statistics—Yearbook 2022; FAO Yearbook of Fishery and Aquaculture Statistics; Food and Agriculture Organization of the United Nations: Rome, Italy, 2025; p. 161. [Google Scholar] [CrossRef]
- Deng, J.L. Introduction to grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Du, J.J.; Chen, Z.W. Carrying out path analysis by linear regression of SPSS. Bull. Biol. 2010, 45, 4–6. [Google Scholar]
- Wang, H.; Shi, W.J.; Wang, L.; Zhang, Y.; Zang, N.W.; Xue, C.P.; Chang, G.L.; Wu, N. Genetic determination of processing traits in the red swamp crayfish, Procambarus clarkii (Girard). Aquaculture 2020, 529, 735602. [Google Scholar] [CrossRef]
- Du, Z.; Hu, Y.G.; Buttar, N.A. Analysis of mechanical properties for tea stem using grey relational analysis coupled with multiple linear regression. Sci. Hortic. 2020, 260, 108886. [Google Scholar] [CrossRef]
- Yu, P.; Li, K. Grey correlation analysis of data on Microsoft Excel. Microcomput. Appl. 2011, 27, 29–30. [Google Scholar] [CrossRef]
- Yan, H.G.; Dong, Z.L.; Li, Y.; Ma, T.T.; Luo, H.; Ye, H.; He, W.P. Relationship Between Morphological Traits and Body Weight of Procypris rabaudi by Path Analysis and Grey Correlation Analysis. J. Southwest Univ. (Nat. Sci. Ed.) 2022, 44, 74–81. [Google Scholar] [CrossRef]
- Chen, Y.H.; Shao, Z.Y.; Zhou, G.L.; Hu, A.; Ding, H.B.; Li, H.Y.; Dong, Z.G.; Niu, D.H.; Li, J.L. Salinity tolerance assessment of different families of the razor clam Sinonovacula constricta using physiological traits. Aquaculture 2025, 595, 741494. [Google Scholar] [CrossRef]
- Li, J.L.; Qin, Q.; Tian, X.; Guo, J.R.; Tang, B.W.; He, Z.G.; Xie, Z.G.; Wang, Y.D.; Wang, D.W. Effects of Different Cultivation Modes on Morphological Traits and Correlations between Traits and Body Mass of Crayfish (Procambarus clarkii). Biology 2024, 13, 395. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.H.; Hu, Z.G.; Su, C.Q.; Yang, T.Z.; Li, C.X.; Cheng, H.X.; Tian, Y.; Guo, X.S. Correlations Between Morphometric Traits and Body Mass Among Different Geographical Populations of Wild Macrobrachium nipponense in Upper Reaches of the Huaihe River, China. Fishes 2025, 10, 413. [Google Scholar] [CrossRef]
- Yuan, Z.F.; Guo, M.C.; Song, S.D.; Xie, X.L.; Liu, J.J.; Du, J.L.; Dong, X.M. Multivariate Statistical Analysis, 3rd ed.; Science Press: Beijing, China, 2018; pp. 125–142. [Google Scholar]
- Chai, Z.; Luan, S.; Luo, K.; Kong, J.; Xu, S.Y. Correlation Analysis of Fillet Yield with Phenotypic Traits for Families from Conservation Population of Litopenaeus vannamei. Prog. Fish. Sci. 2015, 36, 63–70. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Q.C.; Yu, Y.; Zhang, C.S.; Huang, H.; Li, F.H.; Xiang, J.H. Correlation of morphometric attributes to net weight and fillet yield of Litopenaeus vannamei. Oceanol. Limnol. Sin. 2018, 49, 653–661. Available online: https://ols.iocasjournals.cn/thesisDetails#10.11693/hyhz20171100288&lang=zh (accessed on 1 September 2025). [CrossRef]
- Dai, P.; Li, D.Y.; Sui, J.; Kong, J.; Meng, X.H.; Luan, S. Prediction of meat yield in the Pacific whiteleg shrimp Penaeus vannamei. Aquaculture 2023, 577, 739914. [Google Scholar] [CrossRef]

| Trait | Training Group (n = 301) | Holdout Sample (n = 60) | ||||
|---|---|---|---|---|---|---|
| Mean | SD | CV% | Mean | SD | CV% | |
| BW (g) | 1.08 | 0.36 | 33.33 | 1.04 | 0.34 | 32.69 |
| BL (mm) | 42.51 | 4.56 | 10.73 | 42.31 | 5.12 | 12.10 |
| RL (mm) | 11.68 | 2.21 | 18.92 | 11.48 | 2.21 | 19.25 |
| CL (mm) | 10.48 | 1.44 | 13.74 | 10.41 | 1.59 | 15.27 |
| CW (mm) | 5.92 | 0.93 | 15.71 | 5.79 | 0.84 | 14.51 |
| CH (mm) | 6.34 | 0.89 | 14.04 | 6.22 | 0.75 | 12.06 |
| AL (mm) | 31.76 | 3.82 | 12.03 | 32.02 | 3.95 | 12.34 |
| AW (mm) | 5.69 | 0.81 | 14.24 | 5.61 | 0.77 | 13.73 |
| AH (mm) | 6.46 | 0.95 | 14.71 | 6.47 | 0.99 | 15.30 |
| FL (mm) | 9.36 | 1.19 | 12.71 | 9.19 | 1.32 | 14.36 |
| FW (mm) | 13.22 | 2.05 | 15.51 | 12.75 | 1.54 | 12.08 |
| TeL (mm) | 7.15 | 0.87 | 12.17 | 6.85 | 0.76 | 11.09 |
| TeW (mm) | 1.79 | 0.37 | 20.67 | 1.77 | 0.37 | 20.90 |
| TeH (mm) | 1.28 | 0.27 | 21.09 | 1.24 | 0.26 | 20.97 |
| AMW (g) | 0.51 | 0.18 | 35.29 | 0.49 | 0.18 | 36.73 |
| AMP (%) | 46.39 | 4.46 | 9.61 | 46.62 | 4.68 | 10.04 |
| Morphological Trait | AMW (n = 301) | AMP (n = 301) | ||
|---|---|---|---|---|
| Pi (±Standard Error) | VIF | Pi (±Standard Error) | VIF | |
| BW | 0.719 (±0.025) ** | 11.283 | −0.557 (±2.139) ** | 11.283 |
| BL | 0.083 (±0.002) | 11.564 | 0.262 (±0.172) | 11.564 |
| RL | −0.058 (±0.002) ** | 1.881 | −0.207 (±0.144) ** | 1.881 |
| CL | −0.039 (±0.027) | 3.305 | −0.125 (±0.293) | 3.305 |
| CW | 0.140 (±0.007) ** | 6.249 | 0.535 (±0.620) ** | 6.249 |
| CH | −0.018 (±0.007) | 5.778 | −0.128 (±0.625) | 5.778 |
| AL | 0.063 (±0.002) | 5.575 | 0.158 (±0.143) | 5.575 |
| AW | 0.016 (±0.007) | 4.590 | 0.061 (±0.609) | 4.59 |
| AH | 0.033 (±0.005) | 2.797 | 0.110 (±0.408) | 2.797 |
| FL | −0.021 (±0.003) | 2.199 | −0.078 (±0.287) | 2.199 |
| FW | 0.034 (±0.002) | 1.649 | 0.094 (±0.145) | 1.649 |
| TeL | −0.039 (±0.004) | 1.997 | −0.151 (±0.374) * | 1.997 |
| TeW | 0.029 (±0.010) | 1.860 | 0.058 (±0.864) | 1.860 |
| TeH | 0.007 (±0.012) | 1.480 | 0.070 (±1.047) | 1.480 |
| Morphological Trait | AMW (n = 301) | AMP (n = 301) | ||||
|---|---|---|---|---|---|---|
| Direct | Indirect | ∑ | Direct | Indirect | ∑ | |
| BW | 0.517 | 0.147 | 0.664 ** | 0.311 | −0.647 | −0.336 ** |
| BL | 0.007 | 0.114 | 0.121 * | 0.069 | −0.100 | −0.031 |
| RL | 0.003 | 0.001 | 0.004 | 0.043 | −0.072 | −0.029 |
| CL | 0.002 | 0.001 | 0.003 | 0.016 | −0.066 | −0.050 |
| CW | 0.020 | 0.026 | 0.046 | 0.286 | −0.184 | 0.102 ** |
| CH | 0.000 | 0.000 | 0.000 | 0.016 | −0.011 | 0.005 |
| AL | 0.004 | 0.007 | 0.011 | 0.025 | 0.006 | 0.031 |
| AW | 0.000 | 0.000 | 0.000 | 0.004 | 0.004 | 0.007 |
| AH | 0.001 | 0.001 | 0.002 | 0.012 | 0.004 | 0.016 |
| FL | 0.000 | 0.000 | 0.000 | 0.006 | −0.003 | 0.003 |
| FW | 0.001 | 0.001 | 0.002 | 0.009 | 0.003 | 0.012 |
| TeL | 0.001 | 0.001 | 0.002 | 0.023 | −0.001 | 0.022 |
| TeW | 0.001 | 0.001 | 0.002 | 0.003 | 0.001 | 0.004 |
| TeH | 0.000 | 0.000 | 0.000 | 0.005 | 0.000 | 0.005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Hu, Z.; Duan, C.; Zhang, R.; Liu, J.; Guo, X. Modeling Dress-Out Traits Based on Morphological Traits in the Siberian Prawn, Exopalaemon modestus (Heller, 1862). Fishes 2025, 10, 534. https://doi.org/10.3390/fishes10100534
Zhao L, Hu Z, Duan C, Zhang R, Liu J, Guo X. Modeling Dress-Out Traits Based on Morphological Traits in the Siberian Prawn, Exopalaemon modestus (Heller, 1862). Fishes. 2025; 10(10):534. https://doi.org/10.3390/fishes10100534
Chicago/Turabian StyleZhao, Liangjie, Zhiguo Hu, Congying Duan, Ru Zhang, Jiahui Liu, and Xusheng Guo. 2025. "Modeling Dress-Out Traits Based on Morphological Traits in the Siberian Prawn, Exopalaemon modestus (Heller, 1862)" Fishes 10, no. 10: 534. https://doi.org/10.3390/fishes10100534
APA StyleZhao, L., Hu, Z., Duan, C., Zhang, R., Liu, J., & Guo, X. (2025). Modeling Dress-Out Traits Based on Morphological Traits in the Siberian Prawn, Exopalaemon modestus (Heller, 1862). Fishes, 10(10), 534. https://doi.org/10.3390/fishes10100534






