Aspects of Biology and Machine Learning for Age Prediction in the Large-Eye Dentex Dentex macrophthalmus (Bloch, 1791)
Abstract
1. Introduction
2. Materials and Methods
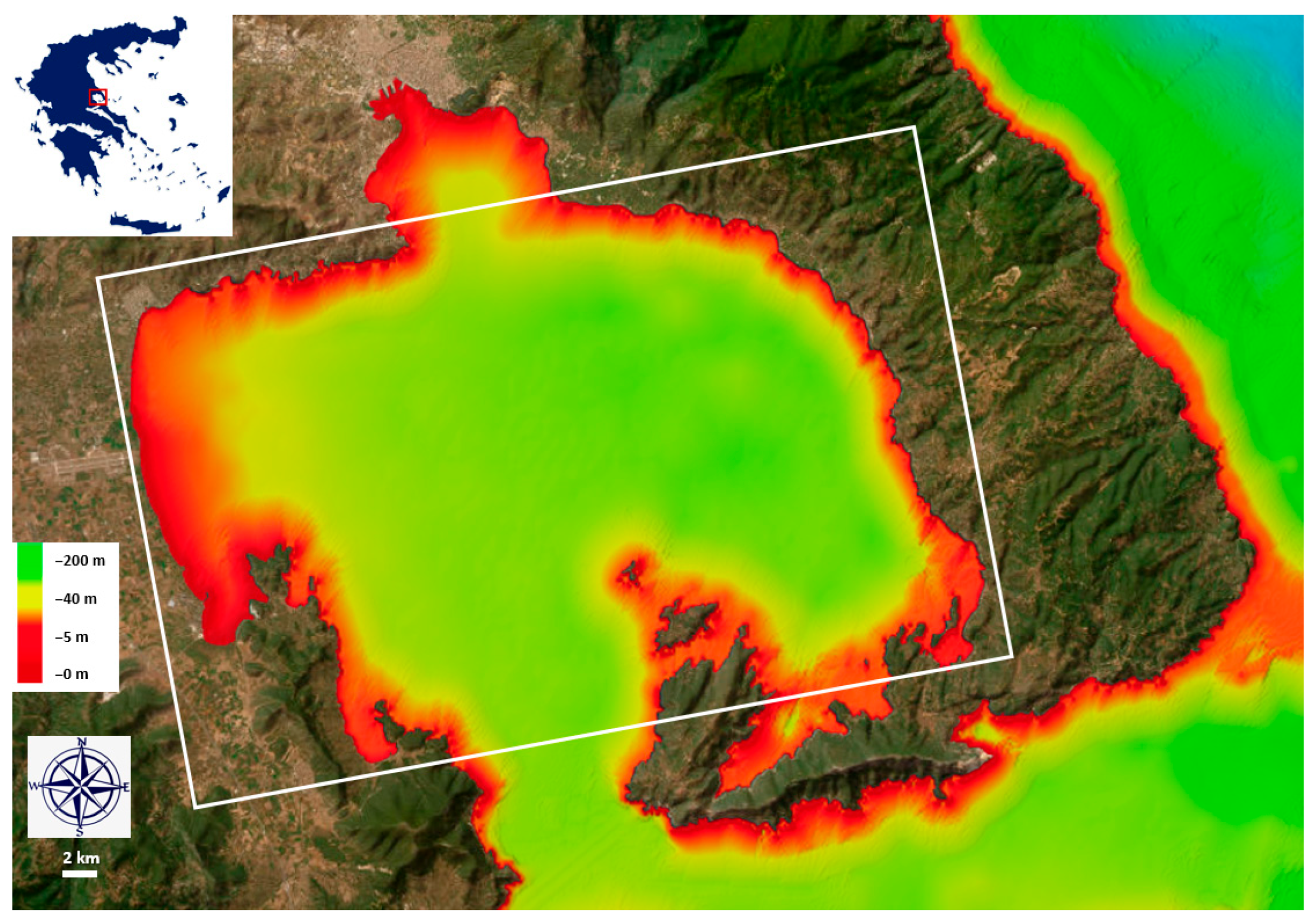
2.1. Study Area and Sampling Methodology
2.2. Otolith Extraction Morphometry and Age Classification
2.3. Statistical Analysis
2.4. Age Composition, Growth, Mortality and Exploitation Rate
2.5. Description of ML Algorithms
2.5.1. Neural Network
2.5.2. Stochastic Gradient Descent
2.5.3. Support Vector Machine (SVM)
2.5.4. Random Forest
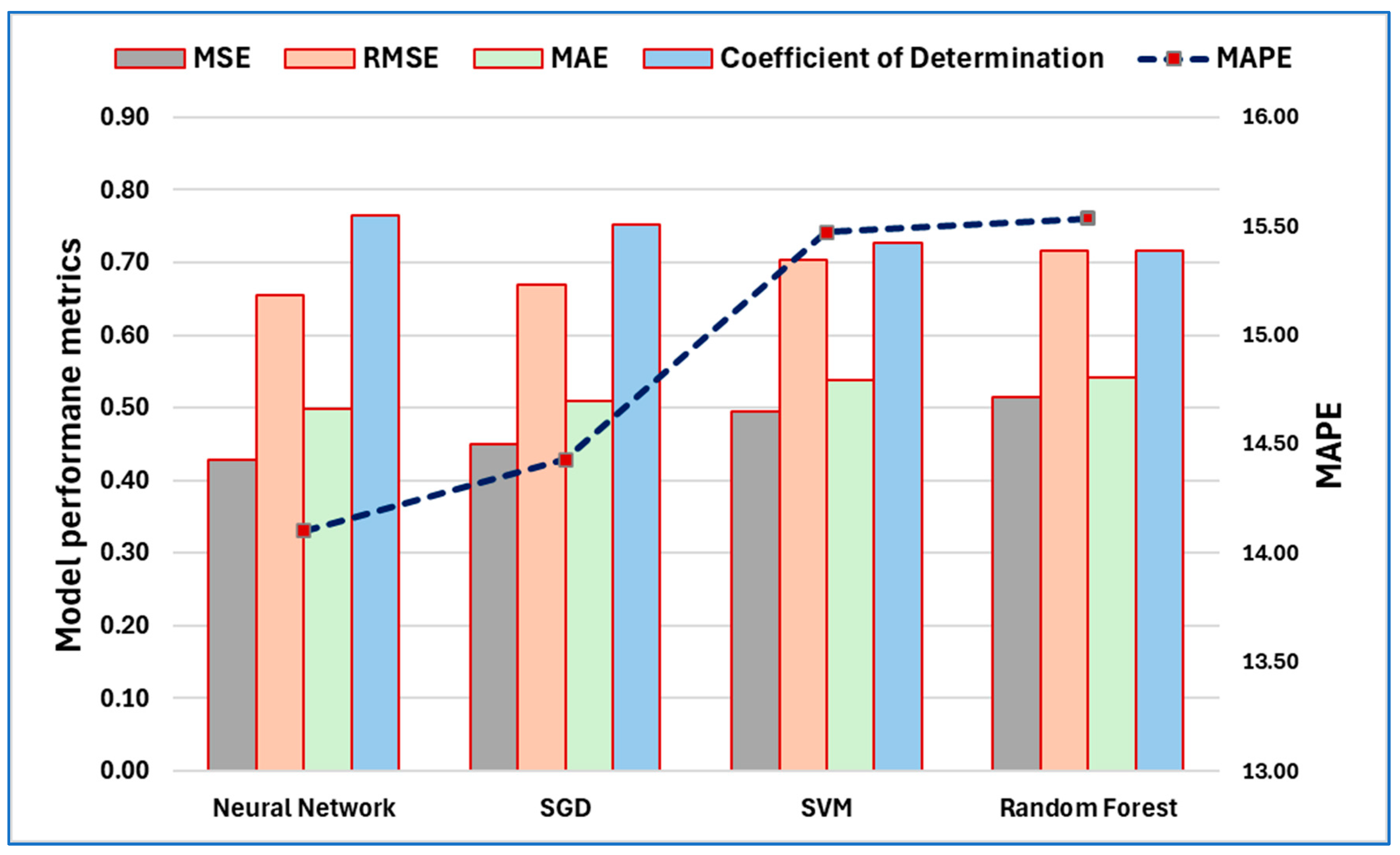
2.6. Assessment of Model Performance
2.6.1. Mean Square Error (MSE)
2.6.2. Root Mean Square Error (RMSE)
2.6.3. Mean Absolute Error (MAE)
2.6.4. Mean Absolute Percentage Error (MAPE)
2.6.5. Coefficient of Determination (R2)
3. Results
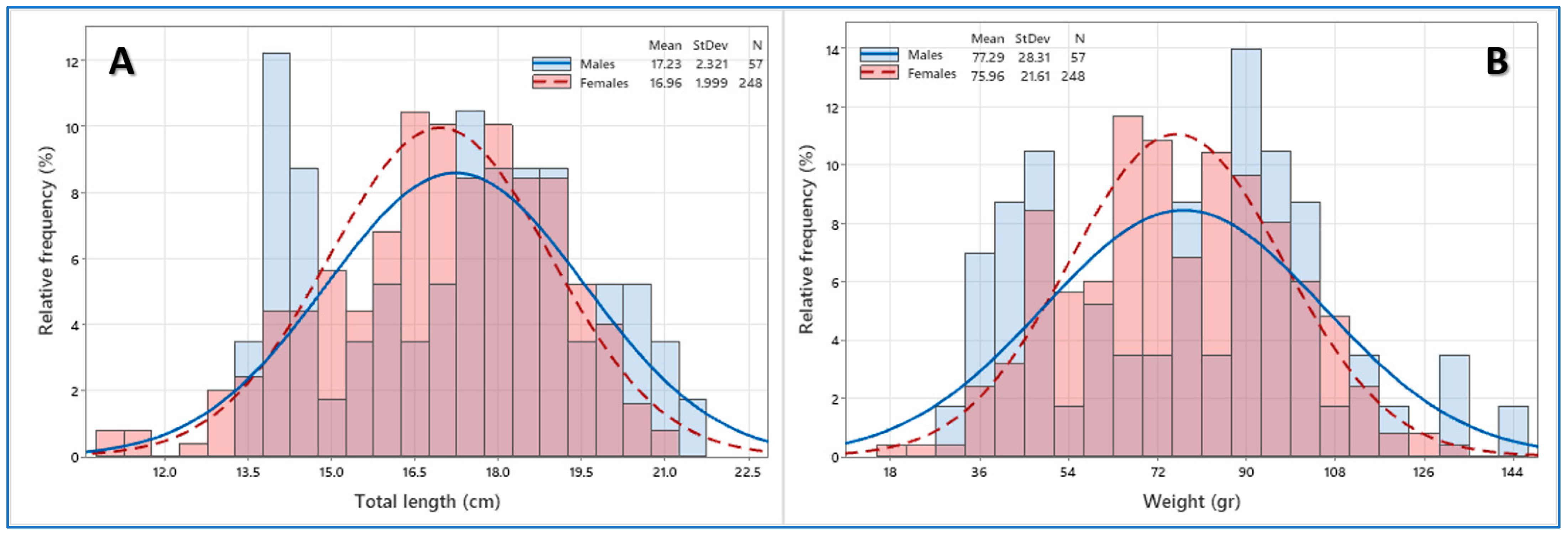
3.1. Population Structure
3.2. Spatial Distribution
3.3. Age Composition, Growth, Mortality and Exploitation Rate
3.4. Inter-Reder Precision and Agreement
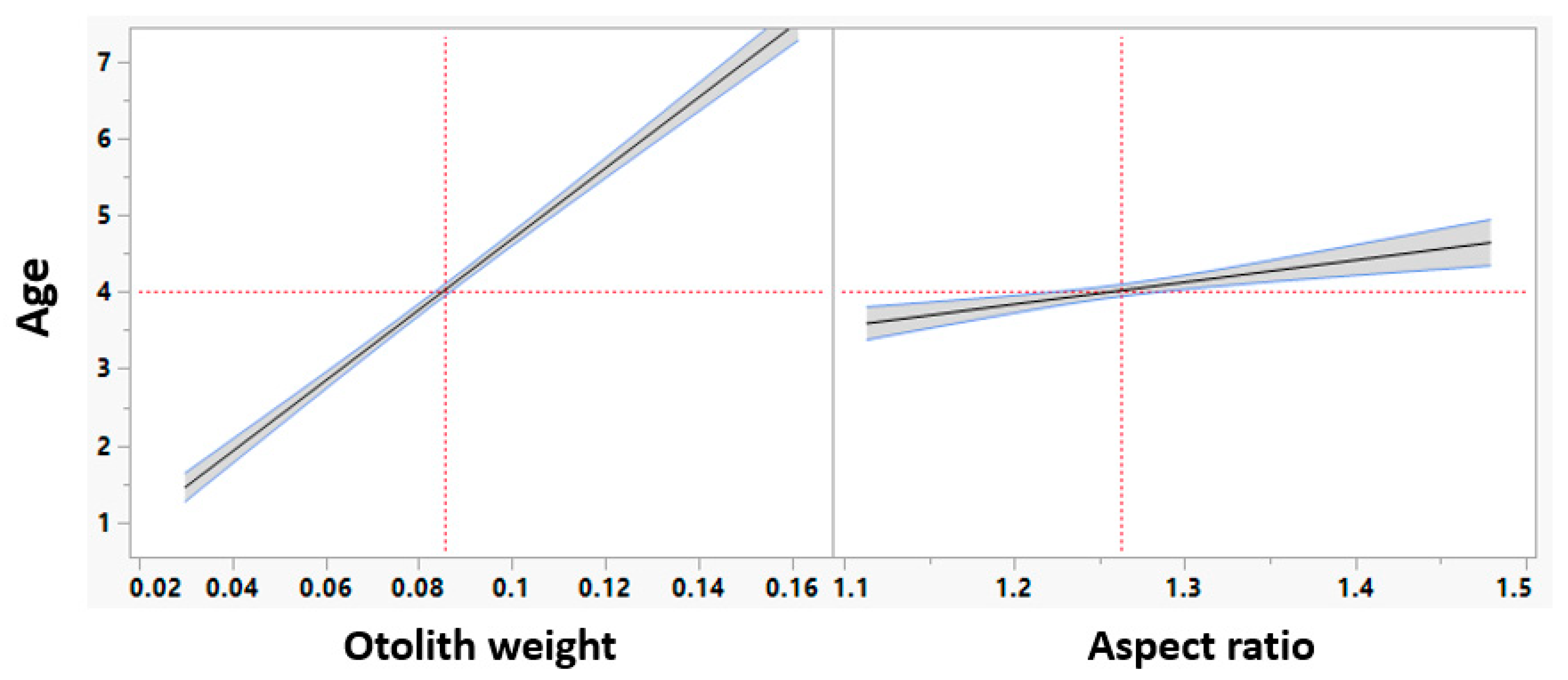
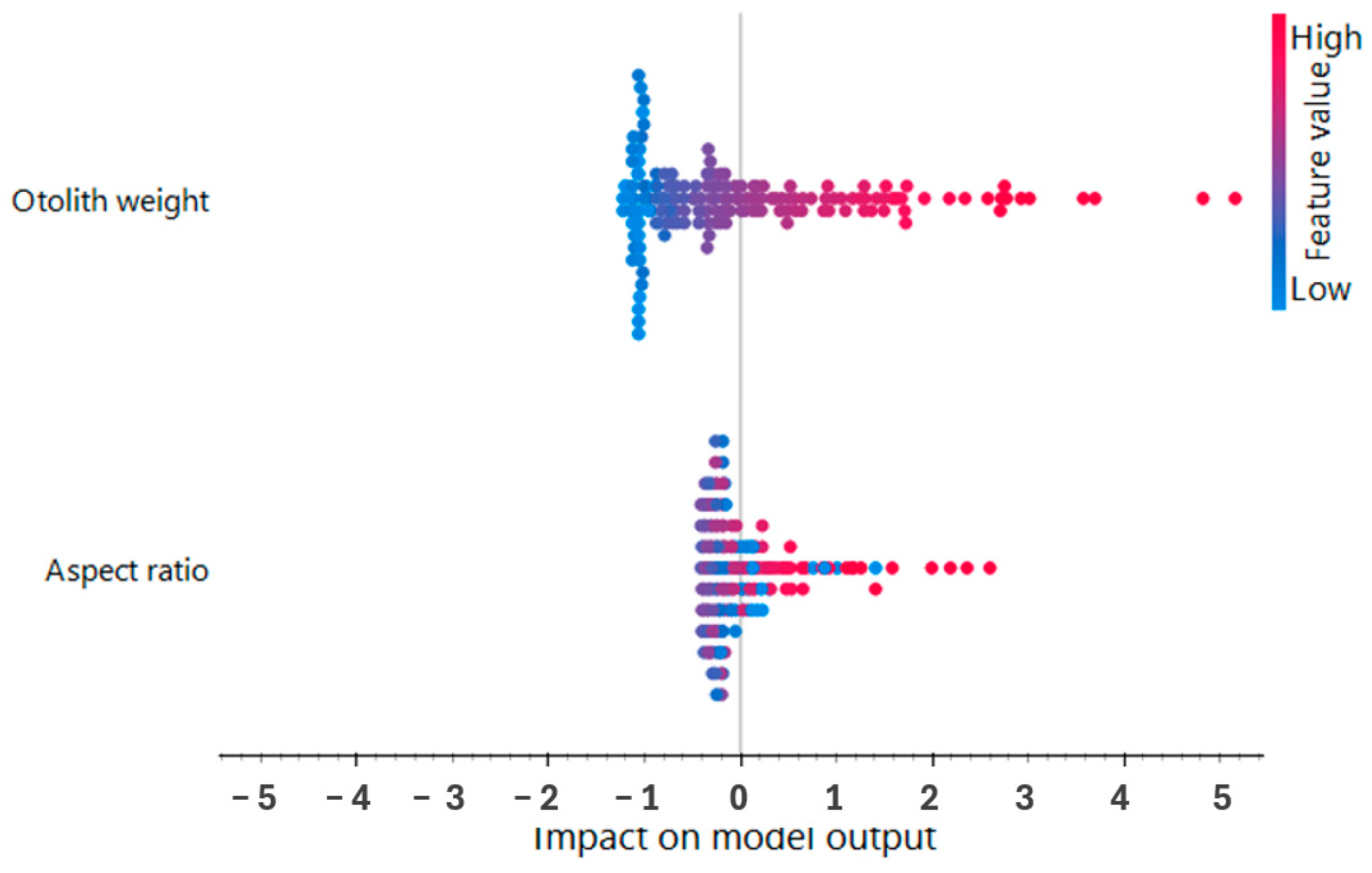
3.5. Machine Learning
3.6. Machine Learning Model Performance Assessment
4. Discussion
4.1. Length Distributions and Length–Weight Relationships
4.2. Age and Growth
4.3. Mortality, Exploitation Rates, and Length at First Capture
4.4. Machine Learning Models for Age Prediction
4.5. Study Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- FAO. The State of World Fisheries and Aquaculture 2024—Blue Transformation in Action; FAO: Rome, Italy, 2024. [Google Scholar] [CrossRef]
- Lloret, J.; Muñoz, M.; Casadevall, M. Threats Posed by Artisanal Fisheries to the Reproduction of Coastal Fish Species in a Mediterranean Marine Protected Area. Estuar. Coast. Shelf Sci. 2012, 113, 133–140. [Google Scholar] [CrossRef]
- Christensen, V.; Coll, M.; Piroddi, C.; Steenbeek, J.; Buszowski, J.; Pauly, D. A Century of Fish Biomass Decline in the Ocean. Mar. Ecol. Prog. Ser. 2014, 512, 155–166. [Google Scholar] [CrossRef]
- Leleu, K.; Pelletier, D.; Charbonnel, E.; Letourneur, Y.; Alban, F.; Bachet, F.; Boudouresque, C.F. Métiers, Effort and Catches of a Mediterranean Small-Scale Coastal Fishery: The Case of the Côte Bleue Marine Park. Fish. Res. 2014, 154, 93–101. [Google Scholar] [CrossRef]
- McClanahan, T.R.; Mangi, S.C. Gear—Based Management of a Tropical Artisanal Fishery Based on Species Selectivity and Capture Size. Fish. Manag. Ecol. 2004, 11, 51–60. [Google Scholar] [CrossRef]
- Humphries, A.T.; Gorospe, K.D.; Carvalho, P.G.; Yulianto, I.; Kartawijaya, T.; Campbell, S.J. Catch Composition and Selectivity of Fishing Gears in a Multi-Species Indonesian Coral Reef Fishery. Front. Mar. Sci. 2019, 6, 378. [Google Scholar] [CrossRef]
- Hiddink, J.G.; Jennings, S.; Sciberras, M.; Szostek, C.L.; Hughes, K.M.; Ellis, N.; Rijnsdorp, A.D.; McConnaughey, R.A.; Mazor, T.; Hilborn, R.; et al. Global Analysis of Depletion and Recovery of Seabed Biota after Bottom Trawling Disturbance. Proc. Natl. Acad. Sci. USA 2017, 114, 8301–8306. [Google Scholar] [CrossRef]
- Pusceddu, A.; Bianchelli, S.; Martín, J.; Puig, P.; Palanques, A.; Masqué, P.; Danovaro, R. Chronic and Intensive Bottom Trawling Impairs Deep-Sea Biodiversity and Ecosystem Functioning. Proc. Natl. Acad. Sci. USA 2014, 111, 8861–8866. [Google Scholar] [CrossRef]
- Hinz, H.; Prieto, V.; Kaiser, M.J. Trawl Disturbance on Benthic Communities: Chronic Effects and Experimental Predictions. Ecol. Appl. 2009, 19, 761–773. [Google Scholar] [CrossRef]
- Bănaru, D.; Harmelin-Vivien, M.; Boudouresque, C.F. Man Induced Change in Community Control in the North-Western Black Sea: The Top-down Bottom-up Balance. Mar. Environ. Res. 2010, 69, 262–275. [Google Scholar] [CrossRef]
- Myers, R.A.; Worm, B. Rapid Worldwide Depletion of Predatory Fish Communities. Nature 2003, 423, 280–283. [Google Scholar] [CrossRef]
- Touloumis, K.; Tsikliras, A.C.; Dimarchopoulou, D. The Cascading Effect of Fishing down Marine Top Predators in the Northeastern Mediterranean Sea. Discov. Ocean. 2025, 2, 22. [Google Scholar] [CrossRef]
- Piroddi, C.; Coll, M.; Liquete, C.; Macias, D.; Greer, K.; Buszowski, J.; Steenbeek, J.; Danovaro, R.; Christensen, V. Historical Changes of the Mediterranean Sea Ecosystem: Modelling the Role and Impact of Primary Productivity and Fisheries Changes over Time. Sci. Rep. 2017, 7, 44491. [Google Scholar] [CrossRef]
- Boudouresque, C.F. Marine Biodiversity—Warming vs. Biological Invasions and Overfishing in the Mediterranean Sea: Take Care, ‘One Train Can Hide Another’. MOJ Ecol. Environ. Sci. 2017, 2, 172–183. [Google Scholar] [CrossRef]
- Coll, M.; Piroddi, C.; Steenbeek, J.; Kaschner, K.; Ben Rais Lasram, F.; Aguzzi, J.; Ballesteros, E.; Bianchi, C.N.; Corbera, J.; Dailianis, T. The Biodiversity of the Mediterranean Sea: Estimates, Patterns, and Threats. PLoS ONE 2010, 5, e11842. [Google Scholar] [CrossRef] [PubMed]
- Nauen, C.E. When Mediterranean Artisanal Fishers Protect Coastal Ecosystems. Fishes 2024, 9, 472. [Google Scholar] [CrossRef]
- Cömert, N.; Deniz, T.; Göktürk, D. Sustainable Fisheries and Non-Target Species Management: A Seasonal and Depth-Based Study in the Deep-Sea Fisheries of Antalya Bay. Sustainability 2025, 17, 5040. [Google Scholar] [CrossRef]
- Caddy, J.F. Options for the Regulation of Mediterranean Demersal Fisheries. Nat. Resour. Model. 1990, 4, 427–475. [Google Scholar] [CrossRef]
- Papaconstantinou, C.; Farrugio, H. Fisheries in the Mediterranean. Mediterr. Mar. Sci. 2000, 1, 5–18. [Google Scholar] [CrossRef]
- Stergiou, K.I.; Somarakis, S.; Triantafyllou, G.; Tsiaras, K.P.; Giannoulaki, M.; Petihakis, G.; Machias, A.; Tsikliras, A.C. Trends in Productivity and Biomass Yields in the Mediterranean Sea Large Marine Ecosystem during Climate Change. Environ. Dev. 2016, 17, 57–74. [Google Scholar] [CrossRef]
- Fiorentino, F.; Vitale, S. How Can We Reduce the Overexploitation of the Mediterranean Resources? Front. Mar. Sci. 2021, 8, 674633. [Google Scholar] [CrossRef]
- FAO. The State of World Fisheries and Aquaculture 2020; Sustainability in Action; General Fisheries Commission for the Mediterranean: Rome, Italy, 2020. [Google Scholar] [CrossRef]
- Colloca, F.; Cardinale, M.; Maynou, F.; Giannoulaki, M.; Scarcella, G.; Jenko, K.; Bellido, J.M.; Fiorentino, F. Rebuilding Mediterranean Fisheries: A New Paradigm for Ecological Sustainability. Fish Fish. 2013, 14, 89–109. [Google Scholar] [CrossRef]
- Sumaila, U.R.; Bellmann, C.; Tipping, A. Fishing for the Future: An Overview of Challenges and Opportunities. Mar. Policy 2016, 69, 173–180. [Google Scholar] [CrossRef]
- Kondylatos, G.; Theocharis, A.; Mandalakis, M.; Avgoustinaki, M.; Karagyaurova, T.; Koulocheri, Z.; Vardali, S.; Klaoudatos, D. The Devil Firefish Pterois miles (Bennett, 1828): Life History Traits of a Potential Fishing Resource in Rhodes (Eastern Mediterranean). Hydrobiology 2024, 3, 31–50. [Google Scholar] [CrossRef]
- Blanco, M.; Sotelo, C.G.; Chapela, M.J.; Pérez-Martín, R.I. Towards Sustainable and Efficient Use of Fishery Resources: Present and Future Trends. Trends Food Sci. Technol. 2007, 18, 29–36. [Google Scholar] [CrossRef]
- Gracia, A.; Vázquez-Bader, A.R.; Lozano-Alvarez, E.; Briones-Fourzán, P. Deep-Water Shrimp (Crustacea: Penaeoidea) Off the Yucatan Peninsula (Southern Gulf of Mexico): A Potential Fishing Resource? J. Shellfish Res. 2010, 29, 37–43. [Google Scholar] [CrossRef]
- Paramo, J.; Saint-Paul, U. Deep-Sea Shrimps Aristaeomorpha foliacea and Pleoticus robustus (Crustacea: Penaeoidea) in the Colombian Caribbean Sea as a New Potential Fishing Resource. J. Mar. Biol. Assoc. United Kingdom 2012, 92, 811–818. [Google Scholar] [CrossRef]
- Harrington, J.M.; Myers, R.A.; Rosenberg, A.A. Wasted Fishery Resources: Discarded by-Catch in the USA. Fish Fish. 2005, 6, 350–361. [Google Scholar] [CrossRef]
- Corrales, X.; Coll, M.; Ofir, E.; Heymans, J.J.; Steenbeek, J.; Goren, M.; Edelist, D.; Gal, G. Future Scenarios of Marine Resources and Ecosystem Conditions in the Eastern Mediterranean under the Impacts of Fishing, Alien Species and Sea Warming. Sci. Rep. 2018, 8, 14284. [Google Scholar] [CrossRef]
- Parenti, P. An Annotated Checklist of the Fishes of the Family Sparidae. FishTaxa 2019, 4, 47–98. [Google Scholar]
- Bargelloni, L.; Alarcon, J.A.; Alvarez, M.C.; Penzo, E.; Magoulas, A.; Reis, C.; Patarnello, T. Discord in the Family Sparidae (Teleostei): Divergent Phylogeographical Patterns across the Atlantic–Mediterranean Divide. J. Evol. Biol. 2003, 16, 1149–1158. [Google Scholar] [CrossRef]
- Hanel, R.; Tsigenopoulos, C.S. Phylogeny, Evolution and Taxonomy of Sparids with Some Notes on Their Ecology and Biology. In Sparidae; Pavlidis, M.A., Mylonas, C.C., Eds.; Wiley: Hoboken, NJ, USA, 2011; pp. 51–73. ISBN 978-1-4051-9772-4 978-1-4443-9221-0. [Google Scholar]
- Vandewalle, P.; Parmentier, É.; Chardon, M. The Branchial Basket in Teleost Feeding. Cybium 2000, 24, 319–342. [Google Scholar]
- Antonucci, F.; Costa, C.; Aguzzi, J.; Cataudella, S. Ecomorphology of Morpho—Functional Relationships in the Family of Sparidae: A Quantitative Statistic Approach. J. Morphol. 2009, 270, 843–855. [Google Scholar] [CrossRef]
- De Azevedo, A.M.; Fontanillas, R.; Owen, M.A.G.; Busti, S.; Parma, L.; Bonaldo, A.; Witten, P.E.; Huysseune, A. A Quantitative Analysis of Gilthead Seabream (Sparus aurata) Juvenile Dentition as a Tool to Assess the Effect of Diet. Can. J. Zool. 2021, 99, 548–556. [Google Scholar] [CrossRef]
- Theocharis, A.; Vardali, S.; Klaoudatos, D. Age, Growth, and Mortality of the Common Pandora (Pagellus erythrinus, L. 1758) in the Central Aegean Sea: Insights into Population Dynamics. Fishes 2025, 10, 160. [Google Scholar] [CrossRef]
- Marguin, A.; Bussotti, S.; Guidetti, P.; Rossi, F. A Systematic Review of Fishing Impacts on the Trophic Level of Fish Populations and Assemblages in the Mediterranean Sea. Front. Mar. Sci. 2025, 12, 1489965. [Google Scholar] [CrossRef]
- Clottey, M.N.K.; Aggrey-Fynn, J.; Blay, J.; Kwasi Arizi, E. Stock Assessment and Reproductive Biology of Bluespotted Seabream Pagrus caeruleostictus (Family: Sparidae). Aquac. Fish Fish. 2024, 4, e163. [Google Scholar] [CrossRef]
- Parker, D.; Winker, H.; Attwood, C.; Kerwath, S. Dark Times for Dageraad Chrysoblephus cristiceps: Evidence for Stock Collapse. African J. Mar. Sci. 2016, 38, 341–349. [Google Scholar] [CrossRef]
- Oosthuizen, C.; Mann, B.; Bloomer, P.; Hoareau, T. Genetic Consequences in the Southern African Endemic Seabream Polysteganus undulosus (Sparidae) after Eight Decades of Overfishing. African J. Mar. Sci. 2024, 46, 205–216. [Google Scholar] [CrossRef]
- Soykan, O.; Ilkyaz, A.; Metin, G.; Kınacıgil, H.T. Growth and Reproduction of Boops boops, Dentex macrophthalmus, Diplodus vulgaris, and Pagellus acarne (Actinopterygii: Perciformes: Sparidae) from East-Central Aegean Sea, Turkey. Acta Ichthyol. Piscat. 2015, 45, 39–55. [Google Scholar] [CrossRef]
- Potts, W.M.; Inácio, L.A.; Santos, C.V.; Richardson, T.J.; Sauer, W.H. Aspects of the Biology and Fisheries of an Economically Important Sparid Dentex macrophthalmus (Bloch 1791) in the Namibe Province, Angola. African J. Mar. Sci. 2010, 32, 601–611. [Google Scholar] [CrossRef]
- FishBase Dentex Macrophthalmus (Bloch, 1791) Large-Eye Dentex. Available online: https://www.fishbase.se/FieldGuide/FieldGuideSummary.php?GenusName=Dentex&SpeciesName=macrophthalmus&pda=1&sps= (accessed on 26 August 2025).
- Ulman, A.; Zengin, M.; Demirel, N.; Pauly, D. The Lost Fish of Turkey: A Recent History of Disappeared Species and Commercial Fishery Extinctions for the Turkish Marmara and Black Seas. Front. Mar. Sci. 2020, 7, 650. [Google Scholar] [CrossRef]
- Roussos, E.; Triantaphyllidis, G.; Ilia, V.; Tsagarakis, K.; Machias, A.; Tziveleka, L.-A.; Roussis, V.; Ioannou, E.; Kotzamanis, Y. Status of Fishery Discards and By-Products in Greece and Potential Valorization Scenarios towards a National Exploitation Master Plan. Mar. Drugs 2024, 22, 264. [Google Scholar] [CrossRef] [PubMed]
- Tsikliras, A.C.; Touloumis, K.; Pardalou, A.; Adamidou, A.; Keramidas, I.; Orfanidis, G.A.; Dimarchopoulou, D.; Koutrakis, M. Status and Exploitation of 74 Un-Assessed Demersal Fish and Invertebrate Stocks in the Aegean Sea (Greece) Using Abundance and Resilience. Front. Mar. Sci. 2021, 7, 578601. [Google Scholar] [CrossRef]
- Kilongo, K.; Barros, P.; Diehdiou, M. Diet of Large-Eye Dentex Dentex macrophthalmus (Pisces: Sparidae) off Angola and Namibia. African J. Mar. Sci. 2007, 29, 49–54. [Google Scholar] [CrossRef]
- Fernández-Corredor, E.; Fuster-Alonso, A.; Ramírez, F.; Giménez, J.; García-Barcelona, S.; Macías, D.; Coll, M.; Navarro, J. Environmental and Human Factors Shape the Trophic Ecology of a Widespread Marine Predator. J. Anim. Ecol. 2025, 94, 1784–1799. [Google Scholar] [CrossRef]
- Bizzarro, J.J.; Field, J.C.; Santora, J.A.; Curtis, K.A.; Wells, B.K. Trophic Guilds of Marine Predators in the California Current Large Marine Ecosystem. Front. Mar. Sci. 2023, 10, 1195000. [Google Scholar] [CrossRef]
- Tuset, V.M.; Lozano, I.J.; González, J.A.; Pertusa, J.F.; García-Díaz, M.M. Shape Indices to Identify Regional Differences in Otolith Morphology of Comber, Serranus cabrilla (L., 1758). J. Appl. Ichthyol. 2003, 19, 88–93. [Google Scholar] [CrossRef]
- Moore, B.R.; Parker, S.J.; Pinkerton, M.H. Otolith Shape as a Tool for Species Identification of the Grenadiers Macrourus caml and M. whitsoni. Fish. Res. 2022, 253, 106370. [Google Scholar] [CrossRef]
- Tuset, V.M.; Lombarte, A.; González, J.A.; Pertusa, J.F.; Lorente, M.A.J. Comparative Morphology of the Sagittal Otolith in Serranus spp. J. Fish Biol. 2003, 63, 1491–1504. [Google Scholar] [CrossRef]
- Russ, J.C. Computer-Assisted Microscopy: The Measurement and Analysis of Images; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; ISBN 1461305632. [Google Scholar]
- Carbonara, P.; Follesa, M.C. Handbook on Fish Age Determination: A Mediterranean Experience. Gen. Fish. Comm. Mediterr. Stud. Rev. 2019, 98, 1–179. [Google Scholar]
- Campana, S. Accuracy, Precision and Quality Control in Age Determination, Including a Review of the Use and Abuse of Age Validation Methods. J. Fish Biol. 2001, 59, 197–242. [Google Scholar] [CrossRef]
- Chang, W.Y.B. A Statistical Method for Evaluating the Reproducibility of Age Determination. Can. J. Fish. Aquat. Sci. 1982, 39, 1208–1210. [Google Scholar] [CrossRef]
- Kimura, D.K. Between-Reader Bias and Variability in the Age-Determination Process. Fish. Bull. 1991, 89, 53–61. [Google Scholar]
- Bowker, A.H. A Test for Symmetry in Contingency Tables. J. Am. Stat. Assoc. 1948, 43, 572–574. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J. A Coefficient of Agreement for Nominal Scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Landis, J.R.; Koch, G.G. The Measurement of Observer Agreement for Categorical Data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [PubMed]
- Morgenthaler, S. Exploratory Data Analysis. Wiley Interdiscip. Rev. Comput. Stat. 2009, 1, 33–44. [Google Scholar] [CrossRef]
- Hampton, R.E.; Havel, J.E. Introductory Biological Statistics; Waveland Press: Long Grove, IL, USA, 2006; ISBN 1577663802. [Google Scholar]
- Krishnamoorthy, K.; Lu, F.; Mathew, T. A Parametric Bootstrap Approach for ANOVA with Unequal Variances: Fixed and Random Models. Comput. Stat. Data Anal. 2007, 51, 5731–5742. [Google Scholar] [CrossRef]
- Şahin, M.; Aybek, E. Jamovi: An Easy to Use Statistical Software for the Social Scientists. Int. J. Assess. Tools Educ. 2019, 6, 670–692. [Google Scholar] [CrossRef]
- Rolke, W.; Gongora, C.G. A Chi-Square Goodness-of-Fit Test for Continuous Distributions against a Known Alternative. Comput. Stat. 2021, 36, 1885–1900. [Google Scholar] [CrossRef]
- Munro, J.L.; Pauly, D. A Simple Method for Comparing the Growth of Fishes and Invertebrates. Fishbyte 1983, 1, 5–6. [Google Scholar]
- Zar, J.H. Biostatistical Analysis, 5th ed.; Pearson Education: Chennai, India, 2014; ISBN 1-292-02404-6. [Google Scholar]
- Sall, J.; Stephens, M.L.; Lehman, A.; Loring, S. JMP Start Statistics: A Guide to Statistics and Data Analysis Using JMP; Sas Institute: Cary, NC, USA, 2017; ISBN 1629608785. [Google Scholar]
- Pebesma, E. Simple Features for R: Standardized Support for Spatial Vector Data. R. J. 2018, 10, 439–446. [Google Scholar] [CrossRef]
- Wickham, H. Data Analysis. In ggplot2: Elegant Graphics for Data Analysis; Springer: Berlin/Heidelberg, Germany, 2016; pp. 189–201. [Google Scholar]
- Amante, C.; Eakins, B.W. ETOPO1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis. 2009. Available online: https://www.ncei.noaa.gov/access/metadata/landing-page/bin/iso?id=gov.noaa.ngdc.mgg.dem:316 (accessed on 1 September 2025).
- Patterson, T.; Kelso, N.V. Natural Earth. Available online: https://www.naturalearthdata.com/ (accessed on 17 July 2025).
- Akima, H. A Method of Bivariate Interpolation and Smooth Surface Fitting for Irregularly Distributed Data Points. ACM Trans. Math. Softw. 1978, 4, 148–159. [Google Scholar] [CrossRef]
- Campitelli, E. MetR: Tools for Easier Analysis of Meteorological Fields. R Package. 2021. Available online: https://eliocamp.github.io/metR/reference/metR.html (accessed on 1 September 2025).
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016; ISBN 978-3-319-24277-4. Available online: https://ggplot2.tidyverse.org (accessed on 1 September 2025).
- Petitgas, P. Geostatistics for Fish Stock Assessments: A Review and an Acoustic Application. ICES J. Mar. Sci. 1993, 50, 285–298. [Google Scholar] [CrossRef]
- Von Bertalanffy, L. A Quantitative Theory of Organic Growth (Inquiries on Growth Laws. II). Hum. Biol. 1938, 10, 181–213. [Google Scholar]
- Haddon, M. Modelling and Quantitative Methods in Fisheries, 2nd ed.; Chapman and Hall/CRC: New York, NY, USA, 2011; ISBN 0429109490. [Google Scholar]
- Cerrato, R.M. Interpretable Statistical Tests for Growth Comparisons Using Parameters in the von Bertalanffy Equation. Can. J. Fish. Aquat. Sci. 1990, 47, 1416–1426. [Google Scholar] [CrossRef]
- Pauly, D. Some Simple Methods for the Assessment of Tropical Fish Stocks; FAO: Rome, Italy, 1983; ISBN 9251013330. [Google Scholar]
- Then, A.Y.; Hoenig, J.M.; Hall, N.G.; Hewitt, D.A. Evaluating the Predictive Performance of Empirical Estimators of Natural Mortality Rate Using Information on over 200 Fish Species. ICES J. Mar. Sci. 2015, 72, 82–92. [Google Scholar] [CrossRef]
- Sparre, P.; Ursin, A.; Venema, S.C. Introduction to Tropical Fish Stock Assessment, Manual. Part 1; FAO Fish. Technical Paper 306; FAO: Rome, Italy, 1989; p. 218. [Google Scholar]
- Froese, R.; Binohlan, C. Empirical Relationships to Estimate Asymptotic Length, Length at First Maturity and Length at Maximum Yield per Recruit in Fishes, with a Simple Method to Evaluate Length Frequency Data. J. Fish Biol. 2000, 56, 758–773. [Google Scholar] [CrossRef]
- Hoggarth, D. Stock Assessment for Fishery Management: A Framework Guide to the Stock Assessment Tools of the Fisheries Management and Science Programme; Food and Agriculture Organization: Rome, Italy, 2006; ISBN 9251055033. [Google Scholar]
- Pauly, D. Theory and Management of Tropical Multispecies Stocks: A Review, with Emphasis on the Southeast Asian Demersal Fisheries. 1979. Available online: https://digitalarchive.worldfishcenter.org/server/api/core/bitstreams/928bc397-ff93-4572-aac0-af3cf5ccd34d/content (accessed on 30 September 2025).
- Demšar, J.; Curk, T.; Erjavec, A.; Gorup, Č.; Hočevar, T.; Milutinovič, M.; Možina, M.; Polajnar, M.; Toplak, M.; Starič, A.; et al. Orange: Data Mining Toolbox in Python. J. Mach. Learn. Res. 2013, 14, 2349–2353. [Google Scholar]
- Zhu, J.-J.; Yang, M.; Ren, Z.J. Machine Learning in Environmental Research: Common Pitfalls and Best Practices. Environ. Sci. Technol. 2023, 57, 17671–17689. [Google Scholar] [CrossRef]
- Wallisch, P.; Lusignan, M.E.; Benayoun, M.D.; Baker, T.I.; Dickey, A.S.; Hatsopoulos, N.G. Chapter 36—Neural Networks Part I: Unsupervised Learning, 2nd ed.; Wallisch, P., Lusignan, M.E., Benayoun, M.D., Baker, T.I., Dickey, A.S., Hatsopoulos, N.G.B.T.-M., Eds.; Academic Press: San Diego, CA, USA, 2014; pp. 489–500. ISBN 978-0-12-383836-0. [Google Scholar]
- Politikos, D.V.; Petasis, G.; Chatzispyrou, A.; Mytilineou, C.; Anastasopoulou, A. Automating Fish Age Estimation Combining Otolith Images and Deep Learning: The Role of Multitask Learning. Fish. Res. 2021, 242, 106033. [Google Scholar] [CrossRef]
- Politikos, D.V.; Sykiniotis, N.; Petasis, G.; Dedousis, P.; Ordoñez, A.; Vabø, R.; Anastasopoulou, A.; Moen, E.; Mytilineou, C.; Salberg, A.-B. DeepOtolith v1. 0: An Open-Source AI Platform for Automating Fish Age Reading from Otolith or Scale Images. Fishes 2022, 7, 121. [Google Scholar] [CrossRef]
- Ruder, S. An Overview of Gradient Descent Optimization Algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Bottou, L. Stochastic Gradient Descent Tricks. In Neural Networks: Tricks of the Trade: Second Edition; Springer: Berlin/Heidelberg, Germany, 2012; pp. 421–436. [Google Scholar]
- Noble, W.S. What Is a Support Vector Machine? Nat. Biotechnol. 2006, 24, 1565–1567. [Google Scholar] [CrossRef] [PubMed]
- Pisner, D.A.; Schnyer, D.M. Chapter 6—Support Vector Machine; Mechelli, A., Vieira, S.B.T.-M.L., Eds.; Academic Press: San Diego, CA, USA, 2020; pp. 101–121. ISBN 978-0-12-815739-8. [Google Scholar]
- Ben-Hur, A.; Weston, J. A User’s Guide to Support Vector Machines. In Data Mining Techniques for the Life Sciences; Springer: Berlin/Heidelberg, Germany, 2009; pp. 223–239. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 2. [Google Scholar]
- Luan, J.; Zhang, C.; Xu, B.; Xue, Y.; Ren, Y. The Predictive Performances of Random Forest Models with Limited Sample Size and Different Species Traits. Fish. Res. 2020, 227, 105534. [Google Scholar] [CrossRef]
- Sun, Y.; Zhao, Y.; Wu, J.; Liu, N.; Kang, X.; Wang, S.; Zhou, D. An Explainable Machine Learning Model for Identifying Geographical Origins of Sea Cucumber Apostichopus Japonicus Based on Multi-Element Profile. Food Control 2022, 134, 108753. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer: Berlin/Heidelberg, Germany, 2013; Volume 103. [Google Scholar]
- Hyndman, R.J.; Koehler, A.B. Another Look at Measures of Forecast Accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the Mean Absolute Error (MAE) over the Root Mean Square Error (RMSE) in Assessing Average Model Performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- De Myttenaere, A.; Golden, B.; Le Grand, B.; Rossi, F. Mean Absolute Percentage Error for Regression Models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef]
- Draper, N.R. Applied Regression Analysis; McGraw-Hill. Inc.: Columbus, OH, USA, 1998. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J.; Franklin, J. The Elements of Statistical Learning: Data Mining, Inference and Prediction. Math. Intell. 2005, 27, 83–85. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice. Available online: https://otexts.com/fpp3 (accessed on 1 September 2025).
- Froese, R. Cube Law, Condition Factor and Weight–Length Relationships: History, Meta-analysis and Recommendations. J. Appl. Ichthyol. 2006, 22, 241–253. [Google Scholar] [CrossRef]
- Akyol, O.; Gamsiz, K. Age and Growth of Adult Gilthead Seabream (Sparus aurata L.) in the Aegean Sea. J. Mar. Biol. Assoc. United Kingd. 2011, 91, 1255–1259. [Google Scholar] [CrossRef]
- Marengo, M.; Durieux, E.D.H.; Marchand, B.; Francour, P. A Review of Biology, Fisheries and Population Structure of Dentex dentex (Sparidae). Rev. Fish Biol. Fish. 2014, 24, 1065–1088. [Google Scholar] [CrossRef]
- Vasilakopoulos, P.; Maravelias, C.D.; Tserpes, G. The Alarming Decline of Mediterranean Fish Stocks. Curr. Biol. 2014, 24, 1643–1648. [Google Scholar] [CrossRef]
- Desouky, M.G.; Azab, A.M.; Maaty, M.M. Length-Weight Relationship and Population Parameters of the Sea Bream, Sparus aurata (Linnaeus, 1758) in Abu Qir Bay, Mediterranean Sea, Egypt. Egypt. J. Aquat. Biol. Fish. 2021, 25, 97. [Google Scholar] [CrossRef]
- Moore, J.W.; Yeakel, J.D.; Peard, D.; Lough, J.; Beere, M. Life-history Diversity and Its Importance to Population Stability and Persistence of a Migratory Fish: Steelhead in Two Large N Orth A Merican Watersheds. J. Anim. Ecol. 2014, 83, 1035–1046. [Google Scholar] [CrossRef]
- King, J.R.; McFarlane, G.A. Marine Fish Life History Strategies: Applications to Fishery Management. Fish. Manag. Ecol. 2003, 10, 249–264. [Google Scholar] [CrossRef]
- Neubauer, P.; Jensen, O.P.; Hutchings, J.A.; Baum, J.K. Resilience and Recovery of Overexploited Marine Populations. Science 2013, 340, 347–349. [Google Scholar] [CrossRef]
- Legaki, A.; Chatzispyrou, A.; Damalas, D.; Sgardeli, V.; Lefkaditou, E.; Anastasopoulou, A.; Dogrammatzi, A.; Charalampous, K.; Stamouli, C.; Vassilopoulou, V.; et al. Decline in Size-at-Maturity of European Hake in Relation to Environmental Regimes: A Case in the Eastern Ionian Sea. Animals 2023, 14, 61. [Google Scholar] [CrossRef]
- Tsagarakis, K.; Coll, M.; Giannoulaki, M.; Somarakis, S.; Papaconstantinou, C.; Machias, A. Food-Web Traits of the North Aegean Sea Ecosystem (Eastern Mediterranean) and Comparison with Other Mediterranean Ecosystems. Estuar. Coast. Shelf Sci. 2010, 88, 233–248. [Google Scholar] [CrossRef]
- Körner, M.; Brandt, P.; Dengler, M. Strength and Timing of Austral Winter Angolan Coastal Upwelling. Sci. Rep. 2024, 14, 27400. [Google Scholar] [CrossRef] [PubMed]
- Imbol Koungue, R.A.; Brandt, P.; Prigent, A.; Aroucha, L.C.; Lübbecke, J.; Imbol Nkwinkwa, A.S.N.; Dengler, M.; Keenlyside, N. Drivers and Impact of the 2021 Extreme Warm Event in the Tropical Angolan Upwelling System. Sci. Rep. 2024, 14, 16824. [Google Scholar] [CrossRef] [PubMed]
- Busch, S.; Mehner, T. Size-Dependent Patterns of Diel Vertical Migration: Smaller Fish May Benefit from Faster Ascent. Behav. Ecol. 2012, 23, 210–217. [Google Scholar] [CrossRef]
- Wang, J.-Y.; Kuo, T.-C.; Hsieh, C. Causal Effects of Population Dynamics and Environmental Changes on Spatial Variability of Marine Fishes. Nat. Commun. 2020, 11, 2635. [Google Scholar] [CrossRef]
- Hussein, A.-S.R.; Younes, G.O.; El-Dakdouki, M.H. Impact of Environmental Conditions on Allometric and Morphometric Traits of Fish in Jiyeh, Lebanon: A Multivariate Analysis. Egypt. J. Aquat. Res. 2025, in press. [CrossRef]
- Mahamat, M.; De León, L.F.; Martínez, M.L. Reproductive Investment in the Knifefish Brachyhypopomus occidentalis. Zoology 2025, 172, 126293. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, D.; Li, Z.; Wang, Y.; Yang, X.; Li, S.; Li, S.; Yang, W.; Li, G. Comparative Physiological and Transcriptomic Profiling Offers Insight into the Sexual Dimorphism of Hepatic Metabolism in Size-Dimorphic Spotted Scat (Scatophagus argus). Life 2021, 11, 589. [Google Scholar] [CrossRef]
- Reich, T.; Ben-Ezra, T.; Belkin, N.; Tsemel, A.; Aharonovich, D.; Roth-Rosenberg, D.; Givati, S.; Bialik, M.; Herut, B.; Berman-Frank, I.; et al. A Year in the Life of the Eastern Mediterranean: Monthly Dynamics of Phytoplankton and Bacterioplankton in an Ultra-Oligotrophic Sea. Deep Sea Res. Part I Oceanogr. Res. Pap. 2022, 182, 103720. [Google Scholar] [CrossRef]
- Keramidas, I.; Dimarchopoulou, D.; Tsikliras, A.C. Modelling and Assessing the Ecosystem of the Aegean Sea, a Major Hub of the Eastern Mediterranean at the Intersection of Europe and Asia. Reg. Stud. Mar. Sci. 2022, 56, 102704. [Google Scholar] [CrossRef]
- Ducklow, H.; Cimino, M.; Dunton, K.H.; Fraser, W.R.; Hopcroft, R.R.; Ji, R.; Miller, A.J.; Ohman, M.D.; Sosik, H.M. Marine Pelagic Ecosystem Responses to Climate Variability and Change. Bioscience 2022, 72, 827–850. [Google Scholar] [CrossRef]
- Fox, J.; Behrenfeld, M.J.; Haëntjens, N.; Chase, A.; Kramer, S.J.; Boss, E.; Karp-Boss, L.; Fisher, N.L.; Penta, W.B.; Westberry, T.K.; et al. Phytoplankton Growth and Productivity in the Western North Atlantic: Observations of Regional Variability From the NAAMES Field Campaigns. Front. Mar. Sci. 2020, 7, 24. [Google Scholar] [CrossRef]
- Hatmar, W.S.M.; Aiman, U. Overfishing and Marine Ecosystem Collapse: A Global Perspective. J. Soc. 2024, 1, 273–289. [Google Scholar]
- Ohlberger, J.; Langangen, Ø.; Stige, L.C. Age Structure Affects Population Productivity in an Exploited Fish Species. Ecol. Appl. 2022, 32, e2614. [Google Scholar] [CrossRef]
- Winemiller, K.O. Life History Strategies, Population Regulation, and Implications for Fisheries Management. Can. J. Fish. Aquat. Sci. 2005, 62, 872–885. [Google Scholar] [CrossRef]
- Klaoudatos, D.; Vlachou, M.; Theocharis, A. From Data to Insight: Machine Learning Approaches for Fish Age Prediction in European Hake. J. Mar. Sci. Eng. 2024, 12, 1466. [Google Scholar] [CrossRef]
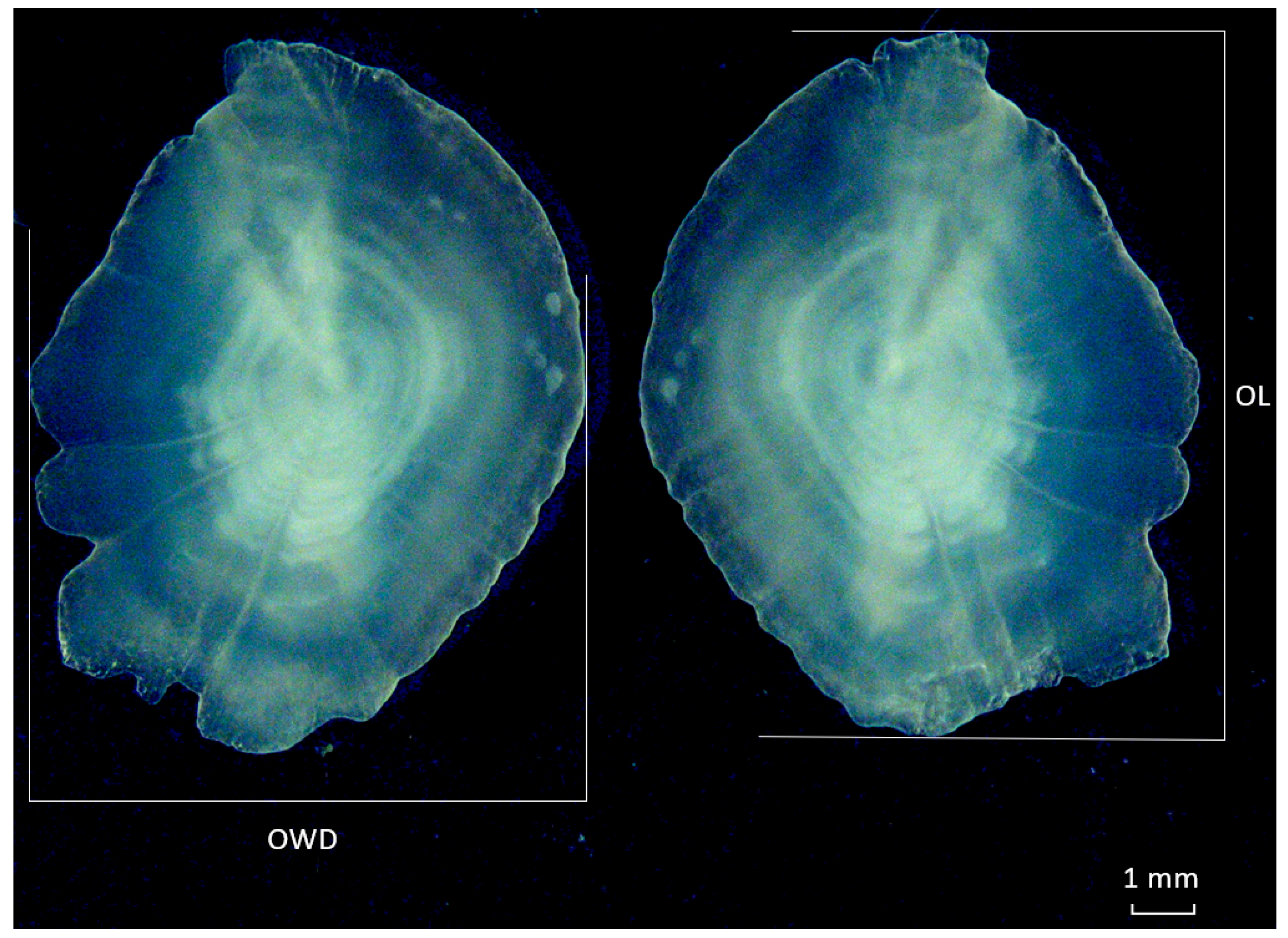

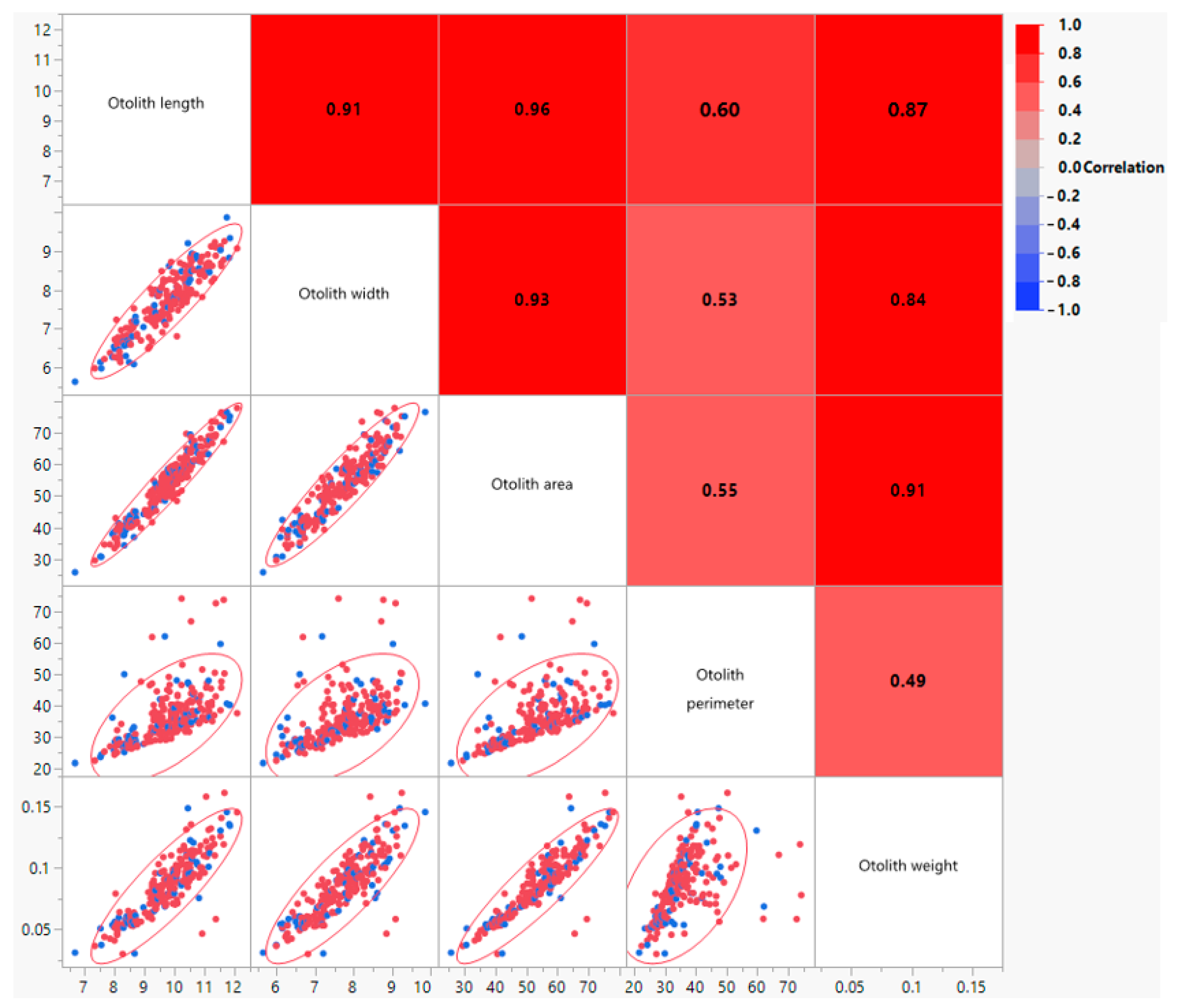

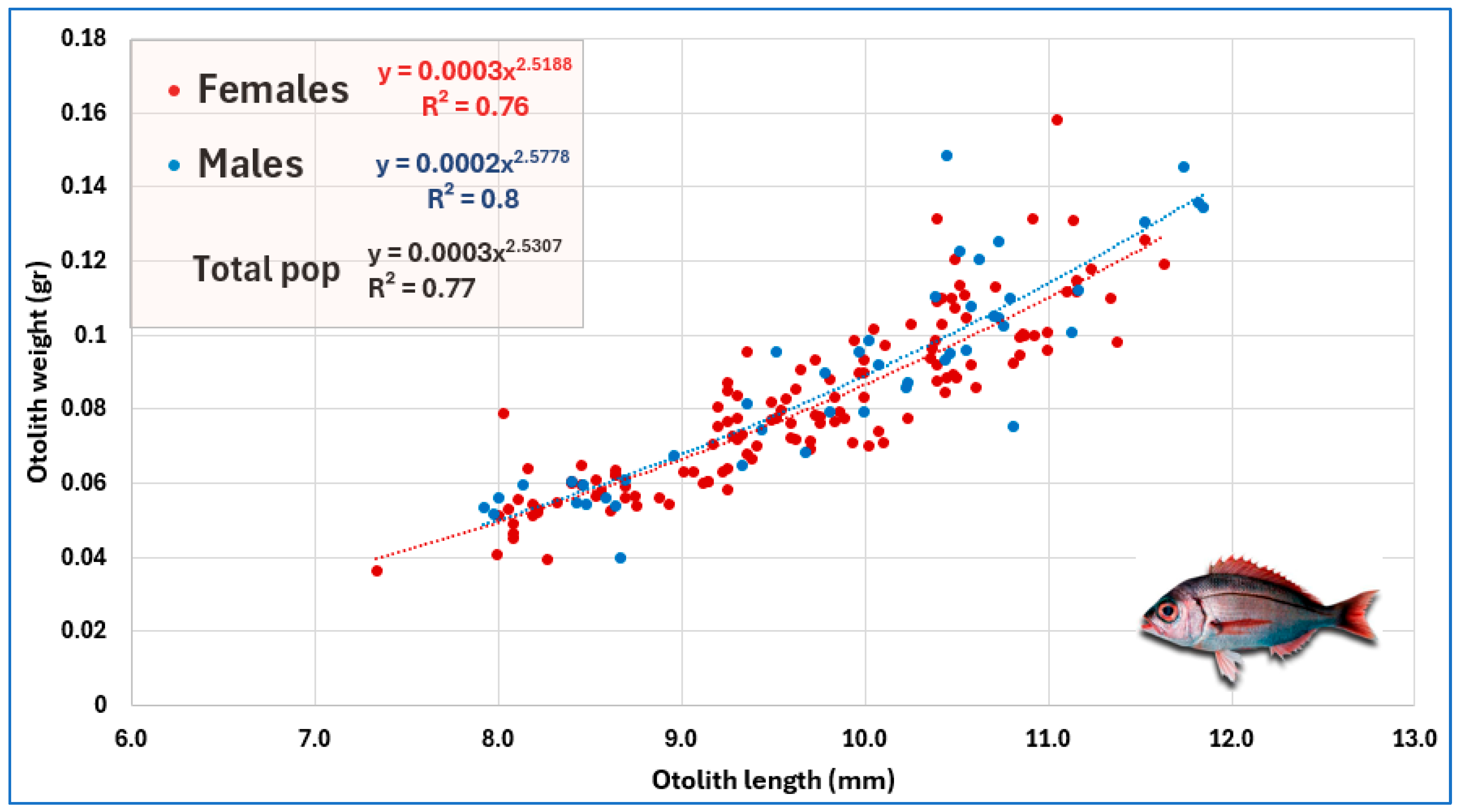
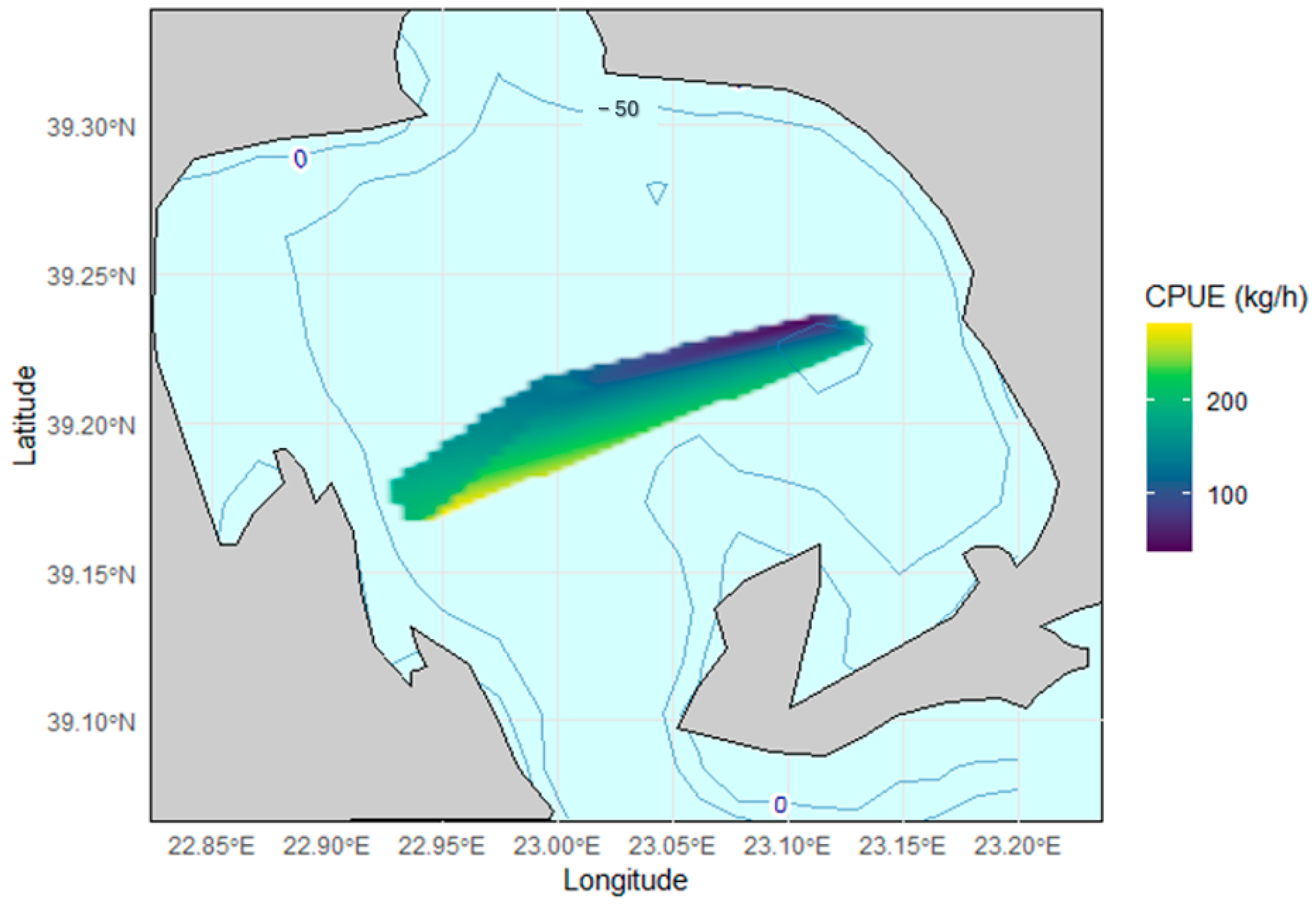


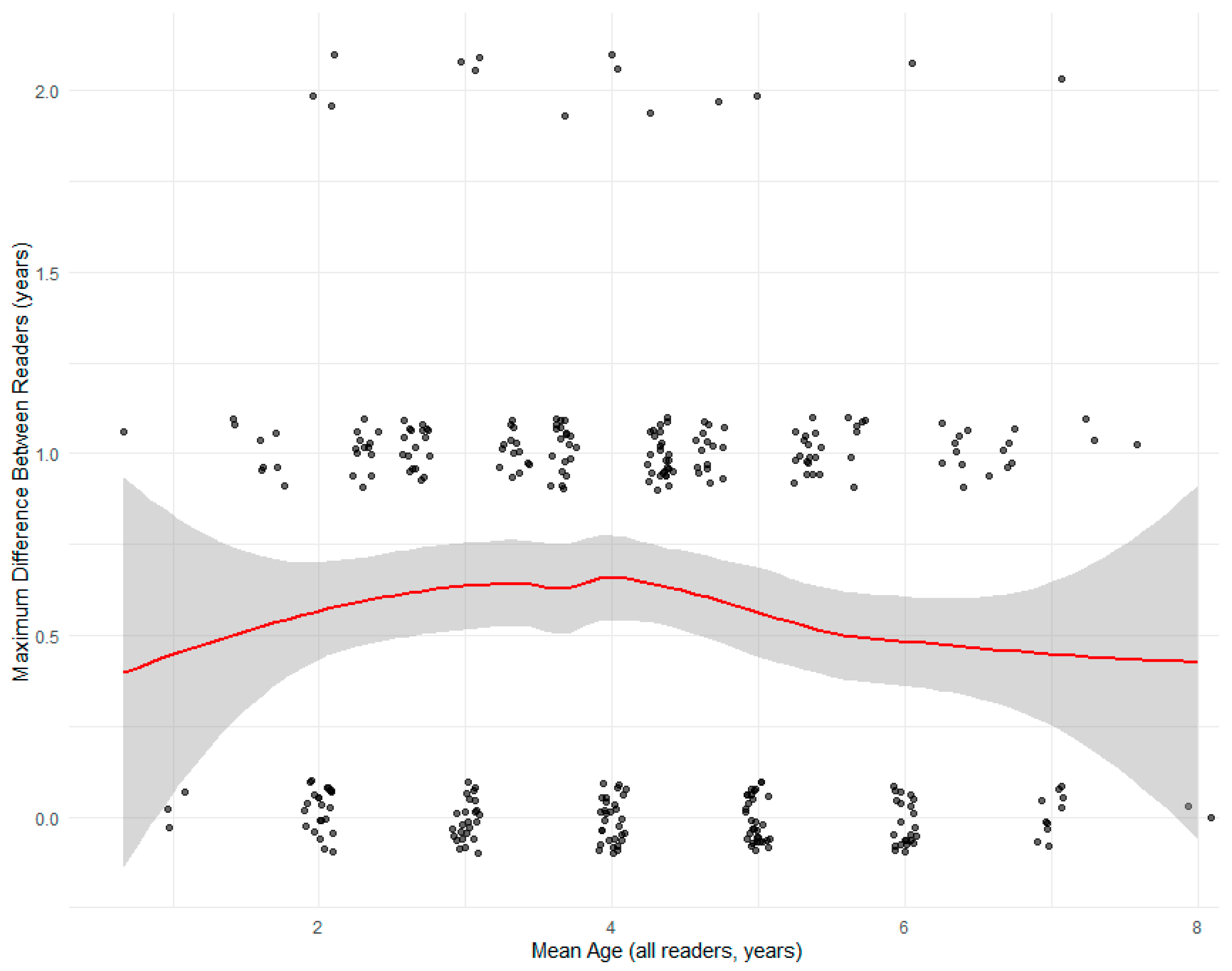

| Otolith Morphometric Characters | Formula | Reference |
|---|---|---|
| rectangularity (R) | [51] | |
| squareness (S) | [52] | |
| ellipticity (E) | [53] | |
| roundness (RO) | 2 | [53] |
| aspect ratio (AR) | [54] | |
| form factor (F) | 2 | [53] |
| circularity (C) | 2 | [51] |
| Relationship | Equation | R2 | t-Test | Allometry |
|---|---|---|---|---|
| OL vs. OW | OW = 0.0008 × OL2.5441 | 75.1% | *** | Negative |
| OL vs. OWD | OWD = 0.9893 × OL0.9024 | 80.3% | *** | Negative |
| OL vs. OA | OA = 0.8540 × OL1.8157 | 91.7% | *** | Negative |
| OWD vs. OW | OW = 0.0006 × OWD2.4343 | 71.3% | *** | Negative |
| OA vs. OW | OW = 0.0003 × OA1.4283 | 82.7% | *** | Negative |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klaoudatos, D.; Theocharis, A.; Vardaki, C.; Pachi, E.; Politikos, D.; Conides, A. Aspects of Biology and Machine Learning for Age Prediction in the Large-Eye Dentex Dentex macrophthalmus (Bloch, 1791). Fishes 2025, 10, 500. https://doi.org/10.3390/fishes10100500
Klaoudatos D, Theocharis A, Vardaki C, Pachi E, Politikos D, Conides A. Aspects of Biology and Machine Learning for Age Prediction in the Large-Eye Dentex Dentex macrophthalmus (Bloch, 1791). Fishes. 2025; 10(10):500. https://doi.org/10.3390/fishes10100500
Chicago/Turabian StyleKlaoudatos, Dimitris, Alexandros Theocharis, Chrysoula Vardaki, Elpida Pachi, Dimitris Politikos, and Alexis Conides. 2025. "Aspects of Biology and Machine Learning for Age Prediction in the Large-Eye Dentex Dentex macrophthalmus (Bloch, 1791)" Fishes 10, no. 10: 500. https://doi.org/10.3390/fishes10100500
APA StyleKlaoudatos, D., Theocharis, A., Vardaki, C., Pachi, E., Politikos, D., & Conides, A. (2025). Aspects of Biology and Machine Learning for Age Prediction in the Large-Eye Dentex Dentex macrophthalmus (Bloch, 1791). Fishes, 10(10), 500. https://doi.org/10.3390/fishes10100500