Figure 1.
Phase diagrams, bifurcation diagrams and Lyapunov exponents.
Figure 1.
Phase diagrams, bifurcation diagrams and Lyapunov exponents.
Figure 2.
Three-level LWT decomposition diagram.
Figure 2.
Three-level LWT decomposition diagram.
Figure 3.
Flow chart of dual watermark encryption algorithm.
Figure 3.
Flow chart of dual watermark encryption algorithm.
Figure 4.
Schematic diagram of the crossing process.
Figure 4.
Schematic diagram of the crossing process.
Figure 5.
Schematic diagram of the mutation process.
Figure 5.
Schematic diagram of the mutation process.
Figure 6.
Flow chart of decryption and dual watermark copyright authentication.
Figure 6.
Flow chart of decryption and dual watermark copyright authentication.
Figure 7.
Simulation results of dual watermark and encryption protection.
Figure 7.
Simulation results of dual watermark and encryption protection.
Figure 8.
Key sensitivity analysis results: (a) β + 10−15, (b) r + 10−15, (c) a1 + 10−15, (d) b1 + 10−15, (e) c1 + 10−15, (f) r1 + 10−15, (g) a2 + 10−15, (h) b2 + 10−15, (i) c2 + 10−15 and (j) r2 + 10−15.
Figure 8.
Key sensitivity analysis results: (a) β + 10−15, (b) r + 10−15, (c) a1 + 10−15, (d) b1 + 10−15, (e) c1 + 10−15, (f) r1 + 10−15, (g) a2 + 10−15, (h) b2 + 10−15, (i) c2 + 10−15 and (j) r2 + 10−15.
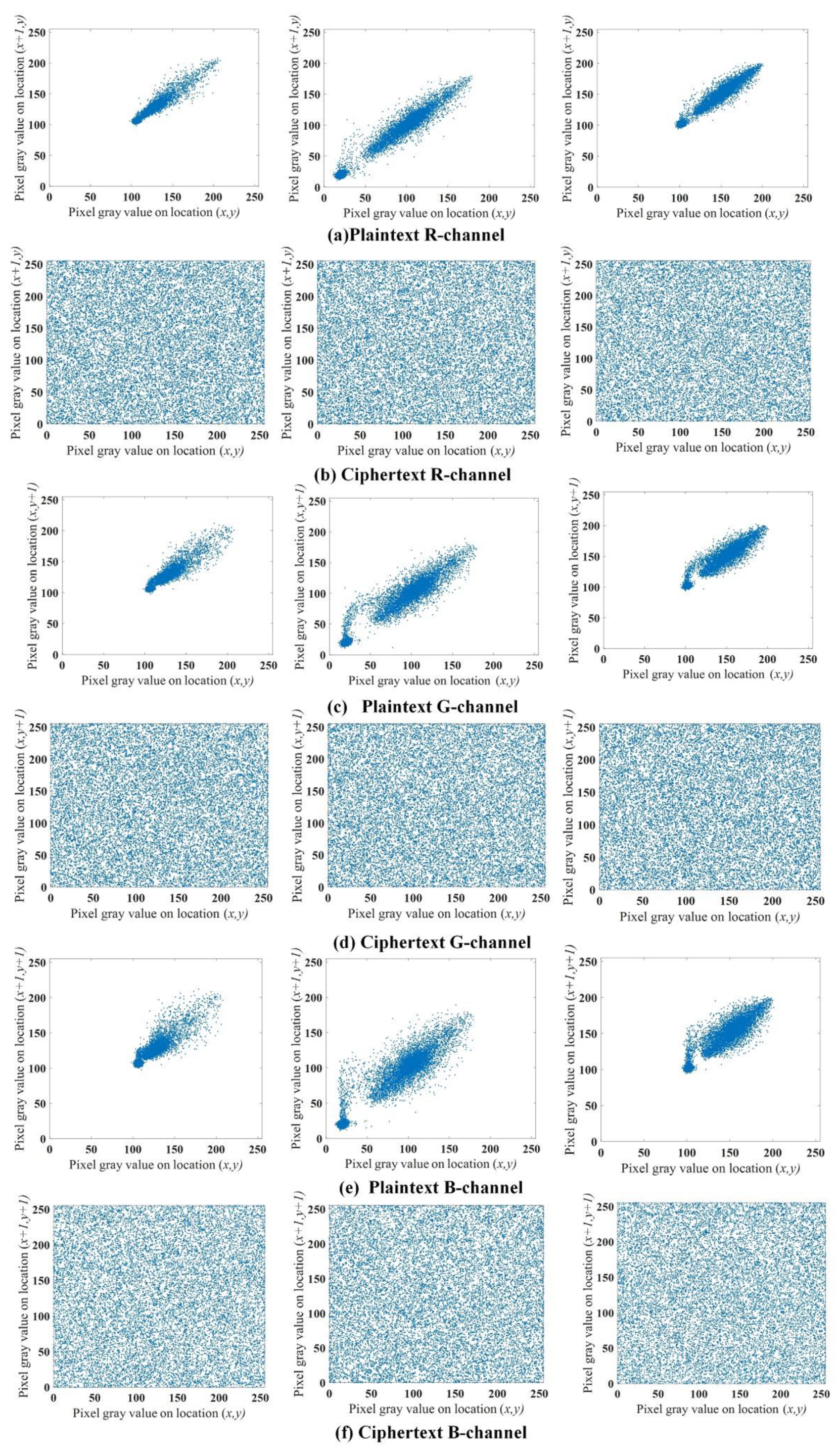
Figure 9.
Correlation analysis result.
Figure 9.
Correlation analysis result.
Figure 10.
Histogram analysis results of ‘Earth’.
Figure 10.
Histogram analysis results of ‘Earth’.
Figure 11.
Experimental results of encryption under noise attack.
Figure 11.
Experimental results of encryption under noise attack.
Figure 12.
Experimental results of encryption under cropping attack.
Figure 12.
Experimental results of encryption under cropping attack.
Figure 13.
Experimental results of watermark under Median filter attack.
Figure 13.
Experimental results of watermark under Median filter attack.
Figure 14.
Experimental results of watermark under noise attack.
Figure 14.
Experimental results of watermark under noise attack.
Figure 15.
Experimental results of watermark under cropping attack.
Figure 15.
Experimental results of watermark under cropping attack.
Figure 16.
Experimental results of zero-watermarking under Median filter and JEPG compression attack.
Figure 16.
Experimental results of zero-watermarking under Median filter and JEPG compression attack.
Figure 17.
Experimental results of zero-watermarking under rotation attack.
Figure 17.
Experimental results of zero-watermarking under rotation attack.
Figure 18.
Experimental results of zero-watermarking under noise attack.
Figure 18.
Experimental results of zero-watermarking under noise attack.
Figure 19.
Experimental results of zero-watermarking under cropping attack.
Figure 19.
Experimental results of zero-watermarking under cropping attack.
Figure 20.
Experimental results of zero-watermarking under combination attack.
Figure 20.
Experimental results of zero-watermarking under combination attack.
Table 1.
NIST test result.
Table 1.
NIST test result.
| Test | p-Value | Pass Rate | Result |
|---|
| Frequency | 0.304126 | 1 | Pass |
| Block Frequency | 0.911413 | 0.96 | Pass |
| Cumulative Sums | Forward | 0.883171 | 1 | Pass |
| Reverse | 0.816537 | 0.99 | Pass |
| Runs | 0.145326 | 0.97 | Pass |
| Longest Run | 0.834308 | 0.99 | Pass |
| Binary Matrix Rank | 0.739918 | 0.99 | Pass |
| FFT | 0.616305 | 0.99 | Pass |
| Non-Overlapping Template Matching | 0.699313 | 0.98 | Pass |
| Overlapping Template Matching | 0.350485 | 0.98 | Pass |
| Maurer’s “Universal Statistical” | 0.978072 | 0.98 | Pass |
| Approximate Entropy | 0.616305 | 0.97 | Pass |
| The Random Excursions | x = −4 | 0.082177 | 0.97 | Pass |
| x = −3 | 0.637119 | 1 | Pass |
| x = −2 | 0.804337 | 1 | Pass |
| x = −1 | 0.134686 | 0.99 | Pass |
| x = 1 | 0.671779 | 1 | Pass |
| x = 2 | 0.602458 | 0.99 | Pass |
| x = 3 | 0.324180 | 1 | Pass |
| x = 4 | 0.862344 | 0.99 | Pass |
| Random Excursions Variant | x = −9 | 0.090936 | 1 | Pass |
| x = −8 | 0.082177 | 0.99 | Pass |
| x = −7 | 0.568055 | 1 | Pass |
| x = −6 | 0.739918 | 1 | Pass |
| x = −5 | 0.066882 | 1 | Pass |
| x = −4 | 0.739918 | 0.99 | Pass |
| x = −3 | 0.888137 | 0.99 | Pass |
| x = −2 | 0.637119 | 0.98 | Pass |
| x = −1 | 0.350485 | 0.99 | Pass |
| x = 1 | 0.407091 | 0.98 | Pass |
| x = 2 | 0.568055 | 0.99 | Pass |
| x = 3 | 0.350485 | 1 | Pass |
| x = 4 | 0.500934 | 1 | Pass |
| x = 5 | 0.931952 | 1 | Pass |
| x = 6 | 0.568055 | 1 | Pass |
| x = 7 | 0.706149 | 1 | Pass |
| x = 8 | 0.324180 | 1 | Pass |
| x = 9 | 0.213309 | 1 | Pass |
| Serial | p-value1 | 0.319084 | 1 | Pass |
| p-value2 | 0.699313 | 0.99 | Pass |
| Linear Complexity | 0.554420 | 0.97 | Pass |
Table 2.
DNA encode rules.
Table 2.
DNA encode rules.
| Rule | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| 00 | A | A | T | T | G | G | C | C |
| 01 | C | G | C | G | T | A | T | A |
| 10 | G | C | G | C | A | T | A | T |
| 11 | T | T | A | A | C | C | G | G |
Table 3.
DNA addition and subtraction rules.
Table 3.
DNA addition and subtraction rules.
| + | A | C | G | T | − | A | C | G | T |
|---|
| A | A | C | G | T | A | A | T | G | C |
| C | C | G | T | A | C | C | A | T | G |
| G | G | T | A | C | G | G | C | A | T |
| T | T | A | C | G | T | T | G | C | A |
Table 4.
Comparison of visual security simulation results.
Table 4.
Comparison of visual security simulation results.
| Algorithm | Proposed | Ref. [19] | Ref. [10] |
|---|
| Earth | Baboon | Peppers | Mean | Mean |
|---|
| Number character | 43.2671 | 37.0417 | 47.0893 | 32.0359 | 42.0000 |
| English character | 49.3960 | 37.0798 | 45.7277 |
| Logo design | 43.2634 | 33.7379 | 47.3498 |
Table 5.
Key space for different algorithms.
Table 5.
Key space for different algorithms.
| Algorithm | Proposed | Ref. [20] | Ref. [22] | Ref. [23] | Ref. [24] |
|---|
| Key space | 21046 | 2233 | 2250 | 2280 | 2294 |
Table 6.
Experimental results of watermark correlation coefficient.
Table 6.
Experimental results of watermark correlation coefficient.
| Watermark | Proposed |
|---|
| Number Character | English Character | Logo Design | Mean |
|---|
| NC | 0.5414 | 0.5044 | 0.5327 | 0.5262 |
Table 7.
Correlation coefficient analysis.
Table 7.
Correlation coefficient analysis.
| Image | Channel | Plain Image | Cipher Image |
|---|
| Horizontal | Vertical | Diagonal | Horizontal | Vertical | Diagonal |
|---|
| Earth | R | 0.9374 | 0.9485 | 0.9024 | −0.0017 | −0.0043 | −0.0012 |
| G | 0.9386 | 0.9505 | 0.9061 | 0.0058 | −0.0005 | −0.0001 |
| B | 0.9256 | 0.9381 | 0.8860 | 0.0018 | 0.0045 | 0.0021 |
| Baboon | R | 0.9474 | 0.9208 | 0.9014 | 0.0085 | 0.0017 | 0.0019 |
| G | 0.8728 | 0.8380 | 0.7905 | 0.0002 | 0.0012 | 0.0084 |
| B | 0.9216 | 0.9139 | 0.8767 | −0.0009 | −0.0007 | −0.0000 |
Table 8.
Information entropy of different images.
Table 8.
Information entropy of different images.
| Image | Proposed Scheme | Ref. [25] | Ref. [26] |
|---|
| Earth | Baboon | Peppers | Lena | Baboon | Peppers | Mean |
|---|
| Plain image | 7.2753 | 7.6785 | 7.7038 | 7.2544 | 7.6599 | 7.2118 | 6.8030 |
| Cipher image | 7.9990 | 7.9989 | 7.9991 | 7.9959 | 7.9959 | 7.9959 | 7.9980 |
Table 9.
The equalization test results of zero-watermarking.
Table 9.
The equalization test results of zero-watermarking.
| Image | Proposed | Ref. [27] | Ref. [28] | Ref. [5] |
|---|
| Lena | 0.0046 | 0.0137 | 0.0117 | 0.0107 |
| Baboon | 0.0098 | 0.0083 | 0.0156 | 0.0093 |
| Peppers | 0.0091 | 0.0142 | 0.0176 | 0.0098 |
| Mean | 0.0078 | 0.0122 | 0.0137 | 0.0085 |
Table 10.
NPCR and UACI test results.
Table 10.
NPCR and UACI test results.
| Image | Earth | Baboon | Peppers | Airplane | Sailboat | Fruit |
|---|
| NPCR | 99.6104 | 99.6147 | 99.6181 | 99.6251 | 99.6150 | 99.6282 |
| UACI | 33.4423 | 33.4632 | 33.4214 | 33.4945 | 33.4964 | 33.4288 |
Table 11.
Comparison of experimental results under ciphertext noise attack.
Table 11.
Comparison of experimental results under ciphertext noise attack.
| Attack | Gaussian Noise | Salt and Pepper Noise |
|---|
| 0.0001 | 0.0003 | 0.0005 | 0.01 | 0.05 | 0.1 |
|---|
| Proposed | 31.0475 | 29.7909 | 29.2037 | 40.1298 | 33.8694 | 31.4819 |
| Ref. [12] | 11.8431 | 11.0575 | 8.6600 | - | 21.4684 | 18.4260 |
| Ref. [29] | - | - | - | 28.4866 | - | 18.5106 |
| Ref. [30] | - | - | - | 20.28 | 13.84 | 11.61 |
Table 12.
Comparison of experimental results under ciphertext cropping attack.
Table 12.
Comparison of experimental results under ciphertext cropping attack.
| Cropping Area | Cropping Attack |
|---|
| 10% | 25% | 50% |
|---|
| Proposed | 31.6300 | 28.8645 | 27.7738 |
| Ref. [29] | 18.7021 | 14.572 | 11.5940 |
| Ref. [30] | 17.35 | 14.48 | 11.60 |
| Ref. [23] | 17.28 | 14.47 | - |
Table 13.
Comparison of experimental results under Median filter attack.
Table 13.
Comparison of experimental results under Median filter attack.
| Attack | Factor | Proposed | Ref. [10] | Ref. [11] | Ref. [31] | Ref. [32] |
|---|
| Median filtering | 3 × 3 | 0.9955 | 0.9873 | 0.9930 | 0.9746 | 0.93 |
| 5 × 5 | 0.8410 | 0.9539 | - | 0.7266 | - |
| 7 × 7 | 0.7959 | 0.9120 | 0.9755 | - | 0.87 |
Table 14.
Comparison of experimental results under noise attack of rubust watermark.
Table 14.
Comparison of experimental results under noise attack of rubust watermark.
| Algorithm | | Proposed | Ref. [10] | Ref. [33] | Ref. [34] |
|---|
| Gaussian noise | 0.001 | 1.0000 | 0.9869 | 0.9466 | 0.8984 |
| 0.002 | 0.9910 | 0.9816 | 0.8748 | - |
| 0.005 | 0.9114 | 0.9299 | - | 0.7283 |
| Salt and pepper noise | 0.005 | 0.9928 | 0.9381 | 0.9886 | 0.8823 |
| 0.01 | 0.9410 | - | 0.9286 | 0.8077 |
| 0.02 | 0.8873 | - | 0.8673 | 0.7028 |
Table 15.
Comparison of experimental results under cropping attack of rubust watermark.
Table 15.
Comparison of experimental results under cropping attack of rubust watermark.
| Cropping Area | 8% | 10% | 15% | 19% | 32% | 35% |
|---|
| Proposed | 0.9991 | 0.9955 | 0.9846 | 0.9810 | 0.9429 | 0.9382 |
| Ref. [32] | 0.81 | 0.80 | 0.74 | 0.75 | 0.59 | 0.63 |
| Ref. [31] | 0.9863 | 0.9824 | - | 0.8789 | - | - |
| Ref. [31] | 0.984 | 0.957 | - | 0.849 | - | - |
| Ref. [11] | - | 0.8608 | - | 0. 8201 | - | - |
Table 16.
Comparison of experimental results under Median filter and JEPG compression attack.
Table 16.
Comparison of experimental results under Median filter and JEPG compression attack.
| Attack | Factor | Proposed | Ref. [27] | Ref. [35] | Ref. [7] | Ref. [36] | Ref. [37] |
|---|
| Median filtering | 3 × 3 | 0.9991 | 0.9954 | 0.9961 | 0.9987 | 1 | 0.95 |
| 5 × 5 | 0.9973 | 0.9911 | 0.9883 | - | 0.999 | 0.86 |
| 7 × 7 | 0.9964 | 0.9874 | 0.9844 | - | 0.998 | 0.80 |
| JPEG compression | 90% | 1.0000 | 0.9964 | 0.9922 | 1 | - | 1 |
| 70% | 1.0000 | 0.9911 | 0.9805 | 1 | - | 1 |
| 50% | 1.0000 | 0.9899 | 0.9727 | 0.9994 | 0.9997 | 0.99 |
| 30% | 0.9991 | 0.9872 | 0.9570 | 0.9993 | 0.999 | 0.90 |
Table 17.
Comparison of experimental results under rotation attack.
Table 17.
Comparison of experimental results under rotation attack.
| Angle | Proposed | Ref. [38] | Ref. [6] | Ref. [39] | Ref. [27] |
|---|
| 1° | 0.9919 | 0.980 | 0.9211 | 0.9971 | 0.9536 |
| 3° | 0.9928 | 0.936 | 0.8203 | 0.9902 | 0.8691 |
| 5° | 0.9937 | - | 0.7569 | 0.9863 | 0.8123 |
| 10° | 0.9955 | 0.823 | 0.6636 | 0.9775 | 0.7152 |
| 20° | 0.9937 | 0.773 | - | - | - |
| 30° | 0.9982 | - | 0.5579 | - | - |
Table 18.
Comparison of experimental results under zero-watermarking noise attack.
Table 18.
Comparison of experimental results under zero-watermarking noise attack.
| Algorithm | | Proposed | Ref. [40] | Ref. [41] | Ref. [42] | Ref. [43] |
|---|
| Gaussian noise | 0.001 | 0.9991 | 1 | 0.9981 | 0.8508 | 1 |
| 0.02 | 0.9946 | 1 | 0.9974 | 0.7645 | 0.9688 |
| 0.025 | 0.9909 | 0.840 | - | - | 0.9063 |
| Salt and pepper noise | 0.001 | 1.0000 | 1 | 0.9885 | 0.9461 | 0.9688 |
| 0.02 | 0.9991 | 0.949 | 0.9846 | 0.9157 | 0.9375 |
| 0.025 | 0.9973 | 0.919 | 0.9559 | 0.8952 | - |
Table 19.
Comparison of experimental results under zero-watermarking cropping attack.
Table 19.
Comparison of experimental results under zero-watermarking cropping attack.
| Cropping Area | Proposed | Ref. [43] | Ref. [38] | Ref. [31] |
|---|
| R/G/B | RGB |
|---|
| 1/4 | 0.9602 | 0.9337 | 0.9063 | 0.892 | 0.9004 |
| 1/8 | 0.9874 | 0.9730 | 0.9063 | 0.949 | 0.9824 |
| 1/16 | 0.9937 | 0.9873 | 0.9688 | 0.969 | 0.9863 |
Table 20.
Comparison of experimental results under combination attack.
Table 20.
Comparison of experimental results under combination attack.
| Combination Attack | Proposed | Ref. [27] | Ref. [6] |
|---|
| Median filtering (5 × 5) + Gaussian noise (0.3) | 0.9723 | 0.9504 | 0.8901 |
| Median filtering (5 × 5) + JPEG compression (90%) | 0.9964 | 0.9835 | 0.9762 |
| JPGE compression (90%) + Gaussian noise (0.3) | 0.9558 | 0.9379 | 0.9551 |
| Rotation (2°) + JPEG compression (90%) | 0.9955 | 0.8989 | 0.8628 |
| Wiener filtering (5 × 5) + salt and pepper noise (0.3) | 0.9720 | 0.9215 | 0.8926 |