Composable Privacy-Preserving Framework for Stakes-Based Online Peer-to-Peer Applications

Abstract

As the demand for expansive back-end systems in online applications continues to grow, novel frameworks are necessitated to address the escalating operational demands, energy consumption, and associated costs. Traditional Client–Server models, while offering centralized security and reliability, are characterized by their high deployment and maintenance expenses. Conversely, Peer-to-Peer (P2P) models, despite being cost-effective and scalable, are hindered by inherent security and data integrity challenges. Moreover, the lack of a central authority in P2P systems complicates a definitive resolution of scenarios involving stakes, where users cannot withdraw without incurring a tangible loss. In this research work, a hybrid back-end framework is introduced, combining the advantages of both models through the utilization of cryptographic algorithms and Secure Multi-Party Computation (MPC) protocols. The baseline solution is lightweight and fully composable, making it capable of utilizing different more complex slot-in MPC techniques. The proposed framework’s effectiveness is demonstrated through a simplified two-player Spades game, although it is fully generalizable to any application. Evaluations across multiple case studies reveal substantial performance enhancements compared to conventional approaches, particularly post-initialization, highlighting the scheme’s potential as a cost-effective, energy-efficient, and secure solution for modern online applications.

1. Introduction

In the realm of online applications, a diverse array of techniques and back-end implementations are necessary to facilitate user communication. This requirement spans from social media platforms to online video games, collaborative workspaces, e-commerce websites, etc. On many occasions, there is a great demand for real-time data synchronization, low-latency connections, and robust server architectures. Traditionally, developers have favored more centralized Client–Server models, wherein a central entity manages all participants. These models are straightforward to implement, ensure a certain level of security, and prevent malicious modifications to core data as the server assumes an authoritative role and has the final say on any action. However, these setups are associated with significant drawbacks, primarily the need for costly infrastructure and high-maintenance expenses.

An often overlooked but increasingly critical concern with centralized Client–Server architectures is their substantial energy demand. The environmental footprint of data centers—especially those operated by large corporations and supporting services like massive online gaming platforms—has sparked growing scrutiny. Studies show that the Information and Communication Technologies (ICT) sector currently accounts for between 2.5% and 3% of global greenhouse gas emissions, with projections climbing to as high as 14% by 2040 [1]. These energy-intensive facilities, which may consume up to 100 megawatts (MW) each, contribute to over 190 terawatt-hours (TWh) of electricity usage annually in certain sectors [2]. As developers grapple with escalating operational costs tied to server maintenance, data storage, and bandwidth, there is an urgent need for sustainable solutions that reduce energy consumption without compromising performance or reliability [3].

In contrast, the decentralized Peer-to-Peer (P2P) model, which establishes a network of interconnected nodes of equal status, presents an alternative approach to traditional centralized systems. While this model is more economical to create, scale, and maintain [4,5], it introduces notable security challenges. The openness of P2P networks makes them susceptible to attacks such as data tampering or unauthorized access. Without a central authority, ensuring data integrity and confidentiality is challenging as information can pass through potentially compromised nodes. Addressing these limitations is critical to realizing the full potential of P2P systems.

Furthermore, a conventional approach when a malicious user is encountered in a P2P environment is to end the interaction with them and avoid future communication. However, when a participant has some stakes in the process, this becomes an unsuitable response. The term stakes can mean any user investment in participating in (and terminating) an honest session between peers without dishonest actions. A very simple example can be an online game with a prize pool or money on the line. If a cheater is detected, the honest user cannot simply leave; an authoritative resolution must be made.

This study seeks to demonstrate that, through a carefully structured combination of certain cryptographic techniques, developers can establish a hybrid back-end that optimally retains the advantages of both the Client–Server and Peer-to-Peer (P2P) models. By merging these architectures, this approach aims to deliver not only the reliability and enhanced security typical of the Client–Server model but also mitigate its high energy costs, as well as utilize the notable cost efficiency associated with the P2P structure. This hybrid back-end thus stands as a balanced, economically viable alternative that addresses critical challenges in performance, operational costs, and energy consumption. Moreover, the proposed framework is focused on providing an identical security level as centralized alternatives with minimal computational overhead. Lastly, since the aim is a general solution, a substantial effort has been made to present a baseline scheme that is fully composable with more complex cryptographic or MPC protocols. In other words, advanced techniques for privacy-preserving computation can be slotted in while retaining complete functionality.

1.1. State of the Art

P2P has been widely studied for its potential. As described beforehand, it can offer self-scaling, robust, and cheap alternatives to traditional Client–Server applications. However, it presents unique security problems that are also the subject of numerous publications throughout the years. For instance, Chopra et al. [6] offer an analysis of security solutions in P2P networks for real-time communication, including reputation systems and cryptographic methods to manage node admission, secure routing protocols and encrypted communications to protect data during transmission, digital signatures, hash functions, and data replication to ensure authenticity and integrity. Additionally, they propose intrusion detection systems and reputation-based mechanisms to identify and mitigate malicious nodes, resource management techniques and challenge-response mechanisms to prevent denial of service attacks, and techniques for NAT and firewall traversal, secure user registration, and location lookup. Qureshi et al. [7] propose a comprehensive framework aimed at enhancing security and privacy within Peer-to-Peer (P2P) content distribution networks. The framework addresses critical challenges associated with piracy and privacy violations, which remain pressing concerns in such decentralized systems. By incorporating advanced techniques, including collusion-resistant fingerprinting and robust privacy protection mechanisms, the proposed solution seeks to safeguard user identities and prevent unauthorized redistribution of content. Kumar et al. [8] focus on developing a secure P2P communication protocol for the Internet of Things (IoT). It proposes a unified IoT framework based on the Mobile Security IP IoT Architecture, designed to address security challenges in P2P IoT interactions. Central to this structure is the IoT-Name Determination Check (NDC), a middleware component that facilitates secure P2P communication by establishing trust between IoT devices through a lightweight keying protocol. The manuscript highlights solutions to common P2P security problems, such as ensuring reliable message transmission and safeguarding against unauthorized access. The effectiveness of the proposed protocol is validated through comprehensive assessments and studies, demonstrating its potential for secure P2P communication in IoT environments.

Examining architectural and system-level techniques, malicious peers in P2P networks can be tackled by coupling architectural safeguards with lightweight cryptography. Jia et al. [9] propose a framework that executes critical P2P protocol code inside Intel SGX enclaves, reducing a compromised peer’s power to little more than dropping messages and thereby simplifying reliable broadcast and randomness services. Al-Otaiby et al. [10] introduce AntTrust, a bio-inspired reputation system that updates pheromone-like scores to reward honest behavior and steer traffic away from dishonest nodes. Ahmed et al. [11] develop a context-aware, blockchain-backed trust architecture that records pseudonymous credentials and evolving reputation on an immutable ledger, enabling ad hoc networks, such as vehicular systems, to expel insiders who inject bogus data. Together, these works exemplify hybrid approaches that blend trusted hardware, adaptive reputation, and blockchain immutability to preserve privacy and integrity in fully decentralized applications. Beyond these safeguards, recent studies have proposed complementary detection mechanisms that flag malicious activity and network breaches at the content layer, further broadening the defense surface of centralized and decentralized systems [12,13].

In spite of addressing different P2P applications, each of the described publications utilizes some mixture of cryptography, authentication protocols, node verification, and specific network organizations to address their respective security concerns. Our research work tackles a more narrow scope, and, instead of attacking broad areas such as data transfer or the IoT, we offer a specific solution in the context of well-defined sessions between multiple users with tangible stakes. Additionally, our approach draws more from the existing research on Secure Multi-Party Computation (MPC) [14,15], offering significant computational speed-ups based on state-of-the-art algorithmic optimizations.

Analyzing MPC focused work, researchers have proposed several cryptographic frameworks to enforce honest behavior or detect cheating in P2P applications without relying on central authorities. These schemes leverage tools like oblivious primitives, secure multiparty computation, and zero-knowledge proofs to guarantee protocol integrity and privacy. Specifically, Minhye Seo et al. [16] propose a fair SMC protocol that detects any cheating party before the final output is reconstructed so that no malicious participant learns the result if misbehavior occurs. The protocol builds on the SPDZ MPC framework and introduces a semi-honest “judge” server that cannot see private inputs but uses broadcast encryption, commitments, and non-interactive zero-knowledge proofs to verify each party’s output share for consistency. By catching malicious behavior prior to revealing the computation outcome, the scheme guarantees fairness (all honest parties get the output or none do) even if multiple parties are corrupted. Moreover, Carsten Baum et al. [17] present a lightweight dishonest-majority MPC protocol that achieves identifiable abort, meaning that if the computation aborts due to misbehavior, the honest peers can agree on which party cheated. Instead of heavy cryptographic machinery, the solution carefully combines inexpensive detection techniques with pairwise MAC-based commitments from state-of-the-art MPC with abort. The core idea is a homomorphic multi-receiver commitment scheme (built from efficient oblivious linear evaluations) that allows the extraction of a proof of misbehavior. This approach thwarts denial-of-service by malicious nodes and mitigates fairness issues while adding minimal overhead to the base MPC protocol.

These works are much closer in nature to our research as expensive server-side processing is avoided and cryptography is utilized for P2P fairness. The presented computing is kept as lightweight as possible, specifically in [17]. However, our work is more tailored to instances where a simple abort after malicious detection is not viable due to session stakes, thus covering a gap in the P2P field.

Moving on to the context of online video games, which are a natural application of our scheme, there is also a vast number of publications trying to secure P2P implementations. The following article [18] explores cheating detection in online games, particularly time cheats in P2P Multiplayer Online Games (MOGs), presenting a framework for modeling game time advancements to identify and prevent cheaters effectively. It proposes real-time cheat detection strategies and discusses two types of time cheats: altering game event generation rates and a real-time look-ahead cheat. The paper introduces a general framework for modeling game time advancements to detect time cheats by monitoring network latencies, with simulation assessments confirming its viability. The authors suggest using effective models to manage game time advancements as a means to prevent time cheats in P2P MOGs.

Buyukkaya et al. [19] introduces VoroGame, a hybrid Peer-to-Peer architecture for massively multiplayer games proposed to address scalability issues in traditional Client–Server setups. It combines a structured overlay using a Distributed Hash Table (DHT) for data distribution and storage with an unstructured overlay based on a Voronoi diagram for game world partitioning. In this system, peers have dual responsibilities: storing data objects mapped by the DHT and managing a specific zone in the game world. The DHT ensures random and balanced data distribution among peers, while the Voronoi diagram facilitates efficient state update dissemination to relevant peers based on their area of interest. VoroGame handles both peer and object movements, updating region boundaries, responsibilities, and peer lists as needed. The authors claim this architecture is the first to offer fully distributed P2P state and data management while leveraging players’ locality of interest for efficient updates.

Baughman et al. [20] explore cheat-proof playout mechanisms for both centralized and P2P gaming structures. The authors propose the Lockstep Protocol and the Asynchronous Synchronization Protocol to prevent cheating in online games. They provide a formal proof of correctness for the Lockstep Protocol and introduce the concept of spheres of influence to define the areas of interaction between players.

Lastly, Han et al. [21] introduce a “Peercraft” framework for browser-specific P2P multiplayer, focusing on cheat-proofing protocols like Random Authority Shuffle and Speculation-Based State Verification. It addresses synchronization challenges with Resynchronizing-at-Root to minimize re-simulation. The implementation includes concepts like Input Delay for synchronized input execution and a Lag Catch-up Mechanism.

Overall, multiple attempts are made to secure decentralized distributed games utilizing all sorts of network-related algorithms, player verification, and arbitrage or cryptographic frameworks. However, the proposals lack a cohesive answer to the question of P2P cheating prevention. In the context of online video games, where sessions between multiple users with some stakes are always present, we believe the offered solution can take a step in establishing a universal setup for securing P2P implementations in this area.

1.2. Manuscript Organization

The manuscript is structured as follows. Section 2 describes all the necessary components for the proposed solution. This includes a simplified game used as an example for the research, an overview of the needed cryptographic constructs, and a layout of the algorithm design. Section 3 states key experimental outcomes obtained from profiling different implementations. Section 4 analyzes said outcomes. Section 5 presents some conclusions and future research lines.

2. Materials and Methods

2.1. Cryptographic Constructs

This research work makes use of certain conventional and well-established cryptographic primitives and protocols described next (in Section 2.1.1, Section 2.1.3 and Section 2.1.4).

2.1.1. Hash Function

Cryptographic hashing is a process that transforms a message, typically of arbitrary length, into a fixed-size output that seems like random noise. This transformation is performed by a hash function that must have certain properties:

• One-way functionality: the result is not reversible.
• Deterministic behavior: a specific input always produces the same output.
• Collision resistance: different inputs never produce identical outputs.

Cryptographic hashing serves as a fundamental tool for ensuring data integrity, secure password storage, and the creation of digital signatures. By generating a fixed-length hash value from input data, it guarantees that any alteration to the original data is immediately detectable. This mechanism is essential for verifying authenticity and maintaining the integrity of sensitive information across various applications.

2.1.2. Oblivious Pseudo-Random Function

An Oblivious Pseudo-Random Function (OPRF) is a two-party protocol in which a client holds a secret input x and a server holds a secret key $k_{OPRF}$; after one brief exchange, the client learns the value $y=F_k\left(x\right)$, while the server learns nothing about x and the client learns nothing about $k_{OPRF}$. Because the output is pseudo-random to everyone who does not know $k_{OPRF}$, an OPRF acts like a keyed hash of the input. This property underpins privacy-preserving systems such as Privacy-Pass tokens and anonymous rate-limiting, password-based key derivation that hides password guesses from servers, private-set-intersection and contact-discovery services, and verifiable randomness beacons where the generator cannot link queries to users.

A standard Diffie–Hellman OPRF [22] based on elliptic curve is described. A prime-order cyclic group $\mathbf{G}$ of order q and generator G is chosen. Specifically, an elliptic-curve group (e.g., ristretto255, P-256, and P-384). All arithmetic is performed in $\mathbf{G}$. Two users are involved: User A has a message x and wants the keyed hash $h_k$ of said value; User B has the hash key $k_{OPRF}$. The protocol is as follows.

• User A maps its value to a point in the chosen elliptic curve $X=H_1\left(x\right)$ using a proper hash to point function.
• User A picks a random value $r\leftarrow {\mathbf{Z}}_q\setminus \left\{0\right\}$, blinds the input $S=r·X$, and sends it to B.
• User B hashes the blinded point $T=k_{OPRF}·S$ and sends the result back.
• User A removes the blinding factor $R=r^{-1}·T$.
• User A performs an unmapping obtaining the final output $y=H_2\left(R\right)$ using a proper point to hash function.

At the end of the protocol, User A has an effective hash of x that can only be obtained using key $k_{OPRF}$. When given $\langle x,y\rangle$, User B can guarantee x has not been changed since the computing of the OPRF as nobody else can evaluate a valid hashing without the private key $k_{OPRF}$. In other words, the OPRF achieves a pre-commitment of its input. A correctness and security proof is provided in Appendix B.

A Verifiable Oblivious Pseudo-Random Function (VOPRF) is an OPRF in which B proves non-interactively and in zero knowledge that it evaluated the hash with its advertised secret key $k_{OPRF}$. Concretely, the server publishes a public key $Y=k_{OPRF}·G\in \mathbf{G}$, and, on a blinded input $S=r·X$ from A, returns not only the evaluation $T=k_{OPRF}·S$ but also a Chaum–Pedersen DLEQ zero-knowledge proof [23] $\pi$ that there is a single scalar $k_{OPRF}\in {\mathbf{Z}}_q$ such that $Y=k_{OPRF}·G$ and $T=k_{OPRF}·S$. With this additional process, malicious security is achieved.

A practical limitation of this VOPRF optimization is its reliance on fast elliptic-curve arithmetic and Chaum–Pedersen DLEQ proofs. Hardware acceleration for the recommended curves (e.g., Ristretto255 or P-384) is inconsistent: many mobile SoCs expose constant-time multipliers only for P-256, while low-power IoT microcontrollers lack any dedicated support, forcing all group operations into slower, potentially side-channel-vulnerable software. The DLEQ proof roughly doubles the number of scalar multiplications per evaluation, one to blind, one to sign, and two to verify, so the client incurs several milliseconds of extra CPU time and a few kilobytes of transient RAM per key on commodity ARM cores. When hundreds of keys are pre-committed, this cost scales linearly and can dominate start-up latency and battery usage on devices without specialized cryptographic engines.

2.1.3. Garbled Circuits

Garbled circuits (GCs) [24,25] enable two parties to securely evaluate an arbitrary function while ensuring that their inputs remain confidential. The function is implemented at the logic gate level, where each gate input bit is substituted with a randomly chosen label and each output bit with a generated ciphertext. The two parties involved in a GC are the generator and the evaluator. The generator prepares the garbled circuit, while the evaluator computes the results. For GC evaluation, one Oblivious Transfer (OT) [26] is required for every evaluator input bit. The foundational concept was introduced in Yao’s seminal work [27]. A correctness and security proof is provided in Appendix A.

GCs have the advantage of being able to compute any arbitrary finite function between two parties, but the longer the function, the more computation and data exchange required. More specifically, a linear dependency is maintained between the length of the function and the circuit cost. Several techniques have been used to address this issue, such as [28,29,30,31,32,33,34,35].

2.1.4. One-Time Pad

A One-Time Pad (OTP) is a single-use encryption method that maps a plaintext message to a ciphertext, offering information-theoretic security. As established in Shannon’s seminal work, any OTP must satisfy certain essential properties [36]:

• The construct must be used once for a single message and then discarded.
• The key of the OTP must be generated randomly.
• The key space K and resulting ciphertext space C must be equal to or greater than the message space M.
• Every possible key must map each distinct message to a distinct ciphertext.

There are many variants of OTPs. In this research work, a classic XOR OTP is utilized. Let m be a message selected from the message space M. Let k be a key randomly selected from the set $K=\{n\in \mathbb{N},n<|M\left|\right\}$. Lastly, let c be the resulting ciphertext. Encryption and decryption are carried out using a bitwise XOR operation:

$$\begin{array}{cc}\hfill & c=m\oplus k\hfill \\ \hfill & m=c\oplus k\hfill \end{array}$$

(1)

2.2. Spades—Proposed Framework

As previously suggested, the approach taken in this work is tailored for scenarios in which multiple users wish to join a shared session where their interactions carry specific, tangible stakes. To illustrate the strengths of this framework, a simplified two-player variant of the card game Spades is used as an example. The game is based on straightforward rules: a standard 52-card deck is dealt so that each player receives 13 cards. During each turn, both players play one card with the goal of earning “points” by playing the highest-ranked card ($A>K>Q>J>10>9>\dots$).

The turn begins with one player playing the first card, after which the opponent must match the suit if they have a card of the same suit. If they do not possess a matching suit, they may play any card. However, failing to follow the suit results in an automatic loss of the turn, with one exception: if the initiating card is not a spade but the response is, the responding player wins the turn. Turns alternate between players until all cards have been played.

Implementing this game with a traditional Client–Server architecture is trivial. Players communicate directly with the server, which keeps track of the game and has the final say on how each round proceeds. Cheating is extremely hard as all the vital information relating to the game state is kept on the server and is not accessible to either player. Additionally, neither player can learn private information (their opponent’s hand, for example) as they have no access to it.

However, if a P2P model is used, where the 2 users directly talk to each other, some problems become apparent. It is important to note that the following complications are inherent to all P2P applications, not only our trivial Spades implementation. Therefore, to achieve a valid solution for any generic application, these problems must be addressed. Before enumerating the specific issues, it is assumed, for a P2P interaction, that a malicious actor can send any desired message to their opponent. The program’s UI can never offer sufficient protection as a user can bypass the interface of an application by running some separate software or reverse engineering the application itself. Once bypassed, any information can be sent to opposing users. Furthermore, the malicious party can view all data related to the session stored locally on their machine. With this critical aspect taken into account, the resulting vulnerabilities can be summarized into 3 main problems.

• Absence of Authority. In the absence of a central server and relying solely on a network of distributed nodes, detecting and preventing dishonest actors from disrupting processes, interactions, or transactions between users becomes a significant challenge. A system with a trusted central entity that holds all authority and oversees that all participants can ensure a higher degree of integrity. However, as illustrated in Figure 1a, this crucial aspect is inherently lacking in Peer-to-Peer (P2P) networks.
• Absence of Secrecy and Privacy. Relying on a network of equal nodes makes maintaining the confidentiality of core data a significant challenge. This data is often essential for verifying the integrity of processes within the system. Furthermore, the issue becomes even more pronounced when an online application needs to perform operations or evaluate functions involving hidden data from multiple user nodes. This limitation is exemplified in Figure 1b.
• Using the System Against Itself. Any proposed solution must consider the possibility that the system could be exploited to target “innocent” users who are falsely accused by malicious actors. In other words, the tools provided cannot operate under the assumption that every allegation of wrongdoing is made in good faith. This scenario is exemplified in Figure 1c.

Lastly, the concept of stakes is important to describe. Stakes are any user investment in participating in an honest session without malicious or dishonest actions. For our Spades example, perhaps there is money on the line and a bet has been made on who wins, perhaps there is an online ranking and winning advances your position in it, or perhaps the players are competing in a tournament with prize money. An application with no stakes is easier to implement using the P2P model. In such cases, if a user detects dishonest or malicious actions, they can simply terminate the session and exit without further consequences. However, when stakes are involved, any instance of cheating must be thoroughly resolved by a trusted authority to ensure fairness and resolution. Once more, using the Spades example, a participant cannot simply walk away when a cheater is detected without losing whatever they initially staked.

This requirement renders the use of a purely P2P model impossible. To address this limitation, a hybrid architecture is proposed. The solution incorporates a small, centralized trusted server, referred to as a “lazy server”, which remains dormant during normal operation and only intervenes when malicious activity is detected.

2.3. Algorithm Design

The presented solution is a combination of several different systems.

2.3.1. Lazy Server

As previously mentioned in Section 1, the scheme incorporates a small central server used for session initialization or when malicious actions are detected by a user. This server is only active during specific key moments; for the rest of the time, it remains dormant, which is why it is referred to as “lazy”. The result is a hybrid system that combines the advantages of both centralized and decentralized architectures.

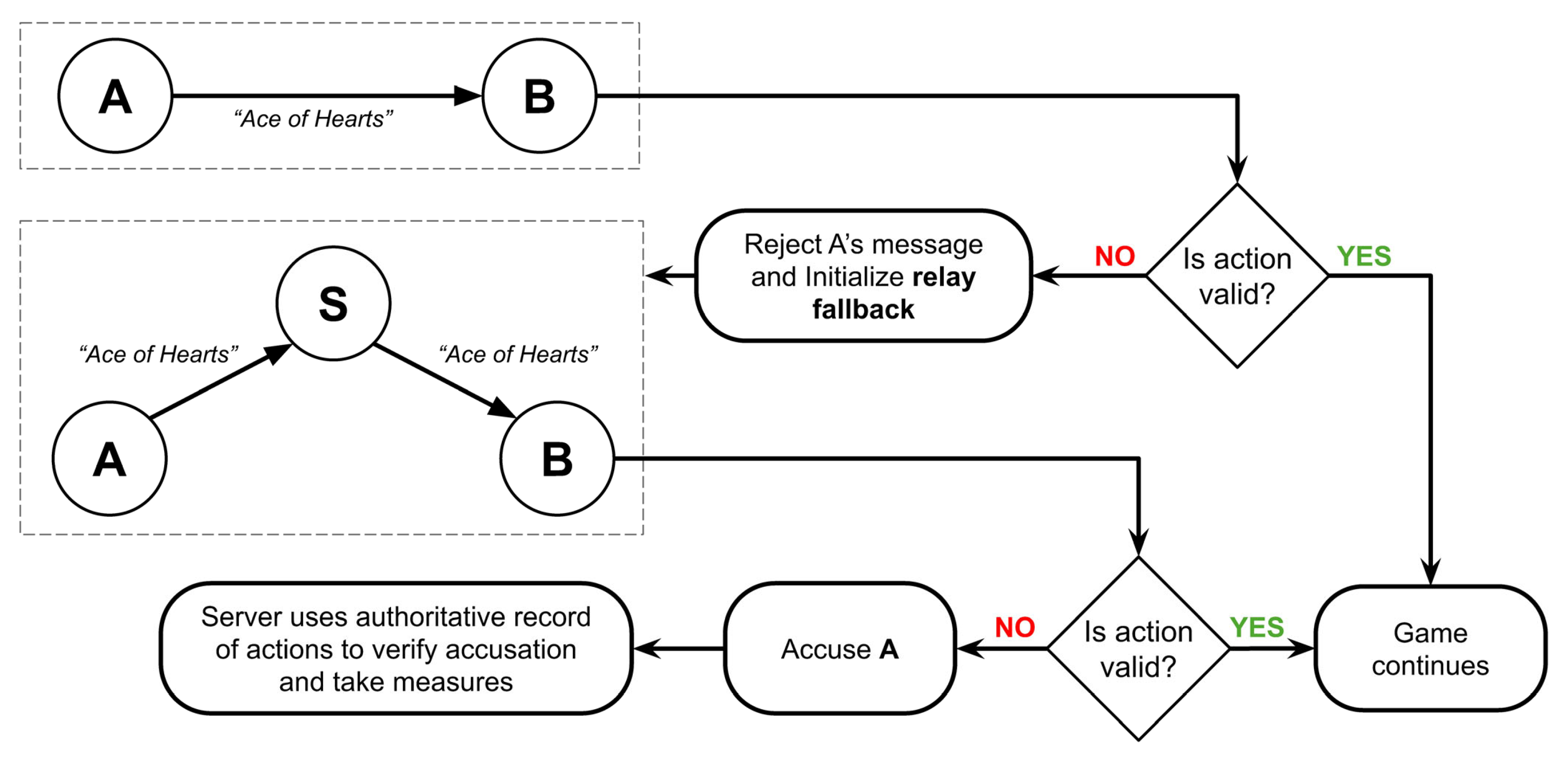
Once a session begins, the two parties communicate exclusively with each other using a P2P protocol or framework (e.g., WebRTC). However, at any point during the session, either user can request a relay fallback from the server. When this occurs, the communication scheme shifts for the remainder of the session, with the lazy server assuming a more active role by relaying messages between the parties. This mechanism introduces complete non-repudiation. Specifically, when a player detects malicious behavior from their opponent, they can reject the action and immediately trigger a relay fallback. With the server now acting as an authority, any further attempts by the opponent to cheat by sending malicious messages must go through the relay, thus creating an authoritative record. The honest player can then use this record to formally accuse the opponent and definitively prove the dishonest behavior.

Intuitively, networking requirements, CPU usage, memory consumption, and overall costs remain minimal when the server is completely dormant. However, once the relay fallback is invoked, these metrics increase. Consequently, the resources required for the proposed solution depend partially on the percentage of malicious actors present in each session, a relationship further explored in Section 3. Even in relay mode, it is important to note that the server remains agnostic to the session’s content, performing no computation or memory-intensive tasks related to the session itself. Its sole responsibility is to relay messages between the parties. Aside from the required networking, a small amount of RAM is allocated to store each user’s most recent message, enabling proper handling of accusations if they arise. This design ensures that, even in this more active role, the overall costs remain significantly lower than those of traditional implementations. This point is further analyzed in Section 3. Lastly, it is worth highlighting that problem 3, depicted in Figure 1c, is effectively resolved since accusations can only be made in relay mode, where the server maintains a trustworthy record of the accused user’s potential misconduct. This guarantees that false accusations are impossible.

2.3.2. Action Verifier

Each action is independently verified by the participants. If a discrepancy is detected, the action is rejected, and the aforementioned server is notified to initiate a relay fallback. This whole construct is applied to our Spades example and is shown in Figure 2.

With this first step, problem 1, showcased in Figure 1a, is partially tackled. The lack of authority is addressed by “summoning” an authoritative source only when necessary. However, an obvious flaw becomes evident in the Action Verifier. It only works with public data. In the provided example (Figure 2), Player B has no way of verifying whether Player A truly holds the Ace of Hearts without exposing Player A’s entire hand. Such a verification process would compromise secrecy and privacy, directly leading to problem 2 (Figure 1b). To address this issue, a new system is introduced.

2.3.3. Encrypted Data Blocks

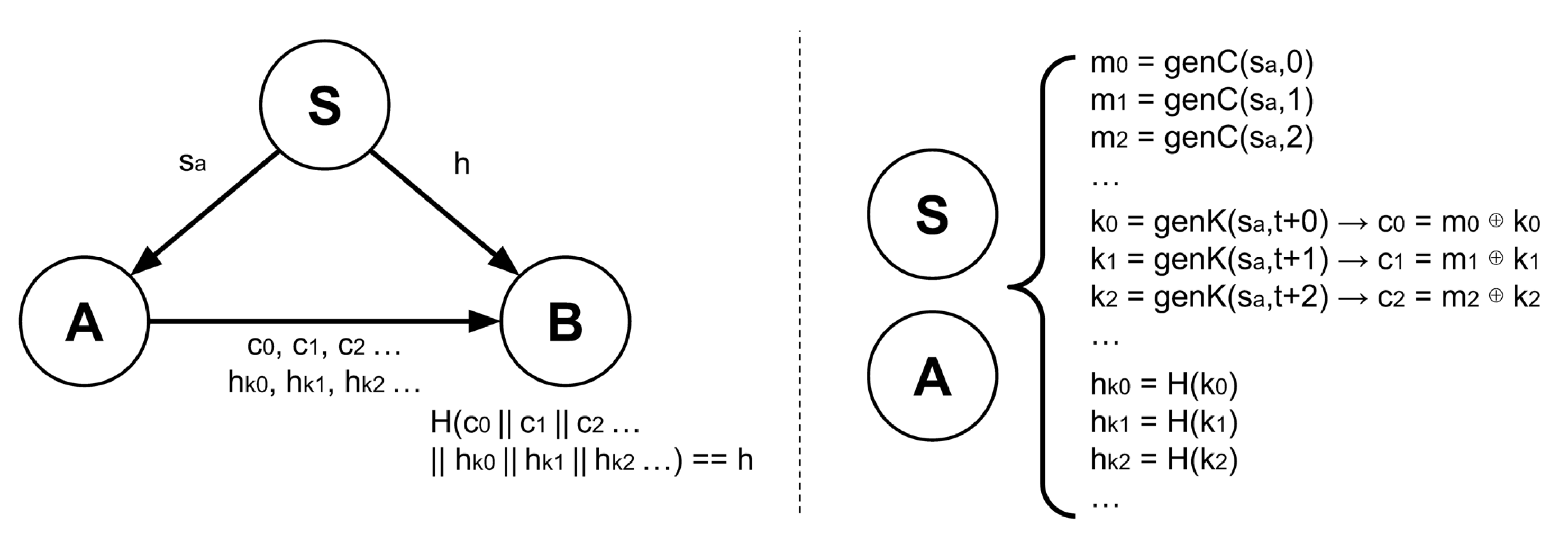
The aforementioned flaw is resolved by encrypting each user’s data using an OTP on the server. The OTP is chosen for its lightweight performance and, above all since it allows subsequent, more complex protocols to be integrated with little overhead. This aspect is further explored in Section 2.3.8.

Each user receives their respective plaintext messages $m_i$ and keys $k_i$, while their opponent is provided with the corresponding ciphertexts $c_i$. In the context of the Spades example, each player is sent 13 plaintext cards and their respective 13 keys, while their opponent receives 13 ciphertexts. During each turn, when a player uses a card, instead of sending that card’s information, they send the position within the data block and the corresponding key, as shown in Figure 3.

This solution is suboptimal because the server’s data transmission requirements scale linearly with the size of the data blocks. In the case of Spades, where a total of 26 cards are needed for two players, this limitation is negligible. However, for applications with larger information requirements, this scaling can become a significant bottleneck. To address this inefficiency, three distinct optimizations are proposed. The process is described for User A’s case but must also be applied symmetrically for User B.

• Rather than transmitting each individual message $m_i$ (e.g., each card), a seed $s_a$ is used. User A expands the seed to generate the required number of messages efficiently, reducing the amount of data transmitted. Note that this technique can only be utilized because drawing cards in Spades is random.
• Instead of sending each individual key $k_i$, the same seed $s_a$ is used. User A expands the seed $s_a$ even more to obtain as many keys as needed.
• Each ciphertext $c_i$ is computed locally by User A using the formula $c_i=m_i\oplus k_i$ and is transmitted directly to User B without involving the server. Note that this optimization is not applicable when dealing with fully hidden information unknown to both players. This limitation is discussed in Section 2.3.7.

Lastly, it is important to mention the lack of malicious security. Specifically, at the start of a session, User A could send fictitious ciphertexts, or during each turn, they could transmit a fabricated key to User B. Player B has no means to verify the authenticity of the received information, leaving the system vulnerable to such actions. Two alternatives based on hash functions are considered for ciphertext and key verification: direct server hashing and a VOPRF.

2.3.4. Direct Server Cipher-Text and Key Hashing

In the first approach, the server sends the opponent (in this case, User B) a hash of all concatenated ciphertexts, $h_c=H(c_0\left|\right|c_1\left|\right|c_2\dots )$. User B can subsequently verify the data sent by Player A at the start of a session by performing $H(c_0\left|\right|c_1\left|\right|c_2\dots )==h_c$. As discussed in Section 2.1, cryptographic hash functions are collision-resistant and deterministic, ensuring that User A cannot generate “fake” data to deceive User B.

For key verification, a naive initial scheme involves creating a hash for each key $k_i$ on the server, defined as $h_i=H\left(k_i\right)$. The resulting hashes are then sent to the opponent (in this case, User B). During each turn, when Player A sends a concatenated position and key $i\left|\right|k_i$, Player B can verify the validity of the message by performing the comparison $h_i==H\left(k_i\right)$. As discussed in Section 2.1, cryptographic hash functions are irreversible, ensuring that the opponent cannot derive any information about the underlying keys.

Naive key hashing addresses the problem but requires additional data transmission from the server during a session. This introduces a linear dependency between the length of the data block and the required exchange, which can become a limiting factor. To mitigate this issue, the responsibility of transmitting each key hash $h_{ki}$ is delegated to User A. The server instead provides User B with a single hash of all concatenated key hashes for verification: $h_k=H(h_{k0}\left|\right|h_{k1}\left|\right|h_{k2}\dots )=H(H\left(k_0\right)\left|\right|H\left(k_1\right)\left|\right|H\left(k_2\right)\dots )$ for verification. User B validates the entire set by performing the comparison $h_k==H(h_{k0}\left|\right|h_{k0}\left|\right|h_{k0}\dots )$.

As a last optimization, the ciphertext and key hashes ($h_c$ and $h_k$) can be combined into a single combined hash: $h=H\left(c_0\right|\left|c_1\right||c_2\dots |\left|h_{k0}\right|\left|h_{k1}\right||h_{k2}\dots )$. The entire process is illustrated in Figure 4.

Note that the OPT encryption speeds up hashing as both keys and ciphertext will end up being as long as the messages, unlike most schemes where these can be several times larger.

2.3.5. VOPRF Key Hashing

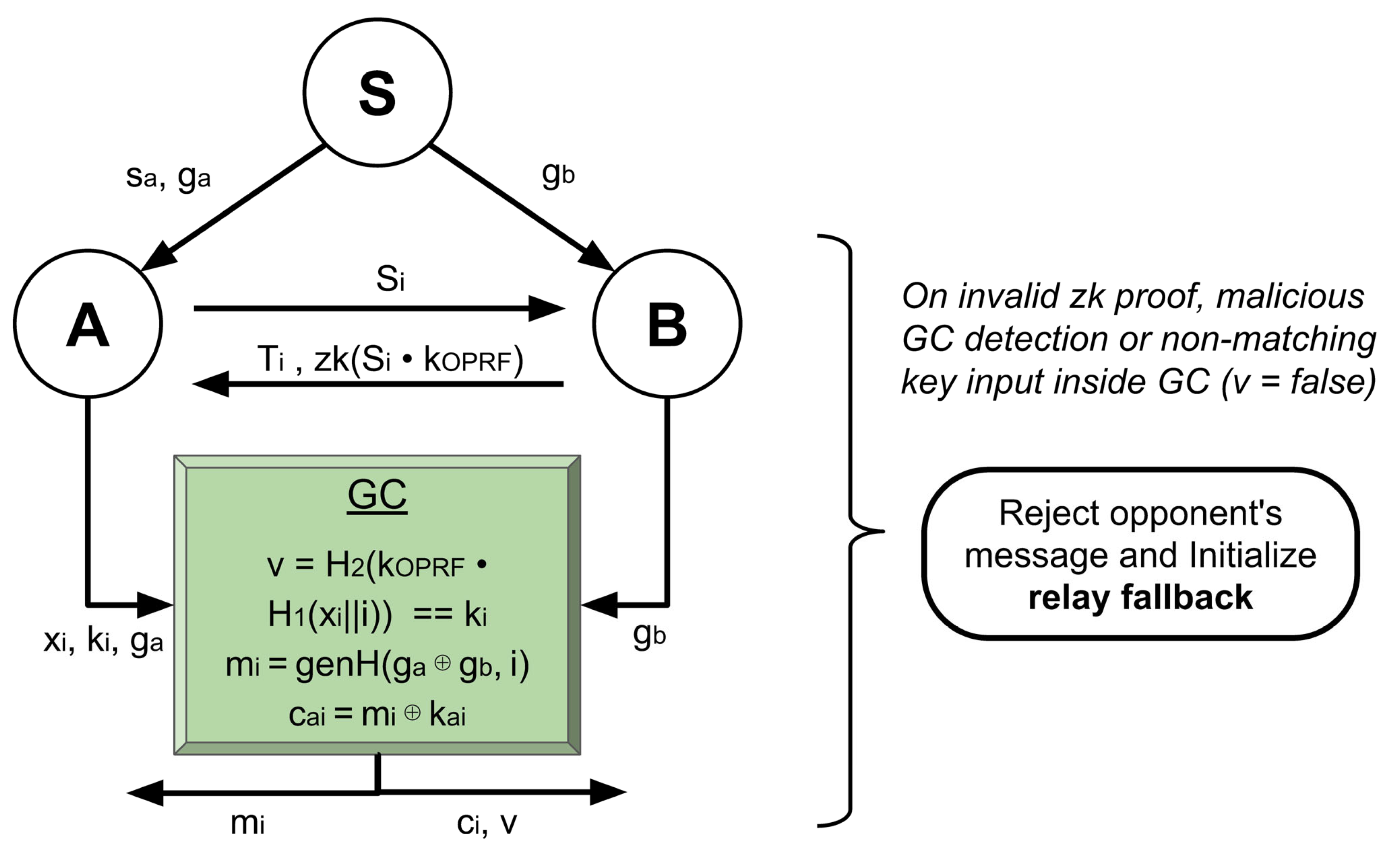
As aforementioned in Section 2.3.4, direct server hashing has a constant networking requirement that greatly minimizes application latency. However, it still demands a linear computational cost. To somewhat reduce such cost, an alternative is proposed: VOPRF in Section 2.1.2.

For each key $k_i$,

• User A generates a random value $x\leftarrow {\mathbf{Z}}_q\setminus \left\{0\right\}$ with seed $s_a$ sent by the server.
• User A appends the index $x^{\prime }=x\left|\right|i$, thus tying the final key to its position in the encrypted data blocks.
• User A maps its value to a point in the chosen elliptic curve $X=H_1\left(x^{\prime }\right)$ using a proper hash to point function.
• User A picks a random value $r\leftarrow {\mathbf{Z}}_q\setminus \left\{0\right\}$, blinds the input $S=r·X$, and sends it to B.
• User B hashes the blinded point $T=k_{OPRF}·S$ and sends the result back alongside a Chaum–Pedersen zero-knowledge proof $\pi$ of the performed operation achieving a maliciously secure protocol.
• User A removes the blinding factor $R=r^{-1}·T$.
• User A performs an unmapping obtaining the final output $k_i=H_2\left(R\right)$.

Note that instead of using the initial value x, the final output is utilized. The usage of suitable EC hash functions $H_1\left(\right)$ and $H_2\left(\right)$ as well as the randomness of the initial setup x gives no hint to B as to how to construct further keys. Since $k_{OPRF}$ is pre-committed for the Chaum–Pedersen zk proof, B has no opportunity to mess with the protocol. Additionally, even if A chooses an opportunistic value x, the multiplication by $k_{OPRF}$ in step number five assures a completely random result. When transferring a key for decrypting a ciphertext, User A will send the values x, $k_i$, and i. User B, by reproducing the keyed hash, will demonstrate whether the random key is the pre-committed one and whether it is of correct index i.

With this optimization, part of the linear computational cost of initialization is removed. The keys are handled entirely by the users. The ciphertext can be hashed on the server as previously or computed with a subsequent MPC protocol. For instance, in the current Spades example, each message (card to draw) is sampled randomly. Thus, these can be generated with a simple non-cryptographic pseudo-random algorithm inside a GC and subsequently XOR-ed with their corresponding keys. An example implementation of this idea can be seen in Figure 5. Malicious security for these constructs will be discussed in subsequent sections.

The combination of ciphertext and key hashing provides a maliciously secure system. However, one final challenge remains. Consider the scenario depicted in Figure 1b, where Player A is unable to follow suit and decides to play the six of spades. How can Player A definitively prove to Player B that they had no heart cards while simultaneously preserving their privacy? This issue is addressed in the following subsection.

2.3.6. Privacy-Preserving Processor

The scenario depicted in Figure 1b illustrates the functionality of the privacy-preserving processor. Player B plays first, selecting the Seven of Hearts. Player A, lacking any hearts, is unable to follow suit and instead plays the Six of Spades, thereby winning the turn (since spades always win when the suit is not followed). The objective is to provide proof to Player B that Player A holds no hearts, without revealing any additional information about Player A’s hand.

As a first slottable proposal, GCs will be used. Let us begin by defining how each card is represented. Any card can be encoded using 6 bits. The first 2 bits contain the card’s suit (diamonds = 00, hearts = 01, clubs = 10, and spades = 11), while the remaining 4 bits represent the card’s value. Four bits are sufficient to represent 16 distinct values, which is adequate for our purposes. A composite GC is built to examine the first two bits of every card in Player A’s hand. For each pair of bits, the circuit outputs a single output indicating whether a specific suit has been detected. For n cards in Player A’s hand, n circuits are prepared, each computing $\overline{b_0}\wedge b_1$, where $b_0$ and $b_1$ are the two bits representing the card’s suit. This circuit is specifically designed to detect hearts. A more general circuit can be inferred for any suit using $(b_0\oplus \overline{s_0})\wedge (b_1\oplus \overline{s_1})$, where $s_0$ and $s_1$ represent the target suit to be examined.

As a final remark, once more, it should be noted that this initial implementation does not provide malicious security. Player A could generate a compromised circuit that consistently returns a desired output in their favor. Extensive research has been conducted on efficiently achieving maliciously secure GCs, such as [37,38,39]. A simple cut-and-choose [37] technique can be leveraged, or if security can be slightly relaxed to 1 bit leakage, a dual execution with swapped roles can be chosen [39,40,41]. Alternatively, there are also more modern proposals and implementations [42,43]. Lastly, GCs require one Oblivious Transfer (OT) per evaluator input bit. Any OT should also be generated in a maliciously secure manner.

Any malicious approach plays nicely with our message verifier as any GC discrepancy will trigger a relay fallback. Note that, in relay mode, GCs are no longer needed and the central server can be asked to perform the desired checking whilst preserving privacy (this process is identical in the traditional Client–Server architecture). Developers can make the choice of maintaining session agnosticism or reducing data transfer by eliminating GCs.

As a GC alternative, a Function Secret Sharing (FSS) [44,45] scheme is considered where two parties obtain additive shares of a specific function. In this case, we create XOR additive shares of a comparison as presented in [46]. The comparison is achieved by altering a distributed point function.

Instead of garbled circuits, we adopt Function Secret Sharing (FSS) [44,45] and, in particular, its two-party distributed comparison function (DCF) variant [46]. The key–generation algorithm takes a threshold $\alpha$ and a payload $\beta$, producing two short keys $(k_0,k_1)\leftarrow {\mathsf{KeyGen}}_{\mathsf{DCF}}(\alpha ,\beta )$ such that for every input $x\in {\{0,1\}}^{\lambda }$

$$\mathsf{Eval}(k_0,x)\oplus \mathsf{Eval}(k_1,x)=\left\{\begin{array}{cc}\beta \hfill & \mathrm{if}x<\alpha ,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

In our card-game setting, we encode the suit with the two high-order bits and instantiate a DCF. A one-time setup hands each player its key share (≈128 bits for classical security); at runtime, each player computes a local $\mathsf{Eval}(k_i,x)$ and sends the 32-bit result to their opponent. XOR-aggregating the two shares reveals only the one-bit predicate. Online bandwidth is thus constant versus one malicious-secure oblivious transfer per input bit in the GC approach, and active security can be added by appending lightweight MACs over the pseudo-random tapes.

To finalize this subsection, some speculation is provided on the compatibility of our slotabble solution with existing well-established MPC frameworks. As stated, every intermediate word in the protocol is protected by an XOR OTP, so a value can be exported from the processor and imported into an external MPC engine with a single XOR operation. This constant-time “glue layer” lets the processor embed directly inside widely used tool chains such as SPDZ, EMP-toolkit, and ABY—without modifying their internals.

SPDZ [47]: Values under the OTP are interpreted as field elements mod p. On entry to SPDZ, the global session MAC key is added once; on exit, the value is re-masked with the OTP. The standard SPDZ workflow regarding offline triple generation, online computation, and reveal runs unchanged. As future research, the same solution can be implemented with additive OTP, reducing external computation even further.

EMP-toolkit [48]: EMP already works in the XOR domain. The OTP key can be treated directly as the garbled-wire mask bit vector, so no conversion is required: pass the ciphertext as a garbled label, evaluate the circuit and then XOR with the same key before transmission.

ABY [49]: For Boolean shares, the procedure is identical to EMP. For arithmetic shares, the same trick as SPDZ applies. For Yao shares, the OTP mask can serve as the global offset $\Delta$. ABY’s built-in converters allow seamless switching between share types, while the OTP remains the outer envelope. Once more, future work can examine an additive OTP for additional speedup.

The XOR-OTP layer remains advantageous: it adds only a single XOR for masking or unmasking, regardless of field size or circuit width, so no extra cryptography is incurred; the same OTP uniformly protects Boolean and arithmetic data, simplifying auditing and fallback logic.

2.3.7. Hidden Data

A concept mentioned in Section 2.3.3 is properly explained. The example provided in this research involves two types of information: public data, which is known to both players (e.g., the card played during a specific turn), and private data, which is only known to one player (e.g., a player’s hand). However, depending on the application, it is possible to encounter a third kind, hidden data. This type is not known by either participant. Imagine a game where each turn a player must draw a card from a shuffled deck. The deck’s order, meaning each card in it, must remain hidden from both users and can only be revealed at an appropriate time. This third kind of information makes initialization harder as it requires different considerations. Using, once more, an OTP where each block of hidden data $m_i$ is encrypted with a random key $k_i$ to generate a cipher $c_i$, some particularities become apparent.

First, both players must maintain a record of this hidden data, requiring each party to have ciphertexts of the same message along with corresponding keys specific to the other player. Therefore, ciphertexts are generated as $c_{ai}=m_i\oplus k_{ai}$ and $c_{bi}=m_i\oplus k_{bi}$. Furthermore, the optimization described in Section 2.3.3 becomes infeasible. From Player A’s perspective, while all necessary keys $k_{ai}$ can still be generated from a single seed, the ciphertexts cannot be computed locally as Player A does not know the messages (they remain hidden). Player B encounters the same limitation. Since the objective of this study is to provide a versatile, general-purpose framework suitable for various types of applications, addressing the initialization of hidden data is essential, even if such functionality is not required for a Spades game.

The first solution involves having the server send each individual ciphertext $c_i$ directly to Player B. While this approach is simple and straightforward, it introduces a linear dependency between the amount of data exchanged by the server and the quantity of hidden data, which may become a limiting factor for certain applications.

As an alternative, a GC can be designed to compute the hidden messages, encrypt them using the provided keys, and output the resulting ciphertexts. In this sense, the respective keys and ciphertexts become homomorphic secret shares of the message. This second approach minimizes server involvement, maintaining it at a constant level regardless of the amount of hidden data. An example of this implementation is illustrated in Figure 6.

2.3.8. OTP Homomorphism and Composability

For more advanced applications that require more intricate functions, the XOR OTP can significantly reduce protocol overhead. For example, by exploring its innate homomorphism, some operations can be trivially solved without any additional privacy-preserving computation. Specifically, this construct presents a partially homomorphic property where XORing a plaintext value v to a ciphertext is equivalent to XORing it to the message itself $E\left(m\right)\oplus v=E(m\oplus v)$. While this attribute is often regarded as a drawback due to its potential for malicious data manipulation, it can be leveraged to optimize certain processes under controlled conditions. For instance, if a player needs to flip a specific bit within an encrypted data block, this operation can be performed without decrypting the block or involving the other user.

Additionally, XOR OTP can combine multiple ciphertexts. For $c_1=m_1\oplus k_1$ and $c_2=m_2\oplus k_2$, these can be XOR-ed together, forming a new encrypted value $c_3=(m_1\oplus m_2)\oplus k_3$ where $k_3=k_1\oplus k_2$

For GC operations where the value inside a ciphertext must be altered or when a newly formed value must be encrypted (similar to Figure 6), encryption is completely free. This is due to the Free XOR GC optimization [28], which, given specific OT generation, allows for the evaluation of XOR gates at no extra cost. Thus, ciphertext manipulation becomes incredibly easy.

For additional MPC protocols, this composability holds as well. Most schemes are either based on additive secret sharing (such as HSS or FSS) or can be trivially adapted to it. For example, take the comparison function evaluated in Section 2.3.7. If there was a need for the output to be OTP encrypted, one of the parties (or both) can XOR a secret key. The result will still match the comparison, but it will be contained within a ciphertext. This also holds for the other examined frameworks such as SPDZ, EMP, and ABY.

In short, the XOR one-time pad acts as a “lossless glue layer” between otherwise disparate MPC components: any intermediate wire value—whether it comes from a garbled-circuit gate, an additive share, or an FSS evaluation—can be (re)encrypted or combined with another ciphertext by a single local XOR, incurring literally zero extra cryptographic cost. It is thus the perfect choice to ensure a composable solution.

2.4. Security Model and Threat Analysis

To complete Section 2, we state the exact assumptions under which our hybrid framework is secure and explain how the protocol is compiled from a semi-honest design into a maliciously secure one with identifiable abort as long as the dormant lazy relay behaves honestly.

Each session involves two peers, A and B, who exchange messages through a fully adversarial network and, when necessary, interact with a third party S that stores pre-commitments and relays traffic after a timeout. The adversary controls scheduling can delay or drop packets and may statically corrupt one of the peers. Baseline analysis is performed in the universally composable (UC) semi-honest model, where a corrupted party follows the code but inspects the entire transcript.

Malicious behavior is detected by binding every secret input to a session-unique tag before any computation starts; when the real value is later revealed, an honest verifier checks that it matches the original tag, and any mismatch exposes the cheater with probability $1-2^{-\lambda }$. Two alternative binding channels are implemented and exactly one is chosen per deployment. Either variant suffices to lift the whole protocol to the malicious model:

(H)

Hash pre-commitment: the relay sends each opponent a single Merkle-style digest $h=H\left(c_0\right|\left|c_1\right||c_2\dots |\left|h_{k0}\right|\left|h_{k1}\right||h_{k2}\dots )$ that covers every ciphertext and every key hash. Verification is purely deterministic hashing.

(V)

VOPRF pre-commitment: the relay holds a static secret key $k_{OPRF}$ and returns to each player a blinded evaluation $F_k(x\parallel i)$ together with a Chaum–Pedersen proof. The resulting tag is a keyed hash that can only be reproduced with the same key, giving sound binding and zero-knowledge privacy.

Above the tag layer, every message is encrypted under an XOR one-time pad, so any two-party primitive that outputs authenticated additive shares can be slotted in without additional cryptographic glue. Typical choices are Free-XOR/half-gate garbled circuits hardened by modern cut-and-choose schedules; IKNP or Ferret OT extension with correlation checks; and two-party function-secret-sharing for comparisons. Each primitive has a known compilation path to malicious security with constant-factor overhead; hence, the framework inherits privacy, correctness, and fairness in the strong adversarial setting.

All security arguments presented above implicitly require the relay to behave with perfect honesty. The server chooses the per-player seeds $s_a,s_b$ that expand into every ciphertext, one-time-pad key and Merkle/VOPRF tag; it also stores the sole authoritative copy of those tags and, once a fallback is triggered, mediates every subsequent message. If the relay deviates from the prescribed code or secretly colludes with a corrupted peer, both the semi-honest and malicious guarantees collapse entirely. A cheating server can inject biased seeds that allow it (or its confederate) to reconstruct private inputs, swap the public hash or substitute a fresh VOPRF secret key so that forged data looks legitimate, and finally reorder, drop, or fabricate relay traffic so that the observable transcript matches any outcome it wishes. In such a scenario, confidentiality, integrity, fairness, and non-repudiation all fail: the server can learn, publicize, or arbitrarily alter user inputs and session results, while honest players lack any cryptographic evidence to prove misconduct.

Under the hardness of discrete logarithms in the chosen elliptic-curve group, the collision resistance of the hash, and the secrecy of the XOR one-time pad, the protocol UC realizes the ideal stakes-based two-party functionality: (i) a coalition of one corrupted peer plus the network learns nothing beyond its prescribed output; (ii) honest peers either agree on the same deterministic result or obtain a cryptographic proof that identifies a cheater; and (iii) the construction remains secure when several instances run concurrently.

3. Results

Four distinct case studies are evaluated using the emulation code provided in [50]. Each scenario consists of a game with a different amount of private information and turns. Additionally, CPU usage, memory consumption, and network activity are measured across all scenarios. The results are presented in two tables: one for the initialization phase and another for the gameplay phase. Each table compares the traditional Client–Server approach (base) with the hybrid solution proposed in this research work (hybrid). The hybrid implementation utilizes the direct server key and ciphertext hashing presented in Section 2.3.4. The results are aggregated from 100,000 executions and were obtained using a single core (and one logical processor) of an AMD Ryzen 9 5900X CPU. This setup was specifically chosen to provide a clear assessment of process speed, enabling direct comparison with similar solutions. It is important to highlight that the calculations are highly parallelizable and could achieve significant acceleration with multiple cores or GPU support. The use of a single logical processor in this evaluation demonstrates the baseline execution speed of the process. The four cases are the following:

• Basic Spades. Each player is dealt 13 cards and the game consists of 13 turns. The results for this scenario are presented in

  Table 1. CPU execution times, memory usage, and data transfers for a game initialization involving 13 cards and 13 turns. Average of 100,000 executions.

  Setup	CPU	Memory	Network	Network
  	(ms)	(MB)	in (MB)	out (MB)
  Base	281	7.63	0	2.48
  Hybrid	485	3.05	0	9.16

  and

  Table 2. CPU execution times, memory usage, and data transfers for a game involving 13 cards and 13 turns. Average of 100,000 executions.

  Setup	Relay	Cheater	CPU	Memory	Network	Network
  	Fallback	Detected	(ms)	(MB)	in (MB)	out (MB)
  Base	No	No	14	7.63	2.48	2.48
  Hybrid	No	No	0	3.05	0	0
  Hybrid	Yes	No	3	3.24	1.24	1.24
  Hybrid	Yes	Yes	1	3.24	0.29	0.29

  .
• Increased Number of Cards. The number of cards per player is increased to 100, while the number of turns remains 13. This modification can be generalized to games or applications with a larger amount of private data. For instance, a more complex card game or a turn-based strategy game may require such conditions. The results are shown in

  Table 3. CPU execution times, memory usage, and data transfers for a game initialization involving 100 cards and 13 turns. Average of 100,000 executions.

  Setup	CPU	Memory	Network	Network
  	(ms)	(MB)	in (MB)	out (MB)
  Base	336	24.22	0	19.07
  Hybrid	1212	3.05	0	9.16

  and

  Table 4. CPU execution times, memory usage, and data transfers for a game involving 100 cards and 13 turns. Average of 100,000 executions.

  Setup	Relay	Cheater	CPU	Memory	Network	Network
  	Fallback	Detected	(ms)	(MB)	in (MB)	out (MB)
  Base	No	No	15	24.22	2.48	2.48
  Hybrid	No	No	0	3.05	0	0
  Hybrid	Yes	No	3	3.24	1.24	1.24
  Hybrid	Yes	Yes	1	3.24	0.29	0.29

  .
• Increased Number of Turns. The number of turns is significantly increased to 6000, while the number of cards remains at 13. Adding more turns simulates a longer-lasting application or a real-time game. For this example, a scenario is modeled where a session lasts an average of 10 min, with the state updated 10 times per second. The results are detailed in

  Table 5. CPU execution times, memory usage, and data transfers for a game initialization involving 13 cards and 6000 turns. Average of 100,000 executions.

  Setup	CPU	Memory	Network	Network
  	(ms)	(MB)	in (MB)	out (MB)
  Base	278	7.63	0	2.48
  Hybrid	491	3.05	0	9.16

  and

  Table 6. CPU execution times, memory usage, and data transfers for a game involving 13 cards and 6000 turns. Average of 100,000 executions.

  Setup	Relay	Cheater	CPU	Memory	Network	Network
  	Fallback	Detected	(ms)	(MB)	in (MB)	out (MB)
  Base	No	No	4798	7.63	1144	1144
  Hybrid	No	No	0	3.05	0	0
  Hybrid	Yes	No	1471	3.24	572	572
  Hybrid	Yes	Yes	1	3.24	0.29	0.29

  .
• Increased Cards and Turns. The previous two scenarios are combined, resulting in a longer real-time application with substantially more private data. This setup can represent, for instance, a real-time strategy game between two players. The results for this scenario are presented in

  Table 7. CPU execution times, memory usage, and data transfers for a game initialization involving 100 cards and 6000 turns. Average of 100,000 executions.

  Setup	CPU	Memory	Network	Network
  	(ms)	(MB)	in (MB)	out (MB)
  Base	337	24.22	0	19.07
  Hybrid	1218	3.05	0	9.16

  and

  Table 8. CPU execution times, memory usage, and data transfers for a game involving 100 cards and 6000 turns. Average of 100,000 executions.

  Setup	Relay	Cheater	CPU	Memory	Network	Network
  	Fallback	Detected	(ms)	(MB)	in (MB)	out (MB)
  Base	No	No	4044	24.22	1144	1144
  Hybrid	No	No	0	3.05	0	0
  Hybrid	Yes	No	1472	3.24	572	572
  Hybrid	Yes	Yes	2	3.24	0.29	0.29

  .

Finally,

Table 9. Improvement comparison for each metric based on case study and depending on cheating percentage. Initialization NOT included.

Case	Cheater	CPU	Memory	Network	Network
Study	Percentage	Improv	Improv	in Improv	out Improv
(#)	(%)	(%)	(%)	(%)	(%)
1	10	98.57	59.78	96.92	96.92
	25	96.43	59.40	92.29	92.29
	50	92.86	58.78	84.58	84.58
2	10	98.67	87.33	96.92	96.92
	25	96.67	87.21	92.29	92.29
	50	93.33	87.01	84.58	84.58
3	10	98.46	59.78	97.50	97.50
	25	96.16	59.40	93.75	93.75
	50	92.32	58.78	87.49	87.49
4	10	98.18	87.33	97.50	97.50
	25	95.44	87.21	93.75	93.75
	50	90.89	87.01	87.49	87.49

and

Table 10. Improvement comparison for each metric based on case study and depending on cheating percentage. Initialization included.

Case	Cheater	CPU	Memory	Network	Network
Study	Percentage	Improv	Improv	in Improv	out Improv
(#)	(%)	(%)	(%)	(%)	(%)
1	10	−64.47	59.90	96.92	−86.22
	25	−64.58	59.71	92.29	−88.53
	50	−64.75	59.40	84.58	−92.39
2	10	−245.36	87.37	96.92	57.14
	25	−245.44	87.31	92.29	56.61
	50	−245.58	87.21	84.58	55.72
3	10	88.88	59.90	97.50	96.71
	25	86.70	59.71	93.75	92.96
	50	83.07	59.40	87.49	86.72
4	10	70.52	87.37	97.50	96.75
	25	67.99	87.31	93.75	93.06
	50	63.79	87.21	87.49	86.91

provide a comprehensive summary of the improvements or potential drawbacks introduced by the hybrid approach across the different case studies, based on the percentage of games involving a cheater. Table 9 focuses exclusively on gameplay performance, while Table 10 includes measurements from both the initialization phase and the gameplay. These results are further visualized in Figure 7, offering a clear graphical representation of the data.

4. Discussion

Before conducting a detailed analysis, several aspects of the methodology deserve attention. First, the obtained values are based on emulation. While this approach provides highly informative data, it inherently sacrifices some precision compared to real-world implementations.

Second, our current experiments use a single-threaded CPU emulator that runs all parties on one machine. This choice simplifies instrumentation but omits key practical aftereffects such as network latency, packet loss, and user churn, and it restricts the evaluation to a two-player scenario. As a result, we do not yet measure real-world overhead or potential advantages of parallel message processing and concurrent MPC engines. Future work will deploy the framework on a distributed testbed with variable RTTs and fault injection, extend the case studies to n-player coordination tasks, and enable true multi-threaded execution so that parties can overlap cryptographic work with network I/O. Such experiments will expose scalability bottlenecks and allow us to quantify how far parallel code paths, both within an MPC engine and across independent engines running simultaneously, can hide individual cryptographic latencies.

Third, as discussed in Section 3, increasing the two variable parameters, namely, the number of cards and turns, is employed to emulate different scenarios. Since the original software [50] was designed specifically for the game Spades, measurements obtained with an artificially higher number of cards and turns lose some specificity. Therefore, in this analysis, greater emphasis is placed on the relative values, such as the comparison between the base and hybrid versions or across different tables, rather than on the absolute values themselves. Future work will focus on profiling a real-world complex application to obtain more practical and representative results.

Analyzing the initialization phase across the four case studies (Table 1, Table 3, Table 5 and Table 7), the following observations can be made:

CPU times for both the base and hybrid implementations are proportional to the number of cards (these represent the amount of private information generated by the server for each player). Intuitively, this behavior is expected as a larger dataset requires increased computational effort during the initialization of a game. This includes tasks such as creating corresponding classes and data structures, generating random values for each player’s cards, and other preparatory operations. Furthermore, the hybrid solution always requires greater computation. Once more, this is expected as additional cryptography must be performed.

The memory requirements of the base implementation scale proportionally with the number of cards, whereas the hybrid scheme maintains constant memory usage. This behavior arises from the compute-and-hash approach employed by the hybrid architecture. In this approach, the necessary data is generated “chunk by chunk” and incrementally processed by the chosen hash function. Each generated chunk is introduced into the hash function’s digest, updating the hash registers. Once the registers are updated, the next chunk is generated and processed. This method requires only a constant amount of memory, sufficient to store a single chunk and the hash registers, regardless of the total amount of data.

The incoming network traffic remains at 0 for both implementations. Outgoing network traffic, however, scales proportionally with the number of cards in the base implementation, whereas it remains constant in the hybrid approach. This difference arises because the hybrid scheme sends only a seed, which is subsequently expanded by the respective players to generate the required information locally. It should be noted that this result is not entirely conclusive as the traditional approach could be similarly optimized using the same seed expansion method.

Analyzing the game or application itself across the four case studies (Table 2, Table 4, Table 6 and Table 8), it is important to note that the hybrid section is divided based on two conditions: whether the fallback protocol has been initialized and whether a cheating accusation has been made. For the purposes of this analysis, it is assumed that, on average, the relay mode is initiated at the midpoint of the game. Additionally, if an accusation occurs, it is assumed to take place immediately after the relay is engaged. The final table subdivision (last two rows) accounts for scenarios in which a malicious player, upon entering relay fallback mode, decides to either cheat or cease cheating and continue playing honestly for the remainder of the game. If the relay is triggered, the two most probable outcomes for a potential cheater are being immediately caught or choosing to continue playing honestly until the end.

Returning to the analysis, the following observations can be made: CPU times for the base implementation are proportional to the number of turns. This behavior is expected as the traditional approach requires continuous server-side computation throughout the session. For the hybrid implementation, three key aspects stand out.

First, in sessions where no dishonest actions are detected, the lazy server performs no computation, resulting in minimal resource usage. Second, when a cheating accusation is made during relay mode (last row), some additional CPU time is required to verify the claim. However, this required computational demand is trivial and remains constant regardless of the session’s length. Lastly, the worst-case scenario for the hybrid approach happens when the fallback protocol is triggered, and the malicious player decides to continue playing honestly. In this situation, computation becomes proportional to the number of turns. Even so, the hybrid approach remains significantly more efficient, requiring approximately 3–4 times less CPU time than the base implementation. This efficiency is attributed to the fact that simply transferring messages and performing occasional comparisons are far less resource-intensive than evaluating the full game logic. The performance gap becomes even more pronounced when compression is utilized as the relay can bypass decompression for most messages and simply forward them directly.

Memory usage in the base implementation scales proportionally with the number of cards, while it remains constant in the hybrid approach. Similar to the initialization phase, the hybrid scheme maintains only a single seed per player, which is expanded as needed. In contrast, the traditional architecture retains and uses each player’s private data throughout the entire session, making it infeasible to store the information as a seed alone.

Incoming and outgoing network usage in the base implementation scales proportionally with the number of turns. This behavior is intuitive as longer sessions naturally involve more communication. For the hybrid implementation, the network usage follows a pattern similar to CPU times. When no relay is triggered, the server remains completely dormant, requiring no network activity. If the fallback protocol is activated and a cheater is detected, a constant (and negligible) amount of network usage is required for verification. Lastly, if the potentially malicious player decides to play honestly after the relay is engaged, even in this case, the network usage remains lower than that of the base implementation due to the reduced communication overhead in the hybrid approach.

In summary, the proposed hybrid solution trades some additional CPU time during the initialization phase to optimize all performance aspects once the game begins, including CPU usage, memory consumption, and incoming and outgoing network traffic. These improvements become significantly better as the amount of private player data (e.g., number of cards) and the session duration (number of turns) increase. Even in the worst-case scenario, where one player detects some dishonest behavior, triggers the server involvement, and the opponent subsequently decides to play honestly for the remainder of the game, the required hardware resources remain lower than those of the traditional approach. In practical terms, this translates into substantial reductions in back-end costs and a corresponding decrease in overall energy consumption.

Moreover, the increased computation can be optimized away by leveraging the VOPRF scheme described in Section 2.3.5. This algorithm removes the linear dependency between CPU timings and the number of cards. Instead of hashing each card key and ciphertext, the players resolve the entire initialization by themselves. The trade-off is a more complex P2P handshake that relies on an elliptic-curve VOPRF with a small zero-knowledge proof. In practice, this can bring hardware and software hurdles, as mentioned in Section 2.1.2. Only a subset of devices ship with fast curve instructions (often limited to P-256), while others must perform every scalar multiplication in constant-time software. The proof step roughly doubles those multiplications, so batching many keys can still add a few milliseconds of CPU and some extra RAM on low-power or mobile hardware. These limitations should be taken into consideration when utilizing this alternative.

4.1. Cheater-Percentage-Dependent Improvements

Combining all the described results data, we can theorize about the percentage of sessions involving at least one malicious actor (referred to as the “cheater percentage”) and determine the corresponding hardware requirements to highlight the improvements offered by the hybrid solution. To establish baseline percentages, we reference existing studies and reports on cheating in video games.

First, Blackburn et al. [51] conducted a quantitative study analyzing Steam users, examining how many were banned for cheating. Out of 10,191,296 profiles analyzed, 720,469 were identified as cheaters, resulting in a 7% cheating ratio. Additionally, in 2018, the cybersecurity company Irdeto, specializing in digital platform security, published a report [52] based on a survey of 9,436 adults, including 5911 gamers aged 18 and older. One of the key findings is that 23% of participants admitted to regularly using third-party software to cheat (3% always, 8% often, and 12% sometimes).

From these findings, we consider three distinct cheater percentage scenarios. An optimistic assumption of 10%, closely aligned with Blackburn et al.’s results; a less optimistic percentage of 25%, reflecting Irdeto’s report; and a highly pessimistic, albeit somewhat unrealistic assumption of 50%, intended as a stress test for the system.

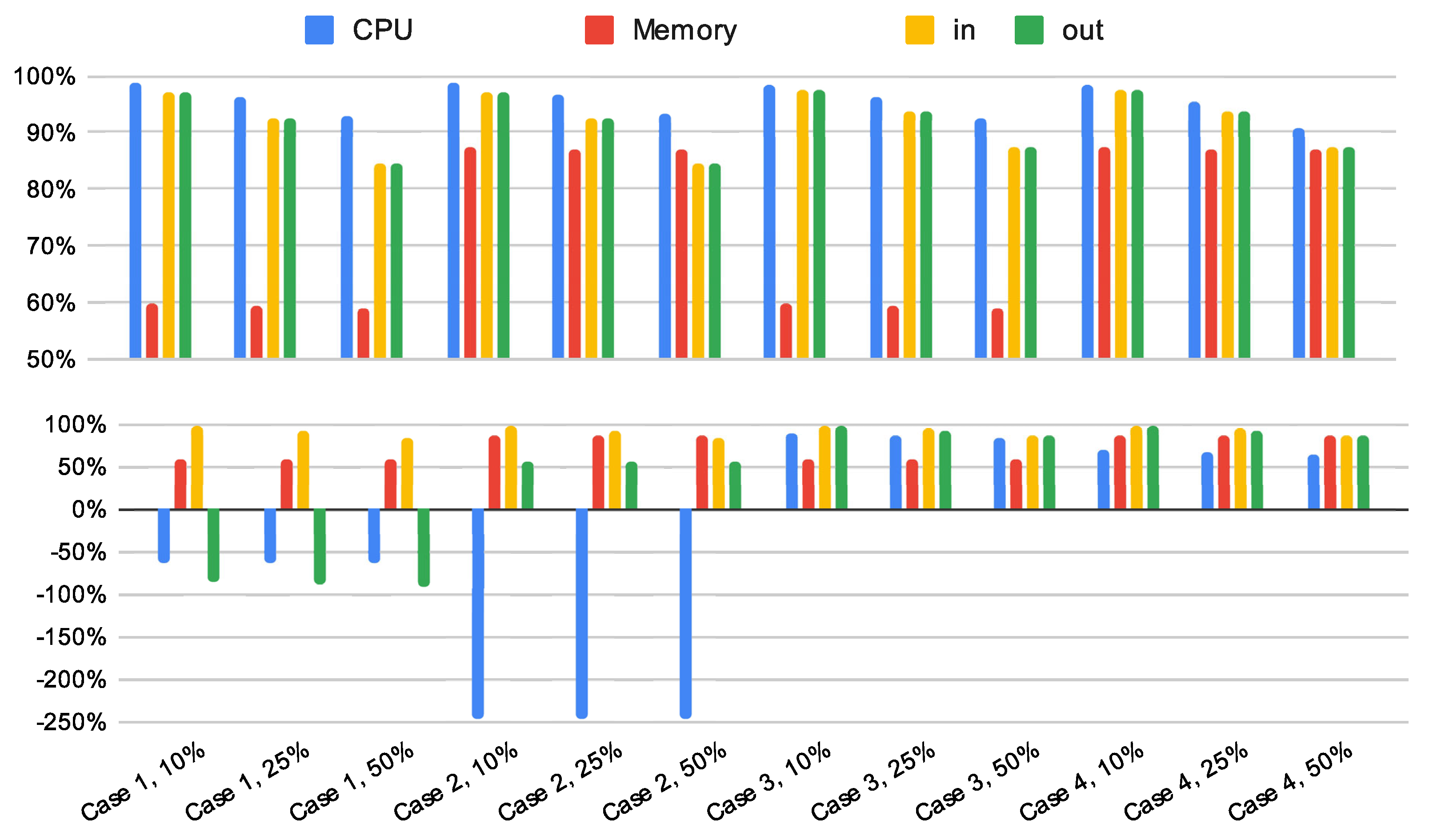
Table 9 and Table 10 showcase the improvements (or potential drawbacks) of the hybrid system compared to the traditional base approach. Table 9 focuses exclusively on the gameplay phase for each case study, whereas Table 10 includes both the initialization phase and gameplay. Two key conclusions can be extracted from these results, both of which are clearly visualized in Figure 7.

On the one hand, cheater percentage has an effect on resource consumption, although it is smaller than anticipated. Initially, it was assumed that a significant proportion of malicious users would slow the system down to the point where the base scheme might become a preferable alternative. However, this was not the case. As shown in Figure 7, the percentage of improvement offered by the hybrid system remained relatively stable regardless of the proportion of cheaters.

On the other hand, comparing the two tables and their corresponding graphs reveals a notable trade-off in CPU utilization when the initialization phase is included. This trade-off is only observed in simpler case studies (1 and 2), where the profiled game sessions are shorter and involve less private information. In practice, we argue that the additional milliseconds of computation during initialization are negligible as they have a minimal, almost imperceptible, impact on user waiting times. Additionally, as mentioned previously, if initialization becomes a bottleneck, it can be sped up by making use of the VORPF setup discussed in Section 2.3.5. Conversely, resources used during gameplay, such as memory and networking, pose greater challenges. Excessive usage in these areas can lead to system failures and back-end downtime in the short term and may necessitate hardware upgrades in the long term.

Consequently, we conclude that the hybrid solution provides a clear improvement for more complex applications with longer sessions and a sufficient enhancement for simpler, shorter applications.

4.2. Mitigating Strategic Relay Abuse

Although entering relay mode prevents further deviations, the very first cheating attempt inside an optimistic P2P phase leaves no cryptographic proof for the server to punish the instigator. A determined attacker could, therefore, mount a “single-probe” strategy: try a speculative deviation once per session, and, if challenged, immediately behave honestly under the relay. While the attempt itself always fails, it still wastes time, leaks side-channel information about edge cases, and consumes relay resources if repeated across many sessions.

A natural extension is to layer a meta-protocol that deters abusive relay triggers without altering the core cryptographic flow:

• Trigger frequency ledger. The relay already authenticates users and can, therefore, maintain a per-identity counter of how often a session escalates. Thresholds may map to exponential back-off, higher escrow requirements, or temporary blacklisting, echoing reputation schemes in decentralized networks [53].
• Reputation staking. Each account locks a small stake that is slashed if its relay-trigger rate exceeds a moving average. Honest users rarely pay, whereas serial abusers face an ever-growing cost.
• Probabilistic post-mortems. On a randomly chosen fraction of relay activations, the server demands the last k P2P messages together with their one-time-pad keys (which the honest party can safely reveal after escalation). A cheater caught by this spot audit forfeits a larger penalty; the probability can be tuned so that the expected loss outweighs any putative gain from probing, conceptually similar to [54].

Because these defenses operate above the existing protocol, they require only minor changes to the relay’s bookkeeping and no extra cryptographic assumptions. Future work will quantify the optimal audit probability and stake schedule that minimizes false positives while strongly discouraging strategic relay abuse.

4.3. Comparison with Related Work

We contrast our hybrid stakes-aware framework with the discussed state of the art as well as additional research in P2P security. The analysis is split into three groups:

Overlay-level defenses. Initial surveys and frameworks secure message routing, admission control, or privacy but stop short of handling tangible stakes. The survey by Chopra et al. [6] catalogs reputation systems and encrypted signaling for VoIP overlays; Qureshi et al. [7] protect copyright in P2P content distribution through collusion-resistant fingerprinting; and Kumar et al. [8] propose a key-establishment layer for IoT peers. Follow-up work enhances trust by using SGX enclaves [9], ant-inspired reputation [10], or blockchain ledgers [11]. All these approaches improve communication security but do not resolve session-level fairness: if a peer cheats, honest users still lack an authoritative path to recover their stake. Our lazy-server fills that gap: it stays dormant during honest play yet becomes an online arbiter when misbehavior is detected, producing incontrovertible proofs that let the victim claim damages.

Efficient cheat resolution. Time-cheat detection via game-time modeling [18], hybrid Voronoi/DHT overlays for load balancing [19], Lockstep and asynchronous playout protocols [20], and more recent WebRTC-based cryptographic engines [21] all thwart specific exploits (e.g., look-ahead or message reordering). However, none provide a general, composable mechanism to enforce penalties; most simply abort the match or rely on out-of-band moderation. Card-game systems such as Kaleidoscope [55] and Royale [56] do enforce deposits but hard-wire blockchain contracts, incurring continuous on-chain fees. Our framework attains comparable fairness while preserving pure P2P latency in the typical case by invoking heavy cryptography or trusted arbitration only on demand.

Cryptographic fairness protocols. Fair-MPC with cheater detection [16] and identifiable-abort MPC [17] guarantee that a corrupted party cannot learn the output after deviating, yet the session ends in an abort that forfeits everyone’s effort. By contrast, our stakes-based design lets the honest peer finish the session (or obtain restitution) through the relay’s signed transcript, offering both cryptographic privacy and practical recourse.

Relative to overlay defenses and cheat-specific engines, we supply the missing fairness layer for stake-centric applications; relative to abort-based MPC, we deliver an outcome without deadlock. The lazy-server’s trigger-on-dispute model keeps common-case overhead minimal (benchmarks show up-to-$100\times$ CPU and bandwidth savings when cheaters are rare), while its OTP-based glue permits easy insertion of MPC sub-protocols for stricter privacy. These properties collectively advance the state of the art in secure, cost-efficient P2P back-ends.

5. Conclusions

Online applications, such as social media sites, email providers, mobile applications, online video games, file-sharing systems, and media streaming platforms, often require expansive back-end infrastructures to accommodate ever-increasing requirements. These architectures typically fall into two categories: centralized Client–Server models and decentralized Peer-to-Peer (P2P) models, each offering distinct advantages and trade-offs.

In this research work, we present a composable framework that enables developers to achieve the low implementation and maintenance costs of P2P systems while leveraging their inherent self-scaling capabilities and robustness. At the same time, the framework preserves the security, reliability, and privacy typically associated with centralized architectures, offering a balanced hybrid solution.

Three critical challenges associated with this approach are identified: the Absence of Authority, the Absence of Secrecy and Privacy, and the Potential for Using the System Against Itself. An initial solution to address these issues is proposed, combining a hybrid back-end architecture (featuring a minimal “lazy” server) with an action verification scheme. This scheme leverages the strategic use of OTP encryption, cryptographic hashing, and different slot-in MPC protocols.

Several experiments were conducted to emulate different real-world scenarios with distinct computational needs. After profiling each case, concrete results were obtained, indicating the areas of improvement achieved using the solution detailed in this study. Notably, significant enhancements were observed in every metric when the initialization phase was excluded. CPU utilization improved by 90.89–98.67%, memory consumption by 58.78–87.33%, and incoming and outgoing network usage by 84.58–97.50%.

When the initialization phase is included, the overall improvements remain substantial, though some exceptions show performance degradation. Specifically, in case study 1, outgoing network usage worsened by 86.22–88.53% and CPU times increased by 64.47–64.75%. Additionally, in case study 2, CPU times increased by 245.36–245.58%.

These results indicate that the efficiency of the proposed framework is proportional to the complexity of the application. Scenarios with larger amounts of private data and longer-lasting sessions achieve greater improvements with the hybrid back-end. Even in simpler cases, where some deterioration occurs, the impact is isolated to the initialization phase. We argue that this localized spike in resource usage is less critical than a sustained increase throughout the session. Furthermore, we propose an alternative VORPG setup for complete server detachment. This more complex scheme can be implemented if initialization becomes a bottleneck.

Moreover, the XOR-OTP mask acts as a universal gateway: one XOR turns a value into the share format expected by or compatible with any MPC engine. Send Boolean circuits to garbled circuits, arithmetic operations to SPDZ, mixed workloads to ABY, bitwise logic to EMP, and bulk look-ups to FSS without any extra encryption or loss of security.

Importantly, the resource efficiency gains also translate to improved energy consumption, with lower CPU utilization and reduced network activity leading to substantial decreases in power demands. These improvements address the environmental and operational costs associated with traditional centralized architectures, making the hybrid model a more sustainable option.

From a developer’s perspective, it is important to acknowledge that, despite the benefits of robustness, self-scalability, and low maintenance offered by P2P systems, this proposal introduces additional complexities. Certain application actions must be implemented within garbled circuits (GCs) or equivalent circuit-based MPC protocols, a process that can be tedious and requires expertise in cryptography and circuit design. Additionally, every function invoked after a user’s input must be accompanied by appropriate verification algorithms, adding to the development effort.

Lastly, the two-tiered communication structure, where a session begins with a direct P2P transmission and may change to a relay server network, can present implementation challenges. For instance, ensuring seamless transitions while maintaining performance and security is non-trivial. Finally, unresolved issues remain, such as time management in real-time applications. The current approach could trigger the relay fallback if a user exceeds a response time threshold, but questions arise regarding its precision and the potential for exploitation by malicious users to gain an advantage.

Overall, providing a secure implementation while fulfilling all these different needs for stakes based sessions is very technically complicated. We firmly believe it is achievable. As stated beforehand, this proposal represents an initial approach, with significant opportunities for further refinement and enhancement.