Auditable Anonymous Electronic Examination

Abstract

Ensuring security in electronic examination systems represents a significant challenge, particularly when practical considerations dictate that most involved parties cannot be fully trusted due to self-interest. To enhance the security, we introduce auditability to e-exam systems, enabling an auditing authority to verify the system integrity. This auditability not only ensures system robustness but also creates an opportunity to grant communication between candidates and examiners, allowing for clarification on unclear questions during exams. Additionally, the implementation of attribute-based certifications ensures anonymity for both candidates and examiners throughout all stages of the exam, with the option for revocation in case of audit-detected fraud.

1. Introduction

The rapid emergence of digital technologies and the World Wide Web simultaneously gave rise to e-learning systems. While these systems have already made a significant impact on education, their importance has been further amplified by the social distancing measures necessitated by the COVID-19 pandemic. However, this widespread deployment presents both existing and new challenges on a larger scale, encompassing not only system functionality but also various aspects of security.

In terms of security, e-exam management stands out as the most challenging component of an e-learning system. Unlike other areas, such as educational material management, which predominantly rely on authorization and data encryption, the examination and assessment process necessitates authenticity, verifiability, anonymity, and accountability. Anonymity plays a crucial role in ensuring unbiased grading—a mandatory requirement, given that assessment results significantly impact the lives of examinees. For instance, professionals like train drivers and Chinese officials must undergo regular exams, and failure in these exams may result in job loss.

An effective e-exam system not only replicates all the features available in a traditional in-person exam but also strives to enhance them with additional benefits unique to the digital platform. This is why we consider the concept proposed by Huszti and Pethő [1] to be essential. According to their proposal, candidates should have the ability to communicate with the examiners during an exam, allowing them to seek clarification on unclear questions or tasks. Furthermore, following the principles outlined in the Huszti–Pethő protocol, an e-exam system should establish a communication channel that preserves the anonymity of both parties, thereby mitigating threats or fraudulent grading. This approach further reinforces the integrity of the system.

Nevertheless, in such systems, it is necessary to minimize the number of trusted parties. In a real-world scenario, the secure approach is to assume that individuals may act in their own self-interest, potentially leading to fraudulent behavior [2,3,4,5,6]. The concept of auditability is common in the case of election systems to reduce the trust in participants. Following the same trend, an e-exam management system should support a thorough logging and auditing procedure as well, which includes all phases of the exam and communication between the participants. Such measures are crucial in identifying and mitigating potential fraudulent behaviors.

Despite all efforts, if a participant attempts to cheat and is detected, the system should support de-anonymization and accountability, applicable to candidates, examiners, or even the examination authority.

To address these challenges, we propose a design for an e-exam protocol that satisfies the aforementioned properties. Utilizing attribute-based credentials [7,8], we can generate pseudonyms linked to certificates of attributes required for exam registration. To implement the timed release function of the test and support additional constraints on the candidates, we use attribute-based encryption [9]. To satisfy the verifiability requirements, the participants use an identity-based signature [10] with the use of pseudonyms. Through the use of identity and attribute-based cryptography, we do not rely on traditional public key infrastructures, thereby supporting flexible access control and more efficient key management and potentially reducing the reliance on central authorities, especially if the implementation employs distributed identity-/attribute-based protocols. Furthermore, to ensure anonymity, it is essential to conceal not only the identity but also the metadata attached to direct communication; otherwise, it could lead to the identification of the communicating parties. To prevent this, we employ the Scalix mix network [11] as it can provide anonymity for the participants of communication against adversaries who can observe the entire network. However, we propose a slight modification to the mix network to support logging for an auditing authority, thus enabling the universal verifiability of the entire system. The use of attribute-based credentials is beneficial in the case of de-anonymization too, as justified anonymity revocation is usually natively supported. To minimize the number of trusted parties in the protocol, we introduce a $\Sigma$-protocol to support identity-based proof of correct decryption, which is used by the auditing authority and other parties as well.

In the subsequent sections, we delve into a detailed exploration of our proposed system. Section 2 provides a comprehensive review of related works, establishing the context for our contributions. In Section 3, we present the theoretical foundation of our approach, highlighting the key concepts and methodologies. Following this, in Section 4, we detail the security goals, with informal definitions, the included roles in the system, and their threats. The section also includes a complete description of the phases of the exam protocol. Section 5 presents a protocol that enables proof of correctness in identity-based decryption, without revealing information about the secret key. Moving forward, in Section 6, we discuss the auditing capabilities of our protocol through a slight modification of Scalix. Section 7 addresses the processes in the case of fraudulent behavior or unreadable log scenarios. In Section 8, we conduct a comprehensive security analysis, evaluating our security goals. We conclude the paper in Section 9, summarizing the key contributions.

2. Related Work

One of the first e-exam management systems that addressed the challenge of a student’s anonymity was proposed by Castella-Roca et al. [12]. Their work covers several authenticity, privacy, correction integrity, and secrecy, which are considered essential for current e-exam protocols. However, their system is designed to be implemented in a supervised environment, where exams are taken electronically but with face-to-face oversight, with the central manager as a trusted party.

Further improvements were introduced by Huszti and Pethő [1] as their protocol focuses on authentication and privacy requirements in the presence of malicious candidates and exam authorities. They introduced the novel approach of employing a mix network to generate pseudonyms for the participants in the protocol, thereby ensuring anonymity, while taking advantage of this technology, providing anonymous communication during the exam.

The next major step in electronic assessment was connected to the WATA family. Their development dates back to 2004. The first published version was WATA II [13], which aimed to replace the double envelope system (with a larger envelope containing an anonymous exam sheet and a smaller envelope sealing the candidate’s identity). WATA II was designed for secure written exams that need both authentication and anonymity. The authors implemented it with a double barcode system, where one barcode was placed on a token containing the candidate’s personal information, verified by the examiner. The other barcode was placed on the test paper, pairing the candidate’s token with the test answers. While WATA II requires operation on a local computer, WATA III [14] functions as a web service, allowing examiners to prepare, mark, and publish results remotely. Furthermore, candidates can securely access their marks, providing a seamless and secure solution for the complex interplay between authentication and anonymity in written exams. Although the WATA family previously focused only on authentication and anonymity in paper-based exams, WATA IV [15] introduces a comprehensive list of security and privacy challenges and their solutions as a computer-assisted exam protocol. This system also aims to minimize the amount of trust in the participants. The threat model of the protocol includes a malicious observer, malicious candidates, an honest-but-curious anonymizer with lightweight participation, and a malicious manager with intensive participation.

The protocol Remark! [16] follows the idea of mixnet-based pseudonym creation, introduced by Huszti and Pethő. It achieves authentication, verifiability, and (conditional) anonymity without relying on trusted parties. However, it does not exploit the benefits of mixnet for anonymous communication during the exam; it only relies on it during registration. Similar to the Huszti–Pethő protocol, Remark! maintains a distinction between candidate and examiner registration. This approach ensures that only the candidate is potentially de-anonymizable, allowing them to receive their marks. However, this design choice also grants examiners immunity from potential punishment.

Bella et al. [17] presented an onsite exam protocol designed for both paper-based and computer-based exams, eliminating the need for any trusted parties. The authors established a well-defined set of security and privacy requirements, all of which their protocol successfully satisfies. However, the authors achieved the absence of trusted parties by foregoing the verification of candidate and examiner eligibility, a task that was already included in the Huszti–Pethő protocol, where it was considered the responsibility of the examination authority working from a trusted database.

Bella et al.’s subsequent work [18] builds upon the concepts introduced in [17]. This extension not only expands the scope of the security and privacy requirements but also introduces additional roles within the exam protocol, effectively distributing responsibilities. Despite these advancements, the new design continues to omit the eligibility check within the system.

Küppers et al. [19] developed an electronic assessment system designed to address in-person examinations, even when students use their own devices. The system achieves this by establishing a trusted platform on students’ devices, effectively preventing cheating. The authors prioritize properties such as equality of treatment, leading them to implement the exam client as a multi-platform software program, ensuring accessibility for all students. Central to the system is student identification, tightly integrated with proof of authorship. This involves identifying students during the registration phase, establishing a TLS connection, and subsequently requesting a digital signature for each set of answers.

Rakeei et al. [20] introduced the concept of coercion-resistant e-exams. To achieve this objective, the authors defined two novel properties: anonymous submission and single blindness. To fulfill these properties, they extended the Remark! protocol with a new technique called shuffled answers. The underlying concept involves examiners receiving tests for marking, where the question and answer pairs originate from a set of candidates, as opposed to only one candidate for each test.

3. Preliminaries

3.1. Attribute-Based Credential

The concept of breaking away from traditional credential systems, which are often exploited for malicious data collection and exchange, originated with Chaum [21]. He proposed the adoption of anonymous credential systems that enable individuals to engage in transactions without revealing their complete identity. This is achieved through the use of pseudonyms, ensuring that, after authentication, organizations cannot link the identity to additional information.

This foundational idea evolved into a more sophisticated category of credential systems known as attribute-based credential (ABC) systems. Within ABC systems, users can assert specific attributes without compromising their overall anonymity. The concept of selective disclosure has also emerged, allowing individuals to share relevant information while safeguarding sensitive data. Pioneering works in this field include [7,8], which form the basis of today’s most recognized ABC engines, namely U-Prove [22,23] and Idemix [24,25].

The ABC4Trust consortium has also significantly advanced ABC systems and demonstrated their practicality through two pilot applications [26]. Another research direction focuses on more practical implementations of ABC systems, as seen in projects like IRMA [27] and IoT implementations [28,29].

3.2. Identity-Based Cryptography

The concept of identity-based cryptography (IBC) was introduced by Shamir [30], who developed an identity-based signature (IBS) scheme based on factorization. However, its performance was impractical. Identity-based encryption (IBE) remained an unsolved problem until Boneh and Franklin created their pairing-based scheme [31], offering practical performance for real-world applications. Soon after this, the first pairing-based IBS scheme was also published by Hess [10].

The uniqueness of IBC lies in the fact that its public key is a string that identifies an entity in a particular domain. Examples of such identifiers are an email address, a username, or a phone number. This novelty directly aligns with the core idea of IBC, which aims to simplify certificate management and eliminate the need for certification authorities. In the traditional public key infrastructure scenario, public keys and user identities are bound together with certificates. With IBC, however, there is no need for such certificates since the public key corresponds directly to the user’s identity.

Furthermore, the public key may contain more information than merely the identity of the user. This extension of the public key with domain-specific data enables a wide spectrum of advanced use cases where fine-grained access control is necessary. Moreover, Vécsi and Pethő proposed a solution [32] that facilitates extension with an authorization formula—a policy governing the attributes required for decryption. Notably, this solution offers the advantage of maintaining performance even as the formula expands.

Since this protocol family eliminates the need for certification authorities, it requires a trusted third party responsible for user key generation, known as the private key generator (PKG). The PKG responds to every extraction request based on the user identity, system parameters, and master secret. Typically, in the IBC model, only the PKG knows the master secret; otherwise, all users’ private keys would be at risk. A reference implementation in C and WebAssembly can be found in [33].

3.3. Attribute-Based Encryption

Attribute-based encryption (ABE) originated from the concept of fuzzy identity-based encryption [34]. It offers a solution for fine-grained access control by incorporating access structures and attributes. These structures permit the use of logical operators between attributes to define authorization policies, such as ((Title = “Examiner” AND Status = registered) OR Title = “Auditor Authority”). ABE enables the targeting of a specific group of people, locations, or time through cryptographic access policies.

There are two types of ABE schemes: key-policy [35], where the policy is linked to the user’s secret keys and the ciphertexts contain sets of descriptive attributes; and ciphertext-policy [9], where the secret key is associated with sets of descriptive attributes and the ciphers are associated with policies. Ciphertext-policy grants the encryptor control over who can access the data, while key-policy requires the encryptor to trust that the key issuer has issued appropriate keys.

The key generation for ABE is similar to that of IBC. A trusted central authority—or, in the case of multi-authority attribute-based encryption [36], multiple authorities—creates the decryption keys for individuals using a master secret key and additional descriptive information. With these keys, users can decrypt ciphertexts if their attributes satisfy the policy associated with the ciphertext. Therefore, there is no requirement to use certificates provided by the PKI.

3.4. Mix Network

Mix networks are designed to provide strong anonymity for communicating parties by executing multistage cryptographic transformations and permutations on messages, a process known as mixing. This mixing operation alters the appearance and transmission order of the messages, making it challenging for even a robust adversary observing all communications in the network to trace the messages.

The first mixnet, created by Chaum [37], utilized a single cascade of n mix nodes, where each message was sealed multiple times, addressing each mix node and the receiver of the communication. While this system successfully provided anonymous emailing for users prioritizing anonymity, it suffered from high latency due to the required permutation on each node and the need to wait for a batch of messages before forwarding them. Additionally, the design had a disadvantage: a single malfunctioning node could cause the entire service to stop working. These shortcomings prompted the emergence of other anonymity protocols like Tor [38], which offered low latency with slightly weaker anonymity.

However, further improvements were introduced by adopting the stratified topology for the mix nodes, enhancing the availability and permeability of the system. To address the latency problem, the Stop and Go mix strategy [39] was introduced. Combining these as foundations, Loopix [40] introduced the Poisson mix strategy, making it possible to offer a low-latency practical mix network. Later, Scalix [11] adopted this ideology into the identity-/attribute-based model.

An important feature developed in some mix networks is the anonymous return channel [41], which enables senders to communicate with a receiver in such a way that the receiver does not know the sender’s identity but can still reply to their messages. This feature is essential in our case to provide fair grading while allowing candidates to communicate with examiners.

Scalix

Scalix’s [11] primary objective is to provide a mix network protocol and an anonymous return channel, ensuring scalability in the number of both users and mix nodes. It achieves this goal by leveraging identity- and attribute-based cryptography, enabling the implementation of load balancers between the mix layers and encryption for unknown mix nodes. This approach securely targets the mix node through encryption, which will be chosen by the load balancer in the future.

Scalix adopts a stratified topology, with a combination of $AA+LB$ nodes that serve as both the attribute authority and load balancer. Although Figure 1 depicts it as a single node, it can function as a distributed system with multiple nodes on one $AA+LB$ layer.

Additionally, Scalix introduces an entity known as the provider. The provider functions similarly to a service provider in real-world messaging scenarios, acting as an intermediary between end-users. In Scalix, all messages traverse through providers, which also serve as storage for messages, allowing users to retrieve their messages when available. Providers are not limited to a single-message relationship with users; they support long-term interactions, and one provider can serve multiple users.

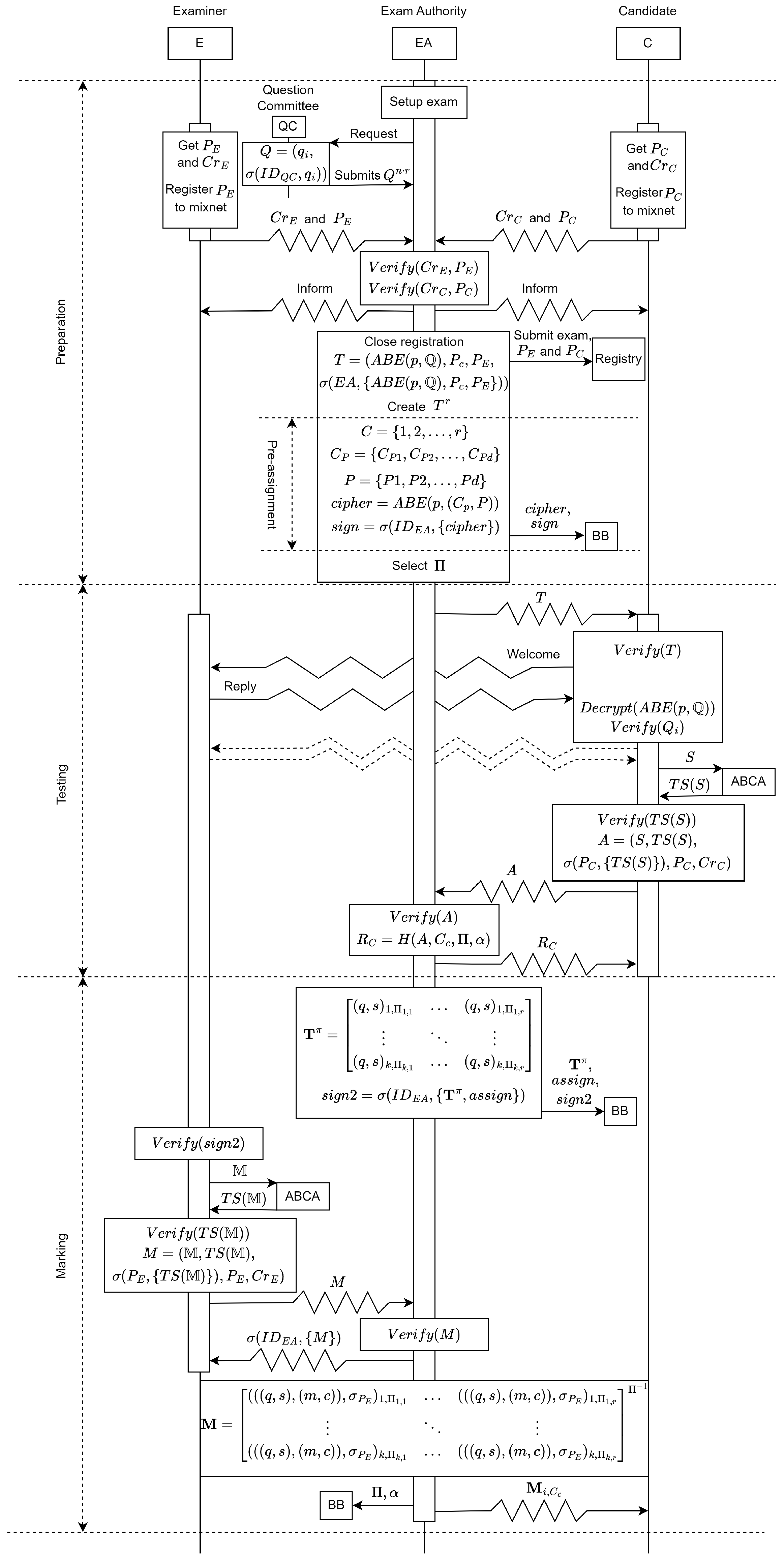
4. Our Protocol

4.1. Roles

• Question Committee (QC): Creates questions for all tests included in exams.
• Attribute-Based Certificate Authority (ABCA): Provides certificate issuance and timestamp generation services. Trusted and honest party in the system.
• Registry: Maintains database of institute regarding examiners and candidates. Trusted and honest party in the system. Also works as an attribute authority for ABC and ABE services.
• Exam Authority (EA): Responsible for organizing exams and maintaining authenticity. The EA is not a trusted party; there is potential for it to be malicious.
• Auditor Authority (AA): All auditing procedures are fulfilled by the AA; in the case of fraudulent behavior, it provides proof for the supervisory board. Not a trusted party; could be malicious.
• Candidate: The exam taker or student. Acts out of self-interest; not trusted; could be malicious.
• Examiner: Marks answers and responds to questions from candidates during the testing phase. Not a trusted party; has potential to be malicious.
• Supervisory Board (SB): A group of people whose task is to examine any complaint and, by majority vote, decide how to respond. Considered to be trusted to a certain level as they make decisions in a distributed manner.

4.2. Goals and Security Requirements

Our objective is to design an electronic examination protocol that ensures anonymity for all participants, while maintaining the possibility of communication between candidates and examiners during exams. Simultaneously, the protocol must incorporate auditability (universal verifiability) to prevent or detect fraudulent behavior, also allowing for de-anonymization and appropriate penalties in such cases. This approach aligns with the overarching goal of minimizing the number of trusted parties involved in the examination process.

In establishing the foundation for our system, we build upon the list of requirements outlined by Giustolisi [42], which includes well-defined fundamental requirements along with their formalizations. Additionally, we incorporate concepts from the Huszti–Pethő protocol [1] and introduce a few additional requirements to align with our specific objectives.

There are four structures in our protocol: question, test, answer and mark. Briefly, a test is built from multiple questions and is sent out to candidates and examiners. The answer is the candidate’s response to a given test and the mark is the examiner’s response to a given answer. A detailed description can be found in Section 4.3. The following are the informal definitions of the security requirements that we seek to satisfy.

4.2.1. Authentication

• Candidate Authorization: Only registered candidates can take an exam. If a candidate submits an answer, then the candidate was correctly registered for the exam.
• Examiner Authorization: Only registered examiners can mark an exam. If an examiner submits a mark, then the examiner was correctly registered for the exam.
• Answer Authenticity: It states that the exam authority should consider only answers that candidates have actually submitted, and that the contents of all collected answers are not modified after submission. An answer must be bound to a candidate.
• Answer Origin Authentication: The exam authority should accept only answers that originate from registered candidates. In addition, only one answer from each registered candidate is actually collected.
• Answer Authenticity: The examiner only marks the answers intended for them. Moreover, the contents of each answer may not be modified until after the answers are marked by the examiner.
• Mark Authenticity: A mark should be correctly recorded for the corresponding answer and candidate, i.e., the examination authority should store the mark assigned to an answer during marking by the examiner.
• Mark Authentication: The candidate should be notified with the same mark that has been stored by the examination authority.

4.2.2. Privacy

• Question Indistinguishability: The questions should not be revealed until the testing phase begins. Two processes with different questions have to be observationally equivalent until the end of the preparation phase.
• Anonymous Marking: The examiner should mark an answer while ignoring its author, namely an anonymous answer. It is a clear contribution to the fairness of the marking.
• Anonymous Examiner: It concerns all phases of an exam because examiner anonymity could be required to hold forever to prevent bribing or coercion. Thus, it is required that no candidate knows which examiner marked their answers. The examiner should only be de-anonymized in the case of proven fraud.
• Examiner Accountability: If an examiner is found to engage in fraudulent behavior, it is necessary to de-anonymize them and retrieve their identity. This ensures accountability for their actions.
• Anonymous Candidate: A candidate should hold anonymity through all phases of the exam until the grading, before which they should de-anonymize themselves or become de-anonymizable, therefore being able to receive their grade.
• Mark Privacy: The mark ultimately attributed to a candidate is treated as valuable personal information. More specifically, no party learns the marks, besides the examiner, the concerned candidate, and the authority responsible for the notification. This means that the marks cannot be made public.
• Mark Anonymity: No one should learn the association between a mark and the corresponding candidate.
• Candidate–Examiner Communication Anonymity: The exam system should provide a communication channel between candidates and examiners in such a way that the examiners cannot learn anything about the candidates.

4.2.3. Individual Verifiability

• Question Validity: The candidate can check that they have received the questions actually generated by the question committee.
• Marking Correctness: The candidate can verify that the mark received is correctly computed on their answer.
• Answer Integrity: The candidate can check that their answer is accepted and marked as they submitted it.
• Answer Markedness: The candidate can check that the answer submitted is marked without modification.
• Mark Integrity: The candidate can verify that the mark attributed to their answer is assigned to them without any modification.
• Mark Notification Integrity: The candidate can check that they have received the mark assigned to them.

4.2.4. Universal Verifiability

• Registration Universal Verifiability: An auditor can check that all accepted answers are submitted by registered candidates and all accepted marks are submitted by registered examiners. Thus, the exam authority should have considered only answers that originated from eligible candidates and marks that originated from eligible examiners.
• Marking Correctness Universal Verifiability: An auditor can check that all marks attributed by the examiners to the answers are computed correctly.
• Answer Integrity Universal Verifiability: An auditor can verify that all and only accepted answers are marked without any modification. This means that the auditor can be sure that no answer is modified, added, or deleted until the end of marking.
• Mark Integrity Universal Verifiability: An auditor can check that all and only the marks associated to the answers are assigned to the corresponding candidates, with no modifications.
• Communication Universal Verifiability: An auditor can check that, during the communication between candidates and examiners, no rules were violated.

4.2.5. Our Requirements for ABC Systems

To satisfy our needs, the ABC system should support two key features: (1) anonymity revocation, which allows the verifier to de-anonymize the presented certification proofs if the circumstances require it; (2) non-transferability, which prevents users from sharing their pseudonyms or credentials with other users.

Both U-Prove [7] and Idemix [8] support these features as extensions of their base feature sets.

For anonymity revocation, they both require a trusted authority that can be referred to as an auditor or revocation manager [8,43]. In the case of Idemix, both the issuers and the central authority (CA) retain information about the user’s pseudonyms and identity. In situations necessitating justified anonymity revocation, the revocation manager provides a secret to the verifier, which can then be used at the issuer or CA to de-anonymize the user. On the other hand, U-Prove requires less communication since the user’s identity is always encrypted in the certification proof using verifiable encryption. Consequently, in the event of malicious activity, the revocation manager/auditor can directly de-anonymize the user.

Non-transferability is achieved similarly in both systems. Both systems follow the approach of publishing some confidential information about the user in encrypted form. Thus, if a user shares their credentials and keys with a friend, the friend will also be able to reveal this confidential information.

4.3. Structures

To provide additional clarity,

Table 1. Table of symbols introduced in Section 4.3.

Symbol	Description
$q_i$	A question plaintext
$\sigma (X,\{p{t}_1,p{t}_2,\dots \})$	A digital signature created by the user X, signing the listed data $p{t}_1,p{t}_2,\dots$
${\sigma }_X$	A digital signature created by the user X, signing all data listed before the signature
$Q_i$	A question package, which is a pair $(q_i,\sigma (I{D}_{QC},q_i))$
$ABE(p,pt)$	An attribute-based encryption of some plaintext $pt$ with policy p
$P_X$	A pseudonym of the user X
T	A test created by the EA
$s_i$	A candidate’s solution to $q_i$
S	A candidate’s solution to T, built as a list of $(q_i,s_i)$ pairs
$TS\left(pt\right)$	A timestamp created by the ABCA to the data $pt$
$C{r}_X$	An attribute-based credential of the user X
A	An answer created by a candidate
$m_i$	A mark given by an examiner to $s_i$
$c_i$	A comment given by an examiner to $s_i$
$\mathbb{M}$	A set of signed marks and comments to questions and solutions
M	A mark package created by an examiner

collects the symbols, which are introduced during the description of the structures.

There are four main structures during the phases of an exam.

• The question is the product of the QC. Based on the security requirements of the system, we distinguish two types of this structure.
  In the first case, the questions created by the QC are part of a public database; therefore, the QC does not perform encryption, but only provides a signature. Here, the question Q is a pair $(q,\sigma (I{D}_{QC},\left\{q\right\}))$, where q is a plaintext (the text of the question) and $\sigma (I{D}_{QC},\left\{q\right\})$ is the digital signature of the QC.
  The second case is when the QC wishes to keep the questions secret until the candidates start their tests. In this case, the question Q is a pair $(ABE(p,q),\sigma (I{D}_{QC},\left\{ABE(p,q)\right\}))$, where $\sigma (I{D}_{QC},\left\{ABE(p,q)\right\})$ is the digital signature of the QC and $ABE(p,q)$ is the q question encrypted with ABE, under p policy. In this case, the policy may include useful constraints. If the EA shares some details of the exam that they requested the questions for, the QC can include a candidate eligibility check in the policy. It also has to include a constraint on the decryption key’s freshness, as a timed release (check if generated after the start of the exam) could also add a constraint to ensure that the candidate is registered to the exam. The combination of the latter property and the time constraint would also enable the question to only be usable in the given exam.
• A test is created by the EA. Similarly to the question, we can consider two cases for this structure, based on the security requirements and based on the structure of the question.
  First, let $\mathbb{Q}=\{Q_1,Q_2,\dots ,Q_n\}$ be a list of questions, and the test $T=(ABE(p,\mathbb{Q}),P_c,P_E,$ $\sigma (I{D}_{EA},\{ABE(p,\mathbb{Q}),P_c,P_E\}))$, where $ABE(p,\mathbb{Q})$ is the attribute-based encryption of a list of questions, under p policy. Here, p has to include a timed release constraint and may include the same constraints as described in the second case of the question or any other extensions, based on the needs of the implementation. $P_C$ is the pseudonym of a candidate, which is necessary to bound the test to the candidate. $P_E$ is the pseudonym of an examiner, with whom the candidate can communicate through the mixnet during the exam, and $\sigma (I{D}_{EA},\{ABE(p,\mathbb{Q}),P_c,P_E\})$ is the digital signature of the EA.
  Second, let $\mathbb{Q}=\{Q_1,Q_2,\dots ,Q_n\}$ be a list of questions, with the test $T=(\mathbb{Q},P_c,P_E,$ $\sigma (I{D}_{EA},\{\mathbb{Q},P_c,P_E\}))$. In this case, the list of questions is not encrypted, assuming that they were already encrypted previously.
• An answer is the product of a candidate. The structure of an answer A is represented as $(S,TS\left(S\right),\sigma (P_C,\left\{TS\left(S\right)\right\}),P_C,C{r}_C)$. The solution S is defined as a set of pairs $\left\{(q_i,s_i)\right\}$, where, for each $i=1,2,\dots ,n$, $q_i$ is the question included in $Q_i$ and $s_i$ is the candidate’s solution for $q_i$. $T{S}_S$ is the timestamp generated for S, $\sigma (P_C,\left\{TS\left(S\right)\right\})$ is the candidate’s digital signature, generated using his pseudonym $P_C$, and $C{r}_C$ is the required credentials of the candidate.
• A mark is the product of an examiner. A mark $M=(\mathbb{M},TS\left(\mathbb{M}\right),\sigma (P_E,\left\{TS\left(\mathbb{M}\right)\right\}),P_E,C{r}_E)$, where $\mathbb{M}$ is a set $\left\{(((q_i,s_i),(m_i,c_i)),\sigma (P_E,\left\{((q_i,s_i),(m_i,c_i))\right\}),P_E)\right\}$, where, for each $i=1,2,\dots ,n$ $(q_i,s_i)$ is a question–solution pair originating from a candidate and $(m_i,c_i)$ is the mark and comment given by the examiner. Moreover, the examiner digitally signs each element of the set $\mathbb{M}$ (denoted as $\sigma (P_E,\left\{((q_i,s_i),(m_i,c_i))\right\})$) with his pseudonym $P_E$. $TS\left(\mathbb{M}\right)$ is the timestamp generated for $\mathbb{M}$, following which $\sigma (P_E,\left\{TS\left(\mathbb{M}\right)\right\})$ denotes the digital signature of $TS\left(\mathbb{M}\right)$ generated with the examiner’s pseudonym $P_E$. Finally, $C{r}_E$ denotes the examiner’s required credentials.

In this paper, we will use $Q=(q,\sigma (I{D}_{QC},\left\{q\right\}))$ and $T=(ABE(p,\mathbb{Q}),P_c,P_E,\sigma (I{D}_{EA},$$\{ABE(p,\mathbb{Q}),P_c,P_E\}\left)\right)$. However, the other versions could be considered in a future extension of this work.

Since our protocol is built on the identitity- and attribute-based paradigm, we suggest the use of IBS as the digital signature algorithm. It is important to mention that, in every structure where a digital signature is used, it denotes the digital signature of every building block of the structure that appeared before the signature itself.

4.4. Phases

To provide additional clarity, Figure 2 illustrates the communication between entities during the preparation, testing and marking phases.

4.4.1. Preparation

The steps for the preparation phase are as follows.

(P1)

The EA files the exam in their system, setting all the necessary information, including a deadline for marking. It also establishes eligibility criteria, specifying the required attributes for exam registration. This information, accessible to the public, covers both candidates and examiners. Additionally, a bulletin board (BB) is introduced for each exam, inspired by Remark! [16]. Only the EA can publish information on the BB, while the examiners, candidates, and AA can only read it. In this step, the EA informs the QC to submit questions for the exam.

(P2)

The QC submits signed questions to the EA.

(P3)

The candidates and examiners create new pseudonyms and submit them to the mix network service provider. The provider accepts them if they are unique pseudonyms and, therefore, maintains the anonymous communication service for them.

(P4)

The candidates and examiners register for the exam, providing their attribute-based credentials and pseudonyms to the EA anonymously through a mix network. The EA verifies the authenticity and eligibility of the credentials and pseudonyms. Subsequently, the EA informs the candidates and examiners about the success or failure of their registration through the mix network. The EA submits the pseudonyms of the registered candidates and examiners to the registry, along with information about the exam that they have registered for, essential for the ABE decryption of the test.

(P5)

After the registration closes, the EA creates tests from the submitted questions, assigning each test to a candidate. Each candidate is assigned to exactly one test. The questions in the test are encrypted with ABE, using exam eligibility constraints, along with a timed release attribute and an attribute requiring the decryptor to be registered for the exam. The tests are then signed by the EA. For timed release, Ref. [44] provides an overview, which includes this idea in the case of identity-based encryption. However, it is more convenient with attribute-based encryption due to the flexible means of applying attribute constraints. In our case, we require that the decryption key be fresh, created close to the time of the exam. The specific timing can be determined by the system owner or the EA.

(P6)

During preparation, a pre-assignment, introduced by Rakeei et al. [20], is implemented to assign examiners to mark a subset/partition of answers without revealing this partition to the public. In their protocol, the distribution of the pre-assignment is handled through secure channels to each examiner. The examiners send back a signature on the pre-assignment, and, as proof that they all received the same pre-assignment, the signatures are redistributed.

Rakeei and his colleagues aimed to achieve coercion resistance by permitting examiners to provide false information about the pre-assignment in the event of coercion, as the assignment details are never disclosed, even in encrypted form. They also assumed that a coerced examiner would publish his private keys. Hence, it would be unrealistic to expect the examiner not to reveal all proof signatures confirming the pre-assignment.

To simplify this process, we use the BB in combination with ABE for distribution. Assuming r candidates and d examiners registered for the exam, the EA forms a set $C=\{1,2,\dots ,r\}$ representing registered candidates. The EA forms d partitions as $C_P=\{C_{P1},C_{P2},\dots ,C_{Pd}\}$ and labels them as $P=\{P1,P2,\dots ,Pd\}$. The EA encrypts $C_P$ and P with ABE using a policy allowing only eligible registered examiners and the AA to decrypt it, resulting in a ciphertext $cipher$. The EA digitally signs $cipher$ and publishes both the ciphertext and the digital signature on the BB. The examiners and the AA check the signature and, if correct, decrypt $cipher$.

(P7)

Finally, the EA selects a secure permutation matrix $\Pi$, which will be relevant during the marking phase.

The tasks of requesting questions from the QC can be skipped if the EA is using a public database of questions that includes questions created properly beforehand by the QC.

4.4.2. Testing

The steps during the testing phase are the following.

(T1)

The EA sends the tests to the candidates through the mix network.

(T2)

The candidates verify the tests by checking if their pseudonyms are included and by verifying the EA’s signature. Additionally, they confirm the validity of the examiner’s pseudonym with a welcome message sent through the mix network’s anonymous return channel. Eligible candidates decrypt the questions in the test and then verify the QC’s signatures for each question. The candidates can then start their tests.

(T3)

During the test, the candidates can communicate with the examiners through the anonymous return channel if necessary. The communication is logged so that, after or even during the exam, the AA can verify that the communication does not involve cheating.

(T4)

Upon finishing their work on the test, candidates can request a timestamp from the ABCA. They can verify the correctness of the timestamp and sign it using IBS. Afterward, they submit the answer to the EA through the mix network.

(T5)

The EA verifies, for every answer, that the candidate was registered for the exam by confirming their pseudonym and checks their eligibility using their credentials. The EA also checks if this is the candidate’s first time submitting an answer. Following this, the EA verifies the correctness of the signature in the answer and checks if the timestamp is accurate, with the included time falling before the end of the exam. If all the checks are fulfilled, the EA accepts the answer.

(T6)

The EA notifies the candidate about the acceptance or rejection of the answer through the mix network. In the case of acceptance, the EA also creates a receipt $R_C=H(A,C_c,\Pi ,\alpha )$, where A is the answer submitted by candidate c, $C_c$ is the candidate’s number from the set C, $\Pi$ is the permutation matrix from Step P7 of the preparation phase, $\alpha$ is a random value generated for the current exam (to prevent candidates from prematurely sharing signatures), and H is a cryptographic hash function. Finally, the EA signs $R_C$ and includes the signature in the notification message.

4.4.3. Marking

In the marking phase, we also include the notification of candidates about their marks.

(M1)

To prevent a malicious EA (collaborating with the AA) from sending the same test to multiple examiners and to prevent malicious examiners from fraudulent marking, we will use the shuffled answers technique [20]. The idea behind the technique is that the EA will share all the question–solution pairs on the BB in such a way that the pairs could form tests; however, they are shuffled, so each pair in the shared tests originates from different candidates.

The EA creates a matrix $\mathbf{T}$ of question–solution pairs and applies $\Pi$ to it, forming a new matrix ${\mathbf{T}}^{\pi }$ such that $\Pi \left(\mathbf{T}\right)={\mathbf{T}}^{\pi }$. Assuming that there are r candidates who submitted answers, and the tests had k questions, then ${(q,s)}_{i,j}$ is the answer of candidate j to question i.

$$\mathbf{T}=\left[\begin{array}{ccc}{(q,s)}_{1,1}& \cdots & {(q,s)}_{1,r}\\ ⋮& \ddots & ⋮\\ {(q,s)}_{k,1}& \cdots & {(q,s)}_{k,r}\end{array}\right]\stackrel{\Pi }{\to }\left[\begin{array}{ccc}{(q,s)}_{1,{\Pi }_{1,1}}& \cdots & {(q,s)}_{1,{\Pi }_{1,r}}\\ ⋮& \ddots & ⋮\\ {(q,s)}_{k,{\Pi }_{k,1}}& \cdots & {(q,s)}_{k,{\Pi }_{k,r}}\end{array}\right]={\mathbf{T}}^{\pi }$$

In the matrix $\mathbf{T}$, each column represents a test submitted by a candidate. In ${\mathbf{T}}^{\pi }$, the columns are tests with each question–solution pair originating from a different candidate. The EA randomly assigns each element of P to an examiner’s pseudonym. Then, the EA signs both ${\mathbf{T}}^{\pi }$ and the assignments.

If the implementation does not wish to share all the question–solution pairs with all the candidates, as they might be considered sensitive data, the EA encrypts ${\mathbf{T}}^{\pi }$ using ABE with a policy allowing only eligible registered examiners and the AA to decrypt it. The EA also creates a new matrix ${\mathbf{T}}^{\pi \prime }$ holding the hashed versions of the question–solution pairs using a cryptographic hash function. Finally, the EA digitally signs the cipher of ${\mathbf{T}}^{\pi }$, ${\mathbf{T}}^{\pi \prime }$ and the assignments and publishes all of them on the BB, including the signature.

Otherwise, they simply publish ${\mathbf{T}}^{\pi }$ and the assignments and the signature on the BB.

(M2)

The examiner verifies the signature and then decrypts the cipher if ${\mathbf{T}}^{\pi }$ was encrypted. Based on the assignments, they mark the correct partitions of the matrix in such a way that, for each column of the matrix partition, they will create a mark, which includes requesting a timestamp from the ABCA. They check if the timestamp is correct and sign it with IBS. Once a mark is created, the examiner sends it to the EA through the mix network.

(M3)

The EA verifies, for every mark submission, that the examiner was registered for the exam by confirming their pseudonym and checks their eligibility using their credentials. After this, they check if the signature of the mark is correct and check if the timestamp is correct, with the time included being before the end of the marking deadline. Moreover, they check that the examiner marked the correct partition. If all the checks are fulfilled, they accept the mark. If only the deadline is missed, they still accept the mark but report the delay to the SB. In the case of acceptance, the EA digitally signs the submitted mark and sends the signature to the examiner as a receipt.

(M4)

Once all the marks arrive, the EA constructs a matrix of these marks ${\mathbf{M}}^{\pi }$ and applies ${\Pi }^{-1}$, resulting in the matrix $\mathbf{M}$, where each column holds the mark of a candidate.

$${\mathbf{M}}^{\pi }=\left[\begin{array}{ccc}{(((q,s),(m,c)),{\sigma }_{P_E})}_{1,{\Pi }_{1,1}}& \cdots & {(((q,s),(m,c)),{\sigma }_{P_E})}_{1,{\Pi }_{1,r}}\\ ⋮& \ddots & ⋮\\ {(((q,s),(m,c)),{\sigma }_{P_E})}_{k,{\Pi }_{k,1}}& \cdots & {(((q,s),(m,c)),{\sigma }_{P_E})}_{k,{\Pi }_{k,r}}\end{array}\right]$$

(M5)

The EA notifies the candidates about their marks through the mix network by sending the correct column of $\mathbf{M}$. Meanwhile, the EA publishes $\Pi$ and $\alpha$ on the BB.

4.4.4. Revising and Grading

(G1)

The candidate reviews the marks and comments received from the examiners. If a mistake is identified, they contact the EA by sending $error=\left(\right(((q_x,s_x),(m_x,c_x)),\sigma (P_E,$$\left\{((q_x,s_x),(m_x,c_x))\right\}),P_E),e,{\sigma }_{P_C},P_C)$ through the mix network, where e is a plaintext describing the found mistake, and ${\sigma }_{P_C}$ is the candidate’s digital signature signing all the elements listed before it, with their pseudonym $P_C$. The EA will then contact an examiner who did not mark the problematic answer through the mix network. The examiner reviews $error$, makes remarks if necessary, and sends the new mark to the EA thorugh the mix network. The EA replaces the old mark with the new one and notifies the candidate again through the mix network.

(G2)

The candidate identifies themselves verifiably using the ABC’s de-anonymization (identification) method and also sends a digital signature of the received mark. If a candidate refuses to identify themselves, the EA should contact the SB by sending the candidate’s final mark as proof of the end of the exam. The SB will then use the ABC’s anonymity revocation method to identify the candidate for the EA and also sends a digital signature of the mark.

(G3)

The EA registers the grading to the registry by providing, for each candidate, the candidate’s identity in a verifiable form, the mark and a final grade, the candidate’s or the SB’s signature, and also the EA’s signature on this package.

4.4.5. Auditing

Auditing is a continuous process. The AA receives every message that is sent through the mix network as a log, and the majority of auditing occurs by examining these logs. Details regarding this logging process can be found in Section 6 and the protocol in the case of fraudulent behavior or unreadable logs is given in Section 7.

(A1)

Starting at the preparation phase, the AA obtains public information about the new exam and receives registrations as a log through the mix network. Since the EA responds to registration attempts with success or failure messages, the AA can verify that only eligible candidates and examiners were accepted for the exam. Additionally, if necessary, the AA can verify the EA’s honesty by checking the recipients of the sent-out tests.

(A2)

Following the registration phase, similarly using the logs, the AA can verify that the accepted answers are associated with the pseudonyms of registered candidates, ensuring registration universal verifiability.

(A3)

Furthermore, by utilizing the mix network logs, the AA receives all the marks, enabling compliance with the requirements of marking correctness universal verifiability and answer integrity universal verifiability.

(A4)

However, to achieve mark integrity universal verifiability, the AA should have access to the marks registered in the registry to compare the marks suggested by the examiners with those registered by the EA. Since the registry is a trusted party, the AA can assume that the data provided by it are equivalent to the data that the EA provided to the registry.

(A5)

Finally, communication universal verifiability is attained since all communication through the mix network is logged.

Figure 2. Sequence diagram of the more complex phases (preparation, testing and marking) of our protocol.

Figure 2. Sequence diagram of the more complex phases (preparation, testing and marking) of our protocol.

5. Identity-Based Proof of Correct Decryption

In the course of the exam’s auditing process, if the auditor authority (AA) identifies any suspicious activities, it must provide evidence and proof that the findings were not forged. This includes the communication between the candidate and the examiner during the exam, which undergoes thorough auditing. Once a suspicious message is found, the AA (henceforth called the prover) needs to provide proof of the correctness of the identity-based decryption without disclosing any information about the secret key in use.

To break down this problem into smaller components, first, we introduce the decryption algorithm of the Boneh–Franklin identity-based encryption (BF-IBE) scheme [31].

The algorithm takes a pair <$U,V$> as input, representing the ciphertext to be decrypted. The decryptor employs their secret key $s{Q}_{ID}$, which is generated by the private key generator using the master secret s and a hashed version of the decryptor’s identity $ID$, denoted as $Q_{ID}=H_1\left(ID\right)$. The decryption process is as follows:

$$V\oplus H_2\left(\widehat{e}(s{Q}_{ID},U)\right).$$

Here, $H_2$ represents a cryptographic hash function and $\widehat{e}$ a bilinear pairing operation.

Our goal is to prove the correctness of the computation above without revealing the secret key. Consequently, the disclosure of the ciphertext and the result of the pairing operation $\widehat{e}(s{Q}_{ID},U)$ is permitted, enabling the verifier to carry out the decryption algorithm, allowing the computation of the message as evidence of the activity and also verifying the correctness of the decryption. Therefore, our needs are reduced to Problem 1.

Problem 1.

The prover has to provide Zero-Knowledge Proof (ZKP) that confirms that the secret key $s{Q}_{ID}$ was indeed the value employed in the pairing operation. This implies that the prover must demonstrate their knowledge of $s{Q}_{ID}$, through the fact that it was used in the computation $\widehat{e}(s{Q}_{ID},U)$, and it is equal to the value used in a verifiable computation.

5.1. Zero-Knowledge Proof of Equality of Identity-Based Private Key

5.1.1. $\Sigma$-Protocols

This problem is analogous to the discrete logarithm equality ZKP problem, for which the Chaum–Pedersen protocol [45] offers a solution. In subsequent research, the Chaum–Pedersen protocol, along with several other similar protocols, was categorized as an $\Sigma$-protocol by Cramer [46]. This generalization holds significant importance as Cramer has provided detailed proofs for the properties of $\Sigma$-protocols.

Consider the following 3-move protocol involving a prover, denoted as A, and a verifier, denoted as B. Here, we have a binary relation R, a subset of ${\{0,1\}}^{*}\times {\{0,1\}}^{*}$, a common input Y for both parties, and a private input w belonging to A such that $(Y,w)\in R$:

• A sends a commitment a;
• B sends a challenge c;
• A sends a response k, and B accepts or rejects it.

Now, a protocol is called a $\Sigma$-protocol for relation R if it satisfies the following conditions.

• The protocol is of the above 3-move form.
• The protocol has completeness. If both parties follow the protocol and $(Y,w)\in R$, then the verifier always accepts.
• The protocol has the special soundness property. For any given Y and any pair of accepting transcripts on Y, $(a,c,k),(a,c^{\prime },k^{\prime })$, where $c\ne c^{\prime }$, w is efficiently computable such that $(Y,w)\in R$.
• The protocol has the special honest-verifier zero-knowledge property. There exists an efficient simulator that, when receiving Y and c as input, outputs an accepting transcript $(a,c,k)$ with the same distribution as an accepting protocol conversation between honest parties.

Cramer also introduced a further generalization of such protocols with the proof of knowledge of a homomorphism preimage. Therefore, if $(G_1,+)$ and $(G_2,\times )$ are finite abelian groups and $\Phi :G_1\to G_2$ is a homomorphism, we can define the relation as $R=\left\{\right(Y,w):Y=\Phi (w\left)\right\}$. There are many protocols that fit into this family of ZKPs, including the Chaum–Pedersen protocol, which is also included in the standardization proposal [47].

5.1.2. Our Protocol

Based on the principles outlined above, we propose the following protocol for Problem 1.

Given two groups ${\mathbb{G}}_1$ and ${\mathbb{G}}_2$ of prime order q, and a bilinear map $\widehat{e}:{\mathbb{G}}_1\times {\mathbb{G}}_1\to {\mathbb{G}}_2$, let $P\in {\mathbb{G}}_1$ be a generator and $U\in {\mathbb{G}}_1$ be part of the BF-IBE ciphertext pair. Let $x\in {\mathbb{Z}}_q^{*}$ and $Q_{ID}=H_1\left(ID\right)$ be the prover’s identity $ID\in {\{0,1\}}^{*}$, using a cryptographic hash function $H_1:{\{0,1\}}^{*}\to {\mathbb{G}}_1^{*}$. The verifiable computation is defined as $h=\widehat{e}(s{Q}_{ID},P)=\widehat{e}(Q_{ID},sP)$, utilizing the bilinear property of the pairing and the fact that $sP$ and $Q_{ID}$ are publicly known values in the BF-IBE scheme. We define the homomorphism $\Phi :{\mathbb{G}}_1\to {\mathbb{G}}_2^2:x{Q}_{ID}\to (\widehat{e}(x{Q}_{ID},P),\widehat{e}(x{Q}_{ID},U))$. The witness of the protocol is the prover’s secret key $s{Q}_{ID}\in {\mathbb{G}}_1$. The common inputs are $(h,z)=\Phi \left(s{Q}_{ID}\right)$.

The communication between the prover and the verifier proceeds as follows.

• The prover chooses a random $l\in {\mathbb{Z}}_q^{*}$ and computes $(a,b)=\Phi \left(l{Q}_{ID}\right)$. The prover sends $(a,b)$ to the verifier.
• The verifier chooses a random challenge $c\in {\mathbb{Z}}_q^{*}$ and sends it to the prover.
• The prover computes $K=l{Q}_{ID}+c·s{Q}_{ID}$ and sends it to the verifier. Finally, the verifier accepts the proof; if $(k_1,k_2)=\Phi \left(K\right)$, then $k_1=a{h}^c$ and $k_2=b{z}^c$ hold; otherwise, they reject it.

Theorem 1.

The described protocol for Problem 1 is an Σ-protocol.

Proof. 

The protocol is complete, since $\Phi$ is a homomorphism; hence, $\Phi \left(K\right)=\Phi \left(l{Q}_{ID}\right)·\Phi (c·s{Q}_{ID})=(a,b)·\Phi {\left(s{Q}_{ID}\right)}^c=(a,b)·{(h,z)}^c=(a{h}^c,b{z}^c)$.

The proof of special soundness in our protocol is the following. If we take two accepting transcripts, $((a,b),K_1,c_1),((a,b),K_2,c_2)$, since $c_1\ne c_2$, $\frac{K_1-K_2}{c_1-c_2}=\frac{l{Q}_{ID}+c_1·s{Q}_{ID}-l{Q}_{ID}+c_2·s{Q}_{ID}}{c_1-c_2}$$=s{Q}_{ID}$.

The simulator of our protocol receives a challenge c and the common input $\Phi \left(s{Q}_{ID}\right)$. The simulator generates a random value $K\in {\mathbb{G}}_1$ and computes $(a,b)=\Phi \left(K\right)·\Phi {\left(s{Q}_{ID}\right)}^{-c}$. As a response, the simulator sends $(a,b)$ and K. □

6. Auditable Mix Network

6.1. Scalix’s Packet

The packet structure of Scalix adopts an onion-like architecture, revealing only necessary information at each layer of the packet’s path. While the specifics of the layer construction are currently irrelevant, the content of the core is paramount. The core is the layer that will reach the receiver of the message, and it is constructed in the following way:

$$E_{AES}(K,M)\left|\right|E_{IB}(R,K)\left|\right|E_{IB}(P_R,R)$$

In Scalix, the message M is encrypted using the Advanced Encryption Standard (AES) key K. Subsequently, this AES key is encrypted using identity-based encryption (IBE) with the receiver’s identity R. Additionally, the packet contains encrypted routing information for the receiver’s provider, enabling the delivery to the receiver’s mailbox.

Achieving Auditability with Scalix

To attain auditability, a slight modification is introduced to Scalix’s packet structure.

Firstly, ensuring that the auditor authority (AA) can read all messages flowing through the system without receiving the sender or receiver’s details is essential. Thus, the core packet is extended to

$$E_{AES}(K,M)\left|\right|E_{IB}(R,K)\left|\right|E_{IB}(P_R,R)\left|\right|E_{IB}(AA,K)$$

Here, $E_{IB}(AA,K)$ allows the AA to decrypt the message. Since the AA should access every message, they do not have a specific provider; instead, they will be a user of every provider in the system. Therefore, providers only need to know that the last block is for the AA, without providing further details.

The packet received by the AA is $E_{AES}(K,M)\left|\right|E_{IB}(AA,K)$, and the provider also provides a digital signature ${\sigma }_{P_R}$ on this packet. This digital signature is crucial in verifying that the AA has not altered the packet while detecting any fraud.

Using this information, the AA can read M. If it discovers attempted cheating by the sender, the AA can contact the sender’s provider and request the decryption of the sender’s pseudonym.

6.2. Scalix’s Anonymous Return Channel

Currently, the core packet of Scalix’s anonymous return channel is constructed as follows:

$${\gamma }_0$$

$$=$$

$$E_{AES}(K,M)\left|\right|E_{IB}(R,K)\left|\right|E_{IB}(P_R,R)\left|\right|E_{IB}(S,K)\left|\right|E_{IB}(P_S,S)\left|\right|E_{AES}(K,P_S)$$

This extends the basic core packet by encrypting the AES key K with IBE using the sender’s identity S. Consequently, using K to encrypt the response message enables the construction of the response packet without revealing the original message’s sender, as $E_{IB}(S,K)$ holds the key for them. The encrypted routing information for the sender’s provider is also included.

The encrypted identity of the sender’s provider is crucial as it forms part of the routing details embedded in the response header. Importantly, because a provider serves multiple users, this setup preserves the sender’s anonymity.

While collaborative efforts between providers could theoretically unveil the identities of communicating parties, Scalix’s threat model assumes that a malicious provider adopts an “honest but curious” stance. Therefore, the provider may attempt to gather information for its benefit, but refrains from disclosing information to other parties.

Achieving auditability follows the same procedure as described for the basic packet.

7. Fraudulent Behavior or Unreadable Log

In the case of logs, we can identify three different behaviors. The first occurs when all parties act honestly, resulting in a log that is correctly readable by the auditor authority (AA), and verifications show no cheating. The second scenario arises when the log is still readable by the AA, but verifications indicate suspicious activity. The third case occurs when the log is not readable by the AA.

Handling the first case is straightforward; the AA saves data in its database or performs other processes, depending on the implementation. Meanwhile, the second and third cases are more complicated; however, they can be addressed similarly. The AA initiates a proving procedure using the protocol described in Section 5. By attaching the provider’s digital signature on the packet to this proof system, the AA can demonstrate that it sends the correct packet, including the ciphertext, to the supervisory board (SB) and also proves that it uses the correct decryption key in its computation. Subsequently, the SB can verify the AA’s findings.

7.1. Decision-Making

The SB determines if the provided information is fraudulent (or unreadable and therefore fraudulent as well). In the case of a positive decision (where the SB also detects cheating), we propose using identity-based threshold signatures [48,49] to sign the decision. In this setup, the private key associated with one identity (the SB) is shared among all members so that t members together can create a signature, while $t-1$ members cannot. Additionally, no individual signer’s identity is made public.

A similar approach, with enhanced features, involves using identity-based threshold proxy signatures, as proposed by Liu and Huang [50]. The paper includes two schemes: one providing partial privacy protection to the proxy signers and the other ensuring anonymity for all proxy signers. Nevertheless, each valid signature includes a tag enabling the tracing of all participating proxy signers. Here, the identity owner could be the registry, and the proxies are the members of the SB.

7.2. De-Anonymization

Once the SB digitally signs the findings of the AA, we distinguish two cases based on the packet type.

In the case of a communication packet between an examiner and a candidate, the SB first contacts the provider included in the packet to start the de-anonymization procedure. The valid digital signature compels the provider to disclose the name of the packet receiver, which is the pseudonym of a candidate or an examiner. Using this information, the SB can contact the ABCA and de-anonymize the receiver.

In the second case, we already know the receiver of the packet, as it is the EA.

In the second case, where the receiver of the packet is already known (the EA), if the AES key was unreadable by the AA, the SB should contact the receiver of the packet to obtain the key K. Since, in both packet types, it should be encrypted in the same way ($E_{IB}(R,K)$), the SB, if needed, can also request proof of correct decryption using the same protocol as in the case of the AA, described in Section 5.

With the help of K, the SB can decrypt the message and determine the sender’s pseudonym or decrypt the identity of the sender’s provider and contact it for the pseudonym. Subsequently, the de-anonymization process can proceed with the help of the ABCA.

7.3. Punishment

Having identified the participants in the fraud, the SB should provide every detail to the registry, including the recommended punishment. If the registry finds the information to be accurate, it will execute the punishment.

8. Security Analysis

Our system relies on multiple trusted parties. The attribute-based certificate authority is one of them, responsible for certificate issuance and timestamp generation; in other e-exam systems, it is equivalent to the traditional PKI. The registry must also be trusted as its job is to maintain the database of the exam organization. Our system also requires the use of identity- and attribute-based cryptography, both depending on trusted private key generators, which could be a distributed system. However, a certain level of trust is mandatory; nevertheless, in the case of distributed key generators, the trust is still weaker compared to the traditional PKI’s key generation. The supervisory board is also a semi-trusted part of the system, as they vote with threshold protocols, and a certain percentage of the board needs to be honest. Scalix also includes an honest but curious party called the provider. Although all the other parties in the system—the auditor authority, candidate, examiner, and exam authority—are not trusted, they are potentially malicious actors.

Candidate authorization holds, as the tests are assigned to registered candidates by including their pseudonyms in the structure, and the questions are encrypted using ABE; therefore, only registered parties can decrypt it. Moreover, once an answer is submitted, the EA verifies the submitter’s credentials and pseudonym. Similarly, the requirements of examiner authorization are met, as every mark that is submitted to the EA includes the examiner’s credentials and pseudonym, which is verified by the EA before the acceptance of the mark. Answer authenticity is satisfied, as the answer’s structure includes a timestamp, a digital signature, and also credentials from a registered candidate, which, when combined, bound the answer to the candidate and make it unmodifiable. In this way, additional answers cannot be generated by any party without the knowledge of the secret keys and the identity of a registered candidate. Answer origin authentication is similar to the former properties; however, there is a nuanced difference as the EA should check if a candidate has already submitted an answer, and, in our system, the EA has. The EA also verifies if a submitted mark includes answers that were intended for the submitter examiner; moreover, an answer cannot be modified as it was signed by the candidate’s pseudonym. Therefore, answer authenticity holds. The candidate can also prove that their answer was submitted and accepted after the exam is closed since they receive a receipt from the EA. In the case of the acceptance of a submitted mark, the EA has to send a receipt to the examiner, as proof that the mark was recorded correctly. Moreover, each mark includes the question and the answer that was marked; therefore, it is bound to the corresponding answer, which means that our protocol meets the requirements of mark authenticity. Since all the submitted marks are digitally signed by an examiner, the EA cannot modify them; therefore, the candidates will receive the mark that was submitted and stored, enabling mark authentication.

The questions that are submitted for the exam are stored in an encrypted form. The resulting ciphertexts are indistinguishable, so question indistinguishability is satisfied. The candidates and the examiners are participating in the system while hiding behind a pseudonym. Moreover, during the communication in the testing phase between the candidates and examiners, the used communication channel is an anonymous return channel, which provides anonymity to the sender party; therefore, the examiner cannot connect these messages to candidate pseudonyms either. However, in the case of fraudulent behavior, the ABCA allows the de-anonymization of the malicious party, once the fraud is proven. Moreover, candidates are allowed to de-anonymize themselves at the end of the exam to receive their grades. Therefore, all the anonymity requirements and examiner accountability are met: anonymous marking, anonymous examiner, anonymous candidate, mark anonymity, and candidate–examiner communication anonymity. The marks are always sent through the mix network; therefore, only the receiver and the sender can read them. However, in the case of an accidental data breach, the marks still cannot be connected to the receiving candidate, as all the candidates are anonymous. Therefore, mark privacy holds.

The questions included in the tests are all signed by the question committee, which allows question validity. Marking correctness is satisfied since the examiners are required to include comments or perfect solutions for every answer that they mark. The answers are also included in the marks, which allows the candidate to verify that it was not modified. In the case of modification, they have the receipt from the EA, so they can prove their original answer, which is also required for answer integrity and answer markedness. Furthermore, the marks are signed by the examiners, which makes them unmodifiable by other parties and also verifiable by the candidates, satisfying mark integrity. Since the answers are included in the marks, our protocol meets the needs of mark notification integrity.

For the analysis of the universal verifiability properties, we refer to the auditing phase included in Section 4.4.

To formally model and verify our protocol, we built upon the foundational work of Giustolisi [42], who provided formal definitions for the properties relevant to our protocol and developed a framework implemented in ProVerif [51], specifically tailored to verifying computer-assisted and Internet-based exam protocols. Utilizing these definitions, we translated our protocol into ProVerif and conducted tests to verify the specified properties.

We focused our testing efforts on the properties outlined in Giustolisi’s work, excluding the privacy properties except question indistinguishability, as our protocol does not rely on the identities of participants, thus satisfying these properties by design. Additionally, we omitted testing for universal verifiability, as this property is primarily related to the functionality of the mix network, ensuring that the auditing authority can access the message content. Therefore, if the mix network satisfies this requirement, the associated properties are inherently satisfied. The code used for these tests is publicly available at https://github.com/BeardOfDoom/e-exam-proverif (accessed on 30 April 2024).

Non-Cryptographic Threat

The primary focus of this paper is the cryptographic security aspects of electronic examinations. However, it is important to recognize that candidates can attempt to circumvent the system using traditional methods as well, not solely relying on cryptographic means. Preventing such forms of cheating largely depends on the implementation of the protocol, offering various options to deter candidates from unethical behavior.

One potential enhancement to the system involves the integration of a proctoring function. We propose implementing a proctoring system that operates on the candidate’s device. This system could capture video, audio or other relevant data [52]. Importantly, the review of these recordings would not occur during the exam, so as to uphold the anonymity requirements. Instead, timestamps must be appended to the recordings at the beginning and end to verify their integrity, ensuring that they are not manipulated before or after the exam. Once the examiners have completed the marking, the examination authority (EA) notifies the candidates. However, as the EA is not inherently trusted, it must prove that the examiners have concluded the marking. One approach is for the EA to share a random value on the bulletin board (BB), which the examiners sign and return alongside the marked answers. The EA then posts these signatures on the BB. If everything is in order, the candidates submit their recordings with the timestamps to the EA.

Subsequently, the auditor authority or a designated proctor reviews the recordings for any signs of cheating. If activity is found, the process outlined in Section 7 is followed. If no irregularities are detected, the examination process proceeds with Step M4.

Additionally, in Section 4.2.5, we highlight a requirement from attribute-based credential systems regarding non-transferability. This feature prevents users from sharing their pseudonyms or credentials with others, as they would share some confidential data as well. This measure effectively prevents candidates from outsourcing the examination to others.

9. Conclusions

In this paper, we present an auditable and secure e-exam management system that ensures anonymity for all participating candidates and examiners while maintaining a communication channel. We have identified key security properties, including authentication, privacy, and verifiability, guiding the design of a system that offers a high security level throughout all exam phases.

To achieve anonymity, we implement various cryptographic techniques, such as attribute-based certificates and mix networks. Additionally, we achieve flexible access control and efficient key management through the use of identity- and attribute-based cryptography, while reducing the reliance on central authorities. To minimize the number of trusted parties in the exam management system, we introduce a $\Sigma$-protocol. This protocol allows a prover to demonstrate knowledge of a secret key in the case of identity-based decryption, ensuring that it matches a publicly verifiable value. Utilizing this protocol enables the proof of correctness in identity-based decryption.