Abstract
Priced oblivious transfer (POT) is a cryptographic protocol designed for privacy-preserving e-commerce of digital content. It involves two parties: the merchant, who provides a set of priced items as input, and a customer, who acquires one of them. After the protocol has run, the customer obtains the item they chose, while the merchant cannot determine which one. Moreover, the protocol guarantees that the customer gets the content only if they have paid the price established by the merchant. In a recent paper, the authors proposed a POT system where the payments employed e-coin transactions. The strong point of the proposal was the absence of zero-knowledge proofs required in preceding systems to guarantee the correctness of payments. In this paper, we propose a novel e-coin-based POT system with a fast item retrieval procedure whose running time does not depend on the number of items for sale. This is an improvement over the aforementioned existing proposal whose execution time becomes prohibitively long when the catalog is extensive. The use of zero-knowledge proofs is neither required.
1. Introduction
The wide deployment of broadband Internet technology enables the digitalization of many actions that were traditionally performed in a face-to-face manner. One such example is the buying and selling of goods and services over the Internet. Electronic commerce is a great advantage for merchants since anybody with access to a connected device becomes a potential client. On the other hand, customers benefit from an unbounded range of available products and a better chance of benefiting from offers and promotions.
Advanced data mining techniques applied to the records generated from electronic transactions provide valuable information for areas like stock adjustment and market trends analysis [1]. On the downside, identified e-commerce records enable the inference of personal information about individuals, such as hobbies or income level, which can be used for non-ethical business practices like aggressive marketing or non-authorized targeted advertising [2]. Concerns about personal privacy have set the basis for research on privacy-preserving electronic commerce.
Anonymous digital cash enables customers to pay for products in such a way that the payer’s identity remains secret. In the blind signature-based e-coin paradigm [3,4], customers withdraw e-coins from a bank, which can later be spent anonymously. After an e-coin has been spent by a customer, the merchant has to deposit it to the bank. So, in this paradigm, already spent e-coins cannot be used by the payee in future payments. In transferable e-coins systems, as we have to prevent multiple-spending frauds while allowing e-coin transferability, we need a public ledger recording all the e-coin transactions. Achieving this in a decentralized manner led to the development of blockchain technology with distributed consensus mechanisms [5]. From the privacy point of view, blockchain-based cryptocurrencies allow for some degree of traceability [6] since all the transactions are anonymous yet publicly accessible, so the real degree of privacy is difficult to assess.
When secrecy about the acquired item is needed, oblivious transfer (OT) protocols [7,8] appear as an adequate tool. In the typical merchant–customer setting, a merchant takes a set of items and provides them as input to the OT protocol. Then, the customer can obtain only one of those items while the merchant remains oblivious about which one. OT protocols can accommodate payments by requiring the customer to make a payment before being enabled to participate in the protocol. The identity of the customer remains unrevealed by choosing an anonymous payment system. Unfortunately, OT protocols only fit well when all the items are equally priced.
Priced OT (POT) protocols [9,10,11,12,13,14] were introduced to permit the oblivious acquisition of an item from a catalog with differently priced products. In a POT protocol, the merchant provides as input a set of items alongside the price of each one. The protocol guarantees that the customer gets the requested item if and only if the customer pays the appropriate sum while the merchant remains oblivious to both the acquired item and its price. The degree of privacy of the customer involved in a purchase varies among the different proposals, which is discussed later.
Contribution and Plan of This Paper
In this paper, we present a novel POT protocol where, like in [14], customers manage their balances and make payments using an e-coin electronic wallet. This way of managing payments eliminates the need to use complicated cryptographic techniques required to prove the correctness of payments in a scenario where the paid quantity cannot be disclosed. Apart from the simplicity of the design, similar to that of [14], our proposal has a fast retrieval protocol that can be assumed to run in constant time (when the price of the most expensive item for sale is bounded), which is an improvement over the cost of [14] which grows linearly with the number of items for sale.
Apart from that, the proposal provides, like [11,14], unlinkability, in the sense that the merchant cannot determine whether two purchases were made by the same customer or not, and an easy way to recharge balances.
This paper is structured as follows. Section 1 introduces the topic of POT protocols in the scope of privacy-preserving e-commerce. Next, Section 2 reviews the existing literature on POT protocols. After that, the building blocks of the system proposed in this paper are detailed in Section 3. The novel proposal is described in Section 4, its security is analyzed in Section 5, while its computational cost is discussed in Section 6. Then, Section 7 summarizes the results obtained from a prototype implementation. Finally, Section 8 concludes the paper.
2. Related Work
The greatest challenge of POT protocols is the requirement to guarantee that the price of the requested product has been paid while keeping the paid sum secret. All the existing proposals implement a pre-paid model.
The first proposed POT system [9] tackles the previous issue by requiring the vendor to maintain each customer’s balance in an encrypted form. Each time a customer makes a purchase, they have to send an encryption of the paid price, which is then subtracted from the balance (the use of homomorphic encryption is needed) by the vendor. The correctness of the subtracted quantity is guaranteed by using conditional encryption techniques.
The authors of [10] include an additional party, namely, the neutral adjudicator, which participates in the protocol only in the case of a dispute. The vendor stores an encrypted balance for each customer. The correctness of the paid quantity is guaranteed by using zero-knowledge proofs. Both [9,10] require all the items in a catalog to have different prices.
Another POT protocol is described in [12] in a paper focused on private mobile pay-TV. Like in the previously reviewed systems, the vendor is in charge of storing and updating customers’ balances which are stored in an encrypted form to preserve the secrecy of the balances and the paid amounts.
POT is addressed in [13] using a construction that takes an underlying OT protocol and upgrades it into a POT one. The proposal further enables dynamic pricing and the computation of aggregate statistics.
In all the previously reviewed proposals [9,10,12,13], the vendor stores customers’ encrypted balances. Although the identity behind each encrypted balance could be secret, all the purchases made by a customer can be linked to the encrypted balance selected for payment. Unlinkability in POT protocols has only been addressed before by [11,14].
The proposal presented in [11] provides unlinkability by having customers keep track of their balances, rather than leaving this to the merchant. In this way, the merchant cannot determine which balance is involved in each transaction. The solution involves many complex cryptography operations like pairing-based cryptography, modified Boneh–Boyen signatures, zero-knowledge proofs, and a set membership scheme.
The proposal in [14] provides a radically different approach. It takes an existing OT protocol and embeds it in a construction in which payments are made using an e-coin system. In this way, the balance of each customer is implicitly determined by the quantity of e-coins they possess. Such balance is decreased each time an e-coin is spent and can be increased by acquiring new e-coins. The proposal does not require the inclusion of complicated cryptography to guarantee the proper management of balances. The unlinkability of the construction is inherited from the unlinkability of the underlying e-coin system.
Although [14] provides a simple way to implement a POT protocol from an existing OT scheme and a digital cash system, the temporal cost of retrieving an item is proportional to the number of items for sale. Consequently, the time required for each transaction can be rather long when the catalog is extensive.
In this paper, we make a proposal which, like [14], avoids complexity by employing an e-coin system for payment management. Its main contribution is that its item retrieval protocol has an running time, being a small parameter m. As a consequence, items can be retrieved quickly even in the presence of a large catalog.
3. Preliminaries
The POT protocol presented in this paper is composed of two main building blocks: a blind exponentiation protocol, and an e-coin system allowing dummy transactions. Both cryptographic components are described next.
3.1. E-Coin Paradigm with Valued and No-Valued E-Coins
The POT protocol presented in this paper, like [14], manages the payments by using an e-coin system enabling dummy transactions. Such an e-coin paradigm is described in [15]. It includes a merchant and some customers. The bank role of other e-coin systems [3,4] is played by the merchant itself.
A customer who wants to acquire an e-coin has to contact the merchant, pay for its value, and then engage in a protocol that produces a new coin for the customer. Coins generated in this way are said to be valued. Alternatively, customers can generate no-valued e-coins by themselves.
In this paradigm, an e-coin is a tuple, digitally signed by the merchant, that includes a public key. When an e-coin is to be spent, the customer sends it to the merchant who will extract such public key and use it to encrypt the requested digital item. Then, the resulting ciphertext is transmitted back to the customer. If the spent e-coin is valued, the customer has the private key which allows them to decrypt the product. Otherwise, if the e-coin is no-valued, the encrypted item cannot be decrypted.
No-valued e-coins are used in transactions in which the customer does not obtain any products. The objective of these dummy transactions is to mask the real consumption pattern of customers.
In the proposal presented in this paper, this e-coin paradigm is useful because it provides a way to hide the price of the requested product whose secrecy is of paramount importance in the scope of POT.
3.2. Blind Exponentiation
Let us consider a finite field , p being prime, with a high-order q multiplicative subgroup, . Let g be a generator of , and let q be large enough so that the discrete logarithm problem is hard in . The tuple constitutes an ElGamal [16] public key cryptosystem setup.
A blind exponentiation protocol involves two parties A and B. Party A possesses an element while B possesses a secret integer . After running the protocol, A obtains while B gets no information about h nor about . Furthermore, the value of x remains unknown to A.
The definition of such a protocol is very similar to that of blind signatures [3]. In the blind signature case, the input by A is the hash digest of a message to be signed while the input by B corresponds to B’s private key. As a result, A obtains a digital signature over its input while B learns no information about it. As expected, A cannot learn about B’s private key.
A blind exponentiation protocol can be implemented as follows:
- A chooses a random exponent and computes .
- A computes and sends to B.
- B computes and sends back to A.
- A computes which is the desired output ().
In the previous protocol, A has no way to verify whether B provided the correct value for x as input to its part of the protocol. Verifiability can be provided if B has previously been published (y plays the role of B’s public key). In such a case, at step 3, B could send together with a Chaum–Pedersen zero-knowledge proof of discrete-log equality [17] proving that .
A blind exponentiation protocol is a key component of the POT protocol proposed in this paper.
4. A Simple POT Protocol with a Fast Item Retrieval
This section presents a novel POT protocol. Let be the set of digital items for sale, and let be the price list ( is the price of ).
4.1. Setup
This process is run by the merchant before putting the system into service. Let be the price of the most expensive item for sale. The merchant performs the following steps:
- Choose a finite field , p being prime, with a high-order q multiplicative subgroup, .
- Set parameter m so that .
- For each j in :
- (a)
- Create a private–public key-pair .
- (b)
- Run the setup procedure of an e-coin system allowing dummy transactions (see Section 3.1) whose e-coins will be signed under the key pair. Each e-coin, denoted , issued under this key pair will be worth monetary units.
4.2. Items Preparation
This protocol is run by the merchant after deciding the set of items for sale and their prices. It requires two hash functions: and .
A hash function must be chosen so that if we first choose an element and then generate h as the output produced by a call to , the computation of is computationally infeasible.
The bitlength of the digests produced by must meet the key length of a symmetric key cryptosystem chosen to encrypt the elements for sale. In this paper, we assume that a 128-bit AES is chosen, but any alternative would be admissible.
The merchant prepares the items for sale as follows:
- Let be an identifier of the current set of items. This value should be unique for each catalog. It could be set as the hash digest of a description of the set of items for sale together with their prices.
- For each j in :
- (a)
- Create and store a random secret integer .
- For each item for sale :
- (a)
- Let its price be with .
- (b)
- Compute .
- (c)
- Encrypt using AES under key . Let be the resulting ciphertext.
- Publish together with the set of encrypted items
4.3. Wallet Management
Each customer manages a wallet in which valued and no-valued e-coins are stored. The current balance is determined by the number of valued e-coins of each denomination.
To be able to acquire any item, a customer should store, at least, one valued e-coin of each denomination. When a customer needs to recharge their wallet, they contact the server, make an electronic payment for the overall value of the requested coins and then engage with the server in running the e-coin withdrawal protocol as many times as needed. The use of an anonymous payment method would allow for this operation to be carried out anonymously and eliminate the possibility of the merchant tracing the wallet-loading operations of each customer.
Let us recall that the denomination of an e-coin is determined by the public key used by the merchant to compute its digital signature. In this way, the merchant has direct control over the value of each minted e-coin.
As for no-valued e-coins, these are generated by the customers themselves. Hence, they can choose to generate them just in time when needed or to pre-compute and store them in advance.
4.4. Item Retrieval
A customer interested in acquiring the i-th item (its price is ) asks the merchant to participate in an execution of the following protocol. The customer does the following:
- Let be the identifier of the current set of items.
- Let , with , be the price of item .
- Compute .
- For to :
- (a)
- If , take a valued e-coin, , worth monetary units from the e-wallet.
- (b)
- Otherwise, let be a no-valued e-coin of denomination .
- (c)
- Spend against the merchant.
- (d)
- Ask the merchant to compute a blind exponentiation (Section 3.2) on h using as an exponent. The merchant encrypts the result of this computation under the public key embedded in and sends the result to the customer.
- (e)
- If was a valued e-coin, decrypt the response of the server, unblind it, and rewrite the content of h with the obtained value ().
- (f)
- Otherwise, the response is discarded.
- Compute .
- Decrypt under key in order to retrieve item .
5. Security Analysis
In the electronic commerce of digital content, a customer who has bought an item can forward copies of it to other people with no limitation. Depending on the particular nature of the acquired digital data, copyright protection techniques like watermarking or fingerprinting [18], or other limitations (such as the number of concurrent accesses to digital platforms accounts), may be applied, but these issues fall out of the scope of POT protocols.
In the particular case of POT protocols, customers can share cryptographic keys and all the data they have had access to as a result of previous executions of the protocol. For this reason, in the forthcoming analysis, we consider a scenario with a merchant and just one customer who may correspond to a coalition of customers sharing all their data.
In this context, security for the merchant states that a coalition of customers who may have acquired some items in the past cannot get access to an item unless its full price has been paid (at least once). Lemma 2 addresses this subject over the basis provided by Lemma 1.
Lemma 1.
Let us consider a set of the form with being a secret integer and set I being of polynomial size. Given a random value h, computing is as hard as solving the Computational Diffie–Hellman (CDH) problem.
Proof.
We prove the lemma by reduction. Let us assume a polynomial time algorithm which takes as input a set S of the form described above together with h and returns as a result. Next, we prove that such an algorithm could be used to solve the CDH problem.
Let us assume some party is given g, , and , with being unrevealed secret integers. That party wants to compute (the CDH problem).
This party could generate a set of random integers and generate a set containing and a tuple for each . Note that the elements in set are of the form of those in S. If the size of is polynomial, its generation takes polynomial time. Then, by calling algorithm with and h provided as input, the value would be returned. In such a case, the existence of would allow us to solve the CDH problem in polynomial time. □
Lemma 2.
A customer acquiring an item for the first time, cannot get it unless its full price is paid.
Proof.
Let us assume a customer who wishes to obtain an item priced with . Let us consider some j for which . Let us also assume that the mentioned customer wants to pay an inferior price by not spending a valued e-coin during the j-iteration of the retrieval protocol.
If this customer acquired a previous item for which and a valued e-coin was provided at the j-th iteration of the item acquisition protocol, the customer provided some value as input to the blind exponentiation protocol and obtained as output. Let I be the set composed of all indices for which an item , whose price meets , was purchased in the past. Then, if the customer stored all that data, now they are in possession of a collection of tuples:
At the beginning of the j-th iteration of the current purchase, the customer has a given value and needs to get , but since they do not intend to provide a valued e-coin , they will be unable to decrypt the response sent by the merchant. In this way, the customer shall try to compute it from the previous collection of tuples. As proven in Lemma 1, a polynomial-time algorithm for performing such computation cannot exist under the assumption that the computation of the Diffie–Hellmann problem is hard.
We conclude that a valued e-coin has to be spent for each j with . Consequently, the overall amount paid by the customer adds to , which is the price of . □
Next, we focus on security for the customer. Firstly, Lemma 3 focuses on the privacy about the acquired item. After that, Lemma 4 addresses the impossibility for the merchant to link the different executions made by a given customer.
Lemma 3.
The merchant gets no information about the acquired item.
Proof.
An execution of the “Item retrieval” protocol consists of m iterations in which the customer spends an e-coin of each of the possible denominations. Since the vendor cannot determine which of these e-coins were valued and which were not, it gets no information about the price of the acquired item nor about the iterations j in which the customer obtains . Consequently, the vendor obtains no information about the key obtained by the customer which determines the item the customer has access to. □
Lemma 4.
The vendor cannot determine whether two executions of the item retrieval protocol were run by the same customer or not.
Proof.
An execution of the “Item retrieval” protocol consists of m iterations involving an e-coin payment and an execution of a blind exponentiation protocol each. The underlying e-coin system provides unlinkability so no information about the customer is obtained from it. Regarding the blind exponentiation protocol, the information provided at each execution cannot be related to the customer nor about any execution in the past. Consequently, the proposed protocol provides unlinkability. □
6. Cost Analysis
In this section, the computational cost of the POT protocol presented in this paper is analyzed. Then, we compare it to [11,14], which are the only existing POT protocols providing the unlinkability feature. The analysis is performed according to parameter m, which determines the maximum price of an item to (its actual value is relatively small, i.e., ), and parameter n, which is the number of items for sale (it may be large).
The “Setup” procedure mainly consists of running the setup process of an e-coin system m times; hence, its cost is of . This process is executed just once before putting the system into service.
The “Items preparation” process, which is run each time the catalog of items for sale is updated, includes the following: the creation of m random integers () at an cost; the computation of n keys () whose cost per key is dominated by the computation of a modular product of up to m integers (), so the overall cost of this part is ; and the encryption of the n items for sale. The cost of encrypting each item is proportional to its size which is unknown to us. Hence, we only count the number of encrypted items, which is . The overall cost of this “Items preparation” process is dominated by the term.
Running the “Item acquisition” protocol includes m e-coin transactions and m executions of a blind exponentiation protocol. Hence, its cost is .

Table 1.
Cost comparison.
Next, we compare the cost of our proposal to that of [14]. In both systems, the balance of each customer is managed in the form of e-coins stored in an electronic wallet. The “Setup” process in both systems is equivalent.
The advantage of our system with respect to [14] comes from a faster “Item retrieval” procedure. An running time, with a small m, is faster than an one, with a large n. Regarding “Items preparation”, our procedure is more costly, namely, an cost is higher than an one.
It is worth noting that the “Items preparation” process is run by the merchant itself in an offline fashion so that it has a null impact on the experience of customers. Moreover, this procedure is only run when a new catalog is created. So, in a scenario where the items for sale are stable, it will be run very few times. Regarding the “Item retrieval” process, it is run at each purchase, and it involves the participation of customers who will benefit from its fast execution.
Regarding the proposal in [11], its “Item retrieval” procedure runs at an cost which is, theoretically, better than our . However, since m takes a small constant value, such cost can be considered to be constant too.
7. Experimental Results
We implemented our protocol to assess its running time. Our starting point was the Java prototype used in the experiments of [14]. We applied the implementation and modified it to implement our new proposal. The resulting Java source code is available at GitHub (https://github.com/sergisi/POTSimulator (accessed on 12 March 2024)).
The blind exponentiation building block was developed using a DSA base field () for a 128-bit security level (the bit size of its order-q subgroup is 256) according to the NIST standard. Our protocol requires a large-enough subgroup in which solving the discrete logarithm problem is unfeasible.
Our experiments were executed on a computer with an Intel i7-6700HQ (8 threads) processor with a 3.5 GHz clock rate. Its operating system was Linux 6.7.2, while the installed OpenJDK version was “1.8.0402”. We set parameter (as set in [14]). Under this setting, if the monetary unit (value of the least valued coin) is 1 cent, then the maximum price for an acquirable item is 655.35 (EUR, USD, etc).
For comparison purposes, we also ran the simulator of [14], which requires an OT protocol as a building block. In this case, we used the system selected for the available simulator, whose details are given in [19]. As mentioned by the authors of [14], other options would be available, like [20]. Nevertheless, a deep inspection of the runtime shows that much of the running time corresponds to e-coin transactions so that the impact of choosing an alternative OT protocol would have little impact. We could not provide the running times of [11] because we were not aware of an available implementation of it.
The results of our experiments are summarized in Table 2 and depicted in Figure 1. We ran each experiment eight times and computed the median running time. Taking m = 16, we performed experiments for n = 10, 50, 100, 500, 1000 (number of items for sale).

Table 2.
Running times (in seconds) of [14] and of our proposal. Each row of the table corresponds to an execution for a particular value of n (number of items for sale). Parameter m is 16 in all the experiments.
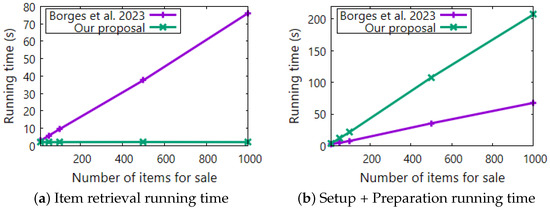
Figure 1.
Graphical representation of the running times of [14] (Borges et al. 2023) and of our proposal. Subfigure (a) shows the results from the “Item retrieval” protocol, while Subfigure (b) depicts the results from the “Setup” and “Items preparation” procedures.
Regarding “Item retrieval”, we can observe how the running time of [14] increases linearly with n while ours is kept constant at around 2 s per execution. Note that for the particular n = 1000 experiment, our running time clearly outperforms that of [14] which is about 76 s per execution. For larger values of n, the difference would be larger.
Putting the system into service requires an execution of the “Setup” and the “Items preparation” procedures. For this reason, we measured the overall time taken by the execution of both processes. As predicted in the cost analysis of Section 6, our system takes a longer time. In our experiments, the system of [14] is three times faster than ours in this part. Nevertheless, let us recall that both procedures are run by the server itself so the time they take has little impact on the quality of the provided service.
8. Conclusions
In this paper, we present a novel priced oblivious transfer (POT) protocol. Most existing proposals require complex cryptographic techniques for the customer to prove that an appropriate payment has been made when neither the purchased item nor its price can be revealed. This issue was smartly addressed in [14] by managing payments in a privacy-preserving way by using an e-coin system enabled with the capacity to perform dummy transactions.
Our proposal also makes use of an e-coin system to manage payments, but it provides a much faster procedure for item retrieval than that of [14]. This enhancement is of great importance because, as our experiments showed, it allows for purchases to be made in around two seconds independently of the number of items for sale.
Author Contributions
Conceptualization, F.S. and S.S.; system design, F.S.; software, S.S.; formal analysis, F.S.; writing—original draft preparation, F.S.; writing—review and editing, S.S.; funding acquisition, F.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Spanish Ministry of Science and Innovation (grant number PID2021-124613OB-I00).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The source code of the prototype used for experimental results is available at https://github.com/sergisi/POTSimulator (accessed on 12 March 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ahmad, A.Y.A.B.; Gongada, T.N.; Shrivastava, G.; Gabbi, R.S.; Islam, S.; Nagaraju, K. E-Commerce Trend Analysis and Management for Industry 5.0 using User Data Analysis. Int. J. Intell. Syst. Appl. Eng. 2023, 11, 135–150. [Google Scholar]
- Bandara, R.; Fernando, M.; Akter, S. Privacy concerns in E-commerce: A taxonomy and a future research agenda. Electron. Mark. 2020, 30, 629–647. [Google Scholar] [CrossRef]
- Chaum, D. Blind Signatures for Untraceable Payments. In Advances in Cryptology; Chaum, D., Rivest, R.L., Sherman, A.T., Eds.; Springer: Boston, MA, USA, 1983; pp. 199–203. [Google Scholar] [CrossRef]
- Brands, S. Untraceable Off-line Cash in Wallet with Observers. In Advances in Cryptology—CRYPTO’ 93; Stinson, D.R., Ed.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 302–318. [Google Scholar] [CrossRef]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: http://www.bitcoin.org/bitcoin.pdf (accessed on 21 February 2024).
- Perlroth, N.; Griffith, E.; Benner, K. Pipeline Investigation Upends Idea That Bitcoin Is Untraceable. The New York Times, 9 June 2021. [Google Scholar]
- Naor, M.; Pinkas, B. Oblivious Polynomial Evaluation. SIAM J. Comput. 2006, 35, 1254–1281. [Google Scholar] [CrossRef]
- Kolesnikov, V.; Kumaresan, R.; Rosulek, M.; Trieu, N. Efficient Batched Oblivious PRF with Applications to Private Set Intersection. In Proceedings of the CCS’16: 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; Association for Computing Machinery: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Aiello, B.; Ishai, Y.; Reingold, O. Priced Oblivious Transfer: How to Sell Digital Goods. In Advances in Cryptology—EUROCRYPT 2001; Pfitzmann, B., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 119–135. [Google Scholar] [CrossRef]
- Rial, A.; Preneel, B. Optimistic Fair Priced Oblivious Transfer. In Progress in Cryptology—AFRICACRYPT 2010; Bernstein, D.J., Lange, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 131–147. [Google Scholar] [CrossRef]
- Camenisch, J.; Dubovitskaya, M.; Neven, G. Unlinkable Priced Oblivious Transfer with Rechargeable Wallets. In Financial Cryptography and Data Security; Sion, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 66–81. [Google Scholar] [CrossRef]
- Biesmans, W.; Balasch, J.; Rial, A.; Preneel, B.; Verbauwhede, I. Private mobile pay-TV from priced oblivious transfer. IEEE Trans. Inf. Forensics Secur. 2017, 13, 280–291. [Google Scholar] [CrossRef]
- Damodaran, A.; Dubovitskaya, M.; Rial, A. UC Priced Oblivious Transfer with Purchase Statistics and Dynamic Pricing. In Progress in Cryptology—INDOCRYPT 2019; Hao, F., Ruj, S., Sen Gupta, S., Eds.; Springer: Cham, Switzerland, 2019; pp. 273–296. [Google Scholar] [CrossRef]
- Borges, R.; Sebé, F. An e-Coin Based Construction for Unlinkable Priced Oblivious Transfer. Comput. J. 2023, bxad031. [Google Scholar] [CrossRef]
- Borges, R.; Sebé, F. A digital cash paradigm with valued and no-valued e-coins. Appl. Sci. 2021, 11, 9892. [Google Scholar] [CrossRef]
- Gamal, T.E. A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Trans. Inf. Theory 1985, 31, 469–472. [Google Scholar] [CrossRef]
- Chaum, D.; Pedersen, T.P. Wallet Databases with Observers. In Proceedings of the CRYPTO ’92: 12th Annual International Cryptology Conference on Advances in Cryptology, Santa Barbara, CA, USA, 16–20 August 1992; Volume 740, pp. 89–105. [Google Scholar] [CrossRef]
- Kadian, P.; Arora, S.M.; Arora, N. Robust Digital Watermarking Techniques for Copyright Protection of Digital Data: A Survey. Wirel. Pers. Commun. 2021, 118, 3225–3249. [Google Scholar] [CrossRef]
- Camenisch, J.; Neven, G.; Shelat, A. Simulatable Adaptive Oblivious Transfer. In Advances in Cryptology—EUROCRYPT 2007; Naor, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 573–590. [Google Scholar] [CrossRef]
- Chou, T.; Orlandi, C. The Simplest Protocol for Oblivious Transfer. In Proceedings of the 4th International Conference on Progress in Cryptology—LATINCRYPT 2015, Guadalajara, Mexico, 23–26 August 2015; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9230, pp. 40–58. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).