Lookup Table-Based Design of Scalar Multiplication for Elliptic Curve Cryptography

Abstract

This paper is aimed at using a lookup table method to improve the scalar multiplication performance of elliptic curve cryptography. The lookup table must be divided into two polynomials and requires two iterations of point doubling operation, for which negation operations are needed. It is well known that an inversion operation requires a lot of multiplication time. The advantage of this paper is that we are able to reduce one inverse element calculation for this problem and also improve the basic operations of finite fields through segmentation methods. If the normal basis method is used in the design of the inverse element operation, it must be converted to the normal basis through the standard basis. However, the conversion process requires a lot of matrix operations. Though the anti-element operation has good speed performance, it also increases the computational complexity. Using number theory and grouping methods will greatly improve the performance of inverse element operations. With application of the two-time point doubling operation in the hardware implementation, the developed approach reduces the computing time by 48% as compared with the conventional approach. The computational time of the scalar multiplication using the presented method is further improved by 67% over the traditional algorithm with only an area increase of 12%. Finally, the proposed lookup table-based technique can be utilized for software and hardware implementation, as the developed arithmetic operations are simple and are consistent in their execution.

1. Introduction

Elliptic curve cryptography (ECC) was presented by N. Koblitz and V. Miller [1,2] in 1986. The ECC is an encryption technique based on the discrete logarithm problem. The public key cryptographic primitives can be implemented by using the elliptic curves over finite fields to generate finite abelian groups. The ECC provides similar security to existing public key cryptography but via application of a smaller key. The ECC with a 160-bit key has the equivalent security level of Rivest–Shamir–Adleman (RSA) and digital signature algorithms (DSA) that require a 1024-bit key. The ECC is defined over prime finite fields GF(p) or binary finite fields GF(2^m). The ECC design over prime fields generally provides more robust resistance to side-channel attacks as compared with those over binary fields. However, the ECC design over binary fields has the carry-free feature and makes arithmetic operations more suitable for hardware implementation.

The authors of [3] presented a method for constructing dynamic lookup tables in order to realize multiplication over a finite field. The Euclidian algorithm can be used for the inverse operation at the expense of computation time. Algorithms for the point multiplication over the ECC have been investigated in many studies. The method of non-adjacent forms (NAF) was presented by Morain et al. [4] to record the scalar in a point multiplication with an aim of reducing nonzero bits and thus the number of point additions. The authors of [5] used the representation of integers in binary form for simplification. Nowadays, most ECC techniques are performed over Koblitz curves [1,6]. Solinas [7] presented the Frobenius map method for data encryption. The projective and affine coordinates were combined in [8] to implement high-efficiency point addition and point doubling operations. There are no inverse operations involved in the exploitation of the coordinate transform techniques. Guo et al. developed [9] a scalar multiplication algorithm based on the step multi-base representation via point halving and the septuple formula to significantly reduce computational cost. The triple-based chain method was proposed in [10] to optimize the time usage in the elliptic curve cryptosystem. The authors of [11] presented a configurable ECC crypto-processor. The ECC operates over the prime field and is defined by the Weierstrass equation. This crypto-processor was verified on a Xilinx FPGA board.

The existing work on modular multipliers over binary finite fields GF(2^m) can be found in [12,13,14]. In [15], a speed-oriented architecture over the finite fields GF(2¹⁶³) and GF(2⁵⁷¹) were implemented by using a balanced quadratic multiplier with high operating frequency. Li et al. [16] exploited the Karatsuba–Ofman multiplier to a scalar multiplication over the finite fields over GF(2⁵⁷¹) and GF(2²⁸³). To minimize the number of point additions without increasing the number of point doubling, the Radix-2^w arithmetic for scalar multiplication was proposed in [17]. The authors of [18] developed a new Montgomery point multiplication algorithm for large field-size ECC over GF(2⁵⁷¹) and GF(2⁴⁰⁹) to optimize resource utilization efficiency. Recently, Zhang et al. [19] introduced a high-performance scalar multiplication architecture over binary fields. A low-latency window (LLW) algorithm was presented for hardware implementation to enhance security, as was an enhanced comb method for point addition and point doubling. The above methods in [15,16,17,18,19] transformed the process of scalar multiplication from an affine coordinate system to a projective coordinate system. These designs were implemented and verified on the FPGA boards.

Different from operations over the projective coordinate system, this paper focuses on the scalar multiplication over the affine system. The hardware architecture and circuit are synthesized for future ASIC implementation. In the affine coordinate system, point addition and point doubling require one modular inversion operation each time. Because the inversion over the finite field is the most time-consuming operation among all of the basic operations. Reducing the number of inverse operations is an important objective of our design. The main idea of this paper can be described as follows: The Fermat’s little theorem [20] is flexibly used for the inverse operation, which controls the critical path easily, as hardware implementation is required. The Horner’s rule is also innovatively exploited to improve the method in [5]. By the binary representation and grouping techniques for constructing lookup tables, the operations of point addition and point doubling are improved. A high-speed scalar multiplication is therefore achieved. The presented approach is applicable to the digital signature [21] for real-time mutual authentication. Finally, the proposed lookup table-based algorithms can be utilized for software and hardware implementations as the developed arithmetic operations are simple and consistent in their execution. From the perspective of the hardware design, the computational time of the scalar multiplication by the proposed method is reduced by 67% over the conventional algorithm. This is because the presented two-time point doubling is superior to the conventional method.

The rest of the paper is organized as follows: The finite field arithmetic is introduced in Section 2. Section 3 briefs the concepts of point addition and point doubling in ECC. The proposed algorithms for the finite field arithmetic is described in Section 4. Section 5 presents the new algorithm for scalar multiplication, which combines the methodology in Section 4. Section 6 concludes this paper.

2. Finite Field Arithmetic

The finite field is a set of finite elements of the field, also known as the Galois field (GF). Multiplication, addition, subtraction and division are defined and certain basic rules are satisfied.

The finite field GF(2) has two elements, with values of 0 and 1. The finite field GF(2) can be extended to GF(2^m) by a primitive polynomial. The finite field GF(2^m) has 2^melements with the values from 0 to 2^m − 1. The primitive polynomial is an irreducible polynomial denoted as $F\left(x\right)$. The national institute of standards and technology (NIST) recommended the primitive polynomials that are applicable to different GF(2^m) finite fields in the public document FIPS 186-4 [22] issued in 2013, as shown in

Table 1. NIST-recommended primitive polynomial.

Finite Field	Primitive Polynomial
$\mathrm{G}\mathrm{F}\left(2^{163}\right)$	$F\left(x\right)=x^{163}+x^7+x^6+x^3+1$
$\mathrm{G}\mathrm{F}\left(2^{233}\right)$	$F\left(x\right)=x^{233}+x^{74}+1$
$\mathrm{G}\mathrm{F}\left(2^{283}\right)$	$F\left(x\right)=x^{283}+x^{12}+x^7+x^5+1$
$\mathrm{G}\mathrm{F}\left(2^{409}\right)$	$F\left(x\right)=x^{409}+x^{87}+1$
$\mathrm{G}\mathrm{F}\left(2^{571}\right)$	$F\left(x\right)=x^{571}+x^{10}+x^5+x^2+1$

.

2.1. Addition and Subtraction

The addition operation over the finite field is $\delta =\gamma +\beta$, where $\beta ,\gamma ,\delta \in \mathrm{GF}\left(2^m\right)$. The element has m-bit representation in a vector form. The addition is based on the bitwise exclusive OR (XOR) operation. Consider an example of GF(2³). Let $\gamma =\left(011\right)$ and $\beta =\left(110\right)$. The result of $\gamma \oplus \beta$ is $\left(101\right)$. The subtraction operation is the same as the addition operation.

2.2. Finite Field Multiplication

Multiplication over the finite field is defined as $\delta =\gamma \cdot \beta$, where $\beta ,\gamma ,\delta \in \mathrm{GF}\left(2^m\right)$. The element $\gamma$ can be represented by the polynomial $A\left(x\right)=a_{m-1}{x}^{m-1}+a_{m-2}{x}^{m-2}+\cdots +a_2{x}^2+a_{1}x+a_0$, where $a_i\in \{0,1\}$. The element $\beta$ is expressed by the polynomial $B\left(x\right)=b_{m-1}{x}^{m-1}+b_{m-2}{x}^{m-2}+\cdots +b_2{x}^2+b_{1}x+b_0$, where $b_i\in \{0,1\}$. The element $\delta$ is represented by $C\left(x\right)=c_{m-1}{x}^{m-1}+c_{m-2}{x}^{m-2}+\cdots +c_2{x}^2+c_{1}x+c_0$, where $c_i\in \left\{\mathrm{0,1}\right\}$. The multiplication result $C\left(x\right)$ is the polynomial multiplication of $A\left(x\right)$ and $B\left(x\right)$ modulo $F\left(x\right)$, where $F\left(x\right)$ is the primitive polynomial. That is,

$$C\left(x\right)\equiv A\left(x\right)B\left(x\right)\left(modF\left(x\right)\right)$$

(1)

Take the field GF(2³) as an example. Let the elements $\gamma$ and $\beta$ be $\left(011\right)$ and $\left(110\right)$, respectively. The primitive polynomial is $F\left(x\right)=x^3+x+1$. The multiplication result of $\gamma$ and $\beta$ is obtained as $\left(001\right)$.

2.3. Finite Field Division

The division operation is $\delta =\gamma /\beta$. It can be viewed as $\delta =\gamma \cdot {\beta }^{-1}$, where ${\beta }^{-1}$ is the inverse element of $\beta$. The inverse element of an element can be obtained quickly by Fermat’s little theorem. Let $A\left(x\right)$ represent the element of a finite field, briefly denoted as $A$. Using the fact that $A^{2^m-1}\equiv 1\left(modF\left(x\right)\right)$, we have $A^{2^m-2}\equiv A^{-1}\left(modF\left(x\right)\right)$. Furthermore,

$$\begin{gathered} A^{2^m-2}=A^{2^1+2^2+\cdots +2^{m-2}+2^{m-1}} \\ =A^{2^1}\cdot A^{2^2}\cdot \cdots \cdot A^{2^{m-2}}\cdot A^{2^{m-1}} \end{gathered}$$

(2)

The inverse element can be calculated efficiently.

3. Arithmetic in ECC

In 1985, Koblitz and Miller proposed the elliptic curve for public key cryptography, elliptic curve cryptography is used in data encryption and decryption, key agreement, digital signature, etc. The definition of the elliptic curve $E$ in the finite field $\mathrm{G}\mathrm{F}\left(2^m\right)$ is expressed as $E\left(\mathrm{G}\mathrm{F}\left(2^m\right)\right)$ where $m$ is a positive integer, as shown in (3).

$$E\left(\mathrm{G}\mathrm{F}\left(2^m\right)\right):y^2+xy=x^3+a{x}^2+b,$$

(3)

where $a,b\in \mathrm{G}\mathrm{F}\left(2^m\right)$ and $b\ne 0$. The point $P$ of the elliptic curve $E$ is defined as $P=\left(x_1,y_1\right)$, where $x_1\in \mathrm{G}\mathrm{F}\left(2^m\right)$ and $y_1\in \mathrm{G}\mathrm{F}\left(2^m\right)$. The inverse of $P$ is $-P=\left(x_1,x_1+y_1\right)$.

Koblitz proposed the elliptic curve $E$ in 1991 as

$$E\left(\mathrm{G}\mathrm{F}\left(2\right)\right):y^2+xy=x^3+a{x}^2+1.$$

(4)

The cases of $a=0$ or $a=1$ refer to a Koblitz curve.

3.1. Point Addition

The point addition of P and Q is defined as $R=P⊞Q$, where $P\ne Q$. Let the points P and Q be $P=\left(x_1,y_1\right)$, and $Q=\left(x_2,y_2\right)$, respectively, where $x_1\ne x_2$. The result of point addition R is $R=\left(x_3,y_3\right)$. The relationships among these are

$$\lambda =\frac{y_1+y_2}{x_1+x_2},$$

(5)

$$x_3={\lambda }^2+\lambda +x_1+x_2+a,$$

(6)

$$y_3=\lambda (x_1+x_3)+x_3+y_1,$$

(7)

where the symbol “+” in (5)–(7) is the addition over the finite field.

3.2. Point Doubling

The point doubling of P is defined as $R=2P$, where $P=\left(x_1,y_1\right)$, $R=\left(x_3,y_3\right)$ and $x_1\ne 0$. The operations of point doubling are

$$\lambda =x_1+\frac{y_1}{x_1},$$

(8)

$$x_3={\lambda }^2+\lambda +a,$$

(9)

$$y_3=x_1^2+\left(\lambda +1\right)x_3.$$

(10)

3.3. The Points at Infinite ($O$ Points)

The elliptic curve $E$ contains a $O$ point in the finite field $\mathrm{GF}\left(2^m\right)$. The $O$ point must comply with the following rules:

$$O=O+O$$

(11)

$$P=P+O=O+P$$

(12)

$$O=P+\left(-P\right)=\left(-P\right)+P$$

(13)

3.4. Elliptic Curve Scalar Multiplication

The elliptic curve scalar multiplication is to add a point P on elliptic curve K times. That is,

$$KP=\underset{K}{\underbrace{P+P+P+\cdots +P+P}},$$

(14)

where K is a positive integer.

4. Proposed Lookup Table-Based Techniques for Arithmetic on $\mathbf{G}\mathbf{F}\left(2^{163}\right)$

This paper focuses on the finite field $\mathrm{G}\mathrm{F}\left(2^{163}\right)$.

4.1. Improved Multiplication Algorithm

Let $H\left(a_i,a_j\right)=a_{i}x+a_j$. By Horner’s rule, $A\left(x\right)$ is expressed as

$$A\left(x\right)=\left(\begin{array}{c}\left(\begin{array}{c}\cdots \left(\begin{array}{c}\left(a_{162}x+a_{161}\right)x^2\\ +\left(a_{160}x+a_{159}\right)\end{array}\right)x^2\\ +\cdots +\left(a_{4}x+a_3\right)\end{array}\right)x^2\\ +\left(a_{2}x+a_1\right)\end{array}\right)x+a_0.$$

(15)

Furthermore, the multiplication of the polynomials $A\left(x\right)$ and $B\left(x\right)$ is re-written as

$$A\left(x\right)B\left(x\right)=\left(\begin{array}{c}\left(\begin{array}{c}\cdots \left(\begin{array}{c}\left(a_{162}xB\left(x\right)+a_{161}B\left(x\right)\right)x^2\\ +\left(a_{160}xB\left(x\right)+a_{159}B\left(x\right)\right)\end{array}\right)x^2\\ +\cdots +\left(a_{4}xB\left(x\right)+a_{3}B\left(x\right)\right)\end{array}\right)x^2\\ +\left(a_{2}xB\left(x\right)+a_{1}B\left(x\right)\right)\end{array}\right)x+a_{0}B\left(x\right).$$

(16)

Define $d$ as the number of input items of $H$.

As $d=1$, $H\left(a_i\right)=a_i$. In the case of $d=2$, $H\left(a_i,a_j\right)=a_{i}x+a_j$. According to (16), one needs only $⌊\frac{163}{d}⌋$ executions to create an H table. The table of $H\left(a_i,a_j\right)$ for $d=2$ is shown in

Table 2. H Table.

Input		Output
$\left\{{\mathit{a}}_{\mathit{i}},{\mathit{a}}_{\mathit{j}}\right\}$	$\mathit{H}\left({\mathit{a}}_{\mathit{i}},{\mathit{a}}_{\mathit{j}}\right)={\mathit{a}}_{\mathit{i}}\mathit{x}+{\mathit{a}}_{\mathit{j}}$	$\mathit{H}\left(\mathit{x}\right)\cdot \mathit{B}\left(\mathit{x}\right)\mathbf{m}\mathbf{o}\mathbf{d}\mathit{F}\left(\mathit{x}\right)$
$\left\{0,0\right\}$	0	0
$\left\{0,1\right\}$	1	$B\left(x\right)$
$\left\{1,0\right\}$	$x$	$x\cdot B\left(x\right)\mathrm{m}\mathrm{o}\mathrm{d}F\left(x\right)$
$\left\{1,1\right\}$	$x+1$	$x\cdot B\left(x\right)\mathrm{m}\mathrm{o}\mathrm{d}F\left(x\right)+B\left(x\right)$

.

4.2. Lookup Table-Based Modulo Operation

Consider the multiplication of $A\left(x\right)\cdot x^q$. We have

$$A\left(x\right)\cdot x^q=\left(\begin{array}{c}{a}_{162}{x}^{162+q}+a_{161}{x}^{161+q}+\cdots \\ +a_2{x}^{2+q}+a_1{x}^{1+q}+a_0{x}^q\end{array}\right)modF\left(x\right),$$

(17)

where $F\left(x\right)=x^{163}+x^7+x^6+x^3+1$. In (17), there are q terms ($a_{162}{x}^{162},a_{161}{x}^{161},\cdots ,a_{163-q}{x}^{163-q}$) to perform a modulo $F\left(x\right)$ operation, because of the degree. As a result, we can establish a table with which to manage these $q$ terms. The table is used to store the results of $\left(a_{162}{x}^{162}+a_{161}{x}^{161}+\cdots +a_{163-q}{x}^{163-q}\right)x^{q}modF\left(x\right)$. Such a table is required when $q<156$. The inputs of the table with q terms are $a_{162},a_{161},\cdots ,a_{163-q}$. The output is $a_{162}{x}^{q-1}\cdot f+a_{161}{x}^{q-2}\cdot f+\cdots +a_{163-q}\cdot f$, where $f=x^7+x^6+x^3+1$. For $q=2$, the M table is constructed as

Table 3. M Table.

Input	Output
$\mathit{M}\left({\mathit{a}}_{162},{\mathit{a}}_{161}\right)$
$M\left(0,0\right)$	0
$M\left(0,1\right)$	$f$
$M\left(1,0\right)$	$x\cdot f$
$M\left(1,1\right)$	$x\cdot f+f$

.

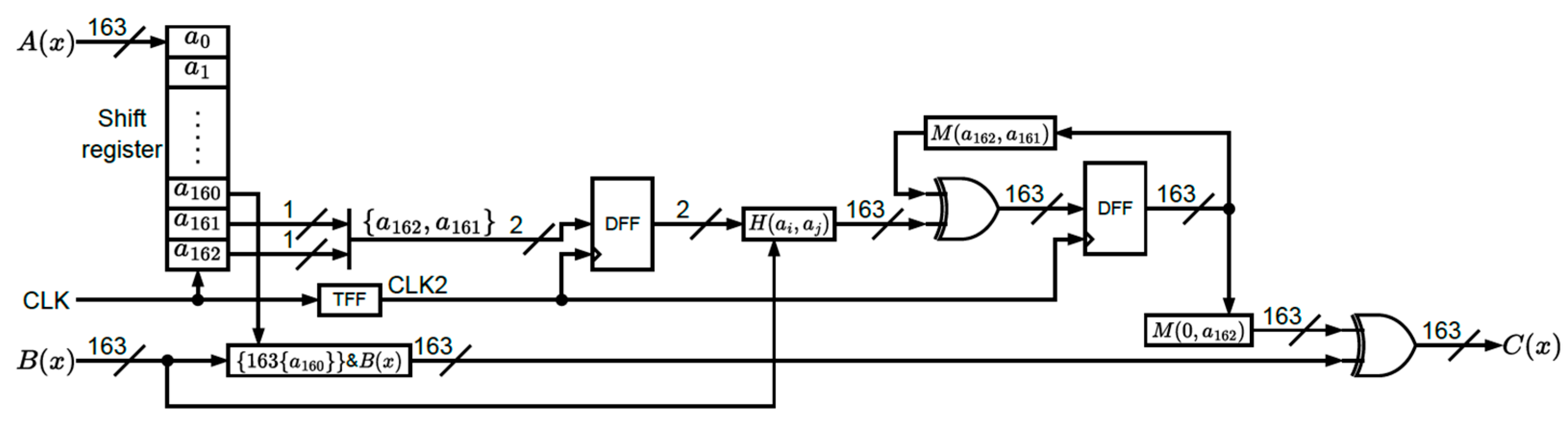
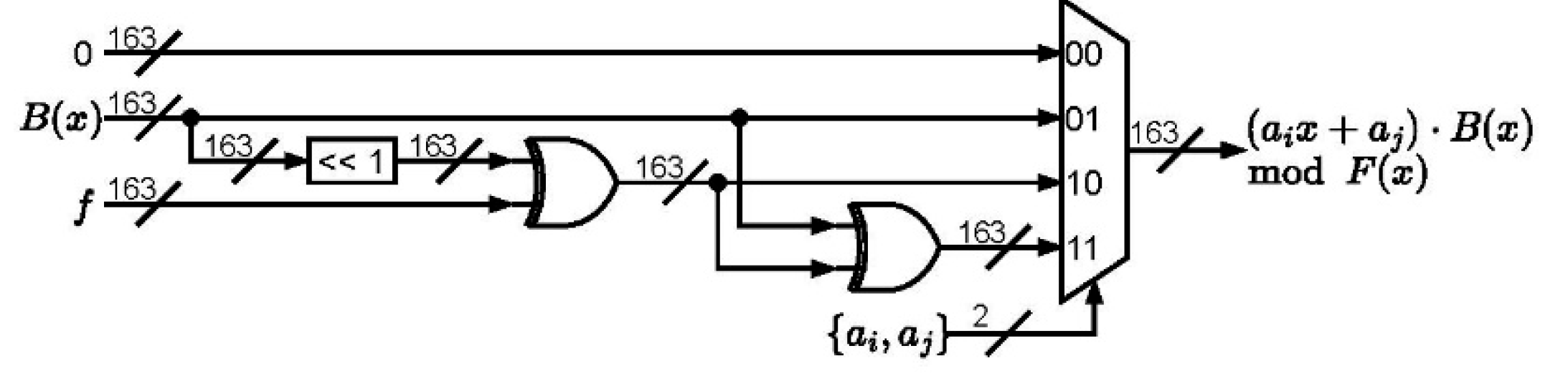
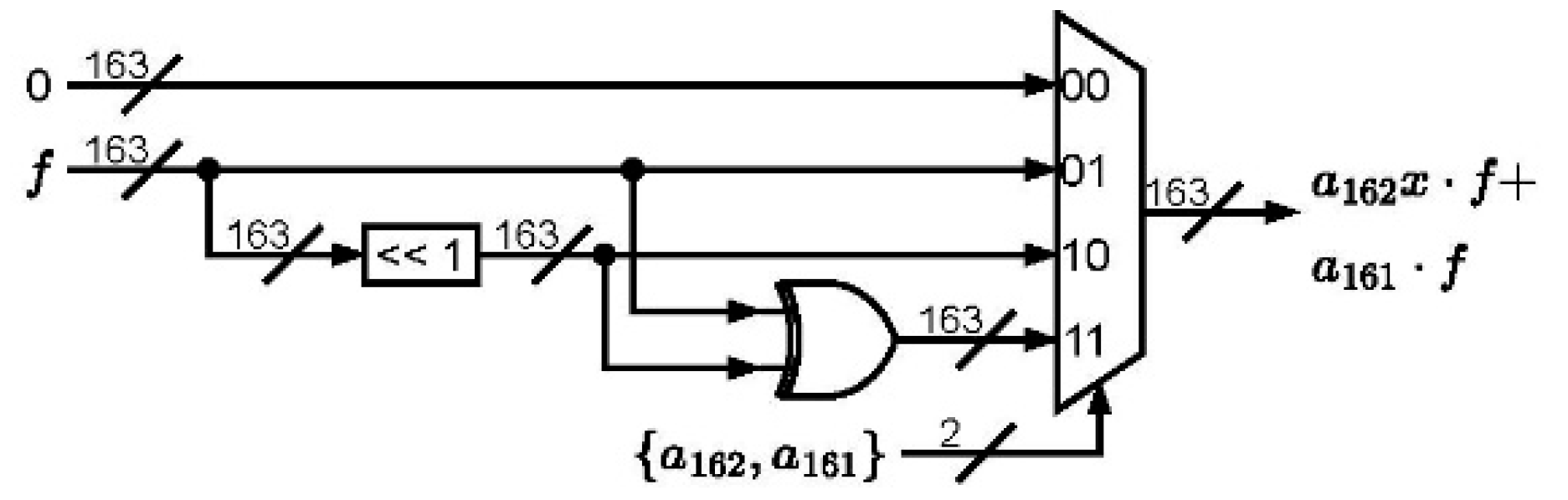
The circuit of the finite field multiplication is depicted in Figure 1, where the H and M tables are included. It can also be observed that the H table dominates the critical path of the whole architecture. Note that two XOR elements and one multiplexer are required for constructing the H table as depicted in Figure 2. The M table includes one XOR logic and one multiplexer in Figure 3.

For the software implementation, there is more time to establish these tables and store the corresponding values. However, the building and searching time for the tables will increase as the tables become large. Additionally, in terms of hardware implementation, more logic elements are required.

4.3. Improved Squaring Operation

The squaring operation of $A\left(x\right)$ is

$$C\left(x\right)\equiv a_{162}{x}^{324}+a_{161}{x}^{322}+\cdots +a_1{x}^2+a_{0}modF\left(x\right).$$

(18)

Consider modulo operations of each term as follows:

$$\begin{gathered} A_{162}\left(x\right)\equiv a_{162}{x}^{324}modF\left(x\right) \\ {A}_{161}\left(x\right)\equiv a_{161}{x}^{322}modF\left(x\right) \\ \dots \\ {A}_1\left(x\right)\equiv a_1{x}^{2}modF\left(x\right) \\ {A}_0\left(x\right)\equiv a_{0}modF\left(x\right). \end{gathered}$$

(19)

Let $A_i\left(x\right)={\sum }_{j=0}^{162}{\rho }_{ij}{x}^j$, where $0\le i\le 162$. In light of (19), we have

$$C\left(x\right)={\sum }_{i=0}^{162}{A}_i\left(x\right)={\sum }_{i=0}^{162}{c}_i\left(x\right),$$

(20)

where $c_i\left(x\right)={\theta }_i{x}^i$.

4.4. Improved Inverse Operation

As shown in (12), we have

$$2^{163}-2=2^{162}+2^{161}+\cdots +2^2+2^1$$

(21)

(21) can be re-written as

$$2^{163}-2=\left(\begin{array}{c}\left(\begin{array}{c}\cdots \left(\begin{array}{c}\left(\sum _{i=1}^w{2}^i\right)2^w\\ +\left(\sum _{i=1}^w{2}^i\right)\end{array}\right)2^w+\cdots \\ +\left(\sum _{i=1}^w{2}^i\right)\end{array}\right)2^w\\ +\left(\sum _{i=1}^w{2}^i\right)\end{array}\right)2^l+sgn\left(l\right)\left({\sum }_{i=1}^l{2}^i\right),$$

(22)

where $l\equiv 162modw$ and $sgn\left(l\right)$ are sign function defined as follows:

$$sgn\left(l\right)=\left\{\begin{array}{cc}0& ,l=0\\ 1& ,l>0\end{array}\right.$$

(23)

Simplification of ${\sum }_{i=1}^w{2}^i$ and ${\sum }_{i=1}^l{2}^i$ in (22) is required.

As $w$ is odd, we have

$${\sum }_{i=1}^w{2}^i=2^w+\left(2^{w-1}+\cdots +2^2+2^1\right).$$

(24)

As $w$ is even, it is derived that

$${\sum }_{i=1}^w{2}^i=\left(2^{w/2}+2^{w/2-1}+\cdots +2^2+2^1\right)2^{w/2}+\left(2^{w/2}+2^{w/2-1}+\cdots +2^2+2^1\right)$$

(25)

According to (24) and (25), (22) is represented as

$$\begin{array}{ll}{A}^{2^m-2}& =A^{2^1+2^2+\cdots +2^{m-2}+2^{m-1}}\\ & =A^{\left(\begin{array}{c}\left(\begin{array}{c}\cdots \left(\begin{array}{c}\left(\sum _{i=1}^w{2}^i\right)2^w\\ +\left(\sum _{i=1}^w{2}^i\right)\end{array}\right)2^w+\cdots \\ +\left(\sum _{i=1}^w{2}^i\right)\end{array}\right)2^w\\ +\left(\sum _{i=1}^w{2}^i\right)\end{array}\right)2^l+sgn\left(l\right)\left(\sum _{i=1}^l{2}^i\right)}\end{array}$$

(26)

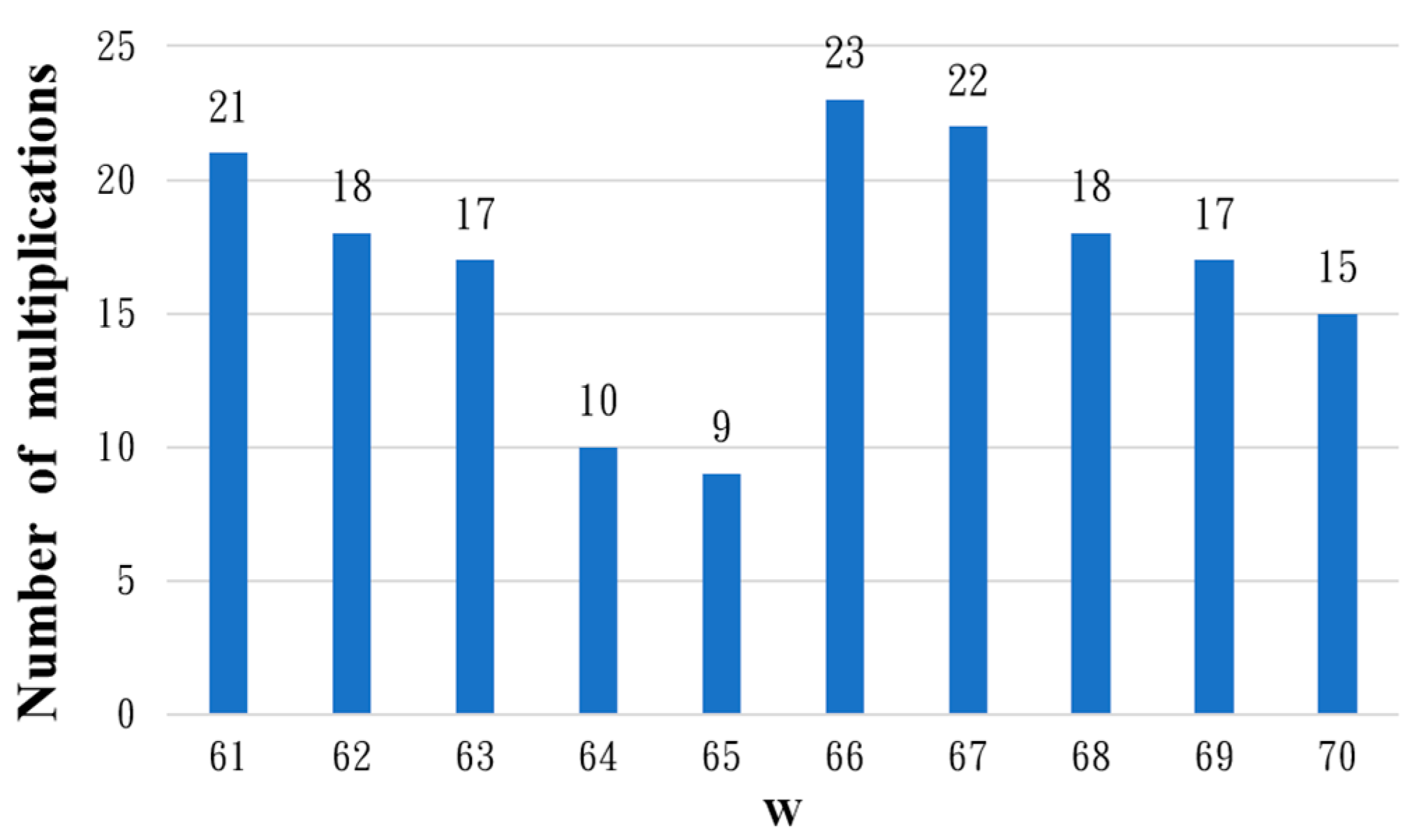
The original Fermat’s little theorem for the inverse element operation needs to go through 162 cycles of power operation and 161 cycles of multiplication operation. The main purpose of the above simplification process is to reduce the number of multiplication operations, but there is also a need to increase the number of different $2^n$ power operations. We investigate the number of multiplications for the inverse operation on the field GF(2¹⁶³) for various $w$. The results are depicted in Figure 4 for $w=61$ to $w=70$.

It can be seen in Figure 1 that grouping by $w=65$ requires the lowest number of multiplications. In the following, the inverse operation of $GF\left(2^{163}\right)$ and grouping by $w=65$ are simplified, where $l=32$, as shown in (27).

$$2^{163}-2=\left(\left({\sum }_{i=1}^{65}{2}^i\right)2^{65}+\left({\sum }_{i=1}^{65}{2}^i\right)\right)2^{32}+\left({\sum }_{i=1}^{32}{2}^i\right)$$

(27)

Simplify ${\sum }_{i=1}^w{2}^i$ and ${\sum }_{i=1}^l{2}^i$ in (27) and let $Z=2^{64}+2^{63}+\cdots +2^2+2^1$. We have

$$\begin{gathered} {\sum }_{i=1}^{65}{2}^i=2^{65}+\left(2^{64}+2^{63}+\cdots +2^2+2^1\right) \\ =2^{65}+Z. \end{gathered}$$

(28)

Using the idea, it is derived as follows:

$$\begin{gathered} Z=\left(2^{32}+2^{31}+\cdots +2^2+2^1\right)2^{32} \\ +\left(2^{32}+2^{31}+\cdots +2^2+2^1\right) \\ =\left(Y\right)2^{32}+Y, \end{gathered}$$

(29)

where $Y=2^{32}+2^{31}+\cdots +2^2+2^1$.

$$\begin{gathered} Y=\left(2^{16}+2^{15}+\cdots +2^2+2^1\right)2^{16} \\ +\left(2^{16}+2^{15}+\cdots +2^2+2^1\right) \\ =\left(X\right)2^{16}+X, \end{gathered}$$

(30)

where $X=2^{16}+2^{15}+\cdots +2^2+2^1$.

$$\begin{gathered} X=\left(2^8+2^7+\cdots +2^2+2^1\right)2^8 \\ +\left(2^8+2^7+\cdots +2^2+2^1\right) \\ =\left(W\right)2^8+W, \end{gathered}$$

(31)

where $W=2^8+2^7+\cdots +2^2+2^1$.

$$\begin{gathered} W=\left(2^4+2^3+2^2+2^1\right)2^4 \\ +\left(2^4+2^3+2^2+2^1\right) \\ =\left(V\right)2^4+V, \end{gathered}$$

(32)

where $V=2^4+2^3+2^2+2^1$.

$$\begin{gathered} V=\left(2^2+2^1\right)2^2+\left(2^2+2^1\right) \\ =\left(U\right)2^2+U, \end{gathered}$$

(33)

where $U=2^2+2^1$.

Among these, $Y$ is the same as the residue ${\sum }_{i=1}^{32}{2}^i$, so there is no need to simplify the residue further, though it does need to store the value of $Y$ after the operation. In this case, where $w=65$, the inverse operation over the field GF(2¹⁶³) requires 9 multiplication operations, 1 squaring operation and $2^2,2^4,2^8,2^{16},2^{32},2^{65}$ power operations.

The circuit for inverse operation over GF(2¹⁶³) is shown in Figure 5. The GFM is the Galois field multiplication unit and the input Ci in the multiplexer means the ith cycle.

5. Proposed Elliptic Curve Scalar Multiplication Operation

By building a table of elliptic curve points and using a table lookup method and an inverse operation that reduces the number of iterations of point doubling by two, the speed of scalar multiplication of elliptic curves is increased.

5.1. Conventional Multiple Time Point Doubling Algorithm

Consider Algorithm 1, called Point_Doubling_Repeating $\left(P,r\right)$, where $P$ is the point of the elliptic curve and $r$ is a positive integer. If $r=2$, the point of $P$ will be subjected to a point doubling operation twice. The coordinate of $P$ is $\left(x_1,y_1\right)$ and the result of point doubling is $\left(x_3,y_3\right)$.

Algorithm 1 Point Doubling Repeating

1: Function Point_Doubling_Repeating $\left(P,r\right)$ 2:    for $i$ from $0$ to $r-1$ do 3:        $\lambda =x_1+\frac{y_1}{x_1}$ 4:        $x_3={\lambda }^2+\lambda +a$ 5:        $y_3=x_1^2+\left(\lambda +1\right)x_3$ 6:        $P\leftarrow P\left(x_3,y_3\right)$ 7:        $x_1=x_3$ 8:        $y_1=y_3$ 9:    end for 10: end function

The computational complexity of Algorithm 1 is listed in

Table 4. Number of finite field operations required for each of the one-time and two-time point doubling operations.

r	$\mathit{r}=1$	$\mathit{r}=2$
Addition	5	10
Multiplication	2	4
Square	2	4
Inverse	1	2

with $r=1$ and $r=2$. It is observed that point doubling two times ($r=2$) requires the inverse operation two times. In fact, $k$ inverse operations are needed as $r=k$.

5.2. Proposed Two-Time Point Doubling Algorithm

Algorithm 2, Point_Doubling_Modify $\left(P,Sel\right)$, is presented, where the input of $P$ point is $P\left(x_1,y_1\right)$. As $Sel=0$, the point doubling is performed once and the output is $P\left(x_3,y_3\right)$. When $Sel=1$, the improved algorithm for point doubling twice is executed and the output is $P\left(x_5,y_5\right)$.

Algorithm 2 Point Doubling Modify

1: Function Point_Doubling_Modify $\left(P,Sel\right)$ 2:    if $Sel=0$ then 3:        $\lambda =x_1+\frac{y_1}{x_1}$ 4:        $x_3={\lambda }^2+\lambda +a$ 5:        $y_3=x_1^2+\left(\lambda +1\right)x_3$ 6:        $P\leftarrow P\left(x_3,y_3\right)$ 7:    else if $Sel=1$ then 8:        $t_0=x_1^2$ 9:        $u_0=t_0+y_1$ 10:       $t_1=a\cdot t_0$ 11:       $t_2=\left(u_0+x_1\right)\cdot u_0$ 12:       $u_1=t_1+t_2$ 13:       $t_3=u_1^2$ 14:       $t_4=u_1\cdot t_0$ 15:       $t_5=t_4^{-1}$ 16:       $x_3=t_3\cdot t_5$ 17:       $t_6=\left(a+1\right)\cdot t_4$ 18:       $t_7=u_0^2$ 19:       $t_8=t_7\cdot u_1$ 20:       $t_9=t_0^2$ 21:       $t_{10}=t_0\cdot t_9$ 22:       $u_2=t_6+t_8+t_{10}$ 23:       $\lambda =u_2\cdot t_5$ 24:       $t_{11}={\lambda }^2$ 25:       $x_5=t_{11}+\lambda +a$ 26:       $t_{12}=x_3^2$ 27:       $t_{13}=\left(\lambda +1\right)\cdot x_5$ 28:       $y_5=t_{12}+t_{13}$ 29:       $P\leftarrow P\left(x_5,y_5\right)$ 30:    end if 31:    return $P$ 32: end function

The number of finite field operations required for improved two-time point doubling is shown in

Table 5. Number of finite field operations for improved two-time point doubling.

	Number of Operations
Addition	10
Multiplication	9
Square	6
Inverse	1

. It can be found that, after simplification, only one inverse operation is required.

Comparison with the conventional two-time point doubling is revealed in

Table 6. Comparison of two-time point doubling.

	Conventional	Proposed
Addition	10	10
Multiplication	4	9
Square	4	6
Inverse	2	1

. Although the proposed two-time point doubling algorithm reduces the number of inverse operations by 1, it increases the number of multiplication operations by 5 and the number of squaring operations by 2.

The proposed architecture of two-time point doubling is presented in Figure 6. The yellow block is used to perform one-time point doubling and the red block is for computing two-time point doubling.

The inverse operation utilizes the framework in Figure 5.

5.3. Proposed Elliptic Curve Scalar Multiplication Algorithm

The elliptic curve scalar multiplication operation is defined in (14). The positive integer K is expressed as follows in the binary form.

$$K=k_{m-1}{2}^{m-1}+k_{m-2}{2}^{m-2}+\cdots +k_2{2}^2+k_1{2}^1+k_0{2}^0,$$

(34)

where $k_i\in \left\{0,1\right\}$.

If $m$ is odd, K is re-written as

$$K=\left(\begin{array}{c}\cdots \left(\begin{array}{c}\left(k_{m-1}2+k_{m-2}\right)2^2\\ +\left(k_{m-3}2+k_{m-4}\right)\end{array}\right)2^2+\cdots \\ +\left(k_{2}2+k_1\right)\end{array}\right)2+k_0$$

(35)

by Horner’s rule. Moreover,

$$KP=\left(\begin{array}{c}\cdots \left(\begin{array}{c}\left(k_{m-1}2P+k_{m-2}P\right)2^2\\ +\left(k_{m-3}2P+k_{m-4}P\right)\end{array}\right)2^2+\cdots \\ +\left(k_{2}2P+k_{1}P\right)\end{array}\right)2+k_{0}P.$$

(36)

It is observed in (36) that the last term is $k_{0}P$ and that the common term is expressed as $k_{i}2P+k_{j}P$. As a result, the L table is motivated and constructed. The L table is listed as

Table 7. L Table.

$\mathit{L}\left({\mathit{k}}_{\mathit{i}},{\mathit{k}}_{\mathit{j}}\right)$	${\mathit{k}}_{\mathit{i}}2\mathit{P}+{\mathit{k}}_{\mathit{j}}\mathit{P}$
$L\left(0,0\right)$	0
$L\left(0,1\right)$	$P$
$L\left(1,0\right)$	$2P$
$L\left(1,1\right)$	$2P+P$

, where the input is $\left(k_i,k_j\right)$. As when one builds the L table, the operations for point addition and doubling once need to be performed first. There are an additional four 163-bit registers required for the table.

The term of $\left(k_{i}2P+k_{j}P\right)$ can be viewed as a point of the elliptic curve. This term requires point doubling once, as $k_i=1$. Furthermore, $\left(k_{i}2P+k_{j}P\right)2^2$ is the operation of two-time point doubling. According to (36), a new scalar multiplication technique is proposed in Algorithm 3.

Algorithm 3 New Scalar Multiplication 1

1: Function New_ScalarM $\left(K,P\right)$ 2:    $Q=\left(\mathrm{0,0}\right)$ 3:    To make a lookup table $L\left(k_i,k_j\right)$ as shown in Table 7 4:    for $i$ from $⌊\frac{m}{2}⌋-1$ to $0$ do 5:    $Q\leftarrow$Point_Doubling_Repeating$\left(Q,2\right)$ 6:    $Q\leftarrow$Point_Addition $\left(Q,L\left(k_{2i+2},k_{2i+1}\right)\right)$ 7:    end for 8: $Q\leftarrow$Point_Doubling_Repeating$\left(Q,1\right)$ 9: $Q\leftarrow$Point_Addition$\left(Q,L\left(0,k_0\right)\right)$ 10: return $Q$ 11: end function

We replace Point_Doubling_Repeating$\left(P,r\right)$ with Point_Doubling_Modify$\left(P,Sel\right)$ in Algorithm 3. Algorithm 4 is therefore obtained.

Algorithm 4 New Scalar Multiplication 2

1: Function New_ScalarM $\left(K,P\right)$ 2:    $Q=\left(\mathrm{0,0}\right)$ 3:    To make a lookup table $L\left(k_i,k_j\right)$ as shown in Table 7 4:    for $i$ from $⌊\frac{m}{2}⌋-1$ to 0 do 5:    $Q\leftarrow$Point_Doubling_Modify$\left(Q,1\right)$ 6:    $Q\leftarrow$Point_Addition$\left(Q,L\left(k_{2i+2},k_{2i+1}\right)\right)$ 7:    end for 8: $Q\leftarrow$Point_Doubling_Modify$\left(Q,0\right)$ 9: $Q\leftarrow$Point_Addition$\left(Q,L\left(0,k_0\right)\right)$ 10: return $Q$ 11: end function

The numbers of arithmetic operations required in Algorithms 3 and 4 are demonstrated in

Table 8. Number of arithmetic operations in Algorithms 3 and 4.

Operation	Number
Number of Point Addition	83
Number of Point Doubling	2
Two-time Point Doubling	81

. The proposed framework of the scalar multiplication by Algorithm 4 is depicted in Figure 7, where Algorithm 2 is applied for point doubling. Note that using the improved two-time point doubling reduces the number of inverse operations by 81. However, the numbers of multiplication and squaring operations will increase by 405 and 162, respectively.

5.4. Performance Evaluation

The results of multiplication over the finite field GF(2¹⁶³) are obtained after computing 163 coefficients. Utilization of the H table by Horner’s rule only needs computation of $⌊\frac{163}{d}⌋$ coefficients. The M table is exploited in order to speed up the modulo operation by the XOR operation. The inverse operation using Fermat’s little theorem is obtained by the simplifications of ${\sum }_{i=1}^w{2}^i$ and ${\sum }_{i=1}^l{2}^i$. The results of $A^{{\sum }_{i=1}^w{2}^i}$ and $A^{{\sum }_{i=1}^l{2}^i}$ are stored in advance. Thus, this leads to improvements in performance of the inverse operation.

The most time-consuming operation over the finite field is the inverse operation. Exploiting Horner’s rule to compute the inverse requires nine multiplication and one squaring operation. The conventional two-time point doubling needs two inverse operations. However, the proposed method requires only one inverse operation at the expense of five multiplication and two squaring operations. Finally, the proposed algorithm reduces four multiplications and increase two squaring operations. Elliptic curve point multiplication KP is improved by using the idea that the integer K is expressed in the binary form with Horner’s rule-based grouping technique. The L table is established to further enhance the efficiency of the scalar multiplication.

The efficiency evaluations for the proposed hardware design are listed in

Table 9. Multiplication designs with various d.

d	Critical Path (ns)	Frequency (MHz)	Area (μm2)	Total Power (mW)	Cycle
1	1.44	694.44	4761.44	3.39	164
2	0.86	1162.79	7705.08	4.53	84
3	0.95	1052.63	8750.62	5.03	57
4	0.95	1052.63	10482.24	6.00	43

,

Table 10. Squaring circuits of 2^n.

2n	Critical Path (ns)	Area (μm2)	Total Power (mW)	Cycle
21	0.18	355.6	0.38	1
22	0.4	709.2	1.09	1
24	0.82	1980.6	4.00	1
28	1.11	5736.1	14.06	1
216	1.22	6569.3	16.44	1
232	1.22	6652.3	16.63	1
264	1.25	6624.6	16.65	1

,

Table 11. Architecture comparison for two-time point doubling.

Two-Time Doubling	Critical Path (ns)	Area (μm2)	Total Power (mW)	Cycle	Delay (ns)
Conventional	2.64	123,197.08	62.15	1795	4738.8
Proposed	2.65	147,547.68	75.11	924	2448.6

and

Table 12. Architecture comparison for scalar multiplication.

	Critical Path (ns)	Area (μm2)	Total Power (mW)	Cycle	Delay (ns)
Algorithm 3	2.76	393,205.19	194.23	464,476	1,281,953.76
Algorithm 4	2.78	441,985.79	219.44	150,925	419,571.5

. All circuits are synthesized with Taiwan Semiconductor Manufacturing Company (TSMC) 40 nm standard cell library by Synopsys Design Compiler

Table 9 indicates the synthesized results of the proposed multiplication method, with various d values. It is observed that the shortest critical path happens as d = 2. For the proposed squaring circuits, Table 10 shows that the critical path becomes short with the increase of n. However, the improvements are not significant from the cases of 2¹⁶ to 2⁶⁵. Table 11 reveals that the proposed two-time point doubling has a 48% shorter computing time when compared with the conventional one, and with low area–time complexity. Take the architectures of scalar multiplication into consideration in Table 12. The delay of Algorithm 4 is improved by 67% over Algorithm 3, with an area increase of only 12%.

6. Conclusions

This paper proposed a methodology and hardware architecture for the scalar multiplication in the affine coordinate system over ECC. Our main idea is to exploit Horner’s rule to efficiently construct the lookup tables for arithmetic operations over the finite field. The time-consuming part in such a system is the inverse operation. The new algorithm for two-time point doubling was therefore developed by reducing the number of inverse operations. Results of the hardware implementations show that the computing time of two-time point doubling is reduced by 48% over the conventional one, with an area increase of only 18%. For the scalar multiplication, including the point addition and doubling operations, the presented hardware architecture has a reduction of delay by 68% as compared with the traditional algorithm. The total power and circuit area increase by only 13% and 12%, respectively. Such results reveal that the proposed lookup table-based design indeed achieves a high-speed performance by reducing the computational complexity of point doubling. However, the current reported hardware designs are still involved in plenty of registers. The size of the lookup tables may be reduced by some merging techniques. These issues will be investigated and addressed for compact design in the future.