ES-HAS: ECC-Based Secure Handover Authentication Scheme for Roaming Mobile User in Global Mobility Networks

Abstract

The design and implementation of two-factor schemes designed for roaming mobile users for global mobility networks in smart cities requires attention to protect the scheme from various security attacks, such as the replay attack, impersonation attack, man-in-the-middle attack, password-guessing attack and stolen-smart-card attack. In addition to these attacks, the scheme should achieve user anonymity, unlinkability and perfect forward secrecy. In the roaming scenario, as mobile users are connected to the foreign network, mobile users must provide authentication details to the foreign network to which they are connected. The foreign network forwards the authentication messages received from the mobile users to their home network. The home network validates the authenticity of the mobile user. In the roaming scenario, all communication between the three entities is carried over an insecure channel. It is assumed that the adversary has the capabilities to intercept the messages transmitted over an insecure channel. Hence, the authentication scheme designed must be able to resist the above-mentioned security attacks and achieve the security goals. Our proposed scheme ES-HAS (elliptic curve-based secure handover authentication scheme) is a two-factor authentication scheme in which the mobile user possesses the password, and the smart card resists the above-mentioned security attacks. It also achieves the above-mentioned security goals. We also extended our two-factor authentication to a multi-factor authentication scheme using the fingerprint biometric technique. The formal security analysis using BAN logic and the formal security verification of the proposed scheme using the widely accepted AVISPA (automated validation of internet security protocols and applications) tool is presented in this article. In comparison with the related schemes, the proposed scheme is more efficient and robust. This makes the proposed scheme suitable for practical implementation.

1. Introduction

With the widespread usage of the internet, there has been an increased demand for internet services. Users are able to access internet services through mobile devices over wireless networks. Hence, securing the network in order to achieve network security goals, such as confidentiality, integrity and availability, becomes imperative. The global mobility network (GLOMONET) facilitates a roaming service for the mobile user (MU) to access various kind of services provided by the home network (HN) while roaming in a foreign network (FN). Authenticating MU in the roaming network is an important security issue. In order to address this issue, researchers have proposed many two-factor and multi-factor authentication schemes in GLOMONET. In two-factor authentication schemes, MU possesses the password and the smart card. In multi-factor authentication schemes, along with the password and the smart card, biometric techniques, such as fingerprint scan, iris scan, etc. are used. When MU roams into any FN, he/she should get authenticated to access the HN services in the FN. Hence, mutual authentication between the MU and the FN becomes important. The mutual authentication process must be supported by the HN. Before any communication takes place in GLOMONET, there are three phases involved in the communication between the three entities. The first is the registration phase, which is carried over a secure channel; the second is the login and the authentication phase; and the third is the password change phase. In the registration phase, MU registers to HN to get access to the HN services, whereas the login and authentication phase is carried over an insecure channel and hence messages transmitted during these phases are vulnerable to security attacks. Hence, securing the messages over an insecure channel becomes important. In order to secure the messages, symmetric key cryptosystem algorithms are used. Another important security property that should be addressed in GLOMONET is the user anonymity. During the message transmission over an open channel, an adversary listening to the open channel can intercept the messages and impersonate the legal MU. So, the protection of the user’s information is also an important task for the researchers.

1.1. Multi-Factor Authentication Schemes in GLOMONET

Many biometric-based user authentication protocols [1,2,3,4,5] have been presented to improve the security flaws associated with the mobile device authentication. Biometric-based schemes are difficult to guess or duplicate or forge, and cannot be stolen or lost.

1.2. Security and Function Requirements

Based on the literature review on the authentication schemes for the roaming MU in GLOMONET, the observation is made that the designed authentication scheme has to satisfy the set of security requirements and functions listed below:

• Quick wrong password detection: MUs use different network-based applications which provide the credentials for users to access their services. To prove the authenticity of the MU using the services, the MU has to input the pair of identity and password. In the event of wrong input of the password, there must be a mechanism to prompt the user about the wrong input login credentials. The mechanism developed must verify the credentials and reject the request of the MUs with invalid credentials, which saves further computational and communication costs.
• Mutual authentication: In the roaming scenario, the MU is away from the HN. Therefore, the MU cannot access the services from the HN. Therefore, the foreign network serves the roaming MU present in the cell area of the FN. To access the services from the FN, the MU has to authenticate HN and FN. The FN forwards the authentication messages sent by the MU to the HN. The HN verifies the authenticity of the MU. After receiving successful verification of the MU credentials, the FN grants access to the services to the MU. In such a roaming environment, where the FN is semi-trusted, the roaming MU is not trusted and the HN is assumed to be fully trusted and thus mutual authentication between all the participating entities in the communication becomes imperative to resist security attacks, such as the man-in-the-middle attack, replay attack, and impersonation attack.
• Fairness of session key: The session key is derived between the FN and the roaming MU to establish secure communication over the insecure channel. The session key establishment requires a contribution from both communicating entities, such as the FN and MU. The derived session should not be known to the third party. Even the HN should not have knowledge of the session key agreed between the FN and MU.
• Session key update: To avoid security attacks, such as the replay attack, etc., the session is updated for every new session that is initiated between the MU and FN. To achieve the freshness of the random numbers for every session, fresh random values are chosen.
• User anonymity: User anonymity is an important security feature that the developed authentication scheme must protect. The identity of the MU should not be disclosed.
• Unlinkability: An attacker should not be able to trace the location of the MU by linking the two different sessions of the same MU.
• Resistance of well known security attacks: The designed authentication scheme should resist the security attacks, such as the replay attack, impersonation attack, stolen-smart-card attack, password-guessing attack, and the man-in-the-middle attack.

1.3. Motivation

The literature survey on the existing authentication schemes for roaming MUs in GLOMONET reveals that the authentication schemes found in the literature survey [6,7,8,9,10] are vulnerable to several security attacks and could not meet the security requirements mentioned in Section 1.2.

• The authentication schemes for the roaming MUs [6,7,8,9,10] are vulnerable to the well-known security attacks, such as the insider attack, replay attack, impersonation attack, and password-guessing attack, in GLOMONETS.
• The session key update phase is a critical security requirement and hence must be implemented carefully while designing the authentication scheme for roaming MUs. The session key update phase maintains the freshness of the random numbers for every new session established between the MU and FN. The literature survey reveals that the authentication schemes designed for roaming MUs in GLOMONET [5,10,11,12] Could not provide the session key update phase in their proposed schemes.
• The authentication schemes developed for roaming MUs in GLOMONET should satisfy all the security requirements presented in Section 1.2.
• The design and development of lightweight secure authentication schemes are essential for resource-constrained mobile devices relative to computing power, memory and battery capacity.

1.4. Contributions of Our Research Work

• We design an efficient and more secure ECC-enabled authentication scheme for roaming MUs in GLOMONET that can potentially resist various known attacks. In the proposed scheme, a roaming MU and a serving network or FN mutually authenticate among each other during the authentication phase, and they also establish a common session key among them for secure communication.
• The BAN logic-based formal security analysis [13] proves the strength of our proposed scheme. Using such a security analysis, it is shown that the proposed scheme provides the session key security. Furthermore, to ensure other existing known attacks, the informal (non-mathematical) security analysis is also presented.
• The proposed scheme is simulated with the help of the broadly accepted automated validation of internet security protocols and applications (AVISPA) tool [14]. AVISPA tools perform formal security verification of the proposed scheme. The simulation results prove that the proposed scheme is secure against passive/active attacks, such as replay attacks and man-in-the-middle attacks.
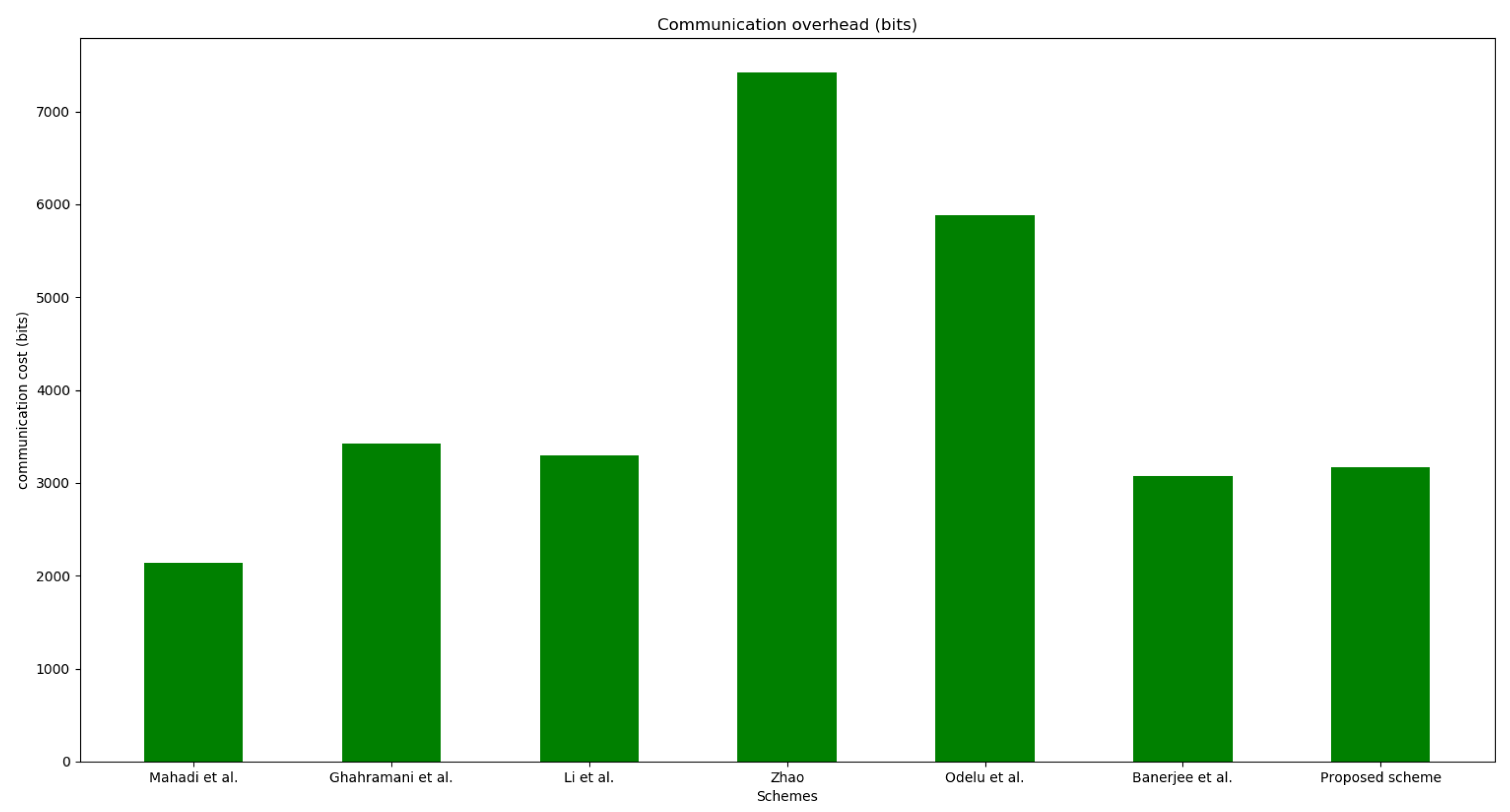
• In addition, the proposed scheme is shown to be comparable with other existing schemes in terms of the communication and the computation costs, and it also provides better security and functionality features in comparison to those of other existing schemes. The comparative study shows that the proposed scheme is efficient and more robust for the authentication of roaming MUs as compared to other authentication schemes in GLOMONET.

1.5. Organization of the Paper

The literature survey on previous authentication schemes is briefed in Section 2. Mathematical preliminaries are explained in Section 3. The system model is presented in Section 4. The proposed scheme is explained in Section 5. Detailed description of the formal security analysis using BAN logic is described in Section 7. Formal security verification of the proposed scheme using the AVISPA tool is illustrated in Section 8. The performance comparison is described in Section 9. Conclusion is given in Section 10.

2. Literature Survey

In 1995, Hwang et al. [15] worked on securing communication over teleconference by sharing a common secret key. In 1999, Hwang [16] further worked on the same topic, securing teleconference, and proposed a new scheme. In 2000, L. Buttyan et al. [17] worked on authentication protocols and came up with a new scheme. The proposed scheme explained the various security attacks to which the authentication schemes designed for GLOMONETs are vulnerable. In 2003, Hwang et al. [18] worked on the authentication schemes of Hwang et al. [15] and L. Buttyan et al. [17]. They proposed a new scheme to provide a secure and efficient authentication scheme.

In 2004, Zhu et al. [19] pointed out that most authentication schemes fail to preserve user anonymity.

Later in 2006, Lee et al. [20] worked on the authentication scheme of Zhu et al. [19]. The study revealed that their scheme is susceptible to forgery attacks and mutual authentication. To overcome the security pitfalls of the scheme of Zhu et al., Lee et al. [20] came up with a new scheme. Later, Wei et al. [21] worked on the scheme of Lee et al. [20]. With a thorough understanding of their scheme, Wei et al. found that their scheme failed to preserve user anonymity and untraceability. Further, Wei et al. also stated that their scheme suffered from password-guessing attacks. To improvise the scheme and to enhance performance, Wei et al. [21] came up with a new scheme.

In 2014, Huang et al. [22] cryptanalyzed the scheme of Juang et al. [23] based on passive attacks and active attacks. The cryptanalysis on the scheme of Juang et al. stated that their scheme has limitations over the smart-card attack, password attack and session key extraction.

In 2015, Ding Wang et al. [24] reviewed the scheme of Tsai et al. [25]. The cryptanalysis was based on the well-known attack in two-factor authentication schemes. For the smart-card-loss attack, with the stolen smart card parameters, the adversary could change the password by initiating the password change phase.

In 2018, Xu et al. [26] reviewed Gope and Hwang’s protocol [27] and identified some of the limitations of the scheme, such as the storage consumption problem, computational burden and replay attack. The scheme of Xu et al. contributes to overcoming the identified limitations.

In 2019, Ref. [28] proposed a privacy-preserving authentication scheme for roaming consumers in GLOMONET. Their work revealed the cryptanalysis of schemes such as those of Arshad et al. [29], Li et al. [4], and Chen et al. [30,31] based on session-specific information attacks. The proposed scheme of Arezou et al. provided countermeasures to the identified security weaknesses. Their scheme achieved security, such as impersonation attack resistance, modified attack resistance, strong MU anonymity and unlinkability, insider attack resistance, replay attack resistance, password-guessing attack resistance, known session-specific temporary information attack resistance, desynchronization attack resistance, known key attack resistance, denial-of-service attack resistance, and stolen verifier attack resistance, as well as security goals, such as perfect forward secrecy. In 2020, in Ref. [32], Wei et al. proposed two-factor authentication for roaming users in GLOMONET. Their scheme is based on the digital signature algorithm. They attempted to achieve the user anonymity using digital signature algorithms. The scheme of Ding et al. [33] cryptanalysed the scheme of Li et al. [34] and claimed that the scheme security proof of Li et al. to protect user anonymity has some weaknesses. Another proof validation was made on the offline password guessing attack and they claimed that the scheme proof of Li et al. has some limitations. The scheme of Ding et al. provided the claim to overcome these identified weaknesses.

In 2013, Shin et al. [35] proposed a secure authentication scheme with user anonymity for roaming users in ubiquitous networks. Later, Farash et al. [36] cryptanalysed the scheme of Shin et al. The cryptanalysis proved that the scheme of Shin et al. is vulnerable to security attacks, such as user traceability, user and server impersonation attacks and session key disclosure. To countermeasure the security attacks identified in the scheme [35], Farash et al. [36] proposed an enhanced secure authentication protocol for ubiquitous networks. The strengths of their proposed scheme are as follows:

• Their scheme provides the mobile node authentication and the FN authentication.
• Their scheme also protects user anonymity and achieves untraceability.
• Their scheme is resistant to the offline password guessing attack.
• No verification table is maintained at the server side for the password. This protects the scheme from such attacks as stolen verifier and modification attacks.

In 2016, Karuppiah et al. [37] reviewed the scheme of Farash et al. [36]. The cryptanalysis on the scheme [36] resulted in the findings of some security weaknesses to the identified attacks: their scheme is vulnerable against replay, forgery, and offline password guessing attacks. In addition, their scheme fails to protect user anonymity, with no local password verification and session key disclosure. Karuppiah et al. [37] proposed a secure lightweight authentication scheme for roaming mobile users. The strengths of their proposed scheme are as follows: user anonymity is protected, user untraceability is achieved, and mutual authentication between the MU, FA and HA are achieved. Their scheme is resistant to such security attacks as the replay attack, offline password guessing attack, forgery attack, stolen verifier and modification attacks, insider attack, man-in-the-middle attack, and known key attack. In addition, forward secrecy and local password verification are achieved.

Gope and Hwang [27] reviewed the scheme of He et al. [38]. The cryptanalysis on the scheme of He et al. revealed their proposed scheme having several security weaknesses, such as vulnerability to forgery attack and unfair key agreement, compromising the untraceability and disclosure of the user identity. Gope and Hwang [27] proposed an efficient mutual authentication and key agreement. Their proposed scheme is resilient to the identified security weaknesses in the scheme of He et al. The security strengths of their proposed scheme are as follows: accomplishment of mutual authentication, fair key agreement, strong user anonymity, resistant to forgery attacks and security assurance in the case of lost smart card.

In 2017, Odelu et al. [39] first reviewed the work proposed by Zhao et al. [40]. The cryptanalysis on the scheme [40] revealed that the scheme is vulnerable to several security attacks, such as known session key attack, and insider attack, with no provision for revocation and reregistration. Odelu et al. [39] proposed a secure anonymity-preserving authentication scheme for roaming mobile users in global mobility networks. The strengths of the proposed scheme are as follows: provides user anonymity; resists impersonation attack, replay attack, man-in-the-middle attack, offline password-guessing attack, and insider attack; provides session key security; provides local password verification; and provides provision for revocation and re-registration.

In 2018, Fan wu et al. [41] proposed a smart healthcare systems under global mobility networks. Their proposed scheme provides security strength against such security attacks as insider attack, offline password guessing attack, forgery attack, de-synchronization attack, replay attack, known key attack, tracking attack and strong forward security.

In 2018, Banerjee et al. [42] proposed an anonymity-preserving group formation-based authentication protocol in global mobility networks. The security strength of the proposed scheme is as follows: protects both user anonymity and untraceability; and the scheme is resilient to security attacks such as impersonation attack, replay attack, man-in-the-middle attack, privileged-insider attack, offline password-guessing attack and stolen-smart-card attack.

In 2018, Madhusudhan and Shashidhara [5] reviewed the scheme of Karuppiah and Saravanan [43]. The cryptanalysis of their scheme [43] demonstrated that it is vulnerable to security attacks such as insider attack, stolen verifier attack, offline password-guessing attack with smart cards, impersonation attack, denial-of-service attack, clock synchronization problem, unfair key agreement and disclosure of user anonymity. Madhusudhan and Shashidhara [5] proposed a secure and lightweight authentication scheme for roaming service in GLOMONETs. The proposed scheme [5] resists the security weaknesses identified in the scheme of [43]. The strengths of the proposed scheme [5] are as follows: user anonymity and untraceability is achieved, mutual authentication is achieved, the proposed scheme is resilient to security attacks such as impersonation attack, replay attack, insider attack, offline dictionary attack, stolen verifier attack and smart-card-loss attack. Their scheme achieves fair key agreement and provides local password verification.

In 2019, Lu et al. [44] reviewed the scheme of Gope and Hwang [45]. The cryptanalysis on the scheme [45] demonstrated that the scheme is vulnerable to security attacks such as known session-specific temporary information attack. To address the identified security weaknesses found in the scheme [45], Lu et al. [44] proposed an elliptic curve cryptography (ECC) based authentication scheme to achieve secure implementation in GLOMONET. The security strengths of the proposed scheme [44] are as follows: mutual authentication is achieved, known session-specific temporary information attack, unlinkability, anonymity and untraceability. The scheme is resilient to security attacks such as forgery attack, insider attack, and stolen-smart-card attack.

In 2019, Aghili et al. [46] proposed authentication and key agreement schemes for IoT environments. The proposed scheme is resilient to security attacks, such as man-in-the-middle attack, impersonation attack, session key security, replay attack, and entity compromised attack, while preserving user anonymity and user untraceability.

In 2020, Wan et al. [47] proposed a roaming authentication protocol based on a heterogeneous fusion mechanism for the IoT environment. Their proposed scheme is resilient to various security attacks, and the experimental results show that their scheme incurs lower packet loss rate and lower energy consumption.

In 2020, Ghahramani et al. [48] reviewed the protocol of Li et al. protocol [4]. The cryptanalysis on the scheme [4] revealed several security weaknesses, such as vulnerability to insider attack, forward and backward security, resistance to offline guess attack, impersonation attack, offline guess attack, and insecure key distributions. Ghahramani et al. [48] proposed a secure biometric authentication scheme for GLOMONETs. The security strength of their proposed scheme is as follows: resilience to offline guess attack, impersonation attack, insider attack, and forward and backward security, and secure key distribution.

Table 1. Literature survey on two-factor authentication schemes in GLOMONET.

Authors	Year	Strengths	Weaknesses
Jiang et al. [49]	2012	Protects user anonymity, user untraceability and provides two-factor security. Mutual authentication between MU, FN and HN are achieved.	Session key agreement is static and depends on static key agreement.
Kuo et al. [6]	2014	Their scheme protects user anonymity with untraceability. Their scheme is resilient to security attacks such as impersonation attack, replay attack, smart-card-loss attack and man-in-the-middle attack. In addition, their scheme also achieves mutual authentication and secrecy of the session key.	User untraceability is not achieved.
Guo et al. [7]	2016	Protects user anonymity and untraceability resists impersonation attack, stolen-smart-card attack, server masquerading attack and replay attacks, achieves mutual authentication and perfect forward security.	Their scheme is vulnerable to insider attack and the scheme provides no session key update.
CC Lee et al. [8]	2017	Protects user anonymity, resilient to masquerade attack, man-in-the-middle attack, stolen-smart-card attack, and offline password-guessing attack. In addition, their scheme achieves perfect forward and backward secrecy.	Their scheme cannot resist replay attacks.
Marimuthu et al. [9]	2017	Provides untraceability and secure against security attacks such as known key, insider, offline password-guessing, replay, stolen verifier, forgery and man-in-the-middle attacks. Achieves mutual authentication, user friendliness and local password verification.	Security pitfalls of their scheme are as follows: absence of user anonymity and vulnerable to security attacks, such as offline password guessing and impersonation attacks, has no password change option and no local password verification.
Shashidhara et al. [5]	2018	Protects user anonymity, and their scheme is resilient to forgery and replay attacks.	Scheme does not provide session key update phase.
Xiong Li et al. [4]	2018	Resists security attacks such as session key, replay, forgery, device lost, and denial-of-service attacks and achieves user anonymity, untraceability and mutual authentication.	Their scheme does not provide local password verification, perfect forward secrecy is not achieved, and is vulnerable to denial-of-service attack.
Madhusudhan and Shashidhara [11]	2020	Resists security attacks such as insider, offline password guessing attack, impersonation attack, bit flipping attack, replay, stolen verifier attack. In addition, their scheme achieves user anonymity, local password verification, perfect forward secrecy and mutual authentication.	Their scheme does not protect user untraceability and does not provide session key update.
Bander et al. [10]	2020	Their scheme achieves user anonymity and untraceability, resilient to security attacks, such as stolen verifier attack, insider attack, stolen-smart-card attack, forgery attack, and known session-specific parameter attack. In addition, their scheme achieves user anonymity and protects user untraceability, perfect forward secrecy and mutual authentication.	Their scheme does not protect against password guessing and does not provide session key update.
Kang et al. [12]	2020	Their scheme achieves user anonymity and untraceability, resilient to security attacks such as mobile node impersonation attack, insider attack, foreign bypass attack and session-key-derived attack. In addition, their scheme achieves perfect forward secrecy and mutual authentication.	Their scheme does not provide session key update.

provides the information about various authentication schemes designed to provide security to the roaming users during handover in GLOMONETs. The strengths and the weaknesses of the authentication schemes are presented in Table 1.

3. Mathematical Preliminaries

In this, we discuss the mathematical background of the cryptographic primitives used in the design of the proposed scheme.

3.1. Basics of Elliptic Curve Cryptography

An elliptic curve defined over finite prime filed $F_p$ is a curve given by the equation of the form

$$y^{2}modp=(x^3+ax+b)modp$$

(1)

There is also a condition that Equation (1) must satisfy $4a^3+27b^2\ne 0$, where $a,b\in Z_p$. A non-singular elliptic curve $E_p(a,b)$ is the set of points $(x,y)$ with $(x,y)\in Z_p\times Z_p$ which satisfy Equation (1). The elements of $Z_p$ are $Z_p=\{0,1,\dots \dots ,p-1\}$. Let $\theta$ be the point at infinity in $E_p(a,b)$. So, E is the set of points on the elliptic curve $E_p(a,b)$ that satisfy Equation (1) along with the point at infinity. Thus,

$$E=\{(x,y)\mid y^2\equiv x^3+ax+b(modp)\}\bigcup \left\{\theta \right\}.$$

3.2. Elliptic Curve Discrete Logarithm Problem (ECDLP)

Given an elliptic curve $E_p(a,b)$ defined over a finite prime field $F_p$, consider two points $P,Q\in E_p(a,b)$ where $Q=rP$ where $r\in Z_p^{\ast }$ is scalar. Computing k from the point P, Q is computationally infeasible if the prime p is a sufficiently large prime number (for example, 160 bits).

3.3. Scalar Multiplication

In ECC, the scalar multiplication of a point $P\in E_p(a,b)$ is denoted by $rP$ where r is a scalar and $rP$ is achieved using repeated point additions and point doubling operations.

3.4. Elliptic Curve Diffie–Hellman Problem (ECDHP)

Given an elliptic curve $E_p(a,b)$ defined over a finite prime field $F_p$ and points $P, \alpha P,$ $\beta P\in E_p(a,b)$, it is difficult to compute $\alpha \beta P$, without the knowledge of either $\left\{\alpha \right\}$ or $\left\{\beta \right\}$ [50].

3.5. Elliptic Curve Diffie–Hellman (ECDH)

ECDH is a key exchange protocol. This protocol allows the communicating entities across the networks to establish a common shared secret key by agreeing to use the shared public domain parameters of ECC explained in Section 5.1.

Steps for Algorithm to compute the shared secret key:

• End system A selects the private key $\alpha \in Z_p^{\ast }$ where $1\le \alpha <n$. A computes the public key as $P{B}_A=\alpha G$, where G is a generator point in the EC domain parameter. Let the private and public key pair of end system A be $\{\alpha ,P{B}_A\}$, respectively. A computes point P with the co-ordinates $P=(x_P,y_p)=\alpha G$.
• End system A transmits $P=(x_P,y_p)=\alpha G$ to end system B over an insecure channel.
• End system B selects the private key $\beta \in Z_p^{\ast }$, where $1\le \beta <n$. B computes the public key as $P{B}_B=\beta G$, where G is a generator point in the EC domain parameter. Let the private and public key pair of end system A be $\{\beta ,P{B}_B\}$, respectively. B computes point Q with co-ordinates $Q=(x_Q,y_Q)=P{B}_{B}G$.
• End system B transmits its public key $Q=(x_Q,y_Q)=P{B}_{B}G$ to end system A over an insecure channel.
• The shared secret key is computed as

  $$\alpha P{B}_B=\alpha \beta G=\beta \alpha G=\beta P{B}_A.$$

3.6. One-Way Hash Function

Hash functions are used to achieve security goals, such as data integrity and message authentication. Hash takes the input of variable length and produces an output of fixed length. $h:{\{0,1\}}^{\ast }\to {\{0,1\}}^l$

A one-way hash function satisfies the following properties [13,51].

• Preimage resistance: For the given input x, it is computationally feasible to compute the hash value of x as $h\left(x\right)=y$. However, it is computationally infeasible to compute for the value x with the output value y.
• Second preimage resistance: It is computationally infeasible to obtain the second input which results in the same hash value output. Ex: If x is one input and y is the other input where $x\ne y$ such that $h\left(x\right)=h\left(y\right)$.
• Collision resistance: A collision resistant one-way hash function $h:{\{0,1\}}^{\ast }\to {\{0,1\}}^{\ell }$ takes the variable length input and generates a fixed length output of ℓ bits. The pair of inputs $(i_1,i_2){\in }_R$ A indicates that an attacker randomly chooses the pair of inputs $i_1,i_2$. It is computationally infeasible for a pair of inputs $i_1,i_2$ where $i_1\ne i_2$ to result in the same hash value such that $h\left(i_1\right)=h\left(i_2\right)$.

3.7. Pseudo-Random Number Generators

A sequence of pseudo-random numbers is generated by a deterministic algorithm and should simulate a sequence of independent and uniformly distributed random variables on the interval $[0,1]$. In order to be acceptable, a sequence of pseudorandom numbers must pass a variety of statistical tests for randomness.

Definition 1.

A pseudo-random number generator (PRNG) is defined by a tuple $(Q,\mu ,f,U,g)$, where Q is a finite set of states, μ is the probability distribution on Q for the initial state called seed, $f:Q\to Q$ is the transition function, U is the output space and $g:Q\to U$ is the output function. The generator P generates the numbers in the following way.

• Select the seed $q_0\in Q$ based on μ. The first number is $u_0=g\left(q_0\right)$.
• At each step $i\ge 1$, the state of the PRNG is $Q_i=f\left(Q_{i-1}\right)$ and output is $u_i=g\left(q_i\right)$. These output $u_{i}n$ of the PRNG are the pseudo-random numbers, where n is some positive integer considered to be the period of the sequence [52].

3.7.1. Properties of Pseudo-Random Function

Here, we list a few of the important properties of the pseudo-random function. A PRNG is called good if it satisfies the below stated properties:

• Uniformity: This property states that the elements in the output space U generated by the pseudo-random function are divided into M equal sub-intervals, and the expected number of samples $\left(e_k\right)$ in each sub-interval k, $\{1\le k\le M\}$ is equal; that is, $\forall k,e_k=N\mid M$, where N is the range of the numbers uniformly distributed over the interval $[0,1]$.
• Independence: The generated numbers in the outspace U should be independent of each other, and there should not exist any correlation between the numbers generated in succession. This implies that, given any length of output sequence $u_i=g\left(q_i\right)$ where $i\ge 1$, one should not be able to predict the next number in the sequence by observing the given numbers.
• Large period: The PRNG is considered to be good if its period is large.
• Reproducibility: This property ensures that for the same seed $s_0$, the same sequence of numbers is generated.
• Cryptographically Secure: The generated output sequence by the PRNGs should be cryptographically secure to be used in cryptographic applications.

3.8. Fuzzy Extractors

Biometrics information, such as fingerprint and iris scans, are noisy data that cannot be reproduced precisely and cannot be used directly in traditional cryptographic algorithms. Fuzzy extractor [53] is an ideal technique to handle noisy data. Noisy data are received from biometric information such as fingerprinting and iris scanning. A fuzzy extractor is composed of two procedures $(Gen,Rep)$.

• Gen $\left(B_i\right)=(R_i,P_i)$. Gen is a probabilistic algorithm. On the biometric input $B_i$, it extracts string $R_i$ and an auxiliary string $P_i$.
• Rep $(B_i^{{}^{\prime }},P_i)=R_i$. Rep is a deterministic algorithm. Rep produces the string $R_i$ on the biometric input from any vector $B_i^{{}^{\prime }}$ close to $B_i$ along with the auxiliary string $P_i$.

4. System Model

The proposed system model consists of three communicating entities: home network (HN), foreign network (FN) and mobile user (MU). The system model consists of four major steps:

• Registration phase: The mobile user registers to the home network by providing credentials, identity and password. The registration phase is carried out over a secure channel. In the registration phase, the HN, after receiving the mobile user request, computes for the secret parameters. HN agrees to the domain parameters of ECC with the mobile user. These are the public key of HN, symmetric encryption key, one-way hash function. P is the generator point on ECC, $a,b,n$ and p, where p is a large prime number and n is the order of the elliptic curve (EC).
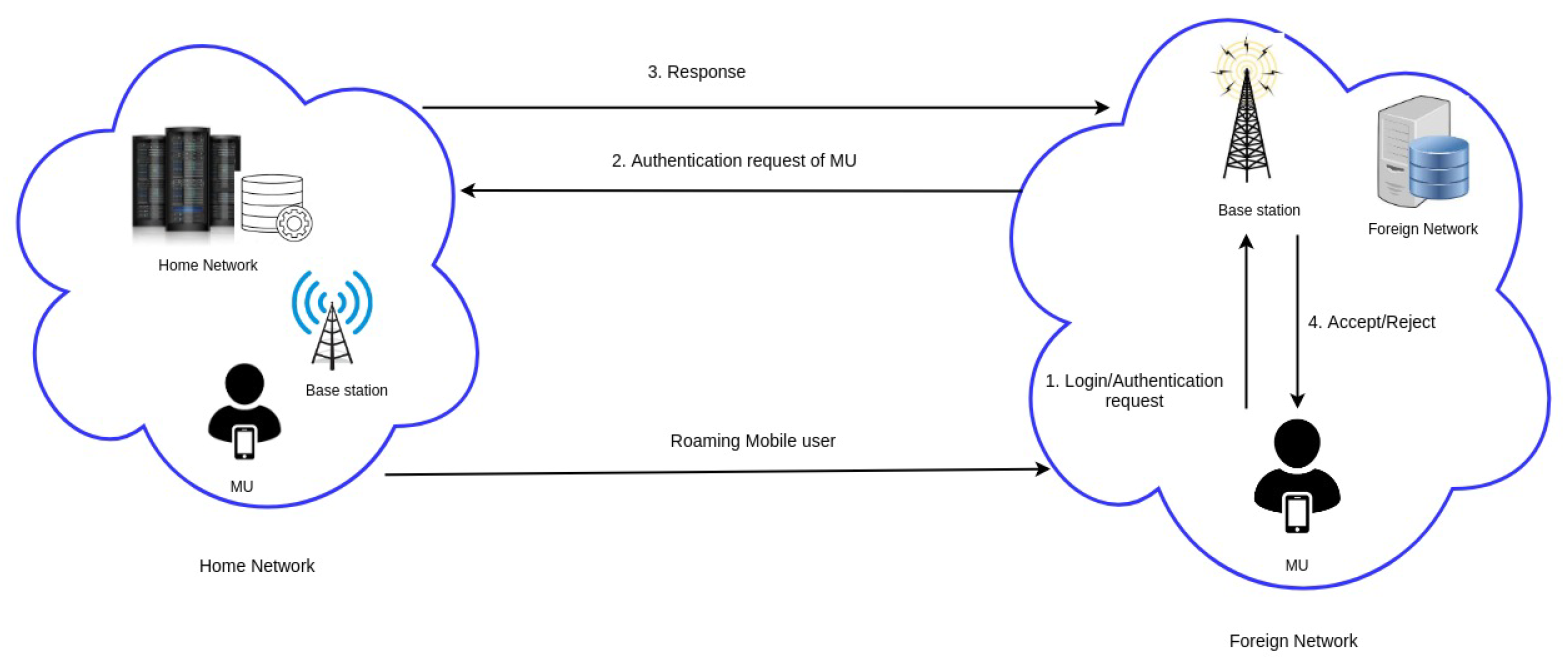
• Login or authentication phase: In the roaming scenario, the mobile user moves from their home network to the foreign network. To access services from the foreign network, the mobile user provides their identity to the foreign network. The login messages are transmitted using a wireless network through radio waves. An adversary listening to the communication channel has full control over the channel, that is, he/she can intercept, modify or alter the messages.
• The foreign network forwards the request received from the MU to the home network for the verification of the MU’s authenticity. The communication between the foreign network and the home network is considered secure.
• The home network verifies the authentication request of the mobile user received via the foreign network.
• If the MU is authentication is verified and the MU is authenticated, FN accepts the MU’s request and allows the roaming user to access the FN services. Otherwise, the FN rejects the login/authentication request sent by the MU.

Figure 1 presents the proposed system model for a roaming MU.

4.1. Trust Model

In the scenario of roaming mobile users in GLOMONET, the communicating entities are the mobile users (MU), foreign network (FN) and home network (HN). MUs are not trusted entities; the FNs are semi-trusted; and the HN is fully trusted.

4.2. Adversary Model

In this section, we illustrate the attacker model during a roaming scenario in the GLOMONET under the two-factor authentication schemes for informal analysis.

• The “Dolev–Yao threat model (DY model)” [54] is considered in our proposed scheme.
• The DY model provides an insecure channel for the communication between the entities MU, FN and HN. The FN is considered to be semi-trusted, whereas the HN is a fully trusted service provider. An attacker listening to an insecure channel has the capability to intercept the messages. The eavesdropped messages can be altered, modified or deleted.
• According to [24], there exist two dictionary spaces for mobile user’s identity and password, respectively: $\left|DID\right|\le \left|DPW\right|\le {10}^6$. Since the dictionary space is finite, an adversary can guess a pair of $\{I{D}_{MU}^{\ast },P{W}_{MU}^{\ast }\}$ in polynomial time. However, it is hard for an attacker to summarize the hash results and the random numbers.
• According to [55], the adversary has full control over the public channel or insecure channel; an adversary can eavesdrop the messages transmitted over an insecure channel and then modify, alter or delete the messages to breach the security services. However, the adversary does not have any control over the secure channel.
• According to [56], the adversary can extract the stored information in the smart card through power consumption.
• An adversary can store all previous session keys. However, if the freshness of the random numbers is changed for every session, then it is difficult for an adversary to arrive at the session keys, even with the knowledge of previous session keys. This property is known as strong forward secrecy.

5. Proposed Scheme

The proposed scheme is divided into four phases: the initialization phase, registration phase that is carried over a secure channel, login and authentication phase, session key update phase that is carried over an insecure channel, and password change phase, which provides local password verification for the MU and is carried over secure channel. The elliptic curve Diffie–Hellman protocol is used to compute the shared secret key between FN and HN to achieve mutual authentication in the proposed scheme. The design goals of our proposed protocol are as follows:

• To establish mutual authentication among the communicating entities under the premise of anonymity;
• To derive and agree on the session key between the communicating entities fairly;
• To resist security attacks, such as stolen-smart-card attack, replay attack attack, offline password-guessing attack and impersonation attack;
• To reduce computational cost and communication cost.

The proposed scheme is simulated using the AVISPA tool. Each phase is explained in detail below. Notations and their representation used in this article are defined in

Table 2. Notations and their representation.

Notation	Representation
MU	Mobile User
FN	Foreign Network
HN	Home Network
$I{D}_i$	MU’s identity
$P{W}_i$	MU’s password
$I{D}_{HN}$	HN’s identity
$I{D}_{FN}$	FN’s identity
$S{K}_{FN}$	Secret key of FN
$P{K}_{HN}$	Public key of HN
$mk$	Server master key is a symmetric key of 128 bit
SK	Session key exchanged with FN and MU
X	Secret key of HN
P	Generator point
p	Large prime number
n	Elliptic curve order
h	Cryptographic hash function, $h:{\{0,1\}}^{\ast }\to {\{0,1\}}^l$, where l = 160 bits
$E_{mk}(.)$	symmetric encryption algorithm
$Z_n^{\ast }$	$Z_n^{\ast }=\left\{a\right|gcd(a,n)=1\}$ where a $\in Z_n$

.

5.1. Initialization Phase

The domain parameters $\{E_{\left(F_p\right)},G,a,b,n,p\}$ of the elliptic curve cryptography are shared among the three communicating entities.

HN performs the following steps to initialize the system parameters:

S1:

The HN considers a non-singular elliptic curve $E_p(a,b)$ of the form $y^2=x^3+ax+b\left(modp\right)$ over a prime (finite) field $Z_p=\{0,1,\dots ,p-1\}$. P is chosen as a generator point on the elliptic curve (EC).

S2:

The HN chooses random number $x\in Z_p^{\ast }$ as its private key and computes the HN’s public key as $P{K}_{HN}=xP$.

S3:

The symmetric encryption key $mk$ of 128 bits is shared with the MU by storing it in the smart card.

S4:

HN computes the secret key for the foreign network as $S{K}_{FN}=h(I{D}_{FN}\left|\right|P{K}_{HN}\left|\right|mk)$

S5:

HN selects the one-way hash function of the form $h:{\{0,1\}}^{\ast }\to {\{0,1\}}^{\ell }$. The input can be a variable bit length string but the output should be of a fixed length.

5.2. Registration Phase

The registration phase of the proposed scheme is presented in Figure 2.

Step 1:

MU → HN: $\{h\left(I{D}_i\right),PID\}$

In the registration phase, the MU is free to choose his/her identity $I{D}_i$ and password $P{W}_i$. After choosing $I{D}_i$, $P{W}_i$ and random number $r_m$, the MU computes the following

$$PID=h\left(h\right(I{D}_i\left|\right|P{W}_i)\oplus h\left(r_m\right))$$

The MU submits $\{h\left(I{D}_i\right),PID\}$ to the HN through a secure channel.

Step 2:

HN → MU:$\{E_p,P,n,a,b,P{K}_{HN},S,E_{mk}(.),h(.)\}$.

The HN receives the request from the MU and the HN chooses its random number $r_h$. HN’s server public key $P{K}_{HN}$ is computed as

$$P{K}_{HN}=xP$$

$$S{K}_{FA}=h(I{D}_{FA}\left|\right|P{K}_{HN}\left|\right|mk)$$

$$S=PID\oplus h\left(mk\right).$$

where x is a random number $\in Z_n$, and P is a generator point on the elliptic curve. For every foreign network $FN$, the HN computes secret key $SK$, where $mk$ is the server shared symmetric key with 128 bits. The HN stores $\{h\left(I{D}_i\right),S\}$ in its database for future communication. The HN sends the smart card with the parameters $\{E_p,P,n,a,b,P{K}_{HN},S,E_{mk}(.),h(.)\}$ to the MU through a secure channel.

Step 3:

MU: $\{E_p,P,n,a,b,P{K}_{HN},S,E_{mk}(.),h(.)\}$

With the received message, the MU computes the following

$$RPW=S\oplus h\left(h\right(I{D}_i\left|\right|P{W}_i)\oplus h\left(r_m\right)).$$

The computed value of $RPW$ is stored in the smart card. The smart contains the parameters $\{E_p,P,n,a,b,P{K}_{HN},RPW,S,r_m,E_{mk}(.),h(.)\}$.

5.3. Login Phase

The login and authentication phase is presented in Figure 3. The detailed description of the steps are stated below.

Step 1:

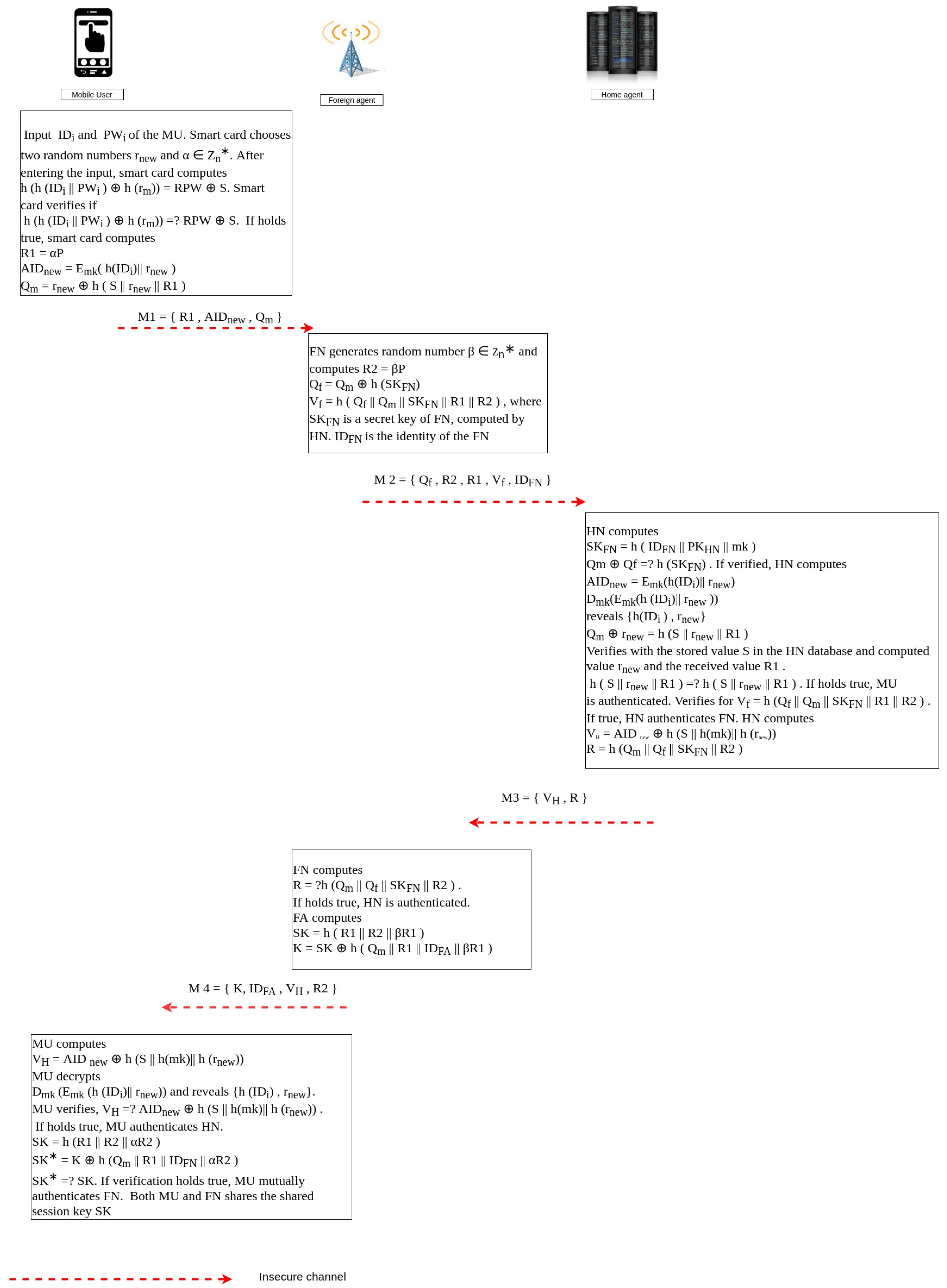
MU → FN: $M_1=\{R_1,AI{D}_{new},Q_m\}$ Smart card is inserted into the smart card terminal by the MU. The smart card terminal asks for the input of $I{D}_i$ and password $P{W}_i$ of the MU. After entering the input, smart card chooses two random numbers $r_{new}$ and $\alpha \in Z_n^{\ast }$. The smart card verifies if

$$h\left(h\right(I{D}_i\left|\right|P{W}_i)\oplus h\left(r_m\right))\stackrel{?}{=}RPW\oplus S. \mathrm{If} \mathrm{it} \mathrm{holds} \mathrm{true}, \mathrm{the} \mathrm{smart} \mathrm{card} \mathrm{computes}$$

$$R_1=\alpha P$$

$$AI{D}_{new}=E_{mk}(h\left(I{D}_i\right)\left|\right|r_{new})$$

$$Q_m=r_{new}\oplus h\left(S\right||r_{new}\left|\right|R_1)$$

The MU sends the message $M_1=\{R_1,AI{D}_{new},Q_m\}$ to FN over insecure channel.

Step 2:

FN → HN: $M_2=\{Q_f,R_2,R_1,V_f,I{D}_{FN}\}$

After receiving the message $M_1=\{R_1,AI{D}_{new},Q_m\}$ from MU. FN generates random number $\beta \in Z_n^{\ast }$ and computes the following

$$R_2=\beta P$$

$$Q_f=Q_m\oplus h\left(S{K}_{FN}\right)$$

$$V_f=h(Q_f\left|\right|Q_m\left|\right|S{K}_{FN}\left|\right|R_1\left|\right|R_2)$$

where $S{K}_{FN}$ is a secret key of FN, computed by HN. $I{D}_{FN}$ is the identity of the FN. FN sends $M_2=\{Q_f,R_2,R_1,V_f,I{D}_{FN}\}$ to HN.

5.4. Authentication Phase

Step 1:

HN → FN: $M_3=\{V_H,R\}$

The HN computes the following:

$$S{K}_{FN}=h(I{D}_{FN}\left|\right|P{K}_{HN}\left|\right|mk)$$

$$Q_m\oplus Q_f\stackrel{?}{=}h\left(S{K}_{FN}\right)$$

If verified, the HN computes the following,

$$AI{D}_{new}=E_{mk}(h\left(I{D}_i\right)\left|\right|r_{new})$$

$$D_{mk}(E_{mk}(h\left(I{D}_i\right)\left|\right|r_{new}\left)\right)$$

$$\mathrm{reveals}h\left(I{D}_i\right),r_{new}$$

$$Q_m\oplus r_{new}=h\left(S\right||r_{new}\left|\right|R_1)$$

verified with the stored value S in the HN database and computed value $r_{new}$ and the received value $R_1$.

$$h\left(S\right||r_{new}\left|\right|R_1)\stackrel{?}{=}h\left(S\right||r_{new}\left|\right|R_1). \mathrm{If} \mathrm{it} \mathrm{holds} \mathrm{true}, \mathrm{the} \mathrm{MU} \mathrm{is} \mathrm{authenticated}.$$

$$V_f\stackrel{?}{=}h(Q_f\left|\right|Q_m\left|\right|S{K}_{FN}\left|\right|R_1\left|\right|R_2). \mathrm{If} \mathrm{true}, \mathrm{HN} \mathrm{authenticates} \mathrm{the} \mathrm{FN}.$$

After the authentication verification is completed between the MU and FN, the HN computes the following:

$$V_H=AI{D}_{new}\oplus h\left(S\right|\left|h\left(mk\right)\right||h\left(r_{new}\right))$$

$$R=h\left(Q_m\right|\left|Q_f\right|\left|S{K}_{FN}\right|\left|R_2\right).$$

After all the computations, the HN sends the message $M_3=\{V_H,R\}$ to the FN over a secure channel.

Step 2:

Foreign Network → Mobile User: $M_4=\{K,I{D}_{FN},V_H,R_2\}$

After receiving the message $M_3$ from the HN, the FN computes the following:

$$R\stackrel{?}{=}h(Q_m\left|\right|Q_f\left|\right|S{K}_{FN}\left|\right|R_2).$$

If it holds true, the HN is authenticated. The FN computes the following:

$$SK=h\left(R_1\right|\left|R_2\right|\left|\beta R_1\right)$$

$$K=SK\oplus h\left(Q_m\right|\left|R_1\right|\left|I{D}_{FN}\right|\left|\beta R_1\right)$$

The FN sends a message $M_4=\{K,I{D}_{FN},V_H,R_2\}$ to the MU over an insecure channel.

Step 3:

MU: $M_4=\{K,I{D}_{FN},V_H,R_2\}$

After receiving the message $M_4$ from the foreign network, the mobile user computes the following:

$$h\left(S\right|\left|h\left(mk\right)\right||h\left(r_{n}ew\right))=AI{D}_{new}\oplus V_H$$

$$\mathrm{The} \mathrm{MU} \mathrm{decrypts} D_{mk}(E_{mk}(h\left(I{D}_i\right)\left|\right|r_{new}\left)\right) \mathrm{and} \mathrm{reveals} \{h\left(I{D}_i\right),r_{new}\}.$$

$$V_H\stackrel{?}{=}AI{D}_{new}\oplus h\left(S\right|\left|h\left(mk\right)\right||h\left(r_{new}\right)).$$

$$\mathrm{If} \mathrm{verification} \mathrm{holds} \mathrm{true}, \mathrm{the} \mathrm{MU} \mathrm{authenticates} \mathrm{the} \mathrm{HN}.$$

$$SK=h\left(R_1\right|\left|R_2\right|\left|\alpha R_2\right)$$

$$S{K}^{\ast }=K\oplus h(Q_m\left|\right|R_1\left|\right|I{D}_{FN}\left|\right|\alpha R_2)$$

$$S{K}^{\ast }\stackrel{?}{=}SK$$

If verification holds true, the MU mutually authenticates the FN. Both the MU and FN share the shared session key $SK$.

5.5. Session Key Update Phase

The detailed description of the session key update phase steps is stated below.

Step 1:

MU → FN: $M_5=\{R_1^{\ast }={\alpha }^{\ast }P\}$

The roaming mobile user periodically updates the session key to achieve freshness in the random numbers. The session key update phase is presented in Figure 4. The MU chooses a new random number ${\alpha }^{\ast }\in Z_n^{\ast }$ and computes.

$$R_1^{\ast }={\alpha }^{\ast }P$$

The MU sends message $M_5=\{R_1^{\ast }={\alpha }^{\ast }P\}$ to the FN over an insecure channel.

Step 2:

FN → MU: $M_6=\{R_2^{\ast }=\left\{{\beta }^{\ast }P\right\},MA{C}_{SK}\}$

After receiving message $M_5$ from the MU, the FN chooses a new random number ${\beta }^{\ast }\in Z_n^{\ast }$. The FN computes the following:

$$R_2^{\ast }={\beta }^{\ast }P$$

$$S{K}_{F{M}_i}=h(R_1^{\ast }\left|\right|R_2^{\ast }\left|\right|{\beta }^{\ast }{R}_1^{\ast })$$

$$MA{C}_{SK}=h\left(h\right(R_1^{\ast }\left|\right|R_2^{\ast }\left|\right|{\beta }^{\ast }{R}_1^{\ast }\left)\right|\left|h\right(R_1\left|\right|R_2\left|\right|\beta R_1\left)\right)$$

The FN sends message $M_6=\{R_2^{\ast }=\left\{{\beta }^{\ast }P\right\},MA{C}_{SK}\}$ to the MU.

Step 3:

Mobile User: $M_6=\{R_2^{\ast }=\left\{{\beta }^{\ast }P\right\},MA{C}_{SK}\}$

After receiving $M_6=\{R_2^{\ast }=\left\{{\beta }^{\ast }P\right\},MA{C}_{SK}\}$ from the FN, the MU computes the following:

$$S{K}_{M{F}_i}=h(R_1^{\ast }\left|\right|R_2^{\ast }\left|\right|{\alpha }^{\ast }{R}_1^{\ast })$$

$$S{K}_{M{F}_{i-1}}=h(R_1\left|\right|R_2\left|\right|\alpha R_2)$$

$$h(S{K}_{M{F}_i}\left|\right|S{K}_{M{F}_{i-1}})\stackrel{?}{=}MA{C}_{SK}.$$

If the verification holds true, message integrity is achieved and message authentication is verified. Therefore, the MU updates the session key as

$$S{K}^{\ast }=h(R_1^{\ast }\left|\right|R_2^{\ast }\left|\right|{\alpha }^{\ast }{R}_2^{\ast })$$

5.6. Password Change Phase

In the password change phase, the terminal allows the MU to change the current password $P{W}_i$ with the new password $P{W}_i^{new}$. The MU has to insert his/her smart card into the terminal. After insertion, the MU has to provide his/her credentials to the terminal. Once the MU has entered $I{D}_i$ and current password $P{W}_i$, the terminal processes the information. Then the smart card computes the following:

Step 1:

$h\left(h\right(I{D}_i\left|\right|P{W}_i)\oplus h\left(r_m\right))=RPW\oplus S$.

Verifies if $h\left(h\right(I{D}_i\left|\right|P{W}_i)\oplus h\left(r_m\right))\stackrel{?}{=}RPW\oplus S$.

Step 2:

If it holds true, the smart card allows the MU to update the current password $P{W}_i$ with the new password $P{W}_i^{new}$. The smart card asks the MU to enter the new password $P{W}_i^{new}$. After that, the smart card computes

$RP{W}^{{}^{\prime }}=S^{{}^{\prime }}\oplus h\left(h\right(I{D}_i\left|\right|P{W}_i^{new})\oplus h\left(r_m\right))$.

The parameter $RPW$, which is stored in the smart card, is replaced with $RP{W}^{{}^{\prime }}$.

5.7. Proposed Two-Factor Authentication Scheme Extended to Multi-Factor Authentication Scheme

The multi-factor authentication schemes includes biometric input from the MU along with the password and the smart card that a MU possesses. Many devices use biometric authentication, such as fingerprint identification. Fingerprint identification is one of the most commonly used biometric technologies integrated in many mobile devices. In our proposed scheme, we describe how the three-factor authentication scheme is implemented during the registration phase. The three-factor authentication provides more security to the authentication schemes for the roaming MU for GLOMONET in the smart city to conform to the security goals designed for the ideal authentication scheme.

5.8. Registration Phase

The registration phase of the proposed multi-factor authentication scheme is as follows.

Step 1:

MU → HN: $\{h\left(I{D}_i\right),PID\}$

In the registration phase, the MU is free to choose his/her identity $I{D}_i$ and password $P{W}_i$ along with the biometric fingerprint. The mobile device extracts the fingerprint information from the fuzzy extractor technique $Gen\left(B_{MU}\right)=(R_{MU},P_M)$. After choosing $I{D}_i$, $P{W}_i$ and random number $r_m$, the MU computes the following:

$$PID=h\left(h\right(I{D}_i\left|\right|P{W}_i)\oplus h\left(r_m\right))$$

The MU submits $\{h\left(I{D}_i\right),PID,R_{MU}\}$ to the HN through a secure channel.

Step 2:

HN → MU:$\{E_p,P,n,a,b,P{K}_{HN},S,E_{mk}(.),Gen,Rep,P_M,h(.)\}$.

The HN receives the request from the MU and the HN chooses its random number $r_h$. The HN’s server public key $P{K}_{HN}$ is computed as

$$P{K}_{HN}=xP$$

$$S=PID\oplus h\left(mk\right)\oplus R_{MU}.$$

where x is a random number $\in Z_n$, and P is a generator point on the elliptic curve. HN stores $\{h\left(I{D}_i\right),S\}$ in it’s database for future communication. HN sends the smart card with the parameters

$\{E_p,P,n,a,b,P{K}_{HN},S,E_{mk}(.),Gen,Rep,P_M,h(.)\}$ to the MU through secure channel.

Step 3:

MU: $\{E_p,P,n,a,b,P{K}_{HN},S,E_{mk}(.),Gen,Rep,P_M,h(.)\}$

With the received message, MU computes the following

$$RPW=S\oplus h\left(h\right(I{D}_i\left|\right|P{W}_i)\oplus h\left(r_m\right)).$$

The computed value of $RPW$ is stored in the smart card. The smart card contains the parameters $\{E_p,P,n,a,b,P{K}_{HN},S,E_{mk}(.),Gen,Rep,P_M,RPW,h(.)\}$.

6. Informal Security Analysis of the Proposed Scheme (ES-HAS)

In this section, through the informal security methods, we prove that the proposed scheme ES-HAS is resilient to the security attacks briefly explained below.

Informal security methods are demonstrated using the knowledge reasoning of the analysis of the protocol messages exchanged between the communicating entities over an insecure channel. With the informal security methods, we can prove the security of the protocol if it is weak or resilient to the security attacks in question.

6.1. Security against User Anonymity

User anonymity is an important security feature in GLOMONETs. The two-factor authentication schemes designed for GLOMONETs should protect user anonymity. In the proposed scheme, during the AESK phase, if an adversary intercepts the message $M_1=\{R_1,AI{D}_{new},Q_m\}$ transmitting on the public channel and gains access to the parameters in $M_1$, it is of no use, as the value of $I{D}_i$ is hashed, encrypted with the shared server secret key, and concatenated with the random number $r_{new}$. To get $r_{new}$ from the computation $D_{mk}(E_{mk}(h\left(I{D}_i\right)\left|\right|r_{new}\left)\right)$, an adversary must know the decryption key $mk$, which is server’s secret key shared between the MU through a secure channel. Therefore, the adversary will not be successful in revealing the $I{D}_i$, the MU’s identity. Thus, the scheme protects user anonymity.

6.2. Security against Stolen Smart Card Attack

With the stolen smart card parameters $\{E_p,G,n,a,RPW,b,P{K}_{HN},S,E_{mk}(.),r_m,h(.)\}$ and the intercepted login message $M_1=\{R_1,AI{D}_{new},Q_m\}$, if an adversary tries to reveal $I{D}_i$ and $P{W}_i$, it is impossible to compute, due to the fact that the parameter $RPW$ is computed as $RPW=S\oplus h\left(h\right(I{D}_i\left|\right|P{W}_i)\oplus h\left(r_m\right))$. To arrive at the identity and password of the MU, an adversary has to guess both $I{D}_i$ and $P{W}_i$ accurately and in addition to this, it must also guess the parameter S, which is computed as $S=PID\oplus S{K}_{HN}$. Thus, even if an adversary possesses the smart card, he/she will still be unsuccessful in revealing the identity and password of the MU. Therefore, the scheme is resilient to the stolen-smart-card attack.

6.3. Security against Offline Password-Guessing Attack

With the interception of the login messages $M_1=\{R_1,AI{D}_{new},Q_m\}$ and $M_2=\{Q_f,R_2,R_1,V_f,I{D}_{FN}\}$ during the AESK phase along with the stolen smart card parameters $\{E_p,G,n,a,RPW,b,P{K}_{HN},S,E_{mk}(.),r_m,h(.)\}$, if an adversary makes a trial to reveal $P{W}_i$ by computing $S=RPW\oplus h\left(h\right(I{D}_i\left|\right|P{W}_i)\oplus h\left(r_m\right))$, to arrive at the correct value of S, he/she should guess the accurate values of $I{D}_i$ and $P{W}_i$. Guessing two parameters at a given time becomes complex, and the hash operations on $I{D}_i$ and $P{W}_i$ makes the guessing more complex. Thus, the scheme is resilient to the password-guessing attack.

6.4. Security against Replay Attack

Suppose, by intercepting the login messages during the AESK phase, that an adversary tries to replay the messages $M_1=\{R_1,AI{D}_{new},Q_m\}$ and $M_2=\{Q_f,R_2,R_1,V_f,I{D}_{FN}\}$ as $M_1^{{}^{\prime }}$ and $M_2^{{}^{\prime }}$ and then sends it to the HN. The HN, on receiving the messages $M_1^{{}^{\prime }}$ and $M_2^{{}^{\prime }}$, computes for the secret key $S{K}_{FN}$ and checks for the freshness of the random number $r_{new}$. Both the parameters can be computed only by the valid HN. After computing, the HN verifies if $V_f\stackrel{?}{=}h(Q_f\left|\right|Q_m\left|\right|S{K}_{FN}\left|\right|R_1\left|\right|R_2)$. If the parameter $V_f$ holds true, then the HN authenticates both the FN and MU. Otherwise, the HN terminates the connection request. It is difficult for an adversary to compute $S{K}_{FN}$ (the secret key of FN), as $S{K}_{FN}$ is concealed with $P{K}_{HN}$ (the public key of the HN) and $mk$ (the secret key of the HN). The random number $r_{new}$ is concealed with S, the secret parameter of the HN. Hence, even if an adversary tries to replay the messages and sends it to the HN which checks for the freshness of the random number $r_{new}$ and also checks for the correctness of the message. If the verification fails, the HN terminates the request. The random number $r_{new}$ is the output sequence generated by the pseudo-random function, satisfying the properties as mentioned in Section 3.7.1. Thus, the proposed scheme is resilient to the replay attack.

6.5. Perfect Forward Secrecy

The session key is computed using the elliptic curve Diffie–Hellman Protocol (ECDHP) as $SK=h\left(R_1\right|\left|R_2\right|\left|\beta R_1\right)$ by FN. During the AESK phase, if an adversary intercepts the messages $M_4=\{V_H,I{D}_{FN},K,R_2\}$ and $M_1=\{R_1,,AI{D}_{new},Q_m\}$ and tries to compute $SK=K\oplus h\left(Q_m\right|\left|R_1\right|\left|I{D}_{FN}\right|\left|\alpha R_2\right)$, even with the disclosure of the session key, it is difficult to calculate the value of $\beta \in Z_n^{\ast }$ due to the fact that, given an elliptic curve E defined over a finite prime field $F_p$ and points $P,\alpha P,\beta P\in E\left(F_p\right)$, it is difficult to compute $\alpha \beta P$ due to the hardness of the ECDH problem. For every new login request, a session key is computed, which makes it difficult for an adversary to arrive at the session key for every new login session. Thus, the scheme achieves perfect forward secrecy.

6.6. Security against Impersonation Attack

• Impersonate a FN.
  If an adversary intercepts the message $M_1=\{R_1,AI{D}_{new},Q_m\}$ and $M_2=\{Q_f,R_2,R_1,$$V_f,I{D}_{FN}\}$ transmitting over an insecure channel during the AESK phase and sends the same message $M_2$ to HN, on receiving $M_2$, the HN computes $S{K}_{FN}=h(I{D}_{FN}\left|\right|$$P{K}_{HN}\left|\right|mk)$. $P{K}_{FN}$ is a public key and $mk$ is a secret key computed by the HN.

  $$V_f\stackrel{?}{=}h(Q_f\left|\right|Q_m\left|\right|S{K}_{FN}\left|\right|R_1\left|\right|R_2).$$
  The HN verifies if $V_f\stackrel{?}{=}h(Q_f\left|\right|Q_m\left|\right|S{K}_{FN}\left|\right|R_1\left|\right|R_2)$.
  If it holds true, the HN authenticates the FN based on its secret key computed by the HN. Thus, it is difficult for an adversary to impersonate a legal FN.
• Impersonate a MU.
  With the interception of message $M_1=\{R_1,AI{D}_{new},Q_m\}$ transmitting over an insecure channel, the adversary tries to reveal the identity of the parameters by capturing message $M_1$ and thus $AI{D}_{new}=E_{mk}(h\left(I{D}_i\right)\left|\right|r_{new})$. The HN uses its secret key for encrypting the identity and random number of MU. To perform decryption, an adversary must have the server secret key. Thus, it is difficult to impersonate a valid MU.

6.7. Man-in-the-Middle Attack

The man-in-the-middle attack is an active security attack. An attacker has the capability to eavesdrop the online authentication messages transmitted over an insecure channel. The intercepted messages are then replayed by an attacker to establish a session among the entities involved in the communication. The entities believe that the communication is carried between the legitimate entities. The legitimate entities are not aware of the session establishment with an attacker. The entire communication channel is controlled by an attacker.

In the proposed scheme, it is difficult for an attacker to mount such an attack. An attacker can eavesdrop all the messages transmitted over the insecure channel as shown in Figure 5. With the interception of the authentic messages $\{M_1,M_4\}$, the attacker would not be able to derive the session key without the knowledge of the private key $\beta$ due to the complexity of the elliptic curve discrete logarithm problem (ECDLP). (The ECDLP is explained in Section 3.2).

6.8. Local Password Verification

In the login phase of the proposed scheme, the mobile device validates the MU credentials through prompting the MU to input the $\{I{D}_{MU},P{W}_{MU}\}$. After the MU input, the following computations are performed.

$$h\left(h\right(I{D}_i\left|\right|P{W}_i)\oplus h\left(r_m\right))\stackrel{?}{=}RPW\oplus S.$$

After successful verification, further computations are performed and the login request message $M_1$ is sent to the FN. An attacker cannot compute the correct $h\left(h\right(I{D}_i\left|\right|P{W}_i)\oplus h\left(r_m\right))$ without the knowledge of $\{I{D}_{MU},P{W}_{MU},r_m\}$ to succeed the verification step $h\left(h\right(I{D}_i\left|\right|P{W}_i)\oplus h\left(r_m\right))\stackrel{?}{=}RPW\oplus S$. Therefore, the proposed authentication scheme is designed to avoid unauthorized use of mobile devices by verifying the password locally.

6.9. Security against User Untraceability

In the proposed scheme, the login message $M_1=\{R_1,AI{D}_{new},Q_m\}$ carries the identity of the MU, which is encrypted with the shared symmetric key between MU and HN. If an attacker attempts to eavesdrop the login message $AI{D}_{new}=E_{mk}(h\left(I{D}_i\right)\left|\right|r_{new})$ transmitted over an insecure channel, decryption of the $I{D}_{MU}$ without the decryption key is not possible. To trace a MU, an adversary keeps track of the authentication sessions between the MU and FN. For every session, the message $\left\{AI{D}_{new}\right\}$ contains the fresh random value. Furthermore, $\left\{AI{D}_{new}\right\}$ varies in each session because it is generated by the random number $r_{new}$. Hence, the proposed scheme satisfies user anonymity and untraceability.

7. Formal Security Analysis of the Proposed Scheme (ES-HAS) Using BAN Logic

In this section, the formal security verification of the proposed scheme ES-HAS using BAN Logic [13] is presented.

BAN logic is a formal tool that enables to analyze the correctness of an authentication protocol. It includes mutual authentication and key distribution. The notations P and Q denote principals; X and Y denote statements; and K is the cryptographic key.

Table 3. Notations used in BAN logic.

Notation	Definition
$P|\equiv X$	P believes X: P would be entitled to believe X.
$P⊲X$	P sees X: P can receive and read X
$P|\sim X$	P said X: P once said X
$P|\Rightarrow X$	P controls X: P has jurisdiction over X
$\#\left(X\right)$	Fresh (X): The formula X is fresh
${\langle X\rangle }_y$	X is integrated with y; y should be kept secret
$P\stackrel{K}{\leftrightarrow }Q$	K is used as a shared key between P and Q
$P\stackrel{y}{\rightleftharpoons }Q$	The formula y is shared between two principals P and Q
$Y={\left(X\right)}_h$	Y is hash of X

provides the meaning for the BAN logic symbols.

Logic postulates of BAN logic

• Message meaning rule for shared secrets: $\frac{P|\equiv Q\stackrel{y}{\rightleftharpoons }P,P⊲{\langle X\rangle }_y}{P|\equiv Q|\sim X}$
• Nonce-verification rule: $\frac{P|\equiv \#(X),P|\equiv Q|\sim X}{P|\equiv Q|\equiv X}$
• Jurisdiction rule: $\frac{P|\equiv Q|\Rightarrow X,P|\equiv Q|\equiv X}{P|\equiv X}$
• Receiving rule: $\frac{P⊲(X,Y)}{P⊲X}$ and $\frac{P⊲{\langle X\rangle }_y}{P⊲X}$
• Freshness-propagation rule: $\frac{P|\equiv \#(X)}{P|\equiv \#(X,Y)}$
• Session-key rule: $\frac{P|\equiv \#(K),P|\equiv Q|\equiv X}{P|\equiv P\stackrel{K}{\leftrightarrow }Q}$

According to the analytic procedure of BAN logic, the proposed scheme must satisfy the following goals to prove the system is secure. G → Goal

G1

: $FN|\equiv R1$

G2

: $FN|\equiv MU|\equiv R1$

G3

: $HN|\equiv \#(R1,R2)$

G4

: $HN|\equiv HN\stackrel{S{K}_{FN}}{\leftrightarrow }FN$

G5

: $FN|\equiv FN\stackrel{SK}{\leftrightarrow }MU$

We summarize the proposed protocol in the following generic form:

• Message M1: $MU\to FN:\{R_1,AI{D}_{new},Q_m\}$
  $R_1=\alpha P, AI{D}_{new}=E_{mk}(h\left(I{D}_i\right)\left|\right|r_{new})$
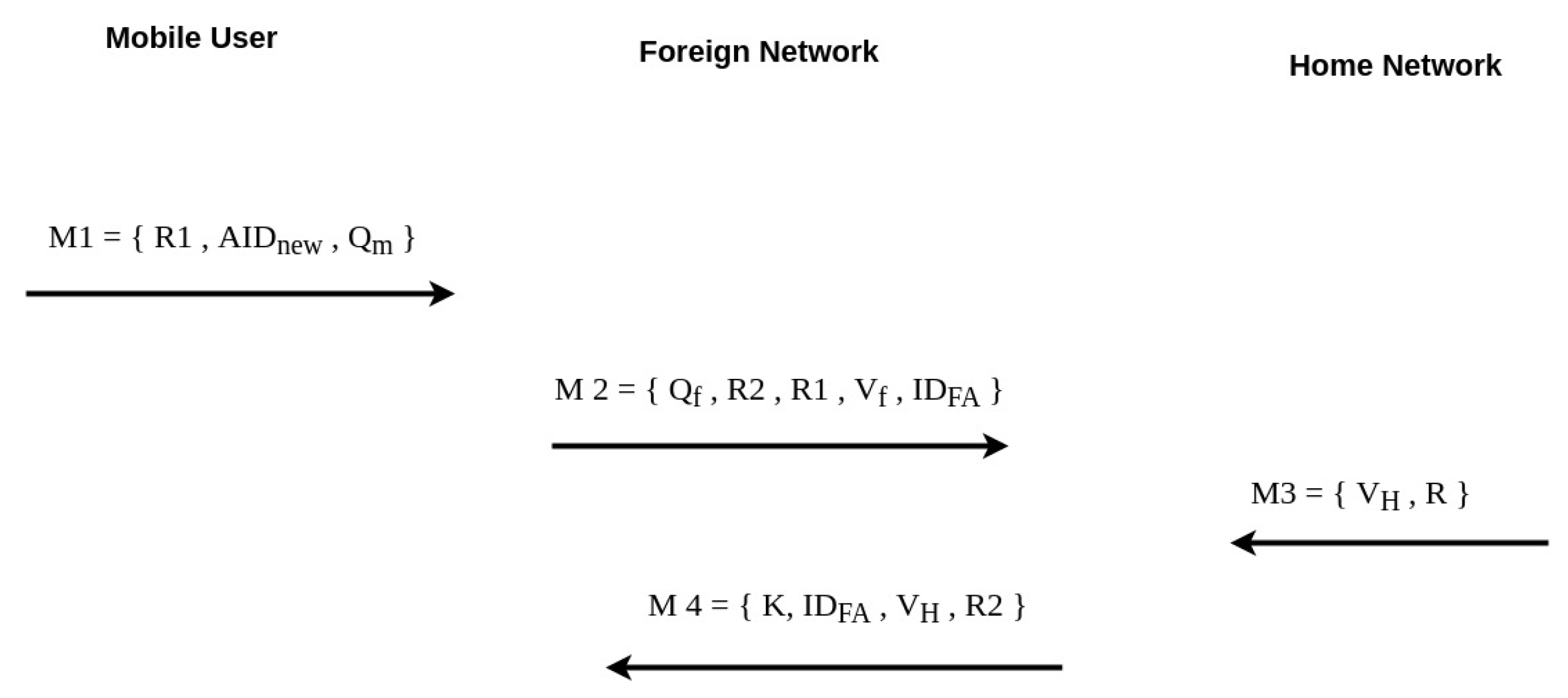
  $Q_m=r_{new}\oplus h\left(S\right||r_{new}\left|\right|R_1)$.
• Message M2: $FN\to HN:\{Q_f,R_2,R_1,V_f,I{D}_{FN}\}$
  $R_2=\beta P, Q_f=Q_m\oplus h\left(S{K}_{FN}\right)$
  $V_f=h(Q_f\left|\right|Q_m\left|\right|S{K}_{FN}\left|\right|R_1\left|\right|R_2)$. Where $S{K}_{FN}$ is a secret key of FN, computed by HN.
• Message M3: $HN\to FN:\{V_H,R\}$
  $V_H=AI{D}_{new}\oplus h\left(S\right|\left|h\left(mk\right)\right||r_{new})$
  $R=h\left(Q_m\right|\left|Q_f\right|\left|S{K}_{FN}\right|\left|R_2\right)$.
• Message M4: $FN\to MU:\{K,I{D}_{FN},V_H,R_2\}$
  $K=SK\oplus h\left(Q_m\right|\left|R_1\right|\left|I{D}_{FN}\right|\left|\beta R_1\right)$.

Hypothesis 1.

The following assumptions about the initial states are made to analyze the proposed scheme:

$I_1$.

$MU|\equiv MU\stackrel{R1}{⟷}FN$

$I_2$.

$FN|\equiv FN\stackrel{R2}{⟷}MU$

$I_3$.

$MU|\equiv MU\stackrel{SK}{\rightleftharpoons }FN$

$I_4$.

$FN|\equiv FN\stackrel{SK}{\rightleftharpoons }MU$

$I_5$.

$MU|\equiv \#(\alpha )$

$I_6$.

$MU|\equiv \#(r_{new})$

$I_7$.

$HN|\equiv \#(R1)$

$I_8$.

$FN|\equiv \#(\beta )$

$I_9$.

$FN|\equiv HA|\Rightarrow {SK}_{FN}$

$I_{10}$.

$MU|\Rightarrow R_1$

$I_{11}$.

$FN|\equiv \#(R1)$

$I_{12}$.

$FN|\equiv MU|\sim R1$

$I_{13}$.

$HA|\equiv \#(R2)$

$I_{14}$.

$HN|\equiv MU|\Rightarrow R_1$

$I_{15}$.

$HN|\equiv FN|\Rightarrow R_2$

$I_{16}$.

$HN|\equiv \#(R2)$

$I_{17}$.

$HN|\equiv \#(S{K}_{FN})$

The generic form of the proposed scheme is transformed into the idealized form. The following assumptions are made to analyze the proposed scheme. The main proofs are stated as follows.

• From message $M_1$, we have the following:
  $S_1$: $FN⊲R_1$. From jurisdiction rule R3 and $I_{11}$, we have
  $\frac{FN|\equiv MU|\Rightarrow R1,MU|\equiv FN|\equiv R1}{FN|\equiv R1}$ (Goal G1)
• From message $M_2$, $I_{12},I_{13}$, we have
  $\frac{FN|\equiv \#(R1),FN|\equiv MU|\sim R1}{FN|\equiv MU|\equiv R1}$ (Goal G2)
• From message $M_3$, $I_7,I_{15},I_{16},I_{17}$ and freshness propagation rule 5, we have
  $\frac{HN|\equiv \#(R1)}{HN|\equiv \#(R1,R2)}$. (Goal G3)
  From session-key rule 6 and $I_9,I_{18}$, we have
  $\frac{HN|\equiv \#\left(S{K}_{FN}\right),HN|\equiv FN|\equiv S{K}_{FN}}{HN|\equiv HN\stackrel{S{K}_{FN}}{\leftrightarrow }FN}$ (Goal G4)
• From message $M_4$, $I_1,I_2,I_3,I_4$ and session-key rule 6, we have
  $\frac{FN|\equiv \#(SK),FN|\equiv MU|\equiv SK}{FN|\equiv FN\stackrel{SK}{\leftrightarrow }MU}$ (Goal G5)

8. Formal Security Verification of the Proposed Scheme (ES-HAS) Using AVISPA Tool

To provide the results of the formal security verification of the proposed scheme, the automated validation of internet security protocols and applications (AVISPA) tool is used. The proposed scheme is simulated and verified against active and passive security attacks. Firstly, the AVISPA tool is introduced; secondly, the implementation details of the proposed scheme using AVISPA are presented; and finally, the output of the simulation is presented.

8.1. Overview of AVISPA

AVISPA is a tool which is widely accepted for the verification of the cryptographic protocols. One of the major advantages of the AVISPA tool is that the same protocol specification can be verified by different verification techniques. The cryptographic protocol is written in HLPSL (high level protocol specification language). HLPSL is an expressive, modular, role-based, formal language. The cryptographic protocol written in HLPSL is first converted into an intermediate format (IF) by the HLPSL2IF translator. Later, this IF is executed by the backend that the AVISPA tool uses. Backend tools supported by AVISPA are on-the-fly model-checker (OFMC), constraint logic based attack searcher (CL-AtSe), SAT-based model checker (SATMC) and tree automata based on automatic approximations for the analysis of security protocols (TA4SP). The AVISPA tool uses the OFMC/CL-AtSe back-end to execute IF, which is then converted to output format (OF) [14]. OF includes the sections which are explained in detail below.

• SUMMARY: It summarizes about the executed protocol safe or unsafe property, where safe signifies that the tested protocol is safe and unsafe signifies that the tested protocol is insecure.
• DETAILS: This section gives details about the conditions that are used in the test to make the protocol safe or unsafe.
• PROTOCOL: This section provides the name of the protocol that is to be tested.
• GOAL: The test’s goal is specified in this section.
• BACKEND: The backend name that is used to execute the test is specified in this section.
• COMMENTS and STATISTICS: This section demonstrates the attacker simulation if the test is unsafe.

The HLPSL basic types are listed below:

• agent: It indicates the principal roles used in the HLPSL language and i denotes the intruder.
• const: It indicates constants.
• public_key: It indicates the public key used by agents in the test.
• symmetric_key: It specifies about the symmetric key used by the agents in the test.
• text: This can be used for nonces or sometimes for messages.
• nat: This signifies the natural numbers that are used in non-message contexts.

In HLPSL, concatenation operation is denoted by the declaration, such as played_by X indicating that X is an agent and knowledge indicating the intruder’s knowledge. $X=\mid >Y$ represents the immediate reaction transitions.

8.2. HLPSL Implementation

HLPSL uses three basic roles: mobileuser played_by the MU, foreignagent played_by the FN, and homeagent played_by the HN. The three supporting roles used in the HLPSL implementation are environment, session and role.

The output of the program using back-end OFMC is presented in Figure 6. The output of the program using back-end CL-ATSE is presented in Figure 7.

9. Performance Analysis and Comparison

This section evaluates performance of the proposed scheme with the other authentication schemes proposed for GLOMONET. These seven authentication schemes are based on the elliptic curve cryptosystem. The proposed authentication scheme is also based on the elliptic curve cryptosystem. These seven schemes are introduced by Mahadi et al. [57], Ghahramani et al. [48], Li et al. [4], Zhao [40], Odelu et al. [39], Banerjee et al. [42] and Li et al. [58], respectively.

The proposed scheme makes the following assumptions to compute the communication overhead during the login phase. The symmetric encryption key length is 128 bits, the one-way hash function output is 160 bits in length, the random number is 128 bits in length, the identity is 32 bits in length, and the elliptic curve point is 256 bits. The proposed scheme establishes four communication rounds with the server. Considering the communication overhead of messages transmission in one authentication session for our proposed scheme, within the login phase, the length of the user’s login request message $M_1=\{R_1,AI{D}_{new},Q_m\}$ is 672 bits, the visited network request to the HN to authenticate the MU’s login request message $M_2=\{Q_f,R_2,R_1,V_f,I{D}_{FN}\}$ is 704 bits in length. The HN server message $M_3=\{V_H,R\}$ is 448 bits in length and the response message $M_4=\{K,I{D}_{FN},V_H,R_2\}$ from the visited network to the MU is 896 bits in length.

Table 4. Comparison on security features.

	S1	S2	S3	S4	S5	S6	S7	S8	S9
Mahadi et al. [57]	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Ghahramani et al. [48]	Yes	No	Yes	No	No	No	Yes	No	No
Li et al. [4]	No	No	No	No	Yes	Yes	Yes	Yes	Yes
Zhao [40]	No	No	No	Yes	Yes	Yes	No	Yes	No
Odelu et al. [39]	Yes	No	Yes	Yes	Yes	Yes	No	Yes	No
Banerjee et al. [42]	No	No	No	No	Yes	Yes	Yes	Yes	Yes
Li et al. [58]	No	No	No	No	Yes	Yes	Yes	Yes	Yes
Ours	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes

S1—user anonymity; S2—resistance to stolen-smart-card attack; S3—resistance to offline password-guessing attack; S4—resistance to replay attack; S5—mutual authentication; S6—resistance to impersonation attack; S7—resistance to man-in-the-middle attack; S7—local password verification; S8—perfect forward secrecy; S9—user untraceability.

compares the security features of the proposed scheme with the four other authentication schemes. The proposed scheme achieves all the listed security features compared to the other schemes. Our scheme requires no intervention of the server during the password change phase, which otherwise creates hassle and increases the communication cost. The password is verified locally in the proposed scheme. Our scheme is secure and efficient with minimal communication overhead compared to the other four schemes to perform handover procedures in GLOMONET.

Table 5. Comparison on computational cost.

	Total Computations
Mahadi et al. [57]	$17T_h+7T_{ecc}+4T_{asymm}+2T_{symm}$
Ghahramani et al. [48]	$22T_h+13T_{ecc}+1T_f$
Li et al. [4]	$21T_h+10T_{ecc}+1T_f+2T_p$
Zhao [40]	$11T_{ecc}+6T_{symm}+2T_{asymm}+15T_h$
Odelu et al. [39]	$15T_{ecc}+2T_a+2T_{symm}+2T_v+17T_h$
Banerjee et al. [42]	$9T_{ecc}+8T_{se}+1T_f+13T_h$
Li et al. [58]	$16T_h+6T_{ecc}$
Ours	$27T_h+5T_{ecc}+3T_{symm}$

gives the computational costs performed both at the user side and server side within the three different phases, including the registration phase, login phase and password change phase. In the proposed scheme, the user side computes three one-way hash functions to compute the parameter $PID=h\left(h\right(I{D}_i\left|\right|P{W}_i)\oplus h\left(r_m\right))$. At the server side, the proposed scheme executes two hash functions and one multiplication of a number over a point on the elliptic curve to compute the secret values $S{K}_{FN}=h(I{D}_{FN}\left|\right|P{K}_{HN}\left|\right|mk)$ and $S=PID\oplus h\left(mk\right)$. Similarly, the login phase at the user side requires seven hash functions, two symmetric functions and two multiplications of a number over a point on the elliptic curve. The login phase at the server side requires four hash functions and three multiplication of a number over a point on the elliptic curve. The password phase at the user side requires two hash functions.

• $T_h$ time taken to execute one hash function.
• $T_{symm}$ time taken to execute one symmetric encryption/decryption operation.
• $T_{E{C}_M}$ time taken to execute multiplication operation on elliptic curve.
• $T_f$ time of a fuzzy extractor.
• $T_{asymm}$ time taken to execute one asymmetric encryption/decryption operation.
• $T_a$ time taken to perform ECC point addition.
• $T_{se}$ time taken for sign operation.
• $T_v$ time of signature verification.

Table 6. Comparison on communication cost.

	Communication Cost
Mahadi et al. [57]	2144
Ghahramani et al. [48]	3424
Li et al. [4]	3424
Zhao [40]	7424
Odelu et al. [39]	5888
Banerjee et al. [42]	3072
Li et al. [58]	3296
Ours	3168

tabulates the communication overhead between the propossed and the other schemes. Based on each round of messages exchange during login and authentication phase, the signal overhead is computed. Figure 8 compares the signal overhead between the proposed scheme and other schemes.

10. Conclusions

In this article, the proposed ES-HAS scheme provides secure services to roaming mobile users. The proposed ES-HAS scheme is resilient to security attacks, such as MU impersonation, stolen-smart-card, offline password-guessing, man-in-the-middle and replay attacks. The ES-HAS scheme also achieves security goals such as user anonymity, user untraceability, perfect forward secrecy and mutual authentication. The shared secret key is computed using elliptic curve cryptography, and this secret key is exchanged between the two communicating entities, FN and HN, during communication to authenticate each other. The proposed scheme is proved using the formal security tool, BAN logic. Furthermore, the ES-HAS scheme is simulated using the AVISPA tool to formally verify whether the proposed scheme is secure against replay and man-in-the-middle attacks. The security features achieved by the different authentication schemes and the proposed scheme are compared. The comparison results shows that the proposed scheme achieves all the security features mentioned. The informal security analysis of the proposed scheme proves that the ES-HAS scheme achieves all the mentioned security features. In comparison with the computational cost and communication overhead of the proposed scheme with the other related schemes, the proposed scheme operates with minimal communication overhead in order to provide better security. Therefore, the proposed scheme is lightweight and practical to implement.