Abstract
Cryptography is traditionally considered as a main information security mechanism, providing several security services such as confidentiality, as well as data and entity authentication. This aspect is clearly relevant to the fundamental human right of privacy, in terms of securing data from eavesdropping and tampering, as well as from masquerading their origin. However, cryptography may also support several other (legal) requirements related to privacy. For example, in order to fulfil the data minimisation principle—i.e., to ensure that the personal data that are being processed are adequate and limited only to what is necessary in relation to the purposes for which they are processed—the use of advanced cryptographic techniques such as secure computations, zero-knowledge proofs or homomorphic encryption may be prerequisite. In practice though, it seems that the organisations performing personal data processing are not fully aware of such solutions, thus adopting techniques that pose risks for the rights of individuals. This paper aims to provide a generic overview of the possible cryptographic applications that suffice to address privacy challenges. In the process, we shall also state our view on the public “debate” on finding ways so as to allow law enforcement agencies to bypass the encryption of communication.
1. Introduction
It is widely known that cryptographic primitives—i.e., symmetric encryption algorithms in various modes of operation, public key algorithms/techniques, hash functions, message authentication codes, digital signatures, etc.,—constitute main building blocks for providing, through appropriate combinations, specific (cyber)security services, such as confidentiality, data and entity authentication, as well as non-repudiation (see, e.g., [1] as a classical cryptographic source, whilst some nice recent sources for cryptography are [2,3]). For example, the Transport Layer Security (TLS) protocol, which is being considered as a somehow de facto standard to secure communications over insecure channels, is highly based on cryptography for ensuring the desired security services. Therefore, cryptography is also explicitly mentioned in several legal instruments regarding cybersecurity and human rights. For example, in Europe, the new Cybersecurity Strategy, presented in December 2020 by the European Commission and the High Representative of the Union for Foreign Affairs and Security Policy, identifies strong encryption as a means of protection fundamental rights and the digital security of individuals, governments and industry [4], thus rendering essential the development, implementation and use of strong encryption.
Apart from the security aspect, cryptography is also relevant with the fundamental human right of privacy. Although there exists, roughly speaking, an overlapping between confidentiality (which is a main goal of security) and privacy in terms of hiding/protecting information concerning individuals, the notions of security and privacy are different—and, sometimes, may be even considered as contradictory (e.g., in cases that security measures put privacy at risk if they are not properly configured) [5]. Therefore, more advanced cryptographic techniques exist to deal with several privacy challenges—and this is one main reason that cryptography goes far beyond encryption [2]. Such advanced techniques had mainly purely academic interest for many years, but advances in technology allow for efficient implementations. The term Privacy Enhancing Cryptography (PEC) has been introduced to describe this aspect of cryptography, whilst the NIST (National Institute of Standards and Technology), being the prominent organisation for cryptographic standards, already runs a project to accompany the progress of emerging technologies in this area [6]. As a characteristic example, cryptographic techniques aiming to protect users privacy have been recently employed for developing COVID-19 contact tracing apps, in order to allow the competent health authorities to trace the chain of infection and take appropriate actions, without affecting users rights (recent surveys on such apps are [7,8]).
Although there is not a unique definition for privacy, a common interpretation is that it should be considered as the indefeasible right of an individual to control the ways in which personal information is obtained, processed, distributed, shared and used by any other entity. Therefore, privacy is somehow related to the so-called protection of personal data. Several legislative instruments exist—such the European General Data Protection Regulation (GDPR) and the California Consumer Privacy Act (CCPA)—for allowing individuals to have more control over their personal information that other entities (e.g., companies) collect and further process; hence these legal frameworks set specific obligations to entities processing personal data. In practice though, the fulfilment of these obligations is not always trivial; for example, the GDPR sets the obligation for the data protection by design principle, meaning that appropriate measures should be implemented at a very early stage of the design of a process, so as to ensure that the necessary safeguards for protecting the rights of individuals are effectively in place, but this is a generic-type obligation for any personal data processing which does not suffice to explicitly guide the organisations on how they should proceed. Advanced cryptographic techniques (more precisely, PEC) may provide efficient solutions so as to protect fundamental human rights, as well as to ensure the compliance of organisations with the legal requirements. However, it seems that—unfortunately—the organisations are not fully aware of such solutions.
This paper aims to provide a survey on advanced cryptographic techniques that could be used to alleviate several personal data protection issues, in light of the relevant legal requirements; to this end, we shall be based on the provisions stemming from the GDPR, which can be considered as a good model for other regulations to adopt, in terms of rights and principles [5]. Therefore, having the GDPR principles as a basis, we shall present such cryptographic solutions in conjunction with possible application areas; when applicable, a comparison with other, less privacy-friendly, solutions that are currently implemented will be also given. The techniques that will be presented are: (i) advanced cryptographic techniques for pseudonymisation, (ii) blind signatures, (iii) ring signatures, (iv) homomorphic encryption, (v) secure multiparty computation protocols (focusing on some important subcategories—namely private set intersection and secret sharing schemes), (vi) functional encryption and (vii) zero-knowledge proofs. Blockchain technology is also discussed, within the same framework for fulfilling data protection requirements. Applications of such techniques to the cybersecurity context are also discussed, to alleviate privacy issues in the framework of collecting data that can be used to analyse possible security incidents. To our knowledge, this is the first such survey which also presents, apart from the cryptographic solutions, the relevant legal requirements that they address, as well as some relevant views that have been stated by data protection authorities. Moreover, since the ultimate goal of this paper is to reveal the importance of cryptography in terms of personal data protection, we shall also discuss—stating our personal view—the public debate with respect to finding ways to allow law enforcement agencies having access to content that has been encrypted.
1.1. Research Methodology and Questions
The paper surveys, based on an extensive literature review, the aforementioned advanced cryptographic techniques, both from a mathematical but also from a practical point of view, towards addressing the following research problem: How these can be used to efficiently address specific data protection legal requirements in challenging real-case scenarios?
More precisely, this review aims to address the following research questions:
- Classification and description of the advanced cryptographic techniques, associating each of them with specific legal provisions.
- Investigation of the possible relationships that exist between these techniques.
- Examination of real use case scenarios in which these techniques are being already implemented, as well as the relative perspectives and areas that need to be further explored.
- Exploration on the relative positions that the competent data protection authorities have stated, regarding the use of these techniques.
To address the above, the relevant provisions stemming from the GDPR are being used as the basis for the legal requirements. Our hypothesis—that it has been verified through our study—is that advanced cryptography suffices to provide solutions to numerous complex cases so as to ensure compliance with the personal data protection principles.
1.2. Structure of the Paper
The paper is organised as follows. First, in Section 2, the necessary background on the provisions of the GDPR with respect to personal data protection is given. Next, Section 3 focuses on cryptography-based pseudonymisation, since this is an important privacy enhancing technology that is also explicitly pointed out within the GDPR. Section 4, being the main part of the paper, presents advanced cryptographic techniques that can be used to promote personal data protection in line with the legal requirements, illustrating their advantages compared to other traditional cryptographic techniques; some of these techniques could be also seen as particular instances of pseudonymisation (which is a more general topic) and this is also explicitly clarified. Moreover, a discussion on how blockchain may also facilitate—under prerequisites—the compliance with the data protection requirements is given in Section 5. The issue of finding ways to allow law enforcement agencies to have access in content that is initially encrypted—i.e., embedding somehow backdoors in cryptographic implementations, for lawful purposes—is discussed in Section 6; the content of this section reflects the author’s personal view on the matter. Finally, concluding remarks are given in Section 7.
2. Background
The right to privacy has been recognised as a fundamental human right by the United Nations Declaration of Human Rights, the International Covenant on Civil and Political Rights, the Charter of Fundamental Rights in European Union and other international treaties. Privacy is strongly related with the personal data protection; as stated in the Charter of Fundamental Rights, personal data (i.e., data relating to an identified or identifiable natural person) must be processed fairly for specified purposes and on the basis of the consent of the person concerned or some other legitimate basis laid down by law under Article 8(2) of the Charter. The Charter furthermore provides that everyone has a right to access personal data relating to them, including a right to have such data rectified or deleted.
The General Data Protection Regulation or GDPR [9], that applies from 25 May 2018, constitutes the main legal instrument for personal data protection in Europe. The GDPR, which has been adopted in 2016 replacing the previous Data Protection Directive 95/46/EC, results in a harmonisation of relevant data processing rules across the European Union and aims to further protect and empower all EU citizens data privacy. Although the GDPR is a European Regulation, its territorial reach is not restricted within the European boundaries, since it applies to all organisations that process personal data of individuals residing in the European Union, regardless of the organizations’ location, which can be outside European Union. As it is stated in [10], the intentionally global reach of the GDPR with the threat of huge fines that it sets if fundamental rights are not properly protected, has led companies around the world to adjust their privacy practices, as well as the countries around the world to update their privacy laws.
The notion of personal data is explicitly defined in the GDPR as any information relating to an identified or identifiable natural person, that is a person who can be identified (being referred as data subject); as it is explicitly stated in the GDPR, an identifiable natural person is one who can be identified, directly or indirectly, in particular by reference to an identifier such as a name, an identification number, location data, an online identifier or to one or more factors specific to the physical, physiological, genetic, mental, economic, cultural or social identity of that natural person. The notion of the personal data is quite wide; the GDPR also describes anonymous data as the data for which the relevant person is no longer identifiable (and, in such a case, GDPR is not applicable since anonymous data are not personal), but it explicitly describes that, towards characterising data as anonymous, all the means reasonably likely to be used to identify the natural person directly or indirectly should be taken into account (see, e.g., [11] for a discussion on fallacies with respect to anonymous data in the smart mobile ecosystem). Therefore, even, e.g., device data, such as the IP address, are generally being considered as personal data.
Personal data processing is defined as any operation that is performed on personal data, including the collection, recording, structuring, storage, adaptation or alteration, retrieval, use, disclosure by transmission, dissemination, combination and erasure. The entity that, alone or jointly with others, determines the purposes and means of the processing of personal data, is the so-called data controller, whereas the entity which processes personal data on behalf of the controller is the data processor.
The GDPR codifies the principles that need to be guaranteed when personal data are collected or further processed and sets specific obligations to those that process personal data (data controllers/data processors). The basic principles that should be in place for any personal data processing are the following:
- Lawfulness, fairness and transparency: Personal data shall be processed lawfully, fairly and in a transparent manner in relation to the data subject;
- Purpose limitation: Personal data should be collected for specified, explicit and legitimate purposes and not further processed in a manner that is incompatible with those purposes (…);
- Data minimisation: Personal data should be adequate, relevant and limited to what is necessary in relation to the purposes for which they are processed;
- Accuracy: Personal data should be accurate and, where necessary, kept up to date (…);
- Storage limitation: Personal data should be kept in a form which permits identification of data subjects for no longer than is necessary for the purposes for which the personal data are processed (…);
- Integrity and confidentiality: Personal data should be processed in a manner that ensures appropriate security of the personal data, including protection against unauthorised or unlawful processing and against accidental loss, destruction or damage, using appropriate technical or organisational measures.
Moreover, any processing of personal data requires a lawful basis; such a possible legal basis could be the individual’s consent—which is defined as a freely given, specific, informed and unambiguous indication of the data subject’s wishes by which he or she, by a statement or by a clear affirmative action, signifies agreement to the processing of personal data relating to him or her—but other legal bases may be also applicable (see art. 6 of the GDPR). In addition, some types of personal data are mentioned as special categories of personal data; there are personal data related to racial or ethnic origin, political opinions, religious or philosophical beliefs, trade union membership, as well as data concerning health or data concerning a natural person’s sex life or sexual orientation. Moreover, the processing of genetic data, as well as of biometric data for the purpose of uniquely identifying a natural person also correspond to processing of special categories of data. In general, there are stricter requirements for legitimate processing of such personal data (which are also referred as sensitive data).
The GDPR sets several rules and obligations for data controllers and processors. First, there exists a number of individuals rights, such as the right to have access to the data or the right to delete the data, which the data controller should satisfy, upon data subject’s request, without undue delay. Moreover, the transparency of the processing, which is—as stated above—a basic principle for legal processing, is also referred as the individuals right to be fully informed for the processing.
Regarding personal data security, the GDPR promotes a risk-based approach, where cryptography is being explicitly stated as a security measure that should be taken into account as a possible appropriate measure, taking into account the state of the art, the costs of implementation and the nature, scope, context and purposes of processing as well as the risk of varying likelihood and severity for the rights and freedoms of natural persons. In addition, there exist specific obligations for data controllers in terms of a personal data breaches; such obligations include the notification of the incident to the relevant competent authority, whereas the affected individuals should be also informed without undue delay in cases that high risks occur for them. Interestingly enough, there is an explicit provision stating that such a communication to the affected individuals is not required if appropriate technical and organisational protection measures are implemented that render the personal data unintelligible to any person who is not authorised to access it, such as encryption. This is a classical use of cryptography for security of data, illustrating the aforementioned overlapping between security and privacy.
However, it becomes evident that personal data protection is much more than personal data security and, thus, additional requirements exist for data controllers (and, in several cases, for processors too). An important one is the so-called data protection by design principle; according to this (see art. 25(1) of the GDPR):
Taking into account the state of the art, the cost of implementation and the nature, scope, context and purposes of processing as well as the risks of varying likelihood and severity for rights and freedoms of natural persons posed by the processing, the controller shall, both at the time of the determination of the means for processing and at the time of the processing itself, implement appropriate technical and organisational measures, such as pseudonymisation, which are designed to implement data-protection principles, such as data minimisation, in an effective manner and to integrate the necessary safeguards into the processing in order to meet the requirements of this Regulation and protect the rights of data subjects.
In other words, from the very early stages of the design of a personal data processing, data protection requirements should be appropriately taken into account—and these requirements go far beyond security. As it is stated in the relevant Recital 78 of the GDPR, appropriate measures that meet in particular this principle could consist of minimising the processing of personal data, pseudonymising personal data as soon as possible, transparency with regard to the functions and processing of personal data, enabling the data subject to monitor the data processing, enabling the controller to create and improve security features. For example, the data controller shall ensure that, according to data minimisation principle, no excessive personal data are being collected or inferred, with respect to desired purpose of the processing; this should be appropriately embedded, as a design requirement, in any data process. Moreover, in specific high-risk personal data processings, there exists the requirement that the data controller should conduct a Personal Data processing Impact Assessment (DPIA), which is—in simple words—an extension of security risk assessment, covering not only security but also all the data protection aspects.
Moreover, recognizing the role of the default settings, the GDPR introduces a relevant obligation to data controllers:
The controller shall implement appropriate technical and organisational measures for ensuring that, by default, only personal data which are necessary for each specific purpose of the processing are processed. That obligation applies to the amount of personal data collected, the extent of their processing, the period of their storage and their accessibility. In particular, such measures shall ensure that by default personal data are not made accessible without the individual’s intervention to an indefinite number of natural persons.
Although this principle, called data protection by default principle, might be perceived only as a substantiation of data protection by design, the task of selecting and implementing the default settings has its own specific significance and challenges [12].
Several data protection requirements, such as, e.g., data minimisation and purpose limitation, could be satisfied by advanced cryptographic techniques (PEC); this is not explicitly mentioned in the GDPR, since cryptography is mentioned therein mainly as a security measure. However, as it will be subsequently discussed, cryptography may also provide other data protection services. For instance, as it is analysed next, advanced cryptography may yield specific-type pseudonymisation approaches to address data protection requirements, which could not be fulfilled by conventional pseudonymisation.
Last, but not least, the GDPR introduces the accountability principle as an obligation for any data controller, in sense that the controller is fully responsible for complying with the data protection requirements, whereas this compliance should be able to be demonstrated through appropriate measures. For example, if the legal basis for the processing is the data subjects consent, then the controller should be able to demonstrate that the individuals consents that have been collected are valid. Again, cryptographic primitives may also help controllers demonstrate compliance, as it will also subsequently discussed.
3. Cryptography as a Pseudonymisation Mechanism
This section illustrates how cryptography can be used as a tool for pseudonymising personal data. Data pseudonymisation is a very important privacy enhancing technology, that may suffice to achieve several important data protection principles, such as data minimisation (e.g., via allowing the processing of pseudonyms instead of the original identifiers) and purpose limitation (e.g., via preserving the unlinkability of individuals across different application domains). Since pseudonymisation is a quite generic term, it is discussed in this review separately from other techniques lying in the field of PEC; however, there clearly exists an overlap between PEC and pseudonymisation, as it will become obvious from the subsequent analysis.
In the discussion that follows, we first present the general notions regarding pseudonymisation, in relation also with the relative legal provisions (Section 3.1) and subsequently we focus on advanced cryptographic techniques for pseudonymisation purposes (Section 3.2). More information can be found in [13,14].
3.1. Classical Cryptographic Techniques for Pseudonymisation
Data pseudonymisation is a well-known data protection technique. According to the ISO/IEC 20889:2018 standard regarding the privacy enhancing data de-identification terminology and classification of techniques [15] , pseudonymisation is a de-identification technique that replaces an identifier (or identifiers) for a data principal (which in turn denotes, according to this definition, any entity such as a person, an organization, a device, or a software application) with a pseudonym in order to hide the identity of that data principal. The pseudonym is defined in the same standard as a unique identifier created for a data principal to replace the commonly used identifier for that data principal. From an engineering perspective, a pseudonym is defined as an identifier of a subject, which is different from the subject’s real name [16,17], whereas the types of pseudonyms may be distinguished by the context of use [16]. In the sequel, we shall assume that identifiers refer to individuals (i.e., data subjects, based on the GDPR terminology), which also include the identifiers of devices corresponding to individuals.
Pseudonymisation can be used to hide the actual identities of individuals, which is essential in several cases from a data protection point of view, such as in processes for research/statistics purposes; for example, in clinical trials, patients data should be processed in a pseudonymised form, according to the European Medicines Agency [18]. Moreover, there are cases where even the data controller does not need to know the exact identities of individuals, in terms of the data minimisation principle, such as, for example, in anonymous smart apps. This may also be the case if the legal basis for the processing is the performance of a task carried out in the public interest; for example, in case that a public health organisation needs to collect patients data from hospital/medical centres, under a provision of a national law, in order to make proper decision on public health issues, it may be necessary to track specific patients for deriving conclusions for their treatment and her/his patient history, but the organisation should not learn the exact identity of the patient or any identifier of her/his, such as her/his social security number, that could allow re-identification (see, e.g., the Opinion 3/2015 of the Hellenic Data Protection Authority [19]).
Typically, any mapping between the space of original identifiers and the space of new identifiers (i.e., pseudonyms) constitutes a pseudonymisation technique; to this end, classical cryptography is a nice—and often preferable—option for implementing pseudonymisation. Indeed, for an identifier of an individual A (e.g., her/his e-mail address), a pseudonym can be derived through encryption , where is the encryption key and E denotes the encryption process (which could be either symmetric or asymmetric); for a robust cryptographic algorithm, only the one with access to the decryption key is able to reverse the pseudonymisation, whilst any two different data subjects will always get two different pseudonyms. The above hold for any type of identifier, even if consists of a number of attributes. Note also that E could be a Message Authentication Code (MAC) or a keyed hash function; similar properties also occur in these cases, but even the owner of the secret key cannot directly reverse the pseudonymisation but she can easily verify whether a given pseudonym corresponds to a given identifier .
Such classical cryptographic techniques for pseudonymisation are already being widely used. For example, in [20], the use of a salted hash function as a pseudonymisation mechanism is being described, which aims to derive pseudonyms for Internet TV users in order to feed an analytics component, so as to ensure that the latter does not have access to the original users’ identifiers (but each user has always the same pseudonym, as required for the analytics purpose). Classical encryption has been also proposed in several contexts for pseudonymising health data—see, e.g., [21]. More recently, due to the COVID-19 pandemic, several contact tracing smart apps have been adopted by many countries, with the aim to have a way of an automatic detection of the contacts of an infected individual, thus allowing the competent health authorities to trace the chain of infection and proceed with appropriate actions (for recent surveys, see, e.g., [7,21]). For deriving pseudonyms of users of these apps, several different approaches exist, with the classical encryption being one of them; for example, in the protocol PePP-PT (Pan-European Privacy-Preserving Proximity Tracing), the derived pseudonyms are encrypted values of the user’s fixed ID [21], where the encryption algorithm is either AES in the so-called PePP-PT Need to Know (NTK) implementation) or 3DES (in the so-called Robert implementation).
The GDPR defines pseudonymisation as the processing of personal data in such a manner that the personal data can no longer be attributed to a specific data subject without the use of additional information, provided that such additional information is kept separately and is subject to technical and organisational measures to ensure that the personal data are not attributed to an identified or identifiable natural person. Pseudonymisation is referred to several times within the GDPR as a possible data protection measure. It should be pointed out that, as the GDPR explicitly states, pseudonymous data are still personal and not anonymous data. The above legal definition of pseudonymisation is in compliance (although actually not identical) with the aforementioned technical interpretation of pseudonymisation; for example, if encryption is being used for pseudonymising data, then the decryption key can be considered as the additional information that is needed to reverse the pseudonymisation and re-identify the individual.
More generally though, even if the pseudonymisation cannot be technically reversed, other available additional information that could allow re-identification of an individual should be also carefully examined on a risk-based approach (see, for example, the famous case of the AOL incident since 2006 [22]); this aspect though will not be discussed in this survey since it is not directly relevant to cryptography (other privacy enhancing technologies apply). A generic survey on pseudonymisation, with emphasis on the use of cryptography from a personal data protection point of view, is given in [23], whilst a more systematic description of possible pseudonymisation scenarios, identifying the roles of the main actors involved in the pseudonymisation process in terms of the personal data protection as well as the possible pseudonymisation policy for each application scenario, is discussed in [13].
3.2. Advanced Cryptographic Techniques for Pseudonymisation
The above describes how classical cryptographic primitives can be used for ensuring data protection goals (e.g., data minimisation, if the actual identities of the individuals are not needed for fulfilling the desired goal of the processing) through pseudonymisation. However, advanced cryptographic techniques may be more powerful than the conventional ones, being able to provide pseudonymisation schemes with properties that cannot be achieved by classical cryptography. For example, for medical records, a technique called polymorphic encryption which has been tested in a real-case scenario of medical research, is presented in [24], in which each user (i.e., patient in case of an e-health system) has a cryptographically generated different pseudonym at different parties; for instance, by a clever use of the El Gamal public key cryptographic algorithm, the patient gets different pseudonyms at doctors X, Y and Z, and at medical research groups U, V and W—that is, domain-specific pseudonyms are generated. By these means, even if these parties lose their data, or they maliciously want to combine their data with others, no privacy risks occur (pseudonymisation reversal is not possible, whereas all the pseudonyms are unlinkable). The same idea has been also used to pseudonymise IP network flows in [25] (recall than an IP address is considered, according to the GDPR, personal data). The main property of polymorphic encryption is that personal data can be encrypted (and stored at a central point) in such a way that there is no need to fix a priori who can decrypt the data later; later on it can be decided who can decrypt the data, via some transformation of the encrypted data which allows ciphertext to be locally decryptable via locally different cryptographic keys, whereas this transformation can be performed in a blind manner, without the party performing this being able to see the original content.
Several other challenges also occur which necessitate more advanced pseudonymisation techniques. A characteristic paradigm is the one that the user’s pseudonym is being generated in the user’s environment—i.e., user-generated pseudonyms. By these means, neither the data controller nor any other (trusted or not) third party is actively employed in the process of deriving the pseudonyms. As it is stated in [26], in such a decentralised approach the following requirements need to be satisfied: (i) ease of use, (ii) linking a pseudonym to its owning user should not be possible for any other than the user herself, unless it is explicitly permitted, (iii) in cases that users may have multiple pseudonyms, it should not be possible to identify different pseudonyms as belonging to the same user, (iv) injectivity, in terms that the pseudonym generation process should avoid duplicates and (v) flexibility, i.e., it should be possible to add new pseudonyms to the user entities with minimal effort. Note that user-generated pseudonyms may be prerequisite for GDPR compliance in cases that the data controller does not need to know the exact identity of the user, unless the user allows such a knowledge (e.g., in cases of temporary identifiers in smart apps).
Hence, to achieve the aforementioned goals, more complex cryptographic schemes are needed to ensure the aforementioned properties, like those presented in [26,27]. More recently, a new technique based on Merkle trees (a type of hash tree) is presented in [28], which allows a user A to generate a pseudonym based on several identifiers , for an integer ℓ, so as all the aforementioned requirements for user-generated pseudonyms are present, whereas additionally A can prove whenever she wants that, for given known , she owns the pseudonym without revealing the remaining identifiers for . By these means, two organisations and having knowledge of the identifiers , respectively, can exchange information for A upon her request without learning any additional identifier—i.e., (resp. ) does not learn (resp. ). According to [28], since the security of this technique rests with the security of the Merkle trees as primitives for building one-time signatures, this pseudonymisation scheme is also post-quantum resistant.
Other advanced cryptographic techniques may also yield powerful pseudonymisation schemes; a generic survey is given in [14], whilst for the special case of IoT applications, a comprehensive survey is given in [17]. It should be noted that [14] also puts emphasis on the cases where pseudonymisation could be utilised in the cybersecurity context, in order to provide for security analytics, while preserving privacy and data protection. As it is described therein, both classical and advanced cryptographic techniques can be used depending on the application scenario and the relevant data protection risks. Interestingly enough, some advanced pseudonymisation techniques discussed in [14,17] include secret sharing protocols, homomorphic encryption and secure multiparty computations; since these techniques are actually more generic than pseudonymisation techniques, they will be discussed separately next as specific types of PEC. However, this observation illustrates the aforementioned overlapping that occurs when classifying PEC technologies (actually, even the polymorphic encryption that is based on the El Gamal cipher as described previously, utilises a homomorphic property of the cipher).
Concluding this subsection, we should discuss the possible applicability of a simple (i.e., unkeyed/unsalted) cryptographic hash function as a pseudonymisation mechanism (see Figure 1). Many organisations/researchers assume that hashing an identifier is a proper way to get a deterministic pseudonymisation—i.e., for the same original identifier, the same (irreversible) pseudonym will be always generated. This is convenient especially in cases that different entities perform pseudonymisation and there is a need to perform a matching between pseudonyms generated by different entities. For example, in the case of the custom audience list that Facebook provides [29], an organisation with its own customers may upload its customer list in the Facebook’s Ads Manager to create a Custom Audience; such an uploading takes places on hashed values of the list. As Facebook states [29]:
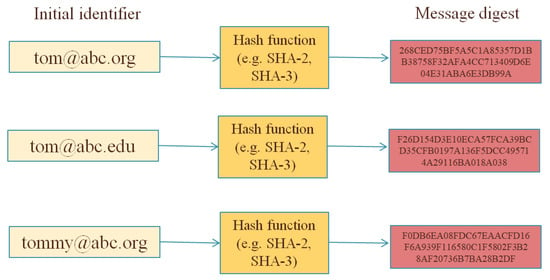
Figure 1.
A simple hash function as a (possibly bad) pseudonymisation technique.
Facebook uses this hashed information and compares it to our own hashed information. Then, we help build your audience by finding the Facebook profiles that match and create a Custom Audience for you from those matches. After your Custom Audience is created, the matched and unmatched hashed information is deleted.
By these means, Facebook receives hashed values of customers’ information of other organisations—and such information could be, e.g., their e-mail addresses. It is implied that Facebook does not learn personal information of non-Facebook users, due to the mathematical irreversibility of cryptographic hash functions. However, this is not fully accurate since the hashing procedure does not utilise any secret key and, thus, having a hashed value (i.e., a message digest) one could try an attack by simply hashing possible input messages; if the inputs space has a specific structure (like e-mail addresses, IP addresses, etc.), such an attack may be feasible and a pseudonymisation reversal may be performed (for example, in Figure 1, having only the list of pseudonyms, it is easy to find out if a given email address (e.g., tom@abc.org) corresponds to a pseudonym of the list). Hence, the data minimisation principle is not ensured, since Facebook is able to learn more information related to individuals than it should learn.
The above weakness of hash functions as pseudonymisation mechanism is analysed in [30], whereas it is also explicitly described in [13,23]. This is another characteristic example illustrating the importance of exploring advanced cryptographic techniques to ensure personal data protection, as it will be subsequently described.
4. Privacy Enhancing Cryptography
In this section, we present some advanced cryptographic methods for mitigating personal data protection challenges, as well as their possible application scenarios. These techniques are the following:
- Blind signatures, which are mainly related to the data minimisation principle.
- Ring signatures, which are mainly related to the data minimisation principle, as well as with the data confidentiality and purpose limitation (since the actual identity of the signer is hidden).
- Homomorphic encryption, which is mainly related to the the data minimisation principle, as well as to the confidentiality of the personal data and the fairness of the processing (since only specific operations are allowed on encrypted data).
- Secure computations, which is mainly related to the data minimisation principle, in conjunction with the fairness of the processing—in the sense that a correct output of a function is jointly computed by several parties in a secure way (the input from each party remains secret from all the remaining parties).
- Functional encryption, which is mainly related to the data minimisation principle as well as the to the data confidentiality and purpose limitation (since only specific processes over the encrypted data are allowed).
- Zero-knowledge proofs, which is mainly related to the data minimisation principle.
It should be pointed out that the classification of these methods is not a straightforward task, since there exist some relationships amongst them in terms of their underlying properties; in the classification that follows, such relationships will be also discussed.
4.1. Blind Signatures
Digital signatures is a well-known cryptographic primitive, being used to provide security services such as message and entity authentication, as well as non-repudiation. The digital signature plays somehow the role of a handwritten signature in the digital world—i.e., the signer validates the content of the message, whereas the validity of the signature can be confirmed by others; forging a signature should not be possible, either in paper or in the digital world. A digital signature has the additional property that is bound not only to the signer but to the message too—i.e., if user A generates the signature for a message m and a signature for a message , then ; that is why the verification of a signature ensures not only the authentication of the signer but also simultaneously the integrity of the message.
There is an important variation of digital signatures, called blind signatures, with additional properties in terms of privacy. Such signatures have been first introduced in [31] (a scheme based on the RSA algorithm was introduced therein), but numerous other blind signature schemes are now well-known (a nice survey of the classical blind signature schemes, up to 2011, is given in [32]). The main privacy property of these signatures is that the signer does not see the content of the message that she/he signs, since the message is blinded before signing; however, despite this, the validity of the signature can be checked, so as to avoid forged signatures. For example, in a RSA blind signature scheme, a user may blind the message m that is to be signed by an authority S via choosing a random value r (satisfying specific properties with respect to the public RSA parameters of S) and computing , where is the RSA public key of S. Hence, S does not see m but and computes the signature , where d is its RSA private key. Then, the user gets the right RSA signature (i.e., the classical RSA signature that S would generate if m was known) by computing .
The necessity of this property was first established in e-cash applications, so as to protect revealing the contents of the individuals payments which could in turn be used to create profiles of the users (in terms of their habits, customer behaviour, etc.). Another characteristic example is the e-voting systems, in which it is essential to ensure that a user’s vote is valid, retaining though the secrecy of the vote.
Other uses of blind signatures are also of importance, in terms of personal data protection. For example, in a recent work [33], blind signatures are building elements for constructing an e-tickets system so as to preserve privacy. More precisely, the authors discuss the issue of reusability of a ticket, which allows the system to link all the journeys made with a given e-ticket, presenting a new privacy-preserving solution that protects users even from internal malicious users having access to the system’s servers. It should be noted that, for an e-ticket system, the absolutely necessary information should be processed without affecting the right of the citizens to come and go anonymously (see, e.g., the Opinion 1/2017 of the Hellenic Data Protection Authority [34], whereas a general study of the issue is given in [35]); such types of information would be, for the general case, excessive and disproportionate compared to the purposes of the system.
Apart from blind signatures, there is also a variation called partial blind signatures [36], which allow a signer to explicitly include necessary information (e.g., expiration date) in the resulting signatures under some agreement with the message owner. The aforementioned scheme in [33] utilizes partial blind signatures.
4.2. Ring Signatures
Another advanced type of digital signatures is the so-called ring signature, first introduced in [37]. By these means, a member of a well-determined group may sign a message such as a third party is able to verify that the signature is valid and stems from a member of a group, but without being able to explicitly identify which member of the group is the actual signer; this is achieved by cryptographic methods based on asymmetric cryptography that do not necessitate the existence of a trusted third party, whereas the verifier can be any user having access to the public keys of all members of the group (actually all the public keys of the members of the group are needed for creating the signature, but once a member of the group signs with her/his secret information that is also needed, her/his identity cannot revealed by her/his signature).
A variant of ring signature is the linkable ring signature, proposed in [38], which allows any of n group members to generate a ring signature on some message, with the additional property that all signatures from the same member can be linked together (which could be of value in some cases). Moreover, a similar concept is the so-called group signature, first introduced in [39], in which there is a group manager with a secret key that may allow finding who was the actually signer. Several nice schemes of group signatures have been proposed since 1991—a recent survey, focusing explicitly on lattice-based group signatures (which also provide post-quantum security) is given in [40].
In the original paper of [37], it is stated—in order to illustrate the importance of this technique— that a ring signature could be used to provide a verifiable signature from ”a high-ranking official”, without revealing who exactly is the official that signed the message (and that is why the title of their work is “How to leak a secret”). Such a technology could be of high value for whistleblowing systems, especially if such an implementation allows a signer to later prove ownership of a signature or a non-signer to repudiate a signature that she/he did not produce [41]. For example, a few months after the date that GDPR came into force, the European Union issued the Regulation (EU) 2018/1725 on the protection of natural persons with regard to the processing of personal data by the Union institutions, bodies, offices and agencies (i.e., it explicitly focuses on European Union legal entities); based on this, the European Data Protection Supervisor (EDPS) issued guidelines on processing personal information within a whistleblowing procedure [42], which explicitly state, amongst others, that the identity of the whistleblower who reports serious wrongdoings or irregularities in good faith should be treated with the utmost confidentiality as they should be protected against any retaliation. Their identity should never be revealed except in certain exceptional circumstances if the whistleblower authorises such a disclosure, if this is required by any subsequent criminal law proceedings, or if the whistleblower maliciously makes a false statement.
Other possible applications of ring (or group) signatures, with respect to personal data protection principles, are related with processing in the context of employment. For example, a company may strictly allow specific employees to have access to restricted areas due to security/safety reasons; by these means, it is ensured that only strictly authorised personnel gets access to these areas (i.e., through a keycard system), without tracking individually the employee’s movements, which could yield further processing for additional purposes, thus contradicting the purpose limitation principle; of course, if an employee abuses this trust, then re-identification could be possible by appropriately using the appropriate re-identification property of the group/ring signature.
4.3. Homomorphic Encryption
Homomorphic encryption is an important area in cryptography, related to specific cryptographic algorithms which preserve the following property: a certain algebraic structure between the plaintext space and the ciphertext space is retained, under the assumption that the encryption key is fixed. By these means, it is possible to perform operations over ciphertexts even if the decryption key is unknown, so as to ensure that the output of this operation corresponds to the encryption of the output that we would get if a well-determined operation were initially performed on the original plaintexts (see Figure 2). For example, a homomorphic property is present if the product of any two ciphertexts , is equal to the ciphertext of the sum of the two corresponding plaintexts, i.e.,
where all the encryption have been performed with the same key k. Actually, the above example corresponds to a well-known homomorphic algorithm, the Paillier’s cryptosystem [43], which has been utilised for e-voting schemes, so as to count encrypted votes without having access to the content of each vote.
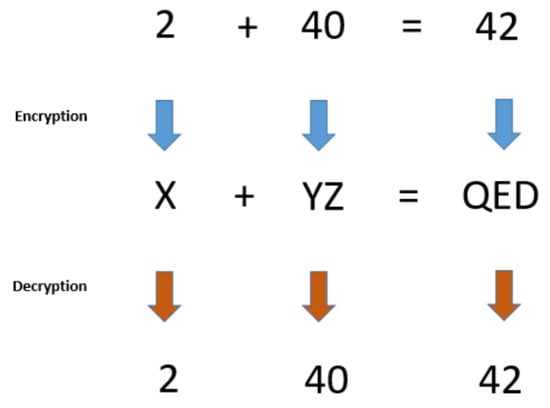
Figure 2.
An additive homomorphic scheme.
Many public key homomorphic cryptographic schemes have been proposed, but most of them are partial homomorphic algorithms—i.e., they support either addition/multiplication, but not both. Fully homomorphic encryption allows both addition and multiplication of ciphertexts, which implies that any computable function can be evaluated on encrypted values solely with knowledge of the public key (i.e., the decryption key is not needed for performing the operations). In other words, given an n-ary function f and encrypted values , , …, one is able to compute efficiently (i.e., in polynomial time in a security parameter) a ciphertext the ciphertext . Such fully homomorphic schemes were not known for many decades, until 2009 with the prominent work by Gentry [44].
It should be pointed out that any homomorphic cryptographic scheme encompasses somehow the malleability property—that is an adversary can modify a ciphertext of m into another ciphertext which is the encryption of , for a known function f, without having knowledge of any information about m. In a malleable encryption scheme, adaptive chosen ciphertext attack is applicable and, actually, this is the case for any homomorphic scheme. Therefore, the notion of targeted malleability has been introduced [45], which ensures that an encryption scheme is only malleable at a specific set of allowable functions; in this work, a mechanism that can add targeted malleability to homomorphic encryption schemes is also presented.
Due to their properties, homomorphic cryptosystems are of high importance in terms of personal data protection. A characteristic example is the use of cloud service providers or of any other environment that is not under the sole control of the data controller in order to store and perform operations on data related to individuals (which can be homomorphically encrypted, thus hiding the original information while still computations are feasible). Another important application scenario is the usage of homomorphic encryption for securing data bases. Indeed, if standard encryption is employed, the encrypted database will not allow any operations on the records (they need to be first decrypted in order to perform operation), whereas other advanced cryptographic techniques that allow some operations like order-preserving encryption still allow some data leakages, such as access/search patterns. Another possible application area, which is of high importance in terms of privacy, is to hide the users requests in search engines; such requests pose several privacy risks, since the search engine may build a concrete profile of the user based on her requests. Through homomorphic encryption, search engines process encrypted data, serve them as the algorithm is designed to, and subsequently respond to the the user with succinct encrypted answer, without having access to the query in plaintext. Hence, the user gets the desired result, while the search engines remain unaware of the data requested.
More generally, several other applications in data analysis may be enhanced, in terms of privacy, through homomorphic encryption, such as predictive analysis on encrypted medical data [46]. More recently, homomorphic encryption was used to secure a typical machine learning pipeline commonly employed in the financial services sector, illustrating that it was possible to run predictions with the same accuracy as without encryption and with adequate performance [47]. According to the results therein, banks can safely outsource the task of running predictions to an untrusted environment (note though that the term untrusted here should be interpreted in terms of personal data protection—that is even if the environment is a cloud service provider with enhanced security measures, it is assumed that even the provider itself should not learn the actual content of the data). Although in the work of [47] an existing encrypted logistic regression model that constitutes sensitive intellectual property is being used in order to demonstrate the feasibility of running a large number of encrypted prediction operations on real, encrypted financial data, it becomes evident that such an approach could be also used when the computations refer to personal data.
Several advancements in implementing homomorphic encryption have been initiated by large companies, such as SEAL (Simple Encrypted Arithmetic Library), which is a set of encryption libraries that allow computations on encrypted data and is developed by Microsoft, Google’s Private Join and Compute which allows organisations gain aggregated insights about the other party’s data, as well as the HElib C++ library by IBM.
Homomorphic cryptography can be also used as a building block for other advanced cryptographic techniques that are classified as PEC; the most notable example is their usage in constructing primitives such as oblivious transfers or, more generally, secure multiparty computations (actually, two-party computations), whereas Gentry in his dissertation has shown how homomorphic encryption may allow construction of non-interactive zero knowledge (NIZK) proofs of small size. The aforementioned Private Join and Compute technology actually implements secure computations. These cryptographic techniques are further discussed next.
4.4. Secure Computations
Secure Multiparty Computation (SMPC) protocols constitute a very important cryptographic field, aiming to allow a set of parties to exchange information so as to jointly make a computation based on their private inputs without though revealing them; this is achieved without the need of a trusted third party, whilst their security can be evaluated based on several assumptions on the honesty of the parties (i.e., some protocols are secure only for strict assumptions on the honesty of the parties).
The underlying idea of the simplest case of secure two-party computation is shown in Figure 3. By their definition, it becomes evident that SMPC protocols are strongly related with the data minimisation principle. The most famous paradigm of SMPC (which is actually a two-party computation, but it can be generalised to parties) is the millionaires problem, i.e., two millionaires are interested in knowing which of them is richer without revealing their actual wealth [48]. After the classical works on the field [49,50], several SMPC protocols have been proposed in several contexts, being efficient. A nice survey on this field is [51] (see also the references therein).
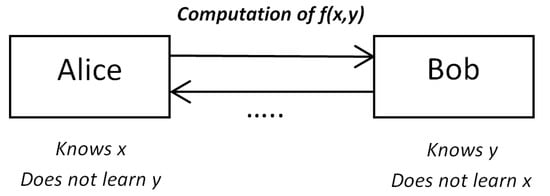
Figure 3.
Secure two-party computation.
A SMPC protocol aims to satisfy the following properties:
- Privacy: Only the output of the function is learned and nothing else.
- Correctness: The parties obtain correct output (even if some parties misbehave).
- Independence of inputs: The parties cannot choose their inputs as a function of other parties’ inputs.
- Fairness: If one party learns the output, then all parties learn the output.
- Guaranteed output delivery: All honest parties learn the output.
There are several different ways to implement MPC protocols. A typical one is the Yao’s garbled circuits [49], by which one party creates a circuit from the function to be calculated and sends it to the other party, whereas the latter evaluates the circuit. The evaluation requires oblivious communication between both parties and, thus, oblivious transfer communications protocols are utilised. There are also other specific cryptographic techniques that could be used for SMPC, which are discussed as specific cases next; note that the homomorphic encryption provides also the means for secure computation and constitutes another alternative for implementing such protocols.
To illustrate the importance of SMPC in terms of personal data protection, we first refer to the example given in [51], regarding the problem of comparing a person’s DNA against a database of patients’ DNA with specific disease, with the goal of finding if the person is in a high risk group for this disease. Note that data regarding DNA are considered as special category of personal data (i.e., sensitive) according to the GDPR provisions and there exist high risks for the individuals by revealing such information to private organisations. An appropriate SMPC protocol may provide a privacy-friendly solution to this problem, so as to ensure that only the category of disease that the person’s DNA is close to (or none) is revealed and nothing else (i.e., neither the DNA of the person being compared nor the DNA of the patients in the database). This is clearly strongly related to the data minimisation principle. Note that the correctness requirement guarantees that a malicious party cannot change the result and such a change could have significant impact to the individuals (e.g., make the individuals erroneously believe that they are at risk).
SMPC protocols have been proposed for several specific application scenarios, in order to alleviate privacy issues. For example, in [52], a SMPC based privacy preserving protocol for smart meter based load management is proposed, so as to ensure that the utility is able to perform real time demand management with individual users, without knowing the actual value of each user’s consumption data (which could allow creating individuals profiles on the habits/daily life, etc.); homomorphic encryption is a building block for this proposal. More generally, SMPC can be used to run machine learning models on data without revealing the model to the data owner, and without revealing the data to the model owner, as well as for statistical analyses between organisations for the purpose of anti money laundering, risk score calculations and more [51].
Some some real-case examples of SMPC protocols are given in [53], including the Sharemind platform [54], which allows users share data in an encrypted form so that nobody except for themselves can access it, whilst Sharemind will process the encrypted data without having to remove the encryption. Sharemind utilises several MPC techniques, including homomorphic encryption (described previously) as well as secret sharing (which will be subsequently described). As an application scenario, in 2015 the Estonian Center of Applied Research used Sharemind to collect governmental tax and education records and ran a big data study looking for correlations between working during studies and failing to graduate in time. The data import by Tax and Customs Board and the Ministry of Education and Research was secured using Sharemind’s file importer tool to protect the uploading of the working and study records. The Estonian Data Protection Authority stated that as identifiable records do not exist outside the input parties and the outputs are highly aggregated statistics, the application is not processing personal data [53]. Although the GDPR was not present in 2015, such a project seems to be also in compliance with the provisions of GDPR with respect to the appropriate safeguards for performing research, taking into account that the processing entity does not have access to the original personal data. Other real-life use cases, with several other available tools, are also described in [53].
4.4.1. Private Set Intersection
There is a specific type of problem, whose solutions lie in the general class of SMPC protocols (actually, two-party computation) but specialised techniques are preferable for efficiently addressing it; this is the so-called Private Set Intersection (PSI), which refers to the problem of how two parties, each having a private set of values (e.g., lists of personal data) can find out the intersection of the sets, without revealing anything but the elements in the intersection (this is illustrated in Figure 4). Variations to this problem exist—the most well-known one is to find out only the cardinality of the intersection.
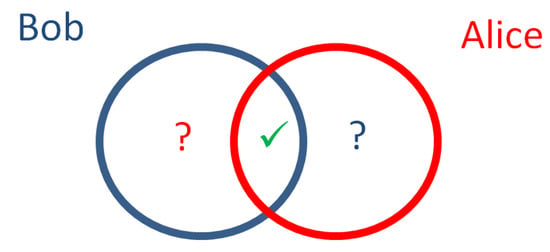
Figure 4.
The notion of private set intersection.
PSI a very important problem with several possible application scenarios, like the one described in Section 3 regarding the Facebook’s custom audience tool (as we described therein, a naive hashing allows for set intersection but it should not be considered as secure) or, more generally, for targeted advertising (note that according at least to the European legal framework, targeted advertising necessitates in principle the explicit informed consent of the user in order to be lawful, but this should not be interpreted that an advertiser may process excessive personal data once the user provides her consent; the data minimisation principle implies that the least possible data, with respect to the desired purpose, should be processed, which is also essential for fulfilling the data protection by design principle). As is it also stated in [51], Google is also using such a protocol (see [55] for the method adopted) in order to compute accurate conversion rates from advertisements to actual purchases; more precisely, Google and the company paying for the advertisement want to share their respective lists in order to compute the intersection size, and this is achieved by the PSI method in [55] which reveals nothing more than the size of the intersection.
PSI is also useful for botnet attack detection and collaborative intrusion detection (see, e.g., [56])—for example, by securely checking suspicious IP addresses. Other possible uses of PSI include COVID-19 contact tracing (see [57,58]), testing human genomes and pattern matching, finding out the patients of a hospital who have participated in the medical tests of different research labs, allowing federal tax authorities to learn whether specific suspected tax evaders have accounts with a certain foreign bank (so as to ensure that bank’s customers data will not be transmitted to the tax authority, as well as that the bank will not find out the list of the suspected tax evaders), etc.
Several different approaches exist for the PSI, under several assumptions on the security model, as well as with different properties in terms of efficiency—i.e., some put emphasis on the computational cost, others on the communication cost in terms of the number of messages that need to be exchanges etc. The traditional way to deal with PSI is the appropriate use of public key cryptography. For example, a PSI protocol that is based on the classical Diffie–Hellman algorithm is the following [59]. Let us assume that the user A (Alice) has the private list , whilst the user B (Bob) has the private list (these lists may be personal data). Then, the PSI protocol proceeds as follows.
- Alice and Bob agree on a large prime p.
- Alice randomly generates a private key a.
- Alice repeatedly hashes each of the values until all the digests be primitive roots modulo p
- For each of these hashed values , , Alice calculates and sends these values to Bob.
- Bob randomly generates a private key b.
- Bob repeatedly hashes each of the values until all the digests be primitive roots modulo p
- For each of these hashed values , , Bob calculates and sends these values to Alice.
- For each received , Bob calculates and sends these values to Alice.
- For each received , Alice calculates .
- Alice compares the sets , in order to find common elements. These correspond to the intersection of the original sets.
Other approaches for PSI are circuit-based (i.e., using the Yao’s ideas for the general SMPC), as well as oblivious transfer (OT) based PSI (note that oblivious transfer is any two-party protocol between a sender and a receiver, by which the sender transfers some information to the receiver, the sender remaining oblivious, however, to what information the receiver actually obtains). As stated in [51], the most efficient PSI protocols today use advanced hashing techniques, are based on OT protocols and can process millions of items in a few seconds [60,61,62]. A high-level description of the work in [60] is given in [51]; this is also described next.
- A chooses a key k for a pseudorandom function F.
- A and B run m oblivious pseudorandom function evaluations: in the i-th execution, , A inputs k and the B inputs . As a result, B learns for all , whereas A does not learn anything on , .
- A locally computes for all , and sends the list to B.
- B computes the intersection between the lists , , and , A and outputs all values for which belongs to the intersection.
Interestingly enough, this protocol (and actually, not only this—see also the approach in the Diffie–Hellman based protocol) is in compliance with the definition of pseudonymisation under the GPDR provisions, as it is illustrated in [14], thus further revealing the connections that exist between PEC tools. Indeed, the values of the pseudorandom function are pseudonymous data (under the assumption that the initial sets correspond to personal data referring to identifiable persons), where the additional information that are needed to re-identify the individuals is actually the key k (in conjunction with the knowledge of the original sets). Hence, such values , are actually not anonymous data but pseudonymous, according to the provisions stemming from the GDPR—and, thus, still personal data. However, this should not be interpreted as a high risk (or even not allowed) processing, since re-identification is not possible in a cryptographically strong SMPC protocol (only the original data owner that generates the “pseudonyms” can re-associate each pseudonym to the original identifier).
More generally, PSI is a rapidly developing field and new techniques are constantly proposed.
4.4.2. Secret Sharing
Secret sharing techniques refer to methods that a secret s is being securely shared into n parties, so as that re-construction of s is possible only if any parties exchange their information, but no less (in other words, for given , no t parties can reconstruct the secret). The first (and most well-known) secret sharing scheme was proposed in 1979 by Shamir [63]. The idea is as follows. Let s the secret value. A prime number is being chosen (which is known to all n parties, whilst it should also hold ) and the user that wants to share the information to these n parties chooses randomly coefficients (where is the Galois field with p elements) of a polynomial
Then, the n shares , , are being computed as follows: , where the computations are performed over . By this way, any users cannot recover the secret value , because any ℓ known pairs , do not suffice to uniquely determine the polynomial L; on the other side, such pairs are adequate to uniquely determine —e.g., through Lagrange interpolation, as suggested in [63]—and, thus, the parties can compute . Such a secret sharing scheme is also called the -out-of-n-threshold secret sharing scheme. For a general survey on secret sharing schemes, the reader can see, e.g., [64,65].
As Shamir states in his seminal paper [63], such schemes can be very helpful in the management of cryptographic keys (i.e., there is no any single point of failure that may allow an adversary to recover the secret key). This is depicted in Figure 5. Recalling Section 3, which illustrates that cryptography may be used for pseudonymisation, as well as the definition of pseudonymisation in the GDPR that states that the additional information that allows re-identification from pseudonymous data should be sufficiently protected, it becomes evident that a secret sharing scheme may be used to protect secret keys in pseudonymisation schemes in order to facilitate compliance with the GDPR (this is also stated in [14]).
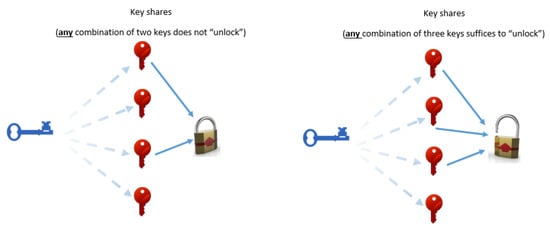
Figure 5.
Secret sharing: “Splitting” the key into several shares (example for ).
However, secret sharing schemes can be also used as primitives for SMPC protocols. For example, let us consider the case that two entities A and B have secret values , respectively and there is need for some other parties to securely compute the sum (the values and should remain secret). The user A (resp. B) shares the value (resp. ) to n parties in a -out-of-n threshold secret sharing scheme. So each party , has two shares; from A and from B (where f and g are the corresponding polynomials that have been chosen by A, B). Then, each party computes the sum . Therefore, any parties (but no less) can reconstruct, if they exchange their information, the polynomial which allows computing . More generally, as it is stated in [51], secret sharing schemes can be used to construct generic SMPC protocols, under the assumption that the majority of the peers are honest—namely, if n entities are involved in a SMPC protocol, such a protocol will work properly if the “corrupted” entities (i.e., the dishonest entities) are less than .
Apart from their significance in the SMPC context, secret sharing schemes may also provide several other privacy-friendly solutions, especially for pseudonymisation (this is also discussed in [14]). For example, in [66] it is described how such a technique can be applied to pseudonymise log files of a system so as to replace original identifiers (e.g., IP addresses) by pseudonyms and, thus, no profiling of users is possible. In other words, the identity of the user is being shared into n shares, where each of them plays a role of pseudonym that does not allow, by itself, pseudonymisation reversal. If a suspicious activity, in terms of (cyber)security, is detected, then recovering the original suspicious identities (i.e., the IP addresses in our example) is possible, by an appropriate number (i.e., the threshold value) of log events analysers who exchange information on their shares for reversing the pseudonyms. This is an interesting use case since log files are indeed necessary for (cyber)security purposes but, on the other side, possible misuse of such files may yield privacy issues (recall the reference in the introduction regarding possible contradictions between security and privacy). More recently, secret sharing schemes have been proposed for privacy preserving in Vehicular Ad Hoc Networks (VANETs) [67], as well as in COVID-19 contact tracing apps [7].
Finally, with respect to secret sharing, a strongly related cryptographic field that actually lies in the SMPC protocols is the so-called threshold cryptography, which refers to cryptographic schemes that allow a set of parties to carry out cryptographic operations (e.g., signatures), without any single party holding the secret key; this key is shared so as no party can reveal it. A characteristic example that illustrates the importance of threshold cryptography is the case that a user has the same software on several devices (e.g., laptop, smart phone, etc.) which necessitates a secret key (e.g., password) for authentication. If any single device with access to this key is compromised, high risks may occur for the rights and freedoms of the user since her/his personal data to all her/his devices become vulnerable, whereas the key must be revoked. This is the scenario that has been studied in several works (see, e.g., [68,69]), where possible solutions based on threshold cryptography are proposed, so as to ensure that no single device has access to the secret key but—despite this—it can perform authentication. NIST initiated in 2021 a call for feedback on criteria for threshold schemes [70].
4.5. Functional Encryption
Functional encryption refers to a type of (public key) encryption that allows decryption keys with the following property: they can only decrypt a specific function of the encrypted plaintext (regardless the content of the plaintext)—see Figure 6. As it is stated in a classical work [71] that initiated the formal study of this field, functional encryption deviates from the classical notion of cryptography in which access to the encrypted data is all or nothing—one can either decrypt and read the entire plaintext or one learns nothing at all about the plaintext other than its length. As a characteristic example that is being mentioned in [71], we may consider the case of a cloud service for storing encrypted images, where law enforcement agencies may require the cloud to search for images containing a particular face and, thus, the cloud needs a suitable restricted secret key that decrypts images that contain the target face, but cannot reveal anything about other images. In the same example, the secret key may only reveal a function of the plaintext image, for example an image that is blurred everywhere except for the target face. Clearly, such properties cannot be achieved by traditional cryptographic techniques.
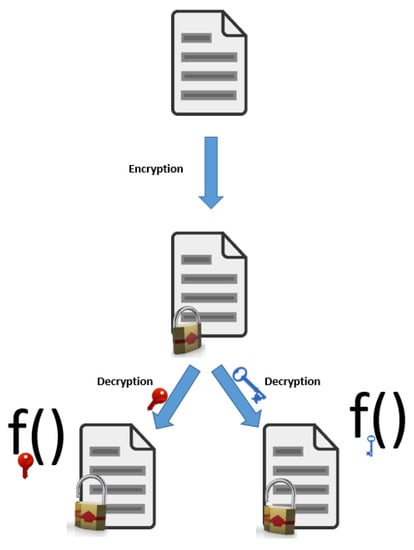
Figure 6.
The generic concept of the functional encryption (inspired by a figure in https://www.esat.kuleuven.be/cosic/people/ward-beullens/, accessed on 1 November 2021).
Functional encryption is actually a very generic term, incorporating several other (advanced) cryptographic techniques, such as identity-based encryption, searchable public-key encryption, hidden-vector encryption, attribute-based encryption and inner-product functional encryption. More precisely:
- Identity Based Encryption (IBE), first introduced by Shamir in 1984 [72], refers to a public key encryption scheme in which any bit string can serve as a public key (where the original motivation was to use the identity of the user as her/his public key, thus eliminating the need for certificates). However, such schemes can be seen as a special case of functional encryption for functions of a certain type—i.e., functions indexed by strings u such that and when x and u are different, where u is interpreted as the identity of a user. Note that encrypting makes the m decryptable only by the user who knows the corresponding private key . The first practical IBE schemes were presented in 2001 [73,74].
- Searchable encryption refers to cryptographic schemes that allow searching for a keyword (in plaintext) within ciphertext (e.g., encrypted documents) and obtaining the resulting outputs without revealing the keyword itself [75]. Searchable encryption is a well-known PEC technique that addresses personal data protection challenges; for example, when storing personal data on remote servers, the search utility on these data is reserved while keeping them hidden (even the server cannot decrypt).
- Hidden-vector encryption refers to cryptographic schemes in which ciphertexts are associated with binary vectors and private keys are associated with with binary vectors with “don’t care” entries (denoted by wildcards ★). A private key can decipher a ciphertext if all entries of the key vector that are not ★ agree with the corresponding entries of the ciphertext vector. Hidden-vector encryption was first proposed in [76] as a special case of the searchable encryption.
- Attribute-Based Encryption (ABE) refers to cryptographic schemes in which the encrypted data is linked with a set of attributes and secret keys along with certain policies that allow to control which ciphertexts can be decrypted depending on the attributes we possess. More precisely, ABE corresponds to functions indexed by a predicate P such that if is true, and if is false, where x is interpreted as a set of attributes, and P is a policy that specifies under what conditions on the attributes a message can be decrypted. ABE was first introduced in 2006 [77].
- Inner-product functional encryption refers to cryptographic schemes in which the plaintext is a vector and the encrypted data can be used along with an evaluation key to compute the inner product of the said vector with another vector. Such a scheme was first presented in 2007 [76] to allow some more complex operations, whereas the first such scheme which outputs a functionality of the encrypted message was presented in 2015 [78].
In the typical scenario of functional encryption, a new party called authority is required, in conjunction with an algorithm called key generation; the authority generates and keeps the master secret key along with the public key. From this master secret key, other secret keys are being generated through the key generation process and are given to users. These secret keys are associated with functions, so as the holder a function key for function f can apply it over a ciphertext (encrypting data m), to learn and nothing else. The example of functional encryption that is given in [79] is that users may encrypt their DNA material and send it to a clinic to check for specific genetic markers (i.e., the function). An authority, say the national health system, may grant to that clinic the function key to carry out the computation. As long as the authority is trusted, the clinic may only compute the function(s) for which it received function key(s).
Functional encryption has attracted much attention especially during the last decade; however, the general-purpose schemes are currently not efficient for being practical. Despite this though, several practical solutions for specific cases do exist. For example, the European Fentec research project [80] focuses on making usable functional encryption schemes, whereas some existing solutions include the management of access to clinical data through ABE, as well as building a heat-map of the location of users in a fully anonymous way though an inner product functional encryption scheme. In general, functional encryption is being considered as a highly promising research field, that may provide solutions in personal data protection that cannot be achieved by other means.
4.6. Zero-Knowledge Proofs
One of the most significant notions of cryptography is the Zero-Knowledge (ZK) proof systems. In simple words, ZK proofs are interactive protocols in which an entity (the prover) attempts to persuade another entity (the verifier) that a mathematical statement is valid, without exposing anything else but the statement itself (i.e., such a statement is derived from sensitive information, but this piece of information is not revealed). This is illustrated in Figure 7. Such protocols were first presented in 1985 [81], whilst a nice source is also [82].
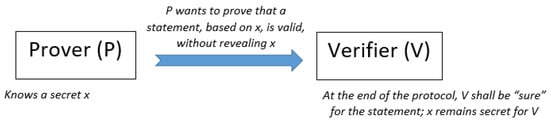
Figure 7.
The notion of zero-knowledge proofs.
A ZK proof system has to satisfy the following properties:
- Completeness: In the case where the statement is correct, the honest prover will persuade the honest verifier that the fact corresponding to the statement is correct.
- Soundness: In the case where the statement is false, the adversarial prover cannot persuade the honest verifier that statement is correct, except with negligible probability.
- Zero-knowledge: In the case where the statement is correct, the verifier figures out nothing more than the fact that the statement is correct.
The first two properties are used in general interactive proof systems, but the third one is the property that provides the full definition of the ZK proof system [82].
By their definition, it becomes evident that ZK proofs are strongly related to the data minimisation principle. A classical application of ZK proofs is for user authentication, in the sense that a user may prove that she knows a secret that allows authentication (which could be, e.g., a secret password) without revealing it (see the famous Fiat–Shamir protocol). Some other interesting applications, in terms of personal data protection, are the following:
- ZK proofs can be used to prove someone is over 18 without revealing her exact age. Since the GDPR also allows individuals over 16 to utilize information society services by their consent (whereas national legislation in each Member State in Europe may provide for a lower age for those purposes, provided that such lower age is not below 13 years), it is important to implement efficient ways to check user’s age in specific circumstances. By ZK proofs, this is possible without requiring the person reveal her exact age or show identity cards. To achieve this, a trusted party is needed to generate a commitment which attests that the relevant information contained in it is correct.
- Since ZK proofs allows to validate that a piece of private information belongs to a specific interval, this can be used to prove that the salary of an individual is above some threshold (without revealing the salary) in order to get, e.g., a mortgage approved.
- In the real estate sector, it is common that estate agents or rental companies can ask their potential tenants to share some information, such as their latest pay cheques or bank statements in order to guarantee that they have a sufficient income to take on the cost. In this case, a system based on ZK proofs could provide users with the possibility to demonstrate that they have sufficient funds without the need to share any personal data with the estate agent.
Although ZK proofs have been widely known for many years, they have attracted much attention recently due to their usage in blockchain technologies. Indeed, in some blockchain structures, smart contracts are being executed with the incorporation of external information from verified sources in order to trigger scheduled orders or events; for example, a payment is made when there is a certain amount of money in an account. In such cases, ZK proofs could facilitate the implementation of the desired purpose without the need to share the external data that trigger a transaction. More generally, ZK proofs can be used in blockchains of several types for allowing validations of transactions without disclosing the underlying data—for example, it can be proved that a user has at least 100 coins in her account, without revealing the actual amount. A recent generic review on privacy features in blockchains, describing also the applications of ZK proofs in this context, is given in [83]. It should be pointed out that, in this framework, a new specific type of ZK proofs are being used, namely the so-called Zero-Knowledge Succinct Non-Interactive Argument of Knowledge (zk-SNARK). In this definition, succinct means that the zero-knowledge proofs can be verified within a few milliseconds, whilst non-interactive means that the proof consists of a single message sent from the prover (i.e., the claimant) to the verifier (which is not the case for the classical zero-knowledge proofs which necessitate a number of interactions between the claimant and the verifier). It is a highly evolving field, where several improvements of zk-SNARKs are being proposed.
An essential element in ZK proofs is the cryptographic commitment, which allows someone to compute a value that hides some message without ambiguity—i.e., nobody can later on claim that this this value corresponds to a different message. A recent survey on zero-knowledge proofs is given in [84]. An open-industry academic initiative has been also constructed [85], aiming to promote best-practice standards for ZK proof schemes.
Despite the fact that ZK proofs are very promising for facilitating the implementation of data minimisation (and purpose limitation), it is interesting to point out that the Spanish Data Protection Authority (AEPD) issued, on 4 November 2020, a statement regarding their effectiveness [86]. As it is stated therein, there is an inherent uncertainty about whether the protected information is correct or not (see the negligible probability that is mentioned above for the soundness property, whereas cryptographic commitments provide probabilistic and not absolute, certainty). Therefore, the AEPD outlines that when applying a ZK proof in the design of data processing, it is necessary to assess whether the said uncertainty reaches values low enough for the risk to be assumed within the framework of said specific processing. Moreover, the AEPD stresses that the differences between mathematical algorithms and their actual implementation in a specific technical, organisational and legal context should be also taken into account; actually, the latter one is an issue that covers all the advanced cryptographic techniques discussed so far in this paper, and we will revisit it at the concluding section.
5. Blockchain Technology and Personal Data Protection
The blockchain technology has met a huge evolution during the last years, with diverse application areas, including—amongst others—the financial, health, IoT and cybersecurity sectors (see, e.g., [87,88,89,90]). In simple words, a blockchain is a distributed database (ledger) across several nodes, being synchronised and updated according to a consensus algorithm. In general, blockchains are append-only ledgers, to which data can be added, whereas removal or modification is actually not possible (these can be achieved, in the general case, by appending new information stating the deemed change on the data already stored). Therefore, the immutability property of the ledgers is possibly the most important feature of the blockchain technology. Blockchain highly relies on cryptographic primitives, such as cryptographic hash functions and digital signatures, independently from its specific nature (e.g., public or private, permissioned or permissionless) or the underlying consensus algorithm.
With respect to personal data protection, there is an ongoing public discussion whether blockchains can be squared with the data protection law (see, e.g., [91] for this issue, in terms of the blockchain’s compliance with the GDPR). It seems that several issues do not have a straightforward answer: for example, in specific settings (e.g., for public permissionless blockchains), even the determination of the data controller(s) or data processor(s) seems to be non-trivial. Moreover, the immutability property of the ledger seems to contradict the fulfilment of specific individuals rights—such as the right to data erasure (also known as right to be forgotten) and the right to rectification. The French Data Protection Authority (CNIL) has issued a document regarding the responsible use of the blockchain in the context of personal data [92]. In this document, it is stated that blockchain is not necessarily the most suitable technology for all data processing. Moreover, some solutions are being presented in terms of processing personal data through blockchain with respect to the data minimisation principle and the fulfilment of data subjects right; these solutions can be implemented under the assumption that a use of blockchain is justified by the purpose of the processing and that a DPIA has proven that the residual risks are acceptable.
Due to the known privacy issues induced by the use of blockchain technologies, there are several advanced cryptographic techniques that are being implemented in the blockchain context in order to alleviate these issues (actually, this was the main motivation for the development of zk-SNARKs described previously). A survey of privacy enhancing technologies for blockchains, with a discussion on which are the main blockchain platforms that support them, is given in [83] (although blockchains for IoT applications are discussed therein, the presented privacy enhancing technologies are actually the same for any application scenario). However, no such technology should be considered as panacea; the choice of the proper privacy enhancing technology highly depends on the specific application.
Despite the above issues, blockchain as technology may be also used to facilitate the implementation of GDPR provisions; this is discussed, e.g., in [91], where several such examples are given therein. First, it is well-known that blockchain may enhance security of the processing (see, e.g., [93]). Apart from this aspect, the inherent property of blockchains that relies on immutability of the ledger may be essential for data controllers in order to ensure the accountability requirement; for example, if the legal basis for a data processing is the users’ consent, storing such time-stamped consents, as well as their possible revocations, into a blockchain may provide the means to prove exactly when an individual provided her consent for a data processing. More generally, verifiable proofs about various transactions related to the user data can be ensured, which in turn facilitates the accountability principle implied by the GDPR. Additionally, blockchains may allow individuals have more control on their data, in terms of providing full traceability and auditability of data access and exchange as well as regulating data access on the basis of user-defined permission/consent settings through a dedicated smart contract (see, e.g., the European research project MyHealthMyData [94]).
In any case though, any blockchain solution for personal data processing should be carefully chosen and designed, taking into account all possible privacy risks. This is a characteristic example of a technology that needs conduction of a DPIA if personal data are to be processed, towards deciding whether it should be the preferable option and, if yes, under which configuration and implementation choices.
6. Discussion on the “Crypto War” for Content Moderation
The previous discussion indicates the importance of cryptography in terms of privacy and personal data protection (which is, roughly speaking, a superset of personal data security). Indeed, as it has been said [95], the two human rights most commonly associated with access to, and use of, encryption are the rights to privacy and the right to freedom of expression. However, it has been said that we are in a period of the second Crypto War (see [95] and the relative references therein), due to the fact that there is a strong public debate on restricting encryption in particular cases. More precisely, such restrictions have been put or implied in several legislations; for example, Australia’s parliament passed legislation in 2018 in order allow the country’s intelligence and law enforcement agencies to demand access to end-to-end encrypted digital communications [96]. In USA, the Department of Justice asked tech companies to deploy responsible encryption [97], where the term responsible indicates that designated authorities will have controlled access to data without creating undue risks. More recently, in 2020, a group of U.S. senators introduced a new bill called the EARN IT act, which is designed to force providers to either solve the encryption-while-scanning problem, or stop using encryption entirely [98]. The specific problem that is discussed now, with respect to encryption scanning, is explicitly the distribution of child sexual abuse material, or CSAM—which is of course of utmost importance to be addressed. This debate has opened a discussion on whether End-to-End-Encryption (E2EE) should be still supported by the providers; alternatively, the providers are obliged to build in a special access mechanism for law enforcement [99]. Such a discussion has been also started in Europe; in the EU’s Cybersecurity Strategy for the Digital Decade [4], it is stated that
Electronic evidence must be readable, thus the Commission will further work on the support to law enforcement capacity in the area of digital investigations, including dealing with encryption when encountered in criminal investigations while fully preserving its function to protect fundamental rights and cybersecurity.
Moreover, on 11 February 2021, the European Commission launched a public consultation on its initiative to fight child sexual abuse online, which aims to impose obligations on online service providers to detect child sexual abuse online and to report it to public authorities [100].
First, why is this the second Crypto War? Because this is not a fully new discussion. Back to 1990s, the US government sought to enforce the controls on those seeking to disseminate free, mass market encryption products for non-military applications [95]. For example, the Microsoft Office 1997 was released with weak encryption (namely, with the RC4 using a 40-bit key) exactly due to such US export restrictions. Now the discussion has indeed been put into a new level, but the same question occurs: How far (or, under which safeguards) can we sacrifice privacy in order to allow law enforcement agencies having access to encrypted communications of individuals?
The current discussion actually concerns E2EE. As it is stated in [99], E2EE refers to implementing encryption on the user’s device so as it can be decrypted only by authorised users who have exchanged the keys with one another; since these users are the only ones with knowledge of the decryption keys, data in E2EE systems remains hidden from any other party, including the service provider. Therefore, intermediate parties that route, store, backup or process by any other means the encrypted data do not have access to the keys and, therefore, cannot learn any information about the data. For example, the Signal messaging app is known to provide E2EE [101], whereas the same also holds for Whatsapp [102]. Clearly, the detection of illegal content (or, more generally, of any content that violates the policies of the service) generated by users becomes a difficult task for service providers and, consequently, for law enforcement agencies—and that is why the relevant public debate is about E2EE.
Our strong belief is that dealing with this issue through simply introducing backdoors on encryption or key escrow schemes (i.e., an arrangement in which the keys needed to decrypt encrypted data are held in escrow so that, under certain circumstances, an authorized third party may gain access to those keys) should be out of the discussion. Any type of deliberated vulnerability on a cryptographic scheme is clearly a vulnerability that can be also exploited by any possible malicious third party, thus posing the security of communications and the protection of personal data at high risk. As it has been aptly stated [103], creating backdoor access would put children at far greater risk by creating new opportunities for criminals and authoritarian governments to further victimise and exploit vulnerabilities in communications. This is because encryption backdoors can be opened by anyone who finds them—including criminals, terrorist organisations, hostile intelligence and other adversaries. There are several well-known security incidents that occurred due to built-in backdoors. A famous one is the case of the Juniper Networks, which is related with a backdoor in the operating system ScreenOS, which could be used to read the entire encrypted VPN traffic of the devices if an internal parameter was known. However, in 2012, hackers exploited this backdoor, and thus unknown third parties were able to read the encrypted VPN data in plain text (and Juniper noticed it after three years). More information on known security issues that were based on built-in backdoors is given in [104].
Apart from the above, since this discussion is actually related with a trade-off between different rights, it is essential—with the aim to strike the proper balance between these rights—to also examine the effectiveness of such backdoors towards achieving the desired goal (i.e., to capture illegal content within encrypted data), compared to the violation of personal rights. To this end, a very interesting work is presented in [105] which exhibits that Dutch law enforcement appears to be as successful in prosecuting offenders who rely on encrypted communication as those who do not; in other words, law enforcement agencies and the public prosecution service are actually not impacted by the use of E2EE in bringing cases to court. This work is based on analysing public court data from the Netherlands. Although it refers to a specific (European) country, it becomes evident that such aspects should be also taken into account.
In any case, any type of backdoor in cryptography opens many directions for malicious actors, thus increasing the risks of successful cyber-theft, cyber-espionage, cyberattack, and cyberterrorism [106]. Moreover, this will highly affect the user’s trust in telecommunication services and governments (since ensuring data protection is indispensable to build trust)—and such a trust is an essential element in societies. At the end, cryptography is an enabler of the rights to privacy and freedom of expression and there can be no backdoors on rights [95].
So, is there any solution? In our view, the requirements stated in the EU’s Cybersecurity Strategy [4]—i.e., as stated above, Commission will further work on the support to law enforcement capacity in the area of digital investigations, including dealing with encryption when encountered in criminal investigations while fully preserving its function to protect fundamental rights and cybersecurity—actually pave the way and provide a definitely negative answer on introducing backdoors. Indeed, there is need to work on the support of the law enforcement capacity, but at the same time with full protection of the fundamental rights; any derogation from this principle should be rejected. In our opinion, this is another research field that advanced cryptographic techniques need to be further explored, but under a proper way and as a part of a holistic approach.
In a very nice report from the Center for Democracy & Technology (CDT) [99], where the more general topic of content moderation is being discussed, several technical proposals that purport to introduce some form of content moderation (specifically, detection of unwanted content), while still providing an E2EE service, are discussed. This report concludes that methods that allow content moderation without sacrificing E2EE are: (i) user-reporting, i.e., (such as, e.g., reporting buttons or complaint forms) that allow users to alert moderators, other intermediaries, or other users of unwanted content. (ii) Meta-data analysis: For E2EE communications, metadata can include unencrypted profile or group chat information, frequency of sending messages, or reports from other users about problematic content. As long as the metadata analysis occurs exclusively on a user’s device and does not result in storage, use, or sending of decrypted messages, the user’s privacy is preserved and the guarantees of end-to-end encryption are not violated. In the same report, it is stated, with well-documented justification, that all other techniques do not preserve the E2EE. Both user-reporting and metadata analysis provide effective tools in detecting significant amounts and different types of problematic content on E2EE services including abusive and harassing messages, spam, mis- and disinformation and CSAM. The report also suggests that Machine-Learning (ML) classifiers on the user’s device that are trained to detect unwanted content, on behalf of the user, may also be a solution, in the sense that such techniques may enable users to avoid receiving sexting images. If this process occurs exclusively on a user’s device, at the user’s instruction, and no information about the message is disclosed to a third party, then the guarantees of E2EE may not be violated—further research though is still needed. We fully support these arguments; we also support further research on advanced cryptographic technologies enhancing privacy, not as panacea (this is further illustrated in the Apple example next), but as building blocks in a generic privacy-oriented approach. For example, we refer to a recent work in [107]—which should be considered only under appropriate safeguards (since it is somehow an one-time backdoor, in the sense that no provider or LEA can decrypt whatever data but only for a single user, but it is still a backdoor)—illustrating that there is plenty of room for further research.
On 5 August 2021, Apple announced that it has designed a technique to to detect known CSAM with user privacy in mind [108]. This technique utilises PSI in order to compare images from user’s device with images in a database that Apple will utilise whose content will be known CSAM images (actually, hashes of images, as described next). Apple claims that the company will not learn anything about user’s private information that is being processed in her/his device, since PSI ensures that Apple will learn only the illegal content (if such exists) and nothing more (namely, Apple will learn of any content that it already exists in its database). At a first glance, implementing PSI seems to be a nice approach in terms of privacy. However, this is a characteristic example to exhibit that PEC is not by itself always a solution, especially in such a critical sector. More precisely:
- First, the comparison between user’s images and known CSAM images will involve hashes of these images—but not the classical cryptographic hashes (which provide fully different outputs for different inputs, even if the inputs are only slightly differentiated) but the so-called perceptual hashes, i.e., an image is being converted to a unique number specific to that image, so as another image that appears nearly identical (differences occur in size or transcoded quality) can produce the same number. Therefore, there is a risk of false positives—i.e., the algorithm will detect a match without ensuring that this is indeed the case.
- Moreover, since Apple’s technique actually requires a client-side scanning of images to detect potential CSAM before allowing users to upload those images to iCloud, it is natural to consider that governments will demand that Apple expand its image scanning tool to include other types of content or that Apple block other types of files (e.g., political messages) [109].
Immediately after Apple’s announcement, experts around the world sounded the alarm that this may turn every Apple device into a device that is continuously scanning all photos and messages that pass through it. Apart from the CDT [109], the Electronic Frontier Foundation (EFF) stated on the matter: It’s impossible to build a client-side scanning system that can only be used for sexually explicit images sent or received by children. As a consequence, even a well-intentioned effort to build such a system will break key promises of the messenger’s encryption itself and open the door to broader abuses (…) That’s not a slippery slope; that’s a fully built system just waiting for external pressure to make the slightest change [110]. The EFF also states specific examples on how Apple’s proposed technology could lead to global abuse: Take the example of India, where recently passed rules include dangerous requirements for platforms to identify the origins of messages and pre-screen content. New laws in Ethiopia requiring content takedowns of “misinformation” in 24 hours may apply to messaging services. And many other countries—often those with authoritarian governments—have passed similar laws. Apple’s changes would enable such screening, takedown, and reporting in its end-to-end messaging. The abuse cases are easy to imagine: governments that outlaw homosexuality might require the classifier to be trained to restrict apparent LGBTQ+ content, or an authoritarian regime might demand the classifier be able to spot popular satirical images or protest flyers.
After all these critiques and comments, Apple announced on 3 September 2021 that, based on feedback from customers, advocacy groups, researchers, and others, it has been decided that additional time is needed to collect input and make improvements before releasing these critically important child safety features [108].
Concluding this discussion, it becomes evident that this is a very important and difficult issue; the response from all stakeholders should be to further promote relevant research and not to implement techniques that violate individuals rights. At the end, the CDT’s report [99] correctly concludes that technological solutions for detecting problematic content alone will not address the larger issues of, e.g., the distribution of disinformation or CSAM, which necessitate to identify and address at their core the social and political causes behind these phenomena.
7. Conclusions
This paper presented a generic survey of advanced cryptographic techniques promoting privacy, with emphasis on describing how they can address specific challenges implied by relevant data protection legislation; to this end, the GDPR has been used as a basis. Specific applications are described, including those in the cybersecurity sector that raise privacy issues, illustrating that difficult tasks, for which traditional cryptography fails to provide the most efficient solution from a data protection point of view, can be addressed by appropriate use of such advanced techniques. It should be pointed out that this survey does not incorporate all possible applications that may already use such advanced cryptographic schemes, whereas the relevant statements or decisions of competent data protection authorities that are presented do not constitute an exhaustive list; however, despite these restrictions, it becomes evident how important is to investigate advanced cryptographic schemes to deal with data protection challenges (whilst their applicability can clearly go beyond the personal data protection field).
This survey focused on the theoretical foundations that suffice to provide security and data protection guarantees; however, it is well-known that cryptography is not only about mathematics but also about implementation. In other words, even the best cryptographic solution may allow backdoors if not properly implemented (e.g., not proper configuration or design of an algorithm/protocol—see, e.g., [111]). From a data protection point of view, this is covered by the data protection by design and data protection by default principles, which are being enforced by the GDPR. Therefore, the discussed cryptographic techniques should be examined, when designing a personal data processing, as possible safeguards that need to be taken into account on a risk-based approach, with specific emphasis on their design (including data flows), and not as already existing concrete solutions.
This paper also aims to contribute to the public discussion which is related on sacrificing cryptography with respect to facilitate content moderation. Although this is a difficult issue to be adequately addressed in a paper’s section, we expressed our personal view, based also on evidence and views that are known to the cryptographic community, as well as to institutions defending human rights. From our perspective, any undermining on cryptography is bound to have significant negative effects for human rights, without even achieving the desired goals—i.e., to prevent crimes; to the contrary, there is no any reason to believe that such an approach will not lead criminals into using other means that rest with several types of hidden communications, thus making law enforcement more difficult. As discussed in Section 6, further research should be done in facilitating law enforcement without violating human rights.
Since it seems that many organisations, having the crucial role of data controllers according to the GDPR’s provisions, ignore such solutions and, thus, they adopt less privacy-friendly techniques, we hope that this survey, apart from its academic interest, will be helpful for all stakeholders (public and private organisations processing personal data, software producers, data protection authorities but also legislators) as a basis for identifying possible solutions in challenging scenarios involving personal data processing.
Funding
This research received no external funding.
Acknowledgments
The author would like to thank the anonymous reviewers for their very constructive comments and suggestions, which helped to greatly improve the manuscript.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ABE | Attribute-Based Encryption |
| AEPD | Spanish Data Protection Authority |
| AES | Advanced Encryption Standard |
| CDT | Center for Democracy & Technology |
| CNIL | French Data Protection Authority |
| CSAM | Child Sexual Abuse Material |
| DNA | Deoxyribonucleic Acid |
| DPIA | Data Protection Impact Assessment |
| E2EE | End-to-End Encryption |
| EFF | Electronic Frontier Foundation |
| ENISA | European Union Agency for Cybersecurity |
| FE | Functional Encryption |
| HDPA | Hellenic Data Protection Authority |
| GDPR | General Data Protection Regulation |
| IBE | Identity Based Encryption |
| IoT | Internet of Things |
| IP | Internet Protocol |
| MAC | Message Authentication Code |
| NIST | National Institute of Standards and Technology |
| NIZK | Non-Interactive Zero Knowledge |
| OT | Oblivious Transfer |
| PEC | Privacy Enhancing Cryptography |
| PePP-PT | Pan-European Privacy Preserving Proximity Tracing |
| PePP-PT NTK | Pan-European Privacy Preserving Proximity Tracing Need To Know |
| PSI | Private Set Intersection |
| RSA | Rivest–Shamir-Adleman (algorithm) |
| SMPC | Secure Multi-Party Computation |
| TLS | Transport Layer Security |
| VPN | Virtual Private Network |
| ZK | Zero Knowledge |
| zk-SNARK | Zero-Knowledge Succinct Non-Interactive Argument of Knowledge |
References
- Menezes, A.J.; van Oorschot, P.C.; Vanstone, S.A. Handbook of Applied Cryptography; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Paterson, K.G. The Cyber Security Body of Knowledge, University of Bristol, 2021, ch. Applied Cryptography, version 1.0.0. Available online: https://www.cybok.org/media/downloads/Applied_Cryptography_KA_webinar_slides.pdf (accessed on 23 August 2021).
- Smart, N. The Cyber Security Body of Knowledge, University of Bristol, 2021, ch. Cryptography, Version 1.0.1. Available online: https://www.cybok.org/ (accessed on 23 August 2021).
- European Union. The EU’s Cybersecurity Strategy for the Digital Decade. Available online: https://digital-strategy.ec.europa.eu/en/library/eus-cybersecurity-strategy-digital-decade-0 (accessed on 23 August 2021).
- Michael, J.; Kuhn, R.; Voas, J. Security or Privacy: Can You Have Both? Computer 2020, 53, 20–30. [Google Scholar] [CrossRef]
- Brandão, L.T.A.N.; Peralta, R.; Robinson, A. Toward a PEC Use-Case Suite. Technical Report (Preliminary Draft), NIST. 2021. Available online: https://csrc.nist.gov/projects/pec/suite (accessed on 23 August 2021).
- Ahmed, N.; Michelin, R.A.; Xue, W.; Ruj, S.; Malaney, R.; Kanhere, S.S.; Seneviratne, A.; Hu, W.; Janicke, H.; Jha, S.K. A Survey of COVID-19 Contact Tracing Apps. IEEE Access 2020, 8, 134577–134601. [Google Scholar] [CrossRef]
- Baumgärtner, L.; Dmitrienko, A.; Freisleben, B.; Gruler, A.; Höchst, J.; Kühlberg, J.; Mezini, M.; Mitev, R.; Miettinen, M.; Muhamedagic, A.; et al. Mind the GAP: Security & Privacy Risks of Contact Tracing Apps. In Proceedings of the IEEE 19th International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom), Guangzhou, China, 29 December–1 January 2021; pp. 458–467. [Google Scholar]
- European Union. Regulation (EU) 2016/679 of the European Parliament and of the Council of 27 April 2016 on the protection of natural persons with regard to the processing of personal data and on the free movement of such data, and repealing Directive 95/46/EC (General Data Protection Regulation). Off. J. Eur. Union 2016, 119, 1–88. [Google Scholar]
- Kaminski, M. A recent renaissance in privacy law. Commun. ACM 2020, 63, 24–27. [Google Scholar] [CrossRef]
- Chatzistefanou, V.; Limniotis, K. On the (non-)anonymity of anonymous social networks. In Proceedings of the E-Democracy—Privacy-Preserving, Secure, Intelligent E-Government Services, Athens, Greece, 14–15 December 2017; Katsikas, S., Zorkadis, V., Eds.; Communications in Computer and Information Science. Springer: Cham, Switzerland, 2017; Volume 792, pp. 153–168. [Google Scholar]
- Hansen, M.; Limniotis, K. Recommendations on Shaping Technology According to GDPR Provisions—Exploring the Notion of Data Protection by Default. European Union Agency for Cybersecurity, Technical Report, Bourka A., Drogkaris, P., Eds., 2018. Available online: https://www.enisa.europa.eu/publications/recommendations-on-shaping-technology-according-to-gdpr-provisions-part-2 (accessed on 23 August 2021).
- Jensen, M.; Lauradoux, C.; Limniotis, K. Pseudonymisation Techniques and Best Practices. European Union Agency for Cybersecurity, Technical Report, Bourka A., Drogkaris, P., Agrafiotis, I., Eds.,2019. Available online: https://www.enisa.europa.eu/publications/pseudonymisation-techniques-and-best-practices (accessed on 23 August 2021).
- Lauradoux, C.; Limniotis, K.; Hansen, M.; Jensen, M.; Efstathopoulos, P. Data Pseudonymisation: Advanced Techniques and Use Cases. European Union Agency for Cybersecurity, Technical Report, Bourka A., Drogkaris, P., Eds., 2021. Available online: https://www.enisa.europa.eu/publications/data-pseudonymisation-advanced-techniques-and-use-cases (accessed on 23 August 2021).
- ISO/IEC 20889:2018(en)—Privacy Enhancing Data De-Identification Terminology and Classification of Techniques. Available online: https://www.iso.org/obp/ui/#iso:std:iso-iec:20889:ed-1:v1:en (accessed on 23 August 2021).
- Pfitzmann, A.; Hansen, M. A Terminology for Talking about Privacy by Data Minimization: Anonymity, Unlinkability, Undetectability, Unobservability, Pseudonymity, and Identity Management. TU Dresden, Dresden Germany, Tech. Rep. V0.34. 2010. Available online: https://dud.inf.tu-dresden.de/literatur/Anon_Terminology_v0.34.pdf (accessed on 23 August 2021).
- Akil, M.; Islami, L.; Fischer-Hübner, S.; Martucci, L.A.; Zuccato, A. Privacy-Preserving Identifiers for IoT: A Systematic Literature Review. IEEE Access 2020, 8, 168470–168485. [Google Scholar] [CrossRef]
- European Medicines Agency. ICH E6 Good Clinical Practice. Available online: https://www.ema.europa.eu/en/documents/scientific-guideline/ich-guideline-e6-good-clinical-practice-draft-ich-e6-principles_en.pdf (accessed on 23 August 2021).
- Hellenic Data Protection Authority—Opinion 3/2015. Available online: https://www.dpa.gr/el/enimerwtiko/prakseisArxis/gia-shedio-nomikis-diataxis-toy-ypoyrgeioy-ygeias-gia-tin-efarmogi-toy (accessed on 23 August 2021). (In Greek).
- White Paper on Pseudonymization drafted by the Data Protection Focus Group for the Safety, Protection, and Trust Platform for Society and Businesses in Connection with the 2017 Digital Summit. Available online: https://www.telekom.com/resource/blob/503396/e646f78275729556fe19ad5ed08b19f8/dl-170912-white-paper-pseudonymisiation-data.pdf (accessed on 23 August 2021).
- Aamot, H.; Kohl, C.D.; Richter, D.; Knaup-Gregori, P. Pseudonymization of patient identifiers for translational research. BMC Med. Inform. Decis. Mak. 2013, 13, 1–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- The New York Times. A Face Is Exposed for AOL Searcher No. 4417749. Available online: https://www.nytimes.com/2006/08/09/technology/09aol.html (accessed on 21 August 2021).
- Limniotis, K.; Hansen, M. Recommendations on Shaping Technology According to GDPR Provisions—An Overview on Data Pseudonymisation. European Union Agency for Cybersecurity, Technical Report, Bourka A., Drogkaris, P., Eds., 2018. Available online: https://www.enisa.europa.eu/publications/recommendations-on-shaping-technology-according-to-gdpr-provisions (accessed on 23 August 2021).
- Verheul, E.; Jacobs, B.; Meijer, C.; Hildebrandt, M.; Ruiter, J. Polymorphic Encryption and Pseudonymisation for Personalised Healthcare—A Whitepaper. Cryptology ePrint Archive, Report 2016/411, 2016. Available online: https://eprint.iacr.org/2016/411 (accessed on 23 August 2021).
- Westerbaan, A.; Hendriks, L. Polymorphic Encryption and Pseudonymisation of IP Network Flows. arXiv 2019, arXiv:1911.02674. Available online: http://arxiv.org/abs/1911.02674 (accessed on 21 August 2021).
- Lehnhardt, J.; Spalka, A. Decentralized generation of multiple, uncorrelatable pseudonyms without trusted third parties. In Proceedings of the 8th International Conference on Trust, Privacy and Security in Digital Business (TrustBus ’11), Toulouse, France, 29 August 2011–2 September 2011; Furnell, S., Lambrinoudakis, C., Pernul, G., Eds.; Lecture Notes in Computer Science. Springer: Heidelberg, Germany, 2011; Volume 6863, pp. 113–124. [Google Scholar]
- Schartner, P.; Schaffer, M. Unique User-Generated Digital Pseudonyms. In Proceedings of the International Workshop on Mathematical Methods, Models, and Architectures for Computer Network Security (MMM-ACNS 2005), St. Petersburg, Russia, 25–27 September 2005; Gorodetsky, V., Kotenko, I., Skormin, V., Eds.; Lecture Notes in Computer Science. Springer: Heidelberg, Germany, 2005; Volume 3685, pp. 194–205. [Google Scholar]
- Kermezis, G.; Limniotis, K.; Kolokotronis, N. User-generated pseudonyms through Merkle trees. In Proceedings of the Annual Privacy Forum (APF) 2021—Privacy Technologies and Policy, Oslo, Norway, 17—18 June 2021; Gruschka, N., Antunes, L.F.C., Rannenberg, K., Drogkaris, P., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2021; Volume 12703, pp. 89–105. [Google Scholar]
- Facebook for Business—About Hashing Customer Information. Available online: https://www.facebook.com/business/help/112061095610075?id=2469097953376494 (accessed on 23 August 2021).
- Demir, L.; Kumar, A.; Cunche, M.; Lauradoux, C. The pitfalls of hashing for privacy. IEEE Commun. Surv. Tutor. 2018, 20, 551–565. [Google Scholar] [CrossRef] [Green Version]
- Chaum, D. Blind Signatures for Untraceable Payments. Advances in Cryptology—Crypto 1982, CA, USA, August 1982; Chaum, D., Rivest, R.L., Sherman, A.T., Eds.; Springer: Boston, MA, USA, 1983; pp. 199–203. [Google Scholar]
- Asghar, N. A Survey on Blind Digital Signatures. Technical Report, University of Waterloo. 2011. Available online: https://cs.uwaterloo.ca/~nasghar/co685.pdf (accessed on 23 August 2021).
- Borges, R.; Sebé, F. A Construction for Providing Reusability to Mobile Phone-Based e-Tickets. IEEE Access 2020, 8, 101386–101397. [Google Scholar] [CrossRef]
- Hellenic Data Protection Authority—Opinion 1/2017. Available online: https://www.dpa.gr/el/enimerwtiko/prakseisArxis/gnostopoiisi-epexergasias-prosopikon-dedomenon-sto-plaisio-toy (accessed on 23 August 2021). (In Greek).
- Kosta, E.; Graux, H.; Dumortier, J. Collection and Storage of Personal Data: A Critical View on Current Practices in the Transportation Sector. In Proceedings of the Annual Privacy Forum (APF) 2012—Privacy Technologies and Policy, Limassol, Cyprus, 10–11 October 2012; Preneel, B., Ikonomou, D., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2012; Volume 8319, pp. 157–176. [Google Scholar]
- Abe, M.; Okamoto, T. Provably Secure Partially Blind Signatures. Advances in Cryptology—Crypto 2000, CA, USA, 20–24 August 2000; Bellare, M., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2000; pp. 271–286. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Tauman, Y. How to Leak a Secret. Advances in Cryptology—Asiacrypt 2001, Australia, December 2001; Boyd, C., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2001; Volume 2248, pp. 552–565. [Google Scholar]
- Liu, J.K.; Wong, D.S. Linkable Ring Signatures: Security Models and New Schemes. In Proceedings of the Computational Science and Its Applications—ICCSA 2005, Singapore, 9–12 May 2005; Gervasi, O., Gavrilova, M.L., Kumar, V., Laganà, A., Lee, H.P., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2005; Volume 3481, pp. 614–623. [Google Scholar]
- Chaum, D.; van Heyst, E. Group signatures. In Proceedings of the Advances in Cryptology—EUROCRYPT ’91, Workshop on the Theory and Application of of Cryptographic Techniques, Brighton, UK, 8–11 April 1991; Davies, D.W., Ed.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 1991; Volume 547, pp. 257–265. [Google Scholar]
- Zhang, L.; Zheng, Z.; Wang, W. Survey of Lattice-Based Group Signature. In Proceedings of the First International Forum on Financial Mathematics and Financial Technology, Financial Mathematics and Fintech, Singapore; Zheng, Z., Ed.; Springer: Berlin/Heidelberg, Germany, 2021; pp. 79–92. [Google Scholar]
- Park, S.; Sealfon, A. It Wasn’t Me!—Repudiability and Claimability of Ring Signatures. In Proceedings of the Advances in Cryptology—CRYPTO 2019, Santa Barbara, CA, USA, 18–22 August 2019; Part III. Boldyreva, A., Micciancio, D., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2019; Volume 11694, pp. 159–190. [Google Scholar]
- European Data Protection Supervisor. Guidelines on Processing Personal Information within a Whistleblowing Procedure. Available online: https://edps.europa.eu/sites/default/files/publication/19-12-17_whisteblowing_guidelines_en.pdf (accessed on 23 August 2021).
- Paillier, P. Public-Key Cryptosystems Based on Composite Degree Residuosity Classes. In Proceedings of the Advances in Cryptology—EUROCRYPT 99, Prague, Czech Republic, 2–6 May 1999; Stern, J., Ed.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 1999; Volume 1592, pp. 223–238. [Google Scholar]
- Gentry, C. Fully homomorphic encryption using ideal lattices. In Proceedings of the 41st Annual ACM Symposium on Theory of Computing (STOC), Bethesda, MD, USA, 31 May–2 June 2009; ACM: New York, NY, USA, 2009; pp. 169–178. [Google Scholar]
- Boneh, D.; Segev, G.; Waters, B. Targeted malleability: Homomorphic encryption for restricted computations. In Proceedings of the 3rd Innovations in Theoretical Computer Science Conference, Cambridge, MA, USA, 8–10 January 2012; ACM: New York, NY, USA, 2012; pp. 350–366. [Google Scholar]
- Bos, J.W.; Lauter, K.; Naehrig, M. Private predictive analysis on encrypted medical data. J. Biomed. Inform. 2014, 50, 234–243. [Google Scholar] [CrossRef] [Green Version]
- Masters, O.; Hunt, H.; Steffinlongo, E.; Crawford, J.; Bergamaschi, F.; Dela Rosa, M.E.; Quini, C.C.; Alves, C.T.; de Souza, F.; Ferreira, D.G. Towards a Homomorphic Machine Learning Big Data Pipeline for the Financial Services Sector. Cryptology ePrint Archive, Report 2019/1113, 2019. Available online: https://eprint.iacr.org/2019/1113 (accessed on 23 August 2021).
- Yao, A.C. Protocols for secure computations. In Proceedings of the 23rd Annual Symposium on Foundations of Computer Science, Chicago, IL, USA, 3–5 November 1982; pp. 160–164. [Google Scholar]
- Yao, A.C. How to Generate and Exchange Secrets. In Proceedings of the 27th Annual Symposium on Foundations of Computer Science (FOCS), Toronto, ON, Canada, 27–29 October 1986; pp. 162–167. [Google Scholar]
- Goldreich, O.; Micali, S.; Wigderson, A. How to Play any Mental Game—A Completeness Theorem for Protocols with Honest Majority. In Proceedings of the 19th Annual ACM Symposium on Theory of Computing, New York, NY, USA, 25–27 May 1987; pp. 218–229. [Google Scholar]
- Lindell, Y. Secure Multiparty Computation (MPC). Cryptology ePrint Archive: Report 2020/300. Available online: https://eprint.iacr.org/2020/300 (accessed on 23 August 2021).
- Thoma, C.; Cui, T.; Franchetti, F. Secure multiparty computation based privacy preserving smart metering system. In Proceedings of the 2012 North American Power Symposium (NAPS), Champaign, IL, USA, 9–11 September 2012; pp. 1–6. [Google Scholar]
- Archer, D.W.; Bogdanov, D.; Lindell, Y.; Kamm, L.; Nielsen, K.; Pagter, J.I.; Smart, N.P.; Wright, R.N. From Keys to Databases—Real-World Applications of Secure Multi-Party Computation. Comput. J. 2018, 61, 1749–1771. [Google Scholar] [CrossRef] [Green Version]
- Sharemind. Available online: https://sharemind.cyber.ee/sharemind-mpc/multi-party-computation/ (accessed on 23 August 2021).
- Ion, M.; Kreuter, B.; Nergiz, E.; Patel, S.; Saxena, S.; Seth, K.; Shanahan, D.; Yung, M. Private Intersection-Sum Protocol with Applications to Attributing Aggregate Ad Conversions. Cryptology ePrint Archive, Report 2017/738. 2017. Available online: https://eprint.iacr.org/2017/738 (accessed on 23 August 2021).
- Nguyen, H.; Ngo, Q.; Le, V. IoT Botnet Detection Approach Based on PSI graph and DGCNN classifier. In Proceedings of the 2018 IEEE International Conference on Information Communication and Signal Processing (ICICSP), Signapore, 28–30 September 2018; pp. 118–122. [Google Scholar]
- Berke, A.; Bakker, M.; Vepakomma, P.; Raskar, R.; Larson, K.; Pentland, A. Assessing disease exposure risk with location histories and protecting privacy: A cryptographic approach in response to a global pandemic. arXiv 2020, arXiv:2003.14412. Available online: http://arxiv.org/abs/2003.14412 (accessed on 21 August 2021).
- Trieu, N.; Shehata, K.; Saxena, P.; Shokri, R.; Song, D. Epione: Lightweight contact tracing with strong privacy. arXiv 2020, arXiv:2004.13293. Available online: http://arxiv.org/abs/2004.13293 (accessed on 21 August 2021).
- Meadows, C. A more efficient cryptographic matchmaking protocol for use in the absence of a continuously available third party. In Proceedings of the IEEE Symposium on Security and Privacy, Oakland, CA, USA, 7–9 April 1986; pp. 134–137. [Google Scholar]
- Kolesnikov, V.; Kumaresan, R.; Rosulek, M.; Trieu, N. Efficient Batched Oblivious PRF with Applications to Private Set Intersection. Cryptology ePrint Archive, Report 2016/799. 2016. Available online: http://eprint.iacr.org/2016/799 (accessed on 23 August 2021).
- Pinkas, B.; Schneider, T.; Zohner, M. Scalable Private Set Intersection Based on OT Extension. ACM Trans. Priv. Secur. 2018, 21, 1–35. [Google Scholar] [CrossRef] [Green Version]
- Pinkas, B.; Rosulek, M.; Trieu, N.; Yanai, A. SpOT-Light: Lightweight Private Set Intersection from Sparse OT Extension. In Proceedings of the Advances in Cryptology—Crypto 2019 (Part III), Santa Barbara, CA, USA, 18–22 August 2019; Boldyreva, A., Micciancio, D., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2019; Volume 11694, pp. 401–431. [Google Scholar]
- Shamir, A. How to Share a Secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Beimel, A. Secret-Sharing Schemes: A Survey. In Proceedings of the International Workshop on Coding and Cryptology (IWCC), Qingdao, China, 30 May–3 June 2011; Volume 6639, pp. 11–46. [Google Scholar]
- Stinson, D.R. An explication of secret sharing schemes. Des. Codes Cryptogr. 1992, 2, 357–390. [Google Scholar] [CrossRef]
- Biskup, J.; Flegel, U. On Pseudonymization of Audit Data for Intrusion Detection. In Proceedings of the International Workshop on Designing Privacy Enhancing Technologies, Berkeley, CA, USA, 25–26 July 2000; Federrath, H., Ed.; Lecture Notes in Computer Science. Springer: Heidelberg, Germany, 2001; Volume 2009, pp. 161–180. [Google Scholar]
- Li, H.; Pei, L.; Liao, D.; Sun, G.; Xu, D. Blockchain Meets VANET: An Architecture for Identity and Location Privacy Protection in VANET. Peer-to-Peer Netw. Appl. 2019, 12, 1178–1193. [Google Scholar] [CrossRef]
- Atwater, E.; Hengartner, U. Shatter: Using Threshold Cryptography to Protect Single Users with Multiple Devices. In Proceedings of the 9th ACM Conference on Security & Privacy in Wireless and Mobile Networks (WISEC), Darmstad, Germany, 18–20 July 2016; Hollick, M., Papadimitratos, P., Enck, W., Eds.; ACM: New York, NY, USA, 2016; pp. 91–102. [Google Scholar]
- Abidin, A.; Aly, A.; Mustafa, M.A. Collaborative Authentication Using Threshold Cryptography. In Proceedings of the 2nd International Workshop in Emerging Technologies for Authorization and Authentication (ETAA), Luxembourg, 27 September 2019; Saracino, A., Mori, P., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2019; Volume 11967, pp. 122–137. [Google Scholar]
- NIST. Multiparty Threshold Cryptography. Available online: https://csrc.nist.gov/projects/threshold-cryptography (accessed on 23 August 2021).
- Boneh, D.; Sahai, A.; Waters, B. Functional Encryption: Definitions and Challenges. In Proceedings of the 8th Theory of Cryptography Conference (TCC), Providence, RI, USA, 28–30 March 2011; Ishai, Y., Ed.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2011; Volume 6597, pp. 253–273. [Google Scholar]
- Shamir, A. Identity-Based Cryptosystems and Signature Schemes. In Proceedings of the Advances in Cryptology—CRYPTO 1984, Santa Barbara, CA, USA, 19–22 August 1984; Blakley, G.R., Chaum, D., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 1984; Volume 196, pp. 47–53. [Google Scholar]
- Boneh, D.; Franklin, M. Identity-based encryption from the weil pairing. In Proceedings of the Advances in Cryptology—Crypto 2001, Santa Barbara, CA, USA, 19–23 August 2001; Kilian, J., Ed.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2001; Volume 2139, pp. 213–229. [Google Scholar]
- Cocks, C. An identity based encryption scheme based on quadratic residues. In Proceedings of the IMA International Conference on Cryptography and Coding, Cirencester, UK, 17–19 December 2001; Honary, B., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 360–363. [Google Scholar]
- Boneh, D.; Di Crescenzo, G.; Ostrovsky, R.; Persiano, G. Public key encryption with keyword search. In Proceedings of the Advances in Cryptology—Eurocrypt 2004, Interlaken, Switzerland, 2–6 May 2004; Cachin, C., Camenisch, J.L., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2004; Volume 3027, pp. 506–522. [Google Scholar]
- Boneh, D.; Waters, B. Conjunctive, subset, and range queries on encrypted data. In Proceedings of the Theory of Cryptography Conference (TCC), Amsterdam, The Netherlands, 21–24 February 2007; Vadhan, S.P., Ed.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2007; Volume 4392, pp. 535–554. [Google Scholar]
- Goyal, V.; Pandey, O.; Sahai, A.; Waters, B. Attribute-based encryption for fine grained access control of encrypted data. In Proceedings of the 13th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 30 October–3 November 2006; Juels, A., Wright, R.N., De Capitani di Vimercati, S., Eds.; ACM: New York, NY, USA, 2006; pp. 89–98. [Google Scholar]
- Abdalla, M.; Bourse, F.; De Caro, A.; Pointcheval, D. Simple functional encryption schemes for inner products. In Proceedings of the IACR International Workshop on Public Key Cryptography (PKC), Gaithersburg, MD, USA, 30 March–1 April 2015; Katz, J., Ed.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2015; Volume 9020, pp. 733–751. [Google Scholar]
- Ambrona, M.; Fiore, D.; Soriente, C. Controlled Functional Encryption Revisited: Multi-Authority Extensions and Efficient Schemes for Quadratic Functions. Proc. Priv. Enhancing Technol. 2021, 1, 21–42. [Google Scholar] [CrossRef]
- The Fentec Project. Available online: https://fentec.eu/ (accessed on 23 August 2021).
- Goldwasser, S.; Micali, S.; Rackoff, C. The knowledge complexity of interactive proof-systems. In Proceedings of the 7th Annual ACM Symposium on Theory of Computing (STOC), Providence, RI, USA, 6–8 May 1985; ACM: New York, NY, USA, 1985; pp. 291–304. [Google Scholar]
- Goldreich, O.; Yair, O. Definitions and properties of zero-knowledge proof systems. J. Cryptol. 1994, 7, 1–32. [Google Scholar] [CrossRef]
- Brotsis, S.; Limniotis, K.; Bendiam, G.; Kolokotronis, N.; Shiaeles, S. On the suitability of blockchain platforms for IoT applications: Architectures, security, privacy, and performance. Comput. Netw. 2021, 191, 108005. [Google Scholar] [CrossRef]
- Morais, E.; Koens, T.; van Wijk, C.; Koren, A. A Survey on Zero Knowledge Range Proofs and Applications. arXiv 2019, arXiv:1907.06381. Available online: http://arxiv.org/abs/1907.06381 (accessed on 21 August 2021). [CrossRef] [Green Version]
- ZK Proof Standards. Available online: https://zkproof.org/ (accessed on 23 August 2021).
- AEPD Statement. Available online: https://www.aepd.es/es/prensa-y-comunicacion/blog/cifrado-privacidad-iv-pruebas-conocimiento-cero (accessed on 23 August 2021). (In Spanish).
- Mohanta, B.K.; Jena, D.; Panda, S.S.; Sobhanayak, S. Blockchain technology: A survey on applications and security privacy challenges. Internet Things 2019, 8, 100107. [Google Scholar] [CrossRef]
- Hölbl, M.; Kompara, M.; Kamišalić, A.; Nemec Zlatolas, L. A Systematic Review of the Use of Blockchain in Healthcare. Symmetry 2018, 10, 470. [Google Scholar] [CrossRef] [Green Version]
- Panarello, A.; Tapas, N.; Merlino, G.; Longo, F.; Puliafito, A. Blockchain and IoT Integration: A Systematic Survey. Sensors 2018, 18, 2575. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brotsis, S.; Kolokotronis, N.; Limniotis, K.; Shiaeles, S.; Kavallieros, D.; Bellini, E.; Pavue, C. Blockchain Solutions for Forensic Evidence Preservation in IoT Environments. In Proceedings of the 2019 IEEE Conference on Network Softwarization (NetSoft), Paris, France, 24–28 June 2019; pp. 110–114. [Google Scholar]
- European Parliament. Blockchain and the General Data Protection Regulation. Available online: https://www.europarl.europa. eu/RegData/etudes/STUD/2019/634445/EPRS_STU(2019)634445_EN.pdf (accessed on 2 November 2021).
- CNIL. Blockchain—Solutions for a Responsible Use of the Blockchain in the Context of Personal Data. Available online: https://www.cnil.fr/sites/default/files/atoms/files/blockchain_en.pdf (accessed on 2 November 2021).
- Kolokotronis, N.; Limniotis, K.; Shiaeles, S.; Griffiths, R. Secured by blockchain: Safeguarding Internet of Things devices. IEEE Consum. Electron. Mag. 2019, 8, 28–34. [Google Scholar] [CrossRef] [Green Version]
- My Health My Data. Available online: http://www.myhealthmydata.eu/ (accessed on 2 November 2021).
- Amnesty International. Encryption: A Matter of Human Rights. Available online: https://www.amnestyusa.org/reports/encryption-a-matter-of-human-rights/ (accessed on 23 August 2021).
- Wired, Australia’s Encryption-Busting Law Could Impact Global Privacy. Available online: https://www.wired.com/story/australia-encryption-law-global-impact/ (accessed on 23 August 2021).
- Green, M. On Ghost Users and Messaging Backdoors. Available online: https://blog.cryptographyengineering.com/2018/12/17/on-ghost-users-and-messaging-backdoors/ (accessed on 23 August 2021).
- Green, M. EARN IT is a Direct Attack on End-to-End Encryption. Available online: https://blog.cryptographyengineering.com/2020/03/06/earn-it-is-an-attack-on-encryption/ (accessed on 23 August 2021).
- Center for Democracy and Technology. Outside Looking In: Approaches to Content Moderation in End-to-End Encrypted Systems. Report. 2021. Available online: https://cdt.org/insights/outside-looking-in-approaches-to-content-moderation-in-end-to-end-encrypted-systems/ (accessed on 23 August 2021).
- European Commission. Fighting Child Sexual Abuse: Detection, Removal and Reporting of Illegal Content Online. Available online: https://ec.europa.eu/info/law/better-regulation/have-your-say/initiatives/12726-Child-sexual-abuse-online-detection-removal-and-reporting-/public-consultation_en (accessed on 23 August 2021).
- Signal. Speak Freely. Available online: https://signal.org/ (accessed on 23 August 2021).
- Whatsapp. Available online: https://www.whatsapp.com (accessed on 23 August 2021).
- Center for Democracy and Technology. Breaking Encryption Myths: What the European Commission’s Leaked Report Got Wrong About Online Security. Available online: https://cdt.org/insights/breaking-encryption-myths-what-the-european-commissions-leaked-report-got-wrong-about-online-security/ (accessed on 23 August 2021).
- Tutanota, Best of Backdoor Fails in Recent History. Available online: https://tutanota.com/blog/posts/encryption-backdoor-fails/ (accessed on 1 October 2021).
- Hartel, P.; van Wegberg, R. Going dark? Analysing the Impact of End-to-End Encryption on the Outcome of Dutch Criminal Court Cases. arXiv 2021, arXiv:2104.06444. Available online: https://arxiv.org/abs/2104.06444 (accessed on 21 August 2021).
- IEEE Global Public Policy, IEEE Position Statement in Support of Strong Encryption. Available online: http://globalpolicy.ieee.org/wp-content/uploads/2018/06/IEEE18006.pdf (accessed on 23 August 2021).
- Chung, K.-M.; Georgiou, M.; Lai, C.-Y.; Zikas, V. Cryptography with Disposable Backdoors. Cryptography 2019, 3, 22. [Google Scholar] [CrossRef] [Green Version]
- Apple, Expanded Protection for Children. Available online: https://www.apple.com/child-safety/ (accessed on 4 October 2021).
- Center for Democracy and Technology. What Could Go Wrong? Apple’s Misguided Plans to Gut End-to-End Encryption. Available online: https://cdt.org/insights/what-could-go-wrong-apples-misguided-plans-to-gut-end-to-end-encryption/ (accessed on 4 October 2021).
- Electronic Frontier Foundation. Apple’s Plan to “Think Different” About Encryption Opens a Backdoor to Your Private Life. Available online: https://www.eff.org/deeplinks/2021/08/apples-plan-think-different-about-encryption-opens-backdoor-your-private-life (accessed on 4 October 2021).
- Limniotis, K.; Kolokotronis, N. Cryptography Threats. In Cyber-Secur. Threat. Actors, Dyn. Mitigation; Kolokotronis, N., Shiaeles, S., Eds.; CRC Press: Boca Raton, FL, USA, 2021; pp. 123–159. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).