Partly-Pseudo-Linear Cryptanalysis of Reduced-Round Speck
Abstract
:1. Introduction
2. Preliminaries
2.1. Notation
- : Addition modulo
- : Subtraction modulo
- ⊕: The bitwise exclusive-or
- : r-bit right rotation on an n-bit word
- : r-bit left rotation on an n-bit word
- : Left word of the Plaintext (Ciphertext)
- : Right word of the Plaintext (Ciphertext)
- : Left (right) word at round j
- : window of state () at round j
- (): window t with size w of the left (right) word x, where the msb is at i and the lsb is at , for and .
- (): Bit at index i of the window where the left (right) word x.
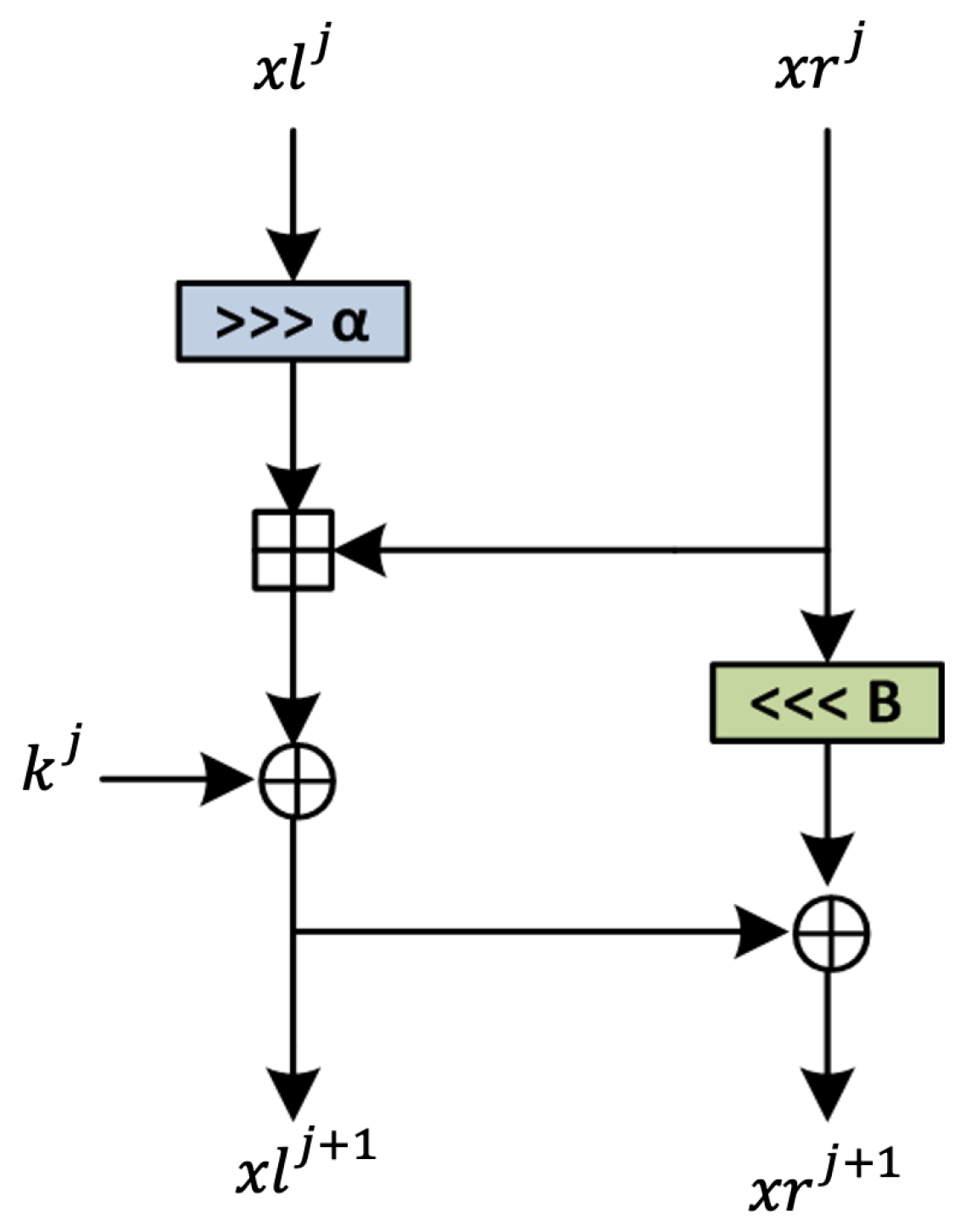
2.2. The Speck Cipher
- Addition modulo , denoted
- Rotation: right rotation by , denoted and left rotation by , denoted
- bitwise XOR, denoted ⊕
3. Related Works
3.1. Linear Cryptanalysis
Linear Cryptanalysis of Modular Addition
- Bitwise rotation breaks the two consecutive bits. After the rotation, one of these two bits will be in the most significant bit position (msb) and the other will be in the least significant bit position (lsb).Example:
- Bitwise exclusive-or breaks the two consecutive bits. These two bits will be not consecutive any more.Example:
3.2. Pseudo-Linear Cryptanalysis
- Suppose and . In this case the approximation is correct because the carry into the window is correctly assumed to be zero (See Figure 3).
- Suppose and . In this case the approximation is incorrect because the carry into the window is incorrectly assumed to be zero (See Figure 4).
3.2.1. Some Observations Regarding the Addition Window
- ⊕ Bitwise exclusive-or
- ⊞ Addition modulo
- Addition modulo
- ⊟ Subtraction modulo
- Subtraction modulo
3.2.2. Pseudo-Linear Approximations of ARX Round Functions
- Base ApproximationThe base approximation is a simple approximation that follows the windows until the target window. All exclusive-or operations and addition modulo operations are preserved, assuming that the carry into all windows is 0 [3].
- Carry PatternsA carry pattern is a series of carry values, ∈ where i denotes to the approximated addition window that may have a carry into it.Multiple carry patterns, indexed by j, = can be constructed for each base approximation; here j denotes a specific carry pattern for the approximation, i the approximated window, and m the total number of windows approximated. If = 1, then the carry going into the approximated addition window is 1. Thus, the base approximation is overlaid by the m carry patterns, to result in m estimates of the target window. [5].
- Computing BiasIf carry patterns are used, the bias may be experimentally computed to be the difference between the probability of the approximation being correct and the probability of correctly guessing a carry pattern at random, with tries. The carry patterns will be correct with probability instead of since each pattern represents a different approximation. According to McKay [3] the bias is computed using Equation (10)
3.3. Comparison between Pseudo-Linear Cryptanalysis and Linear Cryptanalysis
3.4. Cryptanalysis of Speck
3.4.1. Different Methods of Cryptanalysis on Speck
3.4.2. Linear Cryptanalysis of Speck
4. Pseudo-Linear Cryptanalysis Attacks on Reduced-Round Speck 32/64
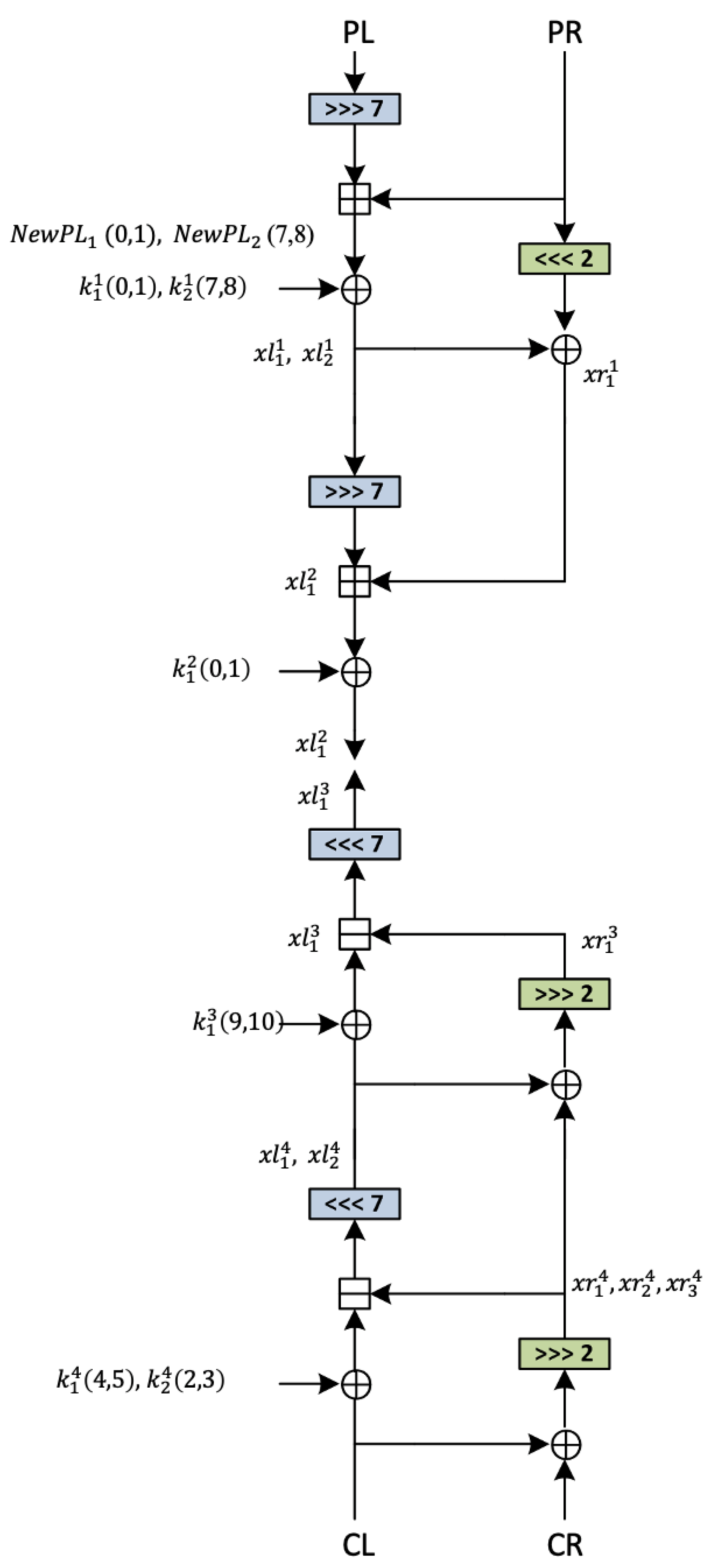
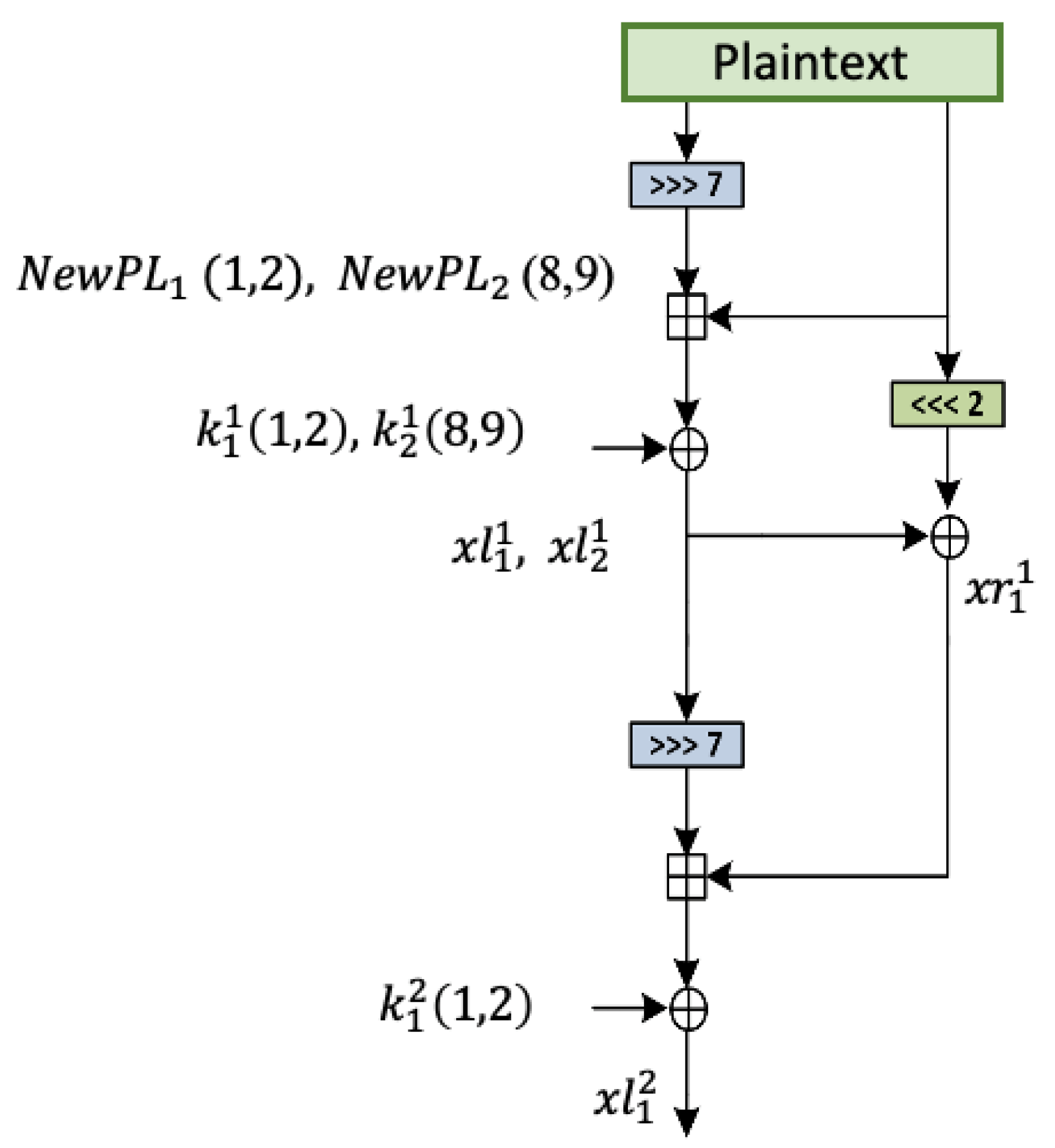
4.1. Four-Round Attack
- = = =
- = = = =
- = 0
- = =
- = = =
- = = = =
- = 0
- = =
- ; the error probabilities are those of , as is approximated with zero error.
- is obtained by adding and . This is the target window and we are trying to compute the entire window correctly, so we compute . If the incoming carry is , we have 16 possibilities for two bit errors in each summand window, 6 of these, with an incoming carry of zero (the possibilities are: both summands have error 00 or 10; with probability half, when both have error patterns 01 or 11; with probability half when the summands are 01 and 11 (two possibilities).), and 8 with an incoming carry of one (with probability half, each of the following pairs of summand errors will result in an error of 00 in the approximated window when the true value of the incoming carry is one; each pair occurs twice: 00 and 01, 00 and 11, 01 and 10, 10 and 11) ,give . The total probability is obtained using the probabilities of errors in windows and computed above to obtain:
- = = .
4.2. Six-Round Attack
5. Partly-Pseudo-Linear Cryptanalysis with Illustration on Speck
- The first part is the bias of xor of the bits of the window when the window is computed using the pseudo-linear approximation.
- The second part is the bias for the linear approximation, computed using traditional linear approaches. The combination of these two biases using the piling up lemma allows us to determine the number of plaintext and ciphertext pairs that we should use in our experiments.
5.1. Implementation of the Partly-Pseudo-Linear Attack on Speck 32/64
5.1.1. Six-Round Partly-Pseudo-Linear Attack
- (a)
- Both bits are zero (and the intermediate carry is zero, its value does not depend on the value of the incoming carry).
- (b)
- Both bits are one (the intermediate carry is one, independent of the incoming carry).
- Bias: The bias for this approximation is a combination of the experimentally-verified bias of the pseudo-linear approximation of the exclusive-or of the two-bit window ()and the bias of the linear approximation () using the piling-up lemma: =
- Data complexity: We use the square of the inverse of the bias of the linear approximation:
- Time complexity: Data complexity multiplied by the complexity of trying all possibilities for the number of key bits in the pseudo-linear approximation:
5.1.2. Nine-Round Partly-Pseudo-Linear Attack
5.2. The Partly-Pseudo-Linear Attack on the Large Variants of Speck
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Four-Rounds Attack of Pseudo-Linear Cryptanalysis
- Window size . The following Table A1 shows the approximation for four rounds meeting at .
| Round | Encryption | Decryption |
|---|---|---|
| 1 | ||
| 2 | ||
| ≡ | ||
| 3 | ||
| 4 | ||
- 2.
- Window size . The following Table A2 shows the approximation for four rounds meeting .
| Round | Encryption | Decryption |
|---|---|---|
| 1 | ||
| 2 | ||
| ≡ | ||
| 3 | ||
| 4 | ||
Appendix B. The Partly-Pseudo-Linear Attack on Speck 48
| Round | Cost | ||||
|---|---|---|---|---|---|
| 1 | 5 | ||||
| 2 | 6 | ||||
| 3 | 3 | ||||
| 4 | 3 | ||||
| 5 | 2 | ||||
| 6 | 1 |
Appendix C. The Partly-Pseudo-Linear Attack on Speck 64
| Round | Cost | ||||
|---|---|---|---|---|---|
| 1 | 5 | ||||
| 2 | 4 | ||||
| 3 | 3 | ||||
| 4 | 3 | ||||
| 5 | 4 | ||||
| 6 | 5 | ||||
| 7 | 3 | ||||
| 8 | 2 | ||||
| 9 | 1 |
Appendix D. The Partly-Pseudo-Linear Attack on Speck 96
| Round | Cost | ||||
|---|---|---|---|---|---|
| 1 | 7 | ||||
| 2 | 6 | ||||
| 3 | 5 | ||||
| 4 | 3 | ||||
| 5 | 2 | ||||
| 6 | 1 |
Appendix E. The Partly-Pseudo-Linear Attack on Speck 128
| R | Cost | ||||
|---|---|---|---|---|---|
| 1 | 7 | ||||
| 2 | 6 | ||||
| 3 | 5 | ||||
| 4 | 3 | ||||
| 5 | 2 | ||||
| 6 | 1 |
References
- Beaulieu, R.; Shors, D.; Smith, J.; Treatman-Clark, S.; Weeks, B.; Wingers, L. The SIMON and SPECK Families of Lightweight Block Ciphers. IACR Cryptol. EPrint Arch. 2013, 2013, 404. [Google Scholar]
- Beaulieu, R.; Shors, D.; Smith, J.; Treatman-Clark, S.; Weeks, B.; Wingers, L. The SIMON and SPECK lightweight block ciphers. In Proceedings of the 52nd Annual Design Automation Conference, San Francisco, CA, USA, 7–11 June 2015; pp. 175:1–175:6. [Google Scholar] [CrossRef]
- McKay, K.A.; Vora, P.L. Analysis of ARX Functions: Pseudo-linear Methods for Approximation, Differentials, and Evaluating Diffusion. IACR Cryptol. EPrint Arch. 2014, 2014, 895. [Google Scholar]
- McKay, K.A. Analysis of ARX Round Functions in Secure Hash Functions. Ph.D. Thesis, The George Washington University, Washington, DC, USA, 2014. [Google Scholar]
- McKay, K.A.; Vora, P.L. Pseudo-Linear Approximations for ARX Ciphers: With Application to Threefish. In Proceedings of the Second SHA-3 Candidate Conference, Santa Barbara, CA, USA, 23–24 August 2010; p. 282. [Google Scholar]
- Cho, J.Y.; Pieprzyk, J. Multiple Modular Additions and Crossword Puzzle Attack on NLSv2. In Proceedings of the 10th International Conference on Information Security (ISC 2007), Valparaiso, Chile, 9–12 October 2007; Lecture Notes in Computer Science. Garay, J.A., Lenstra, A.K., Mambo, M., Peralta, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4779, pp. 230–248. [Google Scholar] [CrossRef]
- Cho, J.Y.; Pieprzyk, J. Algebraic Attacks on SOBER-t32 and SOBER-t16 without Stuttering. In Fast Software Encryption, Proceedings of the 11th International Workshop, (FSE 2004), Delhi, India, 5–7 February 2004; Revised Papers; Lecture Notes in Computer Science; Roy, B.K., Meier, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3017, pp. 49–64. [Google Scholar] [CrossRef] [Green Version]
- Alzakari, S.; Vora, P. Linear and Partly-Pseudo-Linear Cryptanalysis of Reduced-Round SPARX Cipher. IACR Cryptol. EPrint Arch. 2020, 2020, 978. [Google Scholar]
- Bodden, D. Linear Cryptanalysis of Reduced-Round Speck with a Heuristic Approach: Automatic Search for Linear Trails. In Proceedings of the Information Security–21st International Conference (ISC 2018), Guildford, UK, 9–12 September 2018; Lecture Notes in Computer Science. Chen, L., Manulis, M., Schneider, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; Volume 11060, pp. 132–150. [Google Scholar] [CrossRef]
- Ashur, T.; Bodden, D. Linear Cryptanalysis of Reduced-Round Speck. In Proceedings of the 37th Symposium on Information Theory in the Benelux 2016, Louvain-la-Neuve, Belgium, 19–20 May 2016. [Google Scholar]
- Yao, Y.; Zhang, B.; Wu, W. Automatic Search for Linear Trails of the SPECK Family. In Proceedings of the Information Security—18th International Conference (ISC 2015), Trondheim, Norway, 9–11 September 2015; Lecture Notes in Computer Science. Lopez, J., Mitchell, C.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9290, pp. 158–176. [Google Scholar] [CrossRef]
- Fu, K.; Wang, M.; Guo, Y.; Sun, S.; Hu, L. MILP-Based Automatic Search Algorithms for Differential and Linear Trails for Speck. In Proceedings of the Fast Software Encryption—23rd International Conference (FSE 2016), Bochum, Germany, 20–23 March 2016; Revised Selected Papers; Lecture Notes in Computer Science. Peyrin, T., Ed.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9783, pp. 268–288. [Google Scholar] [CrossRef]
- Liu, Y.; Fu, K.; Wang, W.; Sun, L.; Wang, M. Linear cryptanalysis of reduced-round SPECK. Inf. Process. Lett. 2016, 116, 259–266. [Google Scholar] [CrossRef]
- Matsui, M. Linear Cryptanalysis Method for DES Cipher. In Advances in Cryptology—EUROCRYPT ’93, Proceedings of the Workshop on the Theory and Application of of Cryptographic Techniques, Lofthus, Norway, 23–27 May 1993; Lecture Notes in Computer Science; Helleseth, T., Ed.; Springer: Berlin/Heidelberg, Germany, 1993; Volume 765, pp. 386–397. [Google Scholar] [CrossRef] [Green Version]
- Heys, H.M. A Tutorial on Linear and Differential Cryptanalysis. Cryptologia 2002, 26, 189–221. [Google Scholar] [CrossRef]
- Beaulieu, R.; Shors, D.; Smith, J.; Treatman-Clark, S.; Weeks, B.; Wingers, L. SIMON and SPECK: Block Ciphers for the Internet of Things. IACR Cryptol. EPrint Arch. 2015, 2015, 585. [Google Scholar]
- Song, L.; Huang, Z.; Yang, Q. Automatic Differential Analysis of ARX Block Ciphers with Application to SPECK and LEA. In Proceedings of the Information Security and Privacy—21st Australasian Conference (ACISP 2016), Melbourne, VIC, Australia, 4–6 July 2016; Part II; Lecture Notes in Computer Science. Liu, J.K., Steinfeld, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9723, pp. 379–394. [Google Scholar] [CrossRef]
- HoChang, L.; Seojin, K.; HyungChul, K.; Deukjo, H.; Jaechul, S.; Hong, S. Calculating the Approximate Probability of Differentials for ARX-Based Cipher Using SAT Solver. J. Korea Inst. Inf. Secur. Cryptol. 2018, 28, 15–24. [Google Scholar] [CrossRef]
- Liu, Y.; Witte, G.D.; Ranea, A.; Ashur, T. Rotational-XOR Cryptanalysis of Reduced-round SPECK. IACR Trans. Symmetric Cryptol. 2017, 2017, 24–36. [Google Scholar] [CrossRef]
- Dwivedi, A.D.; Morawiecki, P.; Srivastava, G. Differential Cryptanalysis of Round-Reduced SPECK Suitable for Internet of Things Devices. IEEE Access 2019, 7, 16476–16486. [Google Scholar] [CrossRef]




| Block Size, 2n | Key Size, mn | Word Size, n | Rounds | ||
|---|---|---|---|---|---|
| 32 | 64 | 16 | 7 | 2 | 22 |
| 48 | 72 | 24 | 8 | 3 | 22 |
| 96 | 23 | ||||
| 64 | 96 | 32 | 8 | 3 | 26 |
| 128 | 27 | ||||
| 96 | 96 | 48 | 8 | 3 | 28 |
| 144 | 29 | ||||
| 128 | 128 | 64 | 8 | 3 | 32 |
| 192 | 33 | ||||
| 256 | 34 |
| Pairs | ||||
|---|---|---|---|---|
| Rate |
| Linear Cryptanalysis | Pseudo-Linear Cryptanalysis |
|---|---|
| The effect of several approximations can be easily concatenated and simplified because there is only one operation (exclusive-or). | The effect of several approximations cannot be concatenated and simplified because the two operations (exclusive-or and addition modulo ) do not commute. |
| Combining key bits across rounds into a single function of the key, independent of plaintext bits, is possible. | Cannot combine key bits across rounds into a single function of the key independent of plaintext. |
| The approximation may be used for a distinguisher as well as for key recovery. | The approximation includes a non-linear function of key and plaintext bits, and cannot be used as a distinguisher but can be used for key recovery. |
| Approximation of a single modular addition for large window sizes has low bias. | Approximation of a single modular addition can result in high accuracy prediction of large windows. |
| N/K | Ref. | Type of Attack | Number of Rounds | Data Complexity | Time Complexity |
|---|---|---|---|---|---|
| 32/64 | [19] | Rotational | 12 | NA | NA |
| [20] | Differential | 12 | |||
| [17] | Differential | 14 | |||
| [18] | Differential | 15 | |||
| 48/72 | [17] | Differential | 15 | ||
| [18] | Differential | 16 | |||
| 48/96 | [20] | Differential | 13 | ||
| [19] | Rotational | 15 | NA | NA | |
| [17] | Differential | 16 | |||
| [18] | Differential | 17 | |||
| 64/96 | [17] | Differential | 19 | ||
| 64/128 | [19] | Rotational | 13 | NA | NA |
| [20] | Differential | 15 | |||
| [17] | Differential | 20 | |||
| 96/96 | [17] | Differential | 20 | ||
| 96/144 | [19] | Rotational | 13 | NA | NA |
| [20] | Differential | 13 | |||
| [17] | Differential | 21 | |||
| 128/128 | [17] | Differential | 23 | ||
| 128/128 | [17] | Differential | 24 | ||
| 128/128 | [19] | Rotational | 13 | NA | NA |
| [20] | Differential | 15 | |||
| [17] | Differential | 25 |
| N | Ref. | Number of Rounds | Guessed Key Bit/K | Bias | Data Complexity | Time Complexity |
|---|---|---|---|---|---|---|
| 32 | [10] | 7 | LT | |||
| [9] | 8 | LT | ||||
| This work | 9 | 36/64 | ||||
| [12] | 9 | LT | NA | NA | ||
| [13] | 9 | LT | NA | NA | ||
| [11] | 12 | 29/64 | ||||
| 48 | [10] | 8 | LT | |||
| [9] | 9 | LT | ||||
| This work | 10 | 27/72 | ||||
| [12] | 10 | LT | NA | NA | ||
| [13] | 10 | LT | NA | NA | ||
| [11] | 11 | 24/72 | ||||
| This work | 11 | 45/96 | ||||
| [11] | 12 | 48/96 | ||||
| 64 | [9] | 11 | LT | |||
| [10] | 11 | LT | ||||
| [13] | 12 | LT | NA | NA | ||
| This work | 13 | 28/96 | ||||
| [11] | 13 | 31/96 | ||||
| [12] | 13 | LT | NA | NA | ||
| [11] | 14 | 31/96 | ||||
| [11] | 14 | 63/128 | ||||
| This work | 14 | 49/128 | ||||
| [11] | 15 | 63/128 | ||||
| 96 | [11] | 8 | 47/96 | |||
| [11] | 9 | 95/144 | ||||
| [10] | 10 | LT | ||||
| This work | 10 | 46/96 | ||||
| [9] | 12 | LT | ||||
| This work | 12 | 76/144 | ||||
| [12] | 15 | LT | NA | NA | ||
| [13] | 17 | NA/144 | ||||
| 128 | [11] | 7 | 191/256 | |||
| [11] | 8 | 63/128 | ||||
| [11] | 9 | 127/192 | ||||
| [10] | 11 | LT | ||||
| This work | 11 | 50/128 | ||||
| [9] | 13 | LT | ||||
| This work | 13 | 122/192 | ||||
| This work | 14 | 173/256 | ||||
| [12] | 16 | LT | NA | NA | ||
| [13] | 18 | NA/192 | ||||
| [13] | 19 | NA/256 |
| Round | Encryption | Decryption |
|---|---|---|
| 1 | ||
| 2 | ||
| ≡ | ||
| 3 | ||
| 4 | ||
| Approximation | Window Size | Guessed Key Bits | Bias | Data Complexity | Time Complexity |
|---|---|---|---|---|---|
| Table 6 | 2 bits | 12 | |||
| Appendix A | 3 bits | 17 | |||
| Appendix A | 4 bits | 22 |
| Round | Cost | Reason to Stop | ||||
|---|---|---|---|---|---|---|
| 1 | 1 | |||||
| 2 | 2 | |||||
| 3 | 3 | |||||
| 4 | 3 | |||||
| 5 | Broke requirement of consecutive ones for | |||||
| . |
| Round | Encryption | Decryption |
|---|---|---|
| 1 | ||
| 2 | ||
| ≡ | ||
| 3 to 6 | ||
| Approximation | Window | No. of Key Bits Correctly Determined | Bias | Data Complexity | Time Complexity |
|---|---|---|---|---|---|
| Table 9 | 2 bits | 6 |
| Round | Cost | Reason to Stop | ||||
|---|---|---|---|---|---|---|
| 1 | 1 | |||||
| 2 | 2 | |||||
| 3 | 3 | |||||
| 4 | 3 | |||||
| 5 | Broke requirement for consecutive ones for | |||||
| . |
| Round | Encryption | Decryption |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| ≡ | ||
| 6 to 9 | ||
| Approximation | Window Size | Key | Bias | Data Complexity | Time Complexity |
|---|---|---|---|---|---|
| Table 12 | 2 bits | 36 |
| Block Size | Key Size | Rounds | Guessed Key Bits | Bias | Data Complexity | Time Complexity | Approximation |
|---|---|---|---|---|---|---|---|
| 32 | 64 | 9 | 36 | Table 12 | |||
| 48 | 72 | 10 | 27 | Appendix B | |||
| 96 | 11 | 45 | |||||
| 64 | 96 | 13 | 28 | Appendix C | |||
| 128 | 14 | 49 | |||||
| 96 | 96 | 10 | 46 | Appendix D | |||
| 144 | 12 | 76 | |||||
| 128 | 128 | 11 | 50 | Appendix E | |||
| 192 | 13 | 122 | |||||
| 256 | 14 | 173 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alzakari, S.A.; Vora, P.L. Partly-Pseudo-Linear Cryptanalysis of Reduced-Round Speck. Cryptography 2021, 5, 1. https://doi.org/10.3390/cryptography5010001
Alzakari SA, Vora PL. Partly-Pseudo-Linear Cryptanalysis of Reduced-Round Speck. Cryptography. 2021; 5(1):1. https://doi.org/10.3390/cryptography5010001
Chicago/Turabian StyleAlzakari, Sarah A., and Poorvi L. Vora. 2021. "Partly-Pseudo-Linear Cryptanalysis of Reduced-Round Speck" Cryptography 5, no. 1: 1. https://doi.org/10.3390/cryptography5010001
APA StyleAlzakari, S. A., & Vora, P. L. (2021). Partly-Pseudo-Linear Cryptanalysis of Reduced-Round Speck. Cryptography, 5(1), 1. https://doi.org/10.3390/cryptography5010001